DIÉDRICO: SECCIÓN PLANA EN UN HEXAEDRO (unidades en
Anuncio

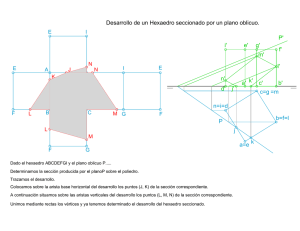
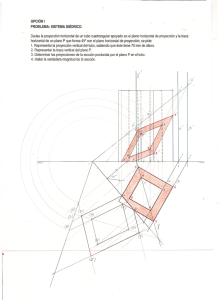
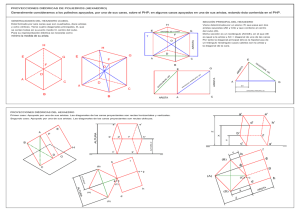
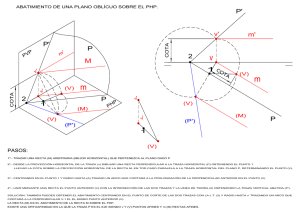
DIÉDRICO 1 / 14 DIÉDRICO: SECCIÓN PLANA EN UN HEXAEDRO (unidades en milímetros) Dibujar un hexaedro apoyado en el plano horizontal de proyección diédrica de forma que su base esté inscrita en una circunferencia de diámetro ɸ = 50 y centro O [ 32, 51, 0]; el hexaedro estará situado en el primer diedro y ninguna de sus caras debe ser paralela al plano vertical de proyección diédrica. Calcular la sección plana producida en dicho cuerpo por un plano perpendicular al segundo bisector que pase por el punto medio del hexaedro y cuyas rectas traza formen 60º con la línea de tierra. Nota: Con los datos presentados, hay infinitas soluciones que responden al planteamiento de este problema. En este ejercicio se muestra una de ellas. DIÉDRICO 2 / 14 Dibujo del hexaedro. Un hexaedro es un cuerpo formado por seis (hexa) caras iguales, seis cuadrados. Como el hexaedro a dibujar tiene que estar apoyado en el plano horizontal de proyección diédrica, habrá una cara situada en dicho plano. Además dicha cara, es decir, un cuadrado, deberá estar inscrito en una circunferencia de diámetro ɸ = 50. Por ello el primer paso es el dibujar un cuadrado inscrito en una circunferencia de diámetro ɸ = 50. Se elige un punto arbitrario en la circunferencia. A partir de dicho punto se construye un cuadrado circunscrito en la circunferencia: será la base del hexaedro. Como los datos del ejercicio especifican que el hexaedro no puede tener caras paralelas al plano vertical de proyección diédrica, hay que tener cuidado en que el cuadrado trazado no tenga ninguno de sus lados paralelo a la línea de tierra. PUNTOS NO PERMITIDOS QUEDARÍAN CARAS PARALELAS AL PLANO VERTICAL PUNTOS SÍ PERMITIDOS NO QUEDAN CARAS PARALELAS AL PLANO VERTICAL DIÉDRICO 3 / 14 Una vez dibujado el cuadrado se obtiene en verdadera magnitud la altura del hexaedro (que es igual al lado del cuadrado). Como la base del hexaedro está situada en el plano horizontal de proyección diédrica, la altura del cuerpo es perpendicular a la base, por lo que la altura del hexaedro será paralela al plano vertical de proyección diédrica, y podrá dibujarse en verdadera magnitud, ya que vendrá representada por una recta perpendicular al plano horizontal. Una vez determinada la altura del hexaedro, ya pueden dibujarse sus proyecciones diédricas. Por facilidad se han nombrado los extremos de las aristas longitudinales con las mismas letras, de tal forma que la base inferior del hexaedro (la que está situada en el plano horizontal) es la ABCD y la base superior del hexaedro (paralela a la anterior y de mayor cota) es la A’B’C’D’. Para determinar la visibilidad de sus aristas, debe prestarse atención a la dirección de proyección sobre el plano V (plano vertical de proyección diédrica). En el caso particular de esta solución, la arista DD’ es oculta en proyección vertical ya ocultada por la cara AA’BB’. que queda DIÉDRICO 4 / 14 El punto medio del hexaedro (punto E) puede determinarse de varias formas. Una de ellas es el trazado de las diagonales del cuerpo: como el orden de notación de las bases inferior (ABCD) y superior (A’B’C’D’) es el mismo, las diagonales vienen representadas por los segmentos AC’ y BD’. Dibujo de la sección plana Se recomienda dibujar primero un plano como el requerido para dar la sección, en una posición arbitraria. Los planos perpendiculares al segundo bisector son aquellos cuyas rectas traza vertical y horizontal coinciden, su dibujo se confunde en una sola. Por otra parte es dato que los ángulos que forman las rectas traza de dicho plano con la línea de tierra son de 60º. Importante: no se trata de los ángulos que forma el plano con el plano horizontal (para determinarlo habría que fijarse en la recta de máxima pendiente) ni con el plano vertical (para determinarlo habría que fijarse en la recta de máxima inclinación). La recta traza vertical de un plano está contenida (por definición de recta traza) en el plano vertical, al igual que la línea de tierra; por ello el ángulo que forman puede ser dibujado directamente ya que se representa en verdadera magnitud. Igualmente la recta traza horizontal de un plano está contenida (por definición de recta traza) en el plano horizontal, al igual que la línea de tierra; por ello el ángulo que forman puede ser dibujado directamente ya que se representa en verdadera magnitud. En este caso los 60º se han tomado “inclinados a la izquierda”; si se hubieran tomado “inclinados a la derecha” el plano también sería válido. DIÉDRICO 5 / 14 Una vez trazado el plano en una posición arbitraria, hay que dibujar un plano paralelo al anterior que pase por el punto medio del hexaedro. En general, para trazar un plano (representado por rectas traza) por un punto (representado por proyecciones) hay que utilizar una recta (que tiene proyecciones y puntos traza). Se ha optado usar una recta horizontal del plano (sólo se ha denotado la proyección vertical de su punto traza vertical tv). DIÉDRICO 6 / 14 DIÉDRICO 7 / 14 Para obtener la sección plana se ha optado por realizar un cambio de plano de proyección vertical, de forma que el plano que va a dar la sección se convierta en proyectante. Para ello se dispone una línea de tierra perpendicular a la recta traza horizontal y se realiza un cambio de plano de proyección vertical. De esta forma, el plano que va a dar la sección se convierte en un plano proyectante vertical (su recta traza horizontal es perpendicular a la nueva línea de tierra): todo lo que esté contenido en dicho plano estará contenido, en proyección vertical v1, en su nueva recta traza vertical Pv1. Al ser un cambio de plano vertical, el plano horizontal permanece, luego las distancias al plano horizontal se mantienen, es decir, se mantienen las cotas de todos los puntos. Se comenzará obteniendo la nueva proyección vertical V1 de la base inferior del hexaedro. DIÉDRICO 8 / 14 La altura del hexaedro se mantiene (se conservan las cotas) por lo que la proyección V1 del hexaedro ya puede ser trazada. En este caso, en proyección vertical V1, la arista BB’ será oculta ya que queda ocultada por las caras AA’DD’ y DD’CC’. DIÉDRICO 9 / 14 Para dibujar la nueva traza vertical Pv1 del plano, simplemente hay que recordar que todo lo que esté en dicho plano estará confundido, en proyección V1, con dicha recta traza Pv1. El punto E (punto medio de la altura del hexaedro) está en el plano, por lo que la recta traza Pv1 se obtiene al unir el punto de corte de la recta traza horizontal Ph con la nueva línea de tierra (las trazas de un plano se cortan en el mismo punto de la línea de tierra) con la proyección V1 del punto E (ev1). DIÉDRICO 10 / 14 La sección plana aparece al determinar la intersección de la recta traza Pv1 con las aristas del hexaedro en proyección V1: como el plano es proyectante vertical, todo lo que esté en dicho plano se confunde con su recta traza Pv1. Importante: hay que determinar la intersección de Pv1 con todas las aristas del hexaedro (hay aristas en las bases inferior y superior que aparecen confundidas). Para mayor claridad se usa una notación numérica: puntos 1-2-3-4-5-6. Importante: debe recordarse el orden utilizado en la notación de los vértices del hexaedro: Base inferior. A-B-C-D Base superior: A’-B’-C’-D’ DIÉDRICO 11 / 14 Una vez determinados los puntos de corte de la recta traza Pv1 con todas las aristas del hexaedro, hay que obtener sus proyecciones horizontales mediante líneas auxiliares perpendiculares a la nueva línea de tierra, dibujadas desde los puntos de corte hasta que corten a las aristas cortadas en su proyección horizontal. DIÉDRICO 12 / 14 Por último sólo queda obtener las proyecciones verticales de los vértices de la sección mediante líneas auxiliares trazadas desde las proyecciones horizontales, perpendiculares a la primera línea de tierra. Este procedimiento es válido para todas las aristas del hexaedro excepto para las aristas longitudinales (la BB’, punto 3, y la DD’, punto 4) que por ser perpendiculares al plano horizontal se confunden con las líneas auxiliares. Para obtener las proyecciones verticales (sobre el plano de proyección V) de los puntos 3 y 4, hay que recordar que la sección se ha obtenido mediante un cambio de plano de proyección vertical, es decir, que al cambiar de planos de proyección de H-V a H-V1 (el plano H no cambia) las cotas se conservan, por lo que las cotas de los puntos 3 y 4 se mantienen iguales. DIÉDRICO 13 / 14 Uniendo los vértices de la sección se obtendrá la representación de dicha sección sobre las caras del hexaedro. Para determinar la visibilidad de las aristas de la sección debe considerarse la visibilidad de las caras seccionadas. DIÉDRICO 14 / 14 Resolución completa del ejercicio a escala 1:1 en formato A4 (puede situarse vertical u horizontalmente).