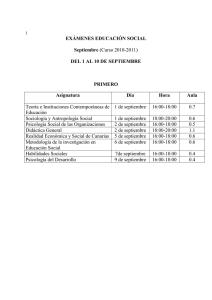
Se desea comprobar si más del 50% de los clientes de un local son

Universidad Autónoma de Madrid
Se desea comprobar si más del 50% de los
clientes de un local son menores de 18 años.
Se toma una muestra de 6 personas y se
registra cuantos de ellos son menores de
edad. A continuación puede verse la
distribución del estadístico X bajo H0 y en el
caso (real pero desconocido) de que el 70%
de los clientes sean menores. Utilizar
α=0,05.
0
1
2
3
4
5
6
π=0,5 0,016 0,094 0,234 0,312 0,234 0,094 0,016
π=0,7 0,001 0,010 0,060 0,185 0,324 0,303 0,118
a) ¿Para qué valores de X se rechaza H0?
b) ¿Cuál es la probabilidad de que el
investigador detecte que H0 es falsa?
c) ¿Cuál es la probabilidad de que el
investigador mantenga H0 (que es falsa)?
d) ¿Cuál hubiera sido la probabilidad de
haber mantenido H0 si fuera verdadera?
e) ¿Cuál sería el nivel crítico si en la muestra
se encuentran tres menores de edad?
Análisis de Datos en Psicología II
Tema 3
Universidad Autónoma de Madrid
Solución:
a) X = 6
b) P (X=6 | π=0,7) = 0,118 (Potencia 1-β)
c) Error tipo II: 1-0,118 = 0,882 (β)
d) P (X≤ 5| π=0,5) = 0,984 (1 - α)
e) P(X≥3 | π=0,5) = 0,656 (p)
Análisis de Datos en Psicología II
Tema 3
Universidad Autónoma de Madrid
Para ampliar el estudio anterior se toma
una muestra de 5 menores y se
contrasta la hipótesis de que la mitad de
los menores gasta más de 6€ en el local.
El investigador decide rechazar H0 si
ninguno o todos los menores de la
muestra gastan más de 6€.
a) ¿Cuál sería la probabilidad
mantener H0 si fuera verdadera?
de
b) ¿Cuál sería la probabilidad de
rechazar H0 si sólo un 40% de los
menores gasta más de 6€?
c) ¿Cuál sería la probabilidad de cometer
un error de tipo I?
d) ¿Cuál sería la probabilidad de cometer
un error de tipo II?
Análisis de Datos en Psicología II
Tema 3
Universidad Autónoma de Madrid
a) Binomial (n=5, π=0,5)
N. de C. Mantener H0 verdadera
P (1≤X≤4 | π=0,5) = P (X≤4) - P (X<1) =
0,969-0,031 = 0,938
b) Binomial (n=5, π=0,4)
Potencia. Rechazar H0 falsa
P(X=0) + P(X=5) = 0,078 + 0,01 = 0,088
c) Error tipo I. Rechazar H0 verdadera
P(X=0) + P(X=5) = 0,031 + 0,031 = 0,062
d) Error tipo II. Mantener H0 falsa
P (1≤X≤4 | π=0,4) = 1 - 0,088 = 0,912
Análisis de Datos en Psicología II
Tema 3
Universidad Autónoma de Madrid
Sabemos que el CI se distribuye normal
(100, 15). Un investigador no se fía de esto y
cree que la media ha disminuido. Decide
realizar un contraste y rechazar H0 si la
media es menor o igual que 94. Toma una
muestra y encuentra que la media es 96. A
continuación
aparece
la
probabilidad
acumulada de obtener cada media muestral
si µ=100 y en el caso (real pero desconocido
por todo el mundo) de que µ=98.
X
94
96
98 100 102 104 106
µ=100 0,023 0,092 0,255 0,5 0,754 0,908 0,977
µ=98 0,092 0,255 0,5 0,754 0,908 0,977 0,996
a) Plantee las hipótesis
b) ¿Cuál es su decisión y qué error ha
cometido?
c) Indique la probabilidad de cada error, el
nivel de confianza y la potencia.
d) ¿Cuánto vale el nivel crítico?
Análisis de Datos en Psicología II
Tema 3
Universidad Autónoma de Madrid
a) H0: µ ≥ 100; H1: µ < 100
b) Zona de aceptación X > 94
Zona de rechazo X ≤ 94
X = 96 la decisión es
Dado que
mantener H0. Ha cometido un error de
tipo II: Mantener H0 siendo falsa.
c)
α = 0,023 (Pr del error tipo I)
β = 1-0,092 = 0,908 (Pr del error tipo II)
1-α = 1 - 0,023 = 0,977 (nivel de confianza)
1-β = 0,092 (potencia)
d)
p = P( X ≤ 96) = 0,092
Análisis de Datos en Psicología II
Tema 3