Las derivadas de los instrumentos de renta fija

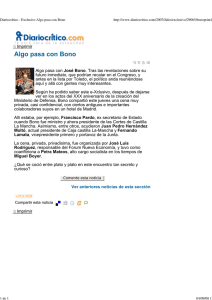
Las derivadas de los instrumentos de renta fija
Estrella Perotti, MBA
Ejecutivo a cargo Capacitación & Desarrollo
Bolsa de Comercio de Rosario
eperotti@bcr.com.ar
Como viéramos en el artículo el dilema entre la tasa de interés y el precio de un bono, la
relación entre los cambios entre el factor de riesgo y el precio de un bono no es lineal
sino que es inversa y convexa.
Esto implica que, ante incrementos en la tasa de interés el precio del bono cae pero no
tanto como si la relación entre ellos fuese lineal (lo contrario también se da, ante una
caída en la tasa, el precio sube más que proporcionalmente). La razón de este
comportamiento es que un bono puede valuarse como el valor presente de los futuros
flujos de fondos que se esperan recibir.
Supongamos que queremos saber qué sucede con el precio del bono ante cambios en
la tasa de interés respecto de su valor inicial, llamémosle y0, a un nuevo valor y1 = y0 +
∆y. Es función del administrador de riesgo valuar los efectos que cambios en el factor
de riesgo pueden tener sobre su cartera de activos. No obstante, esta tarea sería
bastante complicada de ser llevada a cabo en tiempo y forma si no se contara con
métodos que permiten aproximar dichos movimientos.
Cuando los cambios en el factor de riesgo son pequeños, la relación entre el precio del
instrumento financiero y el factor de riesgo (en este caso el bono y la tasa de interés)
puede ser aproximada mediante la fórmula de expansión de Taylor entorno al valor
inicial; esto es, calculando las derivadas de primer y segundo orden respecto del cambio
en la variable de riesgo. En el mundo de los instrumentos de renta fija estas dos
derivadas son tan importantes que tienen nombres propios, la duración (duration) y la
convexidad (convexity).
Valuación local
Taylor nos otorga una fórmula de valuación local en los entornos del valor inicial.
Esto es, el precio de un instrumento financiero en un momento futuro, es función
del factor de riesgo en dicho momento (P1=f (y1)), donde:
P1 = P 0 + f ' ( y0 )∆y +
1
1 ''
f ( y0 )(∆y ) 2 + ... 1
2
Para un mayor entendimiento acerca de este tema puede consultar libros de cálculo matemático.
1
Donde
f ' (.) =
f '' (.) =
dP
es la derivada de primer orden y,
dy
d 2P
dy 2
es la derivada de segundo orden de la función f(.) valuada en el momento inicial.
Esta expansión puede ser generalizada a situaciones donde la función depende
de dos o más variables.
La ecuación presentada es una expansión con infinitos términos, con un poder
de crecimiento de ∆y. Únicamente los dos primeros términos son utilizados en
las finanzas y permiten obtener una buena aproximación de los cambios en el
precio de un instrumento en relación al factor de riesgo (manteniendo siempre
los supuestos de valuación establecidos de antemano).
Determinación matemática
Analicemos primeramente las derivadas de un bono cero cupón. Como
recordará, el precio de cualquier instrumento financiero puede definirse como el
valor presente de los flujos de fondos que se esperan recibir en el futuro. Por
consiguiente, para hallar el precio de un bono es necesario conocer su flujo de
fondos y descontarlos luego a una tasa de interés. Matemáticamente:
n
P=∑
t =1
Ct
(1 + y ) t
Donde:
P es el precio del instrumento financiero
Ct es el flujo de fondos del instrumento al momento t
y es el rendimiento requerido
t es el número de períodos (cantidad de años por cantidad de pagos en el año)
El precio de un bono cero cupón, al no pagar intereses, estará compuesto por un
único flujo de fondos (representado por la devolución del capital al vencimiento
del instrumento) descontado a una tasa apropiada. Esto es:
P=
F
(1 + y )T
Donde:
P es el precio del bono cero cupón
F es el valor nominal del bono
y es el rendimiento requerido
T es el número de períodos (cantidad de años por cantidad de pagos en el año)
2
Un cambio en el precio del bono dado un cambio en la tasa de interés puede
expresarse como:
∂P ⎛ F
=⎜
∂y ⎜⎝ (1 + y ) t
Si recordamos que P =
'
⎞
⎛
⎞
F
⎟⎟ = −T × ⎜⎜
⎟
T +1 ⎟
⎠
⎝ (1 + y ) ⎠
F
, la derivada primera del precio de un bono puede
(1 + y )T
escribirse como:
∂P − T
=
× P = − D* × P ♣
∂y 1 + y
Donde:
P es el precio del bono cero cupón al momento cero
y es la tasa de rendimiento
∂P es el cambio en el precio del bono cero cupón
∂y es el cambio en el rendimiento requerido
D* es la duración modificada, donde D*= D (1 + y ) , donde (1+y) está expresada en el mismo
período de tiempo en que se pagan los cupones (anual, semestral, etc), independientemente de la
medida de tiempo que tome la duración.
T es el número de períodos
El cambio en el precio de un bono, dado un cambio en la tasa de interés será:
∂P = − D * × P × ∂y
Un cambio en el precio del bono dado un cambio cuadrado en la tasa de interés
puede expresarse como (continuando con el ejemplo cero cupón):
∂2P ⎛ F
=⎜
∂y 2 ⎜⎝ (1 + y ) t
''
⎞
⎛
⎞ T × (T + 1)
F
⎟⎟ = −T × [− (T + 1) )]× ⎜⎜
⎟=
×P =C×P
T +2 ⎟
(1 + y ) 2
⎠
⎝ (1 + y ) ⎠
Para instrumentos de renta fija, con flujos de fondos conocidos, es relativamente
sencillo computar las derivadas primera y segunda, tal y como hemos podido
observar en nuestro ejemplo de bono cero cupón.
Al determinar la función de derivada primera obtenemos un término conocido
como duración modificada, que no es más que dividir la duración convencional
♣
Como existe un único flujo de fondos en los bonos cero cupón la duración de Macaulay (D) coincide con
el tiempo al vencimiento (T). Desarrollaremos este punto en mayor detalle al analizarse las derivadas para
bonos con varios flujos de fondos.
3
(o Macaulay duration) por (1+y). La duración de Macaulay2 es una medida de
tiempo e indica el tiempo promedio al vencimiento de cada flujo de fondos.
La duración modificada es apropiada para medir la sensibilidad de un bono ante
cambios en la tasa de interés. El término (1+y) aparece en el denominador de la
función debido a que derivamos el valor presente calculado de manera discreta3.
En la práctica la diferencia entre la duración modificada y la de Macaulay es
generalmente muy pequeña.
Ahora bien, incorporando estas ecuaciones encontradas a la expansión de
Taylor para el cambio en el precio de un bono obtenemos que:
[
]
∆P = − D * × P (∆y ) +
[
1
[C × P ](∆y) 2 + ... ó
2
]
P1 = P0 − D * × P (∆y ) +
1
[C × P](∆y) 2
2
Donde, la duración mide el efecto (lineal) de primer orden de un cambio en la
tasa de rendimiento y la convexidad el efecto de segundo orden o cuadrático.
En la figura a continuación podremos observar la calidad de la aproximación por
series de Taylor.
Figura 1. Aproximación del precio por duración y duración + convexidad de un bono a 20 años,
tasa cupón 8% anual.
250
Precio del bono
200
150
100
$72,42
$70,12
$ 60,73
50
0
1%
2%
3%
4%
5%
6%
7%
8%
9%
10%
11%
12%
13%
14%
15%
16%
Tasa de rendimiento
2
Para un mayor análisis sobre Macaulay Duration, remitirse a Fabbozzi, Frank “Fixed – Income
Mathematics”
3
Cuando se utiliza capitalización continua la duración modificada es idéntica a la duración de Macaulay.
Queda a consideración del lector verificar esto último.
4
Un cambio en el precio del bono dado un movimiento en la tasa de interés
aproximado por duración y convexidad, mejora las estimaciones ya que refleja
de mejor manera la relación precio – tasa de rendimiento de un bono.
Para grandes movimientos en el precio, la función se vuelve más curvada y se
deteriora la calidad de las aproximaciones lineales.
La duración en dólares mide entonces la pendiente (negativa) de la recta
tangente a la curva precio – rendimiento en el momento inicial.
También debería observarse que la curvatura se encuentra lejos del origen, lo
cual es explicado por el término convexidad. Esta curvatura es beneficiosa
debido a que el efecto de segundo orden ( 0.5 × (C × P ) × (∆y ) 2 ) debe ser positivo
cuando la convexidad es positiva (existen algunos instrumentos de renta fija
cuya convexidad es negativa, ejemplo, Mortgage Back Securities (MBS),
Callable Bonds, etc, pero esto será tema para otro artículo). En pocas palabras,
el término cuadrático es siempre beneficioso.
Interpretemos la duración y la convexidad
Hasta el momento hemos mostrado cómo calcular de manera analítica la
duración y la convexidad en el caso de un bono cero cupón; trataremos a
continuación, utilizando el mismo método, de interpretar estas dos medidas.
Si el precio de un bono era equivalente a los flujos de fondos que se esperan
recibir, entonces, un bono con más de un flujo puede denotarse como:
T
P = ∑ Ct (1 + y ) t
t =1
Entonces, el cambio en el precio dado un cambio en la tasa de rendimiento
puede expresarse como:
'
T
⎡ T tC t ⎤
− tCt
∂P ⎡ T
⎤
P
−D
= ⎢∑ Ct (1 + y ) t ⎥ = ∑
=
−
P×
=
×P
∑
⎢
t +1
t ⎥
∂y ⎣ t =1
(1 + y ) (1 + y )
⎦ t =1 (1 + y )
⎣ t =1 (1 + y) ⎦
T
Hecho que define a la duración como D = ∑
t =1
tCt
P
(1 + y ) t
La duración puede ser interpretada económicamente como el tiempo promedio
que hay que esperar por cada pago, ponderando a éstos por el valor presente
5
del total de flujos de fondos a recibir. Si en nuestra última ecuación
reemplazamos P por su valor obtenemos que:
T
Ct (1 + y ) t
D = ∑t ×
=
t × wt
∑
t =1
∑ Ct (1 + y) t t =1
T
En donde, wt representa la razón entre el valor presente de cada flujo de fondos
respecto del total y su suma es equivalente a 1. Esto explica por qué la duración
de un bono cero cupón es igual al tiempo al vencimiento (existe un único flujo de
fondos y su ponderación es igual a 1).
Resumiendo podemos presentar entonces, las propiedades de la duración vistas
hasta el momento:
La duration de un bono cero cupón es igual al tiempo al vencimiento.
-
Manteniendo el plazo al vencimiento constante, la duration aumenta a medida
que disminuye la tasa cupón (caso extremo: bono cero cupón).
-
Manteniendo la tasa cupón constante, la duration crece a medida que aumenta
el plazo al vencimiento.
-
Manteniendo todos los factores constantes, la duration de un bono con cupón
aumenta cuando la tasa requerida (yield) disminuye. Para bonos cero – cupón la
duration es siempre igual al tiempo al vencimiento.
-
La duration asume el período de tiempo en el cual está expresado la tasa, es
decir, si la tasa es semestral, la duración se expresará en semestres, para
llevarla a años simplemente se la multiplica por 2.
- La duración de un bono nos indica:
ƒ El tiempo promedio al vencimiento, ponderando la importancia
relativa del valor presente de cada pago respecto del precio del
bono.
ƒ
El grado de sensibilidad de un bono respecto de otro.
ƒ El momento en que se compensan los efectos del tiempo al
vencimiento y la tasa cupón (Si y sube, el Precio del bono cae por
efecto del tiempo al vencimiento pero los pagos de cupones son
reinvertidos a una mayor tasa, aumentando su valor y
compensando en parte el efecto negativo de la suba de la tasa de
descuento. Si la duration de un bono es 5 años implica que al cabo
de dicho plazo, las variaciones en la yield no afectan el rendimiento
del bono.
6
Importante: la duration no brinda información acerca de cuánto cambia el precio del bono sino
que indica qué bono sufrirá mayores cambios. Si quisiéramos conocer lo primero deberíamos
utilizar como medida la duración modificada.
Pasemos a la interpretación de la derivada segunda…
''
T
t (t + 1)Ct ⎧⎡ T t(t + 1) C t ⎤ ⎫
∂2P ⎡ T
t⎤
Ct
y
(
1
)
=
+
=
∑
⎥ ∑ (1 + y ) t + 2 = ⎨⎢∑ (1 + y) t + 2 ⎥ P ⎬ × P
∂y 2 ⎢⎣ t =1
t =1
⎦
⎦ ⎭
⎩⎣ t =1
⎡ T t(t + 1) C t ⎤
Donde definimos la convexidad como: C = ⎢∑
P.
t +2 ⎥
⎣ t =1 (1 + y) ⎦
t × (t + 1)
× wt en donde wt
2
t =1 (1 + y )
tiene el mismo significado que el dado a conocer en el análisis de la duración.
T
La convexidad también puede denotarse como C = ∑
A modo de resumen podemos describir las propiedades de la convexity:
- Si la tasa se incrementa (decrece) la duración en dólares decrece
(incrementa).
- Para una determinada tasa al vencimiento, un menor cupón significa una
mayor convexidad para ese bono.
- Para una tasa y duración modificada dadas, un menor cupón, significa
menor convexidad. La implicancia de esta propiedad es que para un bono
cero cupón la convexidad será menor para una duración modificada dada.
- La convexidad de un bono aumenta a medida que aumenta su duración.
La relación duration – convexity puede observarse en el siguiente gráfico
(los bonos cero cupón tendrán siempre la mayor convexidad debido a que
tienen un único flujo de fondos y este se produce al vencimiento).
7
Convexity
Duration
Conclusiones
Hemos podido observar a lo largo de este artículo el por qué la derivada primera
(duración) y la segunda (convexidad) son tan importantes al momento de
determinar los cambios en el precio de un instrumento de renta fija (el caso
desarrollado, bonos), basándonos primeramente en las medidas de sensibilidad
para luego adentrarnos en el desarrollo de Macaulay propiamente dicho. Estas
dos medidas permitirán al administrador de riesgo obtener de manera rápida una
buena estimación del cambio en la variable dependiente dado una variación en
el factor de riesgo.
Seguramente muchos temas habrán quedado en el tintero en nuestro afán de
lograr que este artículo resulte amigable al común de los lectores, pero creemos
que nuestro objetivo de mostrar de dónde provienen y para qué se utilizan estas
medidas ha sido cumplido.
Bibliografía
Jorion Philippe, Financial Risk Management Handbook, Wiley Finance 2007
Fabozzi, Frank, Fixed Income Mathematics, Analytical and Statistical
Techniques. Mc Graw – Hill 1997
8