Problemas propuestos PAU 2009

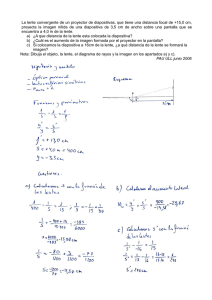
Selección de Problemas de Física
Curso 2008/2009
Problemas relacionados
con los criterios PAU
Selección de Problemas de Física
Curso 2008/2009
Interacción Gravitatoria
1.
Galileo descubrió hacia el 1600 los cuatro satélites mayores de Júpiter mirando a través de su anteojo.
6
Hoy día se sabe que uno de ellos, Ganímedes, describe una órbita circular de radio r =1,071·10 km,
-11
siendo su período de 7,16 días. Con esta información calcula la masa de Júpiter (Dato: G = 6,67·10
2
-2
N m kg )
2.
La astronauta Sunita Williams participó desde el espacio en la maratón de Boston de 2007 recorriendo
la distancia de la prueba en una cinta de correr dentro de la Estación Espacial Internacional. Sunita
completó la maratón en 4 horas, 23 minutos y 46 segundos. La Estación Espacial orbitaba, el día de la
carrera, a 338 km sobre la superficie de la Tierra. Determina:
a. El valor de la gravedad terrestre en la Estación Espacial.
b. La energía potencial y la energía total de Sunita sabiendo que su masa es de 45 kg.
c. ¿Cuántas vueltas a la Tierra dio la astronauta mientras estuvo corriendo?
24
Datos: Masa de la Tierra = 5,97·10 kg, Radio terrestre = 6370 km.
3.
Un astronauta hace experimentos con un péndulo simple de 1 m de longitud en la superficie de un
planeta que tiene un radio que es la quinta parte del radio terrestre y una masa que es la tercera parte
de la terrestre. Determina:
a. El período del péndulo que utiliza el astronauta
b. La velocidad de escape en dicho planeta
c. Si su nave espacial orbita a una altura de la superficie del planeta h=300 km, ¿cuál es el
período de rotación de la misma?
-11
2
-2
Datos: RT = 6370 km; G = 6,67·10 N m kg .
Selección de Problemas de Física
Curso 2008/2009
Interacción Electromagnética
4.
-19
Un átomo de hidrógeno está constituido por un núcleo central puntual de carga e = 1,60· 10
-19
electrón periférico de carga e = -1.61·10
-31
C y masa m = 9·10
C y un
kg. Se admitirá que, debido a la
atracción de estas partículas, el electrón describirá círculos cuyo centro será el núcleo. Siendo el radio
del círculo 0,53 Å, calcula: a) la velocidad del electrón; b) la energía potencial, cinética y total del
sistema.
5.
Considera un conductor rectilíneo de longitud l=1m y recorrido por una corriente eléctrica I=2 A, que se
encuentra en el seno de un campo magnético B= 10T. Calcula la fuerza magnética que actúa sobre el
conductor en las siguientes situaciones:
r
B
I
(a)
6.
r
B
I
(b)
r
B
I
(c)
Dos conductores rectilíneos y paralelos de longitud L y separados una distancia d están recorridos por
sendas corrientes de intensidad I. Dibuja las líneas del campo magnético creado por cada conductor así
como las fuerzas que se ejercen entre sí cuando:
a. las corrientes son del mismo sentido.
b. las corrientes son de sentido contrario.
7.
Dos conductores rectilíneos y paralelos de longitud 1m están separados una distancia de 10cm. Por el
conductor 1 circula una corriente de intensidad 10A y por el 2 una intensidad de 20A, ambas en el
mismo sentido. Determinar:
a. El módulo de la fuerza que se ejercen entre sí los dos conductores.
b. Dibujar los vectores fuerzas que sufre cada conductor.
8.
¿Cuál es la velocidad de un haz de electrones que penetra perpendicularmente en un campo eléctrico
de módulo E= 20000 Vm
-1
, y a un campo magnético de módulo B= 0.4T, que son a su vez
perpendiculares entre sí, si se sabe que los electrones no sufren desviaciones?.
Selección de Problemas de Física
Curso 2008/2009
Vibraciones y Ondas
9.
Una masa de 2 kg está unida a un muelle horizontal cuya constante recuperadora es k = 10 N/m. El
muelle se comprime 5 cm desde la posición de equilibrio (x = 0) y se deja en libertad. Determina:
a. La expresión de la posición de la masa en función del tiempo, x = x(t)
b. Los módulos de la velocidad y aceleración de la masa en un punto situad a 2 cm de la
posición de equilibrio.
c. La fuerza recuperadora cuando la masa se encuentra en los extremos de la trayectoria.
d. La energía mecánica del sistema oscilante.
10. Un resorte de masa despreciable se estira 0,1 m cuando se la aplica una fuerza de 2,45 N. Se fija en su
extremo libre una masa de 0,085 kg y se estira 0,15 m a lo largo de una mesa horizontal desde su
posición de equilibrio y se suelta dejándolo oscilar libremente sin rozamiento. Calcula:
a. La constante elástica del resorte y su periodo de oscilación
b. La energía total asociada a la oscilación
c. Las energías potencial y cinética cuando x = 0,075 m
11. En un extremo de una cuerda tensa horizontal de 5,0 m se provoca un movimiento oscilatorio armónico
perpendicular a la dirección de la cuerda, cuya elongación es de 8,0 cm cuando ha transcurrido 0,10 s
desde su comienzo. Se observa que la onda producida tarda en llegar al otro extremo 2,0 s y que la
distancia entre dos crestas sucesivas es de 1,5 m. Determina: a) la frecuencia y la amplitud del
movimiento ondulatorio; b) la velocidad del punto situado a 1,0 m del origen de la onda, al cabo de 0,6 s
de iniciado el movimiento ondulatorio. (Física Ed. Bruño. Pág. 65)
12. En el centro de una piscina circular de 6 m de radio se produce una perturbación que origina un
movimiento ondulatorio en la superficie del agua. La longitud de onda es de 0,50 m y tarda 12 s en
llegar a la orilla. Calcular:
a. La frecuencia del movimiento ondulatorio.
b. La amplitud del mismo si al cabo de 0,25 s la elongación en el origen es de 4 cm.
c. La elongación en el instante t = 12 s en un punto situado a 6 m del foco emisor.
Selección de Problemas de Física
Curso 2008/2009
Óptica
13. En un proyector de diapositivas se utiliza una lente convergente que permite obtener sobre una pantalla
la imagen de un objeto de tamaño diez veces mayor que el mismo. Si la pantalla está a 4 cm de la
lente, ¿cuál debe ser la posición del objeto? ¿Cuál es la distancia focal de la lente?
Sol: x = -0,4 m; f ‘ = 0,36 m
14. Se pretende duplicar el tamaño de la imagen en el problema anterior sin modificar las posiciones del
objeto y de la pantalla. ¿Cuál debe ser la posición y potencia de la lente a utilizar para obtener la
imagen deseada nítidamente en la pantalla?
Sol: d = 0,21 m del objeto; P = 5 dioptrías
15. Una pantalla está situada a 40 cm de un objeto que se quiere proyectar en la misma. ¿En qué puntos
entre el objeto y la pantalla se puede colocar una lente convergente de 7,5 cm de distancia focal para
que la imagen se forme sobre la pantalla? ¿Cuál es el aumento lateral?
Sol: a. 10 cm y 30 cm del objeto b. -3 y -1/3 respectivamente.
16. a) Halle en forma gráfica y analítica la imagen de un objeto real de 1 cm de altura ubicado a 15 cm de
una lente convergente de distancia focal f’= 10 cm. b) Si a 15 cm de la lente convergente se ubica una
lente divergente, como en la Figura 2,
¿qué distancia focal debe tener la
lente divergente para que la imagen
final se forme sobre una pantalla a 40
cm de la lente divergente?, ¿es esto
posible?
Selección de Problemas de Física
Curso 2008/2009