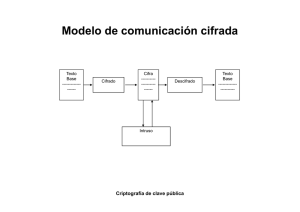
Algoritmos de criptografia asimetrica.
Anuncio

Algoritmos de criptografía asimétrica [3.1] ¿Cómo estudiar este tema? [3.2] Cifradores asimétricos TEMA [3.3] Certificados y firmas digitales TEMA 3 – Esquema man-in-the-middle Ataque Algoritmo DSA Algoritmo El Gammal Algoritmo Diffie-Hellman Vulnerabilidades Seguridad Algoritmo RSA Protección de la información Autenticación Algoritmos Concepto Certificados digitales Firma digital Firma digital y certificados digitales Algoritmos de criptografía asimétrica Criptografía y mecanismos de seguridad Esquema Criptografía y mecanismos de seguridad Ideas clave 3.1. ¿Cómo estudiar este tema? Para estudiar este tema, además de las Ideas clave, lee los apartados 12.1, 12.2, 12.3 y 12.4 del capítulo 12 «Cifrados asimétricos» y los apartados 17.1, 17.2 y 17.3 del capítulo 17 «Autentificación, certificados y firmas digitales» del libro Criptografía y seguridad de computadores de Manuel Lucena, disponible en: http://sertel.upc.es/tdatos/Libros/Lucena.pdf Una vez tratados los algoritmos simétricos, a continuación se presentan los algoritmos que los complementan, los criptosistemas simétricos. Estos sistemas en los que existen dos claves de cifrado, una pública y otra privada, no precisan de un canal seguro para que las partes puedan intercambiar la clave de cifrado. Esta indudable ventaja permite que, disponiendo de la clave pública del destinatario, el emisor pueda enviarle mensajes confidenciales sin necesidad de acordar una clave de cifrado con este. Por otro lado, y a diferencia de esta ventaja de los criptosistemas asimétricos, se trata de criptosistemas generalmente más lentos que los simétricos y que permiten obtener altos niveles de seguridad deben manejar grandes longitudes de clave. Dentro de este tema también se trata la firma digital, que permite mediante el empleo de la clave privada del emisor verificar la autenticidad del emisor; y también de los certificados de clave pública que son necesarios para poder verificar la asociación entre una clave pública (y la privada asociada) y un determinado usuario. Este tema tiene como objetivo principal presentarte los algoritmos de cifrado asimétrico. Así el primer bloque, engloba esos conceptos y el segundo los relacionados con la firma digital y del empleo de certificados digitales de clave pública. TEMA 3 – Ideas clave Criptografía y mecanismos de seguridad 3.2. Cifrados asimétricos La principal característica de este tipo de algoritmos de cifrado es que la clave empleada para el cifrado y descifrado de los mensajes está formada, en realidad, por un par de ellas (clave pública y privada). Su fortaleza está basada en la complejidad computacional que existe a la hora de calcular la clave privada partiendo del conocimiento de la clave pública. Las claves utilizadas por este tipo de algoritmo son de mayor longitud que las de los simétricos y, además, su rendimiento es bastante menor (algoritmos pesados). Debido a estos inconvenientes, el cifrado asimétrico se suele utilizar, en lugar de para cifrar mensajes de longitud considerable, para cifrar las claves de sesión que serán utilizadas por cifradores simétricos que cifrarán dichos mensajes. Protección de la información Teniendo dos entidades A y B que disponen de sus respectivos pares de claves y donde A quiere enviar un mensaje hacia B y B quiere responder a A, el proceso a seguir es el siguiente: 1. A cifrará el mensaje con (clave pública conocida por todos). 2. A envía el mensaje cifrado a B. 3. B descifrará el mensaje con 4. B cifrará el mensaje con (clave privada solo conocida por B). (clave pública conocida por todos). 5. B envía el mensaje cifrado a A. 6. A descifrará el mensaje con (clave privada solo conocida por A). Autentificación Mediante cifrado asimétrico y el empleo de funciones resumen es posible autentificar la procedencia de los mensajes recibidos. TEMA 3 – Ideas clave Criptografía y mecanismos de seguridad A continuación se detalla el método de autentificación en un escenario básico: 1. A recibe un mensaje cifrado con proveniente de B. 2. B genera el resumen del mensaje y lo envía cifrado con 3. A descifra el mensaje proveniente de B con su 4. A calcula el resumen del mensaje descifrado. 5. A descifra el resumen proveniente de B con su 6. A compara para autentificar a B. con . . . Ataque man-in-the-middle Todo algoritmo asimétrico es vulnerable a este tipo de ataque. El atacante se interpone entre A y B en el momento que se intercambian sus claves públicas, las almacena y envía su propia clave pública a A y B para poder suplantar la identidad de ambos. En este momento C podrá descifrar todos los mensajes provenientes de A y B y podrá enviarles mensajes que ellos interpretarán como correctos. La única solución ante tal ataque es confiar en un tercero (redes de «amigos») que asegure que las claves públicas pertenecen a quien la envía. Algoritmo RSA Algoritmo asimétrico más sencillo de implementar y sin vulnerabilidades descubiertas hasta la fecha. La fortaleza de RSA reside en la dificultad para factorizar el producto de dos primos de gran tamaño. TEMA 3 – Ideas clave Criptografía y mecanismos de seguridad Conceptos matemáticos La generación de claves se realiza siguiendo los siguientes pasos: 1. Escoger dos primos grandes y , de forma aleatoria y calcular su producto . 2. La clave pública será donde inversa modulo es un coprimo de que tendrá , de lo que se deduce: 3. Donde es la inversa de módulo . Forma la clave privada. 4. El cifrado se realizará mediante la ecuación . 5. El descifrado por su parte se realizará con . Los primos escogidos suelen tener una longitud de 512 bits (o superior). El cifrado incrementa ligeramente la longitud del texto respecto al original. Los cálculos del algoritmo RSA pueden reducirse mediante el empleo del Teorema Chino del Resto o de la ecuación . Ejemplo: 1. Escogemos y . Por tanto 2. Calculamos . 3. Escogemos 4. Calculamos . , ya que la inversa . (coprimos). módulo , por y la pública 6. Si queremos cifrar el mensaje se calculará con TEMA 3 – Ideas clave que . 5. La clave privada es por tanto 7. Para descifrarlo utilizaremos lo . . . Criptografía y mecanismos de seguridad Seguridad La seguridad de RSA se basa en la complejidad matemática de factorizar el producto de primos grandes, ya que cualquier método que se encuentre para atacar RSA supondrá también encontrar una forma más simple de factorización. Se calculan números que sean «probablemente» primos, ya que no se comprueba que los números sean coprimos (es computacionalmente muy costoso verificar su primaridad con números tan grandes), aunque la probabilidad de que los números escogidos no sean coprimos es despreciable. Vulnerabilidades Aunque la fuerza bruta queda descartada en este algoritmo, existen puntos débiles que pueden ser utilizados por atacantes: Claves débiles: Existen claves en RSA que no alteran el texto original al cifrarlo, donde . Claves cortas: Las claves de RSA deben ser mayores de 1024 bits y recomendablemente, no inferiores a 2048 bits. Texto en claro escogido: Existen dos posibles ataques. o Enviando mensajes y y tal que . Si la víctima los firma obtenemos con lo que podemos obtener el mensaje firmado . o Explotando la posibilidad de que un usuario codifique y firme con el mismo par de claves el mensaje completo (no el resultado del resumen). Módulo común: Si se reutilizan los primos para generar las claves de RSA, el atacante puede obtener el mensaje en claro empleando el algoritmo de Euclides (ya que los valores de TEMA 3 – Ideas clave de la clave antigua y nueva suelen ser coprimos). Criptografía y mecanismos de seguridad Exponente bajo: Existen implementaciones que utilizan valores de bajos para optimizar el rendimiento (recomendable el mismo número de bits que n), esto ocasiona: o Teniendo 3 mensajes cifrados con distintos módulos (probablemente coprimos) y un mismo valor bajo de , utilizando el Teorema Chino del Resto es posible obtener el mensaje original. o Siendo es posible obtener el mensaje original mediante un algoritmo tradicional. Una solución es alargar el mensaje con bits aleatorios. Firma y codificación: Es necesario firmar antes de codificar para evitar ataques. Algoritmo Diffie-Hellman Siendo A y B las entidades que quieren negociar la clave, se procede de la siguiente forma: 1. Calcular un primo y un generador de donde (información pública). 2. A escoge un número aleatorio tal que . A envía el valor . 3. B escoge un número aleatorio tal que . B envía el valor . 4. B calcula la clave . 5. A calcula la clave . Algoritmo ElGamal Su fortaleza reside en el problema de logaritmos discretos. Permite tanto firma digital como cifrado de mensajes. La generación de claves se realiza escogiendo un primo y dos números aleatorios pública está formada por el conjunto TEMA 3 – Ideas clave y menores que . La clave privada es donde: y la clave Criptografía y mecanismos de seguridad Para la firma digital: 1. Escoger un número aleatorio y coprimo con . El valor debe ser secreto y cambiar cada vez. 2. Calcular . 3. Calcular . 4. La firma está formada por y la firma se comprueba mediante: El cifrado y descifrado se realiza de la siguiente forma: 1. Escoger un número aleatorio y coprimo con 2. Calcular . El valor debe ser secreto. . 3. Calcular . Donde 4. El cifrado está formado por es el mensaje original. (doble longitud de ) y el descifrado se realiza mediante: Algoritmo de DSA Variante del método de ElGamal utilizado para realizar firma digital. El algoritmo de generación de claves es el siguiente: 1. Escoger tal que y un número primo 2. Escoger un número primo tal que 3. Seleccionar un elemento 4. Si tal que . y que sea divisor de y calcular . volver al paso 3. 5. Escoger un número entero aleatorio 6. Calcular . 7. La clave pública la componen TEMA 3 – Ideas clave tal que . . . Criptografía y mecanismos de seguridad El proceso de firma y verificación queda descrito a continuación: Siendo la firma y el mensaje original, el algoritmo a seguir es el siguiente: 1. Seleccionar un número aleatorio 2. Calcular . . 3. Calcular . 4. Calcular 5. La firma tal que . es la pareja . La comprobación se realizará mediante los siguientes pasos: 1. Verificar que y 2. Calcular . a partir de 3. Calcular . 4. Calcular y 5. Calcular 6. Si . Rechazar la firma si no se cumple. . . aceptar la firma. 3.3. Certificados y firmas digitales Firmas digitales Firma digital Secuencia de bits añadida a un mensaje y que garantiza su autenticidad. La firma digital está vinculada a un único mensaje, únicamente puede ser generada por el legítimo titular y es públicamente verificable. La firma digital se realiza mediante el cifrado asimétrico del resumen del mensaje original (clave privada). El receptor deberá realizar el resumen del mensaje y comprobar si coincide con el descifrado de la firma digital (clave pública). TEMA 3 – Ideas clave Criptografía y mecanismos de seguridad Certificados digitales Un certificado digital está compuesto por una clave pública y un identificador que son firmados por una autoridad de certificación (entidad que asegura que una clave pública pertenece a un titular). Los certificados en formato X.509 son los más conocidos y usados. Si una clave se quiere revocar (por pérdida o robo) es posible realizar un certificado de revocación. Este certificado contiene la clave pública firmada con la clave privada del titular (de esta forma solo el titular puede revocar un certificado). TEMA 3 – Ideas clave Criptografía y mecanismos de seguridad Lo + recomendado Lecciones magistrales Algoritmos de criptografía asimétrica En esta lección veremos los algoritmos de criptografía asimétrica, que surgen como complemento a los algoritmos simétricos. A diferencia de estos últimos, los algoritmos de criptografía asimétricos permiten una comunicación confidencial sin que exista un canal seguro. La clase magistral está disponible en el aula virtual. No dejes de leer… Cómo trabaja RSA Interesante documento que describe el algoritmo RSA, algunas curiosidades y potenciales vulnerabilidades. El artículo completo está disponible en el aula virtual o en la siguiente dirección web: http://www.muppetlabs.com/~breadbox/txt/rsa.html TEMA 3 – Lo + recomendado Criptografía y mecanismos de seguridad No dejes de ver… Gambling with Secrets (RSA Encryption) Se trata de un interesante vídeo que ayuda a la compresión del algoritmo RSA y de los algoritmos criptografía asimétrica. El vídeo completo está disponible en el aula virtual o en la siguiente dirección web: http://www.youtube.com/watch?v=vgTtHV04xRI TEMA 3 – Lo + recomendado de Criptografía y mecanismos de seguridad + Información A fondo PKCS #1 Texto que describe los aspectos técnicos y de implementación del algoritmo RSA. Se trata del documento de referencia del algoritmo de criptografía asimétrica más utilizado en la actualidad. El artículo está disponible en el aula virtual o en la siguiente dirección web: http://www.rsa.com/rsalabs/node.asp?id=2125 Webgrafía RSA Laboratories Home: RSA Security Research Center Web del laboratorio de investigación de la empresa RSA, la página ofrece documentación técnica sobre los algoritmos y nuevas investigaciones relacionadas. http://www.rsa.com/rsalabs/ TEMA 3 – + Información Criptografía y mecanismos de seguridad Actividades Trabajo: Algoritmo Diffie-Hellman El algoritmo Diffie-Hellman: A y B negocian un nº p (primo) y un g (raíz primitiva módulo p). 1-A) Elección de x aleatorio 2-A) Calcula X= gx mod p 1-B) Elección de y aleatorio 2-B) Calcula Y= gy mod p 3-A) Calcula Yx= gy·x= K 3-B) Calcula Xy= gy·x= k. Partiendo de la negociación de una base g=5 y un módulo p=23 para el algoritmo Diffie-Hellman y supuesto que x= 11 e y=6. Obtén la clave a utilizar. Rellenar los datos pertinentes en el Excel adjunto. NOTA: Aunque solamente se piden los resultados, los ejercicios deben ser desarrollados manualmente como práctica para el examen. En el examen no se podrá usar calculadora. Para realizar la entrega únicamente debes subir al envío de actividades el documento Excel relleno con los resultados obtenidos. TEMA 3 – Actividades Criptografía y mecanismos de seguridad Trabajo: Algoritmo El Gamal Firma digital mediante El Gamal Se elige un número primo p muy grande. Se elige una raíz primitiva g de CG (p). Se escoge un número Xa de forma que 1<Xa<p-1. xy se calcula Ya=gXa.mod p. Posteriormente el emisor del mensaje A: Toma aleatoriamente un número k, 1<k<p-1 tal que m.c.d.(k, p-1)= 1 Calcula r= gK mod p Resolver la congruencia M=Xa·r+Ks mod p-1. Enviar (M,r,s). El receptor cuando recibe el mensaje: 1) Calcula Yar· rS mod p. 2) Calcula gM mod p. 3) Compara los resultados de 1) y 2). Calcula la firma del mensaje M=3, con g=7, p=97, Xa=37, y k=29. Se debe entregar este documento con el ejercicio resuelto y todas las operaciones realizadas. TEMA 3 – Actividades Criptografía y mecanismos de seguridad Trabajo: Sistema RSA En un sistema RSA con p= 11 y q=17, donde se desea firmar digitalmente el mensaje M=6. Supón que e= 7. Obtener el resultado de la firma. Rellenar los datos pertinentes en el Excel adjunto. NOTAS: No aplicar función resumen al mensaje Aunque solamente se piden los resultados, los ejercicios deben ser desarrollados manualmente como práctica para el examen. En el examen no se podrá usar calculadora. Para realizar la entrega unicamente se subirá a la plataforma el documento Excel adjunto relleno con los resultados obtenidos. TEMA 3 – Actividades Criptografía y mecanismos de seguridad Test 1. Los algoritmos de Diffie-Hellman y el RSA: A. Son ambos algoritmos basados en la exponenciación. B. Son criptosistemas de clave pública. C. Ambos pueden sufrir el ataque de hombre en medio. D. Los interlocutores no precisan negociar una clave. 2. Supón un sistema RSA basado en p=9 y q=11: A. Si la clave de cifrado es 3 la clave de descifrado es 67. B. Si la clave de cifrado es 3 la clave de descifrado es 11. C. Las claves no pueden ser calculadas. D. Ninguna de las anteriores. 3. Supuesto el criptosistema RSA, el resultado de cifrar M=34 con la clave pública (11,35) es: A. 32. B. 33. C. 34. D. 35. 4. El esquema de firma ciega basado en RSA… A. Es necesario conocer la clave pública del notario. B. No es un sistema exponencial. C. No se basa en un criptosistema asimétrico. D. Ninguna de las anteriores. 5. La seguridad de RSA se basa en: A. La dificultad del cálculo de la función de Euler. B. La dificultad de factorización de números primos. C. Las respuestas A y B son correctas. D. Ninguna de las anteriores. TEMA 3 – Test Criptografía y mecanismos de seguridad 6. La última etapa de la criptografía está determinada por: A. Los trabajos de Rivest en 1975. B. Los trabajos de Rivest en 1976. C. Los trabajos de Rivest en 1977. D. Ninguna de las anteriores. 7. La seguridad de RSA se basa en: A. El renombre de sus autores. B. La fortaleza de las cajas S. C. La dificultad de factorización de grandes números. D. Ninguna de las anteriores. 8. Supuesto el criptosistema RSA, el resultado de cifrar M=2 con la clave pública (3,35) es: A. 18. B. 2. C. No es una clave pública válida. D. Ninguna de las anteriores. 9. ¿Cuál de los siguientes elementos podría eliminar al contenido de un certificado de clave pública? A. Algoritmo asimétrico empleado. B. Fecha de emisión del certificado. C. Clave privada del usuario. D. Fecha de caducidad del certificado. 10. Las infraestructuras de clave pública son precisas porque: A. Pueden falsificarse las firmas de la autoridad de certificación. B. El certificado de clave pública puede ser robado por un atacante. C. Pueden sustituirse la clave pública en un certificado válido. D. Ninguna de las anteriores. TEMA 3 – Test