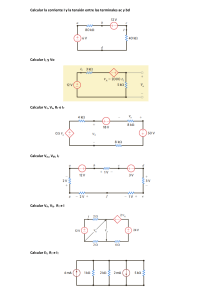
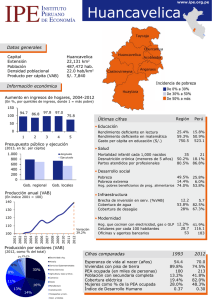
a) Por Ley de Ohm 9 A 8 i = 1 A i = Aplicando la ley de Kirchhoff
Anuncio

a) Por Ley de Ohm 4[Ω] 2[Ω] 9 i1 = ( A ) 8 i2 = 1( A ) 9[V] a i2 i1 6[Ω] b 5[Ω] Aplicando la ley de Kirchhoff para el voltaje desde a hasta b; sea Vab la diferencia de potencial entre a y b. 9 2 ⋅ − 4 + Vab = 0 8 ∴ Vab = 7 (V) 4 Note que éste es el voltaje a través de las terminales del capacitor. b) Dicha configuración es equivalente a la siguiente: Su resistencia equivalente es: 4[Ω] 2[Ω] 1 66 22 Req = 1 1 = = (Ω) + 15 5 6 11 6[Ω] 5[Ω] 3[µF] La expresión para el voltaje a través de un capacitor en un circuito de descarga es: 7 (V ) 4 22 donde: R = ( Ω ) 5 C = 3( µ F ) V0 = V ( t ) = V0 e −t RC , Luego: 7 −665 t V (t ) = e 4 Evaluando en: 5t 1 − 66 =e 10 Aplicando An : t=− 66 ⎛ 1 ⎞ An ⎜ ⎟ 5 ⎝ 10 ⎠ t = 30,39 ( s ) V (t ) = 1 7 ⋅ 10 4