Actividades refuerzo 4º ESO

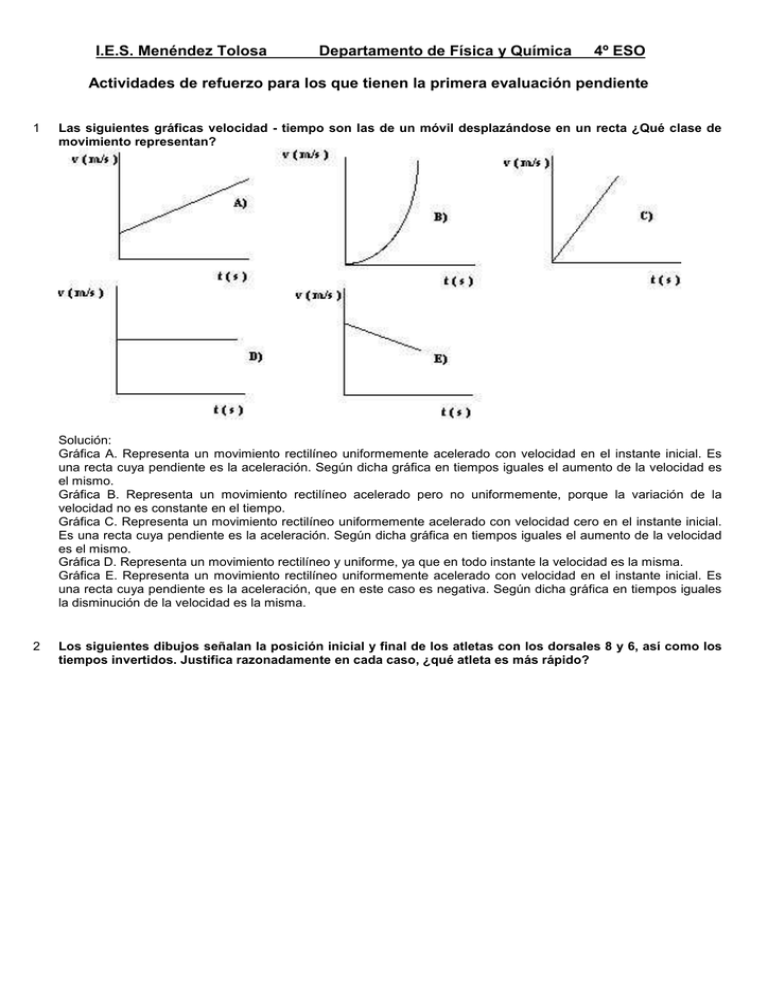
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
1
Las siguientes gráficas velocidad - tiempo son las de un móvil desplazándose en un recta ¿Qué clase de
movimiento representan?
Solución:
Gráfica A. Representa un movimiento rectilíneo uniformemente acelerado con velocidad en el instante inicial. Es
una recta cuya pendiente es la aceleración. Según dicha gráfica en tiempos iguales el aumento de la velocidad es
el mismo.
Gráfica B. Representa un movimiento rectilíneo acelerado pero no uniformemente, porque la variación de la
velocidad no es constante en el tiempo.
Gráfica C. Representa un movimiento rectilíneo uniformemente acelerado con velocidad cero en el instante inicial.
Es una recta cuya pendiente es la aceleración. Según dicha gráfica en tiempos iguales el aumento de la velocidad
es el mismo.
Gráfica D. Representa un movimiento rectilíneo y uniforme, ya que en todo instante la velocidad es la misma.
Gráfica E. Representa un movimiento rectilíneo uniformemente acelerado con velocidad en el instante inicial. Es
una recta cuya pendiente es la aceleración, que en este caso es negativa. Según dicha gráfica en tiempos iguales
la disminución de la velocidad es la misma.
2
Los siguientes dibujos señalan la posición inicial y final de los atletas con los dorsales 8 y 6, así como los
tiempos invertidos. Justifica razonadamente en cada caso, ¿qué atleta es más rápido?
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
Solución:
a) Es más rápido el atleta que lleva el dorsal 8, ya que recorre más distancia en el mismo tiempo que el otro atleta.
b) Es más rápido el atleta que lleva el dorsal 8, ya que recorre más distancia y además en menos tiempo.
c) Es más rápido el atleta que lleva el dorsal 6, ya que recorre la misma distancia en menos tiempo.
d) Es más rápido el atleta que lleve el dorsal 6, ya que ya que recorre en la mitad de tiempo más de la mitad de la
distancia que el otro atleta.
3
En el velódromo de la figura dos parejas de ciclistas se cruzan como señala la figura. Hallar las velocidades
de todos ellos respecto al ciclista A.
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
Solución:
Consideran do positivo el sentido hacia la derecha.
VBA = 45 – 43 = 2 km / h
VCA = - 58 – 43 = - 101 km / h
VDA = - 54 – 43 = - 97 km/ h
4
En una carrera ciclista que se desarrolla por una carretera recta, a las 12 de la mañana, un ciclista A,
aventaja a otro B, en 6 km. Si el que va primero, lleva una velocidad constante de 36 km/h y el que va
segundo, va una velocidad constante de 54 km/h, ¿le habrá alcanzado a las 12 y cuarto? Si no le ha
alcanzado, ¿en qué momento y en qué instante le alcanzará?
Solución:
Consideramos el sistema de referencia la posición por la que pasa el ciclista A, a las 12 de la mañana. El sentido
positivo es el que llevan los corredores.
La ecuaciones del movimiento serán:
Ciclista A: eA = 10 t. Ya que la posición inicial le hemos hecho coincidir con el sistema de referencia y su velocidad
en m/s es 36 km/h = 10 m/s.
Ciclista B: eB = - 6 000 + 15 t. Ya que su posición en el instante inicial es, - 6 000 m respecto al sistema de
referencia elegido y su velocidad en m/s es, 54 km/h = 15 m/s.
En el momento en que el ciclista B alcance al A, las posición de ambos respecto al sistema de referencia será la
misma, por tanto:
10 t = - 6 000 + 15 t
- 5 t = - 6 000
t=
- 6 000 m
= 1 200 segundos = 20 minutos
- 5 m/s
A las 12 y cuarto, no le habrá alcanzado, le alcanzará 5 minutos más tarde. La posición respecto al sistema de
referencia, será :
eA = 10 · 1 200 = 12 000 = 12 km. O bien, eB = - 6 000 + 15 · 1 200 = 12 000 m = 12 km
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
5
El autobús que une Zaragoza con Huesca pasó por el km 26 a las 10 horas y por el km 46 a las 10:15 horas.
¿Cuál ha sido la velocidad media en dicho tramos? Exprésala en km/h y en m/s.
Si la distancia entre la dos ciudades es de 72 km, y en todo el trayecto consigue esa velocidad media, ¿qué
tiempo le costará?
Solución:
(46 - 26) km
∆e
20 k m
vm =
=
=
= 80 km/h
∆ t (10 - 10 : 15) minutos 15 / 60 h
km 1 000 m
1h
80
⋅
⋅
= 22,222... m/s
h
1 k m 3 600 s
∆e
72 km
∆t=
=
= 0,9 horas = 0,9 h ⋅ 60 minutos /hora = 54 minutos.
v m 80 km/h
6
Dos móviles A y B se mueven con movimiento uniformemente acelerado.
2
El A, en el instante t = 2 segundos, su aceleración, velocidad y posición son: a = 2 m/ s , v = 6 m/s y e = 13
m.
2
El B, en el instante t = 3 segundos, su aceleración, velocidad y posición son: a = 4 m/s , v = 10 m/s y e = -5
m.
Escribe las ecuaciones de la velocidad y de la posición respecto al tiempo de cada uno de ellos.
Solución:
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
Móvil A
Determinam os primero la velocidad en el instante t = 0 s
6- v 0
v2 − v0
→2=
→ 4= 6 - v 0 → v 0 = 6 - 4 = 2 m/ s
2
t
Por tanto, la ecuación de la velocidad será : v = 2 + 2 t
a=
Determinam os la posición en el instante t = 0
e2 = e0 + v 0 t +
a t2
2 ⋅ 22
→ 13 = e 0 + 2 ⋅ 2 +
→ 13 = e 0 + 4 + 4 →
2
2
e 0 = 13 - 8 = 5 m
Por tanto, la ecuación de la posición será : e = 5 + 2 t + t 2
Móvil B
Determinam os primero la velocidad en el instante t = 0 s
v3 − v0
10- v 0
→ −4 =
→ -12 = 10 - v 0 → v 0 = 10 + 12 = 22 m/ s
t
3
Por tanto, la ecuación de la velocidad será : v = 22 - 4 t
a=
Determinam os la posición en el instante t = 0
a t2
-4 ⋅ 3 2
→ −5 = e 0 + 22 ⋅ 3 +
→ −5 = e 0 + 66 - 18 →
2
2
e 0 = - 5 - 66 + 18 = - 53 m
e3 = e 0 + v 0 t +
Por tanto, la ecuación de la posición será : e = - 53 + 22 t - 2 t 2
7
Un coche que lleva una velocidad inicial de 2 m/s, acelera durante 10 segundos con aceleración constante
2
de 3 m/s . ¿Qué velocidad tendrá a los 10 segundos? ¿Qué posición tendrá en dicho instante, si en el
instante inicial está en la posición - 3 m? ¿Qué espacio habrá recorrido en dicho tiempo?
Solución:
v = v 0 + a t → v 10 = 2 m/s + 3 m/s 2 ⋅ 10 s = 2 + 30 = 32 m/s
3 m/s 2 (10 s) 2
a t2
→ e 10 = -3 m + 2 m/s ⋅ 10 s +
2
2
= -3 m + 20 m + 150 = 167
e 10 = e 0 + v 0 t +
e 10
∆ e ( espacio recorrido en 10 segundos) = e 10 - e 0 = 167 - ( - 3 ) = 170 m
8
Hallar la velocidad de un móvil que se mueve en línea recta y que se encuentra en la posición - 5 m
en el instante 2 segundos y en la posición 10 metros en el instante 5 segundos. ¿Qué posición tendrá
en el instante inicial y en el instante 20 segundos?
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
Solución:
∆ e e 5 - e 2 10 - ( - 5 ) 15 m
v=
=
=
=
= 5 m/s
t
5-2
3
3s
La posición inicial será :
e 2 = e 0 + 5 t → -5 = e 0 + 5 ⋅ ( 2 - 0 )
e 0 = - 5 - 10 = - 15 m
La posición en el instante 20 será :
e 20 = e 0 + 5 t → e 20 = -15+ 5 ⋅ ( 20 - 0 )= -15 + 100 = 85 m
9
Dadas las ecuaciones del movimiento de dos móviles. A) e = 10 t y B) e = 50 + 10 t .Hacer un dibujo y su
gráfica posición tiempo.
Solución:
10 Un conductor cometiendo una grave infracción de tráfico, va por una carretera a 144 km/h, en un instante
2
dado, ve un obstáculo a 75 m de distancia y frena con aceleración de 8 m/s .
a) ¿Se detendrá antes de chocar?
b) Si hubiera ido a 90 km/h, ¿qué hubiera pasado?
Solución:
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
a ) La velocidad a la que va el coche en m/s es : 144 km/h = 40 m/s.
Cuando se para el coche la velocidad será cero y la aceleració n de frenado es – 8 m/ s 2 .
El tiempo que tarda en pararse en estas condicione s es :
( 0 - 40 ) m / s
- 40 m/s
→t=
= 5s
t
- 8 m/s 2
La distancia recorrida en esos 5 segundos :
- 8 m/s 2 =
- 8 m/s 2 ⋅ (5 s) 2
= 200 - 100 = 100 m, luego chocará.
2
b) Si hubiera ido a 90 km/h = 25 m/ s.
∆e = 40 m/s ⋅ 5 s +
( 0 - 25 ) m / s
- 25 m/s
→t=
= 3,125 s
t
- 8 m/s 2
La distancia recorrida en esos 3,125 segundos :
- 8 m/s 2 =
∆e = 25 m/s ⋅ 3,125 s +
- 8 m/s 2 ⋅ ( 3,125 s) 2
= 78,125 - 39,0625 = 39,0625 m
2
luego, no chocaría.
11 Razonar sobre la veracidad o falsedad de la siguiente afirmación.
“Un cuerpo que no tiene aceleración no experimenta la acción de ninguna fuerza”.
Solución:
Si un cuerpo no tiene aceleración, no habrá fuerza resultante, porque será nula. Pero, sobre el cuerpo si que
pueden actuar fuerzas, de tal manera que la resultante sea cero. Así pues, la afirmación es falsa, aunque no haya
aceleración si que puede experimentar la acción de algunas fuerzas, si su resultante es cero.
12 En las gráficas siguientes, que representan distintos movimientos rectilíneos de un objeto, en cuáles actúa
una fuerza resultante no nula.
Solución:
La gráfica A. Indica que en cualquier instante la aceleración es constante, por lo tanto es necesario que la fuerza
resultante sea distinto de cero.
La gráfica B. Indica que la velocidad es constante en cualquier instante, por lo tanto la fuerza resultante será cero.
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
La gráfica C. Indica que en cualquier instante la posición es la misma, esto quiere decir que estará en reposo. Por
lo tanto la fuerza resultante es cero.
La gráfica D. Indica que la fuerza es constante en cada instante, por lo tanto habrá aceleración y la fuerza
resultante, lógicamente, no será cero.
14 La figura representa 6 fuerzas que actúan sobre un cuerpo. Halla la resultante y calcula su módulo.
Solución:
R 2 = 7,5 2 + 2,5 2 → R = 62,5 = 7,90 N
15 Identificar y dibujar todas las fuerzas que actúan sobre una lámpara colgada del techo y sobre la cuerda
que le sostiene del techo.
Solución:
Sobre la lámpara actúa la fuerza de atracción gravitatoria de la Tierra, peso P. Y, la fuerza que hace la cuerda
sobre la lámpara, tensión T.
Sobre la cuerda actúa la fuerza de atracción gravitatoria de la Tierra, peso P. Y, la fuerza F1, que la ejerce la
lámpara sobre la cuerda y la F2, que la ejerce el techo sobre la cuerda.
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
17 a) Una grúa sostiene un objeto de masa m kg, ¿qué fuerza hace para sostenerlo?
2
b) Una grúa levanta un objeto de masa m en kg. con una aceleración de a m/s , ¿qué fuerza tiene que hace
para levantarlo?
c) Una grúa levanta un objeto de masa m en kg con velocidad constante v m/s, ¿qué fuerza tiene que
hacer para levantarlo?
Suponemos que el rozamiento con el aire es nulo.
Solución:
ΣF = 0 → Fgrúa − P = 0 → Fgrúa = Peso.
a) Si sostiene, no se mueve, luego a = 0, por tanto:
a =
ΣF
F-P
=
→ F = m⋅ a + P
m
m
b) Si la grúa levanta al objeto con aceleración a:
c) Si la grúa levanta al objeto con velocidad constante v, la aceleración será cero y estaremos en el primer caso:
Σ F = 0 → Fgrúa − P = 0 → Fgrúa = Peso.
18 Identificar y dibujar todas las fuerzas que actúan sobre un objeto que está sobre una mesa y que es
arrastrado por la misma con una fuerza F.
Solución:
La fuerza F que le arrastra. La fuerza de atracción gravitatoria de la Tierra sobre el objeto, peso, P. La fuerza que
hace la mesa sobre el objeto, la normal, N. Y, la fuerza de rozamiento del objeto con la mesa, que es contraria al
movimiento FR .
19 ¿Qué sistemas de los siguientes tienen resultante nula?
Solución:
a) Su resultante es 7,5 N hacia la izquierda. No es nula.
b) La resultante es cero.
c) Su resultante es 4 N hacia la izquierda. No es nula.
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
d) La resultante es cero, ya que
la derecha.
R 2 = 4 2 + 4 2 → R = 32 = 5,66 N
, en sentido contrario a la fuerza de 5,66 N, hacia
21 Determinar la distancia recorrida en 3 segundos, por un bloque de madera de 30 kg de masa que está en
reposo, cuando es arrastrado por el suelo con una fuerza de 50 N, si la fuerza de rozamiento entre las dos
superficies es de 12 N.
Solución:
Σ F 50 − 12
a=
=
= 1,27 m/s 2
m
30
a t 2 1,27 m/s 2 ⋅ 3 2
∆ e=0+
=
= 5,7 m
2
2
22 ¿Cómo se halla el centro de gravedad de sólidos irregulares? Haz un dibujo.
Solución:
Se suspende el sólido de un punto de forma sucesiva en dos posiciones diferentes; se marca la vertical en cada
caso y se determina el centro de gravedad por la intersección de las dos líneas marcadas.
23 El dibujo representa las fuerzas a que está sometido un cuerpo de 200 kg sobre la superficie de la Tierra.
Halla la aceleración del cuerpo si la fuerza que actúa es: a) 1 900 N y b) 2 000 N.
Solución:
Si F = 1 900 N
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
P = 200 kg ⋅ 9,8 m/ s 2 = 1 960 N
F − P=m⋅a
a=
F − P 1 900 N − 1960 N − 60 N
=
=
= −0,3 m/s 2
m
2 00 kg
200 kg
El signo negativo indica que va hacia abajo.
Si F = 2 000 N
F − P 2000 N − 1960 N
40 N
=
=
= 0,2m/s 2
m
2 00 kg
200 kg
El signo positivo indica que va hacia arriba.
24 En un instante determinado un disco de hockey sobre hielo de 150 gramos de masa se mueve a 54 km/h
por el suelo de la pista. Si a partir de dicho instante recorre 30 metros hasta pararse. ¿Qué fuerza de
rozamiento se produce entre la superficie del disco y del hielo?
Solución:
54 km/h = 15 m/s.
v 2 − v 0 = 2 a ∆ e → 0 − ( 15 m/s ) 2 = 2 ⋅ a ⋅ 30 → a =
− 225
= − 3,75 m/s 2
60
FR = 0,150 kg ⋅ ( − 3,75 m/ s 2 ) = − 0,5625 N
25 Un bloque de hierro está sobre una mesa. Si se le aplica una fuerza de 80 N se mueve con una aceleración
2
de 2 m/s . Calcula la masa del bloque de hierro, si el rozamiento es de 25 N.
Solución:
(80 − 25) N
55 N
a=
= 2 m/s 2 → m =
= 27,5 kg
m
2 m/s 2
28 ¿Qué fuerza ha de realizar un coche de 1 500 kg de masa para que cambie su velocidad de 36 km/h a 90
km/h en 5 segundos, si el rozamiento con la carretera es de 200 N?
Solución:
36 km/h = 10 m/s y 90 km/ h = 25 m/s.
25 - 15
= 3 m/s 2
5
ΣF
F − 200
a=
→ 3 m/s 2 =
→ F = 4 500 N + 200 N = 4 700 N
m
1 500 kg
a=
29 Un montacargas de 1 000 kg de masa comienza a descender partiendo del reposo de forma que en 4
segundos alcanza la velocidad de 3 m/s.
a) Si la fuerza que hacen los cables es de 8 500 N, ¿cuál es la fuerza de rozamiento?
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
b) Si continúa descendiendo durante 6 segundos a velocidad constante, ¿qué fuerza hacen los cables?
Solución:
La situación será:
a) Considerando como negativo el sentido hacia abajo:
-3 - 0
a=
= −0,75 m/s 2
4
T + FR − P = m ⋅ a
8 500 N + FR − 1000 kg ⋅ 9,8 m/s 2 = 1000 kg ⋅ ( −0,75 ) m/s 2
FR = 9 800 N - 8 500 N - 750 N = 550 N
b) Si se mueve con velocidad constante durante 6 segundos:
a = 0 m/s 2
T + FR − P = m ⋅ a
T + 550 N - 9 800 N = 0
T = 9800 N - 550 N = 9250 N
30 Sobre un cuerpo de 300 kg de masa se aplica una fuerza de 800 N, ¿qué valor tendrá la fuerza de
rozamiento si se mueve con velocidad constante de 10 m/s? ¿Qué valor tendrá dicha fuerza si se mueve
2
con aceleración constante de 2 m/ s ?
Solución:
En el primer caso, si se mueve con velocidad constante, la aceleración es cero. Se cumplirá:
F − FR
ΣF
a=
→0=
→ F − FR = 0 → FR = 800 N
m
m
En el segundo caso, si se mueve con aceleración constante se tiene:
800 − FR
ΣF
a=
→ 2=
→ 800 − FR = 600 → FR = 200 N
m
300
31 Dos personas llevan sujeta una barra de 2 metros de larga de la que cuelga una masa de 40 kg situada a 75
cm de uno de los extremos. Calcula qué fuerza tiene que hacer cada persona.
Solución:
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
F1 + F2 = 40 ⋅ 9,8 = 392 N → F1 = 392 − F 2

F1 ⋅ 0,75 = F2 ⋅ 1,25 → 0,75 · ( 392 − F 2 ) = 1,25 ⋅ F2 → 294 − 0,75 · F2 = 1,25 · F2
2 F2 = 294 → F2 =
294
= 147 N → F1 = 392 − F2 = 392 − 147 = 245 N
2
32 Una persona transporta dos fardos 8 kg y 12 kg, que cuelgan de los extremos de una barra de metro y
medio de largo y masa despreciable. ¿Qué fuerza debe aplicar la persona y en qué punto para que la barra
permanezca horizontal? Indica claramente en que te basas par resolver el problema
Solución:
Para que permanezca en equilibrio se debe cumplir que el momento resultante sea nulo y que la suma de fuerzas
también lo sea. Por tanto:
8 · 9,8 · x = 12 · 9,8 (1,5 - x)
18
= 0,9
20
Despejando: 20 x = 18 ⇒
x=
m
El punto de apoyo se encontrará a 0,9 m del peso menor.
La persona deberá aplicar una fuerza de: 9,8 · (12 + 8) = 196 N
33 Una persona transporta dos fardos 8 kg y 12 kg, que cuelgan de los extremos de una barra de metro y
medio de largo y masa despreciable. ¿Qué fuerza debe aplicar la persona y en qué punto para que la barra
permanezca horizontal?
Solución:
Para que permanezca en equilibrio se debe cumplir que el momento resultante sea nulo y que la suma de fuerzas
también lo sea. Por tanto:
8 · 9,8 · x = 12 · 9,8 (1,5 - x)
18
= 0,9
20
Despejando: 20 x = 18 ⇒
x=
m
El punto de apoyo se encontrará a 0,9 m del peso menor.
La persona deberá aplicar una fuerza de: 9,8 · (12 + 8) = 196 N
35 Para abrir una puerta de 1 metro de ancho hay que aplicar un momento de 35 N · m. ¿Qué fuerza hay que
aplicar a 30 cm del borde de la puerta para abrirla? Y, ¿a 50 cm del borde? ¿Qué conclusión sacas?
Solución:
En el punto B, a 30 cam del borde de la puerta, estará a 70 cm del eje de giro:
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
→ 35 N · m = F · 0,70 → F =
35 N · m
= 50 N
0,70 m
En el punto A, a 50 cm del borde de la puerta, estará a 50 cm del eje de giro:
35 N · m
→ 35 N · m = F · 0,50 → F =
= 70 N
0,50 m
La conclusión es que cuanto más cerca estemos del eje de giro, mayor será la fuerza que habrá que hacer.
37 Halla la resultante de las siguientes fuerzas y su punto de aplicación.
Solución:
a) R = 30 + 70 = 100 N. Si suponemos que su punto de aplicación está a x metros de la fuerza de 70 N. Tendremos
aplicando la condición de los momentos: 70 . x = 30 ( 1 - x ). = 30 - 30 x.
30
→x=
= 0,30 m
100
. El punto de aplicación está a 30 cm de la fuerza de 70 N y a 70 cm de la fuerza de
100 x = 30
30 N.
b)R = 40 - 15 = 25 N. Si suponemos que su punto de aplicación está a x metros a la derecha de la fuerza de 40 N.
Tendremos aplicando la condición de los momentos: 40 . x = 15 (1 + x) = 15 +15 x.
15
→ 25 x = 15 → x =
= 0,6
25
45 x - 15 x = 15
. El punto de aplicación estará a 60 cm de la fuerza de 40 N y a 160 cm
de la otra fuerza.
38 Dos personas transportan una carga de peso P con una barra de 2 metros. Calcular en qué punto de la
barra habrá que colgarlo para que uno de ellas soporte el triple de peso que la otra.
Solución:
Si una soporta un peso de F, la otra soportará 3 F.
Si consideramos que el punto de aplicación está a x metros de la persona que hace el triple de fuerza tendremos,
aplicando momentos respecto a ese punto:
3 F · x = F · (2 - x)
Simplificando la sfuerzas queda: 3 x = 2 - x
2
4x = 2 → x = = 0,5 m
4
La fuerza triple está a 50 cm del punto de aplicación del peso P.
La otra fuerza estará a 150 cm del punto de aplicación del peso P.
39 Un tablón de madera de 5 m de longitud, está apoyado sobre dos caballetes. A 3,5 m de uno de los
caballetes está colocado un objeto de 6 kg. ¿Qué fuerza realiza cada uno de los caballetes para que el
sistema se encuentre en equilibrio?
Solución:
Para que permanezca en equilibrio se debe cumplir que el momento resultante sea nulo y que la suma de fuerzas
I.E.S. Menéndez Tolosa
Departamento de Física y Química
4º ESO
Actividades de refuerzo para los que tienen la primera evaluación pendiente
también lo sea. Por tanto:
F1 + F2 = Peso
F1 · l1 = F2 · l2
Despejando:
F1 =
F1 · l1 = (peso - F1) l2 ⇒
Sustituyendo:
6 · 9,8 · 3,5
F1 =
= 41,2
5
F1 · l1 = peso · l2 - F1 · l2 ⇒
peso · l 2
L
F1 (l1 + l2) = peso · l2 ⇒
N
El otro caballete ejerce una fuerza de: F2 = 6 · 9,8 - 41,2 = 17,6 N
40 Una chica ayuda a su padre a transportar un fardo de 70 kg mediante una barra de 150 cm de longitud. Si la
chica hace el triple de fuerza que el padre, calcula:
a) La fuerza que realiza cada uno para transportar el fardo.
b) ¿A qué distancia del padre deberán de colocar el fardo para que se cumpla el reparto de pesos
indicado?
Solución:
peso 70 · 9,8
=
= 171,5 N
4
4
a) Peso = F1 + F2 = F1 + 3 F1 = 4 F1 ⇒
F2 = 3 F1 = 3 · 171,5 = 514,5 N
F1 =
b) Para que permanezca en equilibrio se debe cumplir que el momento resultante sea nulo y que la suma de
fuerzas también lo sea. Por tanto:
F1 + F2 = Peso
F1 · l1 = F2 · l2
Si una fuerza tiene el valor triple de la otra se tiene:
F1 · l1 = 3 F1 · l2 ⇒ l1 = 3 l2
L = l1 + l2 = 3 l2 + l2 = 4 l2
L 1,5
=
= 0,375 m
4
4
l2 =