PROBLBMAS PROPUESTOS
Anuncio

FUERZAS CENTRIPETA Y CENTRIFUGA
PROBLBMAS PROPUESTOS
{'
un cuerpo de 1,5 kg recorre una circunferenciade 25 cm de radio con
una velocidadde 2 rps. Hallar: a) la
velocidadlineal, ó) la aceleración,c) la fuerzacentripetaaplicadasoure
J *erpo,
Sol. 3,14m/s; 39,48m/s?haciael centro; 59,43N.
1,
Un cuerpo de l0 kg recorreuna circunferenciade 1,5 m de radio con una
velocidadde 4 rps. calcular: a) la
vetocidad linear; ü) ra.acereración,c) la fuerza ce{q.10_e1q
-' --- ,"ür"'ii'"u."po.
Sol, a\ 37,7 mls; b) 941.
,j m/sr hacia el centro; c) 961',25d."pi¡*á"
.8. . Hallar la aceleracióncentrípeta de un punto situado en el ecuador. Tómese el radio ecuatorial
igual
a 6 400 km y el día sideralde 24 horas. Sol. 0,034m/sr.
a queseencuentran
som€tidas
lasmasasde r,6 kg de un reguladoq
centrífugo
.€1 l1111]"^1"::::-Til*t
en el
-rnstante
cn querecorrenunacircunferencia
,.á
de 30cm de radioa una
¿e lOórpm,l
¡ ¡.
"éloci-dad
^So/.5,39kp.
'un tren dc 100 Tm toma una curva sin peraltar de l5_0m de
-- radio
-- a una velocidadde 50 km/h. Hallar la
eje-rc.iÉasob¡,e*.1.9-Talles.
q:::
so/. itt il:-
.l"t'^"]"
-< ll,¡ Un tren toma una curva de 150m de radio a una velocidaddo50-km/h, Hallar
'- la pendienteque debelener
el peraltc para que se ejerzálá misma fuerza sobrecada rafl.
,So/. í,i¿.---
'-
- 12.. Un objeto está situado sobre una plataforma giratoria horizontal a una distancia de 60 cm de su eje. La
plataforma empieza
a moverseaumentandodÑelocidad ¿e-manera
que;i ;;.d'.i;t.
de rozamientoentre el objeto v la plataformaes 0,25,ttiuar ra uóióciáre;;61;;
""ir"i't'ü'i.uien¿o
i. ertu .n et instanteen que
el objeto comienzaa deslizar. ,So/. 2,02 radls,'
t 3. Un objeto estácolocadoen.un c¡bo o calderoque describeuna circunferenciade ó0 cm
de radio situadaen
un plano vertical.calcular la mlnima velocidadque debellevarpáá""-üiiir.Lii"
punto más alto de la trayectoria. So/. 2,43 mli,
.ii¡Éi
.r'ñ;ñ;;i
14. La cargaderoturadeun hilo de.60cm de.longitudesde 8 kp. un cuerpode0,5kp se
unea estehilo y seIe
obligaa.giraren.unplanoverticalrecorriendo
una circunférencia.
Hál.il" m¿iimaviiociáiáingúli,
quepuedegirar sin queserompael hilo, So/, 7,g/r rad/s.
"
15. En una cuerdade 50 cm de longitu-d,ñja por uno de sus extremos,se coloca en el otro un pesoque
recorre
una
circunferenciahorizontar de 30 cm dé radio. Hallar Ia,;i;;liúá;ü;i";'¡;
resultadoen rad/s y en rpm. Sol, 4,95 radls; 47,2 rpm,
h ¿"erd;;;d;s";6';i
16. Un automóvil pasapor-un bj¡dénque sepuedeconsiderarcomo un arco de circunferencia
situadoen un plano;
vertical do ¡10m de radio. Calcular la máxima velocidada la que-puiáe .iiJ"rii
io, ét para no saltar sobre
la carretera. ,Sol. 7l km/h.
t7, Sabiendoque.el cuerpohumano es capaz.desoportar una acaleraciónigual a 9 vecesla correspondiente
a la
gravedad,hallar el radio de curvaturamlnimo que deberátenerta trayect-oria
áe un-ávionqu. r"iJtr".i" aiñu"
dcspuésde haber efectuadoun bombardeo en picado moviéndoséJ"
prr"ó vertical a la veloci4ad
de 750 km/h. Sol, 492m.
""
lE.
Un piloto que pesa75 kp realizacon su aparato un rjzo_enun plano vertical a una velocidad
de 150 km/h,
cuando seencuentrabqc-a-1baig,
en la posñión más alta ¿e ra tiaveciória, i" iu.rru que eiercero¡r. ei aiiinto
del avión es de 25 kp. Hallar el radio del ¡izo.
Indícación:Fuerzacentrlpetasobreel piloto : fuerza.delasientosobreel piloto
* peso del piloto.
.SoL l33 m.
19. Un .cuerpode 45 kp de pesooscilaatado al extremode una cuerda de 6 m de longitud. Cuando pasa por
su
posiciónmás baja lleva una velocidadde l0 m/s. Hallar la tensiónJta cue¿a
eñla citadapoiióiO*'-^fo/. 121,5kp.
20'
Calcularla velocidadcon que_deberíagirar la t ierra alrededorde su eje para que el pesode una persona
en el
ecuadorfuera las 3/4 partesde su pesoreal. Tómeseel radio ecuatorÍal'de6ioo t,ir.
r (pesoreal)
^m M
(2)
l
^ mM
rtp.ro pedido):(r----
mv,2
r
siendo m : masa de_Ia persona,M : masade la tierra, w : mg : pesoreal de la persona,y : velocidad
real de la tierra en el ecuador, ,r : velocidadpcd¡dadé la tierrá
."uá¿oi. Sr¡. 3 9gb m/s.
"nil
VEL OCIDAD Y ACE LE R A C ION
A N C U LA R E S
EcUAcIoNESDEL MovTMIENToDE
RorAcIoN
análogas
A.ELERAD.. son
a lasdelmovimiento
li;al' s-e;;;i,:,i::!üifu;#;ffi.s
'NIF.RMEMENTE
vamente'! vt ! <¡t rascorrespondientes
rinear
y angurar,
respectifinales".
ín .rtu, condiciones.
vú :
vo + a t
( r ) t:( ,ü o + d t
Partiendo del reposo, vo :
vt:
( ,Jt:
g
r:y o , + ! o r
l pzr:vzo
0:o¡o f+ ! o t "
¡ozt:
0o:
at
r:
a2o i
2u0
0, con lo cual
I
ot"
T
v't:
o : l*,
qt
*2as
2as
(')zt :2g.0
PNOBLEMASRESUELTOS
1'
der mderongitud
esde25cmE¡pre.
SiTi?ffiilt; 3f*i:::: i'.:í,:il::" simpre
Solución
0 en ¡adianes_ s(longituddel arco) :_- l 0,25m
: '7 . r a d i á n
t ( t aA¡ o ) - o en grados : 1/¡ rad , __l!9¡gq9r
2' convertir a) 5 radianesen revoruciones,
á) 300
Solución
a ) Srad ,:5ra--dx "
lr ev
: 5
f" rad
};-rev
: Á,3o
revoruciones
en radianes,c) 720 rpmen rady's,
á) 3oorev : 3oo.u ,, jl
tud :
óooz¡rad
c),o# : 720#;
2a,r19
" H,, +# __
3'
H::"T'f;¿"T",u:Tl.:i,i?
deunpunto
cuarquiera
dera
lLftfiif:llJ#.":'T'j1.i:il1?:."
Solución
4'
velocidad angular o : 300 rpm^:
lOn
Velocidadlinéal v para, : i-Á'., y : rad/s es la misma para todos los puntos de Ia rueda.
o/ : l0n radls x)m : 20
m/s.
f.^iñ3'l:lfft::i:itfi:e
unarueda
de3m deradiosabiendo
queraverocidad
rinear
deunpunro
Solución
Velocidadangular,¡ : vlr:
(15 m/s)/(3m) : 5 rad/s
o 5lht revls.
L
+
ó9
VELOCÍDAD Y ACELERAC]ON ANCULARES
5.
La velocidad angular de una rueda aumenta uniformemente a partir del reposo y al cabo de 15 segundos es de 900 rpm (30 zr rad/s). Calcular la aceleración angular a, en rad/sz, y la aceleración lineal a,
en m/dfde un punto situado a una distancia de I m de su centro.
Solución
to
o : -91r
: dr :2n
6.
(30r - 0) rad/s
: 2r radisr
1 5s
-
rad/sr x I m : 2¡ m/sg
La velocidad angular de un motor que gira a I 800 rpm desciendeuniformemente hasta I 200 rpm cn
2 segundos.Hallar a) la aceleración angular del motor y ó) el número de vueltas que realiza.
Solución
o¿ : I 200 rpm :4On rad/s.
r,r¡ = I 800 rpm : 60r radis,
*1--'-L
t
a\ a :
ll
á) 0 :* (-o +
¿-
: -
: -et-=eo'Lfd/1
2s
o r ) x , : - f { 00"
lqrrad/ss.
- ul0r ) r ad/ s
x 2s : l 0 0 r r a d o
50rev.
de 5 rad/s. Calcular el númerode vucltasque da a) en
7. Un disco gira con una aceleración'constante
8 segundoipartiendodel reposo,ó) durante el tercer segundo.
Solución
a) 0 : <,rot
*
\
á ) Pa rat:2 s,
tl
O : 1t . ,
rl
:25'5 tev'
: 160rad o 16012¡
: 0 +;(5 rad/s'¿)(8s)¿
)atz
<¡ c : 5r ad/ s 2 x 2s :
+ o s ) x r:-i tl O+
l0r ad/ s ; Pir a ! : 3 s ,
x (3 -2 )s:
1 5 )ra d /s
orr: 15rad/s.
l 2,5rad osea l 2,5l 2tt: l ,99rcv'
8. La velocidadangularde un motor que gira a 900 rpm desciendeunifor¡nementchasta300 rqm efec'
tuando 50 revolüciones.Calcutara) la aceleraciónangulary D) el tiempo necesariopara realizarlas
50 revoluciones.
Solución
oo : 9(X)rpm : 30t rad/s,t¿¿: 300rpm'1 lo".u'Ol,; 0 : 50 rev : lü)r rad'
a) @f :
ó)'
6:
t'*
602+ 2ú0, . :
99-+- t'
z
Y ¡.
:
'
---.tot 29
;-o J5;
(lor ra9CI'-:-1l9ra¿A)r :
-4n rad/sr.
2 x loor rad
:
s'
-'
flo* -r' 1g*) rad/s
o se a ::'" ::'o' : tt';i T| ti ?"" :-2 ' + ,
t:
oo + o)r
:
2 x 50rev
0sTJtEiE-:
)s
VELOCIDAD Y ACELERACION ANGULARES
PROBLEMAS PROPUESTOS
- 9'
Convertir ¿) 50 revolucionese^nr4dianes,ó) 48r radianes
en revoluciones, c) 72 rpsen rad/s, d) I 500 rpm
rad,ls,e.)l1t,rad,lse1 rpm, /) 2 rad/s en grá¿crr¡r.
on
Sol a) t00r rad; b) ?A rév; c) t44r,"d7t7t'50"
rad/s; e) 210 revlmin;f) I14,6 grados/s.
10. Expresarla velocidadangllar de40 grados/sen a) rps;
ó) rpm; c) rad/s.
Sol. t/9 rps; ffi19 rpm;2¡'19 radls.1l'
una rueda gira a 480 rpm' Hallar la velocidadangular
de un punto cualquierade la misma y la velocidad
lineal de un punto situado a I m de su c€ntro
¡}r. l6n rad/s; lft m/s.
t''
gj:"til?JJIJ;'o"o
t3'
'-ll'
"ntular
de un automóvil que toma una curva de 8 m de radio
Hallar la velocidad angular de una rueda ae 2j,91_alaaio
para que la velocidad lineal de un punto
periferia seade 400-m/min. Expresarel resuláoo
de su
en rpm y en rad/s.
Sol. 800/r rpm; 26,7 rad.ls.
calcular los radianes que se desplazaen 6 horas un punto
de la s¡perficie de la tierra dcbido a la rotación
tmr',áeunlunto
der..uu¿oi
C;;;i&;"*er¿iasiáerar-:
á'ñóá,v or
*J¿tt,T1[l¿?:T".Sff:
Sol. rl2 rad; 0,465km/s.
-
a una velocidad de 4i krn/h.
15'
una rueda que gira a.razón de t 20 rpm incrementa lniformomente
su veloci<radhasta 660 rpm en 6 segundoo.
angular en iev/s'v en-rad/r', ;J;;;;lu-üi"ii"ion
rineal de un punto situado e
3É*l{j".ffleración
Sol, l rev/s¡; 2t radlsz;l,6n m/s¡,
16'
La velocidad angular d¡ u¡ disco-disminuye unif-ormemente
4 rad/s en 16 segundos,calcular la
acereraciónangurarvel número ¿e vuertasque eró-trü';;;ü;;. desde 12 a
v.
rrw'¡¡Pvr" So/' - 0,5 radlss;&ltt weltas.
-*
r7'
i8üilü li:',8:h'á'lffiniii,f,S[H,lil,tirtiendo
derreposo
suacereración
angurar
esde2orad/sr?
Sol. 125lnvueltas;45/r weltas,
lt'
I¿ velocidadangular de una.ruedaes 6,rps. Sabiendoque
su aceleraciónangular es de 4 rad/sr calcular el
nrlmcro de vueltas que dará hasta adquirii u* ;6td;liá;
il;;;;iil,rpo
que €mprearáen alcanzarra.
Sol. 160n vueltas;l0r segundós,
19'
una rueda que gira con una velocidad de 2 100rpm disminuyeésta
uniformemente
hasta 900 rpm cfectuando
B0 weltas. c¿rcurarla aeleración ancura¡ á ti.n,p"lo"",itd;---""
i
,SoL - 12,5nrad/sr; 3,2 segundos.
I
ri '
!!,'|
,h-
Capftulo 10
Fuerzascentrípeta y centrífuga
MovIMIENTo DE RorAcIoN UNIFORME es el de un cuerpoque reoorre
una circunferenciacon
una velocidadlinealde móduloconstante.
ACELERACION CENTRIPETA. Cuando un cuerpo está dotado de
un movimientode rotación
unifo.rme,ar¡nqueel módulo de su velocidades cónstante,ladirecciónvaria constantemente.
Como
la velocidades una magnitud.vectorial
y, por tanto, además¿e m¿duloposeeairecciony,rntiio,
resultaevidenteque en cualquiermovimieniode rotaciónunir*rá .iirie üna aceleracicln
ir""oi"a"
por el cambiocontinuode dirección.
La direccióndel vector aceleraciónes perpendiculara la direcciónde Ia velocidady
su sentido
es haciael centrode la circunferencia..(Si
no fuera asi, habrla uou *rnponente de aeeleración
en la
direcciónde la velocidady el módulo de la velocidadn'ose.""ii"¿¡"-r'"nria¡ir,l
El módulode esta'aceleración
centralo quesedenominaaceleracióncentrlpetaes
(vglocidqd
linealdel.cucrpo)r. _ v'
:
radio de ta trayectoriá-iiEüiái- T t
, _
Otraeexpresiones
son:
A:
Siendo
/:
y¡
-:
r
(2nrI),
:4 tT r
y
yr
A :
T:
lor)r
-:_-i-
:
(Olf
velocidad
angulardel cuerpo en rev/s,o : velocidadangul_,a¡
9n rad/s.
FUERZAS CENTRIPETA Y CENTRIFUGA' La aceleracióncentrípetade un cuerpo
da lugar a una
fuerza,(,F: ma.: mv'lr) dirigidahacia el centrode Ia trayectorialque recibeel nombie
de fuerza
cewrat o centrtDeta,
ley de Newton, a toda acciónIe correspondeuna reacciónigual y opuesta.
fuerzadirigidaensentidocontrarioalacentrípetarecibeeli'o*u'.¿.¿erzaceítrífuga La
"-.^-jtqij-li-,ercera
El valo¡ de la fuerzacentrípeta.Fes
F:
tnd - m
ul
r-
: 4ntfrm:
71
manr
T2
FUERZAS CENTRIPETA Y CENTRIFUGA
PROBLEMASRESUELTOS
l.
se hacegirar horizont"lS.l:.un cuerpo
9r J.tg atado al extremode una cuerdadescribiendouna
circunferencia
de r m de radio a una verocid"ü'.49
r revoruciones
f"r'*e,;id" riñ. ffiñilji
a) la velocidadlineal en mfs,ó) la aceteracio", 1",r"*{'lJiJii""i"o.iu.u..¿"
sobreel cuerpo,
d)lafuerza ejercidasobreél cui.po po. la cueriá,
"l e)
¿eué o.urr. rir. rompera cuerda?
Soh¡ción
a)
v :2 ¡c rf:2 n (t m )(3 /s ):6 ¡m/s.
o y : 2nrf:(ht x t)m/rev x 3rev/s: 6nm/s.
b)
c),ü
¿ - vzlr : (6r mis)ti(l m) : 35,tem/s2haciael centrode la circunferencia.
F : n/ra : m(vllr): (t/9,8utm)(36arm/sr): 3,68r,kp.
Ia fuerzacjercidapor la cuerdasobreel cuerpoesla fuerzacentrípeta.
La fuerzaejercida
poretcuerpo
sobrcla cucrdaesla fuerzacentrífuga.
gstas¿os?ue.zas
sonde
módulo(3,6gr,kp), de la mismadirección,perode sentidocontrario'La fuerzacentripetatienetaigual
áirecciJnlá'ra¿io y su sentidoeshacia
cl centrode la circunferencia'
La fuerzacentiiruiatien"eo ;i;.;-áÉ;ñ,
perosentidocontrario.
e) El cucrpoadquicrcun movimientorectilíneo,
segúnla direcciónde Ia tangente
a la circunferencia.
2. Hallar la máximavelocidada la queun automóvilpuedetomarunacurva
de 25 m de radiosobreuna
carreterahorizontalsi el coeficientede rozamientoentrelas rueoasy
ü""rirt.ru es0,30.
Solución
L¿ fuerzacentralnecesaria
qaramantener
al automóvil.en-ta
curvala proporciona
la füg¡¡;,derozamientoentrelasruedasy la carretera.Seat, el pesodel auiomovil;la máxima
fuurzacent¡aldebidaal rozamiento
esOiXlw'
Fuerza de rozamiento : fuerzacentrip€ta
0 , 3 0r y : m ( v 2 l r ) : ( w l d o z l r )
dedonde ¡ : e30s¡r y , : l/d,nlr:
: 8,59m/s.
3'
1,6J0(rS m/s,)(r5
,
",
una curvade 30m de radioestá-perattada
de maneraqueun automóvilpuedetomarlaa unavelocidad
de 15 m/s. Hallar la pendiente
db la curva.
Solución
[¿s dos fuerzasaplicadasal automóvil en
I son:
l) Su peso w : mg que actúa verticalmentehacia abajo.
2) t¿ reacción P de la carreter? que es normal
a ella.
I.a resultante de estas rlos fuerzas debe ser
91a {ue¡za horizontal en la dirección ,{C de sentido hacia el centro C de la trayectoria cirvitínea
y de módulo mflr.
rg0 :
nvzlr
mg
#%:o,..sl
y 0 : ángulo cuya tangentees 0,754:37,40.
73
FUERZAS CENTRTPETAY CENTRTFUGA
Una bola .B está unida al extremode un hilo de 24 cm de longitud cuyo otro extremoes un punto
fijo O. La bola describeuna circunferenciahorizontal de radio CB como indica la figura. Hallar la
velocidadde la bola sabiendoqueel hilo forma un ángulode 30ocon la vertical.
Solucién
Fieura la)
Las dos fuerzasaplicadasa la bola son:
(a) Su peso, mg.
(b) La tensión en el hilo.
La resultante(>F) de estas dos fuerzas
debeseruna fuérzahorizontal en la direcciónBC
y de sentido hacia C con un módulo igual al
de la fuerza centrlpeta, mv2fr, n*esaria para
mantgner a la bola en su trayectoria circular.
Radio BC :24 cm x sen30o: 12 cm
tg 30o: -^"J'
mg
dedonde, :Vrs tgSO': l6,tñ
0J774: 0,824m/s.
r r,8
-/."
Otro método.VéaseFig.(ó)
La componenteverticalde la tensiónequilibrael pesode labola(mS). La componente,horizontal
de la
tcnsiónes igualal módulode la fuerzacentrípeta(mv'lr). A partir de aquí sesiguecomoen el primermétodo,
5.
Un cuerpo de 2 kp unido a una cuerda describeuna circunferencia
vertical de 3 m de radio. Hallar a) la mínima velocidad yr que debe
tener el cuerpo en la posición más alta para que la cuerda permanezcatirante, á) la mínima velocidad vDen la posición más baja para
que la cuerda siga tirante cuando el cuerpo se dirige hacia la posi
ción superior de la circunfer€ncia, c) la tensión ?¡¿ en la cuerda
cuando el cuerpo está en la posición inferior de la circunferencia
moviéndosea la velocidad critica v¿.
vt
Solucién
a) Cuando el cuerpo se encuentraen la posición superior, actúan sobre
él dos fuerzas: I ) el peso,2) la tensión7¿.La resultantede ambasdebe
ser la fuerza centrípetanecesariapara manteneral cuerpo en su trayectoriacircular.
Fuerzacentrípeta: tensiónen la cúerda * pesodel cuerpo
m ' r tffr :T t*m E
La cuerda se afloja cuando Il : 0, es decir, cuando mv¡gfr : 0 |
+ ms o ,, : ] y ' gr :
Yr , s t 3 : 5, 42m ¡ s .
á) Al pasarde la posicióninferiora la superior,el cuerposeelevaa una altura 2¡.
E. C. en la posicióninferior : E. C. en la posiciónsuperior+ E. P. en la posiciónsuperior
1"1". : :mvtz
| (ng) (2r')
"mvu"
i**n
Si v¡ es menor que VW,
r, será menor quey¡l
Fuerza centrípeta :
c)
mv¡2fr :
Por tanto,
T t:
r 2mgr,y yo:lfw : n,t^tr.
m ( va 2 lr ) ¡ m g :
y la cuerda pierde su tirantezen Ia posición superior.
tensión en la cuerda Ta -
peso del cuerpo
mg
m ( 5 sr lr ) * mg:
mg (5 + l ) :
6w :6(2
kp)':
l 2 kp.
C qp ítulo
'
Velocidad y aceleración angulares
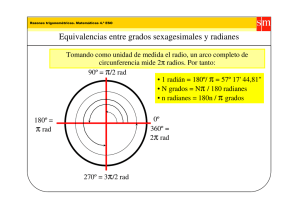
EL DESPLAZAMIENTO ANGULAR
(rev) y radianes (rad).
se expresa,normalmente, en grados ('), vueltas o revoluciones
Un radián es el ángulo subtendidoen el centro de un círculo por un arco cuya longitud es igual a
radio. Como la longitud de la circúnferencia: 2n x radio, el desplazamientoangular corresponclientea I revolución es de 2n radianes.
: 360"- 2nradianes,I radián:
I revolución
#
:
rl.uj;
: 5..,3o
angularen revoluciones.
angularen radianes: 2n x desplazamiento
Desplazamiento
un númeroadimensional.
La medidade un ángutoen radianes(f=t#!,*).,
VELOCIDAD ANGULAR (o) de un cuerpoen movimientode rotaciónen tornoa un ejesedefinecomo
la variación del desplazamientoangular que experimentaen la unidad de tiempo. Se expresaen
(rps) o rev/min(rpm).
rad/s,
'Si o bien, en grados/s,rev/s
su velocidad
un cuerpose desplazaun ángulode 0 radianesen un tiempode r segundos,
angularmediat¿(rad/s)sedefinepor la relación:
: O
r,r(rad/s):
' - tiempo(segundos)invertido en el desplazamiento t
Como I rev/s: 2traófs, to(rad/s):2n
que se denominahertz (Hz).
en rev/sy
x rev/s:2rrl, siendo/ la frecuencia
ACELERACION ANGULAR (a) de un cuerpoen movimientode rotaciónen torno a un ejeesla varia'
ción que experimentasu velocidadangutaren la unidad de tiempo. Se expresaen radianespor
cadasegundo(rad/s'?).
segundo
resulta:
de to. a c,l,rad/sen f segundos,
Si la velocidádangularde un cuerpovariauniformemente
a '(fa O /S=t:
'
RELACION
variación de la velocidad angular (rad/s)
tiempo (s) invertido en la variación
--
ENTRE LAS MAGNITUDES
LINEALES
(ü, -
ú)o
t
Y ANGULARES
s :
0r
s -- longitud del arco, en metros, centimetros,etc.
a
dr
4
v: @r ; =;:Íi:i.'JTillllifllil.-Á:i:
:
:
etc.
aceleración lineal, en m/sr,
donde 0 está en radianes,r,ren rad/s y a en rad/sr.
67