Guía Problemas Resueltos - Unidad 7 versión Alfa2
Anuncio

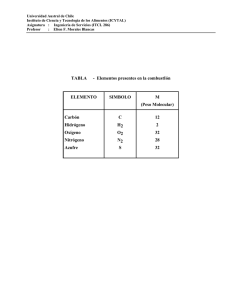
UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas UNIDAD 7: Cinética de Reacción y Procesos Térmicos GUIA DE PROBLEMAS RESUELTOS 1. Con los siguientes datos experimentales que describen la pérdida de caroteno en zanahorias a 135 °C: a) Tiempo (min.) Caroteno retenido (%) 2,0 93 6,0 88 9,0 79 15,0 66 22,0 51 ¿Que orden de reacción siguen los datos experimentales? Solución: De acuerdo a los datos entregados en la tabla, la concentración de caroteno retenido es entregada como concentración relativa (A/A0), lo cual nos da como referente que corresponde a una reacción de orden uno, por lo tanto no es factible realizar un análisis para determinar el orden de la reacción. b) Determine la constante de velocidad de reacción (K). Solución: La constante de velocidad de la reacción, representa la constante de proporcionalidad entre la velocidad de reacción y la concentración del reactante. Realizando una regresión lineal la constate de velocidad esta dada por la pendiente de la recta, por tanto como la reacción es de Primer Orden: ln [ A ] = ln [ A0 ] − Kt y = a − bx Ecuación de la recta Relación Lineal UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ♣ De acuerdo a este análisis los datos obtenidos son los siguientes: b = -0.0308 min.-1 a = 4.6331 %caroteno retenido r2 = 0.9855 K=b K = 0.0308 (min-1) UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 2. Determinar la constante de velocidad de reacción (K) para la descripción de la velocidad de destrucción de esporas bacterianas a 115 °C a partir de los siguientes datos experimentales: Tiempo (min.) Concentración (esporas/g) 0 106 5 2.8 x 105 10 7.8 x 104 15 2.2 x 104 20 6.1 x 103 25 1.7 x 103 Solución: Se procede de igual forma que el ejercicio anterior, primero será necesario determinar el orden de la reacción para luego con la pendiente conocer la constate de velocidad. 2.1 Cinética de reacción de Orden Cero: [A ] = [A0 ] − Kt y = a − bx ♣ Ecuación de la recta Relación Lineal De acuerdo a este análisis los datos obtenidos son los siguientes: b = -33538.285 (esporas/g) / min. a = 650528.571 (esporas/g) r2 = 0.6441 2.2 Cinética de reacción de Primer orden: ln [ A ] = ln [ A0 ] − Kt y = a − bx ♣ Ecuación de la recta Relación Lineal De acuerdo a este análisis los datos obtenidos son los siguientes: UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas b = -0.25503 min.-1 a = 13.8172 (esporas/g) r2 = 0.99999 2.3 Cinética de reacción de Segundo orden: 1 1 = + Kt A A0 y = a − bx ♣ Ecuación de la recta Relación Lineal De acuerdo a este análisis los datos obtenidos son los siguientes: b = 1.9713 x 10 -5 (esporas/g) -1/min. a = -1.105 x 10 -4 (espora/g) r2 = 0.64298 Respuesta: La reacción es de Primer Orden; su constate de velocidad (K) es: ln [ A ] = ln [ A0 ] − Kt b = -0.25503 min.-1 y = a − bx a = 13.8172 (esporas/g) 2 r = 0.99999 K=-b K = 0.255 min−1 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 3. La influencia de la temperatura sobre la velocidad de destrucción de las esporas bacterianas se ilustra mediante los siguientes datos experimentales. T (K) 1/T(K-1) ln K 378.15 0.00264 -7.40205 380.15 0.00263 -6.77673 383.15 0.00261 386.15 389.15 Temperatura (°C) S -1 105 0.00061 107 0.00114 -6.11025 110 0.00222 0.00259 -5.4919 113 0.00412 0.00257 -4.88224 116 0.00758 a) Determinar la energía de activación involucrada en la descripción de esta reacción. Se entiende por Energía de Activación, aquella cantidad de energía suministrada a los reactantes para que la reacción química se inicie. La influencia de la temperatura sobre la velocidad de destrucción de las esporas bacterianas se comporta como una reacción de primer orden esto de acuerdo a la unidad que presenta la constante de velocidad S-1; por lo tanto la regresión lineal se debe realizar con los siguientes datos. K = B×e − Ea RT ⇒ Ecuación de Arrehenius. K = Constante de velocidad de reacción. B = Constante de velocidad en la medida que reacción tiende al infinito. Ea = Energía de activación. R = Constante de gases ideales. T = Temperatura. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ln K = ln B − ⇓ ⇓ y = a b= Y = ax + b b = −33074 .392 Ea ⎛ 1 ⎞ ×⎜ ⎟ R ⎝T ⎠ ⇓ + a = 80 .1538 S 1 bx Ea R r 2 = 0.99518 R = 8314 . 34J / molKg°K Ea = b × R Ea = 33074.392 × 8314.32 Ea = 274991740.4 J / mol Ea = 274991 .74 KJ / mol b) Calcule Q10 y Z Valor de Q10 : Q 10 = e Q 10 = e Ea ⎤ ⎡ 10 R ⎢⎣ T 2 × T 1 ⎥⎦ [ 33074 . 392 10 389 . 5 × 378 . 15 ] Q 10 = 9 . 4646 Por lo tanto, el número de veces que la velocidad de reacción cambia con una variación de la temperatura de 10 º C es 9,46. Valor de Z : Z = 10 × ln 10 ln Q10 Z = 10× ln10 ln 9.4646 Z = 10.24 K Lo cual indica que cada 10,24 K la velocidad de inactivación microbiana varía en un ciclo logarítmico. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 4. Durante la degradación del ácido ascórbico en un jugo de naranja en conserva se obtuvo los siguientes resultados: Temperatura K (°C) (M/día) 29.4 0.00112 37.8 0.0026 46.1 0.0087 Nota: M = Molar a) Calcular la Energía de Activación Ea. El orden de reacción es la suma de los exponentes de los términos de concentración de los reactantes, por lo tanto podemos ver que la degradación del ácido ascórbico en jugo de naranja se comporta como una reacción de orden cero dadas las unidades de K. Como se realizo anteriormente se debe hacer una regresión lineal con la relación: T (K) 1/T(K-1) ln K 302.55 0.0033 -6.7944 310.95 0.00322 -5.9522 319.25 0.00313 -4.7444 Los valores obtenidos de acuerdo a la regresión lineal son los siguientes: Y = ax + b b = −11829 .309 ( M / dias ) a = 32 .2345 M r 2 = 0.9853 1 ln K v sT UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas K = B×e − Ea ln K = ln B − ⇓ ⇓ y = a b= RT Ea ⎛ 1 ⎞ ×⎜ ⎟ R ⎝T ⎠ ⇓ + bx Ea R R = 8 .31434KJ / molKg°K Ea = b × R Ea = 11829.309 × 8.31432 Ea = 98352.897 KJ / mol b) Calcule el valor de Q10 y Z . Valor de Q10 : Para calcular el valor de Q10 , se debe estimar un valor de K ajustado con él se puede usar cualquiera de las temperaturas del problema y no habrán variaciones en al cambio de el número de veces en que cambia la velocidad de reacción cada 10°C. El valor del K ajustado se determina de acuerdo a la ecuación obtenida con la regresión lineal de los datos. Q 10 = e Q 10 = e Ea ⎤ ⎡ 10 R ⎢⎣ T 2 × T 1 ⎥⎦ [ 11829 . 309 10 319 . 25 × 302 . 55 ] Q 10 = 3 . 403 Por lo tanto, el número de veces que la velocidad de reacción cambia con una variación de la temperatura de 10 º C es 3.4. Valor de Z: Para determinar el valor de Z a distintas temperaturas se requiere que la velocidad de reacción sea de Primer Orden, lo cual en este caso no ocurre como se planteo en el comienzo de este ejerció, que esta UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas reacción corresponde a Orden Cero. Por lo tanto no se cuenta con los datos apropiados para determinar el valor Z. c) Determinar el valor de D a 33°C y 42°C. Para determinar el valor D a distintas temperaturas se requiere que la velocidad de reacción sea de Primer Orden; igual condición que se exige para determinar el valor Z, por lo tanto para esta reacción no es posible determinar los valores D y Z, por las razones explicadas con anterioridad. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 5. Un estudio cinético indicó que la destrucción de lisina a diferentes temperaturas de calentamiento sigue una reacción de segundo orden y se obtuvo los siguientes datos experimentales: Temperatura K (°C) (M-1/s) 130 1.54x10-4 160 13.16x10-4 a) Calcule Ea, Q10 y Z . Valor de Ea: Regresión lineal con la relación: 1 ln K v sT T (K) 1/T(K-1) ln K 403.15 0.00248 -8.7785 433.15 0.00231 -6.6331 Los valores obtenidos de acuerdo a la regresión lineal son los siguientes: Y = ax + b b = −12487 .971( K ) a = 22 .197 M −1 / s r2 =1 K = B×e − Ea ln K = ln B − ⇓ ⇓ y = a RT Ea ⎛ 1 ⎞ ×⎜ ⎟ R ⎝T ⎠ ⇓ + bx UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas b= Ea R R = 8 .31434KJ / molKg°K Ea = b × R Ea = 12487.971× 8.31432 Ea = 103829.2368 KJ / mol Valor de Q10 : Q 10 = e Q 10 = e Ea ⎤ ⎡ 10 R ⎣⎢ T 2 × T 1 ⎥⎦ [ 12487 . 971 10 433 . 15 × 403 . 15 ] Q 10 = 2 . 0444 Por lo tanto, el número de veces que la velocidad de reacción cambia con una variación de la temperatura de 10 º C es 2. Valor de Z : Para calcular Z se requiere que los datos cumplan con una velocidad de reacción de primer orden y esto no se cumple, por lo tanto no se puede calcular. b) Determinar el valor de K a 145°C. Para determinar el valor de K utilizamos la ecuación de Arrehenius de forma linealizada: K = B×e − Ea RT ⇒ Ea ⎛ 1 ⎞ ×⎜ ⎟ ln K = ln B − R ⎝T ⎠ ⇓ ⇓ y = a ⇓ + 145°C = 418.15 K bx Ecuación de Arrehenius. Y = ax + b b = −12487 .971( K ) a = 22 .197 M −1 / s r2 =1 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 1 ⎛ ⎞ ln K = 22 . 197 + ( − 12487 . 971 ) × ⎜ ⎟ 418 . 15 ⎝ ⎠ ln K = − 7 . 6678 K = 4.676 x10 −4 M −1 / s UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 6. El valor de F a 121,1°C equivalente a una inactivación del 99,999 % de una cepa del C. botulinum es 1,2 min. Calcular el valor D0 de este microorganismo. N0 N S = log N 0 = Nº de microorganismos viables en el tiempo cero. N = Nº de microorganismos viables en el tiempo t. S = Nº de ciclos logarítmicos. Se asume que la población inicial de C. botulinum es 1. N 0 = 0.99999 N = 1 − 0.99999 = 0.00001 S = log 0.99999 = 4.999 ≈ 5 0.00001 F121.1°C = 1.2 min D0 = F0 S D0 = 1.2 = 0.24 min 5 Por lo tanto, cada 0,24 min. la población microbiana se reduce en un factor de 10 o en un ciclo logarítmico. (Reducción decimal) UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 7. El valor esterilizante de un proceso (F0) ha sido igual a 2,88 min. Si cada lata contiene 10 esporas de un microorganismo con un D0 = 1,5 min., calcular la probabilidad de esporular de este microorganismo. Asuma que el valor F0 fue calculado utilizando el mismo valor de Z para el microorganismo. F0 = 2.88 min N 0 = 10 esporas D0 = 1.5 min Considerando las siguientes ecuaciones: S= F0 = S × D0 F0 D0 S = log N0 N Desarrollo: F0 N = log 0 D0 N 2.88 min 10 = log 1.5 min N 10 ⎛ 2.88 ⎞ ⎟ ⎜ ⎝ 1.5 ⎠ = 10 X 10 N 83.1764 = 10 N N = 0.1202 Existe la probabilidad de que esporulen 0.12 esporas por tarro ya que la carga inicial son 10. O bien que esporulen 12 latas de un conjunto de 100 latas. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 8. La carga de esporas más probable en un alimento enlatado es 100. Calcule un valor de F0 para que un proceso térmico tenga una probabilidad de esporulamiento de 1 en 100.000. Asuma un valor de D0=1,5 min. Si bajo las mismas condiciones el C. botulinum tipo B tiene un D0=0.2 min., ¿el valor F0 calculado satisfacería el tratamiento mínimo 12D para el C. botulinum? Asuma una carga de esporas iniciales de 1 por tarro para el C. botulinum. Datos: N = 1 × 10 −5 esporas N 0 = 100 esporas D0 = 1.5 min ♣ Calculo del valor F0 para que tenga la probabilidad de esporular 10-5 S = log N0 N ⇒ S = log 100 1 × 10 −5 = 7 F0 = S × D0 F0 = 7 × 1.5 min = 10.5 min F0 = 10.5 min ♣ F0 Para C. botulinum tipo B D0 = 0.2 min N0 = 1 S = 12 F0 = 12D0 ⇒ F0 = 12 × 0.2 min F0 = 2.4 min El F0 = 10.5 min , calculado para (a). es mayor al satisfacer el proceso mínimo 12D. F0 mínimo para C. botulinum B requerido para UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 9. Se calculó un proceso tal que la probabilidad de esporular de un microorganismo con un valor Do = 1 min es 1 en 100.000 a partir de una carga de esporas iniciales de 100. Para verificar este proceso, se realiza una inoculación a una conserva. Calcular el nivel de inóculo de un microorganismo con un valor de Do=1,5 min. que debe utilizarse en 100 tarros tal que la tasa de esporulamiento de 5 tarros sea equivalente en letalidad al proceso calculado. Datos: N = 1 × 10 −5 probabilidad de esporular N 0 = 100 carga inicial D0 = 1 min Primer paso a seguir el calcular el valor de F0: N ⎤ ⎡ F0 = D0 × ⎢log 0 ⎥ N⎦ ⎣ 100 ⎤ ⎡ F0 = 1× ⎢log −5 ⎣ 1× 10 ⎥⎦ F0 = 7 Determinación del número de microorganismos inoculados: N0 = ? N= − 5 = 0.05 100 F0 = (log N − log N 0 ) D0 log N 0 = F0 + log N D0 log N 0 = 7 + log 0.05 1.5 ⇒ F0 = (log N 0 − log N ) D0 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas log N 0 = 3.36564 10 X N 0 = 10 3.36564 N 0 = 2320.81 ≈ 2321 Por lo tanto los microorganismos inoculados fueron 2321. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 10. En una incidencia de esporulamiento se encontró que el microorganismo esporulado aislado tiene un valor D0 de 1,35 min. Se desea que la probabilidad de esporulamiento de este microorganismo sea 1 en 100.000. Las cargas de esporas iniciales fueron generalmente del orden de 10 por tarro. Calcular el F0 requerido para este proceso para alcanzar la probabilidad de esporulamiento deseada. Si una conserva se inocula con FS1518 con un nivel de inoculación de 5x105 esporas. Los tarros contienen 200 g de producto, ¿Cuál será el recuento de esporas en el producto procesado tal que la letalidad recibida por los contenidos de los tarros será equivalente a aquella alcanzada por el proceso deseado para eliminar el esporulamiento de los microorganismos aislados? D0 del FS1518 es 2,7 min. Datos: N = 1 × 10 −5 esporas N 0 = 10 carga inicial D0 = 1.35 min Calculo de F0req: − F0 req D0 = (log N − log N 0 ) ⇒ F0 req = (log N − log N 0 ) × D0 F0 req = (log1× 10 −5 − log10) × 1.35 F0 req = 8.1min Se plantea en el problema la condición: Frequerido = F proceso Bajo esta premisa se determina el valor de N: Datos de FS1516: N = 5 × 10 −5 esporas D0 = 2.7 min F0 req D0 = (log N 0 − log N ) UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas log N 0 − log N = log 5 × 10 5 − 10 ⎛ 5 8.1 ⎞ ⎜ log 5×10 − ⎟ 2.7 ⎠ ⎝ F0 D0 8.1 = log N 10 X 2.7 =N N = 500 Por lo tanto se encuentran 500 esporas por tarro (200g), lo cual es equivalente a decir 2.5 (esporas/gr. de producto) UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 11. Los siguientes datos fueron registrados en una prueba de penetración de calor sobre un alimento enlatado para la determinación del proceso térmico: Tiempo (min.) Temp.(°F) Tiempo (min.) Temp. (°F) 0 128 35 245 3 128 40 243 5 139 45 240 10 188 50 235 15 209 55 185 20 229 60 145 25 238 65 120 30 242 70 104 La temperatura de procesamiento fue 250 °F y el tiempo come-up (CUT) fue 2 min. La temperatura del agua de enfriamiento fue 60 °F. Calcular: a) Los valores de fh, fc, jh y jc. Datos: TR = 250°F CUT = 2min. TW = 60°F CUT = Tiempo en que se demora en alcanzar la temperatura de trabajo. Para determinar los valores que se solicitan se debe identificar adecuadamente las etapas de calentamiento y enfriamiento, la grafica de los datos permite una visión bastante amplia de la penetración de calor sobre el alimento enlatado. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 300 Temperatura °F 250 200 150 100 50 0 0 10 20 30 40 50 60 70 80 Tiempo (min) FIGURA 1: Perfil de temperatura para el alimento enlatado. La sección de calentamiento permite calcular los valores de fh y jh, por lo tanto se deben tomar los valores comprendidos entre el tiempo 0 y 35 min. Cuadro 1: Datos correspondientes a la etapa de calentamiento. Paso 1 ♣ Cálculo de 0Corregido: 0Corregido = 0.58 x CUT 0Corregido = 0.58 x 2 min. 0Corregido = 1.16 min. Tiempo (min.) Temp.(°F) 0 128 3 128 5 139 10 188 15 209 20 229 25 238 30 242 35 245 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 2,5 Todos los datos Parte recta 2,0 Lineal (Parte recta) Log (TR-T) 1,5 1,0 0,5 y = -0,0448x + 2,2436 R2 = 0,9968 0,0 0 5 10 15 20 25 30 35 40 Tiem po (m in) Figura 2: Curva de calentamiento. “Ecuación de la Curva de calentamiento”. log( T R − T ) = log( T R − T pih ) − Y a 1 ×t fh bx TR = Temperatura de procesamiento. Tpih = Temperatura pseudoinicial de calentamiento fh = El tiempo que transcurre cuando la porción recta de la curva disminuyendo en un ciclo logarítmico. Se realiza una regresión lineal con los datos de la etapa de calentamiento correspondientes a la parte recta ingresando los datos de la siguiente forma: log( T R − T ) v s De a cuerdo a la regresión lineal se obtienen los siguientes datos: b = −0.044813 a = 2.24357367 r 2 = 0.9968 Paso 2. ♣ Cálculo de fh: t UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas − 1 =b fh fh = ⇒ − 1 = −0.044813 fh 1 = 22.31 0.044813 fh = 22 . 31 min . Luego de 22.31 minutos, la porción recta de la curva pase un ciclo logarítmico. ♣ Calculo de jh: jh = TR − T pih TR − Tih Para determinar el factor de retraso jh; es necesario conocer con anterioridad la temperatura pseudoinicial de calentamiento Tpih. Un factor a considerar es el tomar en cuenta el cero corregido para determinar de manera adecuada el valor de la temperatura seudonicial, ya que el intercepto entregado con la regresión lineal es respecto al tiempo cero. Figura 3: Intercepto de acuerdo al cero corregido. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas Y = 2.24357367 − 0.044813X Y = 2.24357367 − 0.044813× 1.16 Y = 2.19159 ≈ 2.19 log(TR − Tpih ) = 2.19 log(250 − Tpih ) = 2.19 TR = 250°F 10 X (250 − T pih ) = 10 2.19 250 − T pih = 155 T pih = 250 − 155 T pih = 94.5°F Cálculo de jh jh = jh = TR − T pih TR − Tih 250 − 94.5 = 1.27 250 − 128 jh = 1.27 Paso 3. fc y jc corresponde a la etapa de enfriamiento, la cual esta formada por solo aquellos datos que forman parte recta de la curva de enfriamiento; descartando los de la fase Lag UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 2,90 Todos los datos Parte recta Lineal (Parte recta) 2,70 Log (T-Tw) 2,50 2,30 2,10 1,90 1,70 y = -0,0304x + 3,7597 2 R = 0,9988 1,50 0 10 20 30 40 50 60 70 80 Tiempo (min) Figura 4: Curva de enfriamiento. ♣ Ecuación de al curva de enfriamiento: log( T − T w ) = log( T pic − T w ) − Y a 1 ×t fc bx Tpic = Temperatura pseudoinicial de enfriamiento (°F) Para realizar la regresión lineal se ingresan los datos de la siguiente forma: log( T − T w ) v De a cuerdo a la regresión lineal se obtienen los siguientes datos: b = −0.0303585 a = 3.75970959 r 2 = 0.998 Paso 4. ♣ Cálculo de fc: 1 =b fc ⇒ 1 = 0.0303585 fc s t UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas fc = 1 = 32.94 0.0303585 fc = 32 . 94 min . Luego de 32.94 minutos, la porción recta de la curva de enfriamiento pase en un ciclo logarítmico. Figura 5: Identificación de la temperatura seudoinicial de enfriamiento. ♣ Cálculo de jc: jc = T pic − TW Tic − TW Para determinar el factor de retraso jc; es necesario conocer con anterioridad la temperatura pseudoinicial de enfriamiento Tpic. Y = 3.75970959 − 0.0303585X Y = 3.75970959 − 0.0303585 × 50 Y = 2.24178 TW = 60°F UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas log(Tpic − 60) = 2.24178 10 X (T pic − 60) = 10 2.24178 T pic = 60 + 10 2.24178 T pic = 60 + 174.5 T pic = 234.5°F Cálculo de jc jc = jc = T pic − TW Tic − TW 234.5 − 60 = 0.943 245 − 60 jc = 0.943 b) El F0 del proceso por los métodos gráficos (original y mejorado), de Stumbo y de Hayakawa. 1.- MÉTODO GRAFICO MEJORADO: Datos: Z = 18°F Tref = 250°F Paso 1. Etapa de calentamiento; se desarrolla por método de trapecio (i = impar), para lo cual los datos ser deben trabajar del siguiente modo: L= 1 (Tref −T ) / Z 10 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ♣ Tiempo Temp. (min.) °F 0 L Y 128 1.6681x10-7 Y0 3 128 1.6681x10-7 Y1 5 139 6.8129x10-7 Y2 10 188 3.5938x10-4 Y3 15 209 5.2749x10-3 Y4 20 229 0.0681 Y5 25 238 0.2154 Y6 30 242 0.3594 Y7 35 245 0.5275 Y8 i= i= t Δt 35 =7 5 Cálculo de F0h, por método del Trapecio. ⎤ ⎡ Δx ⎤ ⎡ Δx ⎤ ⎤ ⎡ Δx ⎤ ⎡ Δx ⎡ Δx F0 h = ⎢ (Y0 + Y1 )⎥ + ⎢ (Y1 + Y2 )⎥ + ⎢ (Y2 + Y3 )⎥ + ⎢ (Y3 + Y4 )⎥ + ⎢ (Y4 + Y5 )⎥ + ⎦ ⎣2 ⎦ ⎣ 2 ⎦ ⎣ 2 ⎦ ⎣ 2 ⎦ ⎣2 ⎡ Δx ⎤ ⎤ ⎡ Δx ⎤ ⎡ Δx ⎢ 2 (Y5 + Y6 )⎥ + ⎢ 2 (Y6 + Y7 )⎥ + ⎢ 2 (Y7 + Y8 )⎥ ⎣ ⎦ ⎦ ⎣ ⎦ ⎣ ⎡3 ⎤ ⎡2 ⎤ F0 h = ⎢ (1.6681x10 − 7 + 1.6681x10 − 7 )⎥ + ⎢ (1.6681x10 − 7 + 6.8129 x10 − 7 )⎥ + ⎣2 ⎦ ⎣2 ⎦ ⎡5 ⎡5 −7 −4 ⎤ −4 −3 ⎤ ⎢ 2 (6.8129 x10 + 3.5938 x10 )⎥ + ⎢ 2 (3.5938 x10 + 5.2749 x10 )⎥ + ⎣ ⎦ ⎣ ⎦ ⎡5 ⎤ ⎡5 ⎤ ⎡5 ⎤ −3 ⎢ 2 (5.2749 x10 + 0.0681)⎥ + ⎢ 2 (0.0681 + 0.2154)⎥ + ⎢ 2 (0.2154 + 0.3594)⎥ + ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ 5 ⎡ ⎤ ⎢ 2 (0.3594 + 0.5275) ⎥ = 4.5619 ⎣ ⎦ F0 h = 4.6 min . El valor de F0h del proceso para etapa de calentamiento mediante de el método de trapecio es de 4.6 minutos. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas Paso 2. Etapa de enfriamiento; se desarrolla por Método Simpson. Para lo cual los datos se tratar del siguiente modo: Se considera esta desde el punto en que en la tabla de datos se observa un descenso en la temperatura. ♣ Tiempo Temp. (min.) °F L 35 0 245 0.5275 L0 40 5 243 0.4084 L1 45 10 240 0.2782 L2 50 15 235 0.1467 L3 -4 55 20 185 2.45x10 L4 60 25 145 1.47x10-6 L5 65 30 120 5.99x10-8 L6 70 35 104 7.74x10-9 L7 i= i= t Δt 70 = 14 5 Cálculo de F0c, por método de Simpson. Foc = Foc ΔT [L0 + 4 L1 + 2 L2 + 4 L3 + 2 L4 + 4 L5 + 2L6 + L7 ] 3 −4 5 ⎡ 0 . 5275 + 4 × 0 . 4084 + 2 × 0 . 2782 + 4 × 0 . 1467 + 2 × 2 . 45 x10 ⎤ = ⎢ ⎥ 3 ⎣⎢ + 4 × 1 . 47 x10 − 6 + 2 × 5 . 99 x10 − 8 + 7 . 74 x10 − 9 ⎦⎥ Foc = 5.5079 ≈ 5.5 min El valor de Foc del proceso para la etapa de enfriamiento mediante el método de trapecio es de 5.5 minutos. Paso 3. ♣ Cálculo de F0 del Proceso: F0 = F0Calentame int o + F0enfriamiento F0 = (4.6 + 5.5) min . F0 = 10.1min . UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas Por lo tanto el F0 del Proceso para el método grafico mejorado es de 10.1minutos. 2.- METODO GRAFICO ORIGINAL (LETALIDAD) Paso 1. Etapa de calentamiento; se desarrolla por método de trapecio (i = impar), para lo cual los datos ser deben trabajar del siguiente modo: (Treq −Tt ) Z TDT = F(Tref ) ×10 L 1 = TDT F0 req Supuestos: F0req = 5 min. Z = 18 °F ♣ Calculo de L0h, por método del Trapecio. Tiempo Temp. (min.) °F 0 3 5 10 L 1 TDT 128 1.6681x10-7 3.3362 x10-8 Y0 128 -7 -8 Y1 139 188 1.6681x10 -7 6.8129x10 -4 3.5938x10 Y 3.3361x10 -7 Y2 -5 Y3 -3 1.3626x10 7.1876x10 15 209 5.2749x10-3 1.0549x10 Y4 20 229 0.0681 0.01362 Y5 25 238 0.2154 0.0431 Y6 30 242 0.3594 0.0718 Y7 35 245 0.5275 0.1055 Y8 i= i= t Δt 35 =7 5 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ⎤ ⎡ Δx ⎤ ⎡ Δx ⎤ ⎡ Δx ⎤ ⎡ Δx ⎤ ⎡ Δx L0 h = ⎢ (Y0 + Y1 )⎥ + ⎢ (Y1 + Y2 )⎥ + ⎢ (Y2 + Y3 )⎥ + ⎢ (Y3 + Y4 )⎥ + ⎢ (Y4 + Y5 )⎥ + ⎣2 ⎦ ⎣2 ⎦ ⎣ 2 ⎦ ⎣ 2 ⎦ ⎣ 2 ⎦ ⎡ Δx ⎤ ⎤ ⎡ Δx ⎤ ⎡ Δx ⎢ 2 (Y5 + Y6 )⎥ + ⎢ 2 (Y6 + Y7 )⎥ + ⎢ 2 (Y7 + Y8 )⎥ ⎣ ⎦ ⎦ ⎣ ⎦ ⎣ ⎡3 ⎤ ⎡2 ⎤ L0 h = ⎢ (3.3362 x10 −8 + 3.3362 x10 −8 )⎥ + ⎢ (3.3362 x10 −8 + 1.3626 x10 − 7 )⎥ + ⎣2 ⎦ ⎣2 ⎦ ⎡5 ⎡5 −7 −5 ⎤ −5 −3 ⎤ ⎢ 2 (1.3626 x10 + 7.1876 x10 )⎥ + ⎢ 2 (7.1876 x10 + 1.0549 x10 )⎥ + ⎣ ⎦ ⎣ ⎦ ⎡5 ⎤ ⎡5 ⎤ ⎡5 ⎤ −3 ⎢ 2 (1.0549 x10 + 0.01362)⎥ + ⎢ 2 (0.01362 + 0.0431)⎥ + ⎢ 2 (0.0431 + 0.0718)⎥ + ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎡5 ⎤ ⎢ 2 (0.0718 + 0.1055)⎥ = 0.9119 ⎣ ⎦ F0 h = 0.9. Las unidades de letalidad para la etapa de calentamiento según el método del trapecio es 0.9. Paso 2. Etapa de enfriamiento; se desarrolla por Método Simpson. Para lo cual los datos se tratar del siguiente modo: Se considera esta desde el punto en que en la tabla de datos se observa un descenso en la temperatura. ♣ Tiempo Temp. (min.) °F 35 L 1 TDT 245 0.5275 0.1055 L0 40 243 0.4084 0.0817 L1 45 240 0.2782 0.0556 L2 50 235 0.1467 0.0293 L3 55 185 2.45x10-4 4.9x10-5 L4 60 145 1.47x10-6 2.94x10-7 L5 65 120 5.99x10-8 1.198x10-8 L6 70 104 7.74x10-9 1.548x10-9 L7 Cálculo de L0c, por método de Simpson. i= i= t Δt 70 = 14 5 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas Loc = L oc 5 = 3 ΔT [L0 + 4 L1 + 2 L2 + 4 L3 + 2 L4 + 4 L5 + 2 L6 + L7 ] 3 ⎡ 0 . 1055 + 4 × 0 . 0817 + 2 × 0 . 0556 + 4 × 0 . 0293 + 2 × 4 . 9 x10 − 5 ⎤ ⎢ ⎥ −7 −8 −9 ⎢⎣ + 4 × 2 . 94 x10 + 2 × 1 . 198 x10 + 1 . 548 x10 ⎥⎦ Loc = 1.1013 ≈ 1.1 Las unidades de letalidad Loc , para la etapa de enfriamiento es 1.1. Paso 3. ♣ Cálculo de L0 del Proceso: L0 = L0Calentameint o + L0enfriamiento L0 = (0.9119 + 1.1013) L0 = 2.0132 ≈ 2 Las unidades de letalidad total para el método grafico original son 2. Paso 4. ♣ Cálculo de F0 del Proceso; por medio del método grafico original. Letalidad = F0 Freq Freq = 5 min . F0 = Letalidad × Freq F0 = 2.0132 × 5 min . F0 = 10.066 ≈ 10.1 min . Así el F0 del proceso para el método gráfico original es de 10.1min. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 3.- MÉTODOS FORMULA Paso 1. Método de Stumbo ( fh ≈ fc) : De acuerdo a los valores obtenidos en la letra a). fh = fc = 22.31 min → Condición del método Stumbo. Datos: Tih = 128° F fh = 22.31 min jh = 1.27 TR = 250°F CUT = 2 min Tiempo total de calentamiento = 35 min. Tref = 250° F Se tiene como objetivo el calcular el valor de F0 , por el método de Stumbo por lo tanto utilizaremos la siguiente ecuación: F0 = U × 10 (TR −Tref ) Z Primero se debe conocer el valor de U; el cual se determinas en la tabla de valores fh ♣ U V/s g g = j h × I h × 10 − B Cálculo de I h del proceso. I h = T R − T ih I h = ( 250 − 128 )° F I h = 122 ° F ♣ Cálculo de t operador : t operador = ttotal − CUT t operador = 35 − 2 t operador = 33 min . ♣ Cálculo de B (tiempo del proceso): B = t operador + 0.42 × CUT fh → UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas B = 33 min . + 0.42 × 2 min . B = 33.84 min . ♣ Cálculo de g: g = j h × I h × 10 − B fh g = 1.27 ×122 ×10 −33.84 22.31 g = 4.71° F ♣ Cálculo de U: Se utiliza la tabla de valores para procesos térmicas dado por el método de Stumbo, para ello con el valor de g = 4.71 y Z = 18°F (valor supuesto); como este valor no aparece explicito en la tabla se debe interpolar en valores cercanos. fh U g Δg Δj 4.0 4.41 1.34 5.0 5.40 1.59 Antes de interpolar es necesario corregir el valor de g , del siguiente modo: g i = g i =1 + ( j c − 1) × (Δg Δj c ) ♣ Para g = 4.41 6 f h U = 4.0 6 Δg Δj = 1.34 Si jc = 0.943 (calculado en (a)) g j =0.943 = 4.41 + (0.943 − 1) × 1.34 = 4.33 ♣ Para g = 5.4 6 f h U = 5.0 6 Δg Δj = 1.59 Si jc = 0.943 (calculado en (a)) g j =0.943 = 5.4 + (0.943 − 1) ×1.59 = 5.31 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas Ahora con los nuevos valores de g; se interpola de la siguiente manera en la tabla de Stumbo: fh U g 4.0 4.33 X = 4.387 4.71 5.0 5.31 Por lo tanto el valor a utilizar en los cálculos de U son g = 4.71 ♣ 6 f h U = 4.387 Valor de U: U= fh ( f h / U ) g =4.71 U= 22.31 min . = 5.08 4.387 U = 5.08 min . ♣ Cálculo de F0 del proceso: F0 = U × 10 (TR −Tref ) Z F0 = 5.08 × 10(250 − 250 ) 18 F0 = 5.08 min . Así el F0 del proceso, por el método de Stumbo es de 5.08 min. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas Paso 2. Método Hayakawa ( fh ≠ fc ) : a) Etapa de calentamiento. Según la tabla de Hayakawa para determinar la letalidad de la porción de calentamiento del proceso se deben calcular los siguientes parámetros. Datos: Z = 18°F f h = 22.31 min. ♣ Cálculo de KS: KS = Z 20 KS = 18 = 0.9 20 ♣ Cálculo de g K S : g 4.71 = KS 0 .9 g = 5.23 KS ♣ Cálculo de U calentamiento : Interpolando en la tabla de Hayakawa para calentamiento: g KS Uh = 0.1976 fh fh U 6.0 0.1652 5.23 0.1976 7.0 0.2073 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas U h = 0.1976 × f h U h = 0.1976 × 22.31min . U h = 4.408 min . b) Etapa de enfriamiento. Datos: Tw = 60 °F f c = 32.9 min . ♣ Calculo de Tg: g = TR − T g Tg = TR − g Tg = (250 − 4.71)°F Tg = 245.29°F ♣ Cálculo de I c : I c = T g − Tc Tc = Tw I c = (245 − 60)° F I c = 185° F ♣ Cálculo de I c / K S : I C 185 = = 205.55 K S 0.9 De acuerdo al valor de I c / K S , se utiliza la tabla que posea los siguientes rangos: (200 < I c / K S ≤ 400) con j c = 0.943 . ♣ Cálculo de U c' : Se deben realizar tres interpolaciones de acuerdo a la tabla seleccionada para crear la columna correspondiente a jc = 0.943. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas (U 0.943 1.00 210 0.01159 0.01673 0.01878 Por lo tanto: U c? = 0.0171 fc U c' = 0.0171× f c U c' = 0.0171× 32.9 min . U c' = 0.563 min . Uc : U c = U c' × 10 − g Z U c = 0.563 × 10 −4.71 18 U c = 0.308 min . ♣ Cálculo de ) 0.80 205 Cálculo de / f c paraJ C Ic / KS 205.55 ♣ ? c U Total : U Total = U h + U c U Total = (4.408 + 0.308) min . U Total = 4.716 min . 0.0171 0.01189 0.01716 0.01926 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ♣ Cálculo de F 0 del Proceso: U Total = F0 × 10 ( 250−TR ) Z F0 = F0 = U Total 10( 250−TR ) Z 4.716 10( 250−250) 18 F0 = 4.716 min . c) El tiempo de procesamiento y el tiempo total para un F0 requerido de 5 min. y un F240 = 16 min. y Z = 16 °F. Utilizar los métodos fórmula de Stumbo y Hayakawa. Paso 1. Datos. Método de Stumbo: F0req= 5 min. Z = 18 °F. Tref = 250 °F ♣ Cálculo de U del Proceso: U = F0 ref × 10 U = 5 min . × 10( 250−250) 18 U = 5 min . ♣ Cálculo de f h U i : fh 22.31 = U 5 min . (Tref − TR ) Z Z =18 °F; y para UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas fh = 4.462 U ♣ Valor que se debe buscar en la tabla. Cálculo de g : El valor de g no se puede calcular a partir de la formula g = j h × I h × 10 −B fh ya que el valor de B no se conoce y es necesario para responder la pregunta; por lo tanto se determinar el valor de g a través de la tabla de valores interpolando entre los valores de f h U mas cercanos. ♣ fh U g Δg / Δj 4.0 4.41 1.34 5.0 5.4 1.59 Correcciones de los valores de g: g i = g i =1 + ( j c − 1) × (Δg Δj c ) Para g = 4.41 gi=0.943 = 4.41 + (0.943 − 1) × 1.34 gi=0.943 = 4.333 Para g = 5.40 gi=0.943 = 5.40 + (0.943 − 1) ×1.59 g i=0.943 = 5.309 ♣ La tabla con los valores corregidos de g es la siguiente , en la cual se interpolara: fh U g 4.0 4.333 4.462 4.784 5.0 5.309 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas Por lo tanto el valor de g calculado es: g= 4.784 ♣ Cálculo de B: ⎛ j × Ih B = f h × log⎜⎜ h ⎝ g ⎞ ⎟⎟ ⎠ ⎛ 1.27 × 122 ⎞ B = 22.31min× log⎜ ⎟ ⎝ 4.784 ⎠ B = 33.69 min . El tiempo de proceso calculado con método de Stumbo es de 33.69 min. ♣ Cálculo de t total : t total = B + 0.58 × CUT t total = 33.69 min+ 0.58 × 2 min t total = 34.86 min El tiempo total calculado con método de Stumbo es de 34.86 min. Paso 2. Hayakawa Etapa de calentamiento: ♣ Cálculo de Ks : Ks = ♣ Z 20 → Ks = 18 = 0.9 20 Cálculo de g / Ks : Se debe asumir un valor de g, ya que la tabla de Hayakawa no tiene de forma independiente el valor de; “g” esta en función de g / Ks por lo tanto, se deberá estimar un valor de g. Para esto se tiene como referencia que cuando “g” aumenta F0 disminuye; por lo tanto como se sabe que para un g = 5.46, el F0 del proceso es igual a 3.95, por lo tanto se debe asumir un valor de “g” tal que cumpla con F0req = 5min. Se asume: UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas g = 4.0 4 .0 g = = 4.44 K s 0 .9 ♣ Cálculo de U calentamiento : Interpolando en la tabla de Hayakawa para calentamiento: Uh = 0.2397 fh U h = f h × 0.2397 U h = 22.31 min . × 0.2397 U h = 5.347 ≈ 5.35 min . ♣ Cálculo de F0h: Foh = Foh = Uh 10 (250 −TR ) Z 5.35min 10 (250− 250 ) 18 Foh = 5.35min. Etapa de Enfriamiento. ♣ Cálculo de Tg. g = TR − T g Tg = TR − g g Ks Uh fh 5.00 0.2073 4.44 0.2397 4.00 0.2652 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas Tg = (250 − 4.0)º F Tg = 246º F ♣ Cálculo de Ic. Tc = Tw I c = T g − Tc I c = (246 − 60)º F I c = 186º F ♣ Cálculo de I c / K s . I c 186 = K s 0.9 Ic = 206.66 Ks ♣ ' Cálculo de U c . Se debe hacer una interpolación doble primero para el valor de jc=0.943, y luego determinar el valor de (U ' c ) / f c quedando la tabla del siguiente modo: (U ' c / f c Paraj c ) Ic / KS 0.80 0.943 1.00 210 0.01159 0.0167 0.01878 206.66 205 U c' = 0.01705 fc U c' = 0.01705 × 32.9 min . U c' = 0.56 min . 0.01705 0.01189 0.0171 0.01926 jc = 0.943 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ♣ Cálculo de Uc. U c = U c' × 10 − g Z U c = 0.56 × 10 −4.0 18 U c = 0.336 U c = 0.336 min . ♣ Cálculo de U total : U total = U h + U c U total = (5.35 + 0.336) min U total = 5.68 min . ♣ Cálculo de F0 del Proceso. U total = F0 × 10 (250−TR ) Z F0 = U total 10 (250 − 250 ) 18 F0 = 5.68 min ♣ F0 > Freq ; el valor de g se considera como adecuado. Cálculo de B tiempo de proceso. ⎛ j × jh ⎞ ⎟⎟ B = f h × log⎜⎜ h ⎝ g ⎠ ⎛ 1.27 × 122 ⎞ B = 22.31 min× log⎜ ⎟ ⎝ 4.0 ⎠ B = 35.43 min . El tiempo de proceso según Hayakawa es de 35.43min. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ♣ Cálculo de t total t total = B + 0.58 × CUT ttotal = 35.43 min + 0.58 × 2 min ttotal = 36.59 min . Tiempo total según Hayakawa es de 36.59min. Paso 3. Método Stumbo. Datos: F240ºF: 16 min. Z = 16 º F Tref =240 º F ♣ Cálculo de U del Proceso: U = F0 ref × 10 (Tref − TR ) Z U = 16min. × 10( 240−250) 16 U = 3.79min. ♣ Cálculo de f h U i : fh 22.31 = U 3.794 min . fh = 5.88 U ♣ Valor que se debe buscar en la tabla. Cálculo de g : El valor f h U no se encuentra en la tabla de Stumbo, por lo tanto es necesario interpolar para encontrar el valor de “g” correspondiente. Además primeramente es necesario encontrar los valor de “g” y Δg Δj con un Z = 16 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas Z f U h g Δg Δj 14 5.0 4.02 1.32 16 5.0 4.71 1.455 18 5.0 5.40 1.59 14 6.0 4.63 1.56 16 6.0 5.44 1.69 18 6.0 6.25 1.82 Por lo tanto con la tabla que se trabajara será la siguiente: Z = 16 f ♣ g Δg Δj 5.0 4.71 1.455 6.0 5.44 1.69 U h Correcciones de los valores de g: g i = g i =1 + ( j c − 1) × (Δg Δj c ) Para g = 4.71 gi=0.943 = 4.71 + (0.943 − 1) ×1.455 g i =0.943 = 4.627 Para g = 5.44 gi=0.943 = 5.44 + (0.943 − 1) × 1.69 gi=0.943 = 5.344 ♣ La tabla con los valores corregidos de “g” es la siguiente , en la cual se interpolara: UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas fh U g 5.0 4.627 5.88 5.258 6.0 5.344 Por lo tanto el valor de g calculado es: g= 5.258 ♣ Cálculo de B: ⎛ j × Ih B = f h × log⎜⎜ h ⎝ g ⎞ ⎟⎟ ⎠ ⎛ 1.27 × 122 ⎞ B = 22.31 min× log⎜ ⎟ ⎝ 5.258 ⎠ B = 32.78 min . El tiempo de proceso calculado con método de Stumbo es de 32.78 min. ♣ Cálculo de t total : t total = B + 0.58 × CUT t total = 32.78 min+ 0.58 × 2 min t total = 33.94 min El tiempo total calculado con método de Stumbo es de 33.94 min. Paso 4. Hayakawa Etapa de calentamiento: ♣ Cálculo de Ks : Ks = Z 20 → Ks = 16 = 0.8 20 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ♣ Cálculo de g / Ks : Se asume: g = 4.0 4 .0 g = =5 K s 0 .8 ♣ Cálculo de U calentamiento : Interpolando en la tabla de Hayakawa para calentamiento: g Ks Uh fh 5.00 0.2073 Uh = 0.2073 fh U h = f h × 0.2073 U h = 22.31 min . × 0.2073 U h = 4.625 min . Etapa de Enfriamiento. ♣ Cálculo de Tg. g = TR − T g Tg = TR − g Tg = (250 − 4.0)º F Tg = 246º F ♣ Cálculo de Ic. I c = T g − Tc I c = (246 − 60)º F I c = 186º F Tc = Tw = 60º F UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ♣ Cálculo de I c / K s . I c 186 = K s 0.8 Ic = 232.5 Ks ♣ ' Cálculo de U c . Se debe hacer una interpolación doble primero para el valor de jc=0.943, y luego determinar el valor de (U ' c ) / f c quedando la tabla del siguiente modo: (U ) 0.80 0.943 1.00 235 0.01031 0.0149 0.01669 230 U c' = 0.01505 fc U c' = 0.01505 × 32.9 min . U c' = 0.495 min . Cálculo de Uc. U c = U c' × 10 − g Z U c = 0.495 × 10 −4.0 16 U c = 0.278 U c = 0.278 min . ♣ / f c Paraj c Ic / KS 232.5 ♣ ' c Cálculo de U total : 0.01505 0.01054 0.0152 0.01707 jc=0.943 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas U total = U h + U c U total = (4.625 + 0.278) min U total = 4.903 min . ♣ Cálculo de F0 del Proceso. U total = F0 × 10 (240−TR ) Z F0 = 4.903 min . 10 (240 − 250 ) 16 F0 = 20.67 min ♣ F0 > Freq , es adecuado el valor de g = 4.0. Cálculo de B tiempo de proceso. ⎛ j × jh ⎞ ⎟⎟ B = f h × log⎜⎜ h ⎝ g ⎠ ⎛ 1.27 × 122 ⎞ B = 22.31 min× log⎜ ⎟ = 35.43 ⎝ 4.0 ⎠ B = 35.43 min . El tiempo de proceso según Hayakawa es de 35.43min. ♣ Cálculo de t total t total = B + 0.58 × CUT ttotal = 35.43 min + 0.58 × 2 min ttotal = 36.59 min . Tiempo total según Hayakawa es de 36.59min. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas 12.- a) Un alimento en un tarro de 303 x 407 tiene un fh = 8 min. y un jh = jc = 0,9. Para una temperatura inicial de 80°F y una temperatura de retorta de 250 °F, calcular el tiempo de proceso B. Usar un F0 = 6 min. y Z = 18 °F. Utilizar el método de Stumbo y Hayakawa. b) El producto en la parte (a) es procesado en una retorta estacionaria (por Bach), y toma 5 minutos para alcanzar la temperatura de trabajo de 250°F desde que se abre la llave de vapor. ¿Cuantos minutos después de abrir la llave de vapor debe cerrarse? c) En una de las retortas (autoclaves) donde se procesaron los enlatados, hubo un cambio en las condiciones de proceso y la carta de registro de la temperatura de retorta mostró lo siguiente: Tiempo (min.) Temperatura de Autoclave (ºF) 0 70 3 210 10 210 Salto repentino desde 210 ºF a los 10 min. 15 250 16 Cierre la llave de vapor y abertura de la llave de agua. Cuales el F0 de este proceso? La temperatura inicial del producto enlatado fue de 80ºF. NOTA: Utilizar el método de Stumbo y Hayakawa. Paso 1. Método Stumbo. Datos. f h = 8 min . j h = j c = 0 .9 Z = 18 º F T ih = 80 º F T R = 250 º F CUT = 10 min . F 0 = 6 min . ♣ Cálculo de I h . I h = T R − T ih I h = 250 − 80 I h = 170 º F ♣ Cálculo de U del Proceso: UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas U = F0 ref × 10 (Tref −Tg ) Z U = 6min. × 10( 250−250) 18 U = 6min. ♣ Cálculo de f h U i : fh 8 = U 6min. fh = 1.33 U ♣ Valor que se debe buscar en la tabla. Cálculo de g : El valor f no se encuentra en la tabla de Stumbo, por lo tanto es necesario interpolar para U h encontrar el valor de “g” correspondiente con un Z = 16 f h U 1.0 g Δg Δj 0.523 0.192 1.93 0.68 1.33 2.0 ♣ Correcciones de los valores de g: g i = g i =1 + ( j c − 1) × (Δg Δj c ) Para g = 0.523 g i =0.9 = 0.523 + (0.9 − 1) × 0.192 g i =0.9 = 0.504 Para g = 1.93 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas g i =0.9 = 1.93 + (0.9 − 1) × 0.68 g i =0.9 = 1.862 ♣ La tabla con los valores corregidos de “g” es la siguiente , en la cual se interpolara: fh U g 1.0 0.504 1.33 0.9521 2.0 1.862 Por lo tanto el valor de g calculado es: g= 0.9521 ♣ Cálculo de B: ⎛ j × Ih B = f h × log⎜⎜ h ⎝ g ⎞ ⎟⎟ ⎠ ⎛ 0.9 × 170 ⎞ B = 8min × log⎜ ⎟ ⎝ 0.9521 ⎠ B = 17.65min. El tiempo de proceso calculado con método de Stumbo es de 17.65 min. Paso 2. Hayakawa Etapa de calentamiento: ♣ Cálculo de Ks : Ks = Z 20 → Ks = 18 = 0.9 20 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ♣ Cálculo de g / Ks : g 0.9521 = = 1.058 ≈ 1.06 0 .9 Ks ♣ Cálculo de U calentamiento : Interpolando en la tabla de Hayakawa para calentamiento: g Ks Uh fh 1.50 0.5839 1.06 0.7184 1.00 0.7367 Uh = 0.7184 fh U h = f h × 0.7184 U h = 8min. × 0.7184 U h = 5.75min. ♣ Cálculo de F0h: Foh = Foh = Uh 10 (250 −TR ) Z 5.75min = 5.75min. 10 (250− 250 ) 18 Foh = 5.75min. Etapa de Enfriamiento. Datos T w= 60 ºF f c = 8min. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ♣ Cálculo de Tg. g = TR − T g Tg = TR − g Tg = (250 − 0.9521)º F Tg = 249.05º F ♣ Cálculo de Ic. Tc = Tw = 60º F I c = T g − Tc I c = (249.05 − 60)º F I c = 189.05º F ♣ Cálculo de I c / K s . I c 189.05 = Ks 0.9 Ic = 210.05 ≈ 210 Ks ♣ ' Cálculo de U c . ( ' Se debe hacer una interpolación para determinar el valor de U c / f c (U ' c / f c Paraj c ) en la tabla. ) Ic / KS 0.80 0.98 1.00 210 0.01159 0.01518 0.01878 jc=0.9 U c' = 0.01518 fc U c' = 0.01518 × 8min. U c' = 0.1214min. ≈ 0.12min. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ♣ Cálculo de Uc. U c = U c' × 10 − g Z U c = 0.12 × 10 −0.9521 18 U c = 0.106 ≈ 0.11 U c = 0.11min. ♣ Cálculo de U total : U total = U h + U c U total = (5.75 + 0.11)min U total = 5.86min. ♣ Cálculo de F0 del Proceso. U total = F0 × 10 (250−TR ) Z F0 = 5.86 min. 10 (250 − 250 ) 18 F0 = 5.86min ♣ Cálculo de B tiempo de proceso. ⎛ j × Ih B = f h × log⎜⎜ h ⎝ g ⎞ ⎟⎟ ⎠ ⎛ 0.9 × 170 ⎞ B = 8min × log⎜ ⎟ = 17.648min. ⎝ 0.9521 ⎠ B = 17.65min. El tiempo de proceso según Hayakawa es de 17.65min. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas b) Datos. CUT = 5min. B = 17.65 min. t operador = B − 0.42 × CUT t operador = 17.65 − 0.42 × 5min. t operador = 15.55min. c) Para poder calcular el Fo de este proceso es necesario realizarlo en dos etapas, ya que no se puede considerar como un solo proceso Primera etapa: CUT = 3 min., TR = 210 °F, toperador = 7 min. Segunda etapa: CUT = 10 min., TR = 250 °F, toperador = 6 min. Por lo tanto se debe hacer por partes. Para el caso del método de Stumbo se debe considerar calentamiento y enfriamiento de manera conjunta, por lo cual solo se toma la segunda etapa. Para el método de Hayakawa se considera calentamiento y enfriamiento por separado, por lo tanto, se puede realizar el cálculo para todo el proceso pero de forma separada, de la siguiente manera: Uh1 (considera la etapa de calentamiento 1) Uh2 (considera la etapa de calentamiento 2) Uc (considera el enfriamiento) UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas Paso 1. Método Stumbo. Datos: f h = f c = 5min. j h = 0.9 CUT = 10min. Tih = 80º F Tref = 250º F t operador = 6min. ♣ Cálculo de I h . I h = T R − T ih I h = 250 − 80 I h = 170 º F ♣ Cálculo de B. B = t operador + 0.42 × CUT B = (6 + 0.42 × 10 )min. B = 10.2min. UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ♣ Cálculo de t total t total = t operador + CUT t total = 6 min + 10 min t total = 16min . ♣ Cálculo de g. g = jh × I h ×10−TR fh g = 0.9 × 170 º F × 10 −10.2 5 g = 1 . 395 º F ♣ Cálculo de U. Interpolando: U= U= ♣ fh fh U 5min. = 3.08min. 1.62 Cálculo de F0. F0 = U × 10 (TR − 250 ) Z F0 = 3.09 × 10 (250−250 ) 18 F0 = 3.09min. fh /U g 1.0 0.523 1.62 1.395 2.0 1.93 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas Paso 2. Hayakawa Etapa de calentamiento: Para el calentamiento 1 no se calculara un F0 ya que la temperatura de retorta es de 250°F y a esta T° no hay mayor letalidad. Por lo tanto, solo se calculara F0 para el calentamiento 2. Asumiendo el valor de g calculado en (a) g = 1.395 min. ♣ Cálculo de Ks : Ks = ♣ Z 20 → Ks = 18 = 0.9 20 Cálculo de g / Ks : g 1.395 = = 1.55 0.9 Ks ♣ Cálculo de U calentamiento : Interpolando en la tabla de Hayakawa para calentamiento: Uh = 0.574 fh U h = f h × 0.574 U h = 5min. × 0.574 U h = 2.84min. ♣ Cálculo de F0h: Foh = Uh 10 (250 −TR ) Z g Ks Uh fh 2.00 0.4816 1.55 0.574 1.50 0.5839 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas Foh = 2.87 min = 2.87 min. 10 (250− 250 ) 18 Foh = 2.87 min. Etapa de Enfriamiento. Para determinar letalidad en la porción de enfriamiento del proceso se deben calcular los siguientes parámetros. Datos T w= 60 ºF f c = 5min. jc = 0.9 ♣ Cálculo de Tg. g = TR − T g Tg = TR − g Tg = (250 − 1.395)º F Tg = 248.6º F ♣ Cálculo de Ic. I c = T g − Tc I c = (248.6 − 60)º F I c = 188.6º F ♣ Cálculo de I c / K s . I c 188.6 = Ks 0.9 Ic = 209.56 Ks Tc = Tw = 60º F UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas ♣ ' Cálculo de U c . ( ' Se debe hacer una interpolación para determinar el valor de U c / f c (U 0.9 1.00 210 0.01159 0.01518 0.01878 0.01521 0.01189 U c' = 0.01521 fc U c' = 0.01521 × 5min. U c' = 0.07605min. ≈ 0.08min. Cálculo de Uc. U c = U c' × 10 − g Z U c = 0.08 × 10 −1.395 18 U c = 0.0669 ≈ 0.07 U c = 0.07min. Cálculo de U total : U total = U h + U c U total = (2.87 + 0.07)min U total = 2.94min. ♣ ) 0.80 205 ♣ / f c Paraj c Ic / KS 209.56 ♣ ' c ) en la tabla. Cálculo de F0 del Proceso. U total = F0 × 10 (250−TR ) Z 0.01558 0.01926 jc=0.9 UNIVERSIDAD AUSTRAL DE CHILE INSTITUTO E CIENCIA Y TECNOLOGIA / DE LOS ALIMENTOS (ICYTAL) ASIGNATURA : Ingeniería de Procesos III (ITCL 234) PROFESOR : Elton F. Morales Blancas F0 = 2.94min. 10 (250 − 250 ) 18 F0 = 2.94min