La campana de Gauss

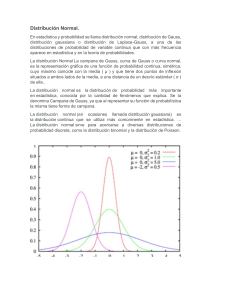
La herramienta que todos
quieren: La Campana de
Gauss
ESCRITO POR: JOSE CARLOS GÁMEZ+MARZO 14, 2013 14 COMENTARIOS EN MATEMÁTICAS PARA REDES
SOCIALES
En este post vamos a hablar, del que es quizás, el resultado matemático más utilizado en
otras disciplinas: La Distribución Normal.
A muchos no os sonará por ese nombre, pero si decimos que hablar de Distribución Normal es
lo mismo que hablar de la Campana de Gauss, la cosa seguro que cambia.
El estudio sobre la distribución normal lo comenzó de Moivre a finales del siglo XVIII, aunque
toma el nombre de Carl Friedrich Gauss (considerado por la comunidad científica como el
matemático más prolífico de la historia), puesto que fue el primero que aplicó esta
herramienta, concretamente, en el análisis de datos astronómicos.
La Campana de Gauss es una función con tres partes diferenciadas: la zona media, en
cuyo centro se encuentra el valor de la media y es cóncava; y losdos extremos, que
son convexos y tienden a aproximarse al “eje x”.
La importancia de esta distribución, reside en que aparece constantemente en la
naturaleza o en la actitud de las personas, puesto que representa el comportamiento de
1
los valores de ciertas variables, cuyas variaciones son influenciadas por fenómenos
aleatorios.
Este hecho, se debe a la forma acampanada y simétrica que posee su función de
densidad, que hace que los elementos más comunes son los que están más centrados,
mientras que los más raros se sitúan en los extremos.
Veamos un ejemplo para entender bien este concepto. Si el “eje x” refleja la altura de todos
los ciudadanos de
España
mayores
de
edad,
y
el “eje
y” el
número
de personas correspondiente a cada medida, está claro que habrá menos personas que
midan 1,98 ó 1,52, que personas que midan 1,75.
Pues esa idea es lo que nos muestra la distribución normal, que en muchos casos, cuando un
resultado es aleatorio, los valores tienden a concentrarse en el centro.
¿En qué disciplinas se suele utilizar? Campos tan distintos como la biología, psicología,
sociología, farmacia o economía, son solo algunos ejemplos de áreas en las que su estudio
es fundamental.
Como ejemplo ilustrativo, veamos una imagen que representa mediante una Campana de
Gauss los datos de los niveles de inteligencia en la población.
¿Y qué aplicación le podemos dar en un entorno digital? En redes sociales como Twitter,
Facebook o Pinterest, los usuarios dan constantemente sus opiniones sobre gustos, datos
personales o intereses. Podemos comprobar que esta cantidad enorme de datos,
en muchos casos, sigue una distribución normal.
Además, una de las ventajas que tiene este estudio, es que si probamos que una muestra
representativa de la población se aproxima respecto a un dato a nuestra distribución, la
población total (tomando como población los elementos de estudio) tenderá a cumplirla,
2
por lo que nos podemos ahorrar el análisis de gran cantidad de datos. Ello conlleva a que
de manera muy sencilla, a partir de la muestra poblacional, podemos aproximar de
manera muy exacta la cantidad de individuos que pertenecen a un cierto intervalo de la
variable que estamos estudiando. Como ejemplo, podríamos aproximar las personas en
España que miden entre 1,70 y 1,80 m ó el número de personas que tienen un pie mayor a la
talla 46, sin necesidad de tener los datos de todos.
La interpretación de esos valores, puede resultar muy interesante para empresas
de publicidad o de venta de productos, puesto que realizando un estudio, pueden conocer
el número de clientes potenciales antes de lanzar una campaña, y así, decidir si les
interesa publicitarse en ese medio o no.
3