1. Estudiar existencia y simplificar: (i) yx ay ax yx ay ax - - + + -
Anuncio
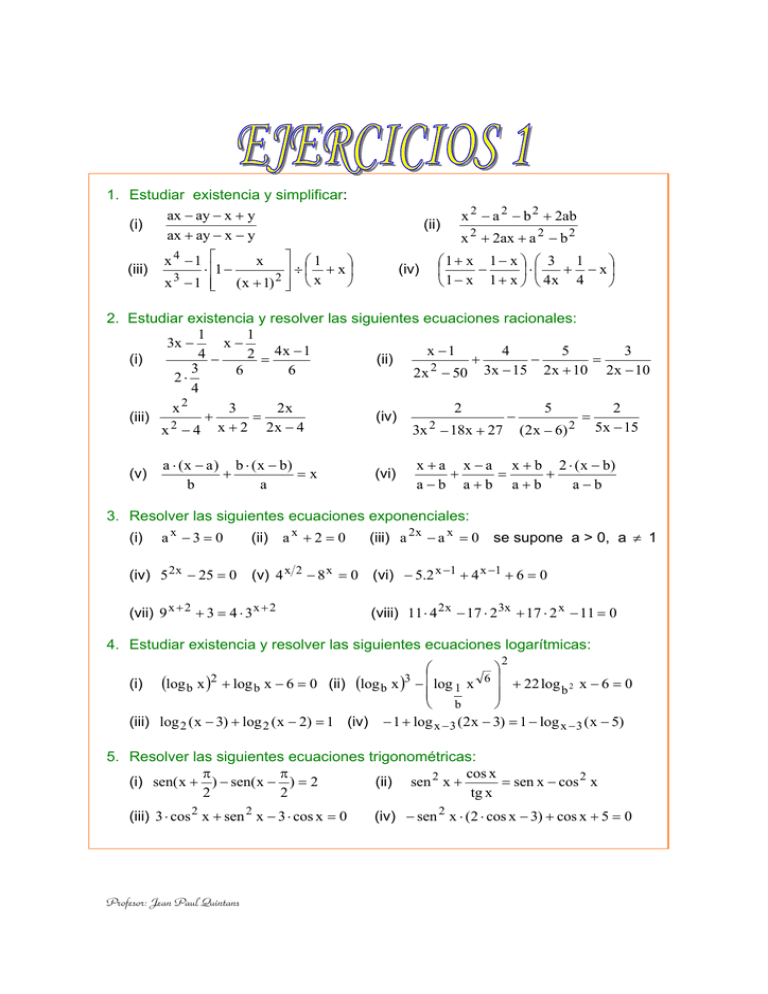
1. Estudiar existencia y simplificar: (i) ax − ay − x + y ax + ay − x − y (iii) x4 −1 x 1 ⋅ 1 − ÷ + x 3 2 x − 1 ( x + 1) x (ii) (iv) x 2 − a 2 − b 2 + 2ab x 2 + 2ax + a 2 − b 2 1+ x 1− x 3 1 − + − x ⋅ 1 − x 1 + x 4x 4 2. Estudiar existencia y resolver las siguientes ecuaciones racionales: 1 1 3x − x− x −1 4 5 3 4− 2 = 4x − 1 (ii) (i) + − = 2 3 6 6 2x − 50 3x − 15 2x + 10 2 x − 10 2⋅ 4 2 x 3 2x 2 5 2 + = − = (iv) (iii) 2 2 2 5x − 15 3x − 18x + 27 (2 x − 6) x − 4 x + 2 2x − 4 (v) a ⋅ ( x − a ) b ⋅ ( x − b) + =x b a (vi) x + a x − a x + b 2 ⋅ ( x − b) + = + a−b a+b a+b a−b 3. Resolver las siguientes ecuaciones exponenciales: (i) ax −3 = 0 (ii) a x + 2 = 0 (iii) a 2 x − a x = 0 se supone a > 0, a ≠ 1 (iv) 5 2 x − 25 = 0 (v) 4 x 2 − 8 x = 0 (vi) − 5.2 x −1 + 4 x −1 + 6 = 0 (vii) 9 x + 2 + 3 = 4 ⋅ 3 x + 2 (viii) 11 ⋅ 4 2 x − 17 ⋅ 2 3x + 17 ⋅ 2 x − 11 = 0 4. Estudiar existencia y resolver las siguientes ecuaciones logarítmicas: 2 (i) (log b x )2 + log b x − 6 = 0 (ii) (log b x )3 − log 1 x 6 + 22 log b 2 x − 6 = 0 b (iii) log 2 ( x − 3) + log 2 ( x − 2) = 1 (iv) − 1 + log x − 3 (2x − 3) = 1 − log x − 3 ( x − 5) 5. Resolver las siguientes ecuaciones trigonométricas: cos x π π = sen x − cos 2 x (i) sen( x + ) − sen( x − ) = 2 (ii) sen 2 x + 2 2 tg x (iii) 3 ⋅ cos 2 x + sen 2 x − 3 ⋅ cos x = 0 Profesor: Jean Paul Quintans (iv) − sen 2 x ⋅ (2 ⋅ cos x − 3) + cos x + 5 = 0
