LICEO SALAZAR Y HERRERA DEPARTAMENTO DE
Anuncio
LICEO SALAZAR Y HERRERA
DEPARTAMENTO DE MATEMATICAS
PREPARACIÓN PARA LAS PRUEBAS ICFES
2012
RESPONDA LAS PREGUNTAS 1 A 4 DE
ACUERDO CON LA SIGUIENTE
INFORMACIÓN
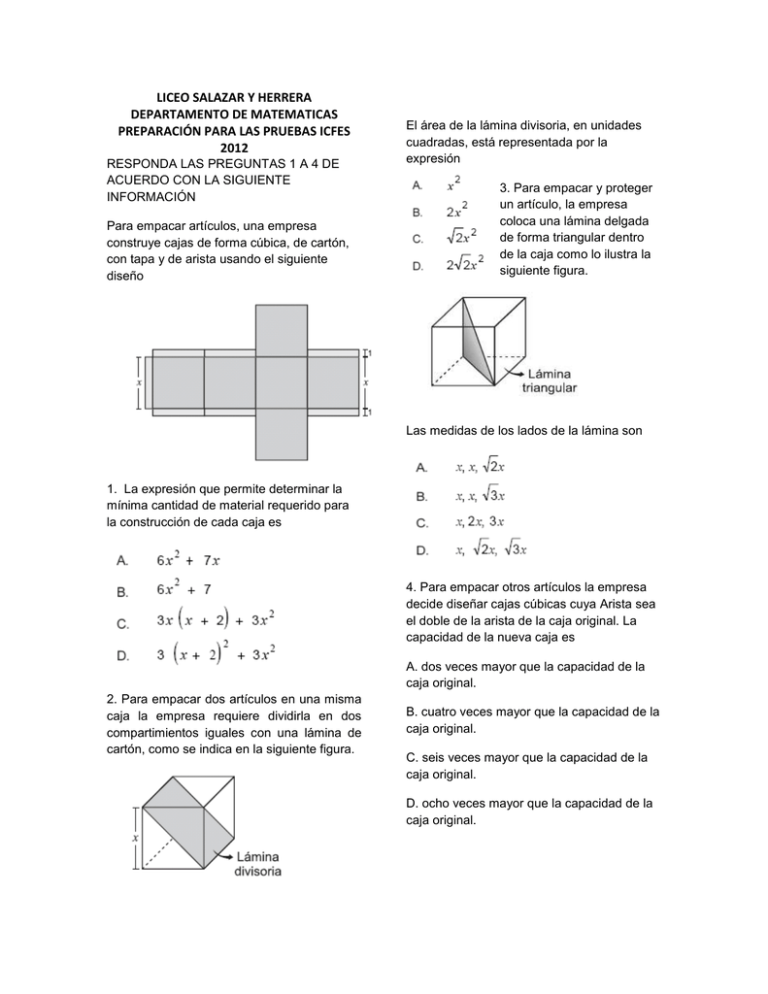
Para empacar artículos, una empresa
construye cajas de forma cúbica, de cartón,
con tapa y de arista usando el siguiente
diseño
El área de la lámina divisoria, en unidades
cuadradas, está representada por la
expresión
3. Para empacar y proteger
un artículo, la empresa
coloca una lámina delgada
de forma triangular dentro
de la caja como lo ilustra la
siguiente figura.
Las medidas de los lados de la lámina son
1. La expresión que permite determinar la
mínima cantidad de material requerido para
la construcción de cada caja es
4. Para empacar otros artículos la empresa
decide diseñar cajas cúbicas cuya Arista sea
el doble de la arista de la caja original. La
capacidad de la nueva caja es
A. dos veces mayor que la capacidad de la
caja original.
2. Para empacar dos artículos en una misma
caja la empresa requiere dividirla en dos
compartimientos iguales con una lámina de
cartón, como se indica en la siguiente figura.
B. cuatro veces mayor que la capacidad de la
caja original.
C. seis veces mayor que la capacidad de la
caja original.
D. ocho veces mayor que la capacidad de la
caja original.
RESPONDA LAS PREGUNTAS 5 A 7 DE
ACUERDO CON LA SIGUIENTE
INFORMACIÓN
La siguiente gráfica muestra la distancia
recorrida por Pedro, Pablo y Juan durante un
entrenamiento de atletismo.
RESPONDA LAS PREGUNTAS 8 A 10 DE
ACUERDO CON LA SIGUIENTE
INFORMACIÓN
En la recta numérica que se muestra se han
señalado algunos puntos con sus respectivas
coordenadas
5. De la gráfica anterior se puede afirmar que
A. los tres atletas recorrieron la misma
distancia.
8. Si M y N son los puntos medios de AB Y
CD respectivamente, la longitud de MN es,
B. los tres atletas estuvieron corriendo
durante el mismo tiempo.
A. 1/2
B. 5/8
C. Pablo recorrió más distancia que Pedro y
que Juan.
D. Pedro corrió durante menos tiempo que
Juan y Pablo
C. 9/16
D. 11/16
6. La velocidad promedio de Pablo durante el
entrenamiento fue de
9. Si DE se divide en n segmentos
congruentes, la longitud de cada uno de los n
segmentos es
A. 0,2 Km/min
A. 1/n
B. 0,25 Km/min
B. 4/n
C. 0,5 Km/min
C. 1/8n
D. 1 Km/min
D. 8/n
7. La relación entre la distancia (d) recorrida
por Juan y el tiempo (t) empleado para
recorrerla está representada por la ecuación
10. De la expresión dada se puede
afirmar que corresponde a un
número
A. racional y se ubica en AB
B. racional y se ubica en BD
C. irracional y se ubica en CD
C. 18 π, 54 π, 36 π
D. irracional y se ubica en DE
D. 0,18 π, 0,54 π, 0,36 π
RESPONDA LAS PREGUNTAS 11 A 13 DE
ACUERDO CON LA SIGUIENTE
INFORMACIÓN
14. Un profesor asigna 3 ejercicios. Pide
a1/4del número de estudiantes que está en
clase que resuelva el primer ejercicio, a 3/8 el
segundo y a 5/16 el tercero. Del total de
alumnos que están ausentes. La cantidad
total de alumnos es
Se tienen los siguientes recipientes, uno de
forma semiesférica, otro cilíndrico y otro de
forma cónica de radio R y altura h como se
muestra en la ilustración
A. 28
B. 32
C. 38
D. 42
11. Respecto al volumen de estos recipientes
NO es correcto afirmar que
A. El volumen del 2 es el triple del 1.
B. El volumen del 3 es el doble del 1.
15. Un agricultor desea cercar un campo
rectángular y luego dividirlo en tres lotes
rectangulares mediante dos cercas paralelas
a uno de los lados. El agricultor necesita
1000 metros de alambre. Si x es el largo del
campo, el área A del campo se expresa
correctamente en
C. El volumen del 3 es la mitad del 1.
D. El volumen del 1 es la tercera parte del 2.
12. Si el recipiente 2 tiene forma de cilindro
circular recto y el material utilizado para
construirlo, sin tapa, es 10 π se puede
determinar el radio de este recipiente
resolviendo la ecuación
A. R2 - 2 = 0
B. R2 - 10 = 0
C. 2R2 - 5 = 0
D. 3R2 - 5 = 0
13. Si R = 3 dm, las capacidades de los
recipientes 1, 2 y 3 expresadas en litros, son
respectivamente
A. 6π, 18 π, 12 π
B. 0,6 π, 1,8 π, 1,2 π
16. Un entero positivo n se denomina un
número perfecto si es igual a la suma de
todos sus divisores propios, el número 1 se
cuenta como un divisor propio pero el
número no.Un ejemplo de número perfecto
es
A. 3
B. 4
C. 5
D. 6
17. Una de las siguientes afirmaciones es
falsa
A. Para todo a, b c pertenecientes a los
reales, (a + b) + c = b + (a + c)
B. Para todo: a perteneciente a los reales,
existe a-1, perteneciente a los
reales, tal que a. a-1 = 1
C. Para todo a perteneciente a los reales,
existe –a, perteneciente a los
reales, tal que a + (-a) = 0
D. Para todo a, b c pertenecientes a los
reales, (a + b). c = (b.c) + (c.a)
18. Un grupo de 30 alumnos recibe 10
paquetes de cuentos, pagando por ellos ¾
del precio total, ya que el colegio paga la
cuarta parte. Sí el precio de cada paquete es
$36000 y los cuentos se reparten por igual
La cantidad X que debe pagar cada alumno
es:
A. X ≤ 5000
B. 10000 ≤ X ≤ 15000
C. 6000 ≤ X ≤ 10000 D. X ≥ 10000
B. 3
2 ) P2
D. (1 - 2
2 ) P2
22. El resultado de 16x+1 + 24x+4 , es:
A. 24x+5
B.28x+8
C.185x+5 D. 325x+5
23. En la figura que se observa, la fracción
que representa la parte sombreada es:
A.
B.
C.
D.
1/5.
1/6.
1/8
1/4.
150°
En una encuesta sobre hábitos de estudio
en matemáticas y ciencias se encontró lo
siguiente:
19. Cuál es el área del triángulo sombreado
si los lados de los cuadrados son 3 y 6
respectivamente?
A. 2
D. 5
C. (3 - 2
U
M
C. 4
C
8
6
4
2
20. Si X = 1 + 2 a, y Y= 1 + 2-a, de las
siguientes formulas. ¿Cuál expresa Y en
A.
términos de X?
A. X
B. X- 1
24. De los alumnos que estudian únicamente
una materia es cierto que son:
C.
x
D. x + 1
X-1
21. El perímetro de un triángulo rectángulo
isósceles es 2P, su área es:
A. (2 +
2)P
B. (2 -
2)P
12
B. 6
C. 8
D. 14
25. La grafica de la función y= cos(x+ π/2) se
obtiene trasladando la grafica de y=cosx , π/2
unidades hacia
A. La derecha
B. Abajo
C.La derecha
D. Arriba
Dados los intervalos reales:
A = (- 2, 2), B = [-2, 2], C = [- 2, 2)
B – A, Equivale a:
A. Ǿ
{2}
B. {-2}
C. {2}
D, {-2, 2}
2. A ∩ B, Equivale a:
A. (- 2, 2),
B. {-2}
D, {-2, 2}
C.

