Actividad 4: Sistemas no Lineales - U

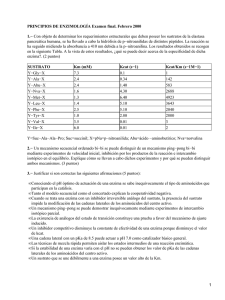
IQ4101, Métodos Matemáticos para Procesos
Profesor: J. Cristian Salgado - jsalgado@ing.uchile.cl
Prof. Aux.: Ximena Barrios – Guillermo Valenzuela
Semestre Otoño 2013
Integrantes: Paulo Arriagada
Actividad 4:
Manuel Warner
Sistemas no Lineales
(a)- Investigue acerca de los métodos multipaso para resolver EDOs. Explique el
funcionamiento de este tipo de métodos. Mencione algunos ejemplos de algoritmos
multipaso. ¿Qué ventajas y desventajas tienen estos métodos con respecto a los métodos
multipaso?
Los métodos multipaso se basan en la obtención de información de puntos anteriores para
calcular el punto que se quiere obtener. Por ejemplo, los métodos de Adams-Bashforth, de
Adams-Moulton y los de predictor-corrector (Heun sin autoinicio, Milne, Hermite, etc.) son de
multipaso. La principal ventaja de estos métodos es que, a diferencia de los de un paso,
disminuyen el error al utilizar valores anteriores con un error más pequeño que el de la
aproximación inmediatamente anterior. Por otro lado, si el coste computacional de la función
objetivo es bajo, conviene utilizar un método de un paso. Sin embargo, si el coste es alto,
conviene utilizar un método de multipaso, pues las distintas evaluaciones de la función en
etapas anteriores se pueden utilizar en varios pasos siguientes, por lo que no es necesario
evaluar la función en cada paso.
(b)- Investigue si matlab y octave tienen implementaciones de integradores multipasos.
Reporte los métodos implementados y una descripción breve de como funcionan.
Se tiene que la velocidad de formación de producto P es igual a la desaparición de sustrato:
−
𝑑[𝑆]
[𝑆]
= 𝑉𝑚𝑎𝑥
𝑑𝑡
𝐾𝑚 + [𝑆]
Esta es una ecuación diferencial ordinaria que determina la variación de la concentración de
sustrato (o producto) respecto al tiempo. Relaciona esta concentración con la velocidad
máxima de reacción y las constantes cinéticas de las reacciones involucradas.
(c)- Implemente la familia de métodos RK orden 1-5 vistos en clase con paso fijo. Compare
el desempeño de los métodos implementados por usted y el integrador ode45 de matlab en
el problema de prueba descrito a continuación.
El principal supuesto que se aplica es el de reacciones de un sustrato. Además, se aplica la
aproximación de estado estacionario, lo que genera que [ES] sea constante. Por otro lado, La
concentración de sustrato ([S]) es mucho mayor que la concentración de enzima ([E]), de
manera que la proporción de sustrato fijo a la enzima es siempre relativamente pequeña. Un
último supuesto recae sobre el uso de velocidades iniciales, esto es que la velocidad de la
reacción debe determinarse tan pronto como el sustrato y la enzima son mezclados. En dicho
tiempo, la concentración de productos es despreciable y, por lo tanto, la reacción inversa de
productos a sustratos puede ser ignorada.
(d)- ¿Qué objetivo tiene el término entre paréntesis en el modelo logístico? explique en base
a sus simulaciones.
A primera vista se observa que a medida que avanza el tiempo, la concentración de sustrato
disminuye, lo cual es lógico dado la reacción química involucrada. Esta disminución es, al
principio de la reacción, casi constante y alta. Sin embargo, a tiempos más grandes, la
pendiente es más horizontal y la disminución de sustrato es más lenta, hasta llegar a cero.
Este perfil se observa en la Figura 1 entregada en la ejecución del archivo “act4_main.m” en
Matlab.
(e)- ¿Qué significado físico/biológico tiene 𝑘2 ? Explique en base a sus simulaciones.
Un aumento de 𝐾𝑚 genera una disminución de la concentración de sustrato más lenta, es
decir, disminuye la velocidad de reacción (ver Figura 2 entregada en la ejecución de
“act4_main.m”). Mientras tanto, un aumento de 𝑉𝑚𝑎𝑥 genera un aumento en la velocidad de
reacción, lo que se ve en el gráfico de la Figura 3. Finalmente, un aumento de 𝑆0 disminuye
la velocidad, lo cual es lógico pues se necesita más tiempo para reaccionar cuando la
concentración inicial es más grande (ver Figura 4).
(f)- ¿Qué efecto tiene un aumento en el orden del método de integración en la calidad de la
estimación de la solución?
La ecuación de Michaelis-Menten ocupa la velocidad de desaparición del sustrato (variación
de la concentración) en función del tiempo, por ello es que a medida que avanza el tiempo
esta concentración disminuye hasta un valor mínimo que es cero, cuando el sustrato
desaparece completamente. Al inicio, reacciona rápidamente el sustrato con la enzima para
formar el complejo ES, lo cual se refleja en que la resta (𝑆0 − 𝑆) domina la ecuación, pues el
logaritmo es pequeño en comparación. A medida que disminuye la concentración de sustrato,
el logaritmo cobra importancia, desde un cierto valor 𝐾𝑚 , cuando la resta se vuelve pequeña
y el logaritmo aumenta de valor. Esto es, la formación de producto comienza a disminuir, por
lo cual la curva toma una forma logarítmica que disminuye lentamente hasta que ya no hay
reactivo que consumir.
(g)- Discuta el efecto del tamaño del paso de integración en el desempeño de los métodos.