Conceptos básicos sobre detección de la radiación ionizante
Anuncio

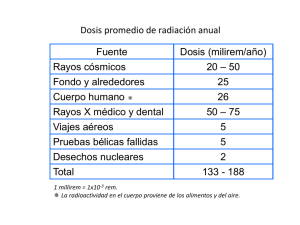
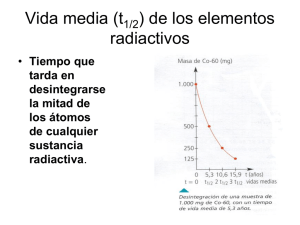
Conceptos básicos sobre detección de la radiación ionizante José Benlliure Curso de Física Nuclear experimental Programa de doctorado inter-universitario de Física Nuclear Universidad de Santiago de Compostela, Febrero de 2007 Indice conceptos generales: radiación ionizante y fuentes de radiación resolución en energía eficiencia de detección tiempo muerto interacción de partículas cargadas con la materia: mecanismos de interacción ionización y excitación pérdida de energía por interacción electromágnetica: fórmula de Bethe-Bloch rango y dispersión de energía interacción de los fotones con la materia: atenuación de la radiación mecanismos de interacción: efecto fotoeléctrico, Compton y creación de pares interacción de los neutrones con la materia: mecanismos de interacción concepto de letargía José Benlliure Curso de Física Nuclear experimental, EDFN, USC Feb.’ 07 Radiación ionizante Radiación con energía suficiente para ionizar la materia que atraviesa (E>10 KeV) partículas cargadas ligeras electrones (β-) y positrones (β+) partículas cargadas masivas mesones (π, µ,k), hadrones (p,∆,… ) deuterones, partículas alfa (α), núcleos pesados (C, O, N, … ) partículas neutras fotones (rayos X y γ), neutrones José Benlliure Curso de Física Nuclear experimental, EDFN, USC Feb.’ 07 Fuentes de radiación ionizante fuentes naturales: radiactividad ambiental (40K, 222Rn) emitiendo radiación α, β+ o β- (E < 5 MeV) radiación cósmica (µ, π, p) (E < 1 GeV) fuentes artificiales: aceleradores de investigación en física nuclear o de partículas (e-,p,núcleos pesados) aceleradores de investiación en física de plasma o materiales (rayos X, radiación sincrotrón o fuentes de neutrones) aceleradores de producción de radioisótopos (aplicaciones médicas o industriales) reactores de investigación reactores de producción de energía ensayos de bombas atómicas … .. (1 MeV < E < 1 TeV) José Benlliure Curso de Física Nuclear experimental, EDFN, USC Feb.’ 07 Detección de la radiación ionizante R= FWHM Eo La radiación ionizante produce cargas en el medio que atraviesa que pueden ser colectadas por los electrodos que generan un campo eléctrico en el medio atravesado. Las cargas colectadas pueden Producir una señal de corriente o de voltaje. interacción de la radiación con la materia: ionización o excitación recolección de la carga (pares ión-catión o electrón-hueco) formación del pulso José Benlliure Curso de Física Nuclear experimental, EDFN, USC Resolución de una medida El proceso de detección de una partícula está sujeto a fluctuaciones estadísticas propias del sistema de detección utilizado definición de resolución: FWHM=0 R= FWHM=1 FWHM FWHM Ho resolución mínima: FWHM=0.5 FWHM < E 2 − E1 Para identificar un núcleo con A=200 E1 R= E2 resolución en energía: 0.5 = 2.5 10­3 200 La fluctuación de la medida está determinada por el número de portadores de carga (E/w, w=energía para crear un par) y sigue la estadística de Poisson FWHM = José Benlliure Eo k ⇒ R = w E Curso de Física Nuclear experimental, EDFN, USC Eficiencia de detección Se define la eficiencia cómo la fracción de cuantos de radiación emitidos por una fuente que son detectados por nuestro dispositivo experimental ε abs = εint εgeo eficiencia intrínseca: Fracción de cuantos de radiación que inciden sobre el detector produciendo una Señal. Es una propiedad del detector eficiencia geométrica: Fracción de cuantos de radiación que inciden sobre el detector produciendo una Señal. Es una propiedad del detector ε José Benlliure Ω d 1 − = Ω = 2 π geo 4π d2 + a 2 Curso de Física Nuclear experimental, EDFN, USC Tiempo muerto Es la fracción de tiempo que el detector necesita para generar una señal m = e­n τ m n = 1 ­ mτ n = tasa de cuentas verdadera m= tasa de cuentas registradas τ = tiempo muerto José Benlliure Curso de Física Nuclear experimental, EDFN, USC Feb.’ 07 Mecanismos de interacción de partículas cargadas interacción Coulombiana con electrones y núcleos: principal mecanismo de interacción de partículas cargadas masivas y electrones y positrones de baja energía (E<10 MeV) emisión de radiación de frenado o bremsstrahlung: importante para electrones y positrones de alta energía (E>10 MeV) emisión de radiación sincrotrón: radiación electromagnética emitida por partículas cargadas en movimiento que siguen una trayectoria circular reacciones nucleares: mecanismo muy poco probable e irrelevante para la detección de radiación emisión de radiación Cerenkov: emisión de radiación electromagnética en el visible cuando una partícula cargada supera la velocidad de la luz en el medio que ésta atraviesa La principal consecuencia de estos mecanismos de interacción es la pérdida de energía o frenado de la radiación que atraviesa un medio Curso de Física Nuclear experimental, EDFN, USC Feb.’ 07 José Benlliure Mecanismos de interacción de partículas cargadas Mecanismos de interacción de β+ y β el mecanismo de interacción predominante es la interacción Coulombiana (ionización) solo para partículas de poca masa (β+,β-) predomina la interacción por frenado o bremsstrahlung a alta energía (E>10 MeV) José Benlliure Curso de Física Nuclear experimental, EDFN, USC Interacción Coulombiana colisiones con los electrones ligados del medio, los cuales se promocionan a niveles superiores de energía (excitación) o bien son expulsados (ionización) el proceso de ionización es dominante si la radiación (partícula) incidente tiene una energía mayor que la energía de ligadura de los electrones atómicos del medio sobre el que incide la radiación. En ese caso se expulsa un electrón de energía cinética T igual a la energía transferida (perdida de energía) por la partícula (Et) ionizante menos la energía de ligadura (potencial de ionización) del medio (I). T = Et - I José Benlliure Curso de Física Nuclear experimental, EDFN, USC Pérdida de energía por ionización y excitación Una partícula cargada moviéndose en un medio interacciona con muchos átomos, por tanto con muchos electrones, a lo largo de su trayectoria dentro del medio Cada interacción ocurre con una cierta probabilidad y en cada una de ellas se pierde una cantidad de energía infinitesimal pero diferente de una difusión a otra (difusión elástica entre dos cuerpos) Es imposible calcular la pérdida de energía debida a cada colisión individual. Se calcula una pérdida de energía promedio por unidad de distancia recorrida en el medio atravesado (fórmula de Bethe-Bloch). El cálculo depende de la naturaleza de la partícula incidente. En el caso de considerar electrones incidentes la radiación incidente pierde mayor cantidad de energía por colisión (proyectil y blanco tienen la misma masa). Las partículas masivas pierden menos energía por colisión. José Benlliure Curso de Física Nuclear experimental, EDFN, USC Fórmula de Bethe-Bloch Electrones: 2 2 βγ γ − 1 ) ( dE mc 1 γ − 1 2 2 2 2 ( MeV / m) = 4πro 2 NZ ln 2mc + 2 β + 1 − γ + 2 γ − 1 ln 2 dx β I 2 γ 8 ( ) Partículas masivas: 2 2mc 2 2 2 2 dE 2 mc ( MeV / m) = 4πro 2 NZ ln β γ − β dx β I José Benlliure ( ) I (eV ) ≈ 9.76 + 58.8Z −1.19 Z Curso de Física Nuclear experimental, EDFN, USC Fórmula de Bethe-Bloch Dependencia con el tipo de radiación: Dependencia con el tipo de material: independiente de la masa de la partícula incidente proporcional al z2 de la partícula incidente depende de la velocidad de la partícula incidente β proporcional a la densidad del material José Benlliure Curso de Física Nuclear experimental, EDFN, USC Curva de Bragg La curva de Bragg nos da el perfil de deposición de energía por unidad de espesor de material atravesado por la radiación José Benlliure Curso de Física Nuclear experimental, EDFN, USC Dispersión en energía y ángulo Cada interacción produce una pérdida de energía y un cambio de dirección La pérdida de energía por colisión es pequeña por lo que cada partícula un número importante de colisiones El número de colisiones está sujeto a fluctuaciones estadísticas que da lugar a una dispersión en pérdida de energía y ángulo de la radiación incidente El haz indicente no tiene dispersión en energía ni en ángulo (función delta) El haz dispersado tiene una energía E1 inferior a la energía inicial Eo y una dispersión en energía ∆E. La distribución angular está centrada entorno a la dirección inicial con una dispersión ∆θ José Benlliure Curso de Física Nuclear experimental, EDFN, USC Rango o alcance El rango corresponde al espesor de material que tras ser atravesado es capaz de detener a la mitad del flujo de partículas que inciden sobre él. Io I dE R=∫ Eo ( dE / dx ) 0 El rango se obtiene integrando la fórmula de Bethe-Bloch (Eo es la energía cinética inicial). José Benlliure Curso de Física Nuclear experimental, EDFN, USC Absorción de partículas beta Los electrones emitidos por una fuente radiactiva tienen un espectro contínuo de energía, por tanto empiezan a ser absorbidos (frenados) con espesores muy finos. El espectro de absorción puede aproximarse mediante la expresión: I(t) = Ioe-µt µ: coeficiente de absorción, depende de la energía del beta y la naturaleza del material atravesado José Benlliure Curso de Física Nuclear experimental, EDFN, USC Detección de partículas cargadas radiación incidente con carga La radiación ionizante se detecta midiendo la carga que ésta genera por ionización (energía depositada) en un determinado material (detector) al atravesarlo. Como la interacción electromagnética es de largo alcance, la probabilidad de interacción Coulombianan es grande y por tanto también lo es la probabilidad de detección (eficiencia) de las partículas cargadas José Benlliure Curso de Física Nuclear experimental, EDFN, USC Mecanismos de interacción de los fotones Existen tres mecanismos de interacción dominantes: efecto fotoeléctrico: El fotón es absorbido por un átomo que a su vez emite un electrón con la misma energía que el fotón incidente. Domina a baja energía (E<100 KeV) efecto Compton: El fotón es difundido por un electrón atómico. El fotón pierde parte de su energía y se la comunica al electrón. Domina a energías intermedias (E=1 MeV) creación de pares: El fotón se materializa en un par e-, e+. Domina a alta energía (E>10 MeV) José Benlliure Curso de Física Nuclear experimental, EDFN, USC Efecto fotoeléctrico Energía cinética del electrón: Te = E γ − Be E γ : energía del fotón incidente Be : energía de ligadura del electrón Probabilidad de interacción: τ(m −1 ) = aN Z [1 − ϑ( Z )] m Eγ n N : densidad del material (átomos/m3 ) Z : número atómico del material a, n, m : constantes Aumenta con el Z del material José Benlliure Disminuye con la energía del fotón Curso de Física Nuclear experimental, EDFN, USC Efecto Compton Energía cinética del electrón: Eγ ' = 1+ θ=π E γmin ' = Temax = Eγ mo c Eγ (1 − cos θ) 2 Eγ 1 + E γ / mo c E γ : energía del fotón incidente θ : ángulo de difusión θ=π Eγmax = Eγ ' 2 2 Eγ / mo c 2 1 + 2 Eγ / mo c José Benlliure E γ ' : energía del fotón difundido 2 Eγ Eγmax Temin = 0 Eγ Curso de Física Nuclear experimental, EDFN, USC Efecto Compton Probabilidad de interacción: σ(m −1 ) ≈ ρ ρ : densidad del material (kg/m3 ) N A : número de Avogadro A : número másico del material Z : número atómico del material NA Zf ( E γ ) A Casi independiente del Z del material Disminuye con la energía del fotón José Benlliure Curso de Física Nuclear experimental, EDFN, USC Creación de pares Energía cinética del electrón: Te − + Te + = Eγ − (mc 2 ) e − − ( mc 2 ) e + = Eγ − 1.022 MeV 1 Te − = Te + = ( Eγ − 1.022 MeV) 2 Probabilidad de interacción: −1 2 κ(m ) ≈ NZ f ( Eγ , Z ) N : densidad del material (átomos/m3 ) Z : número atómico del material Aumenta con el Z del material Aumenta con la energía del fotón José Benlliure Existe un umbral de producción Curso de Física Nuclear experimental, EDFN, USC Absorción de fotones Los fotones que interaccionan desaparecen del haz incidente (excepto para la dif. Compton) La probabilidad de interacción de los fotones es siempre la misma para cualquier diferencial de espesor de material atravesado (dx) dI = − I ( x)µdx ⇓ I(x) = I o e −µx Los fotones transmitidos tienen la misma energía y dirección que los incidentes En cada espesor elemental dx la probabilidad de interacción de los fotones es la misma El número de fotones transmitidos decrece exponencialmente Recorrido libre medio: λ = 1/ µ José Benlliure µ(m-1) = τ(fotoeléctrico)+σ(Compton)+κ(pares) Curso de Física Nuclear experimental, EDFN, USC Detección de fotones γ fotones incidentes e- Los fotones no tienen carga pero generan electrones en movimiento que pueden ionizar o excitar el medio. La probabilidad de interacción de los fotones es muy pequeña y por lo tanto también lo es su probabilidad de detección (eficiencia). José Benlliure Curso de Física Nuclear experimental, EDFN, USC Espectros de energía de fotones La interacción Compton produce un espectro de energía contínuo para los electrones producidos El efecto fotoeléctrico es el único en el que se conserva la energía inicial del rayo-γ. Los electrones producidos originan un fotopico de energía bien definida que nos permite determinar la energía inicial del rayo-γ (espectroscopía) José Benlliure Curso de Física Nuclear experimental, EDFN, USC Mecanismos de interacción de los neutrones Reacciones nucleares con los núcleos de los átomos: difusión elástica: A(n,n)A difusión inelásica: A(n,nγ)A, A(n,2n)B, … producción de partículas cargadas: A(n,p)B, A(n,α)C, … captura radiativa: A(n,γ)B fisión: A(n,FF) José Benlliure Curso de Física Nuclear experimental, EDFN, USC Atenuación de neutrones: cambio letárgico Difusión elástica neutrón-núcleo: vlab Lab sist. vo φlab v cm = θlab 1 V= vo A +1 A CM sist. V vcm θcm A vo A +1 (v ) 2 lab (v ) lab 2 = ( v cm ) + V 2 − 2v cm Vcos( π − θcm ) 2 2 A A 2 1 2 2 = v + v − 2 o o 2 v o cos ( π − θcm ) ( A + 1) A +1 A + 1 vlab φcm A 2 2 A ­1 Eo < E < Eo A + 1 E v lab A 2 + 1 + 2Acosθcm = = Eo vo ( A + 1) 2 0 < E < Eo para A=1: José Benlliure Curso de Física Nuclear experimental, EDFN, USC Atenuación de neutrones: cambio letárgico Cambio letárgico: variación logarítmica de la energía en una colisión 2 E u = ln E o − ln E = ln o E u ( θ) = ln ( A + 1) E v lab A 2 + 1 + 2Acosθcm = = E o v o ( A + 1) 2 2 A 2 + 1 + 2Acosθcm variación media de la letargía por colisión: dΩ 1 ( A + 1) ( A ­ 1) ln A ­ 1 ξ = u ( θ) = ∫ u ( θ) = ∫ ln 2 d ( cosθcm ) = 1 + 4π 2 A + 1 + 2Acosθcm 2A A +1 2 2 Como la variación media de letargía por colisión es constante el número de colisiones para variar la energía del neutrón desde Eo a E’ es: n= u 1 E u = ln o ξ ξ E' José Benlliure 12 C ⇒ ξ = 0.158 H ⇒ ξ =1 Curso de Física Nuclear experimental, EDFN, USC Resumen de conceptos en el laboratorio vamos a trabajar con fuentes radiactivas y rayos cósmicos: radiación α, β y γ (E<5 MeV) rayos cósmicos: pµ,e- (E = 1 GeV) la interacción Coulombiana domina la interacción de partículas cargadas con la materia: pérdida de energía o frenado de la radiación incidente (fórmula de Bethe-Bloch) dispersión en energía y ángulo, rango y absorción ionización del medio (mecanismo de detección) Los mecanismos de interacción de los fotones con la materia son: efecto fotoeléctrico, Compton y creación de pares la inteacción del fotón implica la desaparición o absorción del mismo (excep. Compton) los tres mecanismos producen electrones capaces de ionizar el medio (detección) sólo en el efecto fotoeléctrico los electrones emitidos conservan la energía inicia del γ la probabilidad de interacción de los rayos-γ es pequeña y también su eficiencia de detección ­ G.F. Knoll, Radiation detection measurement, John Wiley and Sons, New York (1979) ­ T. Soulfandis, Measurements and detection of radiation, McGraw­Hill, New York (1983) ­ W.R Leo, Techniques for Nuclear and Particle Physics Experiments, Springer­Verlag (1987) Prácticas del laboratorio detector Geiger-Muller: interacción de radiación α, β y γ con la materia (absorción), detectores gaseosos desintegraciones radiactivas, estadística de la radiación, masa del neutrino espectroscopía γ: interacción de rayos-γ con la materia, detectores de centelleo desintegraciones radiactivas, efecto Compton, fotoeléctrico difusión Compton: interacción de rayos-γ con la materia, detectores de centelleo desintegraciones radiactivas, efecto fotoeléctrico, Compton (cinemática y sec. eficaz) coincidencias γ−γ: interacción de rayos-γ con la materia, detectores de centelleo, coincidencias desint. radiactivas, efecto fotoeléctrico, Compton, correlac. angulares (espín nuclear) cósmicos: interacción de µ y e- con la materia, detectores de centelleo, coincidencias caracterización de la radiación cósmica, vida media del µ http://www.usc.es/genp/docencia/lfnyp.html