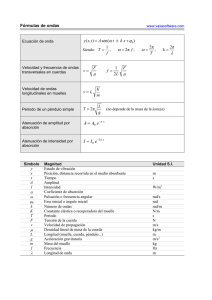
Universidad Veracruzana , Facultad de Ingeniería Mecánica

,
Universidad Veracruzana
Facultad de Ingeniería Mecánica Eléctrica
Región Poza Rica-Tuxpan
TEMA
“MANUAL DE PRACTICAS DE OSCILACIONES Y ONDAS
MECANICAS PARA EL LABORATORIO DE FISICA BASICA”
TRABAJO PRÁCTICO EDUCATIVO
P R E S E N T A N:
CALED DE JESUS LICONA VITE
AGUSTIN JAFET LOPEZ MENDOZA
JOSE JAIME RAMIREZ GARCIA
DIRECTOR DEL TRABAJO RECEPCIONAL
ING. DIONICIO RANGEL ORTA
QUE PARA ACREDITAR LA EXPERIENCIA EDUCATIVA DE
EXPERIENCIA RECEPCIONAL
CATEDRÁTICO DE LA EXPERIENCIA EDUCATIVA
TRABAJO RECEPCIONAL
LIC. MELECIO GONZÁLEZ GÓMEZ
POZA RICA, VER
MARZO 2010
INDICE
Introducción. .…………………………………..………………………………………1
CAPITULO I
Justificación…………………………………………………………………………….3
Tipo y naturaleza del trabajo…………………………………………………………4
Características y funciones esenciales……………………………………………...5
CAPITULO II
2.1. Movimiento Oscilatorio……………………………………………...……..…….9
2.1.1. Concepto de movimiento oscilatorio………………………………….9
2.1.2. Tipos de movimiento oscilatorio………………………..…………...10
2.1.3. Movimiento Armónico Simple………………………………………..12
2.1.4. Comparación de movimiento simple con movimiento circular
Uniforme……………………………………………………………………….13
2.1.5. El péndulo……………………………………………………………...15
2.1.6. Oscilaciones amortiguadas y forzadas…...………………………...19
2.2. Movimiento Ondulatorio….……..……………………………………………...25
2.2.1. Concepto y tipos de onda……………………………………………25
2.2.2. Propagación de perturbación………………………………………..29
2.2.3. Modelo de onda progresiva………………………………………….30
2.2.4. Velocidad de una onda……………………………………………….36
2.2.5. Reflexión y transmisión de ondas…………………………………...38
2.2.6. Transferencia de energía mediante ondas sinusoidales…..……..40
2.3. Equipo de experimentación para oscilaciones mecánicas…………………44
2.3.1. Descripción del marco básico……………………………………….45
2.3.2. Características del contador de oscilaciones…..………………….47
2.3.3. Descripción de los accesorios del contador de oscilaciones….....49
2.3.4. Problemas generales de operación, causas y soluciones………..52
2.3.5. Uso adecuado del contador de oscilaciones………………………55
2.4. Experimentos con sistema de oscilaciones………………...………………..57
2.4.1. Relación entre longitud y el periodo de un péndulo simple……..57
2.4.2. Determinación de la aceleración de la gravedad utilizando un
Péndulo simple…………………………………………………...…61
2.4.3. Determinación de la constante elástica de un resorte……………66
2.4.4. Relación entre la masa del cuerpo y el periodo de oscilación en
el sistema cuerpo resorte……………………………………..…….69
2.5. Equipo para medición de Ondas Mecánicas………………...………………74
2.5.1. Descripción del marco básico……………………………………….75
2.5.2. Generador de Ondas Mecánicas……………………………………76
2.5.3. Generador de funciones……………………………………………...77
2.5.4. Descripción de los accesorios del sistema de Ondas Mecánicas.79
2.5.5. Problemas generales de operación, causas y soluciones………..81
2.5.6. Uso adecuado del sistema de Ondas Mecánicas…..……………..83
2.6. Experimentos con sistema de Ondas Mecánicas………..………………….85
2.6.1. Ondas estacionarias en una cuerda………………………………..85
2.6.2. Velocidad de propagación de una onda longitudinal en un
Resorte……………………………………………………………….90
2.6.3. Velocidad de una onda trasversal en diferentes cuerdas………...94
2.6.4. Modos de oscilación en flejes circular y recto……………………..97
CAPITULO III
Aportaciones y contribuciones al desarrollo…………..…………………………100
Bibliografía……………………..……………………………………………………101
Anexos……………………………………………………………………………….102
Apéndices……………………………………………………………………………103
Introducción
Este trabajo tratara sobre el estudio de las oscilaciones y ondas mecánicas,
iniciaremos con el concepto de oscilaciones. Para lo cual debemos saber que
una oscilación es todo movimiento repetitivo de un objeto, se concentrara la
atención a un caso especial de movimiento periódico, llamado movimiento
armónico simple. Todos los movimientos periódicos se representan como
combinaciones de movimientos armónicos simples. El movimiento armónico
simple también forma la base para comprender las ondas mecánicas, las ondas
sonoras, las ondas sísmicas. A medida que una onda sonora viaja a través del
aire, elementos del aire oscilan de atrás para adelante; conforme una onda en
el agua viaja a través de un estanque, los elementos del agua oscilan arriba y
abajo y en retroceso y hacia delante. El movimiento de los elementos conduce
a una marcada similitud con el movimiento periódico de un péndulo oscilante o
un objeto unido a un resorte.
Para explicar muchos otros fenómenos en la naturaleza, se deben comprender
los conceptos de oscilaciones y ondas. Por ejemplo, aunque los rascacielos y
puentes parecen rígidos, en realidad oscilan, algo que deben tomar en
consideración los arquitectos e ingenieros que los diseñan y construyen. Para
entender como funciona la radio y televisión, debe comprender el origen y
naturaleza de las ondas electromagnéticas y como se propagan a través del
espacio.
Al ser niños la mayoría de las personas han observado lo que es una onda,
cuando soltaron una piedra en un estanque. En el punto donde la piedra choca
con la superficie del agua, se crean ondas. Estas ondas se mueven hacia fuera
a partir del punto de creación en círculos que se expanden hasta que alcanza
la orilla. Esto nos dice que el mundo esta lleno de ondas, los dos tipos
principales son las ondas mecánicas y las ondas electromagnéticas. En el caso
de las ondas mecánicas, algunos medios físicos se perturban. Las ondas
electromagnéticas no requieren un medio para propagarse; algunos ejemplos
de ondas electromagnéticas son la luz visible, las ondas de radio, las señales
de televisión, y los rayos X. En este trabajo solo se estudiaran las ondas
mecánicas.
CAPÍTULO I
Justificación
Conociendo la importancia que tiene la física dentro de la ingeniería, así como
las oscilaciones y ondas mecánicas, el alumno necesita tener un conocimiento
mas profundo no solo desde un enfoque teórico sino también desde el punto de
vista practico, es decir, aplicar conceptos relacionados al tema, fórmulas y
leyes a situaciones en la vida cotidiana que permitan comprobar lo que se
expone durante las clases.
Buscando que el alumno tenga un explicación a lo mencionado en el párrafo
anterior, la
Universidad
Veracruzana región Poza Rica – Tuxpan se
ha
adquirido los sistemas de oscilaciones y ondas mecánicas marca FICER
modelo SOSM-01 y SOM-01 respectivamente. Los cuales están diseñados
para realizar experimentos. Sin embargo, estos sistemas no contaban con un
manual de prácticas que sirviera como apoyo al momento de ponerlo en uso.
Es así como surge la idea de crear un manual teórico practico que cubran las
necesidades que los alumnos
tienen al momento de cursar la experiencia
educativa de física básica y de esta manera complementar su aprendizaje a
Experiencias Educativas posteriores como: Vibraciones Mecánicas, Mecánica
de Materiales, Mecanismos, Dinámica, Instalaciones Mecánicas.
Tipo y naturaleza del trabajo.
La información que aquí se presenta ha sido recopilada y ordenada de forma
que los estudiantes puedan tener un mejor aprendizaje, así como una
herramienta de ayuda para los docentes que imparten la experiencia educativa
de física básica bajo el régimen del MEIF dentro de la Universidad
Veracruzana.
El trabajo comprende una sinopsis de información seleccionada de libros con
diversos autores, así como basada en los instructivos que son incluidos por el
fabricante dentro de los equipos FICER, con el fin de comprobar los principios
básicos y las leyes de la mecánica dentro del tema de oscilaciones y ondas
mecánicas.
Características y funciones esenciales.
El presente trabajo práctico educativo tiene como objetivo despertar al alumno
un interés sobre la mecánica
y las ramas en que se divide. Además
se
pretende que pueda ser utilizado por los alumnos como una herramienta para
la experiencia de física básica, para que así, pueden tener un conocimiento
más extenso sobre las oscilaciones y ondas mecánicas que están contenidas
en experiencias educativas aplicativas.
En este trabajo se incluyen los temas destacados sobre las oscilaciones y las
ondas mecánicas añadiéndosele imágenes de los instructivos de los equipos
FICER para que así los estudiantes puedan tener una mejor comprensión de lo
que se esta tratando.
El capitulado tiene un enfoque teórico práctico educativo que esta estructurado
por tres capítulos de los cuales el capitulo I consta de tres partes, como son:
- Justificación
- Tipo y naturaleza del trabajo
- Características y funciones esenciales
El capitulo 2 hace referencia al desarrollo del trabajo y se encuentra divido en
seis Subtemas.
En el subtema 2.1 se define y explica el movimiento oscilatorio, se describen
algunos tipos de este movimiento, así como la comparación entre alguno de
ellos. Además se conocerá sobre el concepto del péndulo.
En el subtema 2.2 se presenta el movimiento ondulatorio, sus conceptos y tipos
de ondas, propagación de una perturbación, así como la velocidad de una
onda, además, la transferencia de energía mediante ondas sinusoidales.
El subtema 2.3 muestra el uso y manejo del sistema de oscilaciones
mecánicas, describiendo cada una de las partes que lo conforman, también se
presentan soluciones a problemas técnicos que pueden ocurrir durante las
prácticas de laboratorio propuestas en este manual, además de presentar las
recomendaciones y cuidados para el buen funcionamiento del equipo.
El subtema 2.4 expone experimentos que se pueden realizar con el sistema de
oscilaciones como: la relación entre la longitud y un péndulo simple, la
determinación de la aceleración de la gravedad, la determinación de a
constante elástica de un resorte y la relación entre la masa del cuerpo y el
periodo de oscilación en el sistema cuerpo resorte.
El subtema 2.5 describe sobre el uso y manejo del sistema de ondas
mecánicas, marca FICER modelo SOM-01 describiendo cada una de las partes
que lo conforman, además de presentar también algunos problemas técnicos
que pueden encontrarse durante la realización de los experimentos propuestos
en este manual, además de presentar las recomendaciones y cuidados para el
buen funcionamiento del equipo.
Por ultimo se presenta el subtema 2.6 donde encontraremos los experimentos
propuestos en este manual, como lo son: las ondas estacionarias en una
cuerda, velocidad de propagación de una onda longitudinal en un resorte,
velocidad de una onda transversal en diferentes cuerdas y los modos de
oscilación en flejes circular y recto.
Finalmente en el capítulo 3 encontrará las aportaciones o contribuciones al
desarrollo, la bibliografía, los anexos y apéndices.
En el manual se proporcionaran además ejemplos que permitirán al alumno
reafirmar el aprendizaje adquirido en el aula y se incluyen actividades
experimentales realizadas con el sistema de ondas y oscilaciones mecánicas
marca FICER modelo SOM-01 Y SOSM-01 respectivamente.
El objetivo principal de este manual, es facilitar al alumno las bases y los
fundamentos teóricos
y prácticos sobre las oscilaciones y las ondas
mecánicas. Así, como los temas más significativos y
semejantes de los
mismos.
Unas de las funciones principales de este trabajo es comprobar los conceptos
de oscilaciones y ondas mecánicas basadas en ecuaciones y leyes de los
temas antes mencionados.
Además de que servirá como apoyo al alumno al momento de realizar los
experimentos que tratan de comprobar los conceptos y fundamentos de las
oscilaciones y ondas mecánicas, así como dotar al laboratorio de mecánica de
la FIME de un manual de prácticas sobre los temas mencionados en la
experiencia educativa de Física Básica.
CAPITULO II
SUBTEMA 2.1 MOVIMIENTO OSCILATORIO
2.1.1 CONCEPTO DE MOVIMIENTO OSCILATORIO
Uno de los movimientos más importantes, de los observados en la naturaleza,
es el movimiento oscilatorio. Se dice que una
partícula oscila cuando se
mueve periódicamente respecto a una posición de equilibrio.
Tomando un concepto amplio se puede partir que todo movimiento o suceso
que se repite a intervalos regulares se dice que es periódico. En ciertos
movimientos periódicos, un cuerpo se mueve hacia adelante y hacia atrás
siguiendo una trayectoria determinada, entre dos posiciones extremas. Como
ejemplos de este tipo podemos mencionar la vibración de la cuerda de una
guitarra o del cono de un altoparlante, la oscilación de un péndulo, el
movimiento de un pistón en un motor y las vibraciones de los átomos en un
solidó. Tales movimientos periódicos constituyen ejemplos de oscilación. En
general, la oscilación es una fluctuación periódica del valor de una cantidad
física por encima y por debajo de algún valor central o de equilibrio.
En consecuencia, se puede decir que el movimiento oscilatorio es un
movimiento periódico en torno a un punto de equilibrio estable. Los puntos de
equilibrio mecánico son, en general, aquellos en los cuales la fuerza neta que
actúa sobre la partícula es cero. Si el equilibrio es estable, pequeños
desplazamientos darán lugar a la aparición de una fuerza que tenderá a llevar a
la partícula de vuelta hacia el punto de equilibrio. Tal fuerza se denomina
restauradora. Se dice que un punto, o en general un sistema, realiza un
movimiento periódico, cuando en intervalos regulares de tiempo, llamados
periodos, todas las variables que caracterizan su movimiento toman los mismos
valores (posición, velocidad, aceleración).
Dicho lo anterior, se puede concluir que todo movimiento oscilatorio radica en
una estabilidad consistente en un equilibrio siguiendo un patrón regulador que
a través de una fuerza restauradora, vuelve hacia el mismo punto en que parte
aquél.
2.1.2 TIPOS DE MOVIMIENTO OSCILATORIO
Los fenómenos vibratorios u oscilatorios están presentes en toda la naturaleza.
Los péndulos formados por objetos que penden de hilos, los muelles que
oscilan sujetos a un punto fijo, o fenómenos fisiológicos comunes, como el
hecho de tiritar, son ejemplos frecuentes de este tipo de movimientos.
En términos sencillos e idealizados, puede definirse oscilación como un
movimiento rectilíneo de vaivén que alcanza una cierta amplitud a ambos lados
de un punto concreto, que es el que ocuparía la partícula si no se aplicara
sobre ella la fuerza externa que la induce a oscilar. Este punto se denomina
posición de equilibrio, y se elige comúnmente como origen de referencia en la
descripción del movimiento.
Los movimientos oscilatorios o vibratorios se expresan mediante ecuaciones de
movimiento que con frecuencia se apoyan con gráficas que ayudan a
comprender e ilustrar su naturaleza. Estas gráficas son representaciones de la
variación del espacio, de la velocidad y la aceleración de la partícula oscilante
con respecto al tiempo.
GRAFICA 1.-Gráfica de la velocidad con respecto al tiempo de un movimiento
oscilatorio
MOVIMIENTOS OSCILATORIOS PERIÓDICOS
Un caso particularmente interesante de oscilaciones es el constituido por los
llamados movimientos oscilatorios periódicos. En ellos, las partículas describen
una trayectoria que se repite cada cierto tiempo, denominado periodo y
simbolizado por T.
Si la función que describe el movimiento oscilatorio es x(t), se verifica que:
……………………………..ECUACION 1
La magnitud inversa del periodo se llama frecuencia, y es una magnitud básica
de los movimientos oscilatorios. El símbolo de la frecuencia es la letra griega ,
y su unidad de medida es el hertzio (símbolo Hz). El hertzio puede definirse
también como la unidad inversa del segundo, ya que 1 Hz = 1 s-1:
………………………………….ECUACION 2
MOVIMIENTO CIRCULAR
Un ejemplo sencillo de movimiento oscilatorio es la trayectoria descrita por una
partícula que recorre una circunferencia de manera periódica. En tal caso, la
longitud recorrida por la partícula en el período T a una velocidad angular de
giro es igual a la longitud de la circunferencia 2 . Por tanto:
…………………………………….ECUACION 3
Despejando la velocidad angular , se obtiene que:
……………………………….ECUACION 4
Por un sencillo cálculo trigonométrico, la ecuación del movimiento circular, que
permite hallar la posición de la partícula en cualquier instante t, se obtiene
como sigue:
……………………………ECUACION 5
Siendo R el radio de la circunferencia y
partícula en el instante inicial de medida.
el ángulo que fija la posición de la
GRAFICA 2.- Representación gráfica del movimiento circular
2.1.3 MOVIMIENTO ARMONICO SIMPLE (MAS)
Un tipo común de oscilación es el denominado movimiento armónico simple,
descrito como aquel que recorre una partícula que se desplaza en línea recta y
de forma periódica a ambos lados de un punto de equilibrio que se toma como
origen. La posición que ocupa la partícula en un momento dado se denomina
elongación, y su máxima separación con respecto al origen es la amplitud
(simbolizada por A).
El movimiento armónico simple se produce cuando, en todo instante, la
aceleración de la partícula oscilante es proporcional y de sentido contrario a la
coordenada de posición de la misma. Es decir:
…………………………………ECUACION 6
El movimiento armónico simple puede apreciarse como si fuera un movimiento
circular proyectado sobre el diámetro de la circunferencia. Por tanto, las
ecuaciones del movimiento armónico simple son formalmente idénticas a las
del circular. Si la amplitud del movimiento es A, su velocidad angular
posición angular inicial , se tiene que:
y su
…………………………..ECUACION 7
El período y la frecuencia del movimiento armónico simple guardan la misma
relación que en el caso del movimiento circular. Suponiendo que no existe
rozamiento, la energía mecánica del movimiento armónico simple se puede
escribir como:
……………………………....ECUACION 8
2.1.4 COMPARACION DE MOVIMIENTO SIMPLE CON
MOVIMIENTO CIRCULAR UNIFORME
El movimiento armónico simple tiene una simple e interesante relación con una
partícula girando en un círculo con rapidez uniforme. Considere una masa m
girando en un círculo de radio A con rapidez vm encima de una mesa como se
muestra en la figura 1 Visto desde arriba, el movimiento es un círculo. Pero una
persona que observa el movimiento desde el borde de la mesa lo ve como un
movimiento oscilatorio de ida y de vuelta, y esto corresponde precisamente a
un MAS como lo veremos ahora. Lo que la persona ve, y en lo que estamos
interesados, es la proyección del movimiento circular sobre el eje x, figura 1.
Para evidenciar que este movimiento es análogo al MAS, calculemos la
componente x de la velocidad vm designada v en la figura 1. Los dos
triángulos rectos en la figura 1 son semejantes, por lo que:
v
vm
o bien,
A2 x2
A ……………………………….ECUACION 9
v vM
x2
1 2
A
…………………………ECUACION 10
Esta es exactamente la ecuación para la rapidez de una masa oscilando con
MAS, ecuación 9, donde vm vmax . Además, podemos ver en la figura 1 que si
el desplazamiento angular en t=0 es
partícula habrá girado un ángulo
x A cos(
, entonces después de un tiempo t la
= wt , entonces
) A cos(wt
) ………………….…ECUACION 11
Pero que es aquí w ? la velocidad lineal vm de nuestra partícula que
experimenta movimiento rotatorio esta relacionado con w por vm = wA , donde
A es el radio del circulo. Para efectuar una revolución se requiere un tiempo T
, por lo que también tenemos vm 2 A / T , donde 2 A es la circunferencia del
circulo. Por consiguiente
w
vm 2 A / T
A
A
2 / T 2 f …………………..ECUACION 12
Donde T es el tiempo requerido para una revolución y f es la frecuencia. Esto
corresponde precisamente al movimiento de ida y vuelta de un oscilador
armónico simple. Así entonces, la proyección sobre el eje x de una partícula
girando en un círculo tiene el mismo movimiento que una masa bajo MAS.
Ciertamente, podemos decir que la proyección de un movimiento circular sobre
una línea recta es un MAS.
La proyección de un movimiento circular uniforme sobre el eje “y” es también
armónica simple. Así entonces, el movimiento circular uniforme puede
imaginarse como dos movimientos armónicos simples operando según ángulos
rectos.
Figura 1.- Análisis de un movimiento armónico simple como
Una vista lateral (b) de un movimiento circular (a)
2.1.5 EL PENDULO
Un péndulo consiste en un objeto pequeño suspendido del extremo de una
cuerda ligera, figura 2. Suponemos que la cuerda no se estira y que su masa
puede despreciarse respecto a la de la lentejuela. El movimiento de un péndulo
simple al oscilar (figura 2) con fricción despreciable se parece al movimiento
armónico simple: el péndulo oscila a lo largo del arco de círculo con igual
amplitud a cada lado de su punto de equilibrio y al pasar por su punto de
equilibrio tiene su rapidez máxima. Pero, ¿se trata realmente de un MAS? Es
decir,¿es la fuerza restauradora proporcional a su desplazamiento? Veámoslo.
El desplazamiento del péndulo a lo largo del arco esta dado por x
L , donde
es el ángulo que la cuerda forma con la vertical, L es la longitud de la cuerda,
como se muestra en la figura 3. Si la fuerza restauradora es proporcional a x o
a
, el movimiento será armónico simple. La fuerza restauradora es la
componente del peso mg , tangente del arco:
F
mgsen
……………………………….ECUACION 13
Donde el signo menos, como en la ecuación F
kx , significa que la fuerza
tiene sentido opuesto al desplazamiento angular
. Como F es proporcional al
seno de
y no a la misma, el movimiento no es un MAS. Sin embargo, si
pequeño, entonces sen
es casi igual a
es
cuando el último se especifica en
radianes. Esto puede verse observando el desarrollo en serie de sen , o
notando en la figura 3 que la longitud de arco x( Lq) tiene casi la misma
longitud que la cuerda ( Lsen ) , indicada por la línea recta de rayas, si
es
pequeño. Para ángulos menores de 150, la diferencia entre
es
, y sen
menor que 1%. Entonces, con muy buena aproximación para ángulos
pequeños,
F
Usando x
mgsen
mg
………………………….ECUACION 14
L , tenemos
F
mg
x ……………..……………..ECUACION 15
L
Entonces, para desplazamientos pequeños, el movimiento es esencialmente
armónico simple, ya que esta ecuación se ajusta a la ley de Hooke, F
donde la constante de fuerza efectiva es K
Kx ,
mg / L . Podemos entonces
escribir:
max
cos( t
) ………………………...ECUACION 16
Donde
obtener
decir ,
max
es el desplazamiento angular máximo y
2 / T . Para
K
, donde para k sustituimos mg / L , es
m
2
usamos la ecuación
2 f
(mg / L) / m ,o:
g
……………………………...ECUACION 17
L
La frecuencia f es entonces
f
1
2
2
g
………………………..….ECUACION 18
L
Y el periodo T es
T
1
f
2
L
………………………….….ECUACION 19
g
Un resultado sorprendente es que el periodo no depende de la masa del
péndulo. Usted habrá notado eso al empujar a un niño pequeño y a uno grande
en el mismo columpio. El periodo si depende de la longitud L
Sabemos que el periodo de un objeto bajo un MAS, incluido un péndulo simple,
no depende de la amplitud. Se dice que Galileo noto primero esto observando
una lámpara en oscilación en la catedral de Pisa. Este descubrimiento condujo
al reloj de péndulo, el primero realmente preciso, que llego a ser el estándar
durante siglos.
Como un péndulo no experimenta precisamente un MAS, el periodo depende
ligeramente de la amplitud, sobre todo para grandes amplitudes. La exactitud
de un reloj de péndulo será afectada después de muchas oscilaciones, debido
a la fricción; pero el resorte en un reloj de péndulo suministra energía para
compensar la fricción y para mantener la amplitud constante, de manera que el
tiempo indicado permanezca exacto.
Y es como podemos decir que el péndulo es otro sistema mecánico que
presenta movimiento periódico que consiste de una plomada parecida a una
partícula de masa suspendida por una cuerda ligera que es la longitud, donde
el extremo superior ocurre en un plano vertical y se impulsa por la fuerza
gravitacional. Se mostrara que, siempre y cuando el ángulo
sea pequeño, el
movimiento es el de un oscilador armónico simple.
En otras palabras, el periodo y la frecuencia de un péndulo simple solo
dependen de la longitud de la cuerda y de la aceleración debida a la gravedad.
Ya que el periodo es independiente de la masa, se concluye que todos los
péndulos simples que son de igual longitud y están en la misma ubicación
oscilan con el mismo periodo.
El péndulo simple se puede usar como cronometro porque su periodo solo
depende de su longitud y del valor local de g. También es un dispositivo
conveniente para hacer mediciones precisas de la aceleración en caída libre.
Tales mediciones son importantes porque las variaciones en los valores de g
pueden proporcionar información acerca de las ubicaciones de petróleo y otros
recursos subterráneos valiosos.
Figura 2.- fotografía de luz estroboscópica de la oscilación de un péndulo
Figura 3.- péndulo simple
2.1.6 OSCILACIONES AMORTIGUADAS Y FORZADAS
Oscilaciones Amortiguadas.
Los movimientos oscilatorios que se han considerado hasta ahora han
correspondido a sistemas ideales, es decir, sistemas que oscilan de manera
indefinida bajo la ecuación de una fuerza restauradora lineal. En muchos
sistemas reales las fuerzas disipativas, como la fricción, retardan el
movimiento. En consecuencia, la energía mecánica del sistema disminuye en el
tiempo y se dice que el movimiento esta amortiguado.
Un tipo común de fuerza retardadora es donde la fuerza es proporcional a la
rapidez del objeto en movimiento. Esta fuerza retardadora a menudo se
observa cuando un objeto se mueve a través del aire, por ejemplo. Debido a
que la fuerza retardadora puede expresarse como R
bv (donde b es una
constante llamada coeficiente de amortiguamiento) y la fuerza restauradora del
sistema es
kx , la segunda ley de Newton se puede escribir como:
Fx
kx bv max
dx
d 2x
kx b
m 2 ……………………ECUACION 20
dt
dt
Para solucionar esta ecuación se necesitan matemáticas que quizá aun no le
sean familiares, de manera que aquí simplemente se enunciara sin
demostración. Cuando la fuerza retardadora es pequeña, comparada con la
fuerza restauradora máxima, es decir, cuando b es pequeña, la solución para la
ecuación 20 es
b
x Ae2m cos( t
) ……………………...ECUACION 21
Donde la frecuencia angular de oscilación es
k
m
b
2m
2
…………………………ECUACION 22
Este resultado puede verificarse al sustituir la ecuación 20 en la 21
La figura 4a muestra el desplazamiento como una función del tiempo para un
objeto oscilando en la presencia de una fuerza retardadora, y la figura 4b
muestra uno de tales sistemas: un bloque unido a un resorte y sumergido en un
liquido viscoso, en donde se ve que cuando la fuerza retardadora es muy
pequeña comparada con la fuerza restauradora, el carácter oscilatorio del
movimiento se preserva perola amplitud disminuye en el tiempo, y el
movimiento finalmente cesa. Cualquier sistema que se comparte de esta
manera se conoce como oscilador amortiguado. Las líneas punteadas en la
figura 4a, las cuales definen la envolvente de la curva oscilatoria, representan
el factor exponencial en la ecuación 21. Esta envolvente muestra que la
amplitud decae exponencialmente con el tiempo. Para el movimiento con una
constante de resorte y masa de la partícula determinada, las oscilaciones se
amortiguan con mayor rapidez a medida que el valor máximo de la fuerza
restauradora.
(a)
(b)
figura 4.-a) grafica de desplazamiento versus tiempo para un oscilador amortiguado. Advierta la
disminución en amplitud con el tiempo. b) muestra un sistema de oscilación amortiguado.
Es conveniente expresar la frecuencia angular de un oscilador amortiguado en
la forma
2
0
Donde
0
b
2m
2
…………………………….ECUACION 23
k / m representa la frecuencia angular cuando no hay fuerza
retardadora y se llama frecuencia natural del sistema. Cuando la magnitud de
la máxima fuerza retardadora Rmax bvmax kA se dice que el sistema esta
subamortiguado. Conforme el valor de R tienda a kA , la amplitud de las
oscilaciones disminuye más y más rápidamente. Este movimiento se
representa por la curva en la figura 5. Cuando b alcanza un valor critico bc tal
que bc / 2m
0
el sistema no oscila y se dice que esta críticamente
amortiguado. En este caso, una vez liberado desde el reposo en cierta posición
de no equilibrio, el sistema regresa al equilibrio y ahí permanece. La grafica del
desplazamiento versus tiempo en este caso es la curva b en la figura 5.
Si el medio es tan viscoso que la fuerza retardadora es mas grande que la
restauradora, es decir, si Rmax bvmax kA y si b / 2m
0
el sistema esta sobre
amortiguado. Otra vez, el sistema desplazado, cuando tiene libertad de
moverse, no oscila, sino plenamente regresa a su posición de equilibrio.
Conforme aumenta el amortiguamiento el tiempo que le toma al sistema
aproximarse al equilibrio también aumenta, como indica la curva c en la figura
5.
En cualquier caso en que exista fricción, ya sea porque el sistema esta sobre
amortiguado o subamortiguado, la energía del oscilador finalmente tendera a
ser cero. La energía mecánica perdida se disipa en energía interna en el medio
retardador.
Fig.5.- graficas de desplazamiento versus tiempo para a) un oscilador subamortiguado, b)un
oscilador críticamente amortiguado y c) un oscilador sobre amortiguado
OSCILACIONES FORZADAS.
Es posible compensar la pérdida de energía en un sistema amortiguado
aplicando una fuerza externa que efectué trabajo positivo en el sistema. En
cualquier instante la energía puede darse al sistema por medio de una fuerza
aplicada que actúa en la dirección del movimiento del oscilador. Por ejemplo,
una niña en un columpio puede mantenerse en movimiento por medio de
empujones aplicados en el momento apropiado. La amplitud del movimiento
permanece constante si la entrada de energía por ciclo es exactamente igual a
la energía perdida como consecuencia del amortiguamiento. Cualquier
movimiento de este tipo recibe el nombre de oscilación forzada.
Un ejemplo común de una oscilador forzado es un oscilador amortiguado
impulsado por una fuerza externa que varía de modo periódico, tal como
F
Fext cos
t
donde
es la frecuencia angular de la fuerza periódica y Fext es
una constante. La suma de esta fuerza impulsora en el lado izquierdo de la
ecuación 20 produce
Fext cos
t
kx b
dx
d 2x
m 2 …………………….ECUACION 24
dt
dt
Después de un periodo suficientemente largo, cuando la entrada de energía
por ciclo es igual a la perdida de energía por ciclo, se alcanza una condición de
estado estable en el cual las oscilaciones prosiguen con amplitud constante. En
este momento, cuando el sistema esta en estado estable, la solución de la
ecuación 24 es
x Acos( t
) …………………...............ECUACION 25
Donde:
Fext / m
A
2
Y donde
0
2 2
0
b
m
2
………………………...ECUACION 26
k / m es la frecuencia angular del oscilador no amortiguado
(b=0). Se puede argumentar que en estado estable el oscilador debe tener
físicamente la misma frecuencia que la fuerza impulsora, por lo que la solución
que proporciona la ecuación 25 es la esperada. De hecho, cuando esta
solución se sustituye en la ecuación 24, uno descubre que es desde luego una
solución, siempre que la amplitud esta dada por la ecuación 26.
La ecuación 26 muestra que el movimiento del oscilador forzados no esta
amortiguado debido a que esta impulsado por una fuerza externa. El agente
externo proporciona la energía necesaria para cubrir las perdidas debidas a la
fuerza impulsora. En el caso de amortiguamiento pequeño, la amplitud se
vuelve muy grande cuando la frecuencia de la fuerza impulsora se acerca ala
frecuencia se acerca ala frecuencia natural de oscilación. El considerable
aumento en la amplitud cerca de la frecuencia natural
0
en ocasiones recibe
el nombre de frecuencia de resonancia del sistema.
La razón para oscilaciones de gran amplitud en la frecuencia de resonancia es
que la energía se transfiere al sistema en las condiciones más favorables. Esto
puede comprenderse mejor tomando la primera derivada con respecto al
tiempo de x en la ecuación 25, la cual produce una expresión para la velocidad
del oscilador. Al hacerlo se descubre que v es proporcional a sen( t
)
.cuando la fuerza aplicada F hace trabajo sobre el oscilador es igual al producto
punto F.v. Recuerde que la definición de potencia es “rapidez a la cual se
realiza el trabajo”. Dado que el producto F.v es un máximo cuando F y V están
en fase, se concluye que en la resonancia la fuerza aplicada esta en fase con
la velocidad y que la potencia transferida al oscilador es un máximo.
La figura 6 es una grafica de la amplitud como una función de la frecuencia
para el oscilador forzado, con y sin amortiguamiento. Observe que la amplitud
aumenta con la disminución del amortiguamiento (b
0) y que la curva de
resonancia se amplia conforme se incrementa el amortiguamiento. Bajo
condiciones de estado estable y en cualquier frecuencia de impulso se
aumenta
la
energía
perdida
debido
a
la
fuerza
amortiguadora;
en
consecuencia, la energía total promedio del oscilador permanece constante.
Cuando no hay fuerza amortiguadora (b=0), a partir de la ecuación 26 se ve
que la amplitud de estado estable se acerca al infinito cuando
0.
En otras
palabras, si no hubiera pérdidas en el sistema y se continuara impulsando un
oscilador inicialmente sin movimiento con una fuerza periódica que esta en fase
con la velocidad, la amplitud del movimiento se fortalecerá sin límite. Este
fortalecimiento sin límite no ocurre en la práctica debido a que siempre esta
presente algún amortiguamiento.
El comportamiento de un sistema oscilatorio impulsado después de que se
elimina la fuerza impulsora depende de b y de cuán cerca se encuentre
0.
de
Este comportamiento ocasionalmente se cuantifica por un parámetro
llamado factor de calidad Q. Cuanto mas próximo esta en un sistema de ser no
amortiguado, mayor es su Q. La amplitud de oscilación cae por un factor de
e( 2.718...) en Q / ciclos.
Fig 6.- grafica de amplitud versus frecuencia para un
oscilador amortiguado cuando una fuerza
impulsora
periódica esta presente. Cuando la frecuencia de la
fuerza impulsora es igual a la frecuencia natural
0
SUBTEMA 2.2 MOVIMIENTO ONDULATORIO
2.2.1 CONCEPTO Y TIPOS DE ONDAS
El movimiento ondulatorio aparece en casi todos los campos de la Física. Sin
duda alguna, la noción más intuitiva que tenemos del movimiento ondulatorio
está asociada con las ondas producidas por el viento o alguna otra
perturbación sobre la superficie del agua. Oímos un foco sonoro por medio de
las ondas (ondas sonoras) que se propagan en el aire o en cualquier otro
medio material- y las vibraciones del propio foco
constituyen una onda
denominada onda estacionaria. Muchas de las propiedades de la luz se
explican satisfactoriamente por medio de una teoría ondulatoria, estando
firmemente establecido hoy día que las ondas luminosas tienen la misma
naturaleza que las radiondas, las radiaciones infrarrojas y ultravioletas, los
rayos X y la radiación gamma.
Uno de los progresos más importantes de la Física del siglo XX ha sido el
descubrimiento de que toda la materia está dotada de propiedades ondulatorias
(ondas de materia) y que, por ejemplo, un cristal difracta del mismo modo un
haz de electrones que un haz de rayos X.
En este tema vamos a centrar nuestra atención en las ondas que se propagan
en los medios deformables o medios elásticos. Tales ondas, entre las que se
encuentran las ondas sonoras ordinarias, pueden denominarse ondas
mecánicas y se originan al desplazarse alguna porción de un medio elástico de
su posición normal, iniciándose así una oscilación respecto a su posición de
equilibrio. Entonces, debido a las propiedades elásticas del medio material, la
perturbación original se transmite a las porciones de materia vecina, y de ésta a
las siguientes, y así sucesivamente, de modo que la perturbación se propaga
por el medio, alcanzando a todas las porciones de éste, que quedarán
sometidas a movimientos análogos al del punto donde se inició la perturbación.
Obviamente, todos los puntos del medio no serán alcanzados simultáneamente
por la perturbación, ya que ésta se propaga con una velocidad finita que
depende de las propiedades (elásticas e inerciales, como veremos más
adelante) del medio, de modo que las partículas más alejadas del origen de la
perturbación comenzarán a moverse con un cierto retraso. En definitiva,
podemos decir que: la propagación de una perturbación en un medio constituye
un movimiento ondulatorio.
El movimiento ondulatorio transporta energía. Este transporte de energía, que
puede tener lugar a distancias considerables, se realiza sin necesidad de
desplazamiento de materia a gran distancia, ya que cada elemento del medio
transmite energía a los elementos vecinos.
Para que se propaguen las ondas mecánicas es necesario tener como soporte
un medio material. Sin embargo, no es necesario tal medio para la propagación
de ondas electromagnéticas (v.g., la luz), que pueden propasarse en el vacío,
aunque también se propagan en los medios materiales. Las propiedades del
medio material que determinan la velocidad de las ondas mecánicas en él son
su elasticidad y su inercia. Todos los medios materiales (aire, agua, acero, etc.)
poseen esas propiedades y en ellos pueden propagarse las ondas mecánicas.
Es la elasticidad la que da lugar a las fuerzas restauradoras sobre cualquier
elemento que se desplaza de su posición de equilibrio; es la inercia la que
determina la respuesta a esas fuerzas restauradoras.
El término de onda, como tendremos ocasión de comprobar, se refiere a un
modelo matemático que sirve para interpretar de manera análoga fenómenos
físicos de naturaleza muy diferente. En este tema tratamos de los diferentes
tipos de ondas que pueden existir.
Haremos el estudio de las ondas cuya forma es senoidal (ondas armónicas) y
los parámetros que la caracterizan: velocidad de fase, número de ondas,
longitud de onda, período, frecuencia, fase, amplitud, etc.
Las ondas se clasifican según la dirección de los desplazamientos de las
partículas en relación a la dirección del movimiento de la propia onda. Si la
vibración es paralela a la dirección de propagación de la onda, la onda se
denomina longitudinal. Una onda longitudinal siempre es mecánica y se debe a
las sucesivas compresiones (estados de máxima densidad y presión) y
enrarecimientos (estados de mínima densidad y presión) del medio. Las ondas
sonoras son un ejemplo típico de esta forma de movimiento ondulatorio. Otro
tipo de onda es la onda transversal, en la que las vibraciones son
perpendiculares a la dirección de propagación de la onda. Las ondas
transversales pueden ser mecánicas, como las ondas que se propagan a lo
largo de una cuerda tensa cuando se produce una perturbación en uno de sus
extremos, o electromagnéticas, como la luz, los rayos X o las ondas de radio.
En esos casos, las direcciones de los campos eléctrico y magnético son
perpendiculares a la dirección de propagación. Algunos movimientos
ondulatorios mecánicos, como las olas superficiales de los líquidos, son
combinaciones de movimientos longitudinales y transversales, con lo que las
partículas de líquido se mueven de forma circular.
En una onda transversal, la longitud de onda es la distancia entre dos crestas o
valles sucesivos. En una onda longitudinal, corresponde a la distancia entre
dos compresiones o entre dos enrarecimientos sucesivos. La frecuencia de una
onda es el número de vibraciones por segundo. La velocidad de propagación
de la onda es igual a su longitud de onda multiplicada por su frecuencia. En el
caso de una onda mecánica, su amplitud es el máximo desplazamiento de las
partículas que vibran. En una onda electromagnética, su amplitud es la
intensidad máxima del campo eléctrico o del campo magnético.
Atendiendo a la periodicidad de la perturbación local que las origina, las ondas
se clasifican en:
Longitudinales: Tome un resorte y estírelo sobre su escritorio con uno de sus
extremos en su mano y el otro fijo a la pared. Comprima rápido el extremo que
sostiene a lo largo del eje del resorte, como en la fig.7, sin regresar su mano a
la posición original. La compresión se propaga por el eje del resorte con una
velocidad que recibe el nombre de onda.
Si ahora extiende rápido el extremo que sostiene, como en la fig.8 de nuevo sin
regresar su mano a su posición original, se transmite un pulso anticompresivo
denominado rarefacción por eje del resorte. Una serie de compresiones y
rarefacciones que se desplazan a lo largo de los ejes del resorte. En dichas
perturbaciones, la oscilación de las partículas del resorte tiene lugar a lo largo
de la línea de propagación de la onda.
Las ondas cuya oscilación ocurre a lo largo de la línea de propagación de la
onda reciben el nombre de ondas longitudinales.
La velocidad de una partícula determinada del resorte es máxima cuando la
compresión o rarefacción de las espirales es máxima. Esta es una
característica de las ondas mecánicas longitudinales: las velocidades de las
partículas son máximas en el instante de máxima compresión y rarefacción.
Las ondas sonoras en el aire u otros gases son longitudinales; y se consideran
variaciones de densidad o presión que se propagan y son el resultado de
movimientos longitudinales de las partículas que forman el medio a través del
cual viaja la onda sonora. Las regiones de alta densidad son compresiones; las
regiones
de
densidad
reducida,
rarefacciones.
Dichas
variaciones
u
oscilaciones de densidad respecto del valor medio o ambiente son positivas en
el caso de compresiones y negativas en el de las rarefacciones.
Fig 7.- Al comprimir un extremo de un resorte, se propaga un pulso de compresión a lo largo de
el.
Fig 8.- Al tirar del extremo del resorte con
rapidez, se propagara una rarefacción a lo largo
de el.
Transversales: La perturbación del medio se lleva a cabo en dirección
perpendicular a la de propagación. En las ondas producidas en la superficie del
agua las partículas vibran de arriba a abajo y viceversa, mientras que el
movimiento ondulatorio progresa en el plano perpendicular. Lo mismo sucede
en el caso de una cuerda; cada punto vibra en vertical, pero la perturbación
avanza según la dirección de la línea horizontal. Ambas son ondas
transversales. Como se muestra en la figura 9.
Fig 9.- Plano de polarización de una onda trasversal
2.2.2 PROPAGACION DE UNA PERTURBACION.
Una onda es una perturbación que se propaga desde el punto en que se
produjo hacia el medio que rodea ese punto. Las ondas materiales (todas
menos las electromagnéticas) requieren un medio elástico para propagarse.
El medio elástico se deforma y se recupera vibrando al paso de la onda.
La perturbación comunica una agitación a la primera partícula del medio en que
impacta -este es el foco de las ondas- y en esa partícula se inicia la onda.
La perturbación se transmite en todas las direcciones por las que se extiende el
medio que rodea al foco con una velocidad constante en todas las direcciones,
siempre que el medio sea isótropo ( de iguales características físico- químicas
en todas las direcciones ).
Todas las partículas del medio son alcanzadas con un cierto retraso respecto a
la primera y se ponen a vibrar: recuerda la ola de los espectadores en un
estadio de fútbol. La forma de la onda es la foto de la perturbación
propagándose, la instantánea que congela las posiciones de todas las
partículas en ese instante. Curiosamente, la representación de las distancias
de separación de la posición de equilibrio de las partículas al vibrar frente al
tiempo dan una función matemática seno que, una vez representada en el
papel, tiene forma de onda.
Podemos predecir la posición que ocuparán dichas partículas más tarde,
aplicando esta función matemática. El movimiento de cada partícula respecto a
la posición de equilibrio en que estaba antes de llegarle la perturbación es un
movimiento vibratorio armónico simple. Una onda transporta energía y cantidad
de movimiento pero no transporta materia: las partículas vibran alrededor de la
posición de equilibrio pero no viajan con la perturbación.
2.2.3 MODELO DE ONDA PROGRESIVA
Hemos analizado la creación de una perturbación que se mueve a través de un
medio, tal como una cuerda estirada mediante un sencillo desplazamiento
arriba y abajo del extremo de la cuerda. Esto produce un pulso que se mueve a
lo largo del medio. Se si acude continuamente el extremo de la cuerda con un
movimiento armónico simple, se creara una onda continua. Si hacemos esto, la
cuerda adoptara la forma que se muestra en la curva de la figura 10a esta
forma se mantendrá entonces, pero moviéndose hacia la derecha. Esto es lo
que denominamos una onda senoidal, por que la forma de la figura 10 es la de
una función de seno. Al punto situado en la posición mas baja posible se le
denomina valle. La cresta y el valle se desplazan conjuntamente con la onda,
de modo que un determinado punto de la cuerda ira pasando alternativamente
por situaciones de cresta y de valle. En un movimiento ondulatorio ideal en un
medio ideal, cada partícula del medio se somete a un movimiento armónico
simple alrededor de su posición de equilibrio.
A la hora de describir una onda senoidal, hay tres características físicas
importantes: la longitud de onda, la frecuencia y la rapidez de onda. Una
longitud de onda es la distancia minima entre dos puntos idénticos cualesquiera
en una onda como, por ejemplo, crestas adyacentes o valles adyacentes; esto
se ilustra en la figura 10a, que muestra una grafica del desplazamiento en
función de la posición para una onda senoidal en un instante dado. La letra
griega
(lambda) se utiliza para denotar la longitud de onda.
Fig.10(a) la longitud de onda
de una onda es la
Distancia entre crestas adyacentes o valles
Adyacentes
(b) el periodo T de una onda es el tiempo que
tarda la onda en recorrer una long. de onda
onda
La frecuencia de las ondas senoidales es la misma que la frecuencia del
movimientos armónico simple de cada una de las partículas del medio. El
periodo T de la onda es el intervalo de tiempo mínimo que tarda una partícula
del medio al someterse a un ciclo entero de oscilación y es igual al inverso de
la frecuencia:
T
1
……………………….………ecuación 27
f
La figura 10b muestra una grafica de la posición en función del tiempo para una
partícula del medio, como una onda senoidal que pasa a través de su posición.
El periodo es el tiempo que transcurre entre los instantes en los que una
partícula tiene desplazamientos y velocidades idénticos.
Las ondas viajan a través del medio a una determinada rapidez de onda, que
depende de las propiedades del medio que esta siendo perturbado. Por
ejemplo, las ondas sonoras viajan en el aire, cuando éste está a unos 20 0 C,
con una rapidez aproximada de 343m/s, mientras que la rapidez del sonido en
la mayoría de los sólidos es mayor de 343m/s.
Otro parámetro importante de la onda de la figura 10 es la amplitud de la onda.
La amplitud es el máximo desplazamiento de una partícula del medio con
relación a su posición de equilibrio. Se suele denotar por A y equivale a la
amplitud del movimiento armónico simple de las partículas del medio.
En la figura 11 se muestra un método para producir una onda senoidal que se
desplace a lo largo de una cuerda de gran longitud. Se conecta un extremo de
la cuerda a una placa de metal a la que se hace vibrar. A medida que la placa
oscila verticalmente con movimiento armónico simple, se genera en la cuerda
una onda que se desplaza moviéndose hacia la derecha. La figura 11 muestra
una serie de instantáneas de la onda, a intervalos de un cuarto de periodo.
Cada partícula de la cuerda, por ejemplo, P, oscila verticalmente en la dirección
y con un movimiento armónico simple. Por tanto, se puede tratar cada
segmento de la cuerda a la frecuencia de vibración de la placa que mueve a la
cuerda. Aunque cada segmento oscila en la dirección y , la onda viaja en la
dirección xa , una rapidez v . Por supuesto, esto corresponde con la definición
de una onda trasversal. En este caso, la energía transportada por la onda
progresiva es suministrada por la placa que vibra.
Fig 11.- un método para producir una onda senoidal en una cuerda continúa. El extremo
izquierdo de la cuerda se conecta a una placa metálica a la que se hace vibrar. Cada segmento
de la cuerda, como, por ejemplo, el punto P, oscila con un movimiento armónico simple en la
dirección vertical.
En los primeros capítulos de este libro, hemos desarrollado varios modelos
analíticos basados en el modelo de partícula. El modelo de onda nos permitirá
estudiar otros modelos analíticos que nos servirán de ayuda en la resolución de
problemas. Una partícula ideal tiene un tamaño cero; por otro lado, podemos
construir objetos físicos de tamaño distinto de cero como combinaciones de
partículas. Por tanto, podemos considerar la partícula como un elemento
constitutivo básico. Una onda ideal tiene una única frecuencia y es
infinitamente larga; es decir, la onda existe a través de todo el universo. El
modelo de onda parte de una onda ideal que tiene una sola frecuencia, longitud
de onda, rapidez de onda y amplitud. Partiendo de esto, vamos a describir
ondas en una diversidad de situaciones que nos sirvan como modelos
analíticos que nos ayuden a resolver problemas. En la siguiente sección,
vamos a desarrollar un poco más nuestra representación matemática del
modelo de onda.
Analicemos con más detalle los aspectos matemáticos de una onda senoidal.
(Figura 12) la curva punteada representa una instantánea de una onda senoidal
ene l instante t
0 y la curva fija representa una instantánea de la onda en un
momento posterior
t . En los siguientes párrafos desarrollaremos las
características principales y las representaciones matemáticas del modelo de
una onda progresiva. Este modelo analítico se utiliza en situaciones en las que
una onda se mueve a través del espacio sin interactuar con otras ondas o
partículas.
Para
t
0 , la curva punteada de la figura 12. Se puede describir
matemáticamente como
y
Asen
2
x
…………………………ecuación 28
Donde la amplitud A, como siempre, representa el valor máximo del
desplazamiento y
es la longitud de onda, tal como lo definimos en la figura
10a. De esta manera vemos que le valor de y es la misma cuando x se
incrementa en un múltiplo entero de
. Si la onda se mueve hacia la derecha
con rapidez v , la función de onda en un instante posterior t es
y
Asen
2
( x vt)
………………….……ecuación 29
Es decir, la onda senoidal se ha desplazado hacia la derecha una distancia vt
en el instante t como en la figura 12. Observe que la función de onda tiene la
forma
f ( x vt) ……………………….….ecuación 30
y representa a una onda progresiva hacia la derecha. Si la onda fuera
progresiva hacia la izquierda, la cantidad x vt debería ser reemplazada por
x vt .
Dado que el periodo T es el tiempo que tarda la onda en recorrer la distancia
correspondiente a una longitud de onda, la rapidez, la longitud de onda y el
periodo están relacionados mediante la ecuación.
v
T
………………………….…..ecuación 31
Sustituyendo la ecuación 31 en la ecuación 30, tenemos que
y
Asen 2
x
t
T
……………….……ecuación 32
Esta forma de la función de onda muestra la naturaleza periódica de y. Advierta
que con frecuencia se usara y en lugar de y( x, t ) , con una notación abreviada.
En cualquier tiempo dado t , y tiene el mismo valor en las posiciones
x, x
, x 2 , y así sucesivamente. Además, en cualquier posición
determinada x , el valor de y es el mismo en los tiempos t, t T , t 2T , y así
sucesivamente.
La función de onda se expresa en una forma conveniente al definir otras dos
cantidades, el número de onda angular k y la frecuencia angular
Numero de onda angular
2
k
…………………………..ecuación 33
2
T
Frecuencia angular
:
2 f
……………………...ecuación 34
Al usar estas definiciones, la ecuación 34 se puede escribir en la forma mas
compacta
Función de onda para una onda sinusoidal
y Asen(kx
t ) ……………….ecuación 35
Al usar las ecuaciones 34 y 33, la rapidez de onda v originalmente conocida
en la ecuación 31 se expresa en las formas alternativas siguientes:
v
Rapidez de una onda sinusoidal
…………………………..ECUACION 36
k
v
f
…………………………..…..ECUACION 37
La función de onda conocida en la ecuación 35. Supone que la posición vertical
y de un elemento del medio es cero en x 0 y t
0 . Este no necesita ser el
caso. Si no lo es, la función de onda por lo general se expresa en la forma
Expresión general para una onda sinusoidal
y Asen(kx
t
) …….ECUACION 38
Donde
es la constante de fase. Esta constante se determina a partir de las
condiciones iniciales.
Fig.12.- Una onda senoidal unidimensional progresiva hacia la derecha con una rapidez
curva punteada representa una instantánea de la onda en el instante
t
representa una instantánea en un momento posterior
0
v . La
y la otra curva
t
2.2.4 VELOCIDAD DE UNA ONDA.
Recuerde que una onda es una alteración o disturbio que viaja o se mueve.
La velocidad de la onda es una descripción de cuán rápido viaja una onda. La
velocidad de la onda está relacionada con la frecuencia, el período y la
longitud de onda a través de las simples ecuaciones:
……………………………ECUACION 39
…………………………..ECUACION 40
Donde v es la velocidad de la onda,
es la longitud de onda, T es el período,
y f es la frecuencia. La velocidad de la onda se mide en unidades de metros
por segundo (m/s). Por ejemplo, la nota musical “A” es un sonido con una
frecuencia de 440 Hz. La longitud de onda de una onda es de 78.4 cm. ¿Cuál
es la velocidad de una onda sonora?
Para determinar la velocidad de una onda, podemos usar la ecuación 2 y
sustituir los valores dados por longitud de onda y frecuencia, asegurándonos
que estamos usando unidades Standard.
f= 440 Hz
λ= 78.4cm = 0.784 m
v= λf =(0.784m)(440 Hz)=345 m/s
El valor (345 m/s) es el valor aproximado de la velocidad del sonido en el
aire. Cuán interesante es esto, que la velocidad del sonido en el aire depende
de la temperatura y la presión. Un músico que toca un instrumento de viento,
como la trompeta, puede afinar su trompeta en la base de una montaña,
escalar la montaña hasta donde la presión del aire es más baja, y encontrar
que la trompeta ya no está afinada. De manera similar, un cambio de
temperatura en el aire también puede cambiar el tono del instrumento.
Tal como ilustra el ejemplo anterior, las ondas están a nuestro alrededor en la
vida cotidiana. Los antiguos griegos empezaron el estudio de las ondas
pensando sobre la música, pero ahora casi todas las ramas de la física incluyen a
las ondas de una u otra manera.
Del análisis del movimiento ondulatorio y de la definición de velocidad v :
v
d
t
……………………………ECUACION 41.
Donde d es la distancia que se recorre en un tiempo t , se puede determinar
una expresión para la velocidad de la onda. Por definición, el periodo T de
una onda es el tiempo en el que se transmite una oscilación completa. Si la
longitud de la onda es λ. Por lo tanto, la velocidad de la onda será:
v
…………………………………..ECUACION 42
El periodo T esta relacionado con la frecuencia f de la onda de acuerdo
con la siguiente ecuación.
1
f
T
…………………………………ECUACION
43
Sustituyendo esta expresión en la ecuación 42, obtenemos otra expresión
para la velocidad de la onda.
v
f
………………………………….ECUACION 44
2.2.5 REFLEXIÓN Y TRANSMISIÓN DE ONDAS.
Cuando una pulsación que se mueve a lo largo de una cuerda alcanza uno de
sus extremos, se refleja. Si el extremo esta fijo, como en la figura 12a, la
pulsación regresa invertida. Esto se debe a que cuando el borde de entrada
de la pulsación alcanza la pared, la cuerda se levanta por encima del punto de
unión de la cuerda. Según la tercera ley de Newton, la pared empuja hacia
abajo con igual fuerza. La cuerda, siendo mucho más ligera, se mueve hacia
abajo para formar la pulsación invertida. Podemos estudiar el movimiento del
extremo libre de una cuerda atándola a un anillo que se desliza sobre una
varilla, como se ve en la figura 12b. En este caso, la cuerda no esta sujeta a
restricción vertical alguna; por tanto, la pulsación reflejada no está invertida.
Figura 12
a) cuando una pulsación en una cuerda se refleja en un extremo fijo, regresa invertida.
(b) En un extremo libre, la pulsación que se refleja no está invertida .
Figura 13 Los detalles del proceso de reflexión pueden reconstruirse, superponiendo una pulsación
imaginaria y la pulsación real.
Figura 14. Cuando una pulsación llega a la frontera entre dos cuerdas diferentes, en parte se refleja y
en parte se transmite.(a) si la segunda cuerda es mas pesada, la pulsación reflejada se invierte. (b) si la
segunda cuerda es más ligera, la pulsación reflejada no se invierte.
Los detalles del proceso de reflexión pueden reconstruirse superponiendo la
pulsación real y una pulsación imaginaria que se aproxima desde la derecha,
como vemos en la figura 13. El desplazamiento neto en cualquier punto está
dado por el principio de superposición. Nótese que en un instante dado, el
desplazamiento del extremo libre es el doble de la altura de la pulsación
original.
Entre los casos limites de un extremo fijo o de un extremo libre, una pulsación
puede llegar a la frontera entre una cuerda ligera y una cuerda pesada.
Esto da por resultado una reflexión parcial y una transmisión parcial. Puesto
que las tensiones son las mismas, las magnitudes relativas de las velocidades
de onda están determinadas por la densidad de masa. En la figura 14a, la
pulsación proviene de la cuerda ligera. La cuerda pesada se comporta de
manera semejante a una pared pero puede moverse, de modo que se
transmite parte de la pulsación original ala cuerda pesada. En la figura 14b, la
pulsación proviene de la cuerda pesada. La cuerda ligera ofrece muy poca
resistencia y ahora se aproxima a un extremo libre. Así, la pulsación reflejada
no se invierte.
2.2.6 TRANSFERENCIA DE ENERGÍA MEDIANTE ONDAS
SINUSOIDALES.
Las ondas transportan energía de un lugar a otro. Como las ondas viajan a
través de un medio, la energía es transferida como energía vibratoria de
partícula a partícula del medio. Para una onda senoidal de frecuencia f , las
partículas se mueven en un MAS al pasar la onda, y a cada partícula tiene
una energía E
1 2
kD donde DM es el desplazamiento máximo (amplitud)
2 M
de su movimiento, transversal o longitudinal.
E
1
2
kDM
2
2
2 mf 2 DM
……………………ECUACION 45
Para ondas tridimensionales que viajan en un medio elástico, la masa m
pv ,
donde p es la densidad del medio y v es el volumen de una pequeña porción
del medio. El volumen V
Al , donde A es el área transversal a través de la
cual viaja la onda y l la podemos escribir como la distancia que viaja la onda
en un tiempo t , como l = v t , donde v es la rapidez de la onda. Entonces
m pv = pAl = pAvt , y
E 2
2
pAvf 2 DM2
……………………..ECUACION
46
De esta ecuación tenemos el resultado importante de que la energía
transportada por una onda es proporcional al cuadrado de la amplitud y al
cuadrado de la frecuencia. La rapidez promedio de energía transferida es la
potencia promedio P:
_
P
E
I
2 pAvf 2 DM2
……………………..ECUACION 47
Finalmente la intensidad I de una onda se define como la potencia promedio
transferida a través de un área unitaria perpendicular a la dirección del flujo de
energía:
I
P
2 2vpf 2 DM2 …………………….ECUACION 48
A
Si una onda fluye desde la fuente en todas direcciones, se trata de una onda
tridimensional. Ejemplos son las ondas sonoras que viajan en el aire, las
ondas sísmicas y las ondas de luz. Si el medio es isótropo, se dice que la
onda es una onda esférica. Conforme la onda se mueve hacia el exterior, la
energía que lleva se dispersa sobre un área cada vez mayor ya que el área
superficial de una esfera de radio r es 4 r 2 . La intensidad de una onda es
entonces.
P
A
I
P
4 r2
………………………..….ECUACION 49
Si la potencia de salida P es constante, entonces la intensidad decrece
según el cuadrado inverso de la distancia desde la fuente:
1
r2
I
……………….(onda esférica) ECUACION 50
Si consideramos dos puntos a distancias r1 y r2 desde la fuente, como en la
figura 15, entonces P / 4 r12 y I 2
P / 4 r22 , por lo que
r12
r22
I2
I1
………………………………..ECUACION 51
Por ejemplo la distancia se duplica ( r2 / r1
su valor anterior;
I 2 / I1
1
2
2
2 ), la intensidad se reduce a
1
de
4
1
.
4
La amplitud de una onda también decrece con la distancia. Como la
intensidad es proporcional al cuadrado de la amplitud (ecuación 49) entonces
la amplitud debe decrecer según 1/r, de manera que la ecuación 50 será
proporcional a 1/ r 2 ecuación 51; es decir,
Dm
1
r
……………………………..…ECUACION 52
Para ver esto directamente de la ecuación 48, consideremos de nuevo dos
distancias diferentes desde la fuente r1 y r2 . Para una potencia de salida
constante A1DM2 2 , donde DM1 y DM 2 son las amplitudes de la onda en r1 y r2 ,
respectivamente. Como A1
4
2
1
DM 2
DM 1
y A2
4 r22 , tenemos DM2 1r12 = D2M 2r22 ,0
r1
……………………………….ECUACION 53
r2
Cuando la onda esta dos veces mas lejos desde la fuente, la amplitud es la
mitad de grande, siempre que ignoremos el amortiguamiento debido a la
fricción.
Fig 15.- una onda viajando hacia fuera desde la fuente tiene forma esférica. Se muestran dos
crestas diferentes de radio r1 y r2.
SUBTEMA 2.3. EQUIPO DE EXPERIMENTACION PARA
OSCILACIONES MECANICAS
El sistema de oscilaciones mecánicas FICER modelo SOSM-01 es un conjunto
de dispositivos mecánicos y electrónicos que se emplea para el estudio y el
análisis del movimiento oscilatorio del péndulo simple y del sistema masaresorte.
El sistema de oscilaciones mecánicas esta constituido por las siguientes partes:
MARCO BASICO
CONTADOR DE OSCILACIONES
CONJUNTO DE ACCESORIOS
El marco básico modelo SOSMB-01 es una estructura metálica con cubierta de
aluminio que sirve para instalar sistemas oscilatorios, un electro magneto de
sujeción opto electrónico de oscilaciones.
El contador de oscilaciones modelo CDO-01 es un instrumento electrónico con
base en un microprocesador que sirve para medir el numero de ciclos que han
pasado, el tiempo total transcurrido desde el inicio del movimiento y el periodo
de un ciclo dado.
El conjunto de accesorios esta constituido principalmente por el sensor opto
electrónico de oscilaciones modelo SOSSO-01, que se emplea para realizar un
muestreo del movimiento, y por el electro magneto de sujeción modelo ESSFL03, que se utiliza para retener el cuerpo oscilante. Además, tiene un conjunto
de herrajes de sujeción, un resorte metálico, una esfera metálica, un recipiente
cilíndrico, balines y una cuerda inextensible.
2.3.1 DESCRIPCION DEL MARCO BASICO.
En la figura 16 se muestra el marco básico, donde se indican con los números
del 1 al 5 sus diferentes partes.
Fig 16.- marco básico
1.- BASE
Es una estructura metálica con cubierta de aluminio provista de cuatro orificios
para sujetar el marco básico. En la base se instalan los dispositivos del sistema
de oscilaciones mecánicas.
2.- GUIAS
Son dos perfiles metálicos con sección transversal cuadrada, uno colocado en
el centro (guía central) y el otro en la orilla del marco básico. En estas guías se
insertan las nueces que sostienen al electro magneto de sujeción y al sensor
opto electrónico de oscilaciones.
3.- DISPOSITIVOS DE SUJECION DE LOS SISTEMAS OSCILATORIOS.
Esta formado por dos piezas de aluminio anodinado que son unidas por un
tornillo. Tiene dos orificios par pasar la cuerda inextensible.
Sun función es sujetar la cuerda y el resorte de los sistemas oscilatorios. En la
figura 17 se muestra este dispositivo.
Fig17.- Dispositivo de sujeción de los sistemas oscilatorios
4.- GUIAS ANGULARES.
Son cuatro líneas radiales que sirven como referencia para asegurar que en el
modelo matemático del movimiento del péndulo sea valida la aproximación. Las
líneas externas forman un ángulo de diez grados con la vertical y cada línea
interna un ángulo de cinco grados.
2.3.3 CARACTERISTICAS DEL CONTADOR DE OSCILACIONES.
Cara frontal
En la figura 18, se muestra la cara frontal del contador de oscilaciones, en
donde sus diferentes partes y controles se indican con los números del 1 al 5.
Fig 18.- cara frontal del contador de oscilaciones
1.- Control de Encendido
Es un interruptor tipo balancín iluminado y se usa para encender o
apagar el instrumento.
2.-Exhibidor
Es un exhibidor de cristal líquido de dos líneas. En la línea superior
indica el número de ciclos transcurridos desde el inicio del movimiento y
el tiempo acumulado. En la línea inferior se indica el último ciclo y su
respectivo periodo.
3.-Modo
Es in interruptor de tres posiciones. Se usa para controlar el Exhibidor de
Cristal Liquido. Cuando el botón de este interruptor esta en la posición 1,
se retiene fija la línea superior del Exhibidor, permitiendo anotar el total
de ciclos desde el inicio del movimiento y el tiempo empleado en su
ejecución. En la posición 0, el exhibidor estará mostrando las mediciones
continuamente. Con el botón en la posición 2, se mantiene fija la línea
inferior del exhibidor, dando la oportunidad de tomar la última nota del
número del último ciclo y superyodo respectivo. Esto último permite
calcular el amortiguamiento del movimiento del péndulo.
4.-ICA (Indicador del contador activado)
Es un indicador luminoso intermitente que sirve para Mostar que el
contador de oscilaciones esta en operación.
5.-Iniciar
Es un interruptor momentáneo que cuando se mantiene oprimido,
energiza el Electromagneto de Sujeción, y cuando se suelta lo deja sin
energía. Al apretar y soltar este interruptor, se borra la información
mostrada en el Exhibidor y se inicia un nuevo registro de las
oscilaciones.
Cara Posterior
La figura 19 muestra la cara posterior del contador de oscilaciones. Sus partes
se indican con los números del 1 al 4.
Fig 19.- cara posterior del contador de oscilaciones
1.- Censor Optoelectrónico
Es un receptáculo para conector tipo estéreo, en el que se conecta la terminal
del censor Optoelectrónico de Oscilaciones.
2.- Electromagneto
Son dos receptáculos para conector tipo banana, en los que se conectan las
terminales del Electromagneto de sujeción. A través de estas salidas se
suministra el voltaje y la corriente que requiere el Electromagneto.
3.- Cordón de Línea
Esta equipado con clavija polarizada y sirve para conectar el Contador de
Oscilaciones a la línea de alimentación eléctrica de 117 volts, 60 Hz.
4.- Porta fusible
Es el compartimiento para el fusible de 0.5 amperes, a 120 volts, que protege al
instrumento de una eventual sobrecarga en la línea de alimentación eléctrica
2.3.3 DESCRIPCION DE LOS ACCESORIOS DEL CONTADOR
DE OSCILACIONES
1.- Censor Optoelectrónico de Oscilaciones
En la figura cinco, se muestra el Censor Optoelectrónico de Oscilaciones
FICER modelo SOSSO-01.
Fig 20.- sensor Optoelectrónico de oscilaciones
Es un dispositivo provisto de un par acoplado emisor- detector, que funciona en
la banda infrarroja y que cuando esta conectado al contador de oscilaciones,
realiza el muestreo del movimiento en los sistemas oscilatorios que registra el
contador.
Además, este dispositivo esta provisto de una nuez giratoria con la que se
sujeta a la guía central del marco básico y que a su vez le permite colocarse en
posición vertical u horizontal. Se conecta al contador de oscilaciones por medio
de su conector tipo estéreo, en el receptáculo censor Optoelectrónico.
2.- Electromagneto de sujeción
En la figura 21 se muestra el Electromagneto de sujeción FICER, modelo
ESSFL-03.
Fig 21.- electromagneto de sujeción.
Este se utiliza para sujetar magnéticamente las masas de los sistemas
oscilatorios.
Se conecta al contador de oscilaciones, por medio de sus dos conectores, uno
rojo y otro negro, en los receptáculos de los mismos colores de la entrada
ELECTROMAGNETO.
3.- porta electro magneto
El porta electro magneto FICER, modelo SOSPE-01, es una varilla de acero
que tiene un orificio en uno de sus extremos, el cual sirve para instalar el
electro magneto de sujeción, como se indica en la figura siete.
Fig 22.- portaelectromagneto y electromagneto de sujecio
4.-Nuez giratoria
Es un dispositivo de aluminio que tiene tornillos opresores.
Está constituido por dos partes: una que sirve para sujetar el porta electro
magneto y la otra para instalarle en las guías del marco básico. La primera
puede girar sobre la otra, lo que permite ajustar la posición angular del porta
electro magneto, y la segunda para cambiar la posición vertical de este.
En la figura 23 se muestra la Nuez Giratoria FICER, modelo SOSNG-01, con el
porta electro magneto, instalada en el marco básico.
Fig 23.- nuez giratoria
5.-Sistemas Oscilatorios
Estos dispositivos son el péndulo, constituido por una esfera metálica y una
cuerda inextensible, y el sistema cuerpo- resorte, formado por un resorte
metálico y un conjunto de balines colocados en un recipiente cilíndrico.
2.3.4 PROBLEMAS GENERALES DE OPERACIÓN, CAUSAS Y
SOLUCIONES
Problema.
Al conectar el contador de oscilaciones a la línea de suministro de voltaje y
accionar el interruptor de encendido, éste no se ilumina.
Posibles causas.
1.-no hay voltaje en la línea de alimentación eléctrica o este no es el
adecuado.
2.-el fusible esta dañado.
3.-el circuito electrónico de control o alguna de las conexiones se daño.
Soluciones respectivas.
1.-verifique con un voltímetro de corriente alterna si hay voltaje en la
línea de alimentación eléctrica y revise que este sea aproximadamente
117 volts, 60 hz.
2.- verifique con un óhmetro el fusible; si esta dañado, sustitúyalo con
otro en buen estado con las mismas especificaciones.
Nota.- no trate de remplazarlo con un simple alambre(puente); esto
puede causar daños mayores al instrumento.
Problema
Con el contador de oscilaciones conectado a la línea de alimentación eléctrica
e iluminado e interruptor de encendido, no aparece ningún texto en el exhibidor
de cristal líquido.
Posible causa.
1.- El circuito electrónico del contador de oscilaciones se dañó.
Solución respectiva.
1.-Recurra a la facultad de ciencias físico matemáticas, para una pronta
y efectiva solución al problema.
Problema.
Cuando se trabaja con el censor opto electrónico de oscilaciones instalado en
el marco básico y conectado al contador de oscilaciones, el censor no registra
el movimiento oscilatorio.
Posibles causas.
1.- El haz infrarrojo del emisor no es interrumpido por el cuerpo que
oscila.
2.-No hay buen contacto entre el conector del Censor Optoelectrónico de
Oscilaciones y el receptáculo de entrada censor Optoelectrónico del
contador de oscilaciones.
3.-Debido al mal trato, se desoldaron uno o varios hilos del cable en el
conector tipo estéreo del censor.
4.-Debido al mal trato, se rompieron uno o varios hilos del cable del
interruptor en el interior del cuerpo del mismo; o bien, a causa de un
golpe fuerte, se dañó el sistema emisor detector de luz infrarroja en el
interior del censor.
Soluciones respectivas.
1.- Acomode el Censor Optoelectrónico de oscilaciones de tal forma que
el cuerpo que oscila interrumpa el haz infrarrojo; esto es, que el cuerpo
pase entre los orificios del censor.
2.-Insertar totalmente el vástago del conector en el receptáculo
correspondiente del contador de oscilaciones.
3.-Si se cuenta con un técnico, deberá soldar nuevamente los hilos del
cable al conector, teniendo en cuenta dónde estaban soldados
anteriormente.
Problema.
El electro magneto de sujeción, conectado al contador de oscilaciones
(encendido), no retiene el cuerpo metálico que oscila cuando se mantiene
oprimido el botón del interruptor INICIAR.
Posibles causas.
1.- No hay buen contacto entre los conectores del electro magneto de
sujeción y los receptáculos de la salida ELECTROMAGNETO del
contador de oscilaciones.
2.-El contador de oscilaciones se dañó, debido a un corto circuito
causado por conectar una carga inadecuada en las salidas para el
Electromagneto de sujeción.
3.- Debido al uso rudo, se rompieron o desoldaron los cables de los
conductores tipo banana del electro magneto de sujeción.
4.-A causa de un estirón fuerte, uno de los cables del electro magneto de
sujeción o ambos se desprendieron internamente del alambre de
magneto que constituye la bobina del mismo.
5.- La bobina está dañada permanentemente, debido a que el electro
magneto de sujeción se conectó a otra fuente que no es la adecuada.
Soluciones respectivas.
1.-Insertar totalmente los conectores del electro magneto de sujeción en
los receptáculos correspondientes del contador de oscilaciones.
2.-verifique con un voltímetro la diferencia de potencial entre los
receptáculos de la salida del electro magneto; ésta deberá ser
aproximadamente de 15 volts cuando se mantiene oprimido el botón del
interruptor
INICIAR. Esta operación se realiza con el contador de
oscilaciones encendido.
3.- Si cuenta con un técnico, deberá soldar nuevamente los cables a los
conectores.
4.- Si las puntas del alambre del magneto de la bobina se rompieron o
desoldaron de su cable, bastará con soldar nuevamente los cables del
electro magneto de sujeción a las puntas del alambre de la bobina.
5.- Para verificar si existe daño permanente en el interior de la bobina,
bastará medir su resistencia eléctrica con ayuda de un óhmetro; ésta
deberá ser aproximadamente de 46 ohms cuando no hay daño. Si no
hay continuidad, la bobina del electro magneto deberá ser reemplazada
por otra de las mismas características.
2.3.5. USO ADECUADO DEL SISTEMA DE OSCILACIONES
MECÁNICAS.
Del contador de oscilaciones.
1.- NUNCA conecte el contador de oscilaciones a una línea de
alimentación eléctrica que no sea de 117 volts, 60Hz.
2.- NO conecte dispositivo alguno que no sea el indicado, en la salida
electro magneto del contador de oscilaciones; de lo contrario, provocará
un corto circuito que causará daños al instrumento.
Del marco básico.
1.- CUANDO instale el censor Optoelectrónico de oscilaciones y el
electro magneto de sujeción en las guías del marco básico, cerciórese
de que los tornillos opresores de sus nueces presionen adecuadamente
las guías.
2.- NO maltrate la cubierta ni las guías del marco básico.
3.-INSTALE el marco básico en un lugar adecuado de su laboratorio y
nivélelo verticalmente.
De los accesorios
1.- NO maltrate el censor Optoelectrónico de oscilaciones ni el electro
magneto de sujeción; golpearlos o estirarlos de los cables produce
daños, algunos de ellos permanentes.
2.- SI se tiene sospecha o certeza de alguna falla en uno de los
accesorios, no intente repararlo; comuníquese
con los técnicos
autorizados.
3.- NO utilice los accesorios con otros aparatos, ya que pueden ser
dañados permanentemente. Los accesorios han sido diseñados para
funcionar con el sistema de oscilaciones mecánicas, en especial.
SUBTEMA 2.4 EXPERIMENTOS CON SISTEMA DE
OSCILACIONES
EXPERIMENTO 1-SO
2.4.1 Relación entre la longitud y el período de un péndulo simple
2.4.1.1 Objetivo del experimento
Comprobar la relación que hay entre la longitud de un péndulo simple y su
periodo de oscilación.
2.4.1.2 Equipo y material empleado
Marco básico FICER, modelo SOSMB-01
Contador de oscilaciones FICER, modelo CDO-01
Censor Optoelectrónico de oscilaciones FICER, modelo SOSSO-01
Electromagneto de sujeción, modelo ESSFL-03
Porta electromagneto, modelo SOSPE-01
Nuez giratoria, modelo SOSNG-01
Esfera metálica con sistema de sujeción, modelos SOSEM-01
Cuerda inextensible
Cinta métrica (no incluida en el SOSM-01)
2.4.1.3 Diseño del experimento
Para comprobar la relación que existe entre la longitud de un péndulo simple y
su periodo de oscilación, se deben seguir los siguientes pasos.
a) se debe escoger un péndulo cuya masa oscilante sea mucho mayor que
la masa de la cuerda, de tal forma que esta última sea despreciable.
b) El cuerpo se separa de su posición de equilibrio y se suelta para que
comience el sistema oscilatorio. El ángulo que formen la cuerda y la
vertical debe ser igual o menor que 10º para que se cumpla la
aproximación sen θ ≈ θ.
c) Se mide el tiempo de veinte oscilaciones y se obtiene el periodo, el cual
será utilizado como dato experimental. Se registran el periodo y la
longitud del péndulo.
d) Se repiten los pasos anteriores del experimento para diferentes
longitudes del péndulo. Los períodos y las longitudes del péndulo se
registran en una Tabla de Datos.
e) Con los resultados de la Tabla de Datos se hacen dos gráficas; una del
período contra la longitud del péndulo y la otra del cuadrado del período
contra la longitud del péndulo.
f) Se obtiene una relación experimental a partir de las gráficas o bien, se
puede realizar una regresión potencial a partir de los datos registrados.
2.4.1.4 Procedimiento.
1.- Instale el equipo como se muestra en la figura 24 y conecte los dispositivos
en los respectivos receptáculos del contador de oscilaciones. Asegure que el
marco básico se encuentre en posición vertical. Fije una longitud del péndulo
de aproximadamente 0.9 m.
Fig.24 instalación del equipo
2.- Encienda el contador de oscilaciones y coloque el interruptor MODO en la
posición 0. Saque ligeramente el sistema de su posición de equilibrio y déjelo
oscilar.
3.-Con el péndulo oscilando, mueva el censor Optoelectrónico de oscilaciones
hasta que la esfera metálica interrumpa el haz infrarroja del mismo. Esto se
puede comprobar revisando que las lecturas en el Exhibidor del Contador de
Oscilaciones estén cambiando; el indicador ICA estará en estado intermitente.
4.- Mueva el péndulo fuera de la vertical (posición de equilibrio) hasta que la
cuerda forme con ella un ángulo menor o igual que 10º y sosténgalo en esta
posición utilizando el electro magneto de sujeción, tal y como se muestra en la
figura 25
Fig 25.- instalación del electro magneto.
5.- Una vez colocado el electro magneto de sujeción, oprima sin soltar el
interruptor INICIAR del contador de oscilaciones. Esta acción mantendrá
retenida la esfera metálica.
6.- Deje de oprimir el interruptor INICIAR para que la esfera quede libre y el
péndulo comience a oscilar. El contador de oscilaciones comenzará a registrar
las oscilaciones. Inmediatamente después del ciclo 20, cambie el interruptor
MODO a la posición 1 para poder anotar el número de ciclos (20), el tiempo
acumulado y el período del último ciclo.
7.- Calcule el período, dividiendo el tiempo acumulado entre el número total de
ciclos (20). Si existe diferencia entre el período calculado y el período del ultimo
ciclo, del orden de centésimas de segundo, repita el paso anterior asegurando
que no haya perturbaciones en el sistema, como pueden ser las corrientes de
aire y las vibraciones en el marco básico.
8.- Registra el período calculado T. Mida la longitud del péndulo, de acuerdo
con el diagrama de la figura 26 y regístrela.
Fig 26.- medición de la longitud del péndulo
9.-
Repita
los
pasos
anteriores
para
longitudes
del
péndulo
de
aproximadamente 0.8, 0.7, 0.5 y 0.4 m. Registre en cada caso el período y la
longitud del péndulo; llene una tabla de datos como la que se muestra en la fig
27.
T2 (s2)
L (m)
T (s)
0.8
1.912
3.824
0.7
1.70
3.4
0.6
1.57
3.14
0.5
1.45
2.9
0.4
1.30
2.6
Fig 27.- tabla de datos
2.4.2 Determinación de la aceleración de la gravedad utilizando
un péndulo simple.
EXPERIMENTO 2-SO
2.4.2.1 Objetivo del experimento
Determinar experimentalmente el valor de la aceleración de la gravedad
utilizando un péndulo simple.
2.4.2.2 Equipo y material empleados.
Marco Básico FICER, modelo SOSMB-01
Contador de Oscilaciones FICER, modelo CO-01
Censor Optoelectrónico de Oscilaciones FICER
Electromagneto de Sujeción, modelo ESSFL-03
Porta Electromagneto, modelo SOSPE-01
Nuez Giratoria, modelo SOSNG-01
Esfera Metálica con Sistema de Sujeción, Modelo SOSEM-01
Cuerda Inextensible
Cinta Métrica ( no incluida en el SOSM-01)
2.4.2.3 Diseño del experimento.
Para determinar
el valor de la aceleración de la gravedad, empleando el
método del péndulo, el experimentase debe desarrollar de la siguiente manera.
a) Se elije un péndulo con las siguientes características, la masa del
cuerpo oscilante debe ser mucho mayor que la masa de la cuerda, de
tal manera que ésta última sea despreciable. La cuerda deberá ser
inextensible y de longitud por lo menos diez veces mayor que la
mitad del arco que describe el cuerpo oscilante.
b) El péndulo se repara de su posición de equilibrio y se suelta para que
comience el movimiento oscilatorio. El ángulo que forme la cuerda y
la vertical debe ser igual o menor que diez grados para que se
cumpla la aproximación: sen θ = θ.
c) Se mide el tiempo de veinte oscilaciones y se obtiene su promedio,
este será tomado como el periodo de oscilaron. Se registran periodo
y longitud del péndulo.
d) Se repiten los pasos b) y c) para diferentes longitudes del péndulo.
Con los periodos y las longitudes del péndulo se elabora una tabla de
datos.
e) Con los datos del período, longitud, se determina el valor de la
aceleración de la gravedad para cada renglón en la tabla de datos.
f) Se obtiene el promedio de los valores de la aceleración de la
gravedad determinados en los pasos anteriores. Este valor se tomará
como el valor experimental de la aceleración de la gravedad.
g) Opcionalmente se puede obtener el valor de la aceleración de la
gravedad mediante un regresión de los datos experimentales de
longitud y período registrados en la tabla de datos.
2.4.2.4 Procedimiento
1.- Instale el equipo como se muestra en la figura 28 y conecte los dispositivos
en los respectivos receptáculos del contador de oscilaciones. Asegure que el
marco básico se encuentre en posición vertical. Fije una longitud del péndulo
de aproximadamente 0.9 m.
Fig 28.- instalación del equipo
2.- Encienda el contador de oscilaciones y coloque el interruptor MODO en la
posición 0. Saque ligeramente el sistema de su posición de equilibrio y déjelo
oscilar.
3.- Con el péndulo oscilando, mueva el censor Optoelectrónico de oscilaciones
hasta que la esfera metálica interrumpa el haz infrarrojo del mismo. Esto se
puede comprobar revisando que las lecturas en el Exhibidor del Contador de
Oscilaciones estén cambiando; el Indicador ICA estará en estado intermitente.
4.- Mueva el péndulo fuera de la vertical (posición de equilibrio) hasta que la
cuerda forme con ella un ángulo menor o igual que 10º y sosténgalo en esta
posición utilizando el electro magneto de sujeción, tal y como se muestra en la
figura 29.
Fig 29.- instalación del electromagneto
5.- Una vez colocado el electro magneto de sujeción, oprima sin soltar el
interruptor INICIAR del contador de oscilaciones. Esta acción mantendrá
retenida la esfera metálica.
6.- Deje de oprimir el interruptor INICIAR para que la esfera quede libre y el
péndulo comience a oscilar. El contador de oscilaciones comenzará a registrar
las oscilaciones. Inmediatamente después del ciclo 20, cambie el interruptor
MODO a la posición 1 para poder anotar el número de ciclos (20), el tiempo
acumulado y el periodo del último ciclo.
7.- Calcule el período, dividiendo el tiempo acumulado entre el número total de
ciclos (20). Si existe diferencia entre el período calculado y el periodo del último
ciclo, del orden de centésimas de segundo, repita el paso anterior asegurando
que no haya perturbaciones en el sistema, como pueden ser las corrientes de
aire y las vibraciones en el marco básico.
8.- Registre el periodo calculado T. Mida la longitud del péndulo, de acuerdo
con el diagrama de la figura 30 y regístrela.
Fig 30.- medición de la longitud del pendulo.
9.-
Repita
los
pasos
anteriores
para
la
longitud
del
péndulo
de
aproximadamente 0.8, 0.7, 0.6, 0.5 y 0.4 m. Registre en cada caso el período y
la longitud del péndulo; llene una tabla de datos como la que se muestra en la
figura 31.
L (m)
T (s)
T2 (S2)
g ( m/s2 )
g= 4π2 L/T2
0.9
1.92
3.84
19.37
0.8
1.81
3.62
8.72
0.7
1.71
2.34
11.80
0.6
1.58
3.16
7.49
0.5
1.45
2.9
6.80
0.4
1.31
2.62
6.02
Valor promedio de la aceleración de la
gravedad
Fig 31.- tabla de datos
10.09
10.- Obtenga el valor promedio de la aceleración de la gravedad, utilizando los
valores de la aceleración de la gravedad para cada punto experimental
encontrado.
11.- Para encontrar un mejor resultado, en el paso 4 utilice un ángulo menor
que 5º; de esta forma, se tendrá mas cercana la aproximación de sen θ ≈ θ .
2.4.3 Determinación de la constante elástica de un resorte
EXPERIMENTO 3-SO
2.4.3.1 Objetivo del experimento
Determinar la constante elástica de un resorte en forma estática.
2.4.3.2 Equipo y material empleados
Marco Básico FICER, modelo SOSMB-01
Contador de Oscilaciones FICER, modelo CDO-01
Recipiente Cilíndrico, modelo SOSRC-01
Resorte, modelo SOSR-01
Balines
Cinta Métrica
Balanza ( no incluida en el SOSM-01)
2.4.3.3 Diseño del experimento
Para encontrar la constante elástica del resorte, el experimento se debe
desarrollar de la siguiente manera:
a) se sujeta el resorte verticalmente por uno de sus extremos a un punto
fijo y se mide la distancia (x0 ) que hay entre las espiras de los extremos.
b) Después, en el extremo inferior del resorte se cuelga una masa conocida
(m). Se mide la nueva longitud del resorte, se calcula la elongación que
sufre y se registra. Se determina el peso de la masa conocida (en
Newton) y se registra.
c) Se repite el experimento varias veces, utilizando una cantidad de masa
diferente cada vez.
d) Construya una tabla de datos utilizando los resultados experimentales y
en base a ésta, se determina el valor de la constante elástica del resorte
, el cual será el mismo que el de la pendiente de la recta que mejor se
ajuste al conjunto de datos experimentales, tal pendiente puede
obtenerse por medio del método grafico o bien una regresión lineal.
2.4.3.4 Procedimiento
1.- Instale el equipo como se indica en la figura 2. Procure que el resorte esté
bien sujetado en el Dispositivo de Sujeción y que esté colocado verticalmente.
Asegure que el marco básico se encuentre en posición vertical.
Fig 32.- instalación del equipo
2.- utilizando el Indicador Móvil del marco Básico y la cinta métrica, mida
longitud inicial (x0 ).
3.- Coloque dentro del recipiente cilíndrico dos de los balines y obtenga el paso
del conjunto en Newtons (w=mg). Cuelgue en el gancho del resorte el cilindro
con los balines y mida la nueva longitud del resorte. Registre el peso W
obtenido y la longitud X, se incrementó el resorte, respecto a su longitud inicial.
4.- Introduzca otros dos balines dentro del recipiente cilíndrico y obtenga el
peso W del cilindro con los balines en Newtons. Cuelgue de nuevo el cilindro
con los balines en el extremo del resorte y mida la longitud que se incrementa
el resorte a partir de su longitud inicial. Repita 3 veces más esta operación,
agregando dos balines en cada una de ellas.
5.- Registre los diferentes pesos y las correspondientes elongaciones del
resorte (en m) y elabore una tabla de datos, como se muestra en la figura 33.
X (m)
W (N)
0.235
0
0.395
19.62
0.465
39.24
0.545
58.86
0.615
78.48
0.695
98.1
Fig 33.- Tabla de datos
6.- Determinar las constante k del resorte para cada uno de los pares de datos
experimentales.
7.- Opcionalmente, haga una grafica del peso W contra la elongación x del
resorte. En la grafica obtenida, trace la línea recta que pase mas cerca de los
puntos experimentales y obtenga su pendiente. La constante k es igual a la
pendiente.
Otra forma de obtener la relación entre el peso colgado y el alargamiento del
resorte es a partir de una regresión lineal de los datos experimentales. En este
caso, se obtiene una relación de la forma:
W = mX + b…………………………….ECUACION 55
2.4.4. Relación entre la masa del cuerpo y el periodo de
oscilaciones en el sistema cuerpo resorte.
EXPERIMENTO 4-SO
2.4.4.1 Objetivo del experimento
Determinar la relación que existe entre la masa del cuerpo y el periodo de
oscilación de un sistema oscilante cuerpo- resorte.
2.4.4.2 Equipo y material empleados.
Marco Básico FICER, modelo SOSMB-01
Contador de Oscilaciones FICER, modelo CDO-01
Censor Optoelectrónico de Oscilaciones FICER, modelo SOSSO-01
Electromagneto de Sujeción, modelo ESSFL-03
Porta Electromagneto, modelo SOSPE-01
Nuez Giratoria, modelo SOSNG-01
Recipiente Cilíndrico, modelo SOSRC-01
Balines
Resorte, modelo SOSR-01
Balanza (no incluida en el SOSM-01)
2.4.4.3 Diseño del experimento
Para encontrar la relación que hay entre la masa del cuerpo y el período de
oscilación del sistema cuerpo- resorte, el experimento debe desarrollarse de la
siguiente manera.
a) se sujeta el resorte verticalmente por uno de sus extremos a unpunto fijo
y en el otro extremo se cuelga un cuerpo de masa conocida.
b) El cuerpo se desplaza, hacia abajo, de su posición de equilibrio a una
distancia que no exceda el límite del resorte.
c) Se suelta el cuerpo y se deja oscilar libremente el sistema.
d) Se mide y se registra el período de oscilaciones del sistema.
e) Los pasos anteriores se repiten para cuerpos de diferentes masas y se
registran sus respectivos periodos.
f) Con los datos experimentales registrados, se construye una tabla de
datos.
g) A partir de la tabla de datos, se hace un análisis estadístico con el fon de
obtener la relación deseada.
2.4.4.4 Procedimiento
1.- Instale ele quipo como se indica en la figura 34
Fig. 34.- instalación del equipo
2.- Asegure que el Marco Básico se encuentre en posición vertical. Este paso
es muy importante; si el Marco Básico no esta vertical ocurre oscilaciones
complejas del cuerpo y el sensor Optoelectrónico no detecta los tiempos
correctamente.
3.- Revise que el electro magneto de sujeción y el interruptor opto electrónico
de Oscilaciones estén bien conectados al Contador de oscilaciones en sus
entradas posteriores Electromagneto y Censor Optoelectrónico.
4.- Coloque un resorte de constante elástica K conocida en el sistema de
sujeción del marco Básico, sujetándolo por uno de sus extremos. Introduzca
dentro del Recipiente Cilíndrico un balín, mida la masa conjunta y tómela como
la masa m del sistema cuerpo-resorte. Cuelgue el recipiente cilíndrico con el
balín en el extremo inferior del resorte; observe la elongación del resorte.
5.- Encienda el Contador de Oscilaciones. Gire el censor Optoelectrónico de
oscilaciones hasta que quede en posición horizontal, como se indica en la fig
34, y luego muévalo sobre su guía hasta que la línea imaginaria, que une los
dos orificios del censor, quede situada a la mitad de la altura del recipiente
cilíndrico.
6.- Mueva el electro magneto de sujeción hasta que quede a una distancia del
fondo del recipiente cilíndrico aproximadamente igual a la altura del mismo y
fíjelo con el tornillo opresor. Desplace el cilindro verticalmente hacia abajo
hasta que quede en contacto con el electro magneto de sujeción.
7.- Sin soltar el cuerpo, oprima el interruptor INICIAR del Contador de
Oscilaciones; el cuerpo deberá quedar retenido por el electro magneto de
sujeción, mientras se mantenga oprimido este interruptor. Coloque el botón del
interruptor MODO en la posición 0.
8.- Compruebe que tanto el resorte como el cuerpo estén en reposo. Suelte el
interruptor INICIAR y deje que oscile el sistema.
9.- Mueva el botón del interruptor MODO a la posición 1 cuando en el exhibidor
las lecturas correspondientes al periodo numero 20. Registre el tiempo
acumulado y divídalo entre el número de ciclos (20); el valor obtenido es el
periodo promedio T, que se tomará como dato experimental.
Compare el período promedio T con el período registrado en el segundo
renglón del Exhibidor, que corresponde al periodo del último ciclo. Entre estos
dos períodos debe haber una diferencia minima; si la diferencia es de una
centésima de segundo o mayor, revise cuidadosamente que el sistema cuerpo-
Resorte este bien instalado. Compruebe que el censor Optoelectrónico este
detectando todas las oscilaciones del cuerpo. Si no es así, puede sacar el
censor de la posición horizontal de forma que el haz infrarrojo sea cortado, por
el cilindro, más cerca del eje vertical.
10.- Repita el experimento, al menos cuatro veces más, agregando dos balines
encada experimento. Registre para cada experimento el período T y mida la m
correspondiente.
11.- Con los datos experimentales, construya una tabla de datos, como se
indica en la figura 35.
M(kg)
T(s)
T2(s2)
1
2.33
5.42
3
1.30
1.69
5
1.41
2.82
7
1.52
3.04
Tabla de resultados
12.- Con los resultados de la tabla de datos, haga una grafica de T contra m; en
esta grafica se deberá observar un comportamiento parabólico. Haga otra
gráfica de T2 contra m, la cual debe corresponder a una línea recta que pase
por el origen.
Fig 36ª.-
Tcontram
Fig 36b.- T
2
BM
13.- En la grafica de la figura 36b, obtenga la pendiente B de la recta y la
ecuación correspondiente T2 = Bm, o de otra forma:
T = (Bm )1/2
………………………….ECUACION 56
Esta ecuación representa el modelo de la relación que existe entre la masa del
cuerpo y el periodo de oscilación.
Nota: El modelo también se puede obtener a través de una regresión de
potencia de la forma.
T= Amn
……………………….. ECUACION 57
Donde A y n son constantes. Compare el exponente n con el exponente del
modelo teórico (1/2)
14.- Haga una tabla de comparación del periodo T experimental y del valor
calculado con las expresiones 55, 56 y 57, para diferentes valores de la masa
m.
SUBTEMA 2.5. EQUIPO PARA MEDICION DE ONDAS
MECANICAS
El sistema de Ondas Mecánicas FICER modelo SOM-01 es un conjunto de
dispositivos mecánicos y electrónicos que se utilizan para analizar y observar el
movimiento de ondas en cuerdas y resortes.
El sistema de Ondas Mecánicas esta constituido por las siguientes partes:
Marco Básico
Generador de Ondas Mecánicas
Generador de Funciones
Conjunto de accesorios
El Marco Básico modelo, SOMMB-01 es una estructura metálica que sirve para
instalar cuerdas y resortes que son perturbados mecánicamente para generar
ondas.
El Generador de Ondas Mecánicas modelo SOMGO-01 es un dispositivo
electromecánico que se emplea para producir las perturbaciones en las
cuerdas y los resortes, los cuales son los medios en que se propagan las
ondas mecánicas.
El Generador de Funciones modelo GF-02 es un dispositivo electrónico que
produce una señal eléctrica (senoidal) de frecuencia y amplitud variable. Sirve
para suministrar la señal eléctrica adecuada al Generador de Ondas Mecánicas
para que éste a su vez perturbe a las cuerdas y los resortes.
El Conjunto de Accesorios está formado por cuerdas de densidad lineal
constante, un resorte metálico, una polea, un porta polea, un recipiente
cilíndrico con balines y dos flejes metálicos.
2.5.1Descripción del Marco Básico
En la figura 37 se muestra el marco Básico, donde se indican con los números
de 1 al 6 sus diferentes partes.
Fig 37.- marco básico
1.- Base
Es una estructura metálica con cubierta de aluminio anodizado, provista de un
marco circular en el que se fija el Generador de Ondas Mecánicas. En la base
se instalan los dispositivos del Sistema de Oscilaciones Mecánicas.
2.- Perfil Metálico
Es una guía metálica de sección transversal cuadrada sujeta a la base del
Marco Básico. En el perfil Metálico se encuentra la regla graduada y el
indicador móvil
3.- Regla Graduada
Es una regla metálica colocada en el perfil metálico del Marco Básico. Sirve
para medir distancias en los medios mecánicos oscilantes.
4.- Indicador Móvil
Es un apuntador que se desplaza en el perfil Metálico del Marco Básico. Tiene
un tornillo opresor para fijarse en la posición deseada.
El Indicador Móvil sirve para señalar las partes de importancia de ondas (
nodos y antinodos ).
5.- Soporte
Es un dispositivo de aluminio que tiene dos tornillos Opresores laterales y un
orificio en su parte superior. Sirve para instalar el porta polea y el poste de
sujeción.
6.- Poste de Sujeción.
Es una barra metálica que en su parte superior esta provista de una ranura y
de un tornillo opresor lateral. Sirve para sujetar la cuerda o el resorte.
2.5 .2 Generador de Ondas Mecánicas
En la figura 38 se muestra el Generador de Ondas Mecánicas, en donde se
indican sus diferentes partes con los números del 1 al 4.
Fig 38.- generador de ondas mecánicas
1.- Oscilador.
Es un dispositivo electromecánico encerrado en un molde cilíndrico de plástico.
2.- Entradas.
Son dos receptáculos a través de los cuales el Generador de Ondas Mecánicas
recibe la señal eléctrica.
3.- Poste Oscilatorio.
Es un poste metálico que sirve para transmitir las perturbaciones mecánicas a
la cuerda, el resorte y los flejes. En su parte superior se instalan los dispositivos
que permiten sujetar los medios oscilatorios.
4.- Sujetador.
Es un dispositivo metálico que se instala en el poste Oscilatorio. Esta provisto
de una ranura en la que se colocan los extremos de la cuerda y el resorte.
Tiene dos tornillos opresores: uno permite apretar la ranura y sujetar la cuerda
o el resorte y el otro sirve para fijarse al poste Oscilatorio.
2.5.3 Generador de Funciones
2.5.3.1 Cara Frontal
En la figura 39 se muestra la cara frontal del Generador de Funciones, en
donde sus controles y partes se indican con los números del 1 al 6.
Fig 39.- cara frontal del generador de funciones
1.- Control de Encendido
Es un interruptor tipo balancín iluminado y se usa para encender o apagar el
instrumento.
2.-Selec
Es un interruptor de tres posiciones, que se usa para seleccionar el rango de la
frecuencia de la señal eléctrica, cuando el interruptor se activa en la posición
(1) entonces a esta le corresponde un rango de 1Hz a 150 Hz. Si el interruptor
se activa en la posición (2) a esta nueva posición le corresponde el rango de
150 Hz a 2000 Hz.
3.- Salida
Son dos receptáculos (uno negro y otro rojo) mediante los cuales se obtiene la
señal eléctrica. El generador suministra señales eléctricas con las siguientes
características: voltaje pico pico de volts, corriente máxima de 1 ampere e
impedancia de salida de 4 a 8 ohms.
4.- Exhibidor
Es un exhibidor de cristal líquido de una línea, en el que se muestra la
frecuencia de la función (señal eléctrica) seleccionada.
5.- Frecuencia
Es un control que sirve para cambiar la frecuencia de la señal utilizada.
6.- Amplitud
Es un control que se utiliza para ajustar la amplitud de la señal utilizada.
2.5.3.2 Cara Posterior
En la figura 40 se muestra la cara posterior del Generador de Funciones, en
donde sus partes están indicadas con los números 1, 2.
Fig 40.- cara posterior del generador de funciones
1.- Porta fusible.
Es el comportamiento para el fusible de 1 ampere, a 120 volts, que protege al
instrumento de una eventual sobrecarga en la línea de alimentación eléctrica.
2.- Cordón de Línea.
Esta equipado con clavija polarizada y sirve para conectar el Generador de
Funciones a la línea de alimentación eléctrica de 117 volts, 60hz.
2.5.4 Descripción de los accesorios del sistema de ondas mecánicas.
1.- Cuerdas
Son hilos con densidad lineal de masa constante que se utilizan como medio
de propagación para ondas transversales. Se sujeta en el poste de sujeción del
Marco Básico y en el Poste oscilatorio del Generador de Ondas Mecánicas,
como se muestra en la figura 41.
Fig 41.- instalación de la cuerda
2.- Cilindro con Balines.
Es un recipiente cilíndrico en el que se introducen balines. Se instala colgado
de la cuerda, como se muestra en la figura 42. Sirve para tensar la cuerda.
Fig 42.- instalación de la polea, el porta polea y el cilindro
3.- Resorte.
Es un resorte metálico que se emplea como medio de propagación de ondas
longitudinales. Se sujeta en el poste de sujeción del Marco Básico y en el
sujetador del Poste Oscilatorio del Generador de Ondas Mecánicas, como se
muestra en la figura 43
Fig 43.- instalación del resorte en el marco básico y detalle de la sujeción
4.- Polea y porta polea
Son los dispositivos que permiten cambiar la dirección de la fuerza de tensión
de la cuerda. Se instalan y se sujetan en el poste del marco Básico, como se
indican en las figuras 41 y 42
5.- Conectores.
Son dos conectores tipo banana- banana, mediante los cuales se transmite la
señal eléctrica del generador de funciones al Generador de Ondas Mecánicas.
6.- Flejes y Sujetadores de Flejes.
Son dos láminas metálicas que se usan como medio de propagación de ondas
mecánicas. Cada fleje se fija en el poste oscilatorio del Generador de Ondas
Mecánicas, mediante su sujetador de flejes, como se muestra en la fig 44
Fig 44.- instalación de los flejes en el generador de ondas mecánicas
2.5.5 Problemas generales de operación, causas y soluciones.
2.5.5.1 Del generador de funciones
Problema
Al conectar el Generador de Funciones a la línea de alimentación
eléctrica y accionar el Control de Encendido no se ilumina.
Posibles causas
1.- No hay voltaje en la línea de alimentación eléctrica o éste no es el
adecuado.
2.- El fusible esta dañado
3.- El circuito electrónico de control o alguna de las conexiones se dañó.
Soluciones respectivas
1.- Verifique con un voltímetro de corriente alterna si hay voltaje en la
línea de alimentación eléctrica y revise que éste sea aproximadamente
117 volts, 60 HZ.
2.- Verifique con un óhmetro el fusible, si está dañado, sustitúyalo con
otro en buen estado con las mismas especificaciones.
NOTA: No trate de reemplazarlo con un simple alambre (puente); esto
puede causar daños mayores al instrumento.
Problema.
Con el Generador de Funciones conectado a la línea de alimentación
eléctrica e iluminado el control de encendido, no aparece ningún texto en
el exhibidor de cristal líquido.
Posible causa.
1.- El circuito electrónico o alguna de las conexiones del Generador de
Funciones se dañó.
Solución respectiva.
1.- Recurra ala facultad encargada del sistema de ondas mecánicas para
una pronta solución al problema.
Problema.
Cuando se tiene seleccionado un tipo de función y oprimido uno de los
interruptores del selector RANGO, y se gira la perilla del control de
FRECUENCIA, no se observa cambio alguno en el Exhibidor de cristal.
Posible causa
1.- El circuito electrónico del Generador de Funciones está dañado.
Solución respectiva
1.- Recurra ala facultad encargada del sistema de ondas mecánicas para
una pronta solución al problema.
2.5.5.2 Del generador de Ondas Mecánicas.
Problema.
Con el Generador de Ondas Mecánicas conectado a los receptáculos
SALIDA del Generador de Funciones, al girar la perilla del control
AMPLITUD no se observa o no hay movimiento del poste Oscilatorio.
Posible causa.
1.- La tensión de hilo es demasiada y no permite que el poste oscile.
2.- El circuito electrónico del Generador de Funciones o los dispositivos
internos del Generador de Ondas Mecánicas se dañaron.
Solución respectiva.
1.-Ajuste la tensión del hilo de tal forma que permita que oscile el Poste
oscilatorio.
2.- Recurra ala facultad encargada del sistema de ondas mecánicas para
una pronta solución al problema.
2.5.6 USO ADECUADO DEL SISTEMA DE ONDAS MECÁNICAS
2.5.6.1 Del generador de funciones.
1.- NUNCA conecte el Generador de Funciones a una línea de
alimentación eléctrica que no sea de 117 volts, 60 Hz.
2.- NO mueva bruscamente los diferentes controles de su parte frontal.
3.- NO produzca un corto circuito entre los receptáculos de SALIDA del
Generador de Funciones.
2.5.6.2 Del generador de ondas mecánicas.
1.- NUNCA conecte el Generador de Ondas Mecánicas a una señal
eléctrica que no sea provista por el Generador de Funciones FICER, ya
que pudiera causarle daño irreparable.
2.- NO mueva el Poste Oscilatorio manualmente ni
le produzca
tensiones fuertes con la cuerda porque puede dañar los dispositivos
internos del Generador de Ondas Mecánicas.
3.- EVITE golpes y maltratos al Generador de Ondas Mecánicas.
4.- UTILICE el Generador de Ondas Mecánicas solamente en el marco
Básico.
2.5.6.3 De los accesorios.
1.- CUANDO no use la cuerda, guárdela en una bolsa de plástico para
que no se ensucie.
2.- NO estire el resorte a distancias mayores que las requeridas por los
experimentos del Sistema de ondas Mecánicas, ya que pudiera perder
sus propiedades elásticas.
3.- CUANDO estén instalados la cuerda, o el resorte en el Marco Básico,
no les de estirones fuertes porque puede dañar el Generador de Ondas
Mecánicas.
4.- PROCURE no doblar los flejes más de lo señalado en los
experimentos.
5.- CERCIORESE de que la Polea y el Porta polea estén sujetos
correctamente en sus respectivos lugares.
Subtema 2.6 Experimentos con el sistema de ondas mecánicas
EXPERIMENTO 1-OM
2.6.1 Ondas estacionarias en una cuerda
2.6.1.1 Objetivo del experimento
Determinar la velocidad de propagación de una onda mecánica en una cuerda,
para diferentes tensiones.
2.6.1.2 Equipo y material empleados.
Marco Básico FICER, modelo SOMMB-01
Generador de Funciones FICER, modelo GF-02
Generador de Ondas Mecánicas FICER, modelo SOMGO-01
Cables con Terminal Banana
Cuerda
Polea y Porta polea
Recipiente Cilíndrico, modelo SOMRC-01
Balines
2.6.1.3 Diseño del experimento.
El objetivo del experimento es encontrar la velocidad de propagación de una
onda de una cuerda, diferentes tensiones. Para determinar la velocidad, se
necesita conocer la frecuencia, así como la longitud de onda.
Para este fin, se usará una cuerda horizontal tensa que tenga fijo uno de sus
extremos. En el otro extremo, se le producirá una perturbación periódica, de tal
forma que se produzca una onda. Al llegar la onda al extremo fijo, se reflejará y
se superpondrá con la onda incidente, lo que dará origen a una onda
estacionaria; de esta forma, se puede medir fácilmente la longitud de la onda.
Se buscarán al menos cinco diferentes modos de oscilación y se registrarán las
frecuencias y las longitudes de onda. Con estos datos se hará un análisis
grafico, del cual se obtendrá la velocidad de la onda. Asimismo, la velocidad de
la onda puede ser obtenida partir de una regresión lineal de
los datos
experimentales del inverso de la longitud de onda y de la frecuencia.
Los pasos anteriores se realizaran para diferentes tensiones de la cuerda.
2.6.1.4 Procedimiento
1.- Instale el Sistema de Ondas Mecánicas como se muestra en las figuras 45 y
45a.
Fig 45.- instalación del equipo
Fig 45a.-Detalles de la instalación
2.- Revise que la cuerda esté bien sujeta al Poste Oscilatorio del Generador de
Ondas Mecánicas. Introduzca 10 balines en el Recipiente Cilíndrico y cuélguelo
de la cuerda. Apriete el Tornillo Opresor del Poste de Sujeción.
3.-Acomode las ranuras del Poste del Marco Básico y del dispositivo de
sujeción del Poste Oscilatorio del Generador de Señales, de tal forma que
estén en la misma dirección de la cuerda. Para este fin, gire el Poste de
Sujeción y el Generador de Ondas Mecánicas.
4.- Ajuste la horizontalidad de la cuerda de la siguiente manera: libere la cuerda
del Poste de Sujeción del Marco Básico y mediante la elevación de la polea
obtenga la posición adecuada de la cuerda, la cual se logra ubicando a ésta
paralela a la escala graduada. Hecho lo anterior coloque el poste de Sujeción
en su base de forma tal que la cuerda pase libremente a través de la ranura y
de este y sujételo a la base mediante el tornillo correspondiente. A continuación
sujete nuevamente la cuerda al poste. Procure que las ranuras de ambos
postes de sujeción se mantengan en la misma dirección, de acuerdo con el
paso anterior.
5.- Mida la longitud L de la cuerda, mostrado en la figura 45a utilizando el
Indicador Móvil del Marco Básico.
6.- Conecte el generador de Funciones a la línea de alimentación eléctrica y
enciéndalo, active en la posición 1 el interruptor SELEC del generador.
7.- En el generador gire la perilla del control FRECUENCIA y observe si en la
cuerda se forma la onda estacionaria correspondiente al modo fundamental de
oscilación. Si no se observa esta onda, gire de nuevo la perilla del control
FRECUENCIA hasta que en la cuerda se forme la onda estacionaria del modo
fundamental. Enseguida, obtenga la longitud de onda (λ = 2L) y regístrela junto
con a frecuencia que se indique en el Exhibidor del Generador de Funciones.
8.- Aumente la frecuencia en el Generador de Funciones, de acuerdo con el
paso anterior, para encontrar las frecuencias del segundo, tercero, cuarto y
quinto modos de oscilación de la cuerda. Registre las frecuencias y las
longitudes de onda y construya una tabla de datos, como se muestra en la
figura 46.
No. Modo
No. Nodos Distancia
Long.
entre nodos
Frecuencia
Vel.
De
propagación
Onda
1
2
1.04
2.08
16
16.64
2
3
0.52
2.08
32
16.64
3
4
0.26
2.08
50
13
4
5
0.20
2.08
66
13.2
5
6
0.17
2.08
82
13.94
Vel.prom:
14.684
Fig 46.- tabla de datos
9.- De la ecuación
f podemos despejar la frecuencia f :
f
v
1
…………………………………..ECUACION 58
Para ver esta relación de acuerdo con los resultados experimentales, utilice la
tabla de datos para hacer una grafica de f contra 1/ , como se muestra en la
fig 47. Trace la línea recta que pase lo mas cerca de los puntos de la grafica y
obtenga su pendiente B. El valor de la pendiente corresponde al valor de la
velocidad de la onda.
f (Hz)
B=v(m/s)
1/ (m 1)
……………………………ECUACION 59
Opcionalmente, a partir de una regresión lineal de f en función de 1/ ,
determine la velocidad de la onda, la cual es igual al valor de la pendiente de
la recta obtenida.
10.- Opcionalmente mida la masa m, con una balanza analítica y la longitud
total Lt de la cuerda. Calcule la densidad lineal de masa
de la cuerda, de
acuerdo con la siguiente expresión:
m
………………………………ECUACION 60
Lt
Calcule la velocidad de la onda estacionaria empleando la siguiente ecuación
v
F
……………………………….ECUACION 61
Donde F es la fuerza de tensión de la cuerda, la cual es igual al peso del
recipiente cilíndrico con los 10 balines.
11.- Repita los pasos del 7 al 9 para diferentes tensiones de la cuerda, es decir,
con diferentes numero de balines en el recipiente cilíndrico.
2.6.2 VELOCIDAD DE PROPAGACIÓN DE UNA ONDA
LONGITUDINAL EN UN RESORTE
EXPERIMENTO 2-OM
2.6.2.1 Objetivo del experimento
Determinar la velocidad de propagación de una onda longitudinal en un resorte.
2.6.2.2 Equipo y material empleados.
Marco básico FICER, Modelo SOMMB-01
Generador de funciones FICER, Modelo GF-02
Generador de Ondas Mecánicas FICER, Modelo SOMGO-01
Cables con terminal banana.
Resorte, Modelo SOMR-01
2.6.2.3 Diseño del experimento
El objetivo del experimento es determinar la velocidad de propagación de una
onda longitudinal en un resorte. Para cumplir este objetivo, es necesario
conocer la frecuencia y la longitud de la onda.
Se recomienda usar un resorte colocado en posición vertical, fijo en su extremo
superior; en el otro extremo se le debe producir una perturbación periódica, de
tal forma que se cree un tren de ondas. La frecuencia debe ser ajustada para
que se produzcan ondas estacionarias.
Se buscaran al menos cinco diferentes modos de oscilación y se registraran las
frecuencias y las longitudes de onda. Con estos datos se hará un análisis
grafico, del cual se obtendrá la velocidad de la onda. Asimismo, utilizando los
datos experimentales, la velocidad de la onda puede ser obtenida a partir de
una regresión lineal de la frecuencia contra el inverso de la longitud de onda.
2.6.2.4 Procedimiento.
1.- Instale el Sistema de ondas Mecánicas como se muestra en la figura 48.
Fig 48.- instalación del equipo
2.- Revise que el resorte este bien sujetado al poste oscilatorio del Generador
de ondas Mecánicas y al poste de sujeción del Marco Básico (ver el instructivo
para uso y manejo del sistema de ondas mecánicas)
3.- Asegure que el resorte se encuentre en posición vertical. Para lograr esta
posición, acomode el Generador de Ondas Mecánicas hasta lograr la
verticalidad del resorte.
4.- Conecte el Generador de Funciones a la línea de alimentación eléctrica y
enciéndalo.
5.- En el generador de Funciones active el interruptor SELEC en la posición 1 y
gire la perilla del control FRECUENCIA y observe si en el resorte se forma la
onda estacionaria correspondiente a algún modo de oscilación; puede
reconocer la presencia de un modo de oscilación por el hecho de que la espira
mas cercana al Generador de Ondas se un nodo.
Nota: Al establecer un valor de la frecuencia en el generador de funciones, espere un
tiempo para que el resorte se estabilice a onda estacionaria.
Identifique el número de modo de oscilación, que es igual al número de
antinodos que se encuentran presentes en el resorte.
Determine y anote la distancia entre todos los nodos consecutivos, utilizando el
Indicador Móvil y la Regla graduada.
Calcule el valor promedio de dichas distancias y el valor de la longitud de onda,
que es igual al doble de dicho valor promedio.
Anote el promedio de las distancias entre nodos consecutivos, la longitud de
onda y el valor de la frecuencia que indique el exhibidor del Generador de
Funciones en la tabla de datos de la fig 49, obtenga el valor de la velocidad de
propagación de la onda.
6.- Varíe la frecuencia en el Generador de Funciones, para encontrar las
frecuencias de otros modos de oscilación del resorte. Repita el paso anterior y
anote los valores correspondientes para los nuevos modos de oscilación.
Complete la tabla hallando el promedio de las velocidades de propagación en
todos los modos de oscilación estudiados.
No.MODO
No. NODOS
DISTANCIA
LONG.ONDA
FRECUENCIA
PROMEDIO
VEL.
DE
PROPAGACION
ENTRE NODOS
8
9
12.18
148.35
20
2967
10
11
9.8
96.04
25
2401
12
13
8.76
76.73
30
2301.9
14
15
7.97
63.52
35
2223.2
VELOCIDAD PROMEDIO:
Fig 49.- tabla de datos
7.- De la ecuación v
f se puede despejar la frecuencia f :
2473.2
f
1
v ……………………………..ECUACION 62
Para ver esta relación de acuerdo con los resultados experimentales, utilice la
tabla de datos para hacer una grafica de f contra 1/ , como se muestra en la
figura 50. Trace la línea recta que pase lo mas cerca de los puntos de la grafica
y obtenga su pendiente B. El valor de la pendiente corresponde al valor de la
velocidad de la onda.
2.6.3 VELOCIDAD DE UNA ONDA TRANSVERSAL EN DIFERENTES
CUERDAS.
EXPERIMENTO 3-OM
2.6.3.1 Objetivo del experimento.
Determinar la velocidad de propagación de una onda transversal en cuerdas de
diferente densidad lineal de masa para una tensión constante.
2.6.3.2 Equipo y material empleados.
Marco Básico FICER, Modelo SOMMB-01
Generador de Funciones FICER, Modelo GF-02
Generador de Ondas Mecánicas FICER, Modelo SOMGO-01
Cables con Terminal Banana
Cuerdas con diferente densidad lineal de masa
Polea y Porta polea
Recipiente Cilíndrico, modelo SOMRC-01
Balines
2.6.3.3 Diseño del experimento.
El objetivo del experimento es encontrar la velocidad de propagación de ondas
mecánicas en cuerdas de diferente densidad lineal de masa para una tensión
constante en las cuerdas.
Para determinar la velocidad de las ondas en cada una de las cuerdas, se
necesita conocer la frecuencia y la longitud de la onda para diferentes modos
de oscilación.
Una vez obtenidos los valores de las velocidades para cada una de las
cuerdas, se comparará con los resultados experimentales con los valores
teóricos. De acuerdo con las diferentes densidades.
2.6.3.6 Procedimiento.
1.- Instale el sistema de ondas mecánicas como se muestra en la figura 50 con
una de las cuerdas.
Fig 50.- instalación del equipo
2.- Ajuste el sistema de acuerdo con los pasos de los procedimientos del
experimento SOM-1. Coloque en el recipiente cilíndrico 10 balines.
3.- Variando la frecuencia en el generador de funciones logre que en la cuerda
se establezca el tercero o cuarto modo de oscilación. Compruebe que el modo
es estable, oprimiendo la cuerda con los dedos y observando si de nuevo oscila
en el mismo modo cuando se suelta. Determine el valor de la longitud de onda,
de la misma forma que lo hizo en el experimento SOM-1 y anote en la tabla de
datos el valor de la frecuencia y de la longitud de onda.
Calcule el valor de la velocidad de propagación de la onda.
4.- Repita el paso 3 para las otra cuerdas, teniendo cuidado que el modo de
oscilación sea el mismo para todas.
5.- Determine la tensión en las cuerdas, que es igual al peso del recipiente
cilíndrico con los 10 balines.
6.- Calcule la velocidad de propagación de las ondas en cada cuerda, utilizando
la expresión v
F
, los datos de densidad lineal de masa, de la tensión y
complete la tabla de datos, calculando el modulo de la diferencia de los valores
de las ecuaciones.
Nota.- la densidad lineal
de la cuerda, se determina por el método descrito
en el paso 10 del experimento 2.6.1
CUERDA
LONG.ONDA
FRECUENCIA
v
f
v
F
v V
10
.74
80
59.2
2.43
56.77
8
.74
75
55.5
2.63
52.87
6
.74
70
51.8
2.93
48.87
Fig 51.- tabla de datos
7.- Compare los valores de la velocidad obtenidos en el paso 3 con los valores
obtenidos en el paso 6.
2.6.4 MODOS DE OSCILACIÓN EN FLEJES CIRCULAR Y
RECTO
EXPERIMENTO 4-OM
2.6.4.1 Objetivos del experimento
Observar los modos de oscilación de flejes metálicos circular y recto.
2.6.4.2 Equipo y material empleados
Generador de Funciones FICER, Modelo GF-02
Generador de Ondas Mecánicas FICER. Modelo SOMGO-01
Cables con Terminal Banana
Fleje Metálico Circular
Fleje Metálico Recto
2.6.4.3 Procedimiento
1.- Instale el equipo como se indica en la figura. Asegure que el fleje recto de
extremo libre este bien sujeto al poste oscilador del Generador de Ondas
Mecánicas.
Fig 52.- instalación del equipo
2.- Conecte el Generador de Funciones a la línea de alimentación eléctrica y
enciéndalo.
3.- En el Generador de Funciones active el interruptor SELEC en la posición 1 y
gire lentamente la perilla de control FRECUENCIA hasta que el fleje recto de
extremo libre se produzca la onda estacionaria correspondiente al primer modo
de oscilación. Si no se alcanza a distinguir el primer modo, aumente la amplitud
de la señal eléctrica y gire nuevamente la perilla del control FRECUENCIA
hasta que se produzca la onda estacionaria deseada.
4.- Para encontrar los siguientes modos de oscilación, aumente la frecuencia
de la misma forma que en el paso anterior.
5.- Apague el Generador de Funciones e instale el fleje circular. Como se
muestra en la figura 53. Para hallar los modos de oscilación de este fleje,
proceda como en los pasos anteriores y encuentre al menos dos diferentes.
Fig 53.- instalación del equipo
CAPITULO III
3.1. Aportaciones o contribuciones al desarrollo
La principal aportación en este manual es formar alumnos que tengan una
visión real así como enseñanzas que estén totalmente fundamentadas en base
a ecuaciones y análisis teóricos, así, cuando el alumno emprenda el análisis de
estos temas podrá comprender todo lo necesario, así el aprendizaje será mas
rápido y entendible.
Una de las aportaciones es que los alumnos tengan los conocimientos y
conceptos básicos para cuando se trabaje en el área de las oscilaciones y
ondas mecánicas tengan un buen entendimiento.
El presente trabajo esta compuesto de forma que todo lo citado sea lo mas
claro posible y así cuando se consulte no tenga problemas para poder
interpretarlo.
También la forma en que esta estructurado es con el objetivo de brindarle
ayuda al alumno para el entendimiento de oscilaciones y ondas mecánicas al
momento de operar los equipos FICER
Podemos hacer mención sobre este trabajo que se propuso fuera lo mas
posiblemente actualizado en sus conceptos, así como la contribución de tener
una visión mas concreta sobre el conocimiento de las características y
funciones sobres los equipos FICER de oscilaciones y ondas mecánicas.
3.2 Bibliografía
1.- MAXIMO ANTONIO (2003). FISICA GENERAL CON EXPERIMENTOS
SENCILLOS. MEXICO: OXFORD.
2.- GIANCULLI DOUGLAS E. (2002). FISICA PARA UNIVERSITARIOS.
MEXICO: PRENTICE HALL.
3.- JEWETT JOHN W, SERWAY RAYMOND A. (2005). FISICA PARA
CIENCIAS E INGENIERA. E.U.A: THOMSON.
4.- LONE REESE RONALD (2003). FISICA UNIVERSITARIA. MEXICO:
THOMSON.
5.- BENSON HARRIS (1996). FISICA UNIVERSITARIA. MEXICO:
CONTINENTAL.
6.- SERWAY, JEWETT (2005). FISICA PARA CIENCIAS E INGENIERIA.
MEXICO: THOMSON.
7.- MANUALES DE EXPERIMENTOS DE LOS EQUIPOS FICER DE
OSCILACIONES Y ONDAS MECANICAS.
3.3 Anexos
3.4 Apéndices
Alfabeto griego
Mayúsculas
Minúsculas
Nombre español
Alfa
Beta
Gamma
Delta
Épsilon
Dseta
Eta
Zeta
Iota
Kappa
Lambda
Mi
Ni
Xi
Ómicron
Pi
Rho
Sigma
Tau
Ípsilon
Fi
Ji
Psi
Omega