Sensores Generadores - Facultad de Informática
Anuncio

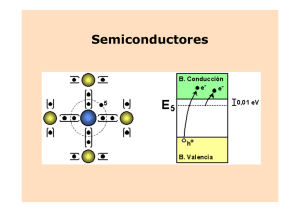
Tecnología y Sistemas Optoelectrónicos aplicados a la Informática Introducción a los Semiconductores 1. INTRODUCCIÓN A LOS SEMICONDUCTORES. .................................................................... 2 1.1. 1.2. 1.3. 1.4. 1.5. 1.6. 1.7. 1.8. 1.9. 2. ESTRUCTURA DE BANDAS. ......................................................................................................... 2 PORTADORES DE CORRIENTE: ELECTRONES Y HUECOS. ............................................................ 3 AGITACIÓN TÉRMICA. DISTRIBUCIÓN DE FERMI-DIRAC. ........................................................... 4 GENERACIÓN Y RECOMBINACIÓN .............................................................................................. 5 IMPULSIÓN. ................................................................................................................................ 6 IMPUREZAS DONADORAS Y ACEPTADORAS. SEMICONDUCTORES N Y P...................................... 7 LA UNIÓN P-N. ............................................................................................................................ 9 EL TRANSISTOR BIPOLAR......................................................................................................... 12 EL TRANSISTOR DE EFECTO CAMPO MOS. .............................................................................. 14 SENSORES FOTOVOLTAICOS ................................................................................................. 19 2.1. 2.2. 2.3. 2.4. 2.5. EFECTO FOTOVOLTAICO ........................................................................................................... 19 EL FOTODIODO ......................................................................................................................... 20 DIODOS PIN ............................................................................................................................. 21 FOTODIODOS DE BARRERA SCHOTTKY ..................................................................................... 22 FOTOTRANSISTORES ................................................................................................................. 22 Depto. de Tecnología Fotónica Facultad de Informática Universidad Politécnica de Madrid Mayo 2003 Rev.: Noviembre 2005 Julio Gutiérrez Ríos SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos 1. Introducción a los Semiconductores. Es sabido que los semiconductores pueden conducir corriente eléctrica mediante dos tipos de portadores que son los electrones y los huecos. La carga de los electrones es negativa (-1.6022×10-19 C), mientras que la de los huecos es exactamente de la misma magnitud, pero positiva. Esto es lo que se denomina conducción bipolar y por eso muchos dispositivos que se basan en ella reciben el nombre de dispositivos bipolares. Los electrones que sirven como portadores de corriente son solamente aquéllos cuya ligazón con los núcleos de los átomos del semiconductor es débil y, por tanto, son susceptibles de moverse por la aplicación de un campo eléctrico externo. Estos electrones son quasi libres porque tienen un nivel alto de energía. 1.1. Estructura de Bandas. Los semiconductores tienen una configuración electrónica tal que existe una banda de energías que no puede estar ocupada por ningún electrón. Ésta es la que se denomina banda prohibida (BP). La parte superior a la banda prohibida sí puede estar ocupada. Y los electrones que la ocupan son los que hemos denominado quasi libres y constituyen portadores de corriente. Por ello, a esta banda de energías superiores a la banda prohibida se le llama banda de conducción (BC). La banda de energías que se encuentra por debajo de la banda prohibida se halla prácticamente repleta de electrones que, sin embargo, por estar ligados a los átomos, no son portadores de corriente. A esta banda se le denomina banda de valencia (BV) y recibe su nombre porque los electrones de la misma que se encuentran al borde de la banda prohibida son los electrones de valencia responsables de los enlaces entre los átomos (ver Fig. 1). La configuración electrónica mencionada se debe a que si considerásemos un átomo aislado, éste tendrá sus niveles estables de energía caracterizados por los números cuánticos. Como es sabido, los electrones en los átomos no pueden tener una energía cualquiera, sino sólo aquellos niveles que cumplen las leyes de la mecánica cuántica. En dichos niveles los electrones se mueven alrededor del núcleo de forma estable, esto es, sin alterar su energía y por consiguiente, no radian. En estado normal, los niveles ocupados más externos son los niveles de valencia y sus electrones son los electrones de valencia. Ahora bien, por diferentes causas tales como la agitación térmica o absorción de energía electromagnética, los electrones de valencia pueden abandonar su nivel normal de valencia y pasar a ocupar otro nivel estable de energía superior. En este caso, los electrones de valencia están excitados y se encuentran menos ligados al núcleo. A su vez, los electrones excitados pueden retornar a su estado normal liberando la diferencia de energía entre el nivel excitado y el normal en forma de fotón o cuanto elemental de energía electromagnética. Si la energía del nivel excitado es Ee y la del nivel normal es En, el fotón emitido al caer un electrón desde el nivel excitado al nivel normal será E = Ee - En, y dicha energía se relaciona con la frecuencia ν de la radiación mediante la constante de Planck (h = 6.63·10-34 J-s) de la siguiente forma: E = Ee − En = h ⋅ν (1) Ahora bien, la materia sólo podría considerarse compuesta por átomos aislados cuando se trata de un gas en el que la interacción entre los átomos es muy reducida. En un sólido, como es el caso de los semiconductores habituales (Si, Ge, AsGa, SbIn···), la 2 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos interacción entre los átomos es por naturaleza muy fuerte (se establecen enlaces) y, en consecuencia, los átomos ya no se comportan como si estuvieran aislados. Si el material es prácticamente puro (semiconductor intrínseco) y el sólido ha podido formarse ordenadamente, la distribución de los átomos es regular, en cuyo caso se dice que el sólido constituye un cristal y los átomos forman una red cristalina. Naturalmente, la estructura de la red cristalina depende de la naturaleza de los átomos y del tipo de enlaces que se establezcan. Pero en cualquier caso, los niveles estables de energía propios de los átomos aislados dejan de ser discretos para pasar a una densa distribución de niveles en un cierto intervalo alrededor del nivel original del átomo aislado. Esto sucede por el principio de exclusión de Pauli según el cual en un mismo sólido no pueden existir electrones con la misma energía. Por tanto, en el momento que un cúmulo de átomos se acercan y enlazan entre sí para formar un sólido en red, los niveles de energía se expanden en bandas de energía que tienen tal densidad de niveles que perfectamente pueden considerarse bandas continuas. Banda de Conducción Ee EC Banda Prohibida En Banda de Valencia Átomo Aislado Eg EV Semiconductor Fig. 1: Niveles discretos de energía del átomo aislado en comparación con las bandas de energía de un semiconductor. En la Fig. 1 se puede apreciar la estructura de bandas de un semiconductor, vista en relación con los niveles discretos de un átomo aislado. En dicha estructura aparece la banda prohibida (BP) ya descrita, junto con las bandas de conducción (BC) y de valencia (BV). Llamaremos EC a la energía del fondo de la BC, EV a la del tope de la BV y Eg a la diferencia entre ambas que es la anchura de la BP (energía del gap). 1.2. Portadores de Corriente: Electrones y Huecos. Como ya se ha dicho, los electrones presentes en la BC constituyen portadores de corriente, ya que se encuentran muy poco ligados a los núcleos de los átomos y, por tanto, pueden moverse con facilidad. También habíamos dicho que los electrones en la BV no son portadores de corriente porque éstos sí están muy ligados a los núcleos. Pues bien, aquí se produce un fenómeno muy importante: tratándose de un semiconductor intrínseco, todos los electrones de la BC son electrones excitados que proceden de la BV. Por tanto, la presencia de electrones en la BC implica también la presencia de lugares vacíos en la banda de valencia. Estos lugares vacíos de la BV reciben el nombre de huecos y tienen la particularidad de que, siendo entidades inmateriales por naturaleza, se comportan como partículas de la misma carga eléctrica que el electrón ( 1.6022·10-19 C) pero de signo positivo. La explicación de este fenómeno es la siguiente: en efecto, los electrones de la banda de valencia están muy ligados y no se mueven por la acción de un campo eléctrico externo, excepto en el caso de los electrones que tienen un lugar vacío (hueco) al lado. En este caso, los electrones son susceptibles de moverse sin salir de la BV porque pueden pasar 3 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos fácilmente a ocupar los lugares vacíos, dejando a su vez un hueco en el lugar donde se encontraban antes. Por consiguiente, da la sensación de que son los huecos los que se mueven como burbujas en una masa de electrones. Así pues, los huecos de la BV son portadores de corriente prácticamente tan ligeros como lo son los electrones de la BC. Por tanto, cuando se aplica un campo eléctrico a un semiconductor se establece una corriente de electrones de la BC que viajan en sentido contrario al campo eléctrico por tener carga negativa y, al mismo tiempo, se establece una corriente de huecos que viajan en el sentido del campo por ser cargas positivas. Conviene aclarar que ambas corrientes se suman aunque sus respectivos portadores viajan en sentido opuesto, ya que también son opuestas las cargas y el sentido convencional de la corriente es el mismo para ambas. Por tanto, la corriente es bipolar porque se debe a dos tipos de portadores de polaridad distinta. En la Fig. 2 se muestra una representación simbólica de ello. EC Sentido Convencional EV Fig. 2: Conducción bipolar en los semiconductores 1.3. Agitación Térmica. Distribución de Fermi-Dirac. Si no hubiera agitación térmica en el sólido, la BV estaría completamente llena de electrones mientras que la BC estaría completamente vacía. Pero esto sólo sucedería si la temperatura fuera el cero absoluto (T = 0 ºK). En consecuencia, igual que en el átomo aislado los electrones de valencia pueden absorber energía y pasar al nivel excitado, en el seno de un semiconductor siempre hay electrones excitados que han adquirido energía suficiente para abandonar la BV y pasar a la BC. Según lo descrito, en el caso de un semiconductor puro (semiconductor intrínseco), la cantidad de electrones en la banda de conducción es la misma que la de huecos en la banda de valencia ya que cada hueco se debe siempre a un electrón que ha subido a la BC. Por ello, se suele hablar de la generación de pares electrón-hueco ya que la generación de un electrón de conducción implica la aparición de un hueco. Naturalmente, ya que la energía de excitación procede en general de la energía térmica de la red cristalina, la concentración de electrones y huecos depende de la temperatura. En efecto, la probabilidad de ocupación de los estados de energía, es decir, la probabilidad de que un nivel de energía E esté ocupado por un electrón siempre que dicho nivel no se encuentre en la banda prohibida (en cuyo caso la probabilidad es cero), viene dada por la distribución de Fermi-Dirac f(E) cuya expresión es la siguiente: f (E ) = 1 exp[(E − E f ) k B T ] + 1 4 (2) SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos donde kB es la constante de Boltzman (kB = 1.3807·10-23 J/ºK), T la temperatura absoluta y Ef es el llamado nivel de Fermi en el cual, como se comprueba fácilmente, la probabilidad de ocupación es ½. indepen-dientemente de la temperatura. En la Fig. 3 se puede ver una representación gráfica de la distribución de Fermi-Dirac según (2) para el caso del Si (similar para otros semiconductores con la diferencia fundamental de la anchura de la BP). Obsérvese que en el cero absoluto de temperatura, la probabilidad conmuta bruscamente del 0 al 1 en el nivel de Fermi. Cuando la temperatura es superior, la distribución es gradual y simétrica respecto a su punto de corte con el nivel de Fermi. Hay dos zonas sombreadas: una representa la probabilidad de ocupación f(E) en la BC, mientras que el significado de la otra es la probabilidad de desocupación [1- f(E)] en la BV. Por tanto, la magnitud de la primera zona sombreada determina la concentración de electrones en la BC y la de la segunda, la concentración de huecos en la BV. Así, la conductividad del semiconductor es proporcional a la suma de ambas, pues ésta reúne la concentración de portadores de corriente (electrones y huecos). Dada la simetría de la distribución, se ve fácilmente que en un semiconductor intrínseco, el nivel de Fermi ha de estar en el centro de la banda prohibida pues, de otra forma, la concentración de huecos sería diferente a la de electrones. Al mismo tiempo, se puede apreciar la fuerte dependencia de la conductividad con la temperatura. Este es el fundamento de diversos dispositivos, tales como los termistores. Fig. 3: Distribución de Fermi Dirac 1.4. Generación y Recombinación De la misma forma que un electrón de valencia de un átomo aislado puede absorber energía y pasar a un nivel excitado y viceversa, en un semiconductor se establecen transiciones de electrónes entre la banda ce valencia y la de conducción. El proceso por el cual un electrón sube a la BC dejando un hueco en la BV es lo que se llama generación.el. El proceso contrario por el cual un electrón de la BC cae a la BV haciendo desaparecer un hueco de la misma es lo que se llama recombinación. En un semiconductor a temperatura normal los procesos de generación y recombinación se producen continuamente en gran número y a grandes velocidades. Por ejemplo, el tiempo de vida medio de un para electrón-hueco en el Si es de unos 100 ns. a la temperatura ambiente (300 ºK), siendo la concentración de huecos y electrones del Si intrínseco a la misma temperatura de 1.5×1010 cm-3. En situación de equilibrio térmico, la generación y la recombinación se contrarrestan, de forma que la concentración de portadores se mantiene constante. La energía que necesita un electrón para dar el salto entre la BV y la de conducción puede ser proceder de diferentes fuentes. Una de ellas, la más habitual y que siempre existe, como se vio en la sección anterior, es la agitación térmica de la propia red 5 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos cristalina. Esto es lo que se denomina generación térmica. Pero otra posibilidad muy importante es la absorción de un fotón con energía suficiente según (1) para provocar este salto. Es decir, la energía hν del fotón ha de ser igual o superior a la anchura de la banda prohibida Eg. En este caso se trata de generación electromagnética y constituye el fundamento del efecto fotoconductivo y de dispositivos como las fotoresistencias, así como del efecto fotovoltaico. Asimismo la recombinación puede producirse, bien por devolución de la energía del salto a los átomos del sólido, lo que se traduce en agitación de la red, o bien se puede producir por la emisión de un fotón. El salto es como mínimo de una energía igual a la anchura de la BP, esto es, Eg = EC - EV. Pero como la probabilidad de ocupación de la banda de conducción es mayor en la parte baja y la probabilidad de desocupación de la BV es mayor en la parte alta, resulta que la gran mayoría de los fotones emitidos tienen una energía muy próxima a la anchura de la BP (Eg) y la luz emitida en conjunto es bastante monocromática, es decir, los fotones tienen todos frecuencias muy próximas entre sí: E ≈ E g = EC − EV = h ⋅ν (3) El que la recombinación sea predominantemente emisiva o no, es una propiedad del semiconductor como se verá en la sección siguiente. 1.5. Impulsión. La dualidad entre las teorías ondulatoria y corpuscular que había planteado Max Planck fue resuelta por De Broglie al enunciar la naturaleza ondulatoria de las partículas, relacionando la impulsión o cantidad de movimiento ‘p’ con la longitud de onda mediante la fórmula de De Broglie: p= h λ = ⋅k ; p = ⋅k (4) donde h es la constante de Planck, ћ = h/2π, λ la longitud de onda, k el número de onda (k= 2π/λ) y k el vector de onda cuyo módulo es el número de onda y cuya dirección y sentido son los de propagación de la onda. A la vista de (4) se comprende fácilmente que las partículas materiales a nivel macroscópico conllevan una longitud de onda infinitamente pequeña, de forma que su naturaleza como onda es completamente imperceptible. Si se tratara de electrones en el espacio libre cuya masa es m0, la energía de los mismos estaría relacionada con la impulsión de la siguiente forma: p2 2k 2 E= = 2m0 2m0 (5) Dependencia que tiene la forma de una parábola. Sin embargo, siendo que los electrones se mueven en el seno de una red cristalina, resulta que los electrones de conducción y los huecos de la banda de valencia están sujetos a una dinámica distinta, de forma que la energía no sólo depende de la impulsión sino también de la dirección en la que el electrón se mueve dentro del cristal. 6 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos E E Eg = 1.42 eV Eg = 1.11 eV k [111] k [111] [100] Silicio [100] Arseniuro de Galio Fig. 4: Energía en función de la impulsión para el Si y el AsGa En la Fig. 4 se ha representado esta función Energía – Impulsión para el Si y el AsGa en dos orientaciones cristalográficas distintas para cada una ([100] y [111]). De esta figura se deduce una carcterística importante: en el caso del AsGa el mínimo de la BC y el máximo de la BV se encuentran en un mismo valor de la impulsión. En este caso se dice que el semiconductor es de Banda Directa. Sin embargo, esto no sucede para el caso del Si y, entonces, se dice que el semiconductor es de Banda Indirecta. La importancia de ello radica en que en los semiconductore de banda directa no requieren un cambio en la impulsión para hacer una transición de energía de la magnitud de la BP, esto es Eg. Por tanto, en los semiconductores de banda directa son fáciles las recombinaciones con emisión de un fotón y por tanto, son materiales eficientes para la emisión de luz. Igualmente sucede con la generación de pares electrón-hueco mediante la absorción de fotones. Sin embargo, en los semiconductores de banda indirecta, una recombinación conlleva un cambio sustancial en la impulsión del electrón de froma que se hace necesaria una colisión con los átomos de la red, con lo que la pérdida de energía se realiza en forma de calor y el material no emite luz. Las colisiones también pueden ser entre electrones. Son semiconductores de banda directa en AsGa, el SbGa, el PIn, el AsIn y el SbIn. Mientras que son semiconductores de banda indirecta el Si, el Ge, el PAl, el AsAl, el SbAl y el PGa. 1.6. Impurezas Donadoras y Aceptadoras. Semiconductores n y p. Lo anteriormente expuesto se corresponde con los semiconductores intrínsecos que, como su nombre indica, están exentos de impurezas. Sin embargo, lo que realmente permite la utilización de los semiconductores para la realización de dispositivos electrónicos es la posibilidad doparles, esto es, introducirles impurezas con características bien definidas en el proceso de fabricación. Dichas impurezas son elementos que se agregan al semiconductor en cantidades minúsculas y que vienen a sustituir a algunos de los átomos de la red cristalina del semiconductor original. Si los átomos del elemento dopante tienen más electrones de valencia que los átomos del semiconductor, las impurezas son donadoras porque aportan más electrones de conducción. En este caso se denominan impurezas tipo n, ya que dan lugar a 7 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos semiconductores tipo n (con mayor concentración de electrones que de huecos) cuya conducción es mayoritariamente de electrones. Si por lo contrario, los átomos de impurezas tienen menos electrones de valencia que los del semiconductor, se trata de impurezas aceptadoras porque lo que aportan son más huecos a la banda de valencia. En este caso, se denominan impurezas tipo p, ya que dan lugar a semiconductores tipo p (con mayor concentración de huecos que de electrones) cuya conducción es mayoritariamente de huecos. Así pues, para los semiconductores de la columna IV de la tabla periódica de los elementos (como el Si y el Ge), las impurezas donadoras proceden de la columna V (p.ej: el P o el As), mientras que las impurezas aceptadoras son de la columna III (como el B o el In). Sin embargo, para los semiconductores del tipo V-III, tales como el AsGa o el SbIn, serán donadoras las impurezas del grupo VI (como el Se o el Te) que vengan a sustituir a átomos del grupo V; mientras que serán aceptadoras las del grupo II (Zn o Cd) sustituyendo a las del grupo III. Se da la circunstancia, además, que las impurezas del tipo IV pueden actuar tanto de tipo n o de tipo p en los semiconductores V-III, según sustituyan a las del grupo II o a las del grupo V. En los semiconductores extrínsecos (dopados) tanto tipo p como tipo n, sigue siendo válida la función de distribución de Fermi-Dirac tal como se vio en la sección 1.3, pero con la diferencia de que el nivel de Fermi deja de estar en el centro de la BP (ver Fig. 3). En efecto, en los semiconductores tipo n, el nivel de Fermi queda desplazado hacia la BC, con el consiguiente aumento de población de electrones de conducción y la disminución de huecos. Por lo contrario, en los semiconductores contaminados tipo p, el nivel de Fermi queda más cercano a la BV, con lo que la población mayor es la de huecos. Fig. 5: Función de Fermi para semiconductores tipo n y tipo p Tanto los huecos como los electrones de conducción son portadores de corriente. Se llaman portadores minoritarios a los portadores que menos abundan y portadores mayoritarios a los que más abundan. Esto es, en un semiconductor tipo p los huecos son 8 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos portadores mayoritarios y los electrones son portadores minoritarios. Lo contrario sucede en los semiconductores tipo n. Cuando el nivel de impurezas es tan alto que el nivel de Fermi sale fuera de la BP y cae dentro de la BV o de la BC, el semiconductor se denomina semiconductor degenerado. Para un semiconductor no degenerado se cumple que el producto de la concentración de electrones en la BV n y la concentración de electrones en la BV p iguala al cuadrado de la concentración intrínseca ni (en el semiconductor intrínseco la concentración de huecos es igual a la de electrones). Esto es: n ⋅ p = ni2 (6) 1.7. La unión p-n. Una unión p-n consiste en una transición brusca entre dos regiones de un semiconductor, una de tipo p y otra de tipo n. Esto significa que se trata de un semiconductor en que la distribución de impurezas, lejos de ser uniforme, pasa bruscamente de n a p. La superficie que separa ambas regiones es lo que se denomina unión pn. Así pues, existe una transición brusca entre una zona con predominio de huecos a otra con predominio de electrones de conducción. Como sucede con todas las partículas que están sujetas a agitación térmica, los huecos y los electrones tienden a trasladarse desde la zona donde son mayoritarios a aquélla en la que son minoría, esto es, las partículas tienden a difundirse desde las zonas de mayor concentración hacia las de menor concentración, tratando de uniformizarse (ley de Fick). Es lo que sucede con una gota de tinta en un vaso de agua. Unión p-n _ _ _ _ _ p a _ _ _ _ _ _ _ _ _ _ + + + + + 0 + + + + + + + + + + n a) b Q b) V c) Fig. 6: Configuración, carga espacial y barrera de Potencial en una unión p-n 9 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos Sin embargo, en el caso de una unión p-n la difusión de los portadores rompe la neutralidad eléctrica y esto impide que las concentraciones se equilibren. En efecto, cuando los huecos de la zona p migran hacia la zona n, la ausencia de huecos implica una zona de carga negativa. Dicha carga no es carga de portadores de corriente, sino carga debida a los átomos de la red que no están neutralizados. En consecuencia es carga fija que no puede moverse. Lo mismo sucede con los electrones que migran de la zona n a la zona p que dejan carga positiva sin neutralizar. En la Fig. 6 a) se puede ver la configuración idealizada de una unión p-n. Es lo que se llama región de carga espacial o carga de espacio A ambos lados de la unión se encuentran estas zonas de carga por vaciamiento de portadores. Aunque la carga total en un lado es igual a la de la otro lado y, en consecuencia, la carga total es nula, lo cierto es que las regiones de carga de espacio no son neutras, como se ve en la representeción gráfica idealizada de la densidad de carga espacial Q de la Fig. 6 b). La consecuencia de esta carga de espacio a ambos lados de la unión es que se induce un potencial eléctrico V a modo de barrera que impide que la difusión de portadores continúe. Esta barrera de Potencial se encuentra representada en la Fig. 6 c) y es consecuencia directa de la carga espacial de la Fig. 6 b). En estas condiciones, si se le aplica una tensión eléctrica a la unión con polaridad positiva en la zona p el resultado es que se disminuye la altura de la barrera de potencial y, en consecuencia se produce un flujo continuo de huecos de la zona p hacia la zona n así como de electrones de la zona n a la zona p. En consecuencia, la unión conduce corriente eléctrica con facilidad. Sin embargo, cuando la polaridad de la tensión aplicada es la contraria, lo que sucede es que la barrera de potencial se hace aún mayor bloqueando con más fuerza el paso de los mayoritarios de cada zona a la opuesta. En tales circunstancias sólo habrá una corriente residual muy pequeña, despreciable en la mayoría de los casos, debida a los minoritarios de cada zona que se desplazan a la zona opuesta. La polarización que da lugar a la conducción, positivo en p y negativo en n se denomina polarización directa, mientras que la polarización contraria se denomina polarización inversa. La relación entre la tensión aplicada a la unión y la corriente que circula es la siguiente: I = I s (exp(qV / k B T ) − 1) (7) Donde Is es la magnitud (muy pequeña) de la corriente inversa de saturación, aquella que circula por la unión con una polarización inversa relativamente grande. q es la carga del electrón en valor absoluto, kB la constante de Boltzman y T la temperatura absoluta. En la Fig. 7 se puede ver la curva característica de una unión p-n de acuerdo con (7). Se puede ver que la corriente inversa de saturación sólo se percibe cuando se manejan señales muy débiles. Finalmente, conviene considerar el proceso de transporte de corriente en las cercanías de una unión p-n. En la Fig. 2 se vio la naturaleza bipolar de la conducción de corriente en un semiconductor: cuando se trata de un semiconductor cuya concentración de impurezas es uniforme, la corriente de huecos y de electrones es también uniforme. Sin embargo, en el caso de una unión p-n la conducción a través de la unión implica que se establezca el paso de portadores mayoritarios de una zona hacia la otra, donde son minoritarios. 10 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos Fig. 7: Curva característica de una unión p-n en dos escalas diferentes Por tanto, se produce una verdadera inundación de minoritarios en cada una de las zonas en las proximidades de la unión. Al haber mucha más concentración de minoritarios que la propia del equilibrio el ritmo de recombinaciones se acelera en proporción a esa concentración ya que los minoritarios van a encontrar una gran cantidad de mayoritarios con los que recombinarse, a medida que avanzan en su trayectoria, una vez han cruzado la unión. En consecuencia, la concentración de minoritarios decae rápidamente a medida que se alejan de la unión. Este proceso se ilustra en la Fig. 8 en la que np0 es la concentración de electrones en la zona p (minoritarios) en condiciones de equilibrio, y np es la concentración de electrones en la misma zona como consecuencia de la corriente establecida. Análogamente, pn0 es la concentración de equilibrio de huecos en la zona n, y pn la concentración fuera del equilibrio a causa de la inyección de huecos desde la zona p. p n pn np pn0 np0 x Fig. 8: Difusión de portadores minoritarios a ambos lados de una unión p-n Se puede ver también en la Fig. 8 que las concentraciones de minoritarios tienden a la concentración de equilibrio a medida que se alejan de la unión, de forma que la 11 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos corriente de huecos en la zona n se va convirtiendo en corriente de electrones y la corriente de electrones en la zona p se va convirtiendo en corriente de huecos, todo ello por efecto de la recombinación. Si la unión p-n se encuentra en un semiconductor de banda directa (ver 1.5), buena parte de las recombinaciones se realizan con emisión de fotón. Este es el principio de la fotoemisión y de los diodos emisores de luz (LEDs (Light Emitter Diodes)). 1.8. El Transistor Bipolar Una vez visto el comportamiento de una unión p-n estamos en condiciones de comprender el efecto transistor que es aquél por el cual se produce una amplificación de corriente. El transistor bipolar se compone de tres zonas semiconductoras de tipos n-p-n o p-n-p. Las transiciones entre dichas zonas son uniones p-n abruptas como las descritas en el apartado 1.7, según se puede ver en la Fig. 9 para el caso n-p-n. En consecuencia, hay dos tipos de transistores bipolares, el transistor p-n-p y el n-p-n. El transistor bipolar, sea del tipo que fuere, no es simétrico, aunque lo parezca en la mencionada figura. Una de las zonas de los extremos está generalmente mucho más contaminada que la zona intermedia y recibe el nombre de Emisor (E). La zona intermedia se denomina base (B) y el otro extremo, colector (C ). Cada una des estas zonas tienen un contacto con un terminal al exterior del dispositivo. Los transistores se simbolizan como elementos de circuito según se muestra en la parte baja de la Fig. 9, donde se puede observar que los tipos p-n-p y n-p-n se diferencian en el sentido de la flecha que se pone en el terminal de emisor, que es el sentido de conducción de la unión correspondiente a dicha zona con la base. Si un transistor n-p-n, como se muestra en la Fig. 9, se polariza con el terminal de colector a una tensión positiva respecto al terminal de emisor, que consideraremos conectada a masa, la unión de colector (entre colector y base) estará inversamente polarizada y, en principio, no podrá conducir. Pero hay que tener en cuenta que una unión no conduce a la inversa porque no dispone de portadores capaces de superar la barrera de potencial. Más propiamente, deberíamos decir que la corriente en una unión p-n inversamente polarizada es ínfima porque sólo los portadores minoritarios de cada zona son capaces de atravesar la unión. Ahora bien, si por algún procedimiento se le suministrara a alguna de las dos zonas portadores minoritarios en cantidades significativas, se establecerá corriente inversa de una magnitud similar a ese aporte de minoritarios. Pues bien, esto es lo que sucede si se polariza directamente la unión de emisor. Es decir, mientras la base se encuentre en circuito abierto o con polarización negativa o cero, la unión de emisor no conducirá y, por tanto, el transistor tampoco conducirá bajo la tensión entre colector y emisor debido a la polarización inversa de la unión de colector. Se dice entonces que el transistor está cortado. Pero si se polariza la base con una pequeña tensión directa, la unión de emisor conducirá una corriente débil. Puesto que el emisor tiene una concentración de impurezas muy superior a la de la base, la mayor parte de esa corriente débil se debe a mayoritarios de emisor que se inyectan en base y sólo una mínima parte será debida a los mayoritarios de base que circulan hacia el emisor. Esta circunstancia de desproporción de contaminación es la que da lugar a una buena eficiencia de emisor, ya que son los minoritarios que se inyectan en la base (mayoritarios para el emisor) los que hacen posible el efecto transistor. 12 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos Para que este efecto transistor se produzca, además de la eficiencia de emisor es también importante que la zona de base sea lo más estrecha posible. Esto se debe a que, como se indica en la Fig. 9-(derecha) en el momento que los mayoritarios de emisor atraviesan la unión, se ven arrastrados hacia la unión de colector por la tensión aplicada a la misma. En consecuencia, si la base es lo suficientemente estrecha, la gran mayoría de los portadores inyectados desde el emisor alcanzarán la unión de colector antes de recombinarse con los mayoritarios de base y sólo una pequeña parte de ellos se recombinará y formará parte de la corriente del terminal de base. + + n n C n C p p _ B C p + B n B n E n E Estructura de TRT npn E TRT npn en estado de Conducción TRT npn en estado de Corte C C B B E E Símbolo de TRT npn Símbolo de TRT pnp Fig. 9: Estructura, funcionamiento y simbología del Transistor Bipolar En consecuencia, con una pequeña corriente en el terminal de base se produce una gran corriente en el terminal de colector (también en el de emisor), aproximadamente proporcional a la corriente en base. Cuando esto sucede se dice que el transistor se halla en zona activa pues es cuando actúa como amplificador de corriente. El factor de proporcionalidad (β) entre ambas es la ganancia en corriente. Es decir: iC = β ⋅ i B ; i E = iC + i B 13 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos Las curvas características de un transistor bipolar pueden verse en la Fig. 10. En ellas puede verse que mientras el transistor permanece en zona activa, la corriente de colector es, en efecto, con bastante aproximación, proporcional a la corriente de base. Sin embargo, a medida que la corriente de colector aumenta, el circuito de polarización externo al transistor puede hacer que la tensión entre colector y emisor disminuya, hasta que llega un punto en que es insuficiente para producir el efecto transistor. De hecho, si VCE es demasiado pequeña mientras estamos polarizando la base para que conduzca, resulta que la tensión en la unión de colector ya dejaría de ser inversa. En estas circuntancias, la corriente de colector se estanca aunque sigamos aumentando la corriente de base. Esto es lo que se denomina saturación del transistor. Cuando el transistor está saturado, el punto de trabajo del transistor se encuentra dentro de la zona marcada en la Fig. 10 como Región de Saturación. IC Región de Región Activa Saturación IB4 IB3 IB2 IB1 IB = 0 Región de Corte VCE Fig. 10: Modelo de Curvas Características de de un Transistor Bipolar npn 1.9. El Transistor de Efecto Campo MOS. La denominación de transistor MOS es un extracto de Metal-Óxido-Semiconductor que define la estructura de este tipo de transistores. Como se ve en la Fig. 11, un transistor MOS se compone de dos regiones semiconductoras de un determinado tipo (n en el caso de la figura) sobre un substrato del tipo opuesto (p en el caso de la figura). Una de las dos regiones recibirá el nombre de fuente por ser ésta la que suministra los portadores de corriente, y la otra se denominará drenador pues será la que recoja los portadores y les dé salida. Ambas regiones tienen contactos al exterior y, puesto que la estructura del transistor es simétrica, cualquiera de ellas puede adoptar la función de fuente y la otra de drenador. En cualquier caso, el drenador y la fuente son los extremos del transistor entre los que se establecerá la corriente del mismo cuando ésta exista. La superficie del semiconductor que se encuentra entre las regiones de drenador y fuente se encuentra cubierta por una fina capa aislante. En la tecnología del silicio dicha capa es de óxido de Si que tiene una rigidez dieléctrica muy elevada. Dicha capa se encuentra metalizada en toda la zona que cubre la separación entre drenador y fuente. Dicha metalización se denomina puerta. Asimismo, el substrato tiene contacto al exterior que se pone a una tensión de referencia. Conviene aclarar que, por razones tecnológicas, en los circuitos integrados MOS actuales se sustituye la metalización de puerta por una capa de silicio policristalino que aunque sólo es un conductor mediano, resulta suficiente. No obstante permanece la denominación Metal-Óxido-Semiconductor (MOS) 14 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos Cuando, como en el caso de la Fig. 11, el drenador y fuente son de tipo n, el transistor se dirá que es de tipo n o n-MOS. En caso contrario, drenador y fuente tipo p y substrato tipo n, será de tipo p o p-MOS. Para estudiar el funcionamiento nos basaremos en un transistor n-MOS como el de la Fig. 11. En este caso el substrato se pondrá a masa. La conducción entre drenador y fuente estará interrumpida (transistor cortado) mientras la tensión entre puerta y substrato sea negativa o cero (Fig. 11 b)), ya que la unión de drenador, donde se aplicaría la tensión positiva estaría inversamente polarizada y no hay aportación de minoritarios a ninguno de los costados de dicha unión. _ Puerta Puerta n n n p Substrato b) Transistor n-MOS Cortado + n Puerta n Puerta ++ Substrato p d) Tensión de Puerta sobre Umbral en n-MOS Puerta + Drenador n n Substrato c) Tensión subumbral de Puerta en n-MOS Fuente ++ n p Substrato p Substrato a) Estructura de un Transistor n-MOS Puerta n ++ Fuente n Drenador n p ++ n Substrato e) Transistor n-MOS en Región Óhmica p f) Transistor n-MOS en Saturación . Fig. 11: Estructura y Comportamiento de un Transistor MOS La estructura puerta-óxido-substrato (conductor-aislante-conductor) es capacitiva por su propia naturaleza. En consecuencia si se aplica tensión en puerta respecto a substrato se producirá una acumulación de carga a ambos lados, siendo su polaridad acorde con el signo de la tensión aplicada. Así pues, si se aplica tensión positiva en la puerta respecto al substrato, la carga acumulada en el lado de la puerta será positiva, y la acumulada en 15 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos el lado del substrato, negativa. Ahora bien, mientras la tensión aplicada sea débil (Fig. 11 c)), la acumulación de carga en el lado del substrato se produce exclusivamente por vaciamiento de los mayoritarios del semiconductor. En nuestro caso se trata de vaciamiento de huecos, con lo que se extiende el dominio de la región de carga espacial, de color blanco en la Fig. 11 c) Sin embargo, cuando la tensión de puerta sobrepasa un cierto umbral, comienza a ser más fácil almacenar carga por acumulación de minoritarios que continuar con el vaciamiento de mayoritarios (Fig. 11 d)). Dichos minoritarios, como cargas móviles que son, forman una conexión entre drenador y fuente que recibe el nombre de canal. En estas condiciones, se hace posible la conducción de corriente entre drenador y fuente. Por tanto, cuando la tensión de puerta sobrepasa un cierto umbral, el transistor pasa de comportarse como un circuito abierto a comportarse como un cortocircuito, haciendo las veces de un interruptor controlado por una tensión (la tensión de puerta). Además, el hecho de que exista un umbral a partir del cual se establece la conducción es extraordinariamente útil a efectos de realizar circuitos digitales que, como es sabido, necesitan un umbral con el fin de distinguir entre los dos estados lógicos (el 1 y el 0, verdadero y falso, etc.). Equiparar el canal formado con un corto circuito no es más que una abstracción. En realidad se trata de una resistencia baja, tanto más baja cuanto mayor sea la concentración de portadortes en el canal o, lo que es lo mismo, cuanto mayor sea la tensión de puerta. Por este motivo se dice que el transistor en estas circunstancias se encuentra en la región óhmica. Sin embargo, dicha resistencia sólo presenta un comportamiento lineal cuando la tensión aplicada entre drenador y fuente es pequeña. Cuando dicha diferencia de tensión se incrementa, la magnitud del canal comienza a reducirse a medida que se acerca al drenador (Fig. 11 e)), lo que provoca un aumento de la resistencia del mismo. Esta reducción se debe a lo siguiente: el canal se forma a consecuencia de la diferencia de tensión entre el substrato y la puerta; si se eleva la tensión por la parte de drenador para hacer conducir al canal, el resultado es que se hace disminuir dicha diferencia, especialmente por la parte más cercana al drenador que es donde se aplica la tensión con polaridad positiva (en el caso de n-MOS). En efecto, como se ha representado en la Fig. 12, la tensión de drenador (VDS) cae a lo largo del canal hasta los cero voltios de la fuente (VS = 0), que se ha puesto a masa igual que el substrato, como sucedería en cualquier conductor. Aun suponiendo que esta caída fuera lineal a lo largo del canal, cuando la tensión aplicada al drenador es tal que la diferencia de tensión entre puerta y canal es inferior al umbral propio del transistor (VT), el canal se extrangula y ya no permite que la corriente siga aumentando cuando se incrementa la tensión de drenador. Conviene detenerse un poco en el fenómeno de la estrangulación del canal porque puede parecer que si el canal se estrangula, la corriente debería interrumpirse pero, en este caso, el estrangulamiento no se produciría porque la tensión no caería a lo largo del canal por falta de corriente, luego existiría canal. Sucede por tanto que la zona del canal vacía de portadores minoritarios es atravesada por ellos a causa de la tensión aplicada, de forma similar a lo que sucede cuando se polariza inversamente una unión p-n con una tensión elevada en cuyo caso, lejos de estar bloqueada la corriente, puede aparecer una corriente alta (efecto de avalancha). Así pues, la corriente fluye pero no aumenta la aumentar la tensión pues al mismo tiempo que se eleva la tensión se alarga la zona estrangulada del canal, ofreciendo mayor impedimento al paso de la corriente. 16 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos VDS VGS Saturación VT VGS -VT Región Óhmica Fuente (S) Drenador (D) Canal Estrangulamiento del Canal (pinch-off) VS = 0 Fig. 12: Esquema de tensiones en un transistor n-MOS ID Región Región de Saturación VGS 4 Óhmica VGS 3 VGS 2 VGS 1 VGS ≤ VT VDS Fig. 13: Curvas características de un Transistor MOS En la Fig. 13 se encuentra una representación de la corriente de drenador ID en función de la tensión aplicada entre drenador y fuente (VDS), según el valor que tenga la tensión de puerta VGS. Para dichas curvas características se ha supuesto que, como es habitual, la fuente y el substrato están interconectados entre sí. Analíticamente, la corriente de drenador se puede calcular con bastante aproximación mediante las siguientes relaciones: En Región Óhmica En Saturación (VDS (VDS 2 VDS I D = K (VGS − VT ) ⋅ VDS − 2 < VGS − VT ) : ≥ VGS − VT ) : I D = 1 K ⋅ (VGS − VT )2 2 En estas expresiones se puede comprobar que la corriente en saturación es independiente de la tensión entre drenador y fuente, que la corriente en región óhmica es bastanete lineal para valores pequeños de VDS y que en el paso de región óhmica a saturación, cuando VGS-VT = VDS, los valores de la corriente obtenidos tanto en región óhmica como en saturación, son coincidentes. En la Fig. 14 se muestran los símbolos utilizados para representar a nivel circuital los transistores MOS: las figuras Fig. 14 a) y b) representan el símbolo completo con indicación del terminal de substrato, que es el que contiene la flecha; la flecha en sentido entrante corresponde al transistor n-MOS, pues es el que tiene substrato tipo p. La flecha saliente es el transistor p-MOS. Lógicamente, el terminal aislado, marcado 17 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos con G es la puerta y los otros dos terminales son la fuente y drenador indistintamente. Las Fig. 14 c) y d) tienen ya realizada la conexión habitual entre puerta y fuente, en cuyo caso ya no es indiferente cuál de los dos extremos se toma como drenador o como fuente. En dichas figuras se ha marcado la polaridad de los terminales para que el transistor conduzca, así como el sentido de la corriente. Finalmente, las Fig. 14 e) y f) muestran los símbolos simplificados, donde el terminal de substrato queda implícito y se distingue entre el transistor n-MOS y p-MOS con un pequeño círculo en el p-MOS que indica que la polaridad de dicho terminal para la conducción es inversa (para incrementar el canal hay que reducir el valor de la tensión, no aumentarlo). + D G G G + S G + D S a) n-MOS b) p-MOS c) n-MOS d) p-MOS e) n-MOS Fig. 14: Símbolos utilizados para representar transistores MOS 18 f) p-MOS SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos 2. Sensores Fotovoltaicos Los sensores fotovoltaicos consisten fundamentalmente en una unión p-n con una de sus zonas, p o n, expuesta a la luz. Otra de sus características es que la superficie expuesta a la luz debe ser lo más cercana posible a la unión por las razones de eficiencia que se verán a continuación. Asimismo, la contaminación de impurezas suele ser baja en la zona de incidencia y bastante alta en la zona contraria. 2.1. Efecto fotovoltaico El principio de funcionamiento es el siguiente: al incidir la luz en una de las zonas se produce un incremento notable en la generación de pares electrón-hueco debido a la excitación por absorción fotónica. Los pares electrón-hueco se producen en la superficie del semiconductor donde incide la luz. Dichos portadores en exceso se difunden por el semiconductor. De ellos, los que son minoritarios en la zona y alcanzan la región de carga de espacio de la unión p-n antes de recombinarse, se verán arrastrados por la barrera de potencial hacia la zona opuesta. Surge, por tanto, una polarización por exceso de mayoritarios en ambas zonas, que da lugar a una tensión entre las mismas en circuito abierto con polaridad positiva en zona p y negativa en n. En consecuencia, si se establece conexión externa entre las zonas p y n, habrá corriente eléctrica. + p n _ a) V b) Fig. 15: Efecto fotovoltaico En la Fig. 15 se ha hecho una representación simbólica del efecto fotovoltaico: los pares electrón-hueco generados por la incidencia de fotones en la zona p se difunden por dicha zona. Algunos de ellos se recombinarán, con la consiguiente pérdida de eficiencia, pero otros alcanzan la región espacial de la unión donde se encuentra la barrera de potencial. La barrera retendrá los huecos en la zona p, pero los electrones serán arrastrados por la barrera por tener polaridad inversa. En la Fig. 15 b) se ha representado en gris la línea inversa de la barrera de potencial que es la forma en que afecta a los electrones. Debido a ello, ambas zonas registran un exceso de mayoritarios que produce la tensión. Es por ello que la zona en la que incide la luz, en el caso de la figura la zona 19 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos p, debe ser lo más estrecha posible, ya que así se impide que los pares generados se recombinen antes de alcanzar la unión. En la Fig. 16 se puede visualizar de otra forma este efecto, a través de la estructura de bandas en una unión p-n. El nivel de Fermi tiene la propiedad de ser constante en todo el sólido y las bandas se deflectan del modo indicado en la figura. Puesto que los electrones tienden a ocupar la EC posición de mínima energía los huecos tienden a ocupar la máxima. En consecuencia, los electrones se precipitan a la zona n Ef y los huecos permanecen en la Eg EV zona p. Lógicamente, en el caso de que la luz incidiera en la zona n, se podría aplicar todo lo dicho para p n este ejemplo en sentido dual. Fig. 16: Estructura de bandas de una unión El hecho de dopar sólo débilmente la zona en la que incide la luz obedece al mismo objetivo de evitar al máximo la recombinación antes de alcanzar la unión: cuanto menos abundantes sean los mayoritarios de esa zona, menor será la probabilidad de recombinación. 2.2. El Fotodiodo Una vez visto el efecto fotovoltaico, es importante distinguir entre dos tipos de dispositivos o sistemas diferentes basados en el mismo efecto: uno es el caso en que se pretende detectar la luz, es decir, aquél cuyo objetivo es saber si el nivel de iluminación sobrepasa un cierto umbral. Otro muy diferente es cuando lo que se pretende es producir energía eléctrica. El principio de funcionamiento es el mismo en ambos casos, pero el dispositivo es esencialmente diferente: los paneles de transformación de energía solar en elécrica constan de una matriz de dispositivos cuya superficie, tanto de exposición como de la unión p-n es lo mayor posible, con el fin de recoger y convertir más radiación. Sin embargo, en el caso de los sensores de luz (fotodiodos y fototransistores) normalmente basta con una pequeña ventana expuesta a la luz. La característica tensión – corriente (V-I) de un fotodiodo I = I s (exp(qV / k B T ) − 1) − I p (1) donde Is es la corriente inversa de saturación de la unión, q en valor absoluto de la carga del electrón, kB la constante de Boltzman, T la temperatura absoluta e Ip la corriente en corto circuito que es proporcional al nivel de incidencia de fotones. Esta característica puede verse representada en la Fig. 17 para tres niveles de iluminación (la línea azul corresponde a la oscuridad absoluta) donde la corriente en corto circuito ha sido marcada con un pequeño círculo en cada uno de los niveles. Obsérvese que la corriente que genera el fotodiodo en corto circuito recorre la unión en el sentido inverso al de conducción de un diodo. En la Fig. 18 se puede ver un conjunto de modos de funcionamiento de un fotodiodo. En las Fig. 18 a) y b) se obtienen la tensión en circuito abierto VCO y la corriente en corto circuito Ip respectivamente. En la Fig. 18 c) se ve el sentido de la corriente en caso de cargar directamente el fotodiodo con una impedancia. Finalmente, el montaje de la Fig. 18 d) es el que se utiliza para efectuar la medida del nivel de iluminación mediante la medida de la corriente en la unión con polarización 20 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos inversa. Ya que lo normal es que la corriente inversa de saturación Is sea despreciable frente a la corriente en corto circuito Ip, la corriente que se registra en Fig. 18 d) es, de acuerdo con (1) y la Fig. 17, Ip. Fig. 17: Curvas características de un fotodiodo + Ip VOC Ip ZL VB _ a) b) c) d) Fig. 18: El fotodiodo en diferentes regímenes de funcionamiento Para la fabricación de fotodiodos y paneles solares se utiliza una gran variedad de semiconductores dependiendo, entre otras cosas, de la parte del espectro electromagnético que se quiere captar, de la eficiencia, sensibilidad y costo. Aunque los semiconductores de banda directa son más eficientes, son perfectamente utilizables semiconductores de banda indirecta, como el Si y el Ge, siempre que la energía de los fotones sea suficientemente grande como para efectuar el salto entre las bandas de valencia y de conducción sin tener que provocar cambios sustanciales en la impulsión (ver Anexo – Introducción a los Semiconductores). Es, por ejemplo, el caso del Si en el espectro visible. 2.3. Diodos PIN Dentro de la variedad de fotodiodos se encuentran los diodos p-i-n que, como su nombre indica, intercalan una capa de semiconductor intrínseco entre las zonas p-n. Con ello se consigue ensanchar la región de carga de espacio disminuyendo la capacidad eléctrica de la unión, con lo que se incrementa la velocidad de respuesta; al mismo tiempo, se reparte mejor la polarización inversa (Fig. 18 d)) en el entorno de la unión y se mejora la eficiencia del dispositivo por estar en mayor proporción el arrastre de la 21 SOE - Introducción a los Semiconductores – J. Gutiérrez Ríos barrera de potencial respecto a la distancia por la que los portadores han de difundirse hasta alcanzar la barrera. 2.4. Fotodiodos de barrera Schottky Otra variante son los fotodiodos con barrera Schottky que consisten en una unión metalsemiconductor tipo n. El metal suele ser en realidad una aleación de metal con semiconductor que se comporta como metal y puede depositarse en el semiconductor con buena continuidad de la estructura atómica. Esta capa metálica puede ser transparente y muy delgada, con lo que la luz incide directamente en la región de carga de espacio de la unión evitándose así la pérdida de eficiencia por recombinación. 2.5. Fototransistores Finalmente, los fototransistores tienen la estructura de un transistor normal, pero sin terminal eléctrico en la base. En lugar de ello tienen la región de base expuesta a la luz donde se produce generación fotónica de pares electrón-hueco igual que en los fotodiodos. Por tanto, por efecto fotovoltaico la unión de colector, inversamente polarizada, conduce a la inversa, dando lugar al efecto transistor: la corriente en la unión de colector atraviesa la unión de emisor polarizada directamente. Esto provoca la inyección adicional de minoritarios en base desde el emisor, multiplicando a su vez la corriente de colector. El fototransistor, por consiguiente, da lugar a corrientes mucho más altas que el fotodiodo, pero tiene una respuesta proporcionalmente más lenta. 22