institución educativa nuestra señora del palmar
Anuncio
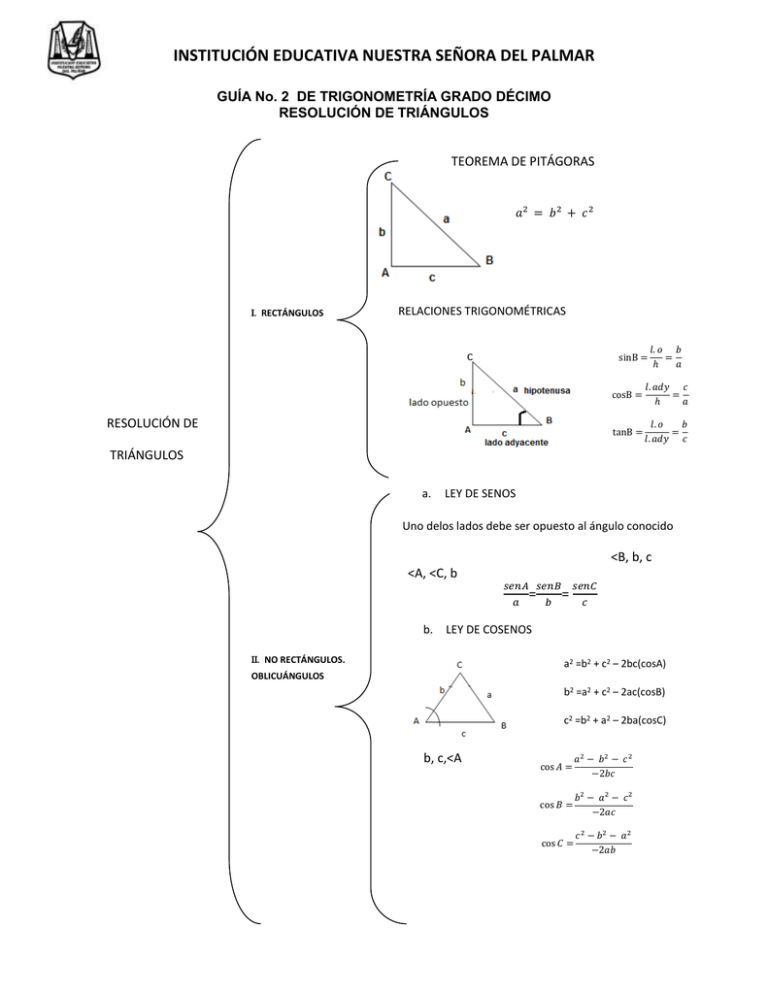
INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR GUÍA No. 2 DE TRIGONOMETRÍA GRADO DÉCIMO RESOLUCIÓN DE TRIÁNGULOS TEOREMA DE PITÁGORAS 𝑎2 = 𝑏 2 + 𝑐 2 I. RECTÁNGULOS RELACIONES TRIGONOMÉTRICAS sinB = RESOLUCIÓN DE 𝑙. 𝑜 𝑏 = ℎ 𝑎 cosB = 𝑙. 𝑎𝑑𝑦 𝑐 = ℎ 𝑎 tanB = 𝑙. 𝑜 𝑏 = 𝑙. 𝑎𝑑𝑦 𝑐 TRIÁNGULOS a. LEY DE SENOS Uno delos lados debe ser opuesto al ángulo conocido <B, b, c <A, <C, b 𝑠𝑒𝑛𝐴 𝑠𝑒𝑛𝐵 𝑎 b. = 𝑏 = 𝑠𝑒𝑛𝐶 𝑐 LEY DE COSENOS II. NO RECTÁNGULOS. a2 =b2 + c2 – 2bc(cosA) OBLICUÁNGULOS b2 =a2 + c2 – 2ac(cosB) c2 =b2 + a2 – 2ba(cosC) b, c,<A cos 𝐴 = 𝑎2 − 𝑏2 − 𝑐 2 −2𝑏𝑐 cos 𝐵 = 𝑏2 − 𝑎2 − 𝑐 2 −2𝑎𝑐 cos 𝐶 = 𝑐 2 − 𝑏2 − 𝑎2 −2𝑎𝑏 c2=a2 +b2 – 2ab(cosC) INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR ÁNGULOS DE ELEVACIÓN Y ÁNGULOS DE DEPRESIÓN Para resolver problemas trigonométricos es importante conocer, entender y aplicar los conceptos de ángulos de elevación y de depresión. Estos conceptos se refieren al ángulo entre la horizontal y la línea visual del observador y la posición del objeto. I. ÁNGULO DE ELEVACIÓN; Si la línea visual del observador y el objeto están por encima de la línea horizontal imaginaria. II. ÁNGULO DE DEPRESIÓN; si la línea visual del observador y el objeto están por debajo de la línea horizontal imaginaria. El ángulo CAB es un ángulo de elevación, el punto B está elevado con respecto al observador en A y la línea horizontal ̅̅̅̅ 𝐴𝐶 que pasa por A. El ángulo DBA es un ángulo de depresión, el punto A queda en la parte de abajo del observador que está en b y ̅̅̅̅ que pasa por B de la línea horizontal 𝐷𝐵 a. Un piloto de un avión observa un punto del terreno con un ángulo de depresión de 30°, 18 segundos más tarde, el ángulo existente sobre el mismo punto es de 55°, si vuela horizontalmente y a una velocidad de 400 millas por hora. Halla la altitud del vuelo. b. La longitud de un hilo que sujeta una cometa es de 15 m, si el ángulo de elevación es de 30°, ¿qué altura alcanza la cometa? c. Una avión vuela a 350 m de altura y el piloto observa que el ángulo de depresión de un aeropuerto próximo es de 15°¿qué distancia le separa del mismo en ese instante? RESOLUCIÓN DE TRIÁNGULOS OBLICUÁNGULOS 1. Dibuja un triángulo equilátero de 4 cm de lado y traza sus alturas. ¿cómo se llama el punto donde se cortan las tres alturas? 2. Dibuja un triángulo rectángulo y otro obtusángulo y encuentra el ortocentro de cada uno. INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR 3. Dado el siguiente triángulo acutángulo sin hacer ninguna construcción auxiliar podrías aplicar los conceptos utilizados en la resolución del triangulo rectángulo anterior Para resolver un triángulo oblicuángulo, necesitamos conocer tres elementos de ellos, uno de los cuales debe ser un lado. Hay cuatro casos distintos: Caso 1. Se conoce un lado y dos ángulos (LAA) ó (ALA) Caso 2. Se conocen dos lados y el ángulo opuesto a uno de ellos (LLA) Caso 3. Se conocen dos lados y el ángulo comprendido entre ellos (LAL) Caso 4. Se conocen tres lados (LLL) Para resolver triángulos oblicuángulos necesitamos conocer dos leyes: III. LEY DE SENOS: la ley de los senos se utiliza para resolver los triángulos de los casos 1 y 2 Esta ley era conocida vagamente por PTOLOMEO (150 D.C) y por NASIN EDADIN ( 1250 D.C) la ley fue enunciada claramente por REGIOMONTANUS en 1464 TEOREMA: “En todo triángulo, la medida de los lados es directamente proporcional a los senos de sus ángulos opuestos”. 𝑎 𝑏 𝑐 𝑠𝑒𝑛𝐴 𝑠𝑒𝑛𝐵 𝑠𝑒𝑛𝐶 = = ó = = 𝑠𝑒𝑛𝐴 𝑠𝑒𝑛𝐵 𝑠𝑒𝑛𝐶 𝑎 𝑏 𝑐 4. Copie en el cuaderno la demostración de este teorema. a. Dado el triángulo ABC, donde se conocen: <A = 38°, <B=52°, lado b=3cm, calcular la medida de los elementos que faltan por conocer. IV. LEY DE LOS COSENOS: la ley de los cosenos se utiliza para resolver los triángulos de los casos 3 y 4. Esta ley aparece por primera vez en los elementos de EUCLIDES (libro II), pero en una forma tal que los cuadrados de los lados del triangulo se suman y se resta un INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR rectángulo que representa el coseno. La forma actual de la le y de los cosenos fue establecida por FRANGOIS VIETA (1540 -1603) TEOREMA: “En todo triángulo, el cuadrado de uno de sus lados es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de dichos lados por el coseno del ángulo que forman” 2 2 2 2 2 2 2 2 2 a =b + c – 2bc(cosA) b =a + c – 2ac(cosB) c =b + a – 2ba(cosC) . 5. a. Copia en tu cuaderno la demostración de la ley de los cosenos b. Dado el triángulo ABC, donde se conocen <A=55°, lado b= 25 cm, lado c = 45 cm, calcular la medidas de sus otros elementos. Tú sabes que el área de un triángulo es igual a 𝑏∗ℎ 2 . Podemos encontrar el área del triangulo aplicando las siguientes formulas: 1 2 1. Conocidos los lados y el ángulo comprendido : “ el área de un triángulo es igual a del producto de los dos lados cualesquiera por el seno del ángulo comprendido, así: 1 Área = 2 𝑏𝑐 𝑠𝑒𝑛𝐴; 1 Área = 2 𝑎𝑐 𝑠𝑒𝑛𝐵; 1 Área: 2 𝑎𝑏 𝑠𝑒𝑛𝐶 2. Conocidos tres lados: “FORMULA DE HERON”: el área de un triángulo es igual a la raíz cuadrada positiva del producto del semiperímetro por la diferencia de éste con cada uno de los lados. A=√𝑝(𝑝 − 𝑎)(𝑝 − 𝑏)(𝑝 − 𝑐), donde P= c. 𝑎+𝑏+𝑐 2 Aplicando las dos fórmulas anteriores encuentra el área de los triángulos de los numerales 4a y 5b TALLER 1. Escribe la oración de Nuestra Señora del Palmar en tu cuaderno 2. Resolver el siguiente triángulo: ABC, donde c=30 cm m<B=50°, m<A=50° 3. Los ángulos de elevación de un globo desde los puntos A y B a nivel del suelo son30° y 40°, respectivamente, los puntos A y B están a 275km entre si y el globo INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR se encuentra entre ambos puntos, con el mismo plano vertical. Calcula la altura del globo sobre el suelo. LEY DE SENOS: En todo triángulo se cumple que los lados son proporcionales a los senos de los ángulos opuestos Hipótesis: el triángulo ABC es un triángulo cualquiera Tesis: Demostración: tracemos sobre el triángulo ABC una de sus alturas, ̅̅̅̅, quedando el triangulo ABC dividido en 2 por ejemplo 𝐶𝐷 triángulos rectángulos En el triángulo ACD se cumple senA = ̅̅̅̅ 𝐶𝐷 𝑏 que: 1 ̅̅̅ b senA = 𝐜𝐝 En el triángulo CDB se cumple senB= ̅̅̅̅ 𝐶𝐷 𝑎 que: ̅̅̅ A senB = 𝐜𝐝 Igualando 1 y 2 queda: 2 b senA = a senB Para obtener la tercera razón = realizado en el paso anterior. 𝒄 𝐬𝐢𝐧 𝑪 𝒃 𝐬𝐢𝐧 𝑩 𝒂 = 𝐬𝐢𝐧 𝑨 A , basta trazar otra de las alturas del triángulo y repetir lo INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR En el triángulo ADC se cumple que: senC = ̅̅̅̅ 𝑨𝑷 ̅̅̅̅ b senC = 𝑨𝑷 𝒃 En el triángulo APB se cumple que: sen B = ̅̅̅̅ 𝐀𝐏 ̅̅̅̅ c sen B =𝑨𝑷 𝐜 Igualando 1 y 2 nos queda: 𝒃 𝐬𝐢𝐧 𝑩 b senC = c senB 𝒄 = 𝐬𝐢𝐧 𝑪 B 𝑏 𝑎 𝑐 = = 𝑠𝑒𝑛𝐵 𝑠𝑒𝑛𝐴 𝑠𝑒𝑛𝐶 Igualando A y B LEY DE COSENOS: En todo triangulo se cumple que el cuadrado de la longitud de uno de los lados es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de estos lados por el coseno del ángulo que forman. Hipótesis: el triángulo ABC es un triángulo cualquiera Tesis: 2 2 2 2 2 2 2 2 2 a =b + c – 2bc(cosA) b =a + c – 2ac(cosB) c =b + a – 2ba(cosC) ̅̅̅̅ Demostración: consideremos el triángulo ABC, trazamos la altura 𝑪𝑫 El triángulo ACD se cumple que: h2 = b2 – x2 1 En el triángulo CDB se cumple que: h2 = a2 – (c - x)2 2 Igualando 1 y 2 nos queda: h2 = b2 – x2 = h2 = a2 – (c - x)2 b2 – x2 = a2 - c2 + 2cx - x2 Ahora bien, en el triángulo ADC se cumple que: 3 INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR cosA = 𝑥 𝑏 X = b cosA Finalmente, reemplazando 4 4 en 3 nos queda: a2 = b2 + c2 – 2bc cosA Este mismo proceso se repite para las otras 2 alturas y se obtienen: b2 = a2 + c2 – 2ac cosB c2 = b2 + a2 – 2ab cosC ACTIVIDAD Resolvamos los siguientes triángulos 1. a. d. b. e. 2. Un poste de 1,2 m de alto se encuentra en la cima de una montaña que forma con su base 20° con la horizontal. Calcula la longitud mínima de cable (x) que llegará a la parte superior del poste a una 2,4 metros cuesta abajo ( medida desde la base del poste) INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR 3. Se desea cultivar sobre un terreno de forma triangular como indica la figura. Calcula el valor del área de dicho terreno ( utiliza la fórmula del Herón) 4. Calcular el valor del ángulo más pequeño entre los lados de un triangulo de medidas 160m, 250m, 320m. 5. Dos vehículos pates de una ciudad al mismo tiempo y circulan en carreteras rectas, separadas por un ángulo de 70°, si viajan a 80 y 100 km por hora representativamente ¿qué distancia se hallarán en uno del otro al cabo de 15 minutos. 6. Inventa el texto de un problema para el siguiente esquema 7. Calcula el valor de la función circular para los siguientes ángulos y arcos: 𝜋 a. Θ= 0° d. β= 2 b. θ = 180° e. β= c. θ= 450° f. β= - 3π(rad) 8. enuncia el TEOREMA DE PITÁGORAS − 3𝜋 2 INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR TALLER DE RESOLUCION DE TRIANGULOS Y NO RECTANGULOS (OBLICUANGULOS) Taller de nivelación 1. el triángulo ABC es rectángulo en B y el triángulo CDE es rectángulo en D. calcular la longitud del lado AB 2. Calcula la medida de la diagonal de un cubo de 4 cm de arista. 3. Las bases de un trapecio isósceles miden 6 cm y 4 cm. El ángulo de la base mida 60°; calcula el área del trapecio. 4. En una carretera para una distancia horizontal de 150 m, se ascienden 12 m. calcula el desnivel en grados. 5. A cierta hora el sol se observa con un ángulo de elevación de 55°, calcula la altura de un árbol que proyecta una sombra de 10,89 m 6. Una escalera de 9 m de longitud se apoya sobre una pared. La escalera forma un ángulo de 54°. Calcula la distancia entre el pie de la escalera y la pared. 7. Calcula la amplitud de los ángulos interiores de un rombo cuyas diagonales mide 6cm y 8 cm. 8. Desde un punto situado 30 m arriba en un faro se observa una pequeña embarcación con un ángulo de depresión de 33°, calcula la distancia al pie del faro que se encuentra la embarcación. 9. Desde la ventana de un edificio a 46 m de altura se observa un automóvil con un ángulo de depresión de 55° calcula la distancia que hay desde el automóvil hasta la base del edificio. 10. Un avión que vuela a 1800m de altura se observa desde una pequeña isla con un ángulo de elevación de 20°, calcula la distancia que hay desde la isla hasta el punto directamente debajo del avión. 11. Un edificio proyecta una sombra de 56m cuando el ángulo de elevación del sol es de 24°11’23”. Calcula la altura del edificio. 12. A cincuenta metros de la base de un edificio se observa la base de la chimenea con un ángulo de elevación de 56° y el punto más alto de la chimenea se observa con un ángulo de elevación de 64°, calcula la longitud de la chimenea. 13. Desde un punto situado a 35 m del pie de un árbol se observa la parte superior con el ángulo de elevación de 48°, calcula la altura del árbol. 14. Uno de los lados congruentes de un triangulo isósceles mide 14 cm y los ángulos de la base miden 36°45’, calcula el área del triángulo. INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR 15. Para alcanzar la cima de un muro se utiliza una escalera de 9,5 m, si la escalera sobresale 0,85 m más allá del muro, calcula la altura del muro. 16. Calcula el área de un paralelogramo cuyos lados miden 6,7m y 8,5m y el ángulo entre los dos es de 37°. 17. Desde un avión que vuela a 186 m de altura se observa una embarcación con un ángulo de depresión de 31° y desde el mismo plano en sentido opuesto se observa el puerto con un ángulo de depresión de 53°. Calcula la distancia que separa a la embarcación de la costa. 18. Calcula la altura del pedestal y de la estatua. 19. Una antena de televisión está instalada en la terraza de un edificio, a 254 m del pie del edificio se observa la parte superior del edificio con un ángulo de elevación de 20° y la parte superior de la antena con un ángulo de elevación de 24°, calcula la altura de la antena. 20. Dibuja un pentágono de 6 cm de lado determina la longitud de la apotema y calcula el área del pentágono. INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR GRÁFICAS DE LAS FUNCIONES TRIGONOMÉTRICAS A. FUNCIÓN SENO Y COSENO: 1. Dibujemos una circunferencia untaría, es decir, con r=1 2. Marquemos un punto P(x,y)de la circunferencia. Este punto determina un ángulo θ en posición normal. 3. Desde este punto P tracemos una perpendicular al semieje positivo de las X, sea M el punto donde la perpendicular corta al eje de las x de tal manera que se forma el triángulo OMP (rectángulo). 4. Encuentra el seno de θ 5. Encuentra el coseno de θ La función que asocia cada número real θ con la ordenada del punto P(x,y) de la circunferencia unitaria y determina el ángulo θ en radianes en posición normal, recibe el nombre de función seno. Seno θ Y, si y solo sí seno θ=Y ó Y= sen θ La función que asocia cada número real θ con la abscisa del punto P(x,y) de la circunferencia unitaria, y determina el ángulo θ en posición normal recibe el nombre de función coseno θ =X 6. Para representar gráficamente la función Y =sen θ y Y = cos θ, construyamos una tabla de valores para 0 < x < 2𝜋 θ 0° 30° 45° 60° 90° 120° 150° 180° 210° 240° 270° 𝜋 𝜋 𝜋 0πrad 6 4 3 0 0,52 0,78 1,05 5𝜋 3 11𝜋 2π 6 Senθ cosθ 7. En hojas de papel milimetrado ubiquemos los puntos (x, sen x); (x, cos x) obtenidos en la tabla anterior. 8. Una los puntos marcados y observa las gráficas obtenidas. B. CARACTERISTICAS DE LAS FUNCIONES SENO Y COSENO Observando cada una de las gráficas del numeral 7, determinar: 1. Dominio y rango de la función seno 2. Dominio y rango de la función coseno C. PROPIEDADES PAR E IMPAR. Simetrías Para poder determinar si las funciones sen θ y cos θ son par o impar debemos tener en cuenta que: 1. Las funciones trigonométricas de un ángulo negativo, vienen dadas por el siguiente teorema sen(-θ) = - sen θ csc (-θ) = - csc(θ) cos(-θ) = cos θ sec(-θ) = sec (θ) INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR 2. 3. 4. 5. tan( - θ) = - tan θ cot (-θ) =- cot(θ) Además las definiciones de: Una función f es par si f(-θ) =-f(θ) Una función f es impar si f(-θ) = -f(θ) Como sen (-θ)= - sen θ, la función y =sen θ es una función par o impar? Como cos (-θ) =cos θ, la función y= cos θ es una función par o impar? Determina si las siguientes funciones son pares o impares ( ó ninguna de las dos) f(x) =3x + 1 f(x)=x2 + 1 f(x)= x2 + 2x 1 f(x) = (x+5)2 – 10(x - 2) f(x)= (8 – x)2 – x(x – 5) f(x) = x3 – 3 f(x)= senx 6. f(x)x3 Una función y=f(x) es simétrica con respecto al eje x Si al sustituir y por –y se obtiene la misma ecuación: x=y2, X = (- y)2 Una función y = f(x) es simétrica con respecto al eje y, si al sustituir x por –x se obtiene la misma ecuación y = x2; y = (- x)2 Una función y = f(x) es simétrica con respecto al origen si al sustituir y por –y y x por – x, simultáneamente, se le obtienen la misma ecuación y = x3, -y =( - x)3 7. Graficar las siguientes relaciones y=x2; x=y2; x2 + y2=1, cada una en papel milimetrado. Dobla la primera por el eje “y”. ¿qué observas? Dobla la segunda por el eje “x” ¿qué observas?. Dobla la tercera por los dos ejes. ¿qué observas? La actividad anterior te permite observar gráficamente cuando una relación o una función es simétrica respecto a uno de los ejes o el origen de coordenadas. 8. Determina que clase de simetría la función y=senx y y=cosx D. PERIODO 1. Completa la siguiente tabla y realice la gráfica en papel milimetrado. Θ Sen θ -720 -630 -540 -450 -360 -270 -180 -90 0 90 180 270 360 450 540 630 720 360 450 540 630 720 2. Observando la gráfica obtenida, ¿cuál es el periodo de la función seno θ? 3 En general senθ = sen(θ+2πK), K ϵƵ 3. Complete la siguiente tabla y realice la gráfica en papel milimetrado Θ cos θ -720 -630 -540 -450 -360 -270 -180 -90 0 90 180 270 4. Observando la gráfica obtenida, ¿cuál es el periodo de la función coseno θ? En general cos θ = cos(θ+2πK), K ϵ Ƶ INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR E. VARIACIÓN Para entender la variación de la función seno y coseno es necesario analizar en cada cuadrante si la función es creciente o decreciente. 1. Una función f(x) es creciente si x1 < x2, entonces f(x1) < f(x2) 2. Una función f(x) es decreciente si x1 < x2, entonces f(x1) > f(x2) 3. Con las gráficas efectuadas en el numeral 7 del literal A, llenar la siguiente tabla con C ( creciente) o D ( decreciente). 1 er cuadrante 2do cuadrante 3er cuadrante 4to cuadrante Sen θ Cos θ 4. Sobre la gráfica escribe las secciones en donde las funciones son crecientes y decrecientes F. MÁXIMOS Y MINIMOS 1. Observando las gráficas del numeral 7 del literal A, ¿cuál es el mayor valor que toma “y” en sen θ y cos θ? 2. ¿cuál es el menor valor que toma y en sen θ y cos θ? 3. ¿Para qué valores de θ, el sen θ es 1? 4. ¿Para qué valores de θ, el cos θ es 1? 5. ¿Para qué valores de θ, el sen θ es - 1? 6. ¿Para qué valores de θ, el cos θ es - 1? Al mayor valor que toma la ordenada de cualquier función, para cambiar de creciente a decreciente, se le llama MÁXIMO Al menor valor que toma la ordenada de cualquier función, para cambiar de decreciente a creciente se le llama MÍNIMO G. AMPLITUD 1. Tabula y grafica en planos individuales y en papel calco las funciones Y=senθ Y=2 senθ 𝟏 𝟐 Y= sen θ 2. Coloca las graficas una sobre la otra en el orden en que se te dieron, ¿qué observas? 3. Halla el dominio y el rango de cada una. INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR En general y=asenx y y = acosx, donde a≠0 satisface en las desigualdades -|A| = a cos x < |A| y -|A|< A sen x < |A| Donde |A| se llama AMPLITUD, la amplitud se utiliza para fijas la escala del eje Y 4. Cuál es la amplitud de y= sen θ Y= 2senθ 1 Y= 2 sen θ 5. Realice los numerales 1,2,3 y 4 para las funciones: y= cos θ Y= 2cosθ 1 Y= 2 cos θ G. El periodo de una función sinoidal se conoce con el nombre de CICLO. El periodo se utiliza para fijar la escala del eje x 𝟏 1. Grafica en papel calco por separado, las funciones y= senθ; y= sen 2θ; y= sen 𝟐θ 2. Coloca las gráficas una sobre la otra en el orden en que se te dieron ¿qué observas? 3. ¿cuál es el periodo de cada una de las funciones? 𝟏 4. Realice los numerales 1,2 y 3 para las funciones y= cos θ; y= cos 2θ; y= cos 𝟐θ Las funciones y = A sen bx y y= A cos bx tienen periodo T = H. 𝟐𝝅 , 𝑩 donde B > 0 Del manual de convivencia escribe 5 deberes que tienes como estudiante de NUESTRA SEÑORA DEL PALMAR. RECUERDA NO BASTA SABER, TAMBIEN SE DEBE APLICAR. NO ES SUFICIENTE QUERER, SE DEBE TAMBIEN HACER. W. GOETHE INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR GRAFICAS DE LAS FUNCIONES TRIGONOMÉTRICAS 1. Determina la amplitud y el periodo de cada función, sin graficar. 9 3 a. Y= 2 sen x e. Y = 5cos ( - 2πx) b. Y = 6 sen πx f. Y = - 4 cos 2x 5 3 2 3 c. Y = sen ( - πx) g. Y = 0.05sen( - 16 x) 5 d. Y= 3 cos x 2. Calcula la amplitud y el periodo y traza la gráfica de cada función a. Y = 6 sen x b. Y = - 4 cos 2x 3. El proceso rítmico de la respiración consiste en periodos alternos de aspiración y espiración. Normalmente un ciclo completo dura 5 segundos. Si f(t). Representa la corriente o flujo de aire en el momento t (en litros / segundos) y si el flujo máximo de aire es 0,6 l/seg, establecer una fórmula que tenga la forma F(t) = a sen bt y que se ajuste a esta información. 4. Asocia cada una de las siguientes gráficas con su función correspondiente. INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR Funciones 𝜋 2 a. Y = 2sen x f. b. Y = 3 cos 2x g. Y =- 2 cos 1 Y = - 3 sen 2x 𝜋𝑥 2 1 sen 2 𝑥 1 cos 2 𝑥 c. Y = -2cos 2 x h. Y = 2 d. Y i. Y=2 j. Y = 3sen 2x e. Y 1 = - sen 2 x 𝜋𝑥 = 2 cos 2 5. Cuando una alarma electrónica o un diapasón se activan, el SONIDO que se produce está formado por vibraciones quedan lugar a una gráfica de tipo sinodal o cosenoidal en un osciloscopio, Figura 1. Figura 1. Estos sonidos se pueden describir por medio de una ecuación de la forma s(t) = Asen(at) Donde t es el tiempo, en segundos, transcurridos después que el sonido se ha originado Algunas características de este tipo de sonido son las siguientes: INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR El VOLUMEN del sonido es la AMPLITUD de la función y se mide en DECIBELES (db) |𝑎| LA FRECUENCIA (f) de las vibraciones está dada por F = 2𝜋 Es decir, la frecuencia es el INVERSO MULTIPLICATIVO del periodo. Ordinariamente, un diapasón en la parte intermedia de la escala musical produce 264 vibraciones por Segundo ¿cuál será la ecuación que describe el sonido que produce un diapasón, si el volumen es de 20 db 6. Dos personas caminan por un sendero pero en un punto se bifurca formando un ángulo de 38° y cada uno va por su lado. Uno camina a 3 k/h y el otro a 5 k/h. ¿a qué distancia se encuentran al cabo de media hora? 7. Una molécula de agua consiste de dos átomos de hidrógeno y una de oxígeno, unidos como indica la figura, la distancia del núcleo de cada átomo de hidrógeno al núcleo del átomo de oxígeno es 4,5 x 10 -9 cm y el ángulo que los une es de 104,8° ¿qué distancia separa los núcleos de los átomos de hidrógenos? H H O 8. encuentra el periodo y la amplitud de las siguientes funciones INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR 9. Encuentra el valor de la base (x) de un banderín de futbol en forma de triángulo isósceles de 1,6 metros de lado y 40° de separación entre los dos lados 10. Desde un punto se observa un edificio cuya parte más alta forma con el suelo un ángulo de 30°, si avanzamos 30 m, el ángulo para a ser de 45°, calcular la altura del edificio. 11. Un edificio proyecta una sombra de 150 m, cuando el sol forma un ángulo de 90° sobre el horizonte, calcula la altura del edificio. 12. Desde el punto A en la orilla de un rio se ve un árbol justo en frente si caminamos 15 m rio abajo, por la orilla recta del rio, llegamos a un punto B desde el cual se ve un pino formando un ángulo de 15° con nuestra orilla, calcula la anchura del rio. 13. En una hoja de papel calco grafica: a. Y = 2 sen2x b. Y = 2sen(2x + 30) c. Y = 2sen (2x – 30) d. Coloca una sobre otra y escribe ¿qué observas? Si y=Asen(Bx +C) o bien y= Acos(Bx+C), donde A y B son números reales distintos de cero, entonces: 1. La amplitud es: |A| y el periodo es T = 2𝜋 𝐵 2. Se puede calcular el desplazamiento de fase y el intervalo que contiene exactamente un ciclo de la curva resolviendo las dos ecuaciones siguientes: 3. Bx +C = 0 ^ Bx + C = 2 π 14. a. b. c. d. e. Graficar las siguientes funciones en papel milimetrado: Y = tan(x) Y = cot(x) Y = cot(x) Y = sec(x) Y= csc (x) INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR f. 15. a. b. c. d. e. En el mismo plano grafica: y = cos(x), y = sen (x + 90|), ¿qué observas? De acuerdo a las gráficas determina: El dominio y rango de cada función Clasificarlas en función par o impar Encontrar si hay simetrías Determinar el período de cada una Analizar en cada cuadrante, donde estas funciones son crecientes y donde son decrecientes 16. Recordar copiando en tu cuaderno cuando una funciones inyectiva, sobreyectiva y biyectiva, realiza ejemplos. 17. Investiga qué es una función inversa y como se encuentran la inversa de una función dada. 18. Escribe en el cuaderno 5 deberes del manual de convivencia para los padres. INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR ACTIVIDAD DE NIVELACIÓN TRIGONOMETRÍA SEGUNDO PERIODO GRADO DÉCIMO 1. Los lados de un triangulo isósceles miden 30,50 y 50 cm calcula en grados la medida de los ángulos 2. Calcula la longitud de la cuerda subentendía por un ángulo central de 110° en un circulo de 24 cm de radio 3. Si caminamos 150 m hacia la base de un edificio y el ángulo de elevación respecto al último piso aumenta de 32° a 45°¿ cuál es la altura del edificio? 1 4. Demuestra que el área del triangulo ABC es 2 x2 tan θ 5. Desde un punto situado a 15 m de la base de un asta, el ángulo de elevación al tope de la misma es de 35°. Halla la altura del asta. 6. Halla el área de un triangulo equilátero en función del lado. 7. Determina el área de cada uno de los siguientes polígonos regulares: a) Pentágono b) Octágono c) Decágono 8. Calcula el área de una circunferencia inscrita en un cuadrado de lado 10 cm. 9. Una escalera tiene 5 m de largo y esta recargada sobre una pared si forma con la pared un ángulo de 60° ¿Que altura alcanzan los extremos de la escalera? 10. Determina la longitud de la base de un triangulo isósceles si el ángulo del vértice no congruente es de 50° y los lados iguales miden 155 cm. 11. Se va a construir una carretera recta para unir las ciudades A y B. Si B está situado a 120 Km al este y 250 Km al norte de A. Encuentra la longitud de la carretera. 12. La longitud del diámetro de las ruedas de un carro es 102 cm ¿Cuánto avanza el carro si uno de los radios de la rueda gira 36°? ¿cuantas vueltas completas debe dar una rueda para que el carro avance 1 Km? 13. Indica a que cuadrante o cuadrantes pertenecen los ángulos que cumplen las siguientes condiciones: a) La tangente es positiva y el seno es negativo. b) La tangente y el coseno tienen el mismo signo. c) El seno y la tangente tienen signos opuestos. INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR 14. Conociendo el valor de una de las razones trigonométricas del ángulo β, halla las demás razones y los posibles valores de β 1 2 √2 - 2 a) Sen β= b) Cos β= 15. Hallar la altura de la torre T del dibujo si d = 40 m, ∞ = 80° β= 65° 16. Una avioneta en vuelo horizontal a 150 Km/h, sobrevuela un pueblo P. si el ángulo ∞ es de 26°, el ángulo β es de 58° y entre el instante A y el instante B han transcurrido 6 seg obtener la altura h del vuelo. 17. Se desea medir la altura de una torre cuya base no es accesible y está situada en un terreno horizontal. Desde un punto A de la torre parece levantar 37°sobre el horizonte. Separándose 12 cm más que A, se llega a un punto B, desde el que la torre parece levantar 28° sobre el horizonte. Hallar la altura de la torre. 18. Hallar la distancia AB representa en el dibujo, para CD = 98 m, ∞ = 98 β= 27° y r=76°, δ =35°. Sera: INSTITUCIÓN EDUCATIVA NUESTRA SEÑORA DEL PALMAR ACTIVIDAD DE PROFUNDIZACION TRIGONOMETRIA GRADO DÉCIMO - SEGUNDO PERIODO 1. Para el siguiente gráfico calcular la medida de las incógnitas 2. 3. 4. 5. 6. 7. 8. 9. 2. Graficar: 𝜋 a. Y = 100 Cos 5 x + 100 f. Y= sen x – Cos x b. Y = - 5 sen 2x + 50 g. Y =( senx)( cosx) c. Y = - 100 sen 3π(x) + 200 h. Y= 𝑠𝑒𝑛 𝑥 𝑐𝑜𝑠𝑥 d. N(t)= 2000 Cos 4 πt + 100 e. Y = senx +Cos x 3. Las coordenadas de los extremos de un vector situado en posición normal son 4 3 P ( 5 , 5 ). Calcula el valor de las siguientes expresiones: a. Sen β + cos β b. 8 sen β + 3 cos β c. (4 tanβ)(3 cotβ) 4. Hallar periodo, amplitud y gráfica de las siguientes funciones trigonométricas. 𝑎. 𝑦=3 𝑠𝑒𝑛 2𝑥 𝑓. 𝑦=2 𝑐𝑜𝑠23𝑥 𝑏. 𝑦=−4cos5𝑥 𝑔. 𝑦=−3cos𝑥 𝑐. 𝑦=2 𝑠𝑒𝑛 𝑥 𝑑. 𝑦=cos13𝑥 𝑒. 𝑦=12𝑠𝑒𝑛 7𝑥