Ejemplo problemas tema 3
Anuncio

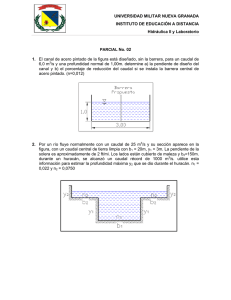
AUTOMATIZACIÓN Y CONTROL DE PROCESOS MEDICIÓN DE CAUDAL DE FLUIDOS PROBLEMA En una instalación se mide caudales de un líquido de densidad 1 g/cc y 1 cP de viscosidad con una turbina Serie 81A de Foxboro de 1 pulg de diámetro. (a) Cuánto vale el caudal mínimo que es capaz de medir el dispositivo con la exactitud de referencia especificada en catálogo? (b) En cuánto cambia el caudal mínimo si se emplea un líquido de 5 cP ? Cuánto vale en estas condiciones el turndown ? (c) Cuánto cambia la pérdida de carga respecto de valor obtenible con el fluido original? PRINCIPIO DE FUNCIONAMIENTO TURBINA Consiste en un aparato que rota, llamado rotor, que está colocado en la cañería de tal forma que la velocidad rotacional es proporcional a la velocidad del fluido; y ésta está relacionada al caudal. 1. Sensor 2. Rotor 3. Brida de montaje 4. Directores de flujo 5. Centro de directores de flujo 6. Eje de rotor, rodamientos 7. Seguros de retención 8. Cuerpo a) De la Tabla 1 del catálogo de FOXBORO 81A Turbine Flowmeters, para un diámtero de 1 pulg. (que es el diámetro de nuestra cañería), los caudales 6 AUTOMATIZACIÓN Y CONTROL DE PROCESOS MEDICIÓN DE CAUDAL DE FLUIDOS límites que se pueden medir con una linelidad de ± 0,5 % son: Qmin = 0,22 lt/s = 3,5 gal/min Qmax = 3,20 lt/s = 50 gal/min b) Para analizar este punto se debe utilizar la Figura 10 de la pág. 6 del catálogo: Se observa que para un fluido cuya viscosidad dinámica de 1 cSt, los límites de caudal que encierran un rango lineal son: Qmin = 0,22 lt/s = 3,5 gal/min Qmax = 3,20 lt/s = 50 gal/min Estos da una rangeabilidad (Turndown) de: Rangeabilidad = Val max 50 = = 14,28 Val min 3,5 Pero cuando se emplea un líquido de 5 cSt, los caudales límites que encierran un rango lineal se ven reducidos: Qmin5 cSt = 1,29 lt/s = 20 gal/min Qmax5 cSt = 3,20 lt/s = 50 gal/min Ahora la rangeabilidad será: Rangeabilidad = 50 = 2,5 20 6 AUTOMATIZACIÓN Y CONTROL DE PROCESOS MEDICIÓN DE CAUDAL DE FLUIDOS c) La Tabla 1 da los valores de pérdida de carga a flujo máximo. Esta información está basada en agua (ρrel= 1, μ = 1 cP a 15 ºC). El valor de pérdida de presión a un flujo determinado menor al máximo puede ser calculado. Para ello la pérdida de presión correspondiente al flujo máximo se multiplica por el cuadrado del valor del flujo divido por el máximo flujo. La ecuación es la siguiente: ⎛ Q ΔPa = ΔPmax ⎜⎜ a ⎝ Qmax ⎞ ⎟⎟ ⎠ 2 Hay otra ecuación más elaborada para calcular la pérdida de presión en una turbina. Esta se utiliza para líquidos cuya densidad relativa y/o viscosidad difieren de la del líquido para el cual la turbina fue calibrado (generalmente agua). En ésta ecuación la pérdida de presión está afectada por factores que consideran el cambio de viscosidad y/o densidad junto con los cambios por caudal: ⎛ ρ ΔPa = ΔPmax ⎜ a ⎜ρ ⎝ agua ⎞ ⎟ ⎟ ⎠ 0 ,81 ⎛ μa ⎜ ⎜μ ⎝ agua ⎞ ⎟ ⎟ ⎠ 0 , 27 ⎛ Qa ⎜⎜ ⎝ Qmax ⎞ ⎟⎟ ⎠ 1,82 Ahora se calcula la pérdida de carga para un fluido de 5 cSt a caudal máximo, de la Tabla 1 se obtiene ΔPmax= 40 kPa: ⎛1⎞ ΔPa = 40kPa⎜ ⎟ ⎝1⎠ 0 ,81 ⎛5⎞ ⎜ ⎟ ⎝1⎠ 0 , 27 ⎛ 50 ⎞ ⎜ ⎟ ⎝ 50 ⎠ 1,82 = 61,77kPa Se observa un aumento de la pérdida de carga de 21,77 kPa. 6 AUTOMATIZACIÓN Y CONTROL DE PROCESOS MEDICIÓN DE CAUDAL DE FLUIDOS PROBLEMA En una citrícola se necesita medir el caudal másico de jugo concentrado de limón que sale del evaporador. Los datos de caudal son vitales ya que se emplearán para calcular los lotes vendidos y eventualmente para realizar mezclas de los mismos. Las condiciones de proceso son: Caudal nominal mínimo: Caudal nominal máximo: Concentración de sólidos: Temperatura: Presión: Pérdida de carga máxima: Diámetro de cañería: 4 ton/hora 16 ton/hora 25 a 45 ° Brix 25 °C a 55 °C 200 Kpa efectiva 70 Kpa 2 pulg (SCh 40) Se dispone de la cotización para caudalímetros másicos por efecto Coriolis (estándar) de dos firmas KROHNE y Schlumberger: Corimas de KROHNE m de Schlumberger Modelo Precio (U$S) Modelo Precio (U$S) 10 P 2500 020/025 3150 60 P 3580 050/075/095 4200 300 P 4930 100/150/195 5460 800 P 6000 200/250/295 6800 1500 P 7000 Los precios corresponden a la presentación estándar del equipo e incluyen el costo de instalación. Seleccionar marca y modelo del equipo más apropiado para esta aplicación. 6 AUTOMATIZACIÓN Y CONTROL DE PROCESOS MEDICIÓN DE CAUDAL DE FLUIDOS PRINCIPIO DE FUNCIONAMIENTO - EFECTO CORIOLIS Un tubo de medición recto es sometido a una oscilación giratoria (ϖ) alrededor de un eje, como se indica en la figura. A través del tubo circula un líquido desde A hasta B. El líquido fluye primero de zonas de alta velocidad rotacional a zonas de menor velocidad rotacional. A medida en que se aproxima al plano del tubo que coincide con el eje de rotación, el movimiento rotacional del fluido es desacelerado de manera uniforme hasta que finalmente llega a cero en el plano del eje de rotación. A medida que el líquido fluye alejándose de este plano hacia zonas de alta velocidad de rotación, el líquido es uniformemente acelerado alcanzando mayores velocidades de rotación. Ambos procesos, desaceleración uniforme y aceleración uniforme del movimiento rotacional del fluido, requiere que una fuerza constante uniformemente distribuida a lo largo del tubo se ejerza en el fluido. Esta fuerza se la conoce como fuerza de CORIOLIS. Si v es la velocidad del fluido en el tubo de medición, ϖ es la velocidad angular instantánea y m la masa de líquido en el interior del tubo, se puede determinar la fuerza de CORIOLIS como: FC = 2m(ϖ X v ) La fuerza de coriolis ,y de esta manera el caudal, son determinados midiendo la cantidad de deformación. Datos: Qnmin = 4 tn/h = 66,6 kg/min 6 AUTOMATIZACIÓN Y CONTROL DE PROCESOS MEDICIÓN DE CAUDAL DE FLUIDOS Qnmax = 16 tn/h = 266,6 kg/min Concentración de sólidos: 25 - 45 ºBx Temperatura: 25 - 55 ºC Presión = 200 kPaef Pérdida de carga máxima: Δpmax = 70 kPa Diámetro cañería: 2 pulg. esc. 40 Con los datos de caudal máximo de 266,6 kg/min y diámetro de cañería 2 pulgadas se analizan ambos catálogos y se obtienen los modelos correspondientes para cada fabricante: • • KROHNE - Corimass MF220 - 300 P SCHLUMBERGER - Mass Flowmeter - Model 195 Ahora con estos dos modelos y sus correspondientes catálogos se arma una tabla comparativa: Características Capacidad [kg/min] Temperaturas Presión [Bar] Densidad Pérdida de Carga [kPa] Exactitud Repetitibilidad Diámetro cañería Precio [U$S] Corimass MF220 300 P 300 -25 - 130 ºC 62 3 0,001- 2 kg/m 60 0,5% 0,1 % rate 1 1/2´´ - 2´´ 4930,00 Schlumberger Model 195 5 - 500 -45 - 204 ºC 103 0,4 - 2 10 0,5% 0,1% 2 ´´ 5460,00 A partir de ésta tabla, se descarta el caudalímetro Corimass 300 P ya que éste que está diseñado para un rango muy bajo de densidades el cual no es suficiente para éste caso. Por lo tanto la opción es el caudalímetro de la firma Schlumberger. 6