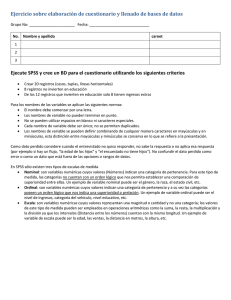
Operacionalización de las variables Las variables se clasifican en

Operacionalización de las variables
Las variables se clasifican en categóricas y continuas.
Las variables categóricas clasifican a los sujetos
distribuyéndolos en grupos, de acuerdo a algún atributo
previamente establecido, por ejemplo, el idioma, la
ocupación, etc. Este tipo de variables se subdividen a su
vez en dos: variables dicotómicas que poseen dos
categorías por ejemplo hombre-mujer, y variables
policotómicas que establecen tres o más categorías, por
ejemplo estado civil, nivel académico, etc.
Son variables continuas cuando se miden atributos que
toman un número infinito de valores, como por ejemplo,
el peso, la talla, la estatura, etc.
• 
Operacionalización de las variables
Las variables categóricas se integra por una serie de
características o atributos que forman una categoría
pero no representan una escala de medición numérica,
por ejemplo los oficios y profesiones. Este tipo de
variables sigue dos reglas:
–  Las categorías diferencian una forma de otra y son
mutuamente excluyentes. Por ejemplo, una persona puede
ser gordo o flaco pero no la suma de las dos categorías.
–  Las categorías de una variable deber ser exhaustivas, es
decir, debe incluir todas las posibles alternativas de variación
en la variable. Por ejemplo, la categoría estado civil incluye
los siguientes rangos potenciales de variación: casado,
soltero, divorciado, viudo, separado, unión libre, etc.
Operacionalización de las variables
•  Variables continuas. Los números utilizados en
esta variable pueden ser discretos o continuos.
•  Por ejemplo en la variable número de hijos, el
rango de números es continuo (1, 2, 3, etc.), en
cambio, si existe la posibilidad de dividirlo en
un continuo de pequeñas fracciones o
cantidades es considerada una variable discreta.
Por ejemplo si se afirma: el ingreso de los
trabajadores operativos de la industria
maquiladora es un promedio de 1.3 salarios
mínimos diario, se tiene una variable discreta.
Operacionalización de las variables
La medición de las variables puede realizarse por
medio de cuatro escalas de medición.
Dos de las escalas miden variables categóricas y las
otras dos miden variables numéricas.
Los niveles de medición son:
-  las escalas nominal
-  Ordinal
-  de intervalo
-  de razón.
Operacionalización de las variables
-  Nominal
En este nivel de medición se establecen categorías
distintivas que no implican un orden especifico.
Por ejemplo, si la unidad de análisis es un grupo de
personas, para clasificarlas se puede establecer
la categoría sexo con dos niveles, masculino
(M) y femenino (F), los respondientes solo
tienen que señalar su género, no se requiere de
un orden real.
Operacionalización de las variables
-  Ordinal
Se establecen categorías con dos o más niveles que
implican un orden inherente entre sí.
La escala de medición ordinal es cuantitativa porque
permite ordenar a los eventos en función de la mayor o
menor posesión de un atributo o característica.
Las formas mas comunes de variables ordinales son ítems
(reactivos) actitudinales
•  Totalmente de acuerdo
•  ___ De acuerdo
•  ___ Indiferente
•  ___ En desacuerdo
•  ___ Totalmente en desacuerdo
Operacionalización de las variables
-  Intervalo
La medición de intervalo posee las características
de la medición nominal y ordinal.
Establece la distancia entre una medida y otra. La
escala de intervalo se aplica a variables
continuas pero carece de un punto cero
absoluto.
Una persona que en un examen de matemáticas que
obtiene una puntuación de cero no significa que
carezca de conocimientos, el punto cero es
arbitrario porque sigue existiendo la
característica medida. Ej. Termómetro.
Operacionalización de las variables
-  Razón
Incluye las características de los tres anteriores
niveles.
Determina la distancia exacta entre los intervalos
de una categoría. Tiene un punto cero absoluto,
es decir, en el punto cero no existe la
característica o atributo que se mide.
Las
variables de ingreso, edad, número de hijos, etc.
son ejemplos de este tipo de escala.
El nivel de medición de razón se aplica tanto a
variables continuas como discretas.