β β β α α
Anuncio
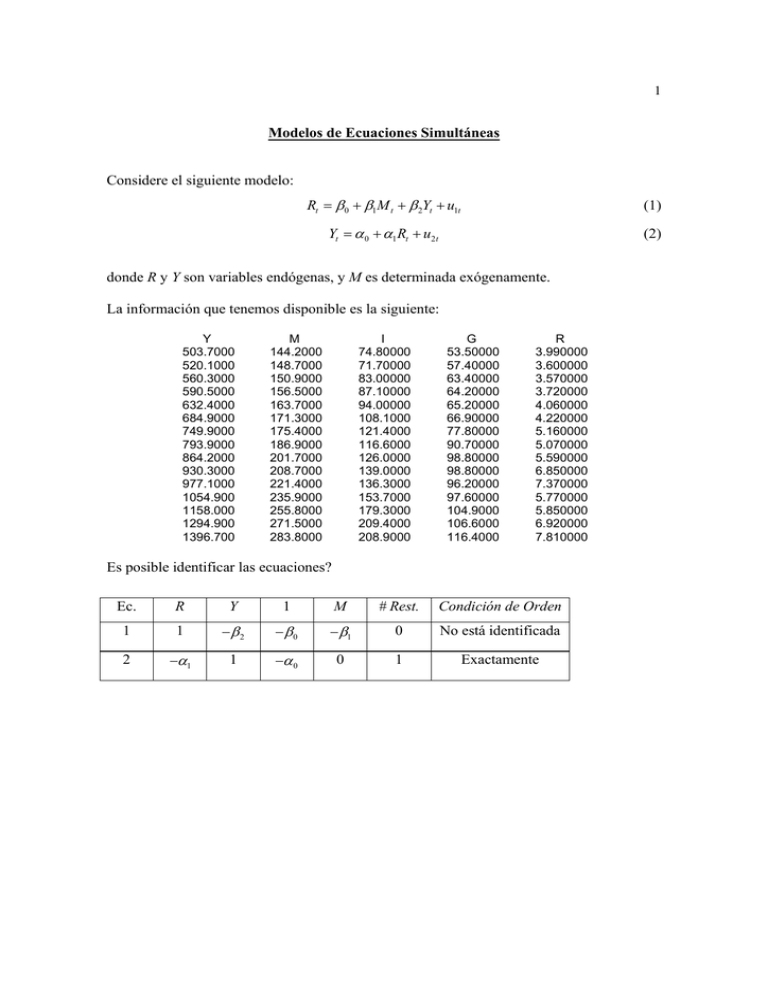
1 Modelos de Ecuaciones Simultáneas Considere el siguiente modelo: Rt = β 0 + β1M t + β 2Yt + u1t (1) Yt = α 0 + α1 Rt + u2t (2) donde R y Y son variables endógenas, y M es determinada exógenamente. La información que tenemos disponible es la siguiente: Y 503.7000 520.1000 560.3000 590.5000 632.4000 684.9000 749.9000 793.9000 864.2000 930.3000 977.1000 1054.900 1158.000 1294.900 1396.700 M 144.2000 148.7000 150.9000 156.5000 163.7000 171.3000 175.4000 186.9000 201.7000 208.7000 221.4000 235.9000 255.8000 271.5000 283.8000 I 74.80000 71.70000 83.00000 87.10000 94.00000 108.1000 121.4000 116.6000 126.0000 139.0000 136.3000 153.7000 179.3000 209.4000 208.9000 G 53.50000 57.40000 63.40000 64.20000 65.20000 66.90000 77.80000 90.70000 98.80000 98.80000 96.20000 97.60000 104.9000 106.6000 116.4000 R 3.990000 3.600000 3.570000 3.720000 4.060000 4.220000 5.160000 5.070000 5.590000 6.850000 7.370000 5.770000 5.850000 6.920000 7.810000 Es posible identificar las ecuaciones? Ec. R Y 1 M # Rest. Condición de Orden 1 1 −β2 −β0 − β1 0 No está identificada 2 −α1 1 −α 0 0 1 Exactamente 2 Cómo estimamos los parámetros de la ecuación (2)? A partir de las ecuaciones (1) y (2), las ecuaciones de forma reducida están dadas por las siguientes expresiones: Rt = β 0 + β 2α 0 β1 Mt + 1 − β 2α1 1 − β 2α1 Yt = α 0 + β 0α1 αβ + 1 1 Mt 1 − β 2α1 1 − β 2α1 Que pueden ser escritas en forma mas compacta como: Rt = π 11 + π 12 M t Yt = π 21 + π 22 M t A partir de las ecuaciones anteriores podemos establecer que: α1π 12 − π 22 = 0 α1 = π 22 π 12 3 Ahora bien, utilizando la información disponible, podemos estimar la ecuación que está exactamente identificada utilizando MCI. Para ello, utilizamos MCO para estimar la ecuación de forma reducida de R: Dependent Variable: R Method: Least Squares Sample: 1960 1974 Included observations: 15 Variable Coefficient Std. Error t-Statistic Prob. C M -0.176195 0.027615 0.811705 0.003991 -0.217068 6.919989 0.8315 0.0000 R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat 0.786487 0.770063 0.691227 6.211332 -14.67152 1.167829 Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic) 5.303333 1.441505 2.222869 2.317276 47.88625 0.000011 y la ecuación de forma reducida de Y: Dependent Variable: Y Method: Least Squares Sample: 1960 1974 Included observations: 15 Variable Coefficient Std. Error t-Statistic Prob. C M -363.7721 6.104147 25.72233 0.126459 -14.14227 48.26975 0.0000 0.0000 R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat 0.994451 0.994025 21.90448 6237.480 -66.51119 1.270539 Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic) 847.4533 283.3689 9.134825 9.229232 2329.969 0.000000 Recordando que: αˆ1 = π 22 6.104147 = = 221.045 π 12 0.027615 Un procedimiento similar se puede utilizar para estimar el parámetro α 0 . Como la ecuación está exactamente identificada, MCI es equivalente a aplicar MC2E. Para aplicar MC2E recordemos en primer lugar que la razón por la cual no podemos aplicar MCO en la ecuación: Yt = α 0 + α1 Rt + u2t 4 es porque la variable del lado derecho es endógena, y por consiguiente debemos utilizar un instrumento. La primera etapa de MC2E es la ecuación de forma reducida de R: Dependent Variable: R Method: Least Squares Sample: 1960 1974 Included observations: 15 Variable Coefficient Std. Error t-Statistic Prob. C M -0.176195 0.027615 0.811705 0.003991 -0.217068 6.919989 0.8315 0.0000 R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat 0.786487 0.770063 0.691227 6.211332 -14.67152 1.167829 Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic) 5.303333 1.441505 2.222869 2.317276 47.88625 0.000011 A partir de esta ecuación encontramos Rˆt . Posteriormente, en la segunda etapa estimamos: Dependent Variable: Y Method: Least Squares Sample: 1960 1974 Included observations: 15 Variable Coefficient Std. Error t-Statistic Prob. C RHAT -324.8250 221.0456 24.93584 4.579381 -13.02643 48.26975 0.0000 0.0000 R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat 0.994451 0.994025 21.90448 6237.480 -66.51119 1.270539 Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic) 847.4533 283.3689 9.134825 9.229232 2329.969 0.000000 5 Si utilizamos la opción TSLS disponible en Eviews, para estimar los parámetros de la segunda ecuación obtenemos: Dependent Variable: Y Method: Two-Stage Least Squares Sample: 1960 1974 Included observations: 15 Instrument list: C M Variable Coefficient Std. Error t-Statistic Prob. C R -324.8250 221.0456 163.5428 30.03408 -1.986177 7.359826 0.0685 0.0000 R-squared Adjusted R-squared S.E. of regression F-statistic Prob(F-statistic) 0.761333 0.742974 143.6615 54.16704 0.000006 Mean dependent var S.D. dependent var Sum squared resid Durbin-Watson stat 847.4533 283.3689 268302.1 1.128420 Los parámetros estimados son idénticos a los que se obtienen cuando aplicamos MC2E “manualmente”. Sin embargo, es importante observar que los errores estándar difieren considerablemente. Para efectos de inferencia debemos utilizar los de arroja la opción TSLS. Para propósitos de comparación, la estimación de la ecuación por MCO produce los siguientes resultados: Dependent Variable: Y Method: Least Squares Sample: 1960 1974 Included observations: 15 Variable Coefficient Std. Error t-Statistic Prob. C R -91.61179 177.0707 129.8351 23.67899 -0.705601 7.477969 0.4929 0.0000 R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat 0.811376 0.796866 127.7155 212046.1 -92.95789 0.922227 Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic) 847.4533 283.3689 12.66105 12.75546 55.92002 0.000005 6 Corrección del error estándar: Y 503.70 520.10 560.30 590.50 632.40 684.90 749.90 793.90 864.20 930.30 977.10 1054.90 1158.00 1294.90 1396.70 Y 847.45 847.45 847.45 847.45 847.45 847.45 847.45 847.45 847.45 847.45 847.45 847.45 847.45 847.45 847.45 Y −Y -343.75 -327.35 -287.15 -256.95 -215.05 -162.55 -97.55 -53.55 16.75 82.85 129.65 207.45 310.55 447.45 549.25 R 3.99 3.60 3.57 3.72 4.06 4.22 5.16 5.07 5.59 6.85 7.37 5.77 5.85 6.92 7.81 R 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 R−R -1.31 -1.70 -1.73 -1.58 -1.24 -1.08 -0.14 -0.23 0.29 1.55 2.07 0.47 0.55 1.62 2.51 Rˆ − Rˆ -1.50 -1.37 -1.31 -1.16 -0.96 -0.75 -0.64 -0.32 0.09 0.28 0.63 1.03 1.58 2.02 2.36 R̂ 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 5.30 R̂ 3.81 3.93 3.99 4.15 4.34 4.55 4.67 4.99 5.39 5.59 5.94 6.34 6.89 7.32 7.66 βˆ2 SLS = 221.0456 σˆ u2 = 1 N ∑ ( y − βˆ 1 2 SLS y2 ) 2 σˆ w2 = 1 N 2856.56 2416.80 9214.54 8655.61 3573.65 5915.57 4338.87 3.90 2173.40 67100.27 107047.35 10876.83 35989.28 8116.14 23.43 σˆ u2 = 17886.8138 σˆ u = 133.7416 ∑ ( y − βˆ 1 ˆ 2 SLS y2 ) 2 162.45 567.13 8.74 1.05 9.47 9.19 1849.42 282.48 10.46 405.49 112.06 453.52 1573.60 1.95 790.47 σˆ w2 = 415.8320 σˆ w = 20.3920 La corrección es entonces: 4.579381(133.7416 20.3920 ) = 30.034 .







