Caso Práctico

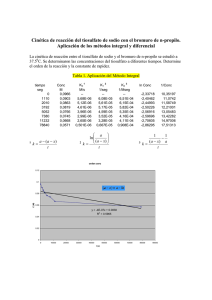
Caso práctico
Administración oral
RESOLUCIÓN
Caso práctico Administración oral
La administración oral de 500 mg de amoxicilina a un paciente de 60 Kg origina la
siguiente curva de concentraciones plasmáticas en función del tiempo:
Tiempo
(h)
0,25
0,5
1
1,5
2
4
6
8
Conc.
(µg/mL)
8,32
14,20
20,60
22,48
21,80
12,24
5,20
1,96
Calcula: Ka, Ke, t1/2, Vd, Cl, ABC0-INF, F, Cmax y Tmax
Caso práctico Administración oral
Calculamos el logaritmo de la concentración y representamos los datos
Tiempo
(h)
0,25
0,5
1
1,5
2
4
6
8
Conc.
(µg/mL)
8,32
14,20
20,60
22,48
21,80
12,24
5,20
1,96
Log conc
0,62
0,85
1,01
1,05
1,04
0,79
0,41
-0,01
2
Log conc (µg/mL)
conc (µg/mL)
12
10
8
6
4
2
0
0
2
4
6
8
10
tiempo (h)
1
0
-1
0
2
4
6
tiempo (h)
8
10
Caso práctico Administración oral
Con los 3 últimos puntos hacemos la regresión lineal para obtener la recta de eliminación
pendiente -0,1989
Log conc (µg/mL)
2
B
y = -0,1989x + 1,5909
R² = 0,9986
1
0
Ke
0,46
h-1
t1/2
1,51
h-1
Ordenada en el origen
1,5909
B
38,99
-1
0
2
4
6
8
10
tiempo (h)
Calculo los residuales para obtener la recta de absorción
tiempo
0,25
0,5
1
valor en la recta conc en la recta
residuales log residuales
de eliminación de eliminación
1,54
1,49
1,39
34,77
31,01
24,66
30,61
23,91
14,36
1,49
1,38
1,16
Log conc (µg/mL)
Residuales
2
y = -0,1989x + 1,5909
R² = 0,9986
1
0
y = -0,4389x + 1,5965
R² = 0,9999
-1
0
2
4
6
tiempo (h)
8
10
Caso práctico Administración oral
Log conc (µg/mL)
2
A
pendiente
Ka
t1/2
y = -0,1989x + 1,5909
R² = 0,9986
1
-0,4389
1,01
h-1
0,69
h-1
0
y = -0,4389x + 1,5965
R² = 0,9999
Ordenada en el origen
A
-1
0
2
4
6
8
1,5965
39,49
10
tiempo (h)
Co,ext:
F·D·Ka/V·(Ka-Ke)
F
Dosis
tmax
tmax
0,92
500
Vd
ln(ka/Ke)/(Ka-Ke)
1,43
Vd
h
F·Ka·D/Co,ext·(Ka-Ke)
21,30
L
Cmax
Co,ext(e-ke*t-e-ka*t)
Cmax
11,06
µg/mL
Cl
Vd·Ke
Cl
9,76
ABC0-inf
A/Ke-B/Ka
ABC0-inf
46,04
ABC0-inf
F·D/V·Ke
ABC0-inf
47,14
L/h
µg h/mL
µg h/mL