valoración de rentas
Anuncio

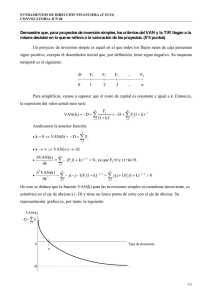
Instrumentos matemáticos para la empresa (4/4) 1º GRADO DERECHO-ADE CURSO 2011-2012. Prof. Pedro Ortega Pulido 1. Matemática Financiera 1.0. Introducción a la matemática financiera. 1.1. Capitales financieros 1.2. Rentas financieras 1.3. Valoración de inversiones 1.3.0. Introducción 1.3.1. El VAN (Valor actual neto) 1.3.2. La TIR (Tasa Interna de Rendimiento) 1.3. Valoración de Inversiones 1.3.0. Introducción ¿QUÉ ES INVERSIÓN? - Concepto complejo - Una aproximación: mediante la INVERSIÓN tiene lugar el cambio de una satisfacción inmediata y cierta a la que se renuncia contra una esperanza que se adquiere y de la cual el bien invertido es el soporte. - PROBLEMAS: - Determinar la rentabilidad de un PROYECTO DE INVERSIÓN para decidir si conviene o no llevarlo. Dada una lista de inversiones alternativas, ordenarlas de mayor a menor rentabilidad con objeto de priorizar las más rentables. 1.3. Valoración de Inversiones 1.3.0. Introducción INVERSIÓN: es una OPERACIÓN FINANCIERA definida por una serie de DESEMBOLSOS que se ESTIMA van a GENERAR una corriente futura de INGRESOS. MÉTODOS PARA VALORAR EL ATRACTIVO DE UN PROYECTO DE INVERSIÓN: - El estudio del VALOR ACTUAL NETO (VAN) - El estudio de la TASA INTERNA DE RENDIMIENTO (TIR) 1.3. Valoración de Inversiones 1.3.0. Introducción Ejemplo 73 Un grupo empresarial está analizando un nuevo proyecto de inversión que requiere una inversión inicial de 450.000€ que genera un flujo de caja de 90.000€ durante los próximos 8 años ¿es una buena o mala inversión? GRÁFICO DE FLUJO DE FONDOS Depósito inicial Corriente de ingresos. Necesitamos conocer el COSTE DE CAPITAL es decir el porcentaje de rentabilidad del proyecto en función de su riesto En el ejemplo podríamos preguntarnos si la inversión es buena si aplicamos una tasa de descuento, dado su nivel de riesgo es del 10% anual. 1.3. Valoración de Inversiones 1.3.1. EL VAN (VALOR ACTUAL NETO) El VAN mide la RENTABILIDAD de un proyecto en VALORES MONETARIOS Mide el valor actual de los desembolsos y de los ingresos, actualizándolos al momento inicial y aplicando un tipo de descuento, conocido también como COSTE DE OPORTUNIDAD DE CAPITAL; en función del riesgo que conlleve el producto. Ejemplo. No conlleva el mismo riesgo invirtiendo en DEUDA DEL ESTADO, en UNA COMPAÑÍA ELÉCTRICA o en una NUEVA COMPAÑÍA DE INTERNET. Cada una de las inversiones utilizaría tasas de descuento diferentes que reflejan distintos niveles de riesgo. 1.3. Valoración de Inversiones 1.3.0. Introducción En el EJEMPLO 73 teníamos el flujo de fondos: Calcularla en el ejemplo y comentar el resultado 1.3. Valoración de Inversiones 1.3.1. EL VAN Supongamos un proyecto de inversión con el siguiente diagrama de flujo de fondos: Un proyecto se ACEPTA si el VAN es positivo, se rechaza si el VAN es negativo. Y entre varios proyectos se elige el que tiene mayor VAN (siempre que tengan inversiones similares) 1.3. Valoración de Inversiones 1.3.1. EL VAN Ejemplo 74. Un proyecto de inversión exige un desembolso inicial de 10 millones de euros y se espera que va a generar los siguientes beneficios durante los próximos seis años: 1º) 600.000€ 2º) 1.000.000 € 3º) 2.000.000 € 4º) 4.000.000 € 5º) 7.000.000 € 6º) 3.000.000 € El tipo de descuento que se aplica a proyectos de inversión con riesgos similares es del 10% anual. Calcular el VAN y extraer conclusiones. 1.3. Valoración de Inversiones 1.3.2. LA TIR (TASA INTERNA DE RENDIMIENTO) Definición. La TIR es la tasa de descuento de un proyecto que hace NULO el van, es decir, la tasa que hace que el beneficio neto actualizado sea igual a la inversión. La TIR es la MÁXIMA TASA DE DESCUENTO que puede tener un proyecto para que sea rentable, pues una tasa mayor ocasionaría que el valor fuese menor que la inversión. Ejemplo 75 En un proyecto de inversión de 6.720,204€ tenemos un cash flow de: 4.000€ el 1er año; 4.000€ el segundo año. Hallar la TIR. La ecuación anterior es relativamente sencilla. Pero en otras ocasiones la ecuación es más compleja de resolver. 1.3. Valoración de Inversiones 1.3.2. LA TIR (TASA INTERNA DE RENDIMIENTO) Ejemplo 76 Un proyecto de inversión de 12.000€ tiene un cash flow de: 4.000€ el 1er año; 4.000€ el 2º año; 4.000€ el 3er años; 4.000€ el 4º año y 5.000€ el 5º año. Halla la TIR. ¿Cómo resolver esta ecuación? (1) Con una calculadora que admita cálculo algebraico (resolución de ecuaciones) (2) MEDIANTE INTERPOLACIÓN (resolvemos el ejemplo anterior con interpolación) 1.3. Valoración de Inversiones 1.3.2. LA TIR (TASA INTERNA DE RENDIMIENTO) Construimos la siguiente tabla (valorando r) r VAN 10% 0,1 3.784,06€ 20% 0,2 364,326€ 25% 0,25 -915,2 Fórmula TIR estará entre el 20% y el 25% Hacemos una proporción Desde el 20%: Una subida de r del 5% -------- VAN baja 1279,52 Una subida de x% ------------- VAN baja 364,326 1.3. Valoración de Inversiones 1.3.2. LA TIR (TASA INTERNA DE RENDIMIENTO) Ejemplo 76 Estamos analizando la posibilidad de instalar un tren de lavado de coches junto a una de nuestras gasolineras. Esta es la información de la inversión: • Cálculo de inversión inicial 150.000€ • El proyecto generará un cash flow de 28.000€ anuales • La vida del proyecto será de 10 años. • El coste de capital para este negocio lo estimo en un 12% anual Calcular el VAN y el TIR y comentar los resultados.