Descargar
Anuncio

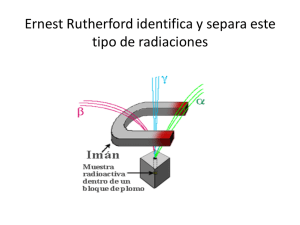
MECÁNICA CUÁNTICA – PLANCK EFECTO FOTOELÉCTRICO – EINSTEIN DUALIDAD ONDA-PARTÍCULA – DE BROGLIE RELATIVIDAD GENERAL – EINSTEIN POSTULADOS GENERALES CONTRACCIÓN DEL TIEMPO FÍSICA NUCLEAR EL NÚCLEO DEFECTO DE MASA Y ESTABILIDAD ENERGÉTICA RADIACTIVIDAD EMISIONES RADIACTIVAS LEY DE DESINTEGRACIÓN REACCIONES NUCLEARES:FISIÓN Y FUSIÓN Año 1900 - Planck La emisión de radiación por parte de la materia no se produce de manera continua, sino de manera discontinua en cantidades discretas, que llamó cuantos de energía(fo tones), proporcionales a la frecuencia de la radiación. E hf siendo h - constante Planck 6,624x10 -34 Js f - frecuencia de la radiación E nhf - múltiplos enteros de un cuanto de energía El efecto Fotoeléctrico - Einstein Emisión de electrones desde la superficie de un metal al ser iluminada Nota: Se puede hablar indistintamente de frecuencia o longitud de onda, ya que ambas se relacionan con la velocidad de propagación. En el caso de la luz=c - c=f 1ev =1,6x10-19J E hf WL hf 0 f0 se invierte - Trabajo(En ergía umbral) de extracción del electrón - frecuencia umbral - Caracterís tica de cada metal M ínima para poder extraer un electrón y lo que sobra en comunicarl e Ecinética Ec E - WL hf - hf 0 h(f f 0 ) Ec 12 mv 2 - Esta energía cinética depende únicamente de la frecuencia de la luz emitida y no de su intensidad Si aumentamos la intensidad lo único que conseguimo s es arrancar un mayor número de electrones , pero darles mayor energía cinética. 1ev =1,6x10-19J Se puede calcular dicha energía cinética, fijando la diferencia de potencial Ec qdV Esta diferencia de potencial se denomina potencial de frenado - T=qdV G Potencial de frenado : Es el necesario para evitar el salto de electrones entre placas. Ajustando el potencial de frenado de frenado podemos calcular la energía cinética de los electrones emitidos - T=qdV G Teoría motivada por la naturaleza ya demostrada dual de la luz Toda partícula tiene un comportamiento dual Como onda Como partícula Parte de la idea de que la luz tiene esta doble naturaleza y la extiende cualquier otra partícula de masa " m" a la que asocia una longitud de onda h h mv p si " m" es relativame nte grande 0 (naturaleza solamente corpuscular) Es una ecuación que relaciona una magnitud ondulatoria con otra lineal E hf Postulados : 1. Todas las leyes físicas se cumplen en cualquier sistema de referencia inercial 2. La velocidad de la luz en el vacío toma el mismo valor en todos los sistemas de referencia inerciales da igual la velocidad con la que se esté moviendo dicho sistema EL TIEMPO SE CONTRAE H PARA EL OBSERVADOR DE DENTRO DEL SISTEMA : 2h t c EL TIEMPO SE CONTRAE h d=vt PARA EL OBSERVADOR DE FUERA DEL SISTEM A : vt 2s 2 h 2 2s ct 2 vt 2 ct 2 h 2 EL TIEMPO SE CONTRAE h DESPEJANDO EL TIEM PO 2 vt 2 2 (ct) 4 h 2 t 2 (c 2 v 2 ) 4 h 2 2h 2h t 2 2 c v v2 c 1 2 c EL TIEMPO SE CONTRAE h t2 2h c2 v2 2h v2 c 1 2 c t1 v2 1 2 c vc t 2 t1 El tiempo es mayor para el observador situado fuera Transcurre más deprisa para el observador situado fuera Relación relativista entre masa y energía : E m c 2 Relaciona las dos magnitudes hasta ese momento considerad as independientes, es decir, la masa es una forma de energía. Cualquier variación pequeña de masa supone una gran varia ción energética y viceversa Ambas relaciones mediante la velocidad de la luz c m Ejemplo : m 1gr E 10 -3 Kg (3 10 8 ) 2 9 1013 J s Para masas muy pequeñas, se utiliza la unidad de masa atómica, equivalent e : 1 10 3 1u.m.a ( gr ) ( Kg ) NA NA 1ev =1,6x10-19J EL NUCLEO: oRUTHERFORD – 1911- LANZANDO ALFA, OBSERVO DESVIACIONES GRANDES EN ALGUNAS DE ELLAS oZONA CENTRAL QUE CONCENTRA TODA LA MASA DEL ÁTOMO oDE CARGA POSITIVA oCONSTITUIDO POR NUCLEONES: PROTONES Y NEUTRONES Z Número Atómico : Número de protones A Número M ásico :Número de nucleones( Protones Neutrones) A Z X Estabilida d de los núcleos : Existencia de una fuerza nuclear fuerte La más intensa que se conoce : superior a la de repulsión eléctrica Actractiva : M antiene los protones y neutrones unidos De corto alcance, solamente actúa a nivel nuclear Energética mente : El núcleo está constituido por nucleones La suma de la masas de todos los nucleones es mayor que la masa del núcleo Existe un defecto de masa en la formación del núcleo : Defecto de masa m m nucleones m núcleo m (Z m protón (A - Z) m neutrón ) m núcleo 1ev =1,6x10-19J Es estable porque : La energía del núcleo es menor que la energía de los nucleones por separado Tiende a poseer menor energía Energía que se libera en la formación del núcleo : E mc 2 Esta energía sería la neceasaria para disgregar un núcleo, es decir, es la energía de enlace nuclear. Dividiendo por el número másico : E En A(número de nucleones que lo constituyen) Energía de enlace por nucleón 1ev =1,6x10-19J LOS NÚCLEOS A PARTIR DE UN CIERTO TAMAÑO (NÚMERO DE PROTONES Y NEUTRONES) COMIENZAN A SER INESTABLES PORQUE LAS FUERZAS DE REPULSIÓN ELÉCTRICAS SON MUY INTENSAS PARA INTENTAR ESTABILIZARSE: PRODUCEN EMISIONES DE PARTÍCULAS – ESTAS EMISIONES ES LO QUE LLAMAMOS RADIACTIVIDAD TRES TIPOS DE EMISIONES: RADIACIÓN ALFA RADIACIÓN BETA RADIACIÓN GAMMA RADIACIÓN ALFA: Son núcleos de Helio 24He Se comprobó que la relación carga/masa se vio que era la misma que la de los iones de He 2 (sin electrones ) Bajo poder de penetración Baja velocidad de emisión 16000 Km/s M ecanismo : A Z X A 4 Z 2 X 4 2 He RADIACIÓN BETA: Son electrones que se producen por desintegra ción de un neutrón Carga negativa M ayorpoder de penetración M ayor velocidad de emisión 260.000 Km/s M ecanismo : A Z X A Z 1 X 10 e RADIACIÓN GAMMA: Es una radiación electromag nética No poseen carga eléctrica M áximo poder de penetración Velocidad de la luz - onda electromag nética M ecanismo : A Z X A Z X Sin cambio pero con emisión energética NOTA: CARGA- se mide al hacerlas atravesar un campo magnético y observar la desviación sufrida Ley de desintegra ción radiactiva : La actividad de una sustancia radiactiva disminuye exponencia lmente con el tiempo. N 0 Número de núcleos iniciales N0 T Periodo de semidesint egración La mitad de ellos 2 T Tiempo que transcurre hasta que se han reducido a la mitad La ley de desintegración radiactiva (1) : t N N 2 T donde t es el tiempo transcurrido 0 Expresión más común para la Ley de desintegra ción radiactiva : Partiendo de la anterior : N N0 2 t T N Ln N0 t - Ln2 T N Ln N0 t tomamos logaritmo Neperiano a ambos lados Ln2 Constante radiactiva T Ley de Desintegración Radiactiva (2) : N N e t donde t es el tiempo transcurrido 0 Ponerla en función del tiempo de vida medio Ley de Desintegración Radiactiva : N N e t 0 1 T Tiempo de vida medio Ln2 Ley de Desintegración Radiactiva (3) : t N N e donde t es el tiempo transcurrido 0 REACCIONES NUCLEARES: FISIÓN NUCLEAR: oNeutrón lanzado contra un núcleo (Uranio-235) oEl núcleo absorbe el neutrón Se excita Se deforma Se fragmenta en dos núcleos Emite nuevos neutrones al fragmentarse(reacción en cadena) oEsta reacción es la que es difícil de controlar(centrales) oEn este proceso se libera gran cantidad de energía por núcleo fisionado oSe debe a que la masa del núcleo original (Uranio) es mayor que la suma de las masas de los núcleos formados. oEste defecto de masa Energía E=mc2 REACCIONES NUCLEARES(II): FUSIÓN NUCLEAR: oNúcleos pequeños se unen para formar otros mayores o2 Núcleos de Hidrógeno se unen para formar núcleos de Helio( partículas alfa). oEn este proceso se libera gran cantidad de energía por núcleo formado oSe debe a que la masa de los reactivos es mayor que la la masa de los productos. oEste defecto de masa Energía E=mc2