Solución del examen del 02-12-2005
Anuncio

UNIVERSIDAD DE SEVILLA – E. T. S. I. INFORMÁTICA
AMPLIACIÓN DE LENGUAJES FORMALES Y AUTÓMATAS
EXAMEN DE DICIEMBRE– CURSO 2004/2005
Apellidos: ___________________________________________________________________________
Nombre: ___________________________________________________________________________
TEST (3 puntos)
Responda si los siguientes enunciados - precedidos por una letra - son verdaderos o falsos utilizando las
tablas que figuran al final. Al rellenar la tabla, coloque una cruz en la fila V si considera que el enunciado
de la correspondiente columna es verdadero. De forma excluyente, coloque una cruz en la fila F cuando
considere que es falso. Las respuestas correctas sumarán 0.2 puntos, las incorrectas restarán 0.2 puntos y
las respuestas en blanco no serán evaluadas. Manifieste nítidamente qué tabla considera su respuesta
final, tachando completamente las demás tablas utilizadas.
•
Sea una GIC G=({a}, VN, S, P).
A. El axioma es generativo si y sólo si S⇒*a
B. El símbolo a es generativo si y sólo si S⇒*αaβ⇒*a con α,β ∈ V*
C. Para limpiar una gramática GIC: primero se deben eliminar las reglas que incluyen símbolos no
generativos y después las que incluyen símbolos inaccesibles
D. Para limpiar una gramática GIC: primero se deben eliminar las reglas que incluyen símbolos
inaccesibles y después las que incluyen símbolos no generativos
E. Para limpiar una gramática GIC se debe eliminar las reglas que incluyen símbolos inaccesibles y
no generativos en el orden que se desee.
Sea un AFP M=({a},{q1,q2},π ,{A(a)}) donde A(a) es la matriz unidad.
F. Si π=(1/2 1/2), el umbral es θ=1/2 y F={q1,q2} entonces L(M)=a*
G. Si π=(1/2 1/2), el umbral es θ=1/2 y F={q1} entonces L(M)=a*
H. Si π=(1/2 1/2), el umbral es θ=1/2 y F={q2} entonces L(M)=a*
I. Si π=(1 0), el umbral es θ=1/2 y F={q1} entonces L(M)= ∅
J. Si π=(0 1), el umbral es θ=1/2 y F={q2} entonces L(M)= ∅
Respecto a la transformación de una GIC G=({a},VN,S,P) en un AP M=({a},{q},q,∅,V,S,δ)
equivalente:
K. Si A →BC∈P entonces δ(q,λ,A)={(q,BC}}
L. Si δ(q, λ ,A)={(q,BC}} entonces A →BC∈P
M. Se verifica que δ(q,a, λ)={(q, λ)}
N. Se verifica que δ(q,a, λ)={(q, a)}
O. Se verifica que δ(q,a, a)={(q, λ)}
•
•
V
F
A
B
X
X
A
B
A
B
C
X
D
E
F
X
G
X
X
X
C
D
E
F
G
C
D
E
F
G
H
X
I
J
K
X
X
X
H
I
J
K
H
I
J
K
L
X
M
N
O
X
X
X
L
M
N
O
L
M
N
O
V
F
V
F
UNIVERSIDAD DE SEVILLA – E. T. S. I. INFORMÁTICA
AMPLIACIÓN DE LENGUAJES FORMALES Y AUTÓMATAS
EXAMEN DE DICIEMBRE– CURSO 2004/2005
Apellidos: ___________________________________________________________________________
Nombre: ___________________________________________________________________________
PROBLEMA 1 (2 puntos)
Dada la siguiente gramática independiente del contexto G=({a,b,c},{S,X,Y},S,P) donde P se define:
S → XY
X → cX | c
Y → aY | bY | bX | a | b
Justifique aplicando el método CYK si la cadena cabaa pertenece a L(G). Nota: Incluya la tabla de
análisis completa utilizada en dicho razonamiento),
La gramática de partida no está en Forma Normal de Chomsky. Para conseguirlo basta con lexicalizarla,
lo que nos conduce a la siguiente gramática:
S → XY
X → CX | c
Y → AY | BY |BX | a | b
A→a
B→b
C→c
Ahora sí podemos aplicar el método CYK sobre cabaa, lo que nos conduce a la siguiente tabla:
S
S
Y
S
Y
Y
S
Y
Y
Y
X,C
A,Y
B,Y
A,Y
A,Y
c
a
b
a
a
Puesto que el axioma pertenece a T[1,5], se verifica que cabaa es una cadena del lenguaje L(G).
Obtenga la expresión regular simplificada asociada para H(L(G)) considerando que h(a)=h(b)=1 y h(c)=0
La expresión que nos piden es 00*1(10*)*
Nota:
El lenguaje de la gramática es el siguiente L(G)= cc*(a+b)*(a+bc*)
Al aplicar el homomorfismo obtenemos H(L(G))= 00*(1+1)*(1+10*)
Al simplificar H(L(G)) obtenemos la expresión que nos piden 00*1*10*
UNIVERSIDAD DE SEVILLA – E. T. S. I. INFORMÁTICA
AMPLIACIÓN DE LENGUAJES FORMALES Y AUTÓMATAS
EXAMEN DE DICIEMBRE– CURSO 2004/2005
Apellidos: ___________________________________________________________________________
Nombre: ___________________________________________________________________________
PROBLEMA 2 (2 puntos)
Obtenga, utilizando el método de Kleene, la expresión regular simplificada que representa al lenguaje
reconocido por el siguiente AF:
M
→q0
q1
*q2
0
q1
q1
q2
1
q2
q0
q2
NOTA: Dibuje la tabla completa y especifique claramente cuál es la expresión regular que representa al
lenguaje reconocido por M.
k=0
k=1
k=2
k=3
R
λ
λ
λ + 0(0 + 10) ∗ 1
λ + 0(0 + 10) ∗ 1
R
0
0
0(0 + 10) ∗
0(0 + 10) ∗
R
1
1
1 + 0(0 + 10) ∗ 11
(1 + 0(0 + 10) ∗ 11)(0 + 1) ∗
1
1
(0 + 10) ∗ 1
(0 + 10) ∗ 1
λ+0
λ + 0 + 10
(0 + 10) ∗
(0 + 10) ∗
θ
11
(0 + 10) ∗ 11
(0 + 10) ∗ 11(0 + 1) ∗
R31k
θ
θ
θ
θ
R32k
θ
θ
θ
θ
R33k
λ + 0 +1
λ + 0 +1
λ + 0 +1
(0 + 1) ∗
k
11
k
12
k
13
R21k
R
R
k
22
k
23
El lenguajes es L(M)=R313 es decir L(M)=(1+0(0+10)*11)(0+1)*
UNIVERSIDAD DE SEVILLA – E. T. S. I. INFORMÁTICA
AMPLIACIÓN DE LENGUAJES FORMALES Y AUTÓMATAS
EXAMEN DE DICIEMBRE– CURSO 2004/2005
Apellidos: ___________________________________________________________________________
Nombre: ___________________________________________________________________________
PROBLEMA 3 (3 puntos)
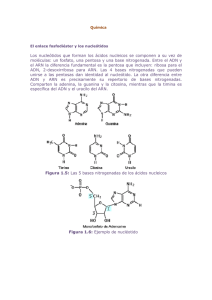
El ADN está formado por pares de 4 tipos de moléculas denominadas bases (adenina, timina, guanina y
citosina). La adenina se empareja con la timina mientras que la citosina se empareja con la guanina. Las
bases de ARN se ordenan de la misma forma aunque en lugar de timina, existe el uracilo. En un
laboratorio que analiza estos componentes, se genera un fichero donde se registran los fragmentos de
pares de bases consecutivos hallados en diferentes secuencias de ADN o ARN. Un ejemplo sería:
Sec0 = <[(G;C)(A;T)][(A;T)(C;G)]>
Sec123 = <[(A;U)(C;G)(U;A)]>
Sec55= <[(A;T) (A;T) (C;G) (T;A)][ (C;G) (G;C)]>
NOTA: A=adenina, T=Timina, G=Guanina y C=Citosina.
Diseñe y atribuya una gramática en bison para reconocer y almacenar los datos descartando los pares de
bases no permitidos y almacenando por separado las secuencias de ADN y ARN. Para la atribución sólo
se podrá usar las funciones incluidas en la siguiente biblioteca
Lista *Agrega_Enlace_a_Lista(Lista *l, Enlace *e);
Secuencia *Agrega_Lista_a_Secuencia(Secuencia *s, Lista *l);
int Comprueba_Tipo_Secuencia(Secuencia *s); //1=ADN,2=ARN
Conjunto *Crea_Conjunto();
Enlace *Crea_Enlace(char *base1, char *base2);
Secuencia *Crea_Secuencia();
int Es_Valido_Enlace(Enlace *e);
void Guarda_Secuencia_ADN(char *id, Secuencia *s);
void Guarda_Secuencia_ARN(char *id, Secuencia *s);
entrada
secuencia
lista_conj
conj_pares
: entrada secuencia
|
;
: ID '=' '<' lista_conj '>'
{if (Comprueba_Tipo_Secuencia($4) == 1)
Guarda_Secuencia_ADN($1, $4);
else
Guarda_Secuencia_ARN($1, $4);}
;
: lista_conj conj_pares
{$$=Agrega_Lista_a_Secuencia($1,$2);}
|
{$$=Crea_Secuencia();}
;
: '[' lista_pares ']'
{$$= $2;}
;
lista_pares : lista_pares par
{if (Es_Valido_Enlace($2))
$$=Agrega_Enlace_a_Lista($1,$2);
else
$$=$1;}
|
{$$= Crea_lista();}
;
par : '(' ID ';' ID ')'
{$$=Crea_Enlace($2,$4);}