Practica No. 6 Objetivo: Que el alumno aplique multiplicadores de
Anuncio

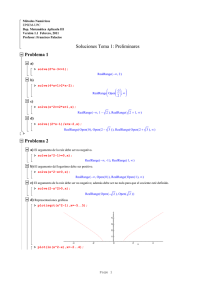
Practica No. 6 Objetivo: Que el alumno aplique multiplicadores de Lagrange para encontrar los puntos criticos en funciones de varias variables. Para el desarrollo de esta practica, el alumno deberá leer la ayuda correspondiente a diff y solve. Para encontrar los puntos críticos de la función f(x,y,z)=y+xz-2x2-y2-z2 sujeto a la restricción z=35-x-y , Teclee las siguientes instrucciones. clear all syms x y z l f=y+x*z-2*x*x-y*y-z*z g=35-x-y-z F=f-l*g Fx=diff(F,x) Fy=diff(F,y) Fz=diff(F,z) Fl=diff(F,l) [x,y,z,l]=solve(Fx,Fy,Fz,Fl) Obtendrá lo siguiente: f= y+x*z-2*x^2-y^2-z^2 g= 35-x-y-z F= y+x*z-2*x^2-y^2-z^2-l*35-x-y-z Fx = z-4*x+l Fy = 1-2*y+l Fz = x-2*z+l Fl = -35+x+y+z x= 21 y= 9 z= 11 l= 15 “La función definida” “La función restricción definida” “La función para analizar puntos criticos” “la derivada parcial de f respecto de x” “la derivada parcial de f respecto de y” “la derivada parcial de f respecto de z” “la derivada parcial de f respecto de l” “El valor de x en el punto critico” “El valor de y en el punto critico” “El valor de z en el punto critico” “El valor de l en el punto critico” ACTIVIDAD Emplee multiplicadores de Lagrange para calcular el valor mínimo absoluto de f si f(x,y,z)=x2+y2+z2 con las dos restricciones x+y+2z=1 y 3x-2y+z=4