PAUTA INTERROGACIÓN 1: P1 y P4 Problema 1: Responda

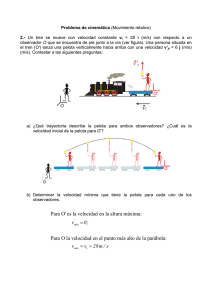
PAUTA INTERROGACIÓN 1: P1 y P4
Problema 1: Responda verdadero (V) o falso (F) justificando las falsas. Sea breve en su
respuesta (no más de 4 líneas). En caso que corresponda puede apoyarse también haciendo
breves cálculos para responder (6 puntos).
i)__F__ Cuando se lanza un objeto hacia arriba, el objeto recorrerá la mayor distancia por
unidad de tiempo cuando esté llegando a la máxima altura.
Debido a la aceleración de gravedad, el objeto irá disminuyendo la velocidad, es decir
cada vez recorrerá menos distancia por unidad de tiempo (1 punto).
ii)__F_ En todos los lanzamientos de proyectil, el módulo de la velocidad primero siempre
disminuye y después siempre crece.
No siempre la afirmación es cierta depende del tipo de lanzamiento de proyectil. Por
ejemplo, la afirmación no es válida cuando se lanza un objeto desde una altura H con una
velocidad horizontal V0, en ese caso el módulo de la velocidad desde el comienzo solo
aumenta hasta hacerse máximo al tocar el suelo (1 punto).
iii)__F__ El gráfico siguiente representa un cuerpo que se
mueve con aceleración positiva hasta T/2, pero después
su velocidad cambia de sentido.
En todo momento la velocidad es positiva (desplazamientos
positivos) nunca cambia de sentido. Efectivamente se
mueve con aceleración positiva hasta T/2, lo que pasa
después es un cambio de sentido de la aceleración
(negativa) (1 punto).
iv)___F__ El gráfico siguiente representa un cuerpo que
va disminuyendo su velocidad con desplazamientos
negativos hasta T/2 para después cambiar de sentido de
desplazamiento aumentando la velocidad.
En todo momento la velocidad es positiva, por lo tanto, los
desplazamientos son en todo momento positivos. Hasta T/2
simplemente la velocidad va disminuyendo para después
aumentar a partir de ese instante (1 punto).
v)___F__El gráfico siguiente representa un movimiento de
dos cuerpos donde uno es a velocidad constante y el otro
a aceleración constante. Además en el tiempo T ambos
cuerpos se encuentran.
Efectivamente un cuerpo se mueve a velocidad constante y
el otro a aceleración constante, pero el grafico indica que
en el tiempo T ambos cuerpos tienen la misma velocidad
NO posición (1 punto).
vi)__V___ En una competencia de lanzar una piedra lo más lejos posible, usted tratará de
lanzar de manera que el vector velocidad tenga un ángulo de 45º con respecto a la
horizontal porque así logrará el máximo alcance que tirando con la misma velocidad pero
con otro ángulo de lanzamiento.
(1 punto).
PROBLEMA 2 Un tren A parte desde el reposo con una aceleración constante de 0, 01 m/s2 , dirigiéndose desde una estación “E1”a una estación “E2”,
las cuales se encuentran separadas por una distancia de 100 km. En ese mismo
instante otro tren “B” que se desplaza a una velocidad constante de 40 km/hr
está pasando por la estación “E2” en dirección a la estación “E1”, por lo cual
ambos trenes se encontrarán en algún punto del tramo entre ambas estaciones.
• a) (2,0 puntos) Determine el tiempo en el cual ambos trenes se encuentran.
• b) (2,0 puntos) Determine la posición y velocidad del tren “A” en el momento del encuentro.
• c) (1,0 ptos.) Grafique como son las velocidades de los dos trenes. Haga
solo 1 gráfico indicando los valores representativos.
• d) (1,0 ptos.) Grafique como son las posiciones de los dos trenes. Haga
solo 1 gráfico indicando los valores representativos.
RESPUESTA
a) Datos del problema:
Posición inicial tren “A” xi,A = 0
Velocidad inicial tren “A” vi,A = 0
Aceleración tren “A” aA = 0, 01 m/s2
Posición inicial tren “B” xi,B = 100 km = 100 000 m
Velocidad inicial tren “B” vi,B = −40 km/hr = −11, 1 m/s
Aceleración tren “B” aB = 0
Notar que la velocidad del tren “B” es negativa dado que hemos tomado
como origen la estación “E1”.
(0.1 puntos)
Utilizando la ecuación de movimiento x = xi + vi × t + a × t2 /2 escribimos
las ecuaciones de movimiento de ambos trenes. La del tren “A” es
xA = 0 + 0 + 0, 005 m/s2 × t2
(1)
(0.3 puntos)
y para el tren “B” es
xB = 100 000 m − 11, 1 m/s × t + 0
(2)
(0.3 puntos)
Ambos trenes se encontrarán cuando xA = xB y llamaremos a ese tiempo
de encuentro como te . Entonces igualando ecuaciones (1) y (2) para t = te se
tiene
1
xA = xB
0, 005 m/s2 × t2e = 100 000 m − 11, 1m/s × te
o escrito de otra forma:
0, 005 m/s2 × t2e + 11, 1 m/s × te − 100 000 m = 0
(0.5 puntos)
√
2
b −4ac
) con a =
Utilizando la solución a la ecuación cuadrática (te = −b± 2a
2
0, 005 m/s , b = 11, 1 m/s y c = −100 000 m se obtiene
√
−11, 1 ± 123, 2 + 2 000
−11, 1 ± 46, 1
te =
=
0, 01
0, 01
donde se escoge el signo positivo para que el resultado tenga sentido fı́sico, o
sea que te = 3 500 s = 58, 3 min.
(0.8 puntos)
b) Para determinar la posición del tren “A” en el momento del encuentro,
se utiliza la ecuación 1 para t = 3 500 s, o sea,
(0.2 puntos)
xA = 0, 005 m/s2 × (3 500 s)2 = 61 250 m
(0.8 puntos)
y para determina la velocidad del tren “B” se utiliza la ecuación de velocidad
v = v0 + a × t para t = 3 500 s, o sea,
(0.2 puntos)
vA = 0 + 0, 01 m/s2 × 3 500 s = 35, 0 m/s
(0.8 puntos)
c) Figura en siguiente página.
Descuentos:
Lı́nea mal dibujada: -0.4
Signo malo: -0.2
No indicar tiempo de encuentro: -0.1
No indicar velocidad en tiempo de encuentro: -0.1
Eje sin unidades: -0.1 (por eje)
Lı́neas terminan en 3500 s: 0.0
2
(1.0 punto)
d) Descuentos:
Lı́nea mal dibujada: -0.4 (solo -0.2 si curvatura mala)
No indicar tiempo de encuentro: -0.1
No indicar posición en tiempo de encuentro: -0.1
Eje sin unidades: -0.1 (por eje)
Lı́neas terminan en 3500 s: 0.0
(1.0 punto)
3
PROBLEMA 3
Dos estudiantes de fı́sica van a medir la altura de un edificio usando lo aprendido
en clases. El estudiante A se pone en lo alto del edificio con una pelota de tenis
y el estudiante B está abajo con un cronómetro. Este último medirá el tiempo
que demora la pelota en llegar al suelo.
• a) (1,5 puntos) Si el estudiante B mide que la pelota demora en llegar al
suelo 15 segundos cuando ésta es soltada por el estudiante A, determine
la altura del edificio.
• b) (1,5 puntos) Para comprobar la medición los estudiantes repiten el
proceso, pero esta vez el estudiante A se equivoca y le da una velocidad
inicial a la pelota. Si ahora la pelota demora en llegar al suelo 18 segundos
y la medición de la altura hecha en el primer intento está correcta (parte
“a” del problema), determine la velocidad inicial de la pelota.
• c) (1,5 puntos) Determine la velocidad que llega la pelota al suelo, para
los dos casos (partes “a”y “b” del problema).
• d) (1,5 puntos) Cuál es la posición respecto al suelo y velocidad de la pelota
despus de 7 segundos en los dos casos (partes “a” y “b” del problema)?
RESPUESTA
a) Datos del problema:
Tiempo de caı́da de la pelota: tf,a = 15 s
Velocidad inicial de la pelota: vi,a = 0
Aceleración de la pelota: ap = −g = −9, 8 m/s2
Notar que se toma como marco de referencia el suelo como origen.
(0.2 puntos)
Este es un problema de caı́da libre donde la ecuación de movimiento de la
pelota está dada por la ecuación y = yi + vi × t + a × t2 /2, que al reemplazar
los datos de esta parte del problema se tiene que
ya = yi − 4, 9 m/s2 × t2
(0.5 puntos)
donde yi es la altura del edificio, la cual se puede encontrar sabiendo que para
t = tf,a el valor de la posición ya = 0, o sea,
0 = yi − 4, 9 m/s2 × (15 s)2
que al despejar yi da que la altura del edificio es de 1102, 5 m.
(0.8 puntos)
4
b) (Nota para el corrector: si la altura determina en a) está incorrecta, pero
el procedimiento está correcto se debe asignar todos los puntos.)
En este caso, la velocidad inicial de la pelota ya no es nula, sino tiene un
valor desconocido que llamaremos vi,b . Con esto la ecuación de movimiento de
la pelota se escribirá como:
yb = 1102, 5 m + vi,b × t − 4, 9 m/s2 × t2
(0.4 puntos)
donde se ha reemplazado la posición inicial con la altura obtenida en a).
Ahora, para determinar la velocidad inicial se utiliza el tiempo de caı́da de
la pelota, la cual será t = tf,b = 18 s donde yb = 0. Por lo tanto la ecuación
anterior queda:
(0.3 puntos)
0 = 1102, 5 m + vi,b × 18 s − 4, 9 m/s2 × (18 s)2
0 = 1102, 5 m + vi,b × 18 s − 1587, 6 m
que despejando vi,b queda
vi,b = 485, 1 m/18 s = 27, 0 m/s
(0.8 puntos)
c) Para determinar las velocidad de llegada de la pelota en los dos casos, se
debe utilizar la ecuación de la velocidad v = vi + a × t, que para la parte “a”
queda:
va = 0 − 9.8 m/s × t
(0.2 puntos)
la cual evaluada para el tiempo de caı́da de ese caso (t = 15 s) da que la velocidad
final es vf,a = −147, 0 m/s.
(0.3 puntos)
Para la parte “b” se tiene que la ecuación de la velocidad queda:
vb = 27, 0 m/s − 9.8 m/s × t
(0.2 puntos)
la cual evaluada para el tiempo de caı́da de ese caso (t = 18 s) da que la velocidad
final es vf,a = −149, 4 m/s.
(0.3 puntos)
5
d) En las partes anteriores del problema se determinaron las ecuaciones
de posición y de velocidad para cualquier tiempo, por lo cual para estimar
las posiciones y velocidades en cada uno de los casos se deben evaluar esas
ecuaciones para t = 7s. Por consiguiente se tiene que la posición y velocidad
para el caso “a” serán:
ya = 1102, 5 m − 4, 9 m/s2 × (7 s)2 = 862, 4 m
(0.375 puntos)
va = 0 − 9.8 m/s × 7 s = −68, 6 m/s
(0.375 puntos)
donde se reemplazó en la ecuación para ya el valor yi = 1102, 5 m. Para el caso
“b” la posición y velocidad en t = 7 s serán:
yb = 1102, 5 m + 27, 0 m/s × 7 s − 4, 9 m/s2 × (7 s)2 = 1051, 4 m
(0.375 puntos)
vb = 27, 0 m/s − 9.8 m/s × 7 s = −41, 6 m/s
(0.375 puntos)
6
PROBLEMA 4
Batman corre en la azotea de un edificio, cuando llega al final, desea saltar horizontalmente
a la otra azotea que se encuentra a 5m bajo la primera y a 6m de ésta (ver figura).
Determine:
a) (3 ptos.) El tiempo de vuelo de Batman.
b) (3 ptos.) La velocidad inicial horizontal
mínima para realizar el salto.
a) Si Batman se lanza horizontalmente, el tiempo de vuelo es independientes de la
velocidad horizontal con que se lanza (recuerde la independencia de los
movimientos en X e Y en un movimiento de proyectil). Entonces simplemente
ocupo la ecuación cinemática de posición en Y para sacar el tiempo de vuelo.
y (t ) = y i + v yi ⋅ t −
1
g ⋅t2
2
[
]
1
0 = 5[m ] + 0 − 9,8 m / s 2 ⋅ t 2
2
0 = 5[m ] − 4,9 m / s 2 ⋅ t 2
t = 1,01s
(3 puntos)
[
]
“Demora 1,01 segundo en caer a la azotea del siguiente edificio”.
b) La velocidad mínima horizontal es la necesaria para alcanzar a recorrer los 6 metros
de separación entre un edificio y otro. Para determinar eso uso simplemente una
ecuación cinemática de posición en X.
x(t ) = xi + v xi ⋅ t
6m = 0 + v xi ⋅ 1s
v xi = 5,94[m / s ]
(3 puntos)
“Entonces la velocidad mínima horizontal para saltar debe ser de 5,94m/s”. Si salta con
menos de eso se cae entre los edificios.