Colección isométrico
Anuncio

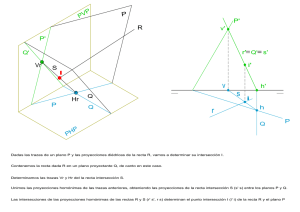
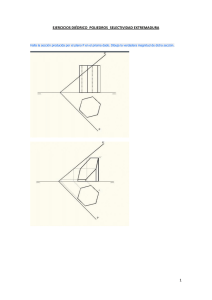
Los puntos en el sistema axonométrico tienen cuatro proyecciones: una sobre cada plano del triedro trirrectángulo, y otra sobre el plano fundamental. Esas cuatro proyecciones y el vértice O del triedro, están en los vértices de un paralelepípedo característico, de manera que la proyección directa del punto (A en la figura) y el punto O son vértices opuestos del mismo La proyección directa de un punto debe quedar unida a la proyección de ese punto sobre un plano del triedro, por medio de una recta que tenga la misma dirección que el eje perpendicular a dicho plano. Por ejemplo, A (proyección directa de A), estaría unido con A’ (proyección de A sobre el plano xy) por medio de una paralela al eje z (eje perpendicular al plano xy) Las proyecciones de un punto sobre dos planos de triedro, deben poder unirse mediante rectas que sigan la direcciones de los ejes que no comparten los planos. Estas rectas se cortan en el eje que dichos planos tienen en común (este eje sería una especie de línea de tierra). z z z A”’ A” A A” A" O A"' A y x A' x y x y A’ A’ A” A”’ A”’ A’ Puntos de los planos del Triedro Puntos del plano xy C=C' z C z D" D y A A"' x 4 1 5 B=B' A" A=A' B" x 2 z y D"' y 3 8 C" D=D' B C"' B"' x 6 7 Octantes en que está dividido el espacio por los planos del Triedro Trirrectángulo Puntos en el sistema isométrico Halla las dos proyecciones que faltan de cada punto. A” A A A”’ A A’ A” A”’ A” A”’ A A”’ A’ A” A A A”’ A’ Rectas en el sistema isométrico Halla las trazas y las proyecciones que falten de la recta r, en cada caso. r r" r" r"' r' r' (los puntos A y B son de r) Tr"' Tr' Tr" r A" Tr"' B' Planos en el sistema isométrico Halla la traza que falta de cada plano. "2 "3 "3 "2 "3 "1 PERTENENCIAS EN ISOMÉTRICO Dibuja las proyecciones y trazas que faltan para que A esté en r y r en el plano alfa. r"' A A" "3 r” "3 r"' A’ "1 Dibuja una recta horizontal del plano, que pase por A "2 Dibuja una recta paralela a yz, contenida en ", que Dibuja una recta paralela a xz, contenida en ", que pase por A. pase por A. "3 A"' A "3 "3 "2 "2 A’ Dibuja la línea de máxima pendiente respecto al plano xy, que pase por A. Halla las trazas del plano cuya línea de máxima pendiente respecto al plano xz es la recta r. Dibuja las trazas del plano del que conocemos r, que es una línea de máxima inclinación respecto a yz. r" r"' "2 r r' A' "1