TECNOLOGÍA INDUSTRIAL I - EJERCICIOS ELECTRICIDAD.
Anuncio

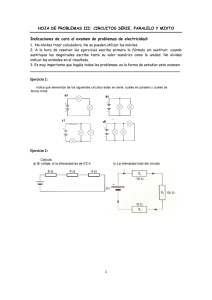
TECNOLOGÍA INDUSTRIAL I - EJERCICIOS ELECTRICIDAD. 1.- Encuentre la resistencia equivalente del siguiente circuito Rab SOLUCIÓN: Requ.= 20Ω 2.- Calcula la resistencia total del circuito 50V 20 100 50 50 100 20 200 3.- Realiza los cálculos solicitados en los siguientes circuitos: 150Ω 250Ω RT IT V1 V2 VT = V1+V2 P1 P2 9V 100Ω 200Ω I1 I2 I3 Req. IT=V/Req. P1 P2 100Ω 30V 4.- En el circuito de la figura se desconoce el valor de la corriente. a) Calcule los valores de la corriente. b) Determine la potencia que disipa cada resistor. P3 TECNOLOGÍA INDUSTRIAL I - EJERCICIOS ELECTRICIDAD. 5.- Calcula la intensidad, la caída de tensión y la potencia que consume cada una de las resistencias del siguiente circuito. ¿Qué potencia eléctrica produce el generador? 6.- En el siguiente circuito, calcula la resistencia equivalente, y posteriormente la intensidad en cada resistencia. 7.- En el siguiente circuito, calcula la resistencia equivalente, y posteriormente la intensidad y la caída de tensión en cada resistencia. 8.- En el siguiente circuito, calcula la resistencia equivalente, y posteriormente la intensidad y la caída de tensión en cada resistencia. TECNOLOGÍA INDUSTRIAL I - EJERCICIOS ELECTRICIDAD. PROBLEMA RESUELTO KIRCHHOFF 1.- Encuentre el valor de las intensidades del circuito de la figura Para la resolución de este circuito utilizaremos las leyes de Kirchhoff. Ley de los nudos: I1 + I2 = I3 Ley de las mallas: Está claro que podéis escoger cualesquiera (dos) de las tres mallas posibles. En este caso se han elegido estas dos, resultando las siguientes ecuaciones: 8-4 = -3I1 + 9I2 8-16 = -3I1 -9I3 Las ecuaciones quedan, por tanto: I1 + I2 = I3 8-4 = -3I1 + 9I2 8-16 = 3I1 -9I3 La reducción sale directamente en las ecuaciones Sustituyendo I3 en la 2ª y 3ª ecuación 4 = -3I1 + 9I2 -8 = -3I1 – 9(I1 + I2) 4 = -3I1 + 9I2 -8 = -12I1 -9 I2 -4 = -15 I1 I1 = -4/-15 I1 0.27 A Sustituyendo en cualquier ecuación obtenemos I2 (por ejemplo esta) -8 = -12 (0.27) – 9I2 I20.54 A Y, por último, de la primera ecuación podemos obtener I3 I1 + I2 = I3 ; I3 = 0.27 + 0.71 ; I3 0.81 A 4 = -3I1 + 9I2 4 = -3I1 + 9I2 -8 = -3I1 – 9I1 -9 I2 -8 = -12I1 -9 I2 TECNOLOGÍA INDUSTRIAL I - EJERCICIOS ELECTRICIDAD. Problemas Propuestos 1. Calcula las intensidades que circulan por cada una de las resistencias de la siguiente red de Kirchhoff. ¿Qué potencia genera cada pila? ¿Qué potencia consume cada resistencia? Comprueba que toda la potencia generada es igual a toda la potencia consumida. ATENCIÓN: ¿Cómo calcular la potencia de cada Resistencia? Pues bien, imaginemos que ya hemos calculado la I2 del circuito. Nosotros sabemos que la potencia consumida se calcula con la fórmula P= V x I. Entonces para calcular la potencia de esa resistencia nos falta saber la caída de tención (V) en ella. Haríamos lo siguiente: Calculamos V con la Ley de Ohm: V= I x R, donde I es lo que hemos calculado (I 2, puesto que es la intensidad que atraviesa a esa Resistencia) y R vale 4Ω. Teniendo ya V2 e I2 calculamos P2 (la potencia consumida en esa resistencia). P2 = V2 x I2 2. Calcula las intensidades que circulan por cada una de las resistencias de la siguiente red de Kirchhoff. ¿Qué potencia genera cada pila? ¿Qué potencia consume cada resistencia?