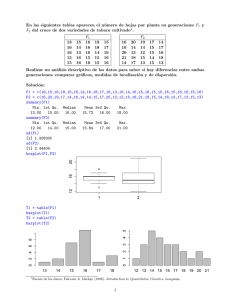
π θ = pV zpppV zp ˆˆ ˆ ˆˆ ˆ + ≤ ≤ -

MÀSTER DE LOGÍSTICA, TRANSPORT I MOBILITAT (UPC).
CURS 09-10 Q1 – EXAMEN EXTRAORDINARI
Mètodes de Captació, Anàlisi i Interpretació de Dades .
(Data: 11/5/2010 9:00-12:00 h
Nom de l’alumne:
Professor responsable:
Localització:
Normativa de l’examen:
Durada del test:
Sortida de notes:
Revisió:
Lloc: Aula – H10.15)
Lídia Montero Mercadé
Edifici C5 D217
ES PERMÉS DE DUR ELS APUNTS PUBLICATS
AULES ESTADÍSTIQUES
ES POT DUR CALCULADORA
2h 00 min
Abans 17/5/10 a les 15:00 al WEB de l’assignatura.
El 17/5/10 a les 15:00 hores (C5-217).
Problema 1 - Puntuació sobre 8 – 1 Punt per Apartat
Para conocer el impacto que tiene una noticia publicada en los medios de comunicación sobre un
incremento extraordinario de las tarifas del transporte colectivo de una ciudad, se escoge una muestra
aleatoria simple sin reposición de 1000 individuos mayores de 18 años, residentes habituales en la
región en la cual se hace el estudio. Entre estas 1000 personas entrevistadas, 132 conocen dicha
noticia.
1. ¿Cuál es la variable de interés?
La variable d’interès és un variable dicotòmica 0, 1 que indica si un individu s’ha assabentat
del canvi de tarifes per els mitjans de comunicació o no.
2. Estimar por punto y por intervalo la proporción p de personas mayores de 18 años que conocen
la noticia bajo estudio al nivel de confianza del 95%.


 Y (intérvalo de confianza bilateral al 95% para la proporción
Para   0.05 y para
poblacional de Y – variable binaria) a partir de la expresión:
s 'y2 
n
n  pˆ 1  pˆ 


Vˆ  pˆ   Vˆ  y   1  
 1  
N n 
N  n 1

pˆ  0.132
1000  0.132  1  0.132 

Vˆ  pˆ   1 
 0.0106 2

999
 100000 
pˆ  z 0,975 Vˆ  pˆ   p  pˆ  z 0,975 Vˆ  pˆ 
con
z 0.975  1.96
0.132  1.96  0.0106   Y  0.132  1.96  0.0106
0.111   Y  0.153
1
3. Sabiendo que en la ciudad residen de forma habitual 100000 de individuos mayores de 18 años,
estimar el total de personas mayores de 18 años enterados de dicha noticia.
TY  Np̂  100000  0.132  13200 habitantes.
4. Sabiendo que en la ciudad residen de forma habitual 100000 de individuos mayores de 18 años,
estimar el intérvalo de confianza al 95% para el total de personas mayores de 18 años enteradas
de dicha noticia.
N 0.132  N1.96  0.0106  N Y  N 0.132  1.96  N 0.0106
11100  TY  15300
5. Sabiendo que en la ciudad residen de forma habitual 100000 de individuos mayores de 18 años,
determinar la precisión absoluta, al nivel de confianza del 95%, del total de personas mayores
de 18 años enteradas de dicha noticia.
 
 
EA TˆY  1.96 Vˆ TˆY  1.96 N Vˆ  pˆ   1.96 100000  0.0106  2077.6
6. Sabiendo que en la ciudad residen de forma habitual 100000 de individuos mayores de 18 años,
determinar la precisión relativa, al nivel de confianza del 95%, del total de personas mayores
de 18 años enteradas de dicha noticia.
 
 
ER TˆY  EA TˆY TˆY  2077.6 13200  0.157  15.7%
7. ¿Qué tamaño de muestra se debe emplear para estimar p con una precisión absoluta de 0.5% y
un nivel de confianza del 95%?
2
0.132  1  0.132 
1.96  0.1146
ˆ
EA pˆ   1.96 V  pˆ   1.96
 0.005  n 
n
0.005 2
n 
n 1
1  
n
N
n
 17606
n  1
17607

 14969.45  14970 hab
n
17606
1 N
1
100000


8. ¿Qué tamaño de muestra se debe emplear para estimar p con una precisión relativa de 5% y un
nivel de confianza del 90%?
n  0.868
 n  pˆ 1  pˆ  ˆ
 n  1  pˆ 

ER pˆ   EA pˆ  pˆ  z0.95 1 
p  z0.95 1 
 1.65 1
 0.05

 N  n-1
 N  pˆ n - 1
 100000  0.132n - 1
n 1
2.1025  6.576
n  0.868 
55305 .16

1.65 2 1
 0.05 2  n 
 55304 .16  n   n 
 35611 hab

.16
1  55304

0.0025
1 N
 100000  0.132n - 1
100000

2

Problema 2 - Puntuació sobre 13 – 1 Punt per Apartat
La recogida de residuos se efectúa parcialmente de forma selectiva en Catalunya, dando lugar a un registro de
los totales recogidos a nivel municipal y de su composición. De la parte que se recoge mezclada (entre el 15% y
el 70%, según el municipio), se conoce el total municipal pero no su composición, de ahí que se tenga que
recurrir a métodos de muestreo para la caracterización de la composición de la fracción de residuos de tipo resto
a nivel municipal, comarcal y global del país. Los datos municipales sobre la cantidad y composición de los
residuos generados en los diversos municipios, clasificados por comarcas son accesibles informáticamente a
través del enlace de la Agencia de Residuos de Catalunya (http://www.arc-cat.net/). Después de acceder a los
datos municipales y unificar en un solo archivo toda la información, se dispone a nivel municipal de las
siguientes variables características de la generación de residuos municipales anuales durantes el año 2007:
 Pob07.1: Padrón de residentes en 2007.
 TotROrga, TotRVidre, TotPaper, TotEnvas, TotVolum, TotPoda, TotPila, TotMede, TotTextil, TotAlter:
Total generado anual de residuos orgánicos, vidrio, papel, envases, objetos voluminosos, poda y jardinaería,
medicamentos, textiles y otros residuos recogidos de manera selectiva.
 PerRecSel: Porcentaje de recogida selectiva municipal, sobre total de residuos generados en 2007.
 FRTracta, FRDipo, FRInci, FRDipoF: Toneladas en 2007 de fracción resto tratada, directa a depósito
controlado, directa a incineradora, directa a disposición final,
 TotFResta: Toneladas totales de residuos de Fracción Resto generados en 2007.
 PerFRsTot: Porcentaje de Fracción Resta sobre el total de Residuos municipales generados en 2007.
 TotRes07: Toneladas totales de residuos municipales generados en 2007.
 Res07pHab: Residuos diarios generados por residente y día en 2007 a nivel municipal (en kg).
 Res07pHabETCA: Residuos diarios generados por persona y día en 2007 a nivel municipal (en kg),
contiene corrección estacionalidad.
 PRSOrga, PRSVidre, PRSPaper, PRSEnvas, PRSVolum, PRSPoda, PRSPila, PRSMede, PRSTextil,
PRSAlter: Porcentaje que supone el Total generado anual de residuos orgánicos, vidrio, papel, envases,
objetos voluminosos, poda y jardinería, medicamentos, textiles y otros residuos recogidos de manera
selectiva sobre el Total anual de residuos de Recogida Selectiva.
La variable de respuesta que se va a estudiar está relacionada con la generación de residuos diarios por
habitante equivalente (en kg): Res07pHabETCA. Las variables explicativas son: porcentaje de recogida
selectiva en 2007, PRSOrga, PRSVidre, PRSPaper, PRSEnvas, PRSVolum, PRSPoda, PRSPila,
PRSMede, PRSTextil, PRSAlter y otras variables sociodemográficas que pudieran desarrollarse durante el
ejercicio.
1. La variable de respuesta que se va estudiar es la generación de residuos municipales por persona y día
con correccion de estacionalidad. ¿Se puede considerar que la generación diaria por persona está
relacionada con la implicación en la recogida selectiva?
> cor.test(rga1$Res07pHabETCA,rga1$PerRecSel)
Pearson's product-moment correlation
data: rga1$Res07pHabETCA and rga1$PerRecSel
t = -3.3166, df = 861, p-value = 0.0009493
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.17771773 -0.04592423
sample estimates:
cor
-0.1123149
Técnicament sí, el p valor de la hipótesi nul.la que indica que no hi ha correlació és de 1 per mil, per tant, es
rebutja la H0 i per tant hi ha una correlación lineal diferent de 0 i negativa, a major recollida selectiva menor
generación diària per persona.
3
2. La variable de respuesta, generación diaria por habitante equivalente, ¿pensais que tiene una distribución de
probabilidad aceptablemente normal?
No, ni de lluny només cal veure l’assimetria que mostra la distribució. A més si s’aplica un contrast de
normalitat de Shapiro-Wilk la normalitat com a hipótesi nula es rebutja.
3. La variable de respuesta, generación diaria por habitante equivalente, ¿pensais que tiene valores atípicos?
Determinar el rango de valores atípicos y atípicos extremos.
S’han donat dades descriptives dels quartils de la variable de resposta. Valors atípics: més petits de 0.56 kg i
més grans de 2.32 kg. Valors extremadamente atípics: generación més gran de 3,0 kg per persona i dia.
> edvr<-summary(rga1$Res07pHabETCA)
> iqr<-edvr[5]-edvr[2]
> ii<-edvr[2]-1.5*iqr;is<-edvr[5]+1.5*iqr;ii;is
1st Qu.
0.56
3rd Qu.
2.32
> ii<-edvr[2]-3*iqr;is<-edvr[5]+3*iqr;ii;is
1st Qu.
-0.1
3rd Qu.
2.98
> edvr<-summary(rga1$Res07pHabETCA);edvr
Min. 1st Qu. Median
Mean 3rd Qu.
Max.
0.400
1.220
1.430
1.502
1.660
5.160
4. Se procede a una discretización de la variable PerRecSel según:
f.RecSel <- factor(cut(PerRecSel, breaks=c(1,15,25,35,100)),labels=c(‘moltbaix’,'baix','mig','alt')).
La variable de respuesta que se va estudiar es la generación de residuos municipales por persona y día
con correccion de estacionalidad. ¿Se puede considerar que la generación diaria por persona tiene una
media diferente según el factor de implicación en la recogida selectiva?
Gràficament l’única cosa que es veu és que la dispersió de la generació diària és clarament diferent en el
grup d’implicació molt baix en la recollida selectiva que en la resta. Hi ha molts valors atípics en aquest
grup (diagrama bivariant i boxplots). Per inferència, el Kruskal – Wallis dona un p valor significativament
menor del 5% per la hipótesis nula d’igualtat entre les mitjanes de generación, malgrat la cautela que s’ha de
tenir devant de l’heterocedasticitat present.
5. ¿Cuál es la generación diaria por persona en la mediana de implicación en la recogida selectiva y el modelo
cuyos resultados se ilustran?
Apliqueu la predicció lineal de la regressió simple: 1.602-0.003779*24.36 = 1.51 kg/persona i dia
> predict(m2,newdata=data.frame(PerRecSel=24.36 ))
1
1.509646
> summary(m2)
Call:
lm(formula = rga1$Res07pHabETCA ~ rga1$PerRecSel)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)
1.601695
0.033810 47.373 < 2e-16 ***
rga1$PerRecSel -0.003779
0.001139 -3.317 0.00095 ***
Ahora se va a estudiar el modelo predictivo para la generación de residuos municipales por persona y día
con correccion de estacionalidad según la implicación en la recogida selectiva (covariante o factor, a
deducir de las preguntas concretas de los apartados) y los porcentajes de esa recogida en algunas de las
tipologías.
4
6. Determinar la suma de cuadrados residual del modelo de nulo.
La suma de quadrats del model nul coincideix amb la suma de quadrats total que és la variança mostral
multiplicada per el nombre d’observacions menys 1: teniu dados de la variança mostral, és a dir,
> var(rga1[,c(2,3)],use="pairwise.complete.obs")
PerRecSel Res07pHabETCA
PerRecSel
184.19186
-0.6960100
Res07pHabETCA -0.69601
0.2084902
> 0.2084902*862
[1] 179.7186
> anova(m0)
Analysis of Variance Table
Response: rga1$Res07pHabETCA
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 862 179.719
0.208
>
7. Determinar ¿ cuál es la suma de cuadrados explicada por el modelo de regresión lineal entre Y e X (en m2)?
El quadrat del coeficient de correlación lineal (-0.1123149* -0.1123149=0.01261) per la suma de
quadrats total que coincideix amb la residual del model nul, és a dir
(0.01261*179.719=2.267) la part de la inèrcia de les dades explicada pel percentatge de
recollida selectiva.
> anova(m2)
Analysis of Variance Table
Response: Res07pHabETCA
Df Sum Sq Mean Sq F value
Pr(>F)
PerRecSel
1
2.267
2.267
11 0.0009493 ***
Residuals 861 177.452
0.206
--Signif. codes: 0 ‘**
8. Calcular el coeficiente de determinación del modelo (m2).
El quadrat del coeficient de correlación lineal (-0.1123149* -0.1123149=0.01261), és a dir 1.3% de
la variabilitat de les dades bé explicada pel percentatge de recollida selectiva.
9. Determinar si la relación entre la generación de residuos por persona depende de la penetración de la
recogida selectiva por valoración de los gráficos disponibles.
S’observa una tendència negativa en les dades, però l’efecte de la sobredispersió de les observacions amb
poca incidència de recollida selectiva sembla que condiciona els resultats.
10. Determinar si la relación entre la generación de residuos por persona depende de la penetración de la
recogida selectiva y de la incidencia de la recogida selectiva de tipo orgánico considerando sólo modelos de
regresión multiple (variables explicativas cuantitativas).
Per inferència es poden comparar per variança incremental si els 2 models són equivalents (amb/sense
percentatge de recollida orgànica): el p valor és del 13% per tant no fa falta el percentatge de recollida
orgànica, en canvi el percentatge de recollida selectiva és estadísticamente significativa a jutjar pel p valor
del coeficiente dins del model (m2) subministrat en un apartat anterior.
> anova(m3,m31)
Analysis of Variance Table
Model 1: rga1$Res07pHabETCA ~ rga1$PerRecSel
Model 2: rga1$Res07pHabETCA ~ rga1$PerRecSel + rga1$PRSOrga
Res.Df
RSS Df Sum of Sq
F Pr(>F)
1
861 177.45
2
860 177.00
1
0.45 2.1862 0.1396
> anova(m0,m3)
Analysis of Variance Table
Model 1: rga1$Res07pHabETCA ~ 1
Model 2: rga1$Res07pHabETCA ~ rga1$PerRecSel
Res.Df
RSS Df Sum of Sq F
Pr(>F)
5
1
862 179.719
2
861 177.452
1
2.267 11 0.0009493 ***
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
11. Interpretar las ecuaciones para la predicción la generación por persona según el modelo aditivo con
tratamiento de la incidencia de recogida selectiva como factor y la incidencia de la recogida selectiva de tipo
orgánico.
Coefficients:
(Intercept)
rga1$f.RecSelbaix
rga1$f.RecSelmig
rga1$f.RecSelalt
rga1$PRSOrga
Estimate Std. Error t value Pr(>|t|)
1.639098
0.032836 49.917 < 2e-16 ***
-0.190895
0.044859 -4.255 2.32e-05 ***
-0.105091
0.046832 -2.244
0.0251 *
-0.111034
0.055259 -2.009
0.0448 *
-0.001882
0.001097 -1.715
0.0867 .
Recollida Selectiva en nivells:
‘molt baix’ : 1.64 +0 – 0.001882 PRSOrga
‘baix’ : 1.64-0.191 – 0.001882 PRSOrga
‘mig’ : 1.64-0.105091– 0.001882 PRSOrga
‘alt’ : 1.64-0.111034
– 0.001882 PRSOrga
12. ¿Cuál será la predicción total de residuos anuales para una ciudad de 30000 residentes en la mediana de
incidencia de la recogida orgánica y un compromiso máximo con el medio ambiente en el modelo aditivo
con tratamiento de la recogida selectiva como factor?
La mediana de PRSORga és 9.8 i d’aquí aplicar l’equació (no importa la població, no intervé) del punt
anterior per nivell alt :
1.64-0.111034
– 0.001882 PRSOrga = 1.64-0.111034
– 0.001882 * 9.8 = 1.509623.
> predict(m32,newdata=data.frame(PRSOrga=9.8 ,f.RecSel="alt"))
1
1.509623
> Generació total de 30000 x 1.509623 = 45289 kg per dia. Por 365 dará el promedio
anual.
Ahora se va a estudiar el modelo predictivo para la generación de residuos municipales por persona y día
con correccion de estacionalidad según la implicación en la recogida selectiva y los porcentajes de esa
recogida en algunas de las tipologías. Se usará la escala logarítmica para las variables cuantitativas.
13. ¿Cuál es la generación diaria por persona según en la mediana de implicación en la recogida selectiva y el
modelo cuyos resultados se ilustran?
> summary(m4)
Call:
lm(formula = log(rga1$Res07pHabETCA) ~ log(rga1$PerRecSel))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)
0.57730
0.05441 10.610 < 2e-16 ***
log(rga1$PerRecSel) -0.06688
0.01709 -3.913 9.84e-05 ***
Manualment, exp(0.5773-0.06688
*ln(24.36))=1,4387
> m4<-lm(log(Res07pHabETCA)~log(PerRecSel),data=rga1 )
> predict(m4,newdata=data.frame(PerRecSel=24.36 ))
1
0.3637511
> exp(predict(m4,newdata=data.frame(PerRecSel=24.36 )))
1
>> Generació total de 30000 x 1.438716 = 43161 kg per dia. Por 365 dará el promedio
anual.
6
RESULTADOS:
> dim(rga1)
[1] 863 33
summary(rga1[,c(91,100:110)])
PerRecSel
Res07pHabETCA
Min.
: 3.21
Min.
:0.400
1st Qu.:16.48
1st Qu.:1.220
Median :24.36
Median :1.430
Mean
:26.39
Mean
:1.502
3rd Qu.:33.02
3rd Qu.:1.660
Max.
:77.60
Max.
:5.160
PRSVolum
PRSPoda
Min.
: 0.000
Min.
: 0.00
0.00
1st Qu.: 0.445
1st Qu.: 0.00
0.00
Median : 5.830
Median : 0.01
6.28
Mean
: 8.488
Mean
: 1.69
:10.69
3rd Qu.:12.550
3rd Qu.: 1.73
Qu.:19.02
Max.
:39.340
Max.
:19.44
:56.66
PRSOrga
PRSVidre
PRSPaper
PRSEnvas
Min.
: 0.00
Min.
: 0.81
Min.
: 0.86
Min.
: 0.010
1st Qu.: 0.00
1st Qu.:11.73
1st Qu.:19.17
1st Qu.: 7.375
Median : 9.80
Median :19.78
Median :28.21
Median :10.420
Mean
:15.04
Mean
:23.14
Mean
:29.34
Mean
:11.266
3rd Qu.:29.21
3rd Qu.:30.90
3rd Qu.:36.98
3rd Qu.:14.890
Max.
:62.06
Max.
:66.38
Max.
:67.16
Max.
:28.460
PRSPila
PRSMede
PRSTextil
PRSAltre
Min.
:0.00000
Min.
:0.01000
Min.
:0.0000
Min.
:
1st Qu.:0.00000
1st Qu.:0.04000
1st Qu.:0.0000
1st Qu.:
Median :0.03000
Median :0.06000
Median :0.0000
Median :
Mean
Mean
Mean
Mean
:0.04159
:0.07479
:0.2178
3rd Qu.:0.05000
3rd Qu.:0.09000
3rd Qu.:0.0700
3rd
Max.
Max.
Max.
Max.
:1.04000
:0.55000
:6.0000
> var(rga1[,c(2,3)],use="pairwise.complete.obs")
PerRecSel Res07pHabETCA
PerRecSel
184.19186
-0.6960100
Res07pHabETCA -0.69601
0.2084902
> cor(rga1[,c(2,3)],use="pairwise.complete.obs")
PerRecSel Res07pHabETCA
PerRecSel
1.0000000
-0.1123149
Res07pHabETCA -0.1123149
1.0000000
>
Residus municipals 2007 per habitant equivalent i dia (kg)
Mirem les dades ...
Density
0.6
0.0
0.0
1
0.2
0.2
0.4
2
0.4
Density
3
0.6
0.8
4
0.8
1.0
1.2
1.0
5
Mirem les dades ...
0
1
2
3
4
5
0
1
2
rga1$Res07pHabETCA
3
N = 863 Bandw idth = 0.07645
> shapiro.test( (rga1$Res07pHabETCA) )
Shapiro-Wilk normality test
data: (rga1$Res07pHabETCA)
W = 0.8628, p-value < 2.2e-16
> plot( rga1$Res07pHabETCA~rga1$f.RecSel )
> kruskal.test( rga1$Res07pHabETCA~rga1$f.RecSel )
Kruskal-Wallis rank sum test
7
4
5
data: rga1$Res07pHabETCA by rga1$f.RecSel
Kruskal-Wallis chi-squared = 13.6471, df = 3, p-value = 0.003427
> fligner.test( rga1$Res07pHabETCA~rga1$f.RecSel )
Fligner-Killeen test of homogeneity of variances
0.5
log(rga1$Res07pHabETCA)
-1.0
1
-0.5
2
0.0
3
rga1$Res07pHabETCA
4
1.0
1.5
5
data: rga1$Res07pHabETCA by rga1$f.RecSel
Fligner-Killeen:med chi-squared = 61.404, df = 3, p-value = 2.946e-13
moltbaix
baix
mig
alt
moltbaix
baix
mig
alt
rga1$f.RecSel
1.5
1.0
0.0
0.5
log(rga1$Res07pHabETCA)
1.0
0.5
log(rga1$Res07pHabETCA)
0.0
3
-0.5
-0.5
2
20
40
60
80
-1.0
-1.0
1
rga1$Res07pHabETCA
4
1.5
5
rga1$f.RecSel
20
40
rga1$PerRecSel
rga1$PerRecSel
8
60
80
1.5
2.0
2.5
3.0
log(rga1$PerRecSel)
3.5
4.0
> summary(m31)
Call:
lm(formula = rga1$Res07pHabETCA ~ rga1$PerRecSel + rga1$PRSOrga)
Residuals:
Min
1Q
Median
-1.03836 -0.27817 -0.06098
3Q
0.16397
Max
3.63676
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)
1.596646
0.033959 47.016
<2e-16 ***
rga1$PerRecSel -0.002650
0.001371 -1.933
0.0535 .
rga1$PRSOrga
-0.001645
0.001112 -1.479
0.1396
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4537 on 860 degrees of freedom
Multiple R-squared: 0.01512,
Adjusted R-squared: 0.01283
F-statistic: 6.601 on 2 and 860 DF, p-value: 0.001429
> step(m31)
Start: AIC=-1361.21
rga1$Res07pHabETCA ~ rga1$PerRecSel + rga1$PRSOrga
Df Sum of Sq
<none>
- rga1$PRSOrga
- rga1$PerRecSel
1
1
0.45
0.77
RSS
AIC
177.00 -1361.21
177.45 -1361.02
177.77 -1359.47
Call:
lm(formula = rga1$Res07pHabETCA ~ rga1$PerRecSel + rga1$PRSOrga)
Coefficients:
(Intercept)
1.596646
rga1$PerRecSel
-0.002650
rga1$PRSOrga
-0.001645
> summary(m32)
Call:
lm(formula = rga1$Res07pHabETCA ~ rga1$f.RecSel + rga1$PRSOrga)
Residuals:
Min
1Q
Median
-1.08913 -0.23820 -0.04498
3Q
0.15809
Max
3.62599
Coefficients:
(Intercept)
rga1$f.RecSelbaix
rga1$f.RecSelmig
rga1$f.RecSelalt
rga1$PRSOrga
--Signif. codes: 0
Estimate Std. Error t value Pr(>|t|)
1.639098
0.032836 49.917 < 2e-16 ***
-0.190895
0.044859 -4.255 2.32e-05 ***
-0.105091
0.046832 -2.244
0.0251 *
-0.111034
0.055259 -2.009
0.0448 *
-0.001882
0.001097 -1.715
0.0867 .
‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4504 on 858 degrees of freedom
Multiple R-squared: 0.03167,
Adjusted R-squared: 0.02716
F-statistic: 7.016 on 4 and 858 DF, p-value: 1.471e-05
> summary(m33)
Call:
lm(formula = rga1$Res07pHabETCA ~ rga1$f.RecSel * rga1$PRSOrga)
Residuals:
Min
1Q
Median
-1.08244 -0.24262 -0.04189
3Q
0.16047
Max
3.69470
Coefficients:
(Intercept)
rga1$f.RecSelbaix
Estimate Std. Error t value Pr(>|t|)
1.647763
0.034106 48.313 < 2e-16 ***
-0.165142
0.049265 -3.352 0.000837 ***
9
rga1$f.RecSelmig
-0.182460
0.056277
rga1$f.RecSelalt
-0.142095
0.080797
rga1$PRSOrga
-0.006105
0.004770
rga1$f.RecSelbaix:rga1$PRSOrga 0.001596
0.005053
rga1$f.RecSelmig:rga1$PRSOrga
0.008516
0.005210
rga1$f.RecSelalt:rga1$PRSOrga
0.004983
0.005262
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’
-3.242
-1.759
-1.280
0.316
1.635
0.947
0.001232 **
0.078992 .
0.200952
0.752186
0.102490
0.343995
0.1 ‘ ’ 1
Residual standard error: 0.4492 on 855 degrees of freedom
Multiple R-squared: 0.0402,
Adjusted R-squared: 0.03234
F-statistic: 5.116 on 7 and 855 DF, p-value: 1.034e-05
> anova(m32,m33)
Analysis of Variance Table
Model 1: rga1$Res07pHabETCA ~ rga1$f.RecSel + rga1$PRSOrga
Model 2: rga1$Res07pHabETCA ~ rga1$f.RecSel * rga1$PRSOrga
Res.Df
RSS Df Sum of Sq
F Pr(>F)
1
858 174.026
2
855 172.494
3
1.532 2.5314 0.05591 .
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> step(m33)
Start: AIC=-1373.47
rga1$Res07pHabETCA ~ rga1$f.RecSel * rga1$PRSOrga
Df Sum of Sq
<none>
- rga1$f.RecSel:rga1$PRSOrga
3
1.53
RSS
AIC
172.49 -1373.47
174.03 -1371.84
Call:
lm(formula = rga1$Res07pHabETCA ~ rga1$f.RecSel * rga1$PRSOrga)
Coefficients:
(Intercept)
1.647763
rga1$f.RecSelalt
-0.142095
rga1$f.RecSelmig:rga1$PRSOrga
0.008516
rga1$f.RecSelbaix
-0.165142
rga1$PRSOrga
-0.006105
rga1$f.RecSelalt:rga1$PRSOrga
0.004983
>
10
rga1$f.RecSelmig
-0.182460
rga1$f.RecSelbaix:rga1$PRSOrga
0.001596