Guía de trabajos prácticos

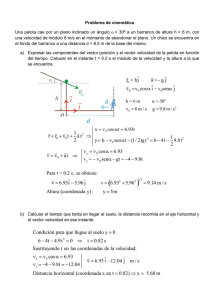
UNGS 1er Semestre 2009
Física General. Guía de Problemas nº 1.
Cinemática
Problemas de Nivel 1.
1- Un auto en movimiento rectilíneo (MR) recorrió la primera mitad del camino con
una velocidad de 80 km/h y la segunda mitad con una velocidad de 40 km/h. ¿Cuál
fué la velocidad media de este auto?
2- Un automóvil en MR llevó, durante la primera mitad del tiempo que estuvo en
movimiento, la velocidad de 80km/h y durante la segunda mitad la velocidad de
40km/h. ¿Cuál fué la velocidad media de este auto?
3- ¿Qué condiciones deben cumplirse en un problema para que el cuerpo en estudio
pueda ser considerado como puntual, es decir como una partícula? ¿Se puede
considerar al planeta Tierra como una partícula?
4- Un auto parte desde San Miguel hacia Mar del Plata que está a 400 Km. Debido al
tránsito, los primeros 100 Km los hace a baja velocidad v1 = 80 Km/h, mientras que
el resto del viaje continúa a una velocidad v2 = 120 Km/h.
a) Realice un esquema de la situación e indique el sistema de coordenadas elegido.
b) ¿Cuánto tardará en llegar a destino?
c) La velocidad media de un cuerpo, corresponde a la velocidad constante (durante
todo el trayecto) con que debería ir el cuerpo de tal forma de recorrer la misma
distancia en el mismo tiempo. Calcule la velocidad media, ¿es lo mismo que sacar
el promedio entre 80 y 120? Discuta.
d) Si el auto, luego de llegar a Mar del Plata, vuelve a San Miguel en 6 horas, ¿cuál es
la velocidad media calculada desde que salió hasta que regresó a San Miguel?
5- Un auto sale de Mar del Plata a las 10:00 hs en dirección a Bs. As., llevando una
velocidad media de v1 = 100 Km/h. A las 11:00 sale un segundo auto pero desde Bs.
As. y en dirección a Mar del Plata, con una velocidad media v2 = 120 Km/h. Si la
distancia entre BsAs y Mar del Plata es de 400 Km.
a) ¿Se puede hallar la ecuación de movimiento con los datos dados? ¿Por qué?
b) Considerando que los autos se mueven con velocidad constante igual a la velocidad
media dada de cada uno; realice un esquema de la situación indicando el sistema de
coordenadas elegido y halle la ecuación de movimiento para cada automóvil, x1(t) y
x2(t), usando un único sistema de coordenadas para ambos.
c) ¿En qué lugar de la ruta se encuentran? Resuelva analítica y gráficamente.
6- Dos coches circulan a lo largo de una carretera recta. El coche A mantiene una
velocidad constante de 80 km/h, el coche B mantiene una velocidad constante de
110 km/h. En t = 0 el coche B está 45 km detrás del coche A. Elija un sistema de
coordenadas y calcule en que posición el coche B va a conseguir pasar al coche A.
1
7- Admitiendo que el radio del Universo es de unos 1028 cm determinar la edad del
Universo a partir de la hipótesis de una estrella que, situada en el radio, ha viajado
alejándose de nosotros desde el principio de los tiempos a una velocidad igual a
2/3. c = 2. 1010 cm/s (c ≡ velocidad de la luz en el vacío).
8- Los siguientes gráficos representan la posición en función del tiempo para diferentes
móviles.
Móvil 1
Móvil 2
x(Km
)
180
x(Km
)
20
Móvil 3
x(Km
)
50
10
7
5t (h)
2
t(h)
4
En cada caso indique:
a) El sistema de coordenadas elegido
b) El tipo de movimiento que describe el gráfico.
c) La posición inicial del móvil
d) La velocidad y aceleración
e) La ecuación de la posición en función del tiempo
f) Sobre el gráfico del móvil 2 dibuje la posición en función del tiempo de dos
móviles uno que se mueve con mayor rapidez que el móvil dos y otro con menor
rapidez. Justifique su respuesta.
9- Un coche pasa por un cruce con una velocidad constante de 72 Km/h y continúa
con la misma velocidad. Cinco segundos después un policía de tráfico que estaba en
el cruce arranca y sale en pos del coche con una aceleración constante de 2 m/s2.
a) Realice un esquema de la situación e indique el sistema de coordenadas elegido.
b) ¿Cuándo y dónde alcanzará el policía al coche? Grafique.
c) ¿A qué velocidad irá marchando el policía en dicho momento?
10- Un tren parte a las 17hs de la estación San Miguel con destino a José C. Paz
(estación Terminal). A las 17hs y 10’ los pasajeros descienden en José C. Paz. El
tren permanece detenido por 10 minutos mientras suben los pasajeros y parte de
regreso hacia Retiro. A las 17hs y 30’ el tren se detiene en San Miguel. Realice un
esquema de la situación e indique el sistema de coordenadas elegido. Grafique la
posición, velocidad y aceleración en función del tiempo, para ello estime valores
razonables de distancias, velocidades y aceleraciones necesarios.
11- El siguiente gráfico representa la posición en función del tiempo para un móvil:
2
t(h)
x(km)
100
90
50
40
20
10
2
a)
b)
c)
d)
e)
f)
g)
h)
4
8
10
12
t(h)
Describa cualitativamente el movimiento del cuerpo.
¿En algún momento la partícula vuelve a pasar por la posición inicial?
¿En qué instantes la velocidad instantánea es nula?
Indique los intervalos de tiempo durante los cuales la velocidad se mantiene
constante y determine la velocidad en dichos lapsos.
¿En qué instante (o lapso) la partícula va a su máxima velocidad (celeridad)?
Indique en que tramos la partícula se acelera o desacelera. Indique el signo de la
aceleración.
Dibuje esquemáticamente un gráfico de velocidad en función del tiempo.
Dibuje esquemáticamente un gráfico de aceleración en función del tiempo.
12- Una persona en una hora anda 1km hacia el oeste y luego 2km hacia el norte.
a) Realice un esquema de la situación e indique el sistema de coordenadas elegido.
b) Halle el vector velocidad media.
c) Halle la celeridad media (Se entiende por celeridad el módulo de la velocidad).
13- Un automóvil se dirige al oeste a 60 Km/h. En un cierto instante toma una curva, y 5
s después está moviéndose en la dirección norte a 60 Km/h. Determine la
aceleración (vectorial) media del automóvil.
14- ** Preguntas:
a) Una bola de boleadoras gira con una rapidez constante, ¿está acelerada? ¿Por qué?
b) ¿Es posible que una partícula siga una curva sin acelerarse?
15- Dado el vector posición en función del tiempo:
r (t) = (3m/s t + 1m) i + ( 1m/s2 . t2 – 1m) j
a) Calcule el vector velocidad en el instante t = 1 s.
b) Calcule el vector aceleración en ese instante.
16- Se lanza una pelota hacia arriba con una velocidad inicial de 20 m/s
a) Realice un esquema de la situación e indique el sistema de coordenadas elegido
b) ¿Cuánto tiempo está la pelota en el aire?
3
c) ¿Cuál es la mayor altura alcanzada por la pelota?
d) ¿En que instante está la pelota a 15 m por encima del suelo?
17- Federico lanza una pelota hacia arriba, luego de transcurrido 1seg vuelve a sus
manos. Si despreciamos la resistencia del aire,
a) Realice un esquema de la situación e indique el sistema de coordenadas elegido.
b) Halle la velocidad y la aceleración de la pelota al alcanzar la altura máxima.
c) Halle la velocidad inicial con que fue lanzada la pelota.
d) Halle la velocidad instantánea al cabo de 0,1seg de lanzada.
e) Halle la altura máxima y el tiempo que demora en alcanzarla.
f) Halle la velocidad con que vuelve a las manos de Fede.
g) Grafique x(t), v(t) y a(t).
18- Un objeto cae desde una altura de 120 m. ¿Qué distancia recorre durante su último
segundo en el aire?
19- Una pelota de baloncesto se deja caer desde una altura de 3 m y rebota en el suelo
hasta una altura de 2 m.
a) ¿Cuál es la velocidad de la pelota justo ante de alcanzar el suelo?
b) ¿Cuál es su velocidad justo cuando deja el suelo?
c) Estime la magnitud y la dirección de su aceleración media durante este
intervalo
20- Un cohete se lanza verticalmente hacia arriba con una aceleración de 20m/s2. Al
cabo de 25 s el combustible se agota y el cohete continúa como partícula libre hasta
que alcanza el suelo. Calcule
a) el punto más alto alcanzado por el cohete.
b) el tiempo total que el cohete está en el aire.
c) La velocidad del cohete justo antes de chocar contra el suelo.
21- En el instante t = 0 se deja caer una piedra desde una cierta altura. Después de 1,6 s
se lanza hacia abajo otra piedra, con una velocidad de 32 m/s, desde la misma altura.
Si ambas piedras chocan contra el suelo al mismo tiempo ¿cuánto vale la altura?
22- Gabriela lanza una pelota al aire, desde un metro del suelo, con velocidad inicial de
vi = 5 m/s formando un ángulo θ = 30 o con la horizontal.
θ
1m
Despreciando el rozamiento con el aire y utilizando la aproximación g = 10 m/s2,
halle:
a) Las componentes x e y de la velocidad inicial. Indicando el sistema de coordenadas
elegido.
b) Las funciones x ( t ), vx ( t ), ax ( t ), y ( t ), vy ( t ) y ay ( t ) y grafíquelas.
c) El vector velocidad en el instante t = 0,1 s. Exprese la solución en cartesianas
(componentes vx y vy)
4
d) La altura máxima que alcanza la pelota y el tiempo que demora en alcanzarla.
e) El tiempo que la pelota demora hasta que vuelve a pasar a un metro del suelo.
f) El vector velocidad (en cartesianas y en polares) en el instante en que la pelota
vuelve a pasar a un metro del suelo. Compare con la velocidad inicial. Discuta.
g) El tiempo total que la pelota está en el aire.
h) La distancia total recorrida (alcance).
i) El vector velocidad en el instante en que la pelota choca con el suelo. Exprese la
solución en cartesianas y en polares.
j) Halle la ecuación de la trayectoria de la pelota, grafíquela. Elija 4 puntos sobre la
trayectoria y dibuje el vector velocidad y el vector aceleración correspondientes a
esos puntos.
k) ¿Con qué ángulo se debería lanzar la pelota para que el alcance sea máximo?
23- Un hombre suelta una pelota de tenis desde la ventana de su auto (1 m del suelo). La
velocidad del auto es de 100 Km/h y avanza por una calle recta. Si estudiamos el
caso ideal en donde no hay rozamiento con el aire,
a) ¿A qué distancia del auto cae la pelota?
b) ¿Cuánto tiempo demora la pelota en caer al suelo?
c) ¿Cómo es que ve moverse a la pelota el hombre que va en el auto?
d) ¿Cómo es que ve moverse la pelota un hombre que se halla parado en la vereda?
Haga un gráfico explicativo.
24- Suponga que usted viaja en su auto a v1 = 100 Km/h. A que velocidad percibe usted
que se desplazan los siguientes cuerpos (velocidad relativa a usted),
a) Auto que viaja en su mismo sentido pero a v2 = 120 Km/h.
b) Auto que viaja en sentido contrario a v3 = 100 Km/h.
c) Persona parada en la vereda.
25- Un tren avanza con una velocidad de 3 m/s. Un pasajero tira una pelota a lo largo
del corredor. Con qué velocidad ha tirado la pelota si la velocidad de la pelota
relativa a un observador parado en la estación es:
a) 4 m/s hacia adelante.
b) 2 m/s hacia adelante.
c) cero.
d) 1 m/s hacia atrás.
26- Un avión de guerra avanza a una velocidad de 2000 Km/h y a baja altura (1 Km)
para no ser detectado por los radares. Detecta un puesto enemigo a 20 Km delante
de él.
a) ¿A cuánta distancia del puesto enemigo debe soltar la bomba? Desprecie el
rozamiento con el aire.
b) Si en lugar de detectar al puesto enemigo a 20 Km lo hace a sólo 2 Km, delante de
él, ¿Qué maniobras podría realizar el avión para soltar la bomba y pegarle? Calcule.
27- En un partido de fútbol un defensor patea la pelota impulsándola hacia delante para
el delantero. En ese mismo instante el delantero comienza a correr también hacia
delante una distancia de 3 m para cabecearla a 2 m de altura y convertir un gol.
Sabiendo que la pelota salió del pie del defensa con una velocidad inicial de 36
Km/h formando un ángulo de 450 con respecto a la horizontal. ¿Cuál es la velocidad
con que debe correr el delantero para cabecear la pelota?
5
25.- Responda y justifique su respuesta.
a) ¿Puede un cuerpo tener velocidad cero y, a pesar de eso, estar
acelerándose?
b) ¿Puede tener un cuerpo una velocidad cuyo módulo es constante y, a
pesar de eso, tener una velocidad variable?
c) ¿Puede tener un cuerpo una velocidad constante y, a pesar de eso, el
módulo de la velocidad ser variable?
d) ¿Si la aceleración es cero, la curva de x en función de t es una línea
recta?
e) Dé un ejemplo de movimiento en el que: (i) la velocidad sea negativa,
pero la aceleración positiva; (ii) tanto la velocidad como la aceleración
sean negativas.
6
Problemas de Nivel 2.
1- En las siguientes figuras se indica la velocidad en función del tiempo para dos autos
(A y B).
Auto B
Auto A
v(Km/h)
v (m/s)
180
20
160
t(s)
4
2
3
4
t(h)
Para cada auto:
a)
b)
c)
d)
Indique que tipo de movimiento realiza en cada tramo
Calcule la aceleración en cada tramo
Escriba la posición en función del tiempo ( x(t) ) correspondiente
Realice un gráfico de posición en función del tiempo y otro de aceleración.
1- El siguiente gráfico, representa la velocidad en función del tiempo para el
movimiento unidimensional de un cuerpo:
V (t)
1m/seg
1
2
4
3
5
6
7 t (seg)
−1m/seg
a) Realice un esquema de la situación indicando el sistema de coordenadas
b) Describa cualitativamente el movimiento del cuerpo. Identifique los tramos en que
avanza, los tramos en que retrocede, los tramos en que acelera y los tramos en que
frena.
c) ¿En qué tramos la velocidad es constante? ¿Puede ser el gráfico de velocidad en
función del tiempo discontinuo?
d) Grafique a(t) ¿Cuándo hay aceleración? ¿Cuándo el movimiento es acelerado y
cuando desacelerado? ¿Puede ser el gráfico de aceleración en función del tiempo
discontinuo?
e) Calcule la posición del móvil a los 3.5 segundos y a los 7 segundos; analice los
resultados
f) Grafique x(t) ¿Cuándo avanza y cuando retrocede? ¿coincide con lo que contestó en
el ítem b?
7
2- La figura representa el gráfico de la aceleración en función del tiempo para una
partícula moviéndose en una dimensión (eje x) :
a (t) (m/seg2)
2m/seg2
−1m/seg
1
3
2
4
5
t (seg)
Sabiendo que en el instante inicial su posición y velocidad eran nulas.
a) Describa el movimiento de la partícula.
b) Obtenga los gráficos de la velocidad y la posición en función del tiempo.
3- Dos cuerpos A y B se mueven a lo largo de la misma línea recta de acuerdo con las
m
m
m
ecuaciones: x A (t ) = −1 t + 2 2 t 2 y x B (t ) = 2 t + 2m , donde x se mide en
s
s
s
centímetros y t en segundos.
a) Describa el tipo de movimiento de cada móvil.
b) Halle gráfica y analíticamente el instante y el lugar donde se encuentran. Analice
cada uno de los resultados y justifique cualquier decisión que tome.
c) ¿Qué velocidad tiene cada cuerpo en el momento del encuentro?
4- El gráfico de la figura muestra la velocidad en función del tiempo correspondiente a
dos autos que en el instante inicial se encontraban en el mismo lugar.
a) Describa el movimiento de cada auto.
b) ¿Se encuentran a los 4 segundos? Justifique su respuesta.
c) Calcule analíticamente tiempo y posición de encuentro.
v(m/s)
100
4
7
10 t (seg)
5- Dos partículas se mueven sobre una recta. El movimiento de la partícula 1 se
m
m
describe a partir de la ecuación de movimiento x1 (t ) = 2m + 2 t 2 + 3 t 3 . La
s
s
partícula 2 describe un movimiento con aceleración no uniforme
m
m
a 2 (t ) = 6 3 t + 4 2 y se sabe que en el instante t = 0 se encontraba en la
s
s
posición x 2 = 1m moviéndose con velocidad instantánea v 2 = −4 m seg . Halle la
posición y el instante en donde se encuentran gráfica y analíticamente.
8
6a)
b)
c)
La distancia mínima para el frenado de un coche, que viaja a 100km / h , es de 80m .
Determine la aceleración (supuesta constante).
¿Cuánto tarda en parar?
Sobre la base del resultado anterior determine la distancia prudente que debe separar
a dos autos que viajan a 100km / h . Tenga en cuenta que dependiendo de la edad del
conductor se demora de medio a un segundo hasta tomar la decisión de frenar.
7- Una maceta cae desde la repisa de un balcón de un edificio. Una persona de un
departamento inferior observa que la maceta tarda 0,2seg en pasar a través de su
ventana que tiene una altura de 4m . ¿A qué altura sobre el borde superior de la
ventana está la repisa?
8- Un arquero dispara una flecha que produce un fuerte ruido al chocar contra el
blanco. La velocidad media de la flecha (en la dirección paralela al piso) es de
150 m seg . El arquero escucha el impacto exactamente 1seg después de disparar el
arco. Si la velocidad del sonido es de 340 m seg ,
a) ¿A qué distancia se encuentra el blanco?
b) Halle el módulo y el ángulo de la velocidad con que fue disparada la flecha
sabiendo que choca contra el blanco a una altura igual a la altura desde donde fue
lanzada.
9- Un río, de 50m de ancho, fluye con una velocidad de 3 m seg . Un muchacho nada
hacia la otra orilla con una velocidad relativa al agua de 2 m seg .
b) ¿Cuánto demora en llegar?
c) ¿Cuánta distancia es arrastrado en dirección de la corriente?
d) ¿Cuál es la velocidad (módulo, dirección y sentido) relativa del muchacho respecto
a un observador parado en la orilla?
r
10- Un barco a vela cuya posición es r1 = 100m i$ + 200m $j ocupa 2 minutos más tarde la
r
posición r2 = 120m i$ + 210m $j .
r r r
a) Halle el vector desplazamiento ∆ r = r2 − r1 .
b) Halle el módulo y el ángulo del vector desplazamiento.
c) Halle las componentes del vector velocidad media, su modulo y su ángulo.
11- Un aeroplano vuela en una circunferencia cuya longitud es de 20 km con una
celeridad constante de 200 km/h.
a) ¿Cuál es cambio de velocidad en un cuarto de vuelta?
b) ¿Cuál es cambio de velocidad en media vuelta?
12- Un proyectil sale disparado, desde un metro del suelo, con una velocidad de 180 km h
y un ángulo de 30 o , con dirección a un tanque enemigo. En el instante del disparo el
tanque enemigo se halla a una distancia de 300m , acercándose al lanza proyectiles
con una velocidad vTanque . Halle la velocidad vTanque sabiendo que el proyectil
impactó sobre él. Exprese el resultado final en km/h.
13- Una botella se deja caer desde el reposo en la posición x=20 m e y=30 m. Al mismo
tiempo se lanza desde el origen una piedra con una velocidad de 15 m/s.
9
a) Determine el ángulo con el que tenemos que lanzar la piedra para que rompa la
botella, calcule la altura a la que ha ocurrido el choque.
b) Dibuje en la misma gráfica la trayectoria de la piedra y de la botella.
14- Se lanza una pelota verticalmente hacia arriba con una velocidad de 20 m/s desde la
azotea de un edificio de 50 m de altura. La pelota además es empujada por el viento,
produciendo un movimiento horizontal con aceleración de 2 m/s2. Calcule:
a) La distancia recorrida horizontalmente entre el punto de lanzamiento y el punto
de impacto.
b) La altura máxima alcanzada.
c) El valor de las componentes tangencial y normal de la aceleración cuando la
pelota se encuentra a 60 m de altura sobre el suelo.
15- El vector velocidad de una partícula depende del tiempo en la forma
r
m
m )
m
m )
v = (3 2 t − 2 )i + (6 3 t 2 − 5 ) j . Si en el instante t = 1s, la posición del
s
s
s
s
r = (3i- 2 j) m. Calcule
móvil es
• El vector posición del móvil en el instante t.
• El vector aceleración.
16- Un tanque avanza a una velocidad de 50 km h . En el instante en que observa que a
2000m delante de él hay un puesto enemigo, dispara un proyectil. Sabiendo que el
proyectil sale del cañón con una inclinación de 30 o y despreciando el rozamiento
con el aire, determine:
a) ¿Con qué velocidad, relativa al tanque, debe salir el proyectil para pegarle al puesto
enemigo?
b) ¿A qué distancia del puesto enemigo se encuentra el tanque en el momento en que el
proyectil impacta?
17- Un hombre malo viaja sobre un tren que se desplaza con velocidad constante de
10m / seg . ¿Con que velocidad (vectorial) debe lanzar una piedra para pegarle a una
ventana de la estación (a 2m de su ventanilla)? Discuta el problema realizando un
esquema de la situación y dé valores a los datos que le falten.
10