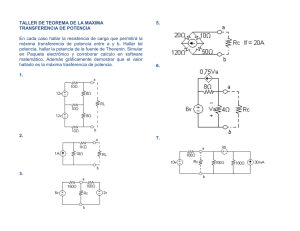
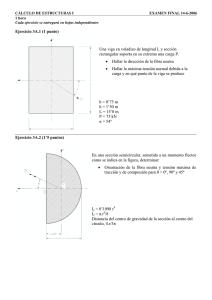
Libro Res - Ingenieria Mecanica y Electromecanica

Prefacio
El presente libro estudia los temas más importantes en Resistencia de Materiales, con
énfasis en aplicación a, solución de problemas y diseño de elementos estructurales y
dispositivos mecánicos. El libro está orientado para alumnos de Ingeniería del segundo o
tercer año.
El desarrollo del curso de Resistencia de Materiales presupone que el alumno posee los
recursos propios del cálculo infinitesimal, cálculo integral, geometría de masas en lo
referente a saber calcular centros de gravedad y momentos de inercia de figuras planas, y,
fundamentalmente, de la Estática, sin cuyo conocimiento es impensable poder obtener un
suficiente aprovechamiento del curso.
En la mayoría de los capítulos el primer objetivo es la determinación de las tensiones
normales y transversales, luego la determinación de los valores máximos de estos tensiones
y finalmente el cálculo de las correspondientes deformaciones. Se estudian como tipos de
carga: Tracción, Corte, Torsión y Flexión. Inicialmente se estudia la teoría y esta se
complementa con un apreciable número de ejemplos o problemas resueltos y luego con
problemas propuestos para que el alumno refuerce su comprensión.
En el primer capítulo se hace una introducción al estudio de la Resistencia de Materiales
marcando sus objetivos y estableciendo los principios generales, que completan las
conclusiones de la teoría de la Elasticidad, para poder desarrollar la disciplina siguiendo el
método lógico-deductivo.
En el resto de los capítulos se hace un análisis sistemático de las acciones que se derivan
de una solicitación externa actuando sobre un prisma mecánico. Y este estudio se hace
considerando los efectos producidos por cada una de las posibles magnitudes causantes,
actuando cada una de ellas independientemente de las otras. Así, las tensiones normal y
cortante que someten al prisma a tracción o compresión y a cortadura, respectivamente, son
tratados en los Capítulos 2 y 3.
En el capítulo 4 se estudia la teoría de la torsión y los tres capítulos siguientes se dedican al
estudio de la flexión, en sus múltiples aspectos. En los dos primeros de éstos se expone la
teoría general haciendo en uno de ellos un análisis del estado tensional que se crea en el
prisma mecánico cuando se le somete a flexión pura o flexión simple, y en el otro, el estudio
de las deformaciones producidas por la misma causa.
El importante tema del pandeo es tratado en el Capítulo 8, en el que hay que abandonar una
de las hipótesis fundamentales admitidas en Resistencia de Materiales cual es la de
pequeñez de las deformaciones.
Finalmente, un último capítulo se dedica al estudio de los estados tensional y de
deformaciones cuando la solicitación que actúa sobre el prisma mecánico es arbitraria. Era
necesario acabar la obra con un tema que nos hiciera ver la generalidad de aplicación de las
teorías de la Resistencia de Materiales a todo tipo de piezas.
En toda la obra se usa el Sistema Técnico de Unidades o el Sistema Internacional de
Unidades y para la solución de muchos de los problemas se usó software matemático.
Agradezco la ayuda y sugerencias de los docentes de Ingeniería Mecánica y
Electromecánica de la UMSA, quienes realizaron valiosos aportes al texto.
Contenido
Prefacio
INDICE
1 Conceptos Básicos de la Resistencia de Materiales
1.1. Objeto y Finalidad de la Resistencia de Materiales
1.2. Concepto de Sólido Elástico
1.3. Modelo teórico de sólido utilizado en Resistencia de Materiales. (Prisma
mecánico)
1.4. Principios generales de la Resistencia de Materiales
1.5. Tipos de Cargas exteriores sobre un prisma mecánico
1.6. Equilibrio estático y equilibrio elástico
1.7. Tipos de Solicitación
1.8. Determinación de las Cargas Internas (Método de las Secciones)
1.9. Tensiones o Tensiones
1.10. Deformación
1.11. Diagrama Tensión y Deformación
1.12. Constantes Elásticas
1.13,- Diagrama Tensión – Deformación para otros materiales
1.14. Diagramas Ideales
1.15. Coeficiente de Seguridad, Tensión Admisible y Carga Admisible
1.16. Falla frente a Cargas Estáticas y Variables
PROBLEMAS RESUELTOS
PROBLEMAS PROPUESTOS
2 Tracción y Compresión
2.1. Introducción
2.2. Diagramas de Fuerzas Normales:
2.3.- Tracción Compresión Mono axial
2.4.- Tracción Compresión Biaxial
2.6.- Problemas Estáticamente Indeterminados (Hiperestáticos)
2.7.- Trabajo de las Fuerzas en Tracción Compresión (Energía Potencial de
Deformación)
PROBLEMAS RESUELTOS
PROBLEMAS PROPUESTOS
3 Corte Puro
3.1. Introducción
2.2.- Tensiones y Deformaciones en Corte Puro
2.3. Problemas Estáticamente Indeterminados (Hiperestáticos)
PROBLEMAS RESUELTOS
PROBLEMAS PROPUESTOS
4.- Torsión
4.1. Introducción
4.2. Diagrama de Momentos de Torsión:
4.3.- Torsión Circular
4.4 Torsión en Elementos con Sección Rectangular
4.5 Tensiones en Secciones Cerradas de Pequeño Espesor
4.6. Problemas Estáticamente Indeterminados (Hiperestáticos)
PROBLEMAS RESUELTOS
PROBLEMAS PROPUESTOS
5.- Flexión - Fuerza Cortante y Momento Flector
5.1. Introducción
5.2. Cargas
5.3. Tipos de Apoyos
5.4. Tipos de Vigas
5.5. Cálculo de Reacciones
5.6. Momento Flector y Fuerza Cortante
5.7. Relación entre el momento Flector y la Fuerza Cortante
5.8. Determinación del Momento Flector y la Fuerza Cortante
5.9. Valores del Momento Flector y la Fuerza Cortante en los extremos
5.10. Cálculo de Momentos por funciones de Singularidad
5.11. Diagrama de Fuerzas Cortantes y de Momentos Flectores
PROBLEMAS RESUELTOS
PROBLEMAS PROPUESTOS
6.- Flexión – Tensiones Normales y Cortantes
6.1. Introducción
6.2. Tensiones Normales en Flexión
6.3. Tensiones Cortantes en Flexión
6.4. Perfiles Comunes Usados en Vigas
PROBLEMAS RESUELTOS
PROBLEMAS PROPUESTOS
7.- Deformaciones en Flexión
7.1. Introducción
7.2 Línea Elástica
7.3 Método de la Ecuación Diferencial de la Elástica o Doble Integración del
Momento
7.4. Método de Superposición
7.5. Método del Área del Diagrama de Momentos o Teoremas de Mohr
7.6. Método de la viga conjugada
7.7. Sistemas Hiperestáticos
PROBLEMAS RESUELTOS
PROBLEMAS PROPUESTOS
8.- Solicitación Compuesta
8.1. Introducción
8.2. Combinación de Tensiones
8.3. Combinación de Deformaciones
8.4 Casos de Solicitación Compuesta
PROBLEMAS RESUELTOS
PROBLEMAS PROPUESTOS
9.- Métodos Energéticos
9.1. Introducción
9.2. Trabajo
9.3 Energía Potencial
9.4 Ecuaciones de la energía
9.5 Teorema de Castigliano
9.6 Ecuaciones de Castigliano
PROBLEMAS RESUELTOS
PROBLEMAS PROPUESTOS
10.- Pandeo de Columnas
10.1. Introducción
10.2 Equilibrio Estable, Inestable e Indiferente
10.3. Tipos de apoyos y Columnas
10.4 Carga Crítica de Euler
10.5. Ecuación de la línea elástica:
10.6. Límites de Aplicación de la Formula de Euler
10.7. Columnas cargadas Excéntricamente – Formula de la Secante
PROBLEMAS RESUELTOS
PROBLEMAS PROPUESTOS
1 Conceptos Básicos de la Resistencia de Materiales
1.1 Objeto y Finalidad de la Resistencia de Materiales
El objetivo del presente libro es establecer los criterios que nos permitan determinar el
material más conveniente, la forma y las dimensiones más adecuadas que hay que dar a los
elementos de una estructura o máquina para que puedan resistir la acción de las fuerzas y
momentos exteriores que los solicitan, así como para obtener este resultado de la forma
más económica posible.
Si se someten dos cables de la misma forma y dimensiones, pero de distinto material como
podían ser de acero y cobre a una misma fuerza por ejemplo el peso de un cuerpo, mismo
que se incrementa paulatinamente, se observa que el cable de cobre es el primero en el que
se produce la rotura. Por lo tanto se puede decir que el acero posee mayor resistencia
mecánica que el cobre, entendiendo por tal la capacidad de oponerse a la rotura al ser
sometido a una solicitación exterior.
En cuanto a las deformaciones que experimentan ambos materiales, también se observa
que son distintas. Se llama rigidez a la propiedad que presenta el material de oponerse a las
deformaciones.
Otro aspecto de gran importancia es la estabilidad, entendiendo por tal la capacidad de
oposición del elemento a grandes desplazamientos y deformaciones como resultado de las
cargas exteriores. El cálculo de la estabilidad de la pieza nos permitirá conocer su capacidad
de conservar las formas de equilibrio que adopta en estado deformado.
Teniendo presentes las anteriores consideraciones, podemos dar una definición más simple
aún que la dada inicialmente, y decir que Resistencia de Materiales es la ciencia que trata
del cálculo de la Resistencia Mecánica, Rigidez y Estabilidad de las piezas de una estructura
o máquina.
En el presente libro se estudiaran principalmente dos problemas fundamentales:
1.° Problema de dimensionamiento. Conocido el sistema de cargas que solicita a una pieza
de una estructura o máquina, calcular sus dimensiones para que la pieza resista y las
deformaciones que se originan no sobrepasen unos valores límites fijados de antemano.
2.° Problema de comprobación. Conocida la solicitación exterior y terminado el
dimensionamiento de una pieza, comprobar su resistencia y calcular las deformaciones.
La Resistencia de Materiales tiene importantes aplicaciones en todas las ramas de la
ingeniería. Sus métodos los utilizan los ingenieros aeronáuticos y navales para el diseño y
construcción de aviones y barcos, respectivamente; los ingenieros civiles, al proyectar
puentes, presas y cualquier tipo de estructura; los ingenieros de minas, para resolver la
necesidad de conocimientos de construcción que exige su profesión; los ingenieros
mecánicos y electromecánicos. para el proyecto y construcción de maquinaria y todo tipo de
construcciones mecánicas, como son los recipientes a, presión; los ingenieros energéticos,
para proyectar los diferentes componentes de un .reactor; los ingenieros metalúrgicos, por la
necesidad que tienen del conocimiento de los materiales actuales para la búsqueda de
nuevos materiales: los ingenieros eléctricos, para el proyecto de máquinas y equipos
eléctricos, y, en fin, los ingenieros químicos, para el diseño de instalaciones en industrias de
su especialidad.
1.2 Concepto de Sólido Elástico
La Estática y la Mecánica Teórica consideran indeformables los cuerpos materiales, ya se
encuentren en estado de movimiento o de reposo. Las conclusiones que se obtienen con
esta suposición son en gran número de casos buenas aproximaciones de lo que realmente
ocurre. Pero para determinar la resistencia de una pieza y sus deformaciones se deben
analizar los cuerpos como deformables.
Según lo indicado se pueden considerar los sólidos como: a) Sólido rígido, b) Sólido elástico
y c) Sólido verdadero.
a) Sólido rígido.- Es aquel que se supone indeformable y que ante cualquier carga (por
grande que sea) a que está sometido, la distancia entre dos moléculas cualesquiera
permanece invariable.
b) Sólido elástico.- Es aquel que ante una tensión exterior se deforma y recupera su forma
original al cesar la causa exterior. A los sólidos elásticos se les supone una serie de
cualidades como son las de isotropía, homogeneidad y continuidad. Un cuerpo es isótropo
cuando sus propiedades físicas no dependen de la dirección en que se han medido en dicho
cuerpo. El sólido es homogéneo si toda región del mismo posee idéntica composición y
características que otra cualquiera. Finalmente el cuerpo es continuo si no existen huecos
entre partículas ni, por consiguiente, distancias intersticiales.
c) Solido verdadero.- Las propiedades de isotropía, homogeneidad y continuidad no
concurren en ningún material, ya sea natural o elaborado por el hombre: no es posible que
se dé un grado de elasticidad exactamente igual en todas las direcciones debido a la
distribución de sus átomos o moléculas en redes cristalinas ordenadamente dispuestas.
Tampoco existe en la realidad la homogeneidad perfecta, así como sabemos por las teorías
modernas de la materia que ésta no es continua y que existen espacios vacíos entre las
moléculas y entre los mismos átomos que la componen. Por lo tanto en algunos materiales
como la madera y el hormigo el cuerpo no puede ser analizado como Solido Elástico y debe
ser analizado como solido verdadero. Entonces sólido verdadero es aquel que resulta de
considerarlo como deformable ante las cargas a que está sometido y falto de isotropía,
homogeneidad y continuidad
El considerar a los sólidos continuo es muy cómoda, pues permite admitir, cuando existe
una deformación debida a la aplicación de una fuerza a unas moléculas del sólido, que el
tensión es absorbido en parte por las moléculas próximas y de esta forma queda repartido
de forma continua y apta para el cálculo. Los materiales a que nos refiramos en lo sucesivo
los consideraremos como sólidos elásticos. Quiere ello decir que si microscópicamente no
son ciertas las hipótesis que se lo hacen, sí lo son macroscópicamente, pues los resultados
que se obtienen quedan sancionados por la experiencia. Aún podremos en muchos casos,
por ejemplo, cuando falte la homogeneidad en un sólido, considerar la existencia de varios
sólidos elásticos dentro del sólido dado, cada uno de los cuales estará concretado por zonas
que posean perfecta homogeneidad, y aplicarles las consideraciones teóricas que hagamos
para los sólidos elásticos en general.
1.3 Modelo teórico de sólido utilizado en Resistencia de Materiales. (Prisma mecánico)
Con objeto de estudiar los sólidos elásticos se crea un modelo teórico que se denomina
prisma mecánico, que desde el punto de vista físico posea las propiedades de isotropía,
homogeneidad y continuidad y que se define atendiendo a un criterio meramente
geométrico.
Se llama prisma mecánico al sólido engendrado por una sección plana S de área cuyo
centro de gravedad G describe una curva llamada línea media o directriz, siendo el plano
que contiene a S normal a la curva.
La mayoría de las piezas pueden considerarse como uno de los siguientes tipos de prismas:
a) Barra. Se llama así al prisma mecánico cuyas dimensiones de la sección transversal son
pequeñas, en comparación con la longitud de la línea media. Pertenecen a este tipo los
elementos de estructuras y los cables, por ejemplo. Este es tipo de prisma mecánico más
usado. Adicionalmente la mayor parte de barras son planos, es decir con línea media
contenida en un plano, siendo éste, además, plano de simetría del prisma.
En estructuras de hormigón armado se emplean sección transversal rectangular y cuadrada,
mientras que en estructuras metálicas secciones muy usuales son el perfil laminado doble te
I en vigas, o dos secciones en U soldadas en pilares.
Fig. 1 Barra
b) Placa. Es un cuerpo limitado por dos planos, cuyo espesor es pequeño en comparación
con las otras dos dimensiones.
Fig. 2 Placa
Pertenecen a este tipo las losas que se fabrican para tapar depósitos subterráneos, as;
como las placas utilizadas como forjados en las edificaciones.
c) Cascara. Es un cuerpo limitado por dos superficies no planas, cuya distancia es pequeña
en comparación con las otras dos dimensiones (Fig. 1.7).
Fig. 3 Cascara
Son de este tipo los depósitos, como los tanques de agua, silos, gasómetros, etc., así como
las tuberías de gran diámetro y, en general, las estructuras laminares. En los últimos tipos,
es decir, en placas y cascaras, en vez de línea media se utiliza la superficie media, que se
define como la constituida por los puntos que dividen el espesor en dos partes iguales.
1.4 Principios generales de la Resistencia de Materiales
Como se mencionó anteriormente la Resistencia de Materiales requiere hipótesis
simplificativas, en el presente texto se asumen las siguientes hipótesis:
a) Los materiales se consideran continuos.- La mayoría de los materiales cumple con esta
hipótesis aun cuando existan poros o se considere la discontinuidad de la estructura de la
materia, compuesta por átomos que no están en contacto rígido entre sí, ya que existen
espacios entre ellos y fuerzas que los mantienen vinculados, formando una red ordenada.
b) Los materiales se consideran homogéneos.- Con esta hipótesis se consideran las
propiedades idénticas en todos los puntos.
c) Los materiales se consideran isótropos.- Con esta hipótesis se consideran las
propiedades idénticas en todas las direcciones. Los metales son materiales homogéneos e
isótropos y la madera, el hormigón y la piedra no lo son.
d) Las fuerzas interiores que preceden a las cargas son nulas.- Las fuerzas interiores entre
las partículas del material se oponen al cambio de la forma y dimensiones del cuerpo
sometido a cargas. Al hablar de fuerzas interiores no consideramos las fuerzas moleculares
que existen en un sólido no sometido a cargas.
e) Es válido el principio de superposición de efectos.- Debido a que las deformaciones de los
cuerpos son pequeños en comparación con las dimensiones del mismo, las ecuaciones de
equilibrio correspondiente a un cuerpo cargado pueden plantearse sobre su configuración
inicial, es decir, sin deformaciones, y que las deformaciones son proporcionales a las
cargas.
f) Es aplicable el principio de Saint Venant.- Según este principio las fuerzas interiores en los
puntos de un sólido, situados lejos de los lugares de aplicación de las cargas no dependen
del modo de aplicación de las mismas, por lo que se puede sustituir un sistema de fuerzas
por otro equivalente
1.5 Tipos de Cargas exteriores sobre un prisma mecánico
Las cargas exteriores sobre una pieza están constituidas por las cargas directamente
aplicadas y las reacciones debidas a los apoyos. Las cargas se clasifican en:
a) Fuerzas de volumen y fuerzas de superficie.- Las primeras actúan sobre todos los puntos
del sólido y se deben a campos de fuerzas tales como el campo gravitatorio, el campo de
fuerzas de inercia, o el campo magnético. Las fuerzas de superficie son las que se aplican a
la superficie exterior del prisma. Pueden ser concentradas o repartidas.
b) Cargas concentradas y distribuidas.- Las cargas concentradas son aquellas que se
aplican en un punto mientras que las cargas distribuidas las que están aplicadas en
porciones de área o volumen, En la naturaleza no existen fuerzas concentradas sino solo
distribuidas sin embargo cuando el área o volumen de aplicación son pequeños las cargas
pueden considerarse como concentradas. Las cargas distribuidas pueden ser de superficie
(presión del viento o del agua sobre una pared) o de volumen (peso propio).
c) Cargas estáticas y dinámicas.- Las cargas cuya magnitud, punto de aplicación y dirección
no varían o lo hacen muy lentamente, se llaman cargas estáticas mismas que no provocan
vibraciones de las estructuras o elementos, mientras que las cargas que varían con el
tiempo se llaman cargas dinámicas y son las que provocan vibraciones
Si la variación de la carga es de carácter periódico, es decir, que los valores máximos de la
carga se repiten cada determinado intervalo de tiempo las cargas se denominan cargas de
régimen estable o cargas de repetición periódica. La resistencia para cargas estables se
analiza en el presente libro pero no para cargas de régimen no estable.
1.6 Equilibrio estático y equilibrio elástico
Para que un sólido rígido se encuentre en equilibrio es necesario y suficiente que se
verifiquen:
1 Que la suma de las fuerzas que actúan sobre el sólido sea igual a cero, o lo que es lo
mismo, que la resultante sea nula. Esta condición asegura que el sólido no tenga
desplazamientos.
2 Que el momento resultante de todas las fuerzas respecto de cualquier punto sea igual a
cero. Esta condición asegura que el sólido no experimente giros.
En un Sólido Elástico estas condiciones son necesarias pero no suficientes, ya que si
suponemos realizado en el sólido un corte ideal y prescindimos de una de las partes, es
necesario que el sistema de fuerzas interiores en los puntos de la sección ideal sea
equivalente al sistema de fuerzas que actúan sobre la parte eliminada. Así, para el equilibrio
en un sólido elástico no sólo se requieren las condiciones del equilibrio estático, sino
también que exista equilibrio entre las fuerzas exteriores y las internas en cada una de las
infinitas secciones.
Esta última condición es la característica del equilibrio elástico: es necesario que las fuerzas
exteriores que actúan sobre el sólido sean contrarrestadas por las fuerzas interiores de
cohesión molecular.
1.7 Tipos de Solicitación
Considérese un cuerpo en equilibrio sometido a la acción de fuerzas y momentos externos,
en cualquier sección interna aparecen una fuerza y un momento resultantes internos que
equilibran las cargas externas. Los valores de la fuerza y el Momento internos se hallan
generalmente con las ecuaciones de la estática
P1
Fue rza In te rn a
P2
M o m en to In te rn o
M2
M1
Pn
P3
M3
P1
Mn
P4
Fig. 4 Fuerza y Momento Internos
La fuerza y el momento internos pueden descomponerse en componentes paralelas y
normales a la sección. Del análisis individual de estas componentes definen los diferentes
tipos de carga. Así la Fuerza Normal produce cargas Normales de Tracción Compresión, la
Fuerza Tangencial produce cargas de Corte, el Momento Normal produce cargas de Torsión
y el Momento Tangencial produce cargas de Flexión.
a) Tracción Compresión.- Un cuerpo está sometido a Solicitación de Tracción o
Compresión, cuando sobre él se apliquen fuerzas paralelas al eje centroidal y
perpendiculares a la sección transversal. Dependiendo si la carga tiende a estirar o a
comprimir la pieza, la carga será de tracción o compresión.
Fig. 5 Tracción
b) Corte.- Un cuerpo está sometido a Solicitación de Corte cuando sobre él se apliquen
fuerzas perpendiculares al eje centroidal y paralelas a la sección transversal.
Fig. 6 Corte
c) Torsión.- Un cuerpo está sometido a Solicitación de Torsión cuando sobre él se aplican
Momentos paralelos al eje centroidal y perpendiculares a la sección transversal.
Fig. 7 Torsión
d) Flexión.- Un cuerpo está sometido a Solicitación de Flexión cuando sobre él se aplican
Fuerzas y Momentos perpendiculares a su eje centroidal y paralelos a la sección
transversal.
Fig. 8 Flexión
e) Cargas Combinadas.- Los cuerpos y elementos en condiciones reales presentan
combinaciones de los anteriores tipos de carga. En el presente texto inicialmente se
analizan los tipos de carga de forma individual y su combinación se analiza posteriormente
1.8 Determinación de las Cargas Internas (Método de las Secciones)
En un cuerpo sometido a fuerzas y momentos, para hallar las cargas internas por el método
de corte o secciones se imagina un plano imaginario que seccione o divida el cuerpo en dos
partes. Para que cada parte este en equilibrio, en la superficie de corte de cada una de las
partes por la interacción que ejerce la otra deben actuar una fuerza y un momento internos
que equilibran las cargas exteriores, que actúan sobre la parte separada. Los valores de la
Fuerza y el Momento internos se pueden hallar generalmente con las ecuaciones de la
estática
P1
Fue rza In te rn a
P2
M o m en to In te rn o
M2
M1
Pn
P3
Mn
M3
P1
P4
Fig. 9 Fuerza y Momento Internos
La fuerza y el momento internos tienen componentes tangencial y normal a la sección. La
componente normal de la fuerza a la sección “N” produce tracción, la componente tangencial
de la fuerza a la sección “Q” produce corte, la componente normal del momento a la sección
“Mt” produce torsión y la componente tangencial del momento a la sección “Mf” produce
flexión. Frecuentemente las fuerzas exteriores se encuentran en un mismo plano, los
momentos exteriores perpendiculares a este plano y no existen momentos de torsión Mt
Fig. 10 Configuración Frecuente
1.9 Tensiones o Tensiones
a) Análisis Molecular
Considérese una barra sometida a la acción de dos fuerzas iguales, opuestas y colineales
en sus extremos. Se verifica el equilibrio: P - P = 0
Fig. 11 Fuerzas en las Moléculas
Realizando un análisis molecular, la fuerza externa se distribuye en pequeñas fuerzas
tirando de cada molécula, que tratan de separarla de sus vecinas, sin embargo la atracción
entre moléculas opone resistencia con una fuerza igual y contraria, lo que finalmente impide
que las moléculas se alejen entre sí. Tomando un par de ellas se verifica que:
-Pi Fi - Fi Pi
(1.1
Donde Pi es la acción sobre cada molécula generada por las fuerzas “P” y “Fi “ la reacción
que opone el material generada por la atracción molecular (o Atómica).
Aumentando “P” aumenta la reacción Fi , que podrá crecer hasta un determinado límite, más
allá del cual las moléculas se separan irremediablemente, y como consecuencia la barra se
deforma permanentemente o se separa.
b) Hipótesis de Navier
Según esta hipótesis los sólidos homogéneos se imaginan como una sucesión de
innumerables secciones transversales paralelas entre si y perpendiculares a su eje
longitudinal (similar naipes pegados entre sí). Cada sección es tan delgada como el
diámetro de un átomo y los átomos están ordenados según un arreglo matricial
Fig. 1.12 Hipótesis de Navier
Entonces :
Pi 
P
n
P y Pi Fuerzas externa e interna sobre cada átomo
“n” el número de átomos que hay en la sección transversal.
(1.2
c) Vector Tensión
Considérese un cuerpo sometido cargas exteriores, si el mismo es cortado idealmente en
dos partes A y B por medio de un plano π y se suprime una de las partes, por ejemplo la B,
de la condición de equilibrio elástico se concluye que en toda la sección S aparece una
distribución continua de fuerzas
Fig. 1.13 Vector Tensión
Si df es la fuerza resultante en un punto P, se define como tensión en el punto a:
Esfuerzo 
Fuerza F

Area
A



f df
t  lim dS0

S dS
(1.3
(1.4
El tensión o tensión es un vector colineal con df.
e) Tipos de Tensiones o Tensiones
El vector tensión puede descomponerse en una componente normal al plano () que recibe
el nombre de tensión normal y en una componente paralela al plano () que recibe el
nombre de tensión tangencial o cortante. A ambas tensiones se denomina componentes
intrínsecas del vector tensión.
Fig. 1.14 Tensiones Normales y Cortantes
La tensión normal provoca que las partículas que están en el plano dado, tiendan a
separarse o a acercarse mientras que las tensiones tangenciales provocan el deslizamiento
de las partículas del material, en el plano de la sección en cuestión.
Los materiales no tienen una determinada resistencia a las fuerzas y momentos, ya que ella
depende de las dimensiones, pero sí tienen determinadas resistencias a las tensiones
normales y cortantes
En las caras de un elemento diferencial cúbico actuarán en el caso general las tensiones de
la figura
Fig. 1.15 Estado tensional
f) Densidad de Tensiones
Fig. 1.16 Densidad de Tensión
Cuando una barra de sección variable se somete a cargas de tracción F, en cualquier
sección transversal aparece una fuerza interna F que equilibra a la externa que se distribuye
en tensiones normales. Sin embargo la magnitud de estos tensiones es variable debido a la
variación del área. Estos tensiones son mayores donde las secciones normales son las
menores y viceversa. Dibujando líneas equidistantes de la periferia se puede apreciar que
ellas tienen mayor “concentración” o “densidad” donde el área es menor. La magnitud de las
tensiones es proporcional a la concentración de líneas equidistantes. Este fenómeno es
similar a la velocidad que adquiere un fluido en una tubería por lo que también es conocido
por flujo de tensiones.
g) Concentradores de tensión
Fig. 1.17 Concentración de Tensiones
Los cambios o variaciones de las secciones transversales de una pieza y especialmente las
variaciones bruscas, resultan en la magnificación de las tensiones efecto conocido como
Concentración de Tensiones.
Las hendiduras, agujeros y cambios de sección bruscos son Concentradores de Tensiones.
Se ha podido verificar que por ejemplo un agujero circular en una placa plana incrementa las
tensiones hasta tres veces.
1.10 Deformación
Consideremos dos puntos P y Q en un sólido elástico en estado neutro, sin carga, es decir,
no sometido a solicitación alguna
Fig. 1.18 Deformación
Aplicadas las cargas externas hay deformación y los dos puntos pasan a las posiciones P' y
Q'. Se definen como deformación total y unitaria a la variación de distancia entre estos dos
puntos y a la variación sobre la distancia original, respectivamente


  P' Q' P' Q'  dr '  dr

P' Q' PQ
PQ


dr '  dr


dr
(1.5
(1.6
Los sólidos, bajo la acción de cargas externas se deforman y cambian sus dimensiones o
forma, Al cambio de dimensión se le denomina deformación lineal y al cambio de forma
deformación angular.
a) Deformación provocada por Cargas de Axiales
Fig. 1.19 Deformación por Cargas Axiales
Una barra sometida a cargas axiales además de experimentar una deformación en la
dirección de axial también presenta otra deformación en la dirección transversal. Las cargas
de tracción provocan alargamiento en la dirección axial y adelgazamiento en la dirección
transversal, mientras que las cargas de compresión provocan acortamiento en la dirección
axial y ensanchamiento en la dirección transversal.
Las deformaciones se cuantifican con:
δ = lf - lo
Deformación longitudinal
(1.7
ε = (lf – lo)/lo
Deformación longitudinal unitaria
(1.8
δq = df - do
Deformación transversal
(1.9
εq = (df – do)/do
Deformación transversal unitaria
(1.10
Donde lf, lo, df y do son las longitudes y diámetros final e inicial
b) Deformación provocada por Cargas de Corte
Las cuerpos sometidos a cargas de corte no presentan deformaciones significativas (no se
verifica cambio de dimensiones) pero si presentan distorsión (se verifica cambio de forma).
Fig. 1.20 Distorsión por Cargas de Corte
La deformación se cuantifica con:
γ
Angulo de inclinación de las caras
c) Deformación provocada por Cargas de Torsión
Las barras sometidas a cargas de torsión no presentan deformaciones longitudinales sino
rotaciones o deformaciones angulares entre secciones. Las secciones transversales giran
una respecto a otra.
Fig. 1.21 Deformación por Cargas de Torsión
La deformación se cuantifica con:
φ
Angulo de rotación entre secciones de los extremos de la barra
d) Deformación provocada por Cargas de Flexión
Los cuerpos generalmente rectos sometidos a cargas de Flexión se vuelven curvos por lo
que presentan deformaciones lineales y angulares.
Fig. 1.22 Deformación por Cargas de Flexión
Las deformaciones se cuantifican con:
ô
Deformación lineal
θ
Deformación angular
1.11 Diagrama Tensión y Deformación
La deformación depende de las cargas externas y consecuentemente de las tensiones y de
fuerzas de atracción molecular, es decir, de la estructura interna del material. Para obtener
la relación entre tensiones y deformaciones se procede por vía experimental mediante
ensayos realizados en el laboratorio, en donde se comprueba, en efecto, que para dos
piezas de distintos materiales, de iguales dimensiones y sometidas al mismo estado de
cargas, las deformaciones son distintas.
El ensayo más simple que se hace es el de tracción. En este ensayo sometiendo una pieza
de dimensiones normalizadas llamada probeta a una carga de tracción que se aumenta
gradualmente hasta la rotura.
En la probeta se realizan previamente dos marcas, que determinan una longitud
denominada distancia entre puntos, sobre las que se efectúa, por medio de un
extensómetro, la medida de los alargamientos.
Si A es la sección de la probeta y P la fuerza aplicada en sus extremos en dirección axial, la
fuerza origina en el interior del material un estado de tensiones que se supone constante.

P
A
(1.11
La probeta, debido al tensión, se alarga. La deformada unitaria longitudinal es:

l f  lo
lo
(1.12
Aumentando progresivamente el valor de P, midiendo ε y llevando los valores a un gráfico,
se obtiene para el acero dulce el diagrama tensión-deformación similar al de la figura
Fig. 1.23 Diagrama ζ - ε
En este diagrama pueden distinguirse ciertas zonas con determinadas características:
a) Período elástico.- Este período queda delimitado por la tensión Se (límite de elasticidad).
El límite de elasticidad se caracteriza porque, hasta llegar al mismo, el material se comporta
elásticamente, es decir que producida la descarga, la probeta recupera su longitud inicial. En
la práctica, este límite se considera como tal cuando en la descarga queda una deformación
especifica remanente igual al 0.001 %.
Este período comprende dos zonas: la primera, hasta el Sp (límite de proporcionalidad),
dónde el material verifica la ley de Hooke. La segunda zona entre Sp y Se, si bien es
elástica, no manifiesta proporcionalidad entre tensiones y deformaciones.
En la primera zona:
d 
 E
d 
(1.13
En la segunda zona
d
 f ( )
d
(1.14
En general, los límites de proporcionalidad y de elasticidad difieren muy poco entre sí.
b) Período elasto-plástico.- Para tensiones superiores al límite elástico, la pieza no recobra
su dimensión original y la deformación es permanente acorde con la carga aplicada. A
medida que aumenta la solicitación, la gráfica disminuye el valor de su tangente, tendiendo a
anularse en el tramo final del período, al cual se llega con un valor de tensión que se indica
como Sy (tensión de fluencia).
c) Período plástico (fluencia).- Una vez arribado al valor de tensión Sy (límite de fluencia),
el material fluye, aumentan las deformaciones sin que existe aumento de tensión. El
fenómeno no es tan simple, ya que la tensión oscila entre dos valores cercanos entre sí,
denominados límites de fluencia superior e inferior, respectivamente. La tensión de
proporcionalidad es aproximadamente 80% la de fluencia
Fig. 1.24 Líneas de Chernov - Lüders
Los experimentos demuestran que durante la fluencia se producen deslizamientos relativos
entre los cristales y en la superficie de la probeta aparecen las llamadas líneas de Chernov Lüders, que forman con el eje de la misma un ángulo de 45º.
d) Período de endurecimiento y de estricción.- Luego de la fluencia hay un
reacomodamiento cristalográfico y el material se endurece e incrementa su resistencia, es
decir, admite un incremento de carga. En este período las deformaciones son muy
pronunciadas. La tensión aumenta hasta alcanzar un valor máximo, denominado “tensión de
rotura”, a partir del cual la tensión disminuye hasta que alcanza una determinada
deformación de rotura, produciéndose la rotura física. La tensión Sut no es en realidad la
máxima tensión que se origina en la probeta sometida a carga. En efecto, alcanzado el valor
de la deformación específica correspondiente a Sut, comienza a manifestarse en la probeta
un fenómeno denominado “estricción”.
Fig. 1.25 Fenómeno de estricción
La estricción es la reducción de una sección central de la pieza, misma que hace que las
tensiones aumenten y que, en realidad, el diagrama efectivo en lugar de presentar su
concavidad hacia abajo muestra un punto de inflexión en las vecindades de Sut y cambia su
curvatura presentando una rama creciente hasta alcanzar la deformación de rotura.
Entonces el diagrama que anterior suele denominarse “diagrama convencional, ya que los
cálculos de las tensiones se realizan siempre sobre la base de suponer la sección
transversal constante, con área igual a la inicial.
La estricción se mide por el “coeficiente de estricción lateral” con la siguiente expresión:

Ai  A f
Af
Dónde:
Ai y Af área inicial y final respectivamente
En los aceros comunes φ ≈ 50 %
(1.15
Fig. 1.26 Diagrama ζ - ε efectivo y convencional
Para tensiones mayores a la fluencia como M en la gráfica la pieza presenta deformaciones
permanentes. Cuando se quita la carga las tensiones y deformaciones desaparecen a través
de una recta paralela a la del período elástico. Si la probeta vuelve a cargarse la curva llega
al punto N, pero con un nuevo recorrido donde ya no existe el período de fluencia y la zona
recta se prolonga hasta un valor ζ'p > ζp.
Fig. 1.27 Endurecimiento mecánico del acero dulce
Este fenómeno se denomina endurecimiento mecánico o por trabajo en frío, y también
puede lograrse por laminado en frío, trefilado o torsión. El trefilado se utiliza para endurecer
alambres o barras circulares finas, y el torsionado especialmente para barras redondas (en
general, con conformaciones superficiales), para hormigón armado.
Para aceros endurecidos mecánicamente o los de dureza natural, logrado por un mayor
contenido de carbono o mediante aleaciones especiales, el diagrama ζ - ε es distinto del
que se vio. Las características más importantes son las siguientes:
- Sus límites de proporcionalidad y elasticidad son más elevados que los aceros comunes.
- No poseen un límite de fluencia definido ni tampoco zonas de escurrimiento plástico.
- La deformación de rotura se reduce considerablemente.
Al no existir un límite de fluencia definido, este se determina en forma convencional como la
tensión para la cual la deformación especifica remanente alcanzan al 0.2 %.
Fig. 1.28 Límite Convencional de Fluencia 0,%
Los materiales como el acero dulce, que presentan una gran capacidad de deformación
antes de alcanzar la rotura, se denominan “dúctiles”. Se puede decir que estos materiales
avisan la rotura física, ya que antes de alcanzarse la misma las deformaciones son tan
grandes, que la estructura llega a la falla por este motivo.
Los materiales como el acero duro, para los cuales la rotura se produce bruscamente, sin
grandes deformaciones previas, se denominan “frágiles”.
e) Elasticidad y Plasticidad.- La propiedad que posee un material de volver parcial o
completamente a su forma inicial una vez que desaparece la carga es lo que se llama
“elasticidad”. Si la pieza recupera completamente su longitud inicial, se dice que el material
es “perfectamente elástico” sino “parcialmente elástico”. Un material es “perfectamente
plástico” cuando al dejar de actuar la carga que lo deforma mantiene su configuración
deformada.
En la realidad ningún material es perfectamente elástico o plástico, pero el acero, aluminio,
goma, la madera y el hormigón se consideran perfectamente elásticos dentro de ciertos
límites. Otros materiales como la arcilla y la masilla pueden considerarse como
perfectamente plásticos.
1.12 Constantes Elásticas
El comportamiento lineal elástico de los sólidos, permite definir las constantes elásticas,
a) Módulo de Elasticidad Longitudinal (E).- Considérese una barra recta sometida a
tracción.
Fig. 1.33 Barra de sección constante sometida a tracción
La deformación unitaria es :

L
L
(1.16
En la zona elástica, las tensiones son proporcionales a las deformaciones
Fig. 1.34 Proporcionalidad entre ζ – ε en la zona elástica
Tg 

E

(1.17
 E
(1.18
Ecuación conocida como de Hooke. La constante E, se conoce como módulo de elasticidad
longitudinal o módulo de Young. Es la más importante de las cuatro constantes elásticas.
b) Módulo de Elasticidad Transversal (G).- Sea un paralelepípedo fijo en su parte inferior
y con una fuerza P en su cara superior.
Fig. 1.35 Distorsión provocada por tensiones cortantes
La deformación se cuantificada por el ángulo

La grafica entre
y la tensión tangencial o cortante es:
P
A
-
(1.19
es similar a la vista anteriormente para las tensiones normales.
Dentro de la zona elástica, la constante que vincula la tensión tangencial con la deformación
angular, es llamada módulo de elasticidad transversal o módulo de rigidez (G).
Tg 

G

(1.20
Esta es la ecuación de Hooke para tensiones cortantes. Para el acero común Sy’ = 0,57 Sy
c) Coeficiente de Poisson
Al someter a una barra a un tensión axial, además de experimentar deformación según la
dirección de la fuerza, el cuerpo también deforma en la dirección normal a ella.
Fig. 1.37 Deformaciones Longitudinal y Transversal
Las deformaciones unitarias son:

L
L
(1.21
a
a
(1.22
q 
Experimentalmente se ha visto que ambas deformaciones son proporcionales
εq = ν ε
(1.23
ν se define como el coeficiente o módulo de Poisson y su valor depende del material, En
general para materiales isótropos, varía entre 0,25 y 0,33. En cualquier caso ν < 0,50
Valores de Constantes Elásticas según el material
Material
E (Ton/cm²)
2.000 a 2.100
1.160 a 1.300
1.100
750 a 1600
760
80 a 120
150 a 350
< 120
0.01
-
Acero
Cobre
Bronce
Hierro fundido
Aluminio
Madera (paralela a la fibra
Hormigón
Mampostería de ladrillo
Caucho
Corcho
γ
0.22 a 0.33
0.31 a 0.34
0.32 a 0.35
0.23 a 0.27
0.32 a 0.36
0.10 a 0.20
0.47
» 0.00
Los módulos de elasticidad longitudinal y transversal están relacionados por:
E=2G(1+ν)
(1.24
ν es el coeficiente de Poisson
Donde
1.13 Diagrama Tensión – Deformación para otros materiales
En la figura 1.29 se presentan los diagramas tensión – deformación para diferentes
materiales. Ahora bien como se observa en la figura 1.30, hay algunos materiales para los
cuales se observa que el diagrama ζ - ε es una curva continua sin tramos rectos, es decir,
que prácticamente en ningún momento se verifica la ley Hooke. Un ejemplo clásico es el
hormigón, donde interesa la curva ζ - ε en compresión.


Mat. Frágil
Acero de Alta Calidad
Acero Media Calidad
Mat. Dúctil
Acero Corriente

Fig. 1.29 Diagramas Tensión Deformación

En estos casos no puede hablarse de un módulo de elasticidad único. Cabe distinguir tres
valores del módulo de elasticidad:
Fig. 1.30 Módulos Tangentes y Secantes
a) Módulo al origen.- Es el valor al origen
E = tg α
(1.25
b) Módulo Instantáneo.- Su valor lo da la pendiente a la curva ζ - ε en cada punto:
E
d
 tg ( o )
d
(1.26
c) Módulo Secante.- Su valor viene dado por la tangente trigonométrica del ángulo α1. Para
estos materiales, Bach, propuso como relación entre ζ - ε una ley de tipo exponencial que
lleva su nombre:
ζk = E e
(1.27
el coeficiente k depende del material (valor medio, ya que depende de muchas variables):
Material
Hormigón
Cobre
Latón
Cuero
Coeficiente k
k = 1,15
k = 1,10
k = 1,085
k = 0,70
Fig. 1.31 Diagramas no lineales ζ - ε
En el caso que k = 1, 0 se obtiene la ley de Hooke. Ciertos materiales presentan un
comportamiento diferente en compresión que a tracción, tal es el caso del hormigón.
1.14 Diagramas Ideales
Los diagramas que se vieron a veces son reemplazados por diagramas idealizados por
Prandtl, resumiendo las características fundamentales de los tres tipos de materiales. El
diagrama ideal correspondiente a un material dúctil se compone de dos tramos rectos: uno
inclinado, correspondiente al período elástico; el otro horizontal, materializando el período de
fluencia. El período de endurecimiento no interesa porque la deformación al final de la
fluencia es tan significativa que el material está en falla antes de llegar a la rotura.
Fig. 1.32 Diagramas ideales a) material dúctil b) material frágil c) material plástico
En los materiales frágiles el límite de proporcionalidad es próximo a la tensión de rotura,
prescindiéndose del tramo curvo y en materiales plásticos el diagrama es una recta
horizontal, lo que significa que sometidos a una carga, se deforman indefinidamente sin
incremento de tensión.
1.15 Coeficiente de Seguridad, Tensión Admisible y Carga Admisible
No hay la seguridad absoluta y las piezas están amenazadas por incertidumbres.
Existen numerosas causas de incertidumbres: Las hipótesis de cargas, las hipótesis de
cálculo, los errores de cálculos, los defectos del material, los errores de las dimensiones, los
errores de ejecución, etc.
La falla de una pieza puede provocar pérdidas económicas y humanas por lo que se debe
buscar la máxima seguridad. Para evitar la falla, la tensión máxima en una pieza no debe
superar un valor límite. Para materiales dúctiles el valor límite es el límite de fluencia y para
de materiales frágiles es el límite de resistencia o tensión de rotura
Sadm = Sy/ 
Para materiales dúctiles
(1.28
Sadm = Sut/ 
Para materiales frágiles
(1.29
Donde  es el coeficiente de seguridad. La elección del coeficiente de seguridad es
compleja pero disposiciones reglamentarias que tratan sobre construcciones de acero;
indican valores que varían entre 1.25 y 1.60, para estructuras de hormigón armado, los
coeficientes de seguridad varían entre 1,75 y 2,10 y en la construcción de máquinas el valor
varía, entre 1.5 a 2.5.
1.16 Resistencia para Cargas Estáticas y Variables
a) Cargas Estáticas.- Son aquellas cuya magnitud no varía con el tiempo,
P
Pmax
Pmin
t
Fig. 1.38 Carga Estática
Como se mencionó anteriormente, la falla frente a cargas estáticas se previene con :
 = E  < Sadm
(1.30
 = G  < S’adm
(1.31
b) Cargas Variables.- Son aquellas cuya magnitud varía con el tiempo. Cuando la variación
es de carácter periódico y los valores máximos de la carga se repiten cada determinado
intervalo de tiempo las cargas se denominan de régimen estable o de repetición periódica.
En el presente libro se analiza la resistencia solo para cargas estables
P
Pmax
t
 P  Pmin 
Pmed   max

2


P
min
Fig. 1.39 Carga variable de régimen estable
Los dos casos más comunes de cargas variables de régimen estable son:
- Cargas Intermitentes.- Son aquellas que aparecen y desaparecen. Es decir que varían
periódicamente de un valor máximo a cero. ( Pmin = 0 )
P
Pmax
P
min
t
P 
Pmed   max 
 2 
Fig. 1.40 Carga Intermitente
- Cargas Alternantes.- Son aquellas cuya magnitud cambia de un valor positivo al mismo
valor negativo. ( Pmax = - Pmin)
P
Pmax
t
 P  Pmin 
Pmed   max
0
2


P
min
Fig. 1.41 Carga Alternante
Existen varias teorías para verificar la falla frente a cargas variables. En el presente libro se
desarrollará sólo la teoría de Goodman Modificado.
Esfu erzos M á xim o s
Sut
Sy
Esfu erzos M ed io s
Se
4 5º
 med
Esfu erzos M íni m o s
-S e
Fig. 1.42 Diagrama de Goodman Modificado
Según esta teoría la pieza no falla mientras las tensiones se encuentran dentro de la región
sombreada.
Para construir el diagrama se necesitan: El Limite de Rotura Sut , El Limite de Fluencia Sy y
el Limite de Resistencia a la fatiga Se (cuyo valor aproximado es la mitad de la resistencia a
la rotura. Se = Sut/2). Por cada una de estas tensiones se traza una línea horizontal que
intersecte a una línea a 45 grados que constituye la línea de Tensiones Medias.
PROBLEMAS RESUELTOS
1.1. Se tiene dos cables metálicos, el primero de Aluminio con un diámetro de 1 mm y el
segundo de Acero con un diámetro de 0.5 mm. Tomar Sy al = 283 Mpa (2884.8 Kg/cm²) y Sy
ac = 428 Mpa (4362.8 Kg/cm²). Se pide hallar la carga máxima que pueden soportar ambos
cables y cuál es el de mayor resistencia
Cable Al

Cable Ac
0.1 [cm]
(a)

0.05 [cm]
(b)
Solución:
Para evitar la falla
 = P/A < Sy
Despejando
P =  d2 Sy /4
Reemplazando valores
Pal = 22.65 Kg
Pac = 8.56 Kg
El cable de aluminio es más resistente.
1.2. Dos piezas “a” y “b” con una longitud inicial de 10 cm y 100 cm, se deforman hasta
alcanzar longitudes finales de 11 cm y 105 cm respectivamente. Se pide calcular la
deformada total y unitaria
Solución:
 = lf – l
 =  / l = (lf - l)/ l
a = 1 cm
a = 0.1 (10%)
b = 5 cm
b = 0.05 (5%)
Nótese que:
a < b pero
a > b
1.3. Si en el problema anterior los diámetros de ambas piezas es de 1 cm. Se pide calcular
la deformada total y unitaria transversal. Tomar  = 0.3
Solución:
q = - 
df = q d + d
qa = - 0.03 (3%)
dfa = 0.97 cm
qb = - 0.015 (1.5%)
dfb = 0.985 cm
1.4. Para el problema 1.2 se pide hallar las tensiones a los que están sometidas las piezas si
son de acero. Tomar E = 2.1 x 10 6 Kg/cm²
Solución:
=E
a = 0.1 (10%)
b = 0.05 (5%)
Entonces
a = 210000 Kg/cm²
b = 105000 Kg/cm²
Ningún material soporta estos tensiones. Estas deformadas (10 y 5 %) son imposibles.
1.5. Cuál es la deformada máxima que puede tener un acero antes de fallar.
Tomar Sy = 428 Mpa (4362.8 Kg/cm²) y E = 2.1 x 10 6 Kg/cm²
Solución:
 < Sy
=E
 < = Sy/ E = 0.00207 (0.2%)
1.6. Una carga de 100 Kg se aplica a dos piezas de aluminio y acero con el mismo diámetro
de 1 cm. Tomando Eacero = 2.1 x 10 6 Kg/cm², Ealuminio = 0.9 x 10 6 Kg/cm², Sy acero = 428 Mpa
(4362.8 Kg/cm²) y Sy aluminio = 283 Mpa (2884.8 Kg/cm²). Se pide hallar : La relación de
deformadas y la relación de factores de seguridad.
Solución:
=/E
 = Sy/
acero = P/A = aluminio
acero/aluminio = Ealuminio / Eacero = 0.428 (42.8 %)
acero / aluminio = Syacero/ Syaluminio = 1,512 (151,2 %)
Estos resultados muestran primero que el acero se deforma menos que el aluminio y
segundo que el acero resiste más que el aluminio
1.7. Hallar los módulos de elasticidad al corte para los materiales del 1.anterior. Tomar  =
0.3 Eac = 2.1 x 10 6 Kg/cm², Eal = 0.9 x 10 6 Kg/cm²
Solución:
G = E/[2 ( 1 +  )]
Gacero = 8,07 x 105 Kg/cm²
Galumino = 3,46 x 105 Kg/cm²
1.8. Construir el diagrama de Goodman Modificado para un material con S y = 4000 Kg/cm²
Sut = 6000 Kg/cm² y Se = Sut/2 = 3000 Kg/cm²
Solución:
S
6000
B
4000
3000
C
A
45º
D
 med
A(0,3000)
B(6000,6000)
C(4000,4000)
E(0,-3000)
-3000 E
1.9. En el anterior 1.hallar las ecuaciones de las tensiones máximas, tensiones medios y
tensiones mínimas.
Solución:
A (0,3000)
B (6000,6000)
C (4000,4000)
E (0,-3000)
La ecuación de la recta conocidos dos puntos es
(y – y1)/(x – x1) = (y2 – y1)/(x2 – x1)
Para (A,B)
(y – 3000)/(x - 0) = (6000 – 3000)/(6000 – 0)
Smax = x/2+3000
para Smax< 4000
Las curvas de tensiones mínimas van de B a E y de C a D
(y – 6000)/(x - 6000) = (-3000 – 6000)/(0 - 6000)
Smin = 1,5 x – 3000
para min < 0
Cuando Smin = 0 se halla que x = 2000 y D = ( 2000,0)
(y – 4000)/(x - 4000) = (0 – 4000)/(2000 - 4000)
y = 2 x – 4000
para min > 0
Smin = 2x – 4000
1.10. Hallar las tensiones admisibles para carga estática, carga intermitente y carga
alternante del material de los problemas 6 y 7
Solución:
a) Carga estática
S = Sy = 4000 Kg/cm²
b) Carga intermitente
S = . Smax = x/2+3000 y x = 2000
S = 4000 Kg/cm²
c) Carga alternante
S = Se = 3000 Kg/cm²
1.11. Para las cargas dadas determinar en cada caso si hay o no falla con el material de los
problemas 6 y 7
 max = 3500 Kg/cm² y  min = – 3500 Kg/cm².
 max = 3500 Kg/cm² y  min = – 500 Kg/cm².
 max = 4500 Kg/cm² y  min = 0 Kg/cm².
 max = 4500 Kg/cm² y  min = 1500 Kg/cm².
Solución:
 med = (max+ min)/2
 a med = 0
 b med = 1500 Kg/cm²
 c med = 2250 Kg/cm²
 d med = 3000 Kg/cm²
S
6000
B
4000
3000
C
A
45º
D(20000,0)
 med
-3000 E
a)
 a med = 0
S max = 3000 <  a max = 3500
Hay falla
b)
 b max = 1500 Kg/cm² < 4000 Kg/cm²
Smax = 3750
y = x/2+3000
>  b max = 3500 Kg/cm²
No hay falla
 b min = - 500 Kg/cm² < 0
Smin = - 750
c)
<  b min = -500 Kg/cm²
No hay falla
 c max = 2250 Kg/cm² < 4000 Kg/cm²
Smax = 4125
d)
y = 1,5 x – 3000
y = x/2+3000
<  b max = 4500 Kg/cm²
Hay falla
 d max = 3000 Kg/cm² < 4000 Kg/cm²
Smax = 4500
y = x/2+3000
<  b max = 4500 Kg/cm²
No hay falla
 d min = 3000 Kg/cm² > 0
Smin = 2000
y = 2x – 4000
>  b min = 1500 Kg/cm²
Si hay falla
1.12. Hallar las ecuaciones genéricas de las tensiones máximas, medios y mínimos.
S
Sut
B
Sy
Se
C
A
45º
D
 med
A(0,0.5*Sut )
B(S ut ,Sut )
C(Sy ,Sy )
D(Descon,0)
E(0,0.5*Sut )
-S e E
La ecuación de la recta conocidos dos puntos es
(y – y1)/(x – x1) = (y2 – y1)/(x2 – x1)
La curva de tensiones máximas va de A a B
(y – 0.5 Sut)/(x - 0) = (Sut – 0.5 Sut)/(Sut – 0)
Smax = (x + Sut)/2
para Smax< Sy
Las curvas de tensiones mínimas van de B a E y de C a D
BE)
(y – Sut)/(x – Sut) = (-0.5 Sut – Sut)/(0 – Sut)
Smin = 1,5 x – 0,5 Sut
CD)
para min < 0
Cuando Smin = 0 se halla que x = Sut/3 y la coordenada de D ( Sut/3, 0)
(y – Sy)/(x – Sy) = (0 – Sy)/(Sut/3 – Sy)
y = (x – Sy)( – Sy)/(Sut/3 – Sy) + Sy
Smin = (x – Sy)( – Sy)/(Sut/3 – Sy) + Sy
para min > 0
PROBLEMAS PROPUESTOS
1.13. Se pide hallar la carga que pueden levantar (resistencia) dos cables metálicos, el
primero de Aluminio con un diámetro de 2 mm y el segundo de Acero con un diámetro de 1
mm. Tomar S y al = 2884.8 Kg/cm² y S y ac = 4362.8 Kg/cm²
1.14. Se pide hallar resistencia de los cables del 1.anterior, para cargas Alternante e
Intermitente.
1.15. Una carga de 100 Kg se aplica a una pieza de Acero con un diámetro de 1 cm y una
longitud de 100 cm. Se pide calcular las deformadas longitudinal y transversal.
1.16. En el anterior 1.se pide calcular la variación del volumen debido a la deformación.
1.17. Que carga aplicada a una pieza cilíndrica de Acero con un diámetro de 1 cm y una
longitud de 100 cm produce una deformación de 0,1 mm.
1.18. Cuál es la deformada máxima que puede tener un Aluminio antes de alcanzar la
fluencia. Tomar Sy = 2884.8 Kg/cm² y E = 0.7 x 10 6 Kg/cm²
1.19. Construir el diagrama de Goodman Modificado para un material con
Sy = 3000 Kg/cm² Sut = 5000 Kg/cm² y Se = Sut/2 = 2500 Kg/cm²
1.20. En el anterior 1.hallar las ecuaciones de las tensiones máximas, tensiones medios y
tensiones mínimas.
1.21. Hallar las tensiones admisibles para carga estática, carga intermitente y carga
alternante del material de los problemas 4 y 5
1.22. Para las cargas dadas determinar en cada caso si hay o no falla con el material de los
problemas 4, 5 y 6
 max = 3000 Kg/cm² y  min = – 3000 Kg/cm².
 max = 3000 Kg/cm² y  min = – 500 Kg/cm².
 max = 4000 Kg/cm² y  min = 0 Kg/cm².
 max = 4000 Kg/cm² y  min = 1500 Kg/cm².
1.23. Hallar las ecuaciones genéricas de las tensiones máximas, tensiones medios y
tensiones mínimas.
PROPIEDADES MECANICAS
Material
Aluminun allys 2014-T4
Aluminun allys 2014-T6
Aluminun allys 2024-T4
Aluminun allys 6061-T6
Aluminun allys 7075-T6
Brass (Red, cold rolled)
Brass (Red, annealed)
Bronze (cold rolled)
Bronze (annealed)
Cast iron (tension)
Cast iron (compression)
Concrete (compression)
Copper (cold-drawn)
Plate glass
Magnesium alloy
Monel (wrough, hot rolled)
Nickel alloy
Nylon
Polyethylene
Rubber (average)
Steel .2% C hardened
Steel .2% C cold-rolled
Steel .2% C hot-rolled
Steel .4% C hot-rolled
Steel .8% C hot-rolled
Steel Stainless (cold-rolled)
Steel Stainless (heat-treated)
Steel, structural
Steel ASTM-A36
Steel ASTM-A572
Steel ASTM-A514
Douglas Fir
Southern Pine
Red Oak
Sy
Sut
E
Ksi
41
60
48
40
70
60
15
75
20
29.5
2
40
22
50
60
0.6
62
60
53
53
76
165
132
MPa
283
410
331
276
483
414
104
772
138
205
13.8
280
150
345
414
4
428
414
366
366
524
1140
911
Ksi
62
70
68
45
80
75
40
100
50
40
125
5
45
10
40
90
80
9
2.5
2
90
85
62
84
122
190
150
MPa
428
480
470
310
552
518
276
515
345
274.5
870
35
310
70
280
621
552
60
17.5
13.5
620
587
428
580
842
1310
1040
36
50
100
6
6.5
4.6
250
340
700
41
45
32
60
70
120
7.4
8.4
6.9
400
500
830
51
58
48
Ksi
10,6
10,6
10,6
10,4
10
15
15
15
15
25
25
4,5
17
10
24
26
30
400
150
.4
30
30
30
30
30
29
29
29
29
29
1,3
1,9
1,8
G
GPa
73
73
73
72
69
104
104
104
104
173
173
31
117
69
166
179
207
2.76
1
.00276
207
207
207
207
207
200
200
200
200
200
9
13.1
12.4
Ksi
4
3,8
3,9
3,9
3,75
5,5
5,5
6,5
6,5
12,5
12,5
6,3
4
20
9,5
11,4
.0007
11,6
11,6
11,6
11,6
11,6
12,5
12,5
11
11
11
-
GPa
27.6
26.2
27
27
26
38
38
44.9
44.9
86.3
86.3
43.5
27.6
138
65.6
78.7
41.5
80
80
80
80
80
86.3
86.3
75.9
75.9
75.9
-

0.33
0.33
0.33
0.33
0.33
0.34
0.34
0.34
0.34
0.28
0.28
0.15
.35
0.2
0.35
.32
0.31
0.4
0.4
0.48
.32
.32
.32
.32
.32
.27
.27
.32
.32
.32
.29
.3
.3
2 Tracción y Compresión
2.1 Introducción
Un elemento está sometido a tracción o compresión cuando al realizar un corte por cualquier
sección recta no aparecen momentos internos, tampoco fuerzas de corte y solo se verifica
una fuerza normal N en el centro de gravedad de la sección, es decir, en todas las
secciones rectas del elemento se anulan el tensión cortante y los momentos torsor y flector.
Dependiendo si la carga tiende a estirar o a comprimir la pieza, la carga será de tracción o
compresión.
Fig. 2.1 Tracción
Ejemplos de elementos sometidos a tracción compresión son: Los cables metálicos, los
arriostres, los elementos de las vigas armadas y elementos de las estructuras metálicas.
Para la validez de las ecuaciones y resultados de este capítulo se asume la veracidad de las
siguientes condiciones:
1.- Se cumple la hipótesis de Bernoulli (Conservación de las secciones planas)
2.- Los elementos tienen secciones transversales uniformes
3.- Los materiales son homogéneos
4.- Las cargas están aplicadas en los centros de gravedad de la sección
5.- Los miembros sometidos a compresión no son tan esbeltos y no hay pandeo.
2.2 Diagramas de Fuerzas Normales:
Se denominan diagramas de fuerzas normales a los diagramas que dan las fuerzas
normales N en cada sección de una barra prismática.
Fig. 2.4 Diagrama de Fuerzas Normales
2.3 Tracción Compresión Monoaxial
a) Tensiones
Considérese una barra prismática sometida a Tracción-Compresión.
Fig. 2.1 Tensiones en Tracción Compresión
Realizando un corte en la barra por la sección recta transversal A, se observa que:
n = P/A
(2.1
n = 0
(2.2
La hipótesis de Bernoulli se comprueba experimentalmente observando que en una barra
sin carga en la que se trazaron líneas rectas paralelas y perpendiculares a su eje
longitudinal, con carga las líneas paralelas al eje longitudinal se alargan por igual (La
deformación longitudinal es constante),
Fig. 2.1 Hipótesis de Bernoulli
Entonces si εX = cte, de la ley de Hooke se concluye que como el área es también
constante, las tensiones resultan constantes. Para una pieza de sección variable las
tensiones varían inversamente proporcionalmente a la magnitud del área
Si en lugar de cortar la barra por la sección recta transversal A, se la corta por una sección
inclinada en un ángulo α
Fig. 2.3 Tensiones en una sección inclinada
Por equilibrio, la fuerza externa P genera una fuerza interna de igual magnitud, sin embargo
esta ya no es perpendicular a la sección y se la puede descomponer en una componente N
perpendicular a la sección que producirá tensiones normales y en otra componente Q
tangencial a la sección que producirá tensiones cortantes. Se tiene:
N = P Cos α
(2.3
Q = P Sin α
(2.4
α = N/Aα
(2.5
α = Q/Aα
(2.6
AN = Aα Cos α
(2.7
De 2.2, 2.3 y 2.6
α = N/Aα = P Cos α /(AN /Cos α) = P Cos2 α / AN
(2.8
α = (P/2AN) (1 + Cos 2 α)
(2.9
De 2.4, 2.5 y 2.6
α = Q/Aα = P Sin α/(AN /Cos α) = P Sin α Cos α / AN
(2.10
α = (P/2AN) Sin 2 α
(2.11
Reemplazando α = 0 en 2.7 y 2.8, se verifican los resultados obtenidos en 2.1
La ecuación de una circunferencia es :
(x – xo)2 + (y – yo)2 = R2
(2.12
Y se verifica que
(α - P/2AN)2 + α2 = (P/2 AN)2
(2.13

 max
P/2AN
 max

Fig. 2.4 Tensiones en una sección normal
Entonces, la relación entre las tensiones α y α puede se representa por una circunferencia
con un radio de P/2AN y con centro desplazado horizontalmente con el mismo valor del
radio.
b) Tensiones Principales
Se llaman tensiones principales a las tensiones máximas. De 2.7, 2.8 y del gráfico
Para α = 0
max = N = P/AN
 min = 0
(2.14
Para α = 45
45 = P/2AN
 max = P/2AN
(2.15
Para cargas de tracción y compresión en una dimensión las tensiones normales máximos
ocurren en una sección transversal α = 0 y las tensiones cortantes máximos en una sección
a α = 45º. Para prevenir la falla, ambos tensiones máximas no deben exceder las fluencias.
max = P/AN < Sy
(2.16
max = P/2AN < S´y
(2.17
c) Deformaciones
Una pieza recta de sección constante y longitud l cargada en sus extremos por una fuerza
de tracción (compresión) sufre una deformación L
Fig. 2.5 Deformación en una pieza de sección constante
En la zona elástica, la deformada es proporcional a la carga y es válida la ecuación de
Hooke
x = P/AN = E x
(2.18
y = z = 0
(2.19
x = /L
(2.20
y = z = - ν x = - ν x /E
(2.21
Entonces
x = PL/EA
(2.22
Resultado válido para piezas con sección constante. Para piezas con sección variable se
aplica la anterior ecuación a un elemento diferencial “dx” donde el área se puede considerar
constante.
dx
P
P
l
lf
Fig. 2.6 Deformación en una pieza de sección variable
d = Pdx/EA
l
 
0
(2.23
Pdx
EA
(2.24
Para una sección transversal constante se obtienen los mismos resultados de 2.17
d) Cargas, Tensiones y Deformadas debido al Peso Propio
En objetos de gran altura como por ejemplo edificios, torres y otros, el peso propio es una
carga que tiene mucha importancia y debe ser tomada en cuenta. El peso es una carga
variable ya que a analizando una sección horizontal a una altura “y”, esta soporta el peso de
la porción del objeto que se encuentra encima de ella. Para entender mejor esto se presenta
la analogía de una torre humana de 3 personas cada una con un peso de 75 Kg. En ésta
torre la persona de arriba no soporta sobre sus hombros ninguna carga, la del medio soporta
75 Kg. y la de abajo soporta 150 Kg. sobre sus hombros.
dy
A
W(y )
Peso
sobre "y "
h
y
Fig. 2.7 Peso Propio
Para un elemento diferencial “dy” el área de la sección se considera constante y su peso es
dW =  A(y) dy
(2.25
El peso de la porción de la pieza que se encuentra sobre una sección a una altura “y” es
h
W ( y )   A( y )dy
y
(2.26
Un error común es tomar el límite inferior como cero, ya que en este caso el peso calculado
es el de toda la pieza. Entonces se enfatiza en que el límite inferior de la integral es “y”.
La tensión en una sección a una altura “y” es:
h
W ( y)
 ( y) 

A( y )
 A( y)dy
y
A( y )
(2.27
La deformación longitudinal debido al peso propio se halla con la ecuación 2.19
reemplazando en ella el peso como carga
h

 A( y )dy dy
h
h 

Pdy
y

 
 
EA
EA
0
0
(2.28
e) Deformaciones debido a la temperatura
Además de las deformadas debido a las cargas externas se presentan deformadas
originados por cambios de temperatura, conocidas como dilataciones y contracciones. Los
cambios de temperatura originan una deformación lineal uniforme en todas las direcciones,
que se calcula por :
Entonces
lf = l +l  T
(2.29
t = l  T
(2.30
t =  T
(2.31
 es el coeficiente de dilatación que es un valor específico de cada material.
Material
Aluminio
Fundición
Cobre
Acero
Hormigón
23.2
10.4
16.7
11.7
10.8
Las deformada total es por consiguiente la suma de las deformadas debido a cargas
externas y la deformada debido a los cambios de temperatura.
tot = mec + t = /E +  T
(2.32
Si la deformación por cambios de temperatura se restringe, provocan tensiones. Para
encontrar estas tensiones, se usa la anterior ecuación escrita en otra forma que se conoce
como la ley de Hooke extendida o la ley de Duhamel – Neumann
 = E (tot -  T)
(2.33
Cuando la expansión térmica de un sistema se restringe por ejemplo anclando una pieza
entre dos paredes rígidas, aun pequeños cambios de temperatura producen grandes
tensiones térmicos. Esto se debe al módulo de Young que para la mayoría de los materiales
usados en Ingeniería es grande
2.4 Tracción Compresión Biaxial
a) Tensiones
Considérese un elemento diferencial sometido simultáneamente a cargas de tracción
compresión en dos direcciones
Fig. 2.8 Tensiones en Tracción Compresión Biaxial
En la sección inclinada aparecen simultáneamente tensiones normales  y cortantes .
Por trigonometría
L Cos  = dy
(2.34
L Sin  = dx
(2.35
 L dz - y dx dz Sin  - x dy dz Cos  = 0
(2.36
 - y Sin2  - x Cos2  = 0
(2.37
 = y (1-Cos 2)/2+ x (1+ Cos 2)/2
(2.38
 = (y+ x )/2+(x - y )(Cos 2)/2
(2.39
 L dz + y dx dz Cos  -x dy dz Sin  = 0
(2.40
 + y Sin  Cos  - x Sin  Sin  = 0
(2.41
 = (x -y )(Sin2)/2
(2.42
De la estática
 F1 = 0
 F2 = 0
Las ecuaciones 2.26 y 2.29 dan las tensiones normales y cortantes para una sección
inclinada.
Ya que
(Sin 2 )2+( Cos 2 )2 = 1
(2.43
Entonces
[-(x + y )/2]2 + 2 = [(x - y )/2]2
(2.44
Similar a una dimensión, las ecuaciones representan una circunferencia con desplazamiento
en  de (x +y )/2, sin desplazamiento en  y radio igual al (x - y )/2. Esta ecuación no
necesariamente pasa por el origen

(x y)/2
 max
(x-y)/2
 max

Fig. 2.9 Circulo de Mohr en Tracción Compresión Biaxial
b) Tensiones Principales
Las tensiones máximas o principales son:
Para  = 0
max = x
 min = 0
(2.45
Para  = 90
max = y
 min = 0
(2.46
Para  = 45
min = 0
 max = (x -y )/2
(2.47
Una pieza sometida a tracción compresión en dos dimensiones tiene tensiones normales
máximas en los ejes “x” y “y”, y tensiones cortantes máximos en secciones inclinadas a  =
45º.
Para que la pieza no falle, las tensiones máximas no deben exceder los límites de fluencia
max < S y
(2.48
 max < S´y
(2.49
c) Deformaciones
En la figura se muestra un elemento sometido a tracción compresión en dos dimensiones o
biaxial
Fig. 2.10 Deformaciones en Tracción Compresión Biaxial
Debido a que las ecuaciones son lineales, se aplica el principio de superposición, donde se
hallan primero las deformaciones originadas sólo por las cargas horizontales y luego las
deformaciones originadas sólo por las cargas verticales. Las deformadas totales se hallan
por la superposición o combinación de ambos resultados parciales.
Considerando inicialmente sólo las tensiones horizontales
x = x /E
(2.50
y = - q = -  x /E
(2.51
Considerando ahora sólo las tensiones verticales
y = y /E
(2.52
x = - q = -  y /E
(2.53
Superponiendo
xt = x /E -  y /E = x- y
(2.54
yt = y /E -  x /E = y- x
(2.55
2.5 Tensiones en Recipientes de Pequeño Espesor
a) Tensiones en Recipientes Cilíndricos de Pequeño Espesor
Considerando recipiente cilíndrico de radio interior r y espesor de pared t, que contiene un
fluido a presión. Se van a determinar las tensiones ejercidos sobre un pequeño elemento de
pared con lados respectivamente paralelos y perpendiculares al eje del cilindro. Debido a la
simetría axial del recipiente y de su contenido, no se ejercen tensiones cortantes sobre el
elemento.
Figura 2.11 Recipiente cilíndrico
Las tensiones ζ1 y ζ2 mostrados en la figura 2.11 son por tanto tensiones principales. El
tensión ζ1 se conoce como tensión de costilla y se presenta en los aros de los barriles de
madera. El tensión ζ2 es el tensión longitudinal. Para determinar las tensiones de costilla se
retira una porción del recipiente y su contenido limitado por el plano “xy” y por dos planos
paralelos al plano yz con una distancia Δx de separación entre ellos. Se aclara que p es la
presión manométrica del fluido.
Figura 2.12 Trozo del cilindro
Con la ecuación de equilibrio de fuerzas en “z” se halla el tensión de costilla:
p (2r) Δx = 2 ζ1 Δx t
(2.56
ζ1 = p r / t
(2.57
Para hallar el tensión longitudinal ζ2 como se muestra en la figura 2.13 se hace un corte
perpendicular al eje x y se considera, el cuerpo libre, consta de la parte del recipiente y de
su contenido a la izquierda de la sección
Figura 2.13 Corte del cilindro
De la sumatoria de fuerzas en z, finalmente se concluiría que:
p (π r2) = ζ2 2 π r
(2.58
ζ2 = p r / (2 t)
(2.59
El tensión en la costilla es el doble del tensión longitudinal
b) Tensiones en Recipientes Esféricos de Pequeño Espesor
Debido a la presión interior p, un elemento diferencial y por la simetría de la esfera estará
sometido a las tensiones ζ2 uniformes
Fig. 2.14 Tensiones en un Recipiente de Pared Delgada Esférico
La tensión ζ2 se halla de una manera similar a la tensión longitudinal en cilindros
De la sumatoria de fuerzas en x, finalmente se concluiría que:
p (π r2) = ζ2 2 π r
(2.60
ζ2 = p r / (2 t)
(2.61
2.6 Problemas Estáticamente Indeterminados (Hiperestáticos)
Cuando en una barra o en una estructura el número de ecuaciones de equilibrio es inferior al
número de incógnitas, se dice que es un caso Hiperestático. Estos casos suelen darse
cuando la barra o la estructura tiene apoyos (ligaduras) de más. Para resolver pues un caso
hiperestático no serán suficientes las Ecuaciones de equilibrio y se buscarán para
complementarlas Ecuaciones de Deformación,
PROBLEMAS RESUELTOS
2.1. Una pieza con una sección de 1 cm² está sometida a una fuerza de tracción en una
dimensión de 100 Kg. Hallar las tensiones en secciones con ángulos de 0º hasta 360º con
un intervalo de 10º.
Solución:
=(P/2An)(1+Cos 2)
100.0
97.0
88.3
75.0
58.7
41.3
25.0
11.7
3.0
0.0
3.0
11.7
25.0
41.3
58.7
75.0
88.3
97.0
100.0
97.0
88.3
75.0
58.7
41.3
25.0
11.7
3.0
0.0
3.0
11.7
25.0
41.3
58.7
75.0
88.3
97.0
100.0
=(P/2An)(Sin 2)
0.0
17.1
32.1
43.3
49.2
49.2
43.3
32.1
17.1
0.0
-17.1
-32.1
-43.3
-49.2
-49.2
-43.3
-32.1
-17.1
0.0
17.1
32.1
43.3
49.2
49.2
43.3
32.1
17.1
0.0
-17.1
-32.1
-43.3
-49.2
-49.2
-43.3
-32.1
-17.1
0.0
60.0
40.0
20.0
Esf Corte
(Gr) (Rad)
0
0.0
10
0.2
20
0.3
30
0.5
40
0.7
50
0.9
60
1.0
70
1.2
80
1.4
90
1.6
100
1.7
110
1.9
120
2.1
130
2.3
140
2.4
150
2.6
160
2.8
170
3.0
180
3.1
190
3.3
200
3.5
210
3.7
220
3.8
230
4.0
240
4.2
250
4.4
260
4.5
270
4.7
280
4.9
290
5.1
300
5.2
310
5.4
320
5.6
330
5.8
340
5.9
350
6.1
360
6.3
0.0
-50.0
0.0
50.0
100.0
-20.0
-40.0
-60.0
Esf Normal
2.2. Hallar las tensiones máximas del 2.1.
Solución:
max = P/AN = 100/1 = 100 Kg/cm²
 max = P/2AN = 100/2 = 50 Kg/cm²
2.3. Una pieza está sometida a cargas de tracción compresión en dos dimensiones con x =
90 Kg/cm² y y = -120 Kg/cm². Hallar las tensiones para ángulos desde 0º hasta 360º con un
intervalo de 10º. Graficar los resultados.
Solución:
 = (x+y)/2 +
( x- y)(Cos 2)/2
90.0
83.7
65.4
37.5
3.2
-33.2
-67.5
-95.4
-113.7
-120.0
-113.7
-95.4
-67.5
-33.2
3.2
37.5
65.4
83.7
90.0
83.7
65.4
37.5
3.2
-33.2
-67.5
-95.4
-113.7
-120.0
-113.7
-95.4
-67.5
-33.2
3.2
37.5
65.4
83.7
90.0
 =(x-y)(Sin 2)/2
0.0
35.9
67.5
90.9
103.4
103.4
90.9
67.5
35.9
0.0
-35.9
-67.5
-90.9
-103.4
-103.4
-90.9
-67.5
-35.9
0.0
35.9
67.5
90.9
103.4
103.4
90.9
67.5
35.9
0.0
-35.9
-67.5
-90.9
-103.4
-103.4
-90.9
-67.5
-35.9
0.0
150.0
100.0
50.0
Esf Corte
(Gr) (Rad)
0
0.0
10
0.2
20
0.3
30
0.5
40
0.7
50
0.9
60
1.0
70
1.2
80
1.4
90
1.6
100
1.7
110
1.9
120
2.1
130
2.3
140
2.4
150
2.6
160
2.8
170
3.0
180
3.1
190
3.3
200
3.5
210
3.7
220
3.8
230
4.0
240
4.2
250
4.4
260
4.5
270
4.7
280
4.9
290
5.1
300
5.2
310
5.4
320
5.6
330
5.8
340
5.9
350
6.1
360
6.3
-150.0
0.0
-50.0
50.0
-50.0
-100.0
-150.0
Esf Norm al
2.4. Hallar las tensiones máximas del problema 2.3.
Solución:
=0
max = x = 90 Kg/cm²
 = 90
max = y = -120 Kg/cm²
 = 45
 max = (x - y )/2 = 105 Kg/cm²
2.5. Una pieza cilíndrica de Acero tiene  = 3 cm y largo L = 100 cm está sometida a una
carga de 1000 Kg. Tomando Sy = 1800 Kg/cm² y Sy´ = 960 Kg/cm²sse pide hallar:
Las tensiones máximas
Las tensiones a 30o
Las deformadas total, unitaria longitudinal y transversal
Los coeficientes de seguridad
Solución:
a)
A = 2/4 = 7,07 Kg/cm²
max = N = P/AN = = 141,47 Kg/cm²
para  = 0o
 max = P/2AN = 70,73 Kg/cm²
para  = 45o
 = (P/2AN )(1 + Cos 2)
b)
30 = 106,10 Kg/cm²
 = (P/2AN) Sin 2
30 = 61,25 Kg/cm²
 = Pl/EA = 6,73 x 10-3 cm
c)
 = /l = 67 x 10-6 ( 67 x 10 –4 %)
q = -  = -20,20 x 10 –6 (-20,20 x 10 –4 %)
q = q d = -60,6 x 10 –6 cm
 = Sy/max = 1800/141,47 = 12,72
d)
 = Sy´/max = 960/70,73 = 13,57
2.6. Una pieza de a = 2 cm de ancho por b = 3 cm de alto y c = 1 cm de profundidad está
sometida a una fuerza horizontal de 100 Kg. y una vertical de 200 Kg. Se pide hallar las
dimensiones finales. Tomar  = 0.3
200[kg]
c
100[kg]
b
a
Solución:
x = Fx/(b c) = 33,33 Kg/cm²
y = Fy/(a c) = 100,00 Kg/cm²
xt = x /E -  y /E = 1,58 x 10-6
yt = y /E -  x /E = 4,28 x 10-5
af = a + a xt = 2,000003 cm
bf = b + b yt = 3,00012 cm
2.7. En la pirámide truncada de área transversal cuadrada de la figura. Se pide calcular:
a) El peso parcial sobre cualquier altura “y”
b) El tensión normal máximo
c) La deformada total
60[cm]
SEC. A-A
dy
A
1000[cm]
A
y
90[cm]
Solución:
b(y) = (- 30/1000) y + 90
a) El peso sobre y es
h
h
y
y
2
W ( y )   A( y )dy     30 / 1000 y  90 dy


1000 
3 

W ( y )   603   30 / 1000 y  90  
 (3)30 
b) El tensión normal es máximo en la base ( y = 0)
 max 
 1000 (603  903 )
903
max = 703.83 
c) La deformada
l
Wdy
0 EA
 
l

0


3
1000  3  30
 
60   
y  90   dy
90 
 1000
 

dy
2
 30

E 
y  90 
 1000



  1000 
1
 1000  1
2
2 1000 
 603 
    60  90

E 90 
2(30) 
 30  60 90 
2.8. En la pieza cónica truncada de la figura, se pide hallar la deformación debida a la acción
de la fuerza P y del peso propio.
P
D/2
SEC. B-B
dy
B
h
B
y
D
Solución:
h
 
P  W ( y)dy
EA
0
D y

  1
2 h

d
d 2
A

4
 D y

  1
4  2  h 
2
2
y
y  D y


W ( y )   A( y )dy       1 dy
0
0 4  2  h 
W ( y) 
h

h
Pdy
 
0
D 2y 2
( y  3 yh  3h 2 )
48h 2
E
 D  y

  1
4  2  h

2

0
D 2 y 2
( y  3 yh  3h 2 )dy
48h 2
2
  D  y 
E    1
4 2 h

h(24P  D 2 h)
3ED 2
2.9. En el sistema de la figura se piden las tensiones en los cables.
l
l
(b)
l/2
P
l
(c)
(a)
a
l
(b)
b
(c)
c
Solución:
 Fy = 0
Ta+ Tb + Tc = P
(i
 Ma = 0
P l/2 – Tb l – Tc 2l = P/2 - Tb –Tc 2 = 0
(ii
El sistema es hiperestático ya que son tres incógnitas (Ta , Tb ,Tc) y sólo 2 ecuaciones. La
tercera ecuación se halla analizando las deformaciones
(a-c)/2l = (b-c)/l
 Tl
Ta l Tcl
T 

 2 b  c 
EAa EAc
EA
EA
c 
 b
Ta –Tc = 2 (Tb – Tc)
Ta – 2 Tb + Tc = 0
De i, ii y iii
(iii
Ta = P - Tb - Tc = 2 Tb - Tc
Tb = P/3
Tc = P/12
Ta = 7P/12
2.10. En el sistema de la figura se piden las tensiones en los cables
  
 
b
a


c
O
P
O'
Solución:
lb = la Sin  = 0.5 la
lb = lc Sin  = 0.866 lc
 Fy = 0
Ta Sin + Tb+Tc Sin  = P
Ta 0.5 + Tb + Tc 0,866 = P
 Fx = 0
(I
Ta Cos  = Tc Cos 
Ta 0,866 = Tc /2
 Ma = 0
(ii
No existe ya que las fuerzas son concurrentes
El sistema es hiperestático ya que son tres incógnitas (Ta , Tb ,Tc) y sólo 2 ecuaciones. De la
ecuación de deformadas




O
O


O'

O'

a = OO´Sin (-) = Ta la / EA
(iii
b = OO´Sin (90-) = Tblb/EA
(iv
c = OO´Sin (+) = Tclc/EA
(v
De iii y iv
Ta la/ Sin (-) = Tb lb/ Sin (90-)
(vi
De iv y v
Tb lb/ Sin (90-) = Tc lc/ Sin (+)
(vii
Del gráfico
la 0.5 = lb
lc 0,866 = lb
De vi
Tala/(Sin Cos - Sin  Cos ) = Tblb/ Cos 
Ta (lb/0.5)/(Cos 0.5- Sin  0,866) = Tblb/ Cos 
Ta = 0.5Tb( 0.5- 0.866 Tan )
0.5 - (Ta / 0.5Tb) = 0.866 Tan 
Tan  = [( 0.52Tb - Ta) / (0.5Tb)]/0.866
De vii
(viii
Tb lb/ Cos = Tc lc/ SinCos+Sin Cos)
Tb lb/ Cos = Tc (lb/0.866)/ (0.866Cos+Sin 0.5)
0.5 Tan  = (Tc/0.866 Tb) – 0.866
Tan  = [(Tc – 0.8662Tb) / (0.866 Tb)]/0.5
De viii y ix
(ix
[( 0.52Tb - Ta) / (0.5Tb)] 0.5 = [(Tc – 0.8662Tb) / (0.866 Tb)] 0.866
( 0.52Tb - Ta) = (Tc – 0.8662Tb)
( 0.52Tb - Ta) = (Tc – 0.8662Tb)
Tb = Ta + Tc
(x
Esta última es la ecuación de deformaciones buscada.
De x y i
Ta 0.5 + (Ta +Tc )+ Tc 0,866 = P
1.5 Ta + 1.866 Tc = P
1.5 Ta + 1.866 (2Ta 0.866) = P
Ta = 0.211 P 0.29 P
Tc = 0.366 P 0.42 P
Tb = 0.577 P 0.5 P
2.11. En el sistema de la figura se piden hallar las tensiones en los cables a y b. La barra
horizontal se supone rígida y articulada en la pared
l/2
(b)
(a)

Tb
Ta



Rx
l/2
l/2
P Ry
l/2
l/2
P
Solución:
Tan  = (l/2)/(l/2) = 1
 = 45º
Tan  = (l/2)/l = 0.5
 = 26,56
 Fx = 0
Rx- TaCos  -Tb Cos  = 0
(i
 Fy = 0
Ry + Ta Sin  +Tb Sin -P = 0
(ii
 Mo = 0
- Ta Sin  l/2 -Tb Sin  l + P l = 0
Ta 0.3535 + Tb 0.4472 = P
(iii
Son tres ecuaciones con cuatro incógnitas Rx , Ry , Ta y Tb
l/2
A

A'
a
Del grafico

B'
b
la Cos  = l/2
lb Cos  = l
a = AA´Sin 
b = BB´Sin 
AA´ = BB´/2
Entonces
AA´ = a / Sin  = BB´/2 = b /2 Sin 
Tala/(EA Sin ) = Tblb/ (2EA Sin )
Ta/(2 Cos  Sin ) = Tb/ (2 Cos  Sin )
Ta/ Sin (2 ) = Tb/ Sin (2 )
Ta/ 1 = Tb/ 0.8
(iv
Que es la cuarta ecuación buscada, De donde
Ta = 1.405 P
Tb = 1.124 P
2.12. Hallar las tensiones en los cables a y b

Ta
(a)

(b)

Rx

Tb


Ry
l/2
l/2
P
P
Solución:
 Fx = 0
Rx + Ta Sin 30 = 0
(i
 Fy = 0
Ry + Ta Cos 30 + Tb -P = 0
(ii
 Mo = 0
-Ta l/2 -Tb Sin 60 l + P Sin 60 l/2 = 0
-Ta 0,5 -Tb 0,866 + P 0,433 = 0
(iii
El 2.es hiperestático con tres ecuaciones y cuatro incógnitas Rx , Ry , Ta y Tb

(a)
A

B
A'

b
B'
lb Cos 30 = la
a = AA´Sin 90
b = BB´Sin 60
AA´ = BB´/2
Entonces
AA´ = a / Sin 90 = BB´/2 = b /(2 Sin 60)
Tala/(EA) = Tblb/ (2EA Sin 60)
Ta lb Cos 30 = Tb lb / (2 Sin 60)
Ta 1,5 = Tb
Resolviendo
(iv
Ta = 0,2406 P
Tb = 0,361 P
2.13. Se pide hallar el diámetro de la barra AC. Tomar Sy = 1800 Kg/cm²
A
TAC
20
30
B

60
2TBC Cos 

B
C
P
Vista Lateral
P
Solución:
 Fy = 0
Tan  = 20/60
 = 18.43
Tan  = 15/60
 = 14.03
TAC Sin  = P
TAC = 3163.09 Kg
 Fx = 0
Tracción
TAC Cos  + 2TBC Cos  = 0
TBC = - 1546.56 Kg
Compresión - Pandeo
Analizando solo la barra AC
AC = TAC/( dAC2/4) < Sy
dAC = 1.49 cm
2.14. En el sistema de la figura se piden las reacciones en A y B
30[cm]
B
Rb
B
T
2
40[cm]
P
y
P
1
x
A
A
60[cm]
Ra
Solución:
 Fy = 0
Rb = Ra + P
(i
El sistema es hiperestático con una ecuación y dos incógnitas Ra y Rb. Las ecuaciones de
los círculos respecto del sistema x - y son
x2+y2 = 302
x2 + (y-40)2 = 152
los diámetros 1 = 2 (302-y2)1/2
2 = 2 [152-(y-40)2]1/2
éstos se igualan a un altura de
2(302-y2)1/2 = 2[152-(y-40)2]1/2
302-y2 = 152- y2+ 80y –1600
y = 28,43
ec deformaciones
t = 1+2 = 0
1 
28.43

0

Ra dy 4
E 2(30  y )


2 1/ 2 2
2
Ra
E 60
28.43

0
 1
1 
 (30  y)  (30  y) dy


Ra
(3.6167)
E 60
1 
40

2 
28, 43
2 

( Ra  P)dy 4


( Ra  P)
1
1

dy


E 30 28, 43 15  ( y  40) 15  ( y  40) 
40
E 2(152  ( y  40) 2 )1/ 2

2

( R a  P)
(2.0472)
E 30
1   2 
Ra
( R  P)
(3.6167)  a
(2.0472)  0
E 60
E 30
Ra = - 0.259 P
Rb = 0.741 P
2.15. Se pide hallar las reacciones en las paredes
2
1
60
30
A
45
RA
P
30
B
10
RA
A
x
P
3
RB
B

Solución:
 Fx = 0
Rb + P = Ra
Los diámetros y deformadas
d1 = -30 x/45 + 60
d2 = 30
d3 = 3 x - 195
(i
45
Ra dy 4
4 Ra
45
dy 
2
E (30 x / 45  60) 30
E  30 x / 45  60
1  
0
1 
4(45) Ra 1 1
(  )  Ra 9,09e 7
E 30 30 60
2 
Ra 30(4)
 Ra 2,02e 8
2
E 30
( Ra  P)dy 4
4( Ra  P)
dy 
2
E (3x  195)(3)
75 E 3 x  195
85
3  
3 
4( Ra  P) 1
1
(  )  ( Ra  P)3,36e 9
E (3) 60 30
La ec de deformadas
t = 1 +2+3 = 
Ra9,09 E-7+Ra2,03 E-8+(Ra-P)3,36 E-9 = 0,001
Ra = 0.75 P
Rb = 0.25 P
2.16. Hallar las tensiones en las barras del sistema de la figura
100 cm
a
b
Tb
a
Ta
30
Ta
P
P
Solución
Fx = 0
Ta Cos 30 = Ta Cos 30
Fy = 0
2 Ta Sin 30 + Tb = P
M = 0
Las fuerzas son concurrentes
No aporta
(i
Se tiene una ecuación y dos incógnitas. De las deformaciones
b
a
a
30
O
b
a
b = OO´
O'
a = OO´Sin 30
b = a /Sin 30
Tb lb/EA = Tala/(EA Sin 30)
la Sin 30 = lb
Tb la Sin 30 = Ta la/Sin 30
Tb = Ta / Sin2 30
4 Tb = Ta
De i y ii
(ii
2 (4 Tb) Sin 30 + Tb = P
Ta = 0.2 P
Tb = 0.8 P
2.17. Tres barras se encuentran articuladas en A para soportar juntas, un peso W como se
indica en la figura. El desplazamiento horizontal del punto A esta impedido por una varilla
corta horizontal AO que se supone infinitamente rígida, a) Determinar las expresiones para
calcular las tensiones en cada una de las barras y la fuerza total sobre la barra AO. b)
Utilizando las anteriores relaciones determinar las tensiones sí: A1 = A2 = A3 = 2 cm²  = 30º;
 = 45º; W = 2500 [ Kg].
L2,A2,E 0
L1,A1,E 0
L3,A3,E 0

L

a
W
Solución.
 Mo = 0
(T1 cos  )a  T2 a  (T3 cos  )a  Wa  0
L2,A2,E0
L1,A1,E 0
T1 cos   T2  T3 cos   W  0
L3,A3,E 0


(i






L

W
Además
cos    1 /  2
cos    3 /  2
(ii
l1 Cos  = l2 = l3 Cos 
A
T1  cos 2  · 1
 A2
(iv

·T2

A 
T3  cos 2  · 3 ·T2
 A2 
T1 
T2 
T3 
(v
cos 2 A1W
A2  cos 3 A3  cos 3 A1
(vi
A2W
A2  cos A3  cos 3 A1
(vii
cos 2 A3W
A2  cos 3 A3  cos 3 A1
(viii
3
Además
y
T2
T1

T3

R
x
W
T3 sen  T1 sen  R  0
W (cos 2 senA3  cos 2 senA1 )
R
A2  cos 3 A3  cos 3 A1
(ix
Con los datos se halla que:
T1 = 936.062 Kg
T2 = 1248 Kg
T3 = 624.041 Kg
R = - 26.768 Kg
2.18. Hallar la deformación total de la barra de la figura, considerando el material Acero con
D = 10 cm, l = 50 cm, E = 2.1x106 Kg/cm² y P = 2000 Kg
P
D/2
2P
l/2
l/2
D/3
D
l/2
T 
l/2

0
P1 dx l P2 dx 3l / 2 P3 dx

 
EA1 l / 2 EA2
EA3
l
P1 = -P (compresión) P2 = -P (compresión) P3 = P (tracción)
D1 
D
2
d1 
D
3
A1   ( D1  d 1 ) 
2
2
5D 2
144
D2 
Dx D
2x  l
  D(
)
2l
4
4l
d2 
D
3
A2   ( D2  d 2 ) 
2
D3 
2
2
D 2  2 x  l 
1
  

4  4l 
9 
Dx D
2x  l
  D(
)
2l
4
4l
d3  0
A3   ( D3  d 3 ) 
2
T 
l/2

0
2
2
D 2  2 x  l  

4  4l
 
 
P1 dx l P2 dx 3l / 2 P3 dx
72 Pl
12 Pl
25
8Pl
 
 


ln

2
2
EA1 l / 2 EA2
EA3
13 3ED 2
5ED
ED
l
Reemplazando T = - 0,00296 cm
2.19. En el sistema mostrado en la figura, se pide determinar las reacciones que soportan
las paredes rígidas por efecto de las cargas que se indican. Considerar una sección
rectangular de espesor constante “b” y los siguientes datos:
L = 30cm; H = 10 cm; h = H/3; E = 2.1x106 Kg/cm² ; P = 5000 Kg; b = 5 cm
Solución:
l
P1 dx 2l P2 dx 5l / 2 P3 dx 3l P4 dx
T  

 

EA1 l EA2
EA3 5l/ 2 EA3
0
2l
 2x 
A1  b1   H
 3l 
A2  bH / 3
bH (l  2 x' )
 H h
A3  A4  b
 x' h 
3l
 l 
Asumiendo que el bloque no llega a chocar en el extremo izquierdo
P1 = 0
P2 = P
P3 = P
P4 = 3P
Reemplazando
l
T  
0
l
2l
0dx
Pdx


bH
 2x 
Eb1   H l E
3
3l 

2l
0dx
Pdx


bH
 2x 
l E
Eb1   H
3
3l 

T  
0
l/2

0
l/2

0
l
Pdx
3Pdx

bH (l  2 x' ) l / 2 bH (l  2 x' )
E
E
3l
3l
l
Pdx
3Pdx

bH (l  2 x' ) l / 2 bH (l  2 x' )
E
E
3l
3l
PL
9
(3  3 ln 2  ln 3)  0.00837cm
EbH
2
T 
ya que ésta deformada es mayor a la tolerancia indicada, hay contacto en la pared izquierda
y se debe tomar en cuenta la reacción R1 sobre la pared izquierda del apoyo. Recalculamos
la deformada con
P1 = -R1
P2 = P - R1
P3 = P - R1
P4 = 3P - R1
Además la deformación iguala a la tolerancia dada ( = 0.001)
l
T  
0
T 
 R1dx
( P  R1 )dx


bH
 2x 
Eb1   H l E
3
 3l 
2l
l/2

0
( P  R1 )dx
(3P  R1 )dx

 0.001
bH (l  2 x' ) l / 2 bH (l  2 x' )
E
E
3l
3l
l
3Pl
3R l
(2  2 ln 2  3 ln 3)  1 (ln 3  1)  0.001
2 EbH
EbH
De donde
R1 = 4657.03 Kg
Además
R2 = P + 2P – R1
R1 P
De donde
R2
2P
R2 = 10342.97 Kg
2.20. Hallar una expresión para determinar la deformación que sufre una barra con sección
variable según una función cuadrática, como se ve en la figura.
y
y
P
D
d
x
D
Dx
dx
f(x2)
x
d
x
l
Solución:
t  
l
0
Pdx
EAx
la variación del diámetro en función de x es cuadrática
Dx  Ax 2  B
para x = 0
Dx = d
para x = l
Dx = D
Resolviendo
Dd 
Dx   2  x 2  d
 l

Ax 
t 
  D  d 
· 
4   l 2
 E··  D  d ·x
l
0
t 
De donde

·x  d 


2
2
P·dx
4   l 2

2

 d 

2
 D  d 
2 P·l 
D

1
arctg
 d (D  d )  
E· ·d ·D 
Dd



2.21. Hallar una expresión para determinar la reacción en cada uno de los apoyos, de los
elementos mostrados en la figura, originados por un aumento de la temperatura T,
considerando como datos: , l, a.
Cu
a
Al
a/2
l
a
l

Solución:
Suponiendo que la deformación por dilatación es mayor a la holgura
Cu
Al
La deformada en la pieza de cobre por tensiones es
 cu  
l
0
Dx 
R·dx
E cu Ax
a x
(  1)
2 l
 cu  
R·dx
l
0
Ecu
 cu 
 a  x

  1
4  2  l

2
8Rl
E cu a 2
En el aluminio la deformación es similar:
 al  
l
0
Dx 
a x
(  1)
2 l
l
R·dx
0
 a  x
 al  
 al 
R·dx
Eal Ax

Eal    1
4 2  l

2
8Rl
Eala 2
La deformación por la variación de temperatura:
 T  lcu T  l alT  l (cu   al )T
Además
 cu   al   T  
Reemplazando, obtenemos:
8Rl
8Rl

 l ( cu   al )T  
2
E cu a
E al a 2
8R * l
2
Ecu *  * a

8R * l
E al *  * a 2
 l * T  cu   al   
De donde:
8Rl
8Rl

 l ( cu   al )T  
2
Ecua
Eala 2
Ecu Eala 2
2
Ecu  Eal
R
l (cu   al )T   
2.22. La pieza mostrada en la figura fue maquinada con las dimensiones mostradas, si la
temperatura aumenta a 120ºC, determinar las reacciones que soportan los apoyos luego de
la dilatación, tomando: l = 20[cm]; D = 5[cm]; d = 2[cm]; cu = 17x10-6[1/ºC]; al = 22.2x105[1/ºC]; Ecu = 1.1x106[ Kg/cm²]; Eal = 7x105[ Kg/cm²
Tº=25 ºC
D
Cu
Al
l
l
d

Solución:
La deformación debido a la dilatación es:
 T  l cu T  l al T  l ( cu   al )T
 T  20(17 x10 6  22.2 x10 5 )(120  25)
 T  0.0745cm
Ya que la deformada es mayor a la holgura, hay contacto en la pared derecha.
 R   T  
dx
Dx
Cu
R
Al
x
x
l
R  
0
2l
P1 dx
P dx
 2
E al Aal l E cu Acu
P1 = R
A1 =  d2/4
P2 = R
A1 =  Dx2/4
El diámetro es lineal
Dx = A x + B
de las condiciones de borde se obtiene que:
Dx 
Dd
x  2d  D
l
Reemplazando:
l
R  
0
2l
Rdx
Rdx

2
2
d
 Dd

l
E al
E cu 
x  2d  D 
4
4 l

Resolviendo:
R 
4 R( DEal  dE cu )
Dd 2E al E cu
Reemplazando
4 R( DEal  dE cu )
Dd 2E al E cu
  T  
Con los datos
R = 2599.39 Kg
2.23. En la siguiente figura determinar las tensiones que ocurren en cada uno de los
alambres flexibles, que soportan a la barra rígida, articulada en uno de sus extremos.
(Considerar los datos mostrado en la figura.
E,A 1,l1
E,A 2,l2



l
l
l
E,A 3,l3
P
Solución:
Las deformaciones


1
a


3
2
b

entonces
a / l = b / (2l)
1 = a Sin 
2 = b Sin 
3 = b Sin 
además
l = l1 Cos 
l = l2 Cos 
l = l3 Cos 
reemplazando:
2
2
sen
1
sen
2  2
 1 sen
sen
3  2
1sen
sen
Las deformadas:
1 
T1l1
EA1
2 
T2 l 2
EA2
3 
T3 l 3
EA3
T2
l
l
T1
cos 
cos sen
2
EA2
EA1 sen
T2 
T3
2sen cos A2T1
sen cos A1
l
l
T1
cos 
cos sen
2
EA3
EA1sen
T3 
2sen cos A3T1
sen cos A1

De la estática
T1senl  Pl  T2 sen 2l  T3sen 2l  0
Donde
T1 
sen cos A1P
K
T2 
sen cos A2 2 P
K
T3 
sen cos A3 2 P
K
K  A1 sen 2 cos   4 A2 sen 2  cos   4 A3 sen 2  cos 
2.24. Determinar la deformación debido al peso propio del bloque mostrado en la figura.
Siendo la sección, circular y variable con la altura, de forma parabólica, según el sistema de
coordenadas, mostrado.
H
x
x
ry
y
H
dy
y
wy
H/3
y
Solución:
T  
H
0
w( y )
dy
EA y
la ec. de la parábola es
x  x o  P( y  y o ) 2
( xo , y o )  (
H
,H)
6
para x = H/2 y = 0
x  rr 
( y  H )2 H

3H
6
El área a cualquier altura “y” es:
( y  H )2 H 
2
A( y )  rr   
 
6
 3H
El peso por debajo de “y” es:
2
w( y )   ry dy
2
Reemplazando y simplificando:
w( y) 

H 2 540
47H
5
 135H 4 y  180 H 3 y 2  140 H 2 y 3  60 Hy 4  12 y 5

La deformada:

 
47 H 5  135H 4 y  180 H 3 y 2  140 H 2 y 3  60 Hy 4  12 y 5
2
H 
H
540
T   
2
0
( y  H )2 H 

E 
 

6
 3H


simplificando:
T 
H 2
90 E
(17  6 ln 3)


dy



PROBLEMAS PROPUESTOS
2.25. Hallar la tensión normal en una barra de sección circular sujeta a una carga de tracción
de 100 Kg si su diámetro es de 1 cm.
2.26. Hallar las tensiones normal y cortante para una sección a 30º en el anterior problema
2.27. Una pieza está sometida a tensiones de tracción compresión en dos dimensiones con
x = - 120 Kg/cm² y y = -150 Kg/cm². Hallar las tensiones para una sección que forma un
ángulo de 30º con la horizontal
2.28. Hallar el círculo de Mohr y las tensiones máximas en el anterior problema.
2.29. Una pieza de acero tiene sección cuadrada de 3 x 4 cm y un largo de 900 cm y está
sometida a una carga de 1500 Kg. Se pide hallar:
Las tensiones máximas
Las tensiones a 30o
Las deformadas total y unitaria longitudinal y transversal
Los coeficientes de seguridad Sy = 1800 Kg/cm² y Sy´ = 960 Kg/cm²
2.30. Una pieza de a = 3 cm de ancho por b = 4 cm de alto y c = 2 cm de profundidad está
sometida a una fuerza horizontal de 150 Kg. y una vertical de -200 Kg. Se pide hallar las
dimensiones finales. Tomar  = 0.3
200[kg]
c
150[kg]
b
a
2.31. En el sistema de la figura la sección transversal es circular y las dimensiones están en
centímetros. Se pide hallar:
a) El peso parcial sobre cualquier altura “y”
b) La tensión normal máxima
c) La deformada total
30
1000
y
500
15
45
2.32. En el sistema de la figura se piden las tensiones en los cables.
l
l
(a)
(b)
(c)
(b)
(a)
l/2
P
2.33. En el sistema de la figura se piden las tensiones en los cables


(a)

(b)
(c)
P
2.34. Hallar las tensiones en los cables
l/4
(a)
l/5
(b)
(c)
l/5
2.35. Hallar las tensiones en los cables
(d)
l/5
(e)
l/5
l/5
P

(a)
(b)

(c)

l/2
l/2
P
2.36. Se pide hallar el diámetro de la barra AC. Tomar Sy = 1800 Kg/cm²
A
A
20
30
B
60

B
C
P
2.37. Hallar la deformación total debido al peso propio. Tomar las unidades en cm
30
40
P
25
60
2.38. Para el sistema de la figura se piden las reacciones en A y B. Tomar las unidades en
cm
B
40
50
P
30
A
50
2.39. Se pide hallar las reacciones en las paredes. Tomar  = 0.01 cm
70
P
40
A
60
50
B
20

2.40. Tres barras se encuentran articuladas en A para soportar juntas, un peso W como se
indica en la figura. El desplazamiento horizontal del punto A esta impedido por una varilla
corta horizontal AO que se supone infinitamente rígida, a) Determinar las expresiones para
calcular las tensiones en cada una de las barras y la fuerza total sobre la barra AO. b)
Utilizando las anteriores relaciones determinar las tensiones sí: A1 = A2 = A3 = 2 cm²  = 30º;
 = 45º; W = 2500 Kg.
l/4
l/4
l/4
l/4
l/3
A
P
2.41. Hallar la deformación total del sistema de la figura. Tomar E = 2.1x106 Kg/cm² y P =
2000 Kg
0.35
P
60
45
45
2.42. Hallar la deformada debido a la fuerza P y el peso propio
P
D
h
dy
A
A
y
D/2
2.43. En el sistema mostrado en la figura determinar las reacciones que soportan las
paredes rígidas por efecto de las cargas y un incremento de la temperatura. Considerar una
sección rectangular de espesor constante “b” y los siguientes datos:
L = 30cm; H = 10 cm; h = H/3; E = 2.1x106 Kg/cm² ; P = 5000 Kg; b = 5 cm T = 90C
l/2
B
P
A
H
2P
h
H
B

l
l
B-B
b
l
2.44. Hallar una expresión para determinar la deformación que sufre una barra con sección
variable según una función cúbica, como se ve en la figura.
y
y
P
D
d
x
Dx
D
dx
f(x2)
x
d
x
l
2.45. Hallar una expresión para determinar la reacción en cada uno de los apoyos, de los
elementos mostrados en la figura, debido a la variación de temperatura T, considerando
como datos: , l, a.
T
a/2
Cu
a
l
Al
l

2.46. Si la temperatura aumenta a 120 º C, determinar las reacciones que soportan los
apoyos luego de la dilatación, tomando: l = 20 cm; D = 5 cm; d = 2 cm; cu = 17x10-6 (1/ºC);
al = 22.2x10-5 (1/ºC); Ecu = 1.1x106[ Kg/cm²]; Eal = 7x105[ Kg/cm²
T
d
Cu
l
a Al
D
l
 cm
2.47. Hallar las tensiones en el sistema de la figura. Cuando las deformaciones además de
la carga P provienen de un incremento de la temperatura T
E,A 1,l1
E,A 2,l2



l
l
l
E,A 3,l3
P
2.48. Determinar la variación que debe tener la sección circular del elemento de la figura, de
modo que las tensiones debido al peso propio sean constantes.
x
y
ry
dy
wy
y
2.49. La barra maciza mostrad en la figura, consta de un tramo troncocónico y otro cilíndrico,
determinar la deformación total del sistema siendo el material el mismo para ambos tramos.
d
D
3P
P
2P
l
l
2.50. Determinar la expresión para calcular la deformación total de la barra, que tiene una
perforación que produce una pared de espesor constante t, como se muestra en la figura, la
barra se encuentra sometida a la acción de las respectivas cargas. La sección de la barra
varía según se ve en dicha figura.
t
P
D
l/2
2P
3P
2P
D/2
l
l
2.51. La barra mostrada en la figura se encuentra sometida a la
mostradas que produce una reacción interna de la barra, debido
muestran, determinar las reacciones que se producen en dichos
además que los materiales tienen diferente módulo de elasticidad, y
es circular y varía en cada tramo.
3P
2P
E2
d
2d
E1
E1
l
l
l
acción de las fuerzas
a los apoyos que se
apoyos, considerando
su sección transversal
2.52. Determinar la ecuación para determinar el Área de las secciones transversales de los
elementos elásticos que se muestran en la figura. Considerar conocidas las longitudes de
cada una de éstas.
1
2
a
P
3
a
2.53. Hallar las tensiones de los elementos mostrados en la figura.
1

2

P
a

2.54. Hallar las tensiones en las barras de la armadura mostrada en la figura cuando se
aplica la fuerza indicada. Considerar E, A igual para todas las barras.
a
1
2
a
a
P
2.55. Una armadura simétrica experimenta las cargas mostradas en la figura. Determinar las
tensiones normales que experimentan cada una de ellas.
1
1
a
3a
3a
2
2
P
2.56. Calcular las tensiones de montaje de los elementos flexibles mostrados en la figura, si
uno de ellos fue fabricado con una falla en su longitud  = 0.5 cm.
a=1[m]

2a

a
2.57. Determinar los desplazamientos, horizontal y vertical, del punto de aplicación de la
fuerza P, además determinar todas las tensiones en las diferentes barras. Considerar, el
módulo de rigidez a la tensión E·A, constante.
l
2l
3
1
l
2
l
P
.
2.58. Determinar el desplazamiento del punto A debido a las cargas aplicadas sobre la
armadura mostrada en la figura.
2l
l
3
1
2
l
A
l
P
3 Corte Puro
3.1 Introducción
Un elemento está sometido a Corte Puro cuando al realizar un corte por cualquier sección
recta no aparecen momentos internos, tampoco fuerzas normales y solo se verifica una
fuerza tangencial Q en el centro de gravedad de la sección, es decir, en todas las secciones
rectas del elemento se anulan la fuerza normal y los momentos torsor y flector.
Fig. 3.1 Corte Puro
Ejemplos de elementos sometidos a Corte Puro son: Vigas de muy pequeña luz donde la
rotura se produce por corte puro y el efecto de flexión es despreciable, el corte de planchas
metálicas mediante cizallado, punzonado o troquelado y las uniones con remaches, bulones,
soldadura, pernos, etc.
Para la validez de las ecuaciones y resultados de este capítulo se asume la veracidad de las
siguientes condiciones:
1.- Se cumple la hipótesis de Bernoulli (Conservación de las secciones planas)
2.- Los elementos tienen secciones transversales uniformes
3.- Los materiales son homogéneos
4.- Las cargas están aplicadas en los centros de gravedad de la sección
5.- Los miembros sometidos a compresión no son tan esbeltos y no hay pandeo.
3.2 Tensiones y Deformaciones en Corte Puro
a) Tensiones
Considérese una pieza sometida a una carga horizontal en su cara superior y anclada en su
cara inferior:
Fig. 3.2 Tensiones en Corte Puro
Realizando un corte en la pieza por la sección recta horizontal A, se observa que:
=0
(3.1
 = Q/A
(3.2
Ahora bien, las tensiones cortantes no aparecen aisladas. Analizando un elemento
diferencial del cuerpo











(a)
(b)
(c)
(d)
No equilibrio en x
Si equilibrio en x
Si equilibrio en x
Si equilibrio en x
Si equilibrio en y
Si equilibrio en y
Si equilibrio en y
Si equilibrio en y
No equilibrio rotación
No equilibrio rotación
No equilibrio rotación
Si equilibrio rotación
Fig. 3.3 Condiciones de Equilibrio
Para que el elemento diferencial este en equilibrio, necesariamente se requiere que:
a) Las tensiones de corte actúen en cuatro caras del elemento diferencial.
b) Las tensiones sean concurrentes o divergentes en las aristas y que tengan igual
magnitud.
Si en lugar de cortar la barra por la sección recta horizontal A, se la corta por una sección
inclinada en un ángulo α
Fig. 3.4 Tensiones en una Sección Inclinada
Geométricamente
dl Cos α = dy
(3.3
dl Sin α = dx
(3.4
α dl dz + y dy dz Sin α + x dx dz Cos α = 0
(3.5
α + y Cos α Sin α + x Sin α Cos α = 0
(3.6
α = - Sin 2α
(3.7
α dl dz - y dy dz Cos α + x dx dz Sin α = 0
(3.8
α - y Cos α Cos α + x Sin α Sin α = 0
(3.9
α =  Cos 2α
(3.10
De la estática
 F1 = 0
 F2 = 0
Cuando α = 0 se verifica que
0 = 90 = 0
(3.11
0 = 90 = 
(3.12
Ya que
(Sin 2 α)2+( Cos 2 α)2 = 1
(3.13
De 3.3 y 3.5
α2 + α2 = 2
(3.14
Que es la ecuación de una circunferencia con centro en el origen.

 max

 max  
Fig. 3.5 Circulo de Mohr
b) Tensiones principales
Los valores máximos de las tensiones normales y cortantes son:
Paαa α = 0
min = 0
 max = P/AN
(3.15
Paαa α = 45 max = P/AN
 min = 0
(3.16
Estos resultados indican que un elemento con cargas cortantes presenta las tensiones
cortantes máximos cuando α = 0 y las tensiones normales máximas en una sección a α =
45º. Para prevenir la falla, las tensiones máximas no deben excedeα las fluencias.
max = P/AN < Sy
(3.17
 max = P/AN < S´y
(3.18
c) Deformaciones
Como se mencionó anteriormente, los elementos sometidos a la acción de fuerzas cortantes
o tangenciales, más que presentar cambios en las dimensiones sufre distorsión o cambios
de forma. Dentro de la zona elástica, las tensiones de corte son proporcionales al ángulo de
deformación.





De la ecuación de Hooke
 = Q/AN = G 
(3.19
 = Q/(AN G)
(3.20
3.3 Problemas Estáticamente Indeterminados (Hiperestáticos)
En algunas ocasiones las ecuaciones de la Estática ( F = 0 y  M = 0) son en número
menores al número de Cargas incógnitas que se desean hallar. Estos problemas se
conocen como estáticamente Indeterminados y en ellos se deben introducir ecuaciones
adicionales de deformaciones.
PROBLEMAS RESUELTOS
3.1. Una pieza con un área de 1 cm² soporta una fuerza cortante de 100 Kg. Se piden: a)
Las tensiones en ángulos de 0 a 360 con intervalos de 10.y b) Graficar  vs. 
Solución:
=(Q/An)Sin 2
0.0
34.2
64.3
86.6
98.5
98.5
86.6
64.3
34.2
0.0
-34.2
-64.3
-86.6
-98.5
-98.5
-86.6
-64.3
-34.2
0.0
34.2
64.3
86.6
98.5
98.5
86.6
64.3
34.2
0.0
-34.2
-64.3
-86.6
-98.5
-98.5
-86.6
-64.3
-34.2
0.0
=(Q/An)Cos 2
100.0
94.0
76.6
50.0
17.4
-17.4
-50.0
-76.6
-94.0
-100.0
-94.0
-76.6
-50.0
-17.4
17.4
50.0
76.6
94.0
100.0
94.0
76.6
50.0
17.4
-17.4
-50.0
-76.6
-94.0
-100.0
-94.0
-76.6
-50.0
-17.4
17.4
50.0
76.6
94.0
100.0
150.0
100.0
50.0
Esf Corte
(Gr) (Rad)
0
0.0
10
0.2
20
0.3
30
0.5
40
0.7
50
0.9
60
1.0
70
1.2
80
1.4
90
1.6
100
1.7
110
1.9
120
2.1
130
2.3
140
2.4
150
2.6
160
2.8
170
3.0
180
3.1
190
3.3
200
3.5
210
3.7
220
3.8
230
4.0
240
4.2
250
4.4
260
4.5
270
4.7
280
4.9
290
5.1
300
5.2
310
5.4
320
5.6
330
5.8
340
5.9
350
6.1
360
6.3
0.0
-100.0
-50.0
0.0
50.0
100.0
-50.0
-100.0
-150.0
Esf Normal
3.2. El remache de la figura une tres piezas y soporta las cargas dadas. Hallar las tensiones.
Tomar d = 25.4 mm y F = 100 kN.
Solución:
 = F/(2AN) = 100000/(2 ( 25.42)/4] = 98,67 N/mm2
3.3. Que diámetro debe tener un remache para unir dos placas que soportan una fuerza de
corte de 1000 Kg. Tomar Sy´ = 900 Kg/cm²
Solución:
max < P/AN = 1000/( d2/4) < 900
d2 = 4(1000)/( 900)
d = 1.19 cm Se adopta d = 1,27 cm
3.4. Dos placas unidas por dos cordones de soldadura a 45º soportan una carga de corte de
6000 Kg. Si el ancho de las placas es de b = 3 cm, se pide hallar las dimensiones de la
garganta y de la base de la soldadura. Tomar Sy´ = 900 Kg/cm².
P
e
P
a
Solución:
El área mínima es
A=eb=e3
max = P/AN = 6000/[2(3)e] < 900
De donde
e = 1.11 cm
Y
a = 2 e Cos 45 = 1.57 cm
3.5. Una pieza de madera con una sección transversal de 3 x 3 cm. está colada como se ve
en la figura. Hallar la fuerza máxima que puede soportar. Tomar Sy´ = 200 Kg/cm²
P
1.
Solución:
60
P
De 2.7 y 2.8
 = (P/2AN) (1 + Cos 2 )
 = (P/2AN) Sin 2 
 60 = (P/2AN) Sin 2  = P/[2(3)(3)] Sin 60 < 200
P = 4156.92 Kg
3.6. Hallar las tensiones cortantes en función del momento torsor en un pasador que
sostiene una polea en un eje
Solución:
El Momento de Torsión
T=Qr
Q=T/r
 = Q/AN = T /(r a b)
3.7. Una polea está fijada a su eje por medio de un pasador cilíndrico. Los ejes del eje y del
pasador son perpendiculares. Si el momento torsor soportado es de 150 Kg cm. y el
diámetro del eje de 3 cm. Se pide hallar el coeficiente de seguridad en el pasador. Tomar
diámetro pasador 0,5 cm. y Sy` = 900 Kg/cm²
Pasador
Polea
Eje
Solución:
T=Fr
F = T / r eje = 150 Kg cm/(3/2) cm = 100 Kg
max = P/AN = 100/( pas2/4) = 509.29 Kg/cm²
 = Sy´/max = 900/509.29
 = 1.76
3.8. En la figura se representan planchuelas, unidas por cordones de soldadura. Se trata de
soldaduras en ángulo compuestas por dos cordones laterales y dos frontales. Se pide la
fuerza P que pueden soportar los cordones
Solución:
g = 0.7 e
AN = (2 a + 2 b) g
 = P/AN = P/ [(a + b) 1.4 e]
3.9. Hallar la intensidad máxima H de la carga que puede soportar la plataforma rígida de la
figura. Los pasadores en A, B y C tienen un diámetro de 1 cm y Sy´ = 900 Kg/cm²
A
30

AC
C
B
40
C
Rx
30
Rv
35
Peq
30
Solución:
 = Arctan(30/40) = 36.86
La carga equivalente
Peq = H 70
Fx = 0
Rx – AC Cos  = 0
(i
Fy = 0
Ry + AC Sin  = Peq
(ii
MB = 0
AC Sin  40 = Peq 35
(iii
AC = H(70)35/(Sin  40) = 102,08 H
Rx = AC Cos  = 81.66 H
Ry = H70 - AC Sin  = 8.75 H
R  ( Rx 2  Ry 2 )  82.12 H
AC = AC/AN = 102,08H/( 12/4) < 900 Kg/cm²
HAC = 6.92 Kg/cm
O = R/AN = 82,12H/( 12/4) < 900 Kg/cm²
HO = 8.6 Kg/cm
Entonces
H = 6.92 Kg/cm.
3.10. La plataforma rígida de la figura está soportada por dos cables a y b. Hallar el diámetro
del pasador en O si Sy´ = 900 Kg/cm² y P = 100 Kg
a
Ta
30
O
30
Rx
b
Tb
30
60
60
Ry
P
P
Solución:
De 2.11
Ta = 0.24 P = 24 Kg
Tb = 0.36 P = 36.1 Kg
 Fx = 0
Rx + Ta Sin 30 = 0
(i
Rx = -12.04 Kg
 Fy = 0
Ry + Ta Cos 30 + Tb -P = 0
(ii
Ry = 43.2 Kg
R  ( Rx 2  R y 2 )  44.64 Kg
O = R/AN = 44.64/( pas2/4) < 900 Kg/cm²
pas = 0.25 cm
3.11. Hallar la fuerza que se necesita para troquelar un disco de 3 cm de diámetro y 0,2 cm
de alto . Tomar Sy´ = 1500 Kg/cm².
P
Solución:
max = P/AN > S`ut
A =   t =  3 0,2 = 1,88 cm²
P > S`ut A = 1500 Kg/cm 2 1.88 cm² = 2827.4 Kg
3.12. Una escalera está diseñada para soportar una persona de 500 Kg y está fijada al piso
por dos pasadores que evitan su deslizamiento. Se pide hallar el diámetro de los pasadores:
Tomar Sy´ = 900 Kg/cm².
P
P
N
x
60
60
Rx
Ry
Solución:
Fx = 0
Rx = N
(i
Fy = 0
Ry = P
(ii
MA = 0
P x Cos 60 – N l Sin 60 = 0
(iii
N = P x Cot 60 /l
Rx = N = P x Cot 60 /l
Ry = P
R  Rx 2  Ry 2
x
R  P 1  ( Cot 60) 2
l
Máx con x = l
R = 1.15 P
max = R/AN = 1.15 (500)/(2 pas2/4) < 900 Kg/cm²
pas = 0.6377 cm
3.13. Una escalera soporta una persona de 500 Kg en su punto medio y está fijada al piso
por dos pasadores que evitan su deslizamiento. Se pide hallar el diámetro de los pasadores:
Tomar Sy´ = 900 Kg/cm².
P
60
Solución: Del anterior problema
x
R  P 1  ( Cot 60) 2
l
para x = l/2
R = 1,04 P
max = R/AN = 1,04 (500)/(2 pas2/4) < 900 Kg/cm²
pas = 0.606 cm
3.14. La pieza de la figura está fijada por cuatro pasadores y soporta una carga de P = 3000
Kg. Se pide hallar el diámetro mínimo de los pasadores. Tomar Sy´ = 1100 Kg/cm².
P
9
A B
9
C
D
Solución:
Por simetría, la carga P se reparte equitativamente entre los cuatro pernos
Fy = 0
Fa = Fb = Fc = Fd = P/4
(i
Fa = Fb = Fc = Fd = 750 Kg
(i
 = F /A < S´y
750 Kg/( d2/4) < 1100 Kg/cm²
d > 0.9317 cm
3.15. La plataforma de la figura soporta una carga de 100 Kg y esta soportada por 2
pasadores de 1 cm de diámetro. Se pide el coeficiente de seguridad en los pasadores.
Tomar Sy´ = 1100 Kg/cm².
P=100[kg]
P
M
75
9
Fa
Fb
Solución:
Los pasadores además de soportar la carga vertical deben soportar el momento que se
origina respecto del centro de los mismos.
Fy = 0
Fa + Fb = P
(i
MA = 0
P (75+9) = Fb 9
(ii
De i y ii
Fb = 933.33 Kg
Fa = - 833.33 Kg
a = Fa /A = 833.33/( 12/4) = 1061.02 Kg/cm²
b = FB /A = 933,33/( 12/4) = 1188.34 Kg/cm²
a = S`y/ a = 1.036 (No hay falla)
b = S`y/ b = 0.925 (Hay falla)
3.16. La plataforma de la figura soporta una carga de 400 Kg y esta soportada por 4
pasadores de 1 cm de diámetro. Se pide el coeficiente de seguridad en los pasadores.
Tomar Sy´ = 1100 Kg/cm².
P=400 kg
9
75
P=400 kg
M=P(75+9/2)
B
D
A
C
d
Solución:
d = (9 )21/2/2 = 6,36
Fy = 0
Fa = Fb = Fc = Fd = P/4 = 100 Kg
(i
Mo = 0
Fa = Fb = Fc = Fd = M/(d4)
(ii
Fa = Fb = Fc = Fd = [400(75+9/2)]/[4(6.36)] = 1250 Kg
La composición da
Fax = -1250 Cos 45 = - 883.88 Kg
Fay = 100-1250 Sin 45 = -783.88 Kg
Fatot = 1181.40 Kg
Fbx = -1250 Cos 45 = - 883.88 Kg
Fby = 100+1250 Sin 45 = 983.88 Kg
Fbtot = 1322.60 Kg
Fcx = 1250 Cos 45 = 883.88 Kg
Fcy = 100-1250 Sin 45 = -783.88 Kg
Fctot = 1181.40 Kg
Fdx = 1250 Cos 45 = 883.88 Kg
Fdy = 100+1250 Sin 45 = 983.88 Kg
Fdtot = 1322.60 Kg
Los pasadores más solicitados son los “b” y “d”, es decir los de la derecha
b = d = F /A = 1322.60/( 12/4) = 1683.98 Kg
 = S`y/  = 0.653 (Hay Falla)
3.17. La plataforma de la figura soporta una carga de 1000 Kg y esta soportada por un
pasador en su extremo izquierdo y dos cables. Se pide el diámetro del pasador O. Tomar
Sy´ = 900 Kg/cm².
Ta
l/2



Rx
l/2
l/2
P
Ry
l/2
Tb

l/2
P
Solución:
De 2.10
Ta = 1.405 P = 1405 Kg
Tb = 1.124 P = 1124 Kg
 Fx = 0
Rx- TaCos  -Tb Cos  = 0
(i
 Fy = 0
Ry + Ta Sin  +Tb Sin -P = 0
(ii
 = 45º
 = 26,56
Rx = 1496.9 Kg
Ry = -496.9 Kg
R  Rx  Ry
2
2
R = 1577.21 Kg
max = R/AN = 1577.21/( pas2/4) < 900 Kg/cm²
pas = 1.49 cm
PROBLEMAS PROPUESTOS
3.18. Una pieza circular con un diámetro de 1 cm soporta una fuerza cortante de 150 Kg. Se
piden a) Las tensiones para ángulos de 0 a 360 con intervalos de 10.y b) Graficar  vs. 
3.19. Cuantos remaches de 2 cm. de diámetro se necesitan para unir dos placas que deben
soportar una fuerza de corte de 1500 Kg. Tomar Sy´ = 900 Kg/cm
P
P
3.20. Dos placas con un ancho de b = 3 cm y un espesor de e = 0,5 cm. están unidas por
cordones de soldadura a 45º: Se pide hallar la carga máxima que la unión soportan. Tomar
Sy´ = 900 Kg/cm²
P
e
P
a
3.21. Una pieza de madera con sección cuadrada soporta una carga de 1000 Kg y está
unida a 70 º. Se piden las dimensiones. Tomar Sy´ = 200 Kg/cm²
P
P
70
3.22. Una polea está fijada a su eje por medio de un pasador rectangular. El momento torsor
soportado es de 150 Kg cm y el diámetro del eje de 3 cm. Hallar el área que debe tener la
chaveta. Tomar Sy` = 900 Kg/cm²
Chav eta
Polea
Eje
3.23. La plataforma de la figura esta soportada por un pasador en su extremo izquierdo y un
cable. Para una intensidad de la carga distribuida de H = 10 Kg/cm. Se pide hallar los
diámetros de los pasadores en A, B y C. Tomar Sy´ = 900 Kg/cm²
A
30

B
40
30
3.24. La plataforma de la figura esta soportada por un pasador en su extremo izquierdo y
dos cables. Para una carga horizontal en su extremo derecho de P = 100 Kg, se pide hallar
el diámetro del pasador en O. Tomar Sy´ = 900 Kg/cm²
30
O
30
60
P
P
3.25. Que fuerza se necesita para troquelar una pieza de sección cuadrada de 6 cm de lado
y 0,3 cm de alto. Tomar Sy´ = 1500 Kg/cm²
P
3.26. Una escalera soporta una carga distribuida de H = 10 Kg/cm y se fija al piso por dos
pasadores para evitar su deslizamiento. Se pide hallar el diámetro de los pasadores. Tomar
Sy´ = 900 Kg/cm².
H
60
3.27. La plataforma de la figura esta soportada por 4 pasadores de diámetro de 1,5 cm y en
ella actúa una fuerza P. Se pide hallar el valor máximo de P que pueden soportar los
pasadores. Tomar Sy´ = 900 Kg/cm².
P
9
A
9
B
C
D
3.28. La plataforma de la figura esta soportada por 4 pasadores con un diámetro de 1 cm y
en ella actúa una fuerza P = 2000 Kg. Se pide el factor de seguridad en los pasadores.
Tomar Sy´ = 1100 Kg/cm²
9
90
A
B
C
D
P = 400 Kg
6
3.29. La plataforma de la figura esta soportada por 3 pasadores con un diámetro de 1 cm y
en ella actúa una fuerza P = 400 Kg. Se pide el factor de seguridad en los pasadores. Tomar
Sy´ = 1100 Kg/cm².
P=400 kg
90
A
C
B
12
3.30. La plataforma de la figura esta soportada por un pasador en su extremo izquierdo y
dos cables. Para las cargas en su extremo derecho de P y 3P, se pide hallar el diámetro del
pasador en O. Tomar Sy´ = 900 Kg/cm² y P = 1000 Kg.


3P
l/2
l/2
P
3.31. La plataforma de la figura esta soportada por un pasador en su extremo izquierdo y
cuatro cables. Para una carga vertical en su extremo derecho de P = 1000 Kg, se pide hallar
el diámetro del pasador en O. Tomar Sy´ = 900 Kg/cm².
P
l/2
l/4
l/4
l/4
l/4
4 Torsión
4.1 Introducción
Un elemento está sometido a torsión cuando al realizar un corte por cualquier sección recta
no aparecen fuerzas internas, tampoco momentos de flexión y solo se verifica un momento
normal Mt en el centro de gravedad de la sección o una cupla que queda contenida en el
plano de la misma, es decir, en todas las secciones rectas del elemento se anulan las
fuerzas y el momento flector.
Fig. 4.1 Torsión
Los ejes y árboles de cualquier maquina son ejemplos de elementos sometidos a torsión.
Los elementos sometidos a torsión son comúnmente de sección circular, sólida o hueca,
debido a que piezas tales como rodamientos, poleas y engranajes en los sistemas de
transmisión de potencia (donde se generan pares de torsión) tienen agujeros circulares que
se montan sobre árboles y ejes.
Para la validez de las ecuaciones y resultados de este capítulo se asume la veracidad de las
siguientes condiciones:
1.- Se cumple la hipótesis de Bernoulli (Conservación de las secciones planas)
2.- Los elementos tienen secciones transversales uniformes
3.- Los materiales son homogéneos
4.- Las cargas están aplicadas en los centros de gravedad de la sección
5.- Los miembros sometidos a compresión no son tan esbeltos y no hay pandeo.
4.2 Diagrama de Momentos Torsores:
Se denominan diagramas de momentos torsores a los diagramas que dan los momentos de
torsión Mt en cada sección de una barra prismática.
Fig. 4.2 Diagrama de Momentos Torsores
4.3 Torsión Circular
a) Tensiones
Aceptando la hipótesis de Coulomb que establece que las secciones normales al eje de la
pieza permanecen planas y paralelas a sí misma luego de la deformación por torsión. Como
consecuencia de lo enunciado resulta que las secciones tienen rotaciones relativas, de
modo que las rectas trazadas sobre ellas continúan siendo rectas y los ángulos mantienen
su medida. Por otro lado, las generatrices rectilíneas de la superficie lateral del cilindro se
transforman en hélices.
Fig. 4.3 Rotación de Secciones en Torsión
Considérese una barra prismática sometida a momentos de torsión en sus extremos. Una
línea recta (A-B) dibujada en su superficie exterior y paralela a su eje axial antes de la
aplicación de los momentos de torsión, se inclina y curvea luego de la aplicación de los
momentos (A-C).
Analizando el giro d entre las secciones laterales en un elemento diferencial de longitud dx
Fig. 4.4 Análisis de un Elemento Diferencial
Se puede apreciar, que una figura rectangular a, b, c, d se distorsiona en la forma romboidal
a´, b´, c, d debido al desplazamiento de los puntos a y b hacia a` y b` en la sección derecha.
Ésta deformación o distorsión es la misma que se producía en cargas de corte. Entonces :
De Hooke
Tg  ≈  = AA’/AAo
(4.1
AA` = r d
(4.2
AAo = dz
(4.3
=G
(4.4
 = G r d/ dz
(4.5
En la ecuación se aprecia las tensiones cortantes son proporcionales al radio (  r ).
Fig. 4.5 Tensiones Cortantes en Torsión
De la estática  Mo = 0
A
 (dA)r  Mt
0
Y de 4.5
(4.6
 Grd 
r 2rdr   Mt
dz 
0
R
 
r 4 d
4 dz
G 2
Mt  GI o
(4.7
R
 Mt
(4.8
0
d
dz
(4.9
De 4.5 y 4.9
Mtr
Io

 max 
(4.10
Mt R
Io
(4.11
Para piezas sólidas
 max
d
T( )
16T
 24  3
d
d
32
(4.12
Las tensiones máximas nunca deben sobrepasar los Límites de Fluencia del material.
 max < S´y
(4.13
b) Deformaciones
El ángulo que giran las secciones laterales de una pieza sometida a torsión.
R
d
Fig. 4.6 Angulo de Rotación entre Secciones en Torsión
Integrando 4.10
l
Mt
dz
GI o
0
 
(4.14
Si el diámetro es constante

MtL
GIo
(4.15
c) Tensiones Principales
Fig. 4.7 Tensiones Tangenciales y Normales
Un elemento diferencial del interior de una barra circular torsionada se encuentra en un
estado de corte puro. Como se vio, las tensiones principales resultan iguales en valor
absoluto y de signo contrario e iguales al valor de las tensiones tangenciales. Además
actúan a 45º con respecto a los planos de las secciones, formando superficies helicoidales.
En vista que las tensiones de la parte central de la sección maciza son pequeñas, no tienen
un aporte significativo, por lo que para torsión son más convenientes las secciones huecas
Fig. 4.8 Tensiones en una Pieza Circular Hueca
4.4 Torsión en Elementos con Sección Rectangular
Fig. 4.9 Torsión en una Pieza Rectangular
En este caso la hipótesis de Coulomb: "las secciones transversales permanecen planas
durante la torsión", válida para secciones circulares, no es válida para secciones
rectangulares ya que las secciones se alabearán.
Fig. 4.10 Alabeo de una Pieza Rectangular
Aun así se supone que sólo aparecerán tensiones cortantes x. El cálculo exacto de
tensiones y deformaciones en una pieza de sección cualquiera sometida a Torsión, se debe
a Saint-Venant y es parte de la Teoría de la Elasticidad. Aquí se exponen solo los resultados
que se obtienen al aplicar dicha teoría al caso se piezas de sección rectangular.
Fig. 4.11 Tensiones en una Pieza Rectangular
El esfuerzo cortante máximo se da en el punto medio del lado mayor y su valor es
 max 
Mt
b 2 h
(4.16
El Angulo

h/b
Mt
Ghb3
1
1,5
0,208
0,231
0,141
0,196
(4.17
1,75
2
2,5
3
4
6
8
10
OO
0,239 0,246
0,258
0,267
0,282
0,299
0,307
0,313
0,333
0,214 0,229
0,249
0,263
0,281
0,299
0,307
0,313
0,333
4.5 Tensiones en Secciones Cerradas de Pequeño Espesor
Para piezas con pequeño espesor las tensiones normales se consideran cero y sólo habrá
tensiones cortantes.
Considérese un elemento diferencial de una pieza de longitud dx sometida a Torsión. Las
tensiones cortantes aparecen solo en las secciones cortadas y son tangentes a ellas
Fig. 4.12 Sección Cerrada de Pequeño espesor
Analizando el elemento b c d e. De la estática en x
Fig. 4.13 Tensiones en Sección Cerrada de Pequeño espesor
b tb dx = c tc dx
(4.18
b tb = c tc
(4.19
 t = Constante (Flujo cortante es constante
(4.20
Las tensiones cortantes, son mayores donde el espesor es menor
Tomando momentos respecto del centro de gravedad G de la sección, de todas las fuerzas
que actúan en la misma:
Fig. 4.14 Momentos de las Tensiones en Sección Cerrada de Pequeño espesor
dF =  dSm t
 (dS
Sm
m
t )r  Mt
Sm Longitud de la Linea Media
(4.21
Mt  t  rdSm  t  2dAm  t 2 Am
Sm

(4.22
Sm
Mt
2tAm
(4.23
Dónde: Am = "área encerrada por la línea media de la sección transversal"
La tensión cortante máxima se da donde el espesor es mínimo, resultando su valor:
 max 
Mt
2t min Am
(4.24
4.6 Problemas Estáticamente Indeterminados (Hiperestáticos)
De manera similar a lo visto anteriormente, cuando las ecuaciones de la Estática ( F = 0 y 
M = 0) son en número menores al número de reacciones incógnitas que se deben hallar, los
problemas se conocen como estáticamente indeterminados o hiperestáticos. En estos casos
se deben complementar las ecuaciones de la estática con ecuaciones de deformaciones
PROBLEMAS RESUELTOS
4.1. Una pieza cilíndrica de Acero de diámetro  = 3 cm y largo L = 100 cm está sometida a
una carga de 1000 Kg. cm. Tomando Sy´ = 960 Kg/cm², se pide: a) Las tensiones máximas
b) El coeficiente de seguridad y c) Las deformadas total y unitaria longitudinal y transversal
Solución:
La inercia es I =  4/32 = 7,95 cm4
a) Tensión máximo
 max = TR/Io = 1000(1,5)/7,95
 max = 188,62 Kg/cm²
b) Coeficiente de seguridad
 = S`y/max = 960/188,62 = 5,08
 = 5,08
c) Deformada  = TL/(GIo) = 1000(100)/(6,67 x 105 7,95)
 = 0,0188 rad
4.2. Un tambor con un diámetro de 30 cm, levanta una carga de 1000 Kg. Calcular el
diámetro del eje. Tomar Sy` = 900 Kg/cm²
Ø
30[cm]
d
1000[kg]
Solución:
El momento
T = 1000(30)/2 = 15000 Kg. cm
De 4.14
max = 16 T/ ( d 3)
d = [16 T / ( S`y)]1/3
d = 4,39 cm
4.3. Un motor de 5 Hp esta acoplado por medio de una transmisión a un eje que gira a 30
rpm. Si el material del eje tiene una fluencia de S`y = 900 Kg/cm². Tomando  = 1,5 se pide
calcular el diámetro del eje.
Solución:
La potencia
Pot (CV) = T ( Kg. m)  (rad/seg)/ 75
 (rad/seg) = (30 rpm) (2 rad / rev) (min/60 s) = 3,14 rad/seg
El momento
T = 5 (75)/3,14 = 119,36 Kg. m = 11942,59 Kg. cm
Tensión
max = 16 T/ ( d 3) < S`y/
d = [16 T  / ( S`y)]1/3 = 4,66 cm
Se adopta
d = 5 cm
4.4. En el sistema de la figura, se pide el ángulo de deformación del extremo libre respecto
al extremo fijo. El material es acero y las dimensiones están en cm
120
40
100 [kg]
3Ø
1Ø
6Ø
Solución:
T = F r = 100(3) = 300 Kg cm
1 = TL/(GIo) = 300(120)/(6.67 x 105  34/32) = 0.00678 rad
2 = TL/(GIo) = 300(40)/(6.67 x 105  14/32) = 0.182 rad
tot = 1 + 2 = 0.189 rad
4.5. Dos piezas cilíndricas del mismo material están cargadas con el mismo momento de
torsión “T”. La primera pieza es sólida con un diámetro “d” y la segunda es hueca con un
diámetro externo “D” y un espesor “e”. Si la fluencia al corte es Sy. Se pide :
La relación de dimensiones
La relación de masas.
d
D
e
Solución:
a) Las tensiones de corte no pueden ser mayores a la fluencia
 max 
TR
 S y ´
Io
I
T
 o
Sy '
R
En el cilindro sólido
T
d 4 2

Sy '
32 d
(i
En el cilindro hueco


T
 D 4  ( D  2e) 4 2

Sy '
32
D
(ii
Ya que ambos tienen la misma carga y el mismo material. Igualando i y ii

d4
D 4  ( D  2e) 4

d
D


 D 4  ( D  2e) 4 
d 

D



1/ 3
(iii
b) La relación de masas
Mh  
Ms  

4
D
2
 ( D  2e) 2
(iv
d 2
4
(v

De iii, iv y v

 

Mh
D 2  ( D  2e) 2
D 2  ( D  2e) 2 D 2 / 3


2/3
Ms
d2
D 4  ( D  2e) 4


4.6. Para un cilindro hueco con un diámetro D = 5 cm y un espesor e = 0,3 cm. Hallar :
a) El diámetro de un cilindro sólido que soporta la misma carga de torsión
b) La relación de masas
d
Solución:

a)

 D 4  ( D  2e) 4 
d 

D


1/ 3
d = 3.6849 cm

b)
Mh
D 2  ( D  2e) 2

Ms
d2

D
e
(Mh/Ms) = 0.41536
Este resultado indica que si bien ambos cilindros tienen la misma resistencia, la pieza hueca
solo pesa el 41,64 % de la pieza sólida.
4.7. El sistema de la figura tiene una forma cónica circular. En ella se pide calcular
La tensión cortante máxima
La deformada total
60
T=1000 kg cm
dy
1000
y
90
Solución:
El diámetro
d(y) = - (30/1000) y + 90
y=0
d = 90
y = 1000
d = 60
a) La tensión máxima se presenta en el menor diámetro
 max = 16 T/( d 3 ) = 16(1000)/ [ (60)3]
 max = 0,0235 Kg/cm²
b) La deformada
h
T
dy 
GI
o
0
 
1000

0
1000(32)
dy
G (0,03 y  90) 4
 = 0.368717 /G
4.8. El sistema de la figura tiene una forma cónica circular hueca. En ellas se pide:
a) La tensión cortante máxima
b) La deformada total
60
45
T=1000 kg cm
dy
1000
y
15
90
Solución:
Las ec. de los diámetros externo e interno son :
D(y) = - (30/1000) y + 90
d(y) = (30/1000) y + 15
La inercia
Io =  [-(30/1000)y + 90]4 - [(30/1000)y + 15]4/32
a) La tensión máxima se presenta en la menor inercia
I o min =  ( 604 - 454)/32 = 869767.09 cm4
 max = TR/I = (1000)(30)/ 869767.09
 max = 0,0344 Kg/cm²
b) La deformada
h
 
0
1000
T
dy 
GIo

0
(1000)(32)
dy
4
4
G  0.03 y  90  0.03 y  15


 = 0,4145 /G
4.9. La pieza de la figura tiene una forma semiesférica truncada, con un diámetro en la base
de 60 cm y una altura de 20 cm. Para un momento torsor T aplicado en su parte superior, se
pide la deformación angular.
y
T
20[cm
]
x
60[cm]
Solución:
Definiendo un sistema de coordenadas en la base. La ecuación del círculo es :
x2+y2 = 302
El diámetro
d = 2x = 2 (302-y2)1/2
20

 G 2(30
T 32dy
2
0

2 1/ 2 4
y )

T2
G
20
 (30
2
0
dy
 y 2 )2
 = 2,3634 10-5 T / G
4.10. La pieza de la figura está formada por dos semiesferas truncadas con diámetros de 60
y 30 cm en sus bases. Para un momento torsor T aplicado en la sección común, se pide
hallar los momentos de reacción en A y B
Tb
30[cm]
B
B
2
T
T
40[cm]
1
y
x
A
A
60[cm]
Ta
Solución:
M=0
Ta + Tb = T
(i
Sistema hiperestático con una ecuación y dos incógnitas. La ec de deformadas
t = 1+ 2 = 0
Se define un sistema de coordenadas en la base. Las ecuaciones de los círculos son :
x2+y2 = 302
x2 + (y-40)2 = 152
Los diámetros
d1 = 2(302-y2)1/2
d2 = 2[152-(y-40)2]1/2
Que igualan a una altura de
d1 = 2(302-y2)1/2 = d2 = 2[152-(y-40)2]1/2
y = 28,43
1 
28.43

0

G 2(30  y )
40

2 
28, 43
T 
Ta 32dy

2

2 1/ 2 4

(Ta  T )32dy
G 2(15 2  ( y  40) 2 )1 / 2
Ta (1.309)10 4
G

4

(Ta  T )(2.761)10 4
G
Ta (1.309)10 4 (Ta  T )(2.761)10 4

0
G
G
De donde
Ta = 0,678 T
Tb = 0,322 T
4.11. La pieza de la figura tiene una sección circular. En ella se pide hallar las reacciones en
las paredes
2
1
4T
T
T
3
4T
Tb
60
30
A
45
30
10
B
Ta
x
A
B
Solución:
M=0
Ta + T + Tb = 4T
(i
Sistema hiperestático con una ecuación y dos incógnitas. La ec de deformadas
t = 1 + 2 + 3 = 0
Los diámetros
d1 = -30 x/45 + 60
d2 = 30
d3 = 3 x + 30
Ta 32dx
Ta (1.65)10 4

4
G
0 G ( 30 x / 45  60)
45
1  
2 
(Ta  T )30(32) (Ta  T )(3.773)10 4

G
G 30 4
(Ta  3T )32dx (Ta  3T )(3.668)10 5

G
G (3x  195) 4
75
85
3  
Resolviendo
T 
Ta (1.65)10 4 (Ta  T )(3.773)10 4 (Ta  3T )(3.668)10 5


0
G
G
G
De donde
Ta = 0,462 T
Tb = -3,462 T
4.12. Determinar la deformación total que se produce en la barra de la figura que consta de
dos tramos, una cilíndrica y otra cónica, sometida a la acción de un momento torsor T en su
extremo libre. Tomar D = 10 cm y l = 50 cm.
T
D/3
D/2
D
l/2
l/2
l/2
Solución:


l
0
2
Tdx

GIo1

l
Tdx

l GI
o2
2

3l
2
l
Tdx
GIo3
(i
ext = D/2
0<x<l/2
int = D/3
I o1 
l/2<x<l

 ( D / 2)4  ( D / 3)4

32
(ii
ext = (D/2) (x/l)+ D/2
int = D/3
Io2 
l<x<3l/2
4

D 
 Dx D 

   ( )4 
2
l
2
3 




32
 
(iii
ext = (D/2) (x/l)+ D/2
int = 0
I o3 
 
Dx D 
 
2
 2l
32

Reemplazando
4
(IV
3l
T (l / 2)32
32dx
32dx
 ll
 l 2
4
4
4
4
 Dx D 
2 
G ( D / 2)  ( D / 3)
D 
 Dx D 
  
     ( ) 4 
3 
 2l 2 
 2l 2 


(V
 = 0.721 T/G
4.13. Hallar una expresión para determinar la deformación que sufre una barra con sección
variable según una función cuadrática, como se ve en la figura.
y
D
Dx
d
x
x
dx
l
Solución:
La variación del diámetro en función de x es cuadrática
 = Ax2 + B
para
x=0
Dx = d
x=l
Dx = D
T
resolviendo
Dd
Dx   2 ·x 2  d
 l 

l T ·dx
 G·I
0


l
0
o
T 32dx
 Dd

G· ( 2 ) x 2  d 
 l

4


 D  d  
10 A tan 


d
(
D

d
)
Tl 

  10  20  16 



G 
d 3 D 3d 2 D 2 3dD 3 
d 3 d (D  d )




4.14. Hallar una expresión para determinar la deformación que sufre una barra con sección
variable según una función potencial, como se ve en la figura.
y
D
Dx
d
x
x
dx
T
l
Solución:
La variación del diámetro en función de x es polinómica
 = A xm + B
Para
resolviendo
x=0
Dx = d
x=l
Dx = D
 = (D - d)(x / l)m + d
l
T ·dx

0 G·I
0
o
 
l
T 32dx
 Dd

G· ( m ) x m  d 
 l

4
4.15. Determinar la deformación angular de la pieza de sección circular, sometida a las
cargas de torsión mostradas en la figura. Tomar D = 10cm; d = 3cm; l = 150cm; Mt = 7000
Kg·m; G = 7.648x105 Kg/cm²
3Mt
D
2Mt
Mt
d
l/4
l/4
l/4
l/4
x
Solución:
D2
d
D1x
D
d
D
x
dx
d
x
x
l/4
x
D1 
2(d  D) x
D
l
D2 
2( D  d ) x
 D  2d
l
l/4
 
 GD
M t 32
0

4
1
l/2

dx 

l/4
M t 32
GD14
128lMt
( D  d )3 (d  D)G

3l / 4
dx 


l/2
M t 32
GD24
16lMt
3d 3 (d  D)G

l/4
dx 

(2  M t )32
0
GD24
dx
32lMt
3D3 (d  D)G
 = - 4.283 Mt/G
4.16. Calcular la deformación angular del eje circular de la figura. Tomar D = 20cm; l = 50
cm Gac = 7.64x105 Kg/cm²; Gal = 2.65x105 Kg/cm²;Gcu = 4.1x105 Kg/cm²; Mt = 2000
Kg·cm
3Mt
Mt
D
GAc D/2
l
Gal
2Mt
Gcu
D/3
l
l
x
Solución:
2l
3l
2M t 32
(2M t  M t )32
(2M t  M t  3M t )32
dx  
dx  
dx
4
4
Gac ( D) 4
0 Gcu  ( D / 3)
l Gal ( D / 2)
2l
l
 

M t l  2(32)(81) 1(32)(16) 4(32)(1) 




Gcu
Gal
Gac 
D 4 
 = 5.866 x 10--5 rad
4.17. Hallar la deformación de la pieza troncocónica y cilíndrica hueca mostrada en la figura.
Tomar D = 20cm, d = 5 cm, Mt = 8000 Kg·cm, G = 7.6x105 Kg/cm².
2Mt
Mt
D d
d/2 D/2
l
l
x
Solución:
0< x < l
Dext = D/2
dint = d/2
l< x < 2l
Dext = (Dx)/(2l)
dint = (dx)/(2l)
l
 
2l
M t 32
 D   d 
0
G     
 2   2 
4
4



dx  
l
M t 32
dx
 Dx  4  dx  4 
G 
   
 2l   2l  
integrando
 = 7.243 x 10-4 Mt/G
4.18. El eje de la figura tiene sección circular. Se pide hallar las reacciones en los extremos.
Ma
Mb
5
4
2Mt
3
2
Mt
D
1
5Mt
D/2
l/3
l/3
D
l/3
x
Solución:
M=0
Ma + 2Mt – Mt – 5 Mt + Mb = 0
0< x < l/3
d = (D/2) (2-3x/l)
Mt1 = Mb
l/3< x < l/2
d = (D/2)
Mt2 = Mb – 5 Mt
l/2< x < 2l/3
d = (D/2)
Mt3 = Mb – 6 Mt
2l/3< x < 5l/6 d = (D/2) (3x/l-1)
Mt4 = Mb – 6 Mt
5l/6< x < l
Mt5 = Mb – 4 Mt
d = (D/2) (3x/l-1)
El sistema es hiperestático. La ecuación de deformadas es :
(i
total = 1 + 2 + 3 + 4 + 5 = 0
 tot 
l /3
M t1 32
 GD
0
l /3

0
Mb
3x 
2  
 l
4
l/2
dx 
M t 2 32
 GD
l /3
1
4
2l / 3
M t 3 32
 GD
dx 
l/2
2
4
(ii
5l / 6
dx 

2l / 3
3
M t 4 32
GD4
4
l
dx 
M t 5 32

5l / 6
GD5
4
dx
2l / 3
5l / 6
l
( M b  5M t )
( M b  6M t )
( M b  6M t )
( M b  4M t )
dx

dx

dx

dx  0
4
4
 14
 14




l /3
l/2
2l / 3  3x
5l / 6  3 x
  1
  1
l 
l 
l/2
dx 
4
Reemplazando
Mb = 4.507 Mt
Ma = - 0.507 Mt
4.19. Hallar la deformación angular del extremo derecho de la pieza mostrada en la figura.
Evaluar el resultado cuando d = D/2 ;
5Mt
Mt
D
2D
d
l
l
x
Solución:
M=0
Ma + 2Mt – Mt – 5 Mt + Mb = 0
0< x < l
D1 = D (l + x)/l
Mt1 = Mt
l< x < 2l
D2 = D (3l - x)/l
Mt1 = -4Mt
l

 G (D
0
simplificando

M t132
4
1
 d 4)
2l
dx 
 G (D
M t 2 32
4
2
l
 d 4)
(i
dx
 9.195M t l
GD 4
4.20. Hallar la deformación angular del sistema. Tomar H = 3R/4 y R = 5 cm
Mt
h
4Mt
R
y
h
Solución:
Definiendo un sistema de coordenadas en la base de la esfera
x2 + y2 = R2
D1 ( y)  2 x  2 R 2  y 2
Cuando
y = h = 3R/4
D1 = D2
D2  2 R2  h2  7 R / 2
3R / 4


0

evaluando
3R / 2
3R / 4

0

3M t 32
 M t 32
dy  
dy
4
GD1 ( y )
GD2 ( y ) 4
3R / 4
3R / 2
3M t 32
G 2 ( R  y )
4
2
2
2
dy 
M t  3 ln 7 36  M t



G  2 R3 7 R3  G

3R / 4
 M t 32(16)
G 49 R 4
dy
 512 3 


3
 49 R 4 
4.21. Hallar las reacciones en los extremos empotrados del eje de sección circular mostrado
en la figura. Tomar m0 = 10 Kg·cm/cm, a = 100 cm y D = 2 cm.
mo
4D
x
Ma
a
a
5D
Mb
Solución:
M=0
Ma + Mb = mo a
El sistema es hiperestático con una ecuación y dos incógnitas. De las deformadas
total = 1 + 2 = 0
2a
( M a  mo x)32
( M a  mo a)32
dx

dx  0
4

G

(
5
D
)
G (4 D) 4
0
a
a
 
a
( M a  mo )
2  ( M a  mo a)  0
(5) 4
(4) 4
entonces
Ma = 0.8547 moa
Mb = 0.1452 moa
4.22. Hallar la longitud que debe tener un eje macizo de acero de d = 13 mm de diámetro
para que sus extremos giren 90º uno respecto del otro. No se debe rebasar un tensión
cortante permisible de 713.8 Kg/cm², y G = 8.1573x105.
max
d
l
Solución:
Las ecuaciones de deformación y tensión
 
M tl
GIo
 max 
l
De ambas
Mtr
Io
rG
 max
l = 116.68 m
4.23. La barra de la figura tiene sección transversal circular sólida en el tramo AB, y sección
transversal circular hueca en el tramo BC. Obtener la expresión de la relación a/L tal que los
momentos de reacción en los apoyos sean iguales.
B
A
D d
d
a
L
Solución:
M=0
Ma + Mb = 2Ma = 2Mb = Mt
(i
El sistema es hiperestático. La ecuación de deformación es :
tot = 1 + 2 = 0

M a a32
Gd 4
Ma 
resolviendo
De i y ii

( M a  M t )(l  a)32
G ( D 4  d 4 )
0
d 4 M t (l  a)
(aD4  2ad 4  d 4l )
2d 4 M t (l  a)
 Mt
(aD 4  2ad 4  d 4 l )
(a / l) = (d / D)4
(ii
4.24. La barra circular de la figura está empotrada en sus extremos. Sobre ella actúa un Par
de Torsión distribuido q(x) en toda su longitud con intensidad cero en A y qo en B. Se piden
los momentos de reacción Ma y Mb.
q(x)
Ma
Mb
x
L
q( x)
q ox
L
Solución:
M=0
Ma + Mb = Mt
(i
El sistema es hiperestático. La ecuación de deformación es :
tot = 0
l


0
[ M a  q( x) x]
dx  0
GIo
resolviendo con
q(x) = qox/l
Ma = qo l / 3
Mb = qo l / 6
4.25. Una pieza está conformada por dos materiales, la exterior de acero y la interior de
latón. Si los diámetros externo e interno son 75 y 60 mm respectivamente y asumiendo las
tensiones permisibles como a = 82 Mpa y l = 50 Mpa en el acero y latón respectivamente,
se pide hallar el momento máximo de torsión que puede aplicarse a la pieza. (Ga = 80 Gpa
Gl = 36 Gpa)
Mp
Latón
d D
L
Acero
Solución:
laton = acero
M latonl 32
Gd 4

M acerol 32
G ( D 4  d 4 )
Mtot = Mlaton + Macero
(i
(ii
M t Glatond 4
M laton 
GaceroD 4  Glatond 4
M acero 
M t GaceroD 4
GaceroD 4  Glatond 4
Las tensiones permisibles par cada barra son:
 laton 
M laton(d / 2)32
 acero 
M acero( D / 2)32
Mt 
Mt 
d 4
 ( D4  d 4 )
 acero(GaceroD 4  Glatond 4 ) ( D 4  d 4 )
16GaceroD5
 laton(GaceroD 4  Glatond 4 )
16Glatond
remplazando Mt = 4.749 x 103 Nm para el acero
Mt = 1.363 x 104 Nm para el latón
Luego
Mt = 4.749 x 103 Nm
PROBLEMAS PROPUESTOS
4.26. Hallar el diámetro de una pieza cilíndrica de Acero con un largo de 100 cm para que
pueda soportar un momento de 1000 Kg cm. Tomar Sy´ = 960 Kg/cm², y  = 2. Hallar
además la deformación.
4.27. Un tambor de una máquina de elevación tiene un diámetro de 30 cm y se encuentra
montado sobre un eje con un diámetro de 3 cm con Sy` = 900 Kg/cm². Se pide hallar el peso
máximo que puede levantar
4.28. Un eje gira a 120 rpm y esta acoplado a un motor de 9 Hp por medio de una
transmisión. Si el material tiene una fluencia de S`y = 900 Kg/cm². Para  = 2 se pide
calcular el diámetro del eje.
4.29. Hallar el ángulo de torsión del extremo libre respecto al extremo fijo del sistema de la
figura. El material es acero y las dimensiones están en cm.
150
60
150 [kg]
6Ø
3Ø
12 Ø
4.30. La pieza de la figura tiene forma cónica truncada. Se pide hallar la deformada total y la
tensión máxima
d
d/2
T=1000[kg .cm]
H
D
4.31. Hallar la deformada total y la tensión máxima en el sistema de la figura
T=1000[kg.cm]
d
H
D
4.32. Hallar la deformada total y la tensión máxima en el sistema de la figura
d
H
T=1000[kg.cm]
D
4.33. Hallar la deformada total y la tensión máxima en el sistema de la figura
D e xt  90[cm] ; d int  45[cm]
T=1000[kg-cm]
A
1000
[cm]
dy
A
y
D e xt  60[cm] ; d int  30[cm]
4.34. Una pieza tiene la forma de cascaron semiesférica truncada de diámetro 60 cm, altura
20 cm y espesor 3 cm. Hallar la deformada angular para un momento torsor aplicado en su
parte superior de T.
3
T
20[cm
]
60[cm
]
4.35. Hallar las reacciones en A y B en el sistema de la figura
B
40[cm]
30[cm]
25[cm]
y
A
60[cm]
T
x
4.36. Se pide hallar las reacciones en las paredes para el sistema de la figura
4T
T
60
30
A
50
30
10
40
B
4.37. En el sistema de la figura se pide hallar las reacciones en las paredes. Las
dimensiones están en cm
T
30
Ø
9
Ø
20
30
45
60
Ø
45
Ø
45
4.38. Para el sistema de la figura, se pide determinar las reacciones en los apoyos. Tomar D
= 10 cm, l = 50 cm, E = 2.1x106 Kg/cm² y P = 2000 Kg
T
D/3
D/2
l/2
l/2
l/2
4.39. Para el sistema de la figura se pide hallar las reacciones. Tomar D = 10cm; d = 3cm; l
= 150cm; Mt = 7000 Kg·m; G = 7.648x105 Kg/cm²
Mt
3M t
d
A
l/4
l/4
D
l/4
l/4
B
4.40. Hallar las reacciones del sistema de la figura, considerar para cada caso los valores
indicados a continuación. D = 10cm; d = 3cm; l = 150cm; Mt = 7000 Kg·m; G = 7.648x105
Kg/cm²
Mt
3M t
D
d
l/4
A
l/4
l/4
l/4
B
4.41. Hallar las reacciones del sistema de la figura, considerar para cada caso los valores
indicados a continuación. D = 10cm; d = 3cm; l = 150cm; Mt = 7000 Kg·m; G = 7.648x105
Kg/cm²
Mt
3Mt
D
d
l/5
A
l/5
l/5
l/5
l/5
B
4.42. Hallar la deformación de la pieza troncocónica hueca mostrada en la figura. Tomar D =
20cm d = 5cm Mt = 8000 Kg·cm G = 7.6x105 Kg/cm²
3Mt
Mt
D
d
B
l/5
A
l/5
l/5
4.43. Hallar las reacciones en los extremos del sistema de la figura.
5
4
2Mt
3
2
Mt
D
Ma
1
5Mt
D/2
l/3
l/3
D/8
l/3
Mb
4.44. Hallar la deformación angular del extremo derecho de la pieza mostrada en la figura.
Evaluar el resultado cuando d = D/2 y e = D/9
Mt
3Mt
e
D
d
A
B
l/4
l/4
l/2
4.45. Hallar la deformación angular de la figura. Tomar H = 3/4R, R = 15 cm y d = 3
d
Mt
h
3M t
h
R
4.46. Hallar las reacciones en los extremos empotrados del bloque de sección circular
mostrado en la figura. Tomar m0 = 10 Kg·cm / cm, a = 100 cm y D = 2 cm.
m
D
d
A
l/2
l/2
B
4.47. Hallar la longitud que debe tener una barra hueca de acero de D = 1.5 cm y d = 0.5 cm
de diámetros para que sus extremos giren 30º uno respecto del otro. No se debe rebasar un
tensión cortante permisible de 713.8 Kg/cm², y G = 8.1573x105.
4.48. La barra cónica de la figura tiene sección transversal circular. Obtener la expresión de
la relación a/L tal que los momentos de reacción en los apoyos sean iguales.
Mt
D
d
a
L
4.49. La barra circular. de la figura, está empotrada en ambos extremos. Sobre ella actúa un
par de Torsión distribuido q(x) que actúa a lo largo de su longitud, y varía de intensidad
desde cero en A hasta qo en B parabólicamente. Calcular los momentos de reacción Ma y
Mb.
q(x)
A
B
4.50. Un cono macizo está constituida por dos materiales, uno exterior, de acero y otro
interior cilíndrico de latón, como se muestra en la figura. Si se supone que las tensiones
permisibles son a = 82 Mpa y l = 50 Mpa en el acero y latón respectivamente, determinar
el momento máximo de torsión permisible que puede aplicarse a la barra. (Ga = 80 Gpa Gl =
36 Gpa) D = 15 cm
l
D D/4
D/2
5 Flexión - Fuerza Cortante y Momento Flector
5.1 Introducción
Un elemento está sometido a torsión cuando al realizar un corte por cualquier sección recta
no aparecen fuerzas ni momentos internos normales a la sección y solo se verifican fuerzas
y momentos internos en el centro de gravedad de la sección y paralelos a ella.
Fig. 5.1 a) Flexión Pura
a) Flexión Simple
Se llama FLEXIÓN PURA cuando actúan únicamente los momentos flectores: Mz y/o My.
(Fig. 5.1.a) y cuando actúan los momentos flectores Mz y/o My y también las fuerzas
cortantes Qy y/o Qz, se llama FLEXIÓN SIMPLE.(Fig.5.1.b). Las vigas, losas de las
viviendas y puentes y pasarelas son ejemplos de elementos sometidos a torsión.
Para la validez de las ecuaciones y resultados se asumen las siguientes condiciones:
1.- Los elementos son rectos
2.- Los elementos tienen secciones transversales uniformes
3.- Las cargas y reacciones en apoyos actúan perpendicularmente al eje de la viga.
4.- Las vigas no están sometidas a torsión
5.- Las vigas son relativamente largas y angostas respecto a su peralte
6.- Los materiales son homogéneos
7.- Las tensiones no exceden al límite de fluencia del material
8.- Las vigas no fallan por pandeo
5.2 Cargas
a) Tipos de Cargas.- Las cargas pueden ser : Puntuales y Distribuidas.
Fig. 5.2 (a) Cargas Puntuales
(b) Cargas Distribuidas
- Cargas puntuales.- Son aquellas que actúan en un solo punto. Son ideales ya que no
existen físicamente, sin embargo las cargas aplicadas en áreas pequeñas pueden
idealizarse como puntuales. Así, las reacciones en las llantas de los vehículos automotores;
las fuerzas en elementos de estructuras metálicas, las tensiones en cables, etc., son cargas
que se pueden idealizar como puntuales
- Cargas distribuidas - Son aquellas que están aplicadas en áreas no muy pequeñas. La
fuerza del viento, el peso de materiales continuos, la presión de los líquidos en superficies
sólidas sumergidas, etc., son ejemplos de cargas distribuidas.
b) Carga Puntual Equivalente de Distribuida.- Las cargas distribuidas deben cuantificarse
y concentrarse en una carga puntual que produzca similares efectos (cargas y momentos).
Esta carga puntual se denomina equivalente de la carga distribuida.
Considérese una carga distribuida cualquiera
P
x
0
x
dx
Fig. 5.3 Carga Distribuida en un Elemento diferencial
Tomando un elemento infinitesimal “dx” en él, la altura es constante p(x) y su peso es :
dw =  dV =  h(x) dx dz
donde
Llamando

es el peso específico del material
h(x)
es la altura de la carga en la posición x
dx
es el ancho diferencial
dz
es la profundidad
p(x) =  h(x) dz
(5.1
e Integrando
l
Peq  W   p( x)dx
0
(5.2
Los momentos que producen las cargas puntual y distribuida deben ser iguales
dM = x dw
(5.3
l
M   p( x) xdx  Peq X eq
0
(5.4
l
X eq 
 p( x) xdx
0
l
 p( x)dx
0
_
X
(5.5
De 5.2 y 5.5 se concluye que :
- El área de una carga distribuida es igual a la carga puntual equivalente
- La carga puntual equivalente debe ubicarse en el centro de gravedad de la carga
distribuida
5.3 Tipos de Apoyos
Los apoyos que sostienen a las vigas son : a) Apoyo móvil, b) Apoyo fijo y c) Empotramiento
Rx
Mr
Rx
Ry
Ry
(a)
Ry
(b)
(c)
Fig. 5.4 Tipos de Apoyos
a) Apoyo Móvil.- Este apoyo restringe el movimiento vertical pero no el horizontal ni los
giros. En él aparecen solo reacciones verticales. Un rodillo es un ejemplo de apoyo móvil
b) Apoyo Fijo.- Este apoyo restringe los desplazamientos vertical y horizontal pero no los
giros. En este apoyo aparecen reacciones verticales y horizontales. Una bisagra es un
ejemplo de un apoyo fijo.
c) Empotramiento.- Este apoyo restringe los desplazamientos vertical, horizontal y los giros.
En este apoyo aparecen reacciones verticales, horizontales y momentos.
5.4 Tipos de Vigas
Los tipos de vigas dependen de los tipos de apoyos. Como hay infinitas combinaciones de
apoyos hay infinito tipos de vigas. Las vigas más comunes son la simplemente apoyada y la
simplemente empotrada.
(b)
(a)
(c)
Fig. 5.4 Tipos de Vigas
a) Viga simplemente apoyada.- Es aquella que descansa sobre un apoyo móvil y otro fijo.
b) Viga simplemente empotrada.- Es aquella que tiene uno de sus extremos empotrado.
c) Viga con apoyos múltiples.- Las vigas que tenga más de un apoyo fijo y otro móvil o un
empotramiento, tiene apoyos múltiples y su cálculo es hiperestático.
5.5 Cálculo de Reacciones
El cálculo de las reacciones en los apoyos se realiza con las ecuaciones de la estática.

M  0

F  0
(5.6
Notas :
- Las cargas distribuidas previamente deben reemplazarse por sus equivalentes puntuales
- Las vigas con múltiples apoyos son hiperestáticas y serán analizadas posteriormente.
5.6 Momento Flector y Fuerza Cortante
Como se vio anteriormente, en cualquier sección plana interna de un cuerpo en equilibrio
sometido a la acción de fuerzas y momentos externos, aparecen una fuerza y un momento
internos que equilibran las cargas externas.
Fig. 5.5 Fuerza Cortante y Momento Flector
Las componentes tangenciales de la fuerza y del momento internos, son respectivamente la
fuerza cortante y el momento flector.
5.7 Relación entre el momento Flector y la Fuerza Cortante
Analizando un elemento diferencial de viga, la carga puede ser tomada constante.
Adoptando las direcciones de la figura para el momento flector y la fuerza cortante.
Peq
M
M+dM
Q
dx
Q+dQ
Fig. 5.5 Relación entre M y Q
Entonces :
Peq = p(x) dx
(5.7
De la estática  Fy = 0
Q = (q+dQ)+p(x)dx
(5.8
dQ/dx = -p(x)
(5.9
 Mder = 0
M - Peq dx/2 + Q dx - (M+dM) = 0
(5.10
M-p dxdx/2 + Q dx - M - dM = 0
(5.11
dM/dx = Q
(5.12
d2M /dx2 = -p
(5.13
De 5.8 y 5.11
Es decir que la derivada de la función del momento flector da la función de la fuerza cortante
y la derivada de esta da la función de la carga.
5.8 Determinación del Momento Flector y la Fuerza Cortante
Para la determinación del Momento Flector y la Fuerza Cortante se emplean generalmente
dos métodos: El cálculo estático y el cálculo por integración.
a) Cálculo estático.- Por este método se realiza un corte y el momento flector y la fuerza
cortante se calculan aplicando las ecuaciones de la estática

F  0

M  0
(5.13
b) Cálculo por integración.- Por este método el momento flector y la fuerza cortante se
calculan aplicando las EC. 5.8, 5.11 y 5.12., es decir integrando una vez la función de la
carga se obtiene la Fuerza Cortante e integrando dos veces la función de la carga se
obtiene el Momento Flector.
5.9 Valores del Momento Flector y la Fuerza Cortante en los extremos
Cuando se emplea el método de doble integración para el cálculo de la fuerza cortante y del
momento flector, la integración de la función de la carga origina constantes que deben
hallarse por las condiciones de borde, las mismas que se describen a continuación
a) M y Q para extremo izquierdo empotrado
Peq
Mr
M(x)
Rx
x
Rv
Q
Fig. 5.6 Valores de M y Q en los extremos extremo izquierdo empotrado
Cuando x  0. Peq = 0 y de la estática
Q = Ry
(5.14
M = -Mr
(5.15
b) M y Q para extremo izquierdo con apoyo fijo o móvil
Q = Ry
(5.16
M=0
(5.17
c) M y Q para extremo izquierdo libre
Q=0
(5.18
M=0
(5.19
d) M y Q para extremo derecho empotrado
Peq
Mr
M(x)
Rx
l-x
Q
Rv
Fig. 5.7 Valores de M y Q en los extremos extremo derecho empotrado
Cuando x  l Peq = 0 y de la estática
Q = -Ry
(5.20
M = - Mr
(5.21
e) M y Q para extremo derecho con apoyo fijo o móvil
Q = -Ry
(5.22
M=0
(5.23
f) M y Q para extremo derecho libre
Q=0
(5.24
M=0
(5.25
5.10 Cálculo de Momentos por funciones de Singularidad
Las funciones de singularidad se emplean para integrar cargas puntuales
Funcion
Forma
Valor
-2
<x-a>
Momento Puntual
x
<x-a>-2 = 1 si x=a
<x-a>-2 = 0 si x<>a
 <x-a> dx = <x-a>
-2
a
x
-1

<x-a>-1
Fuerza Puntual
x

a
x
x

<x-a>1
a
x
Carga Lineal
<x-a>-1dx = <x-a>0

<x-a>0
Carga Constante
<x-a>-1 = 1 si x=a
<x-a>-1 = 0 si x<>a
<x-a>0 = 0 si x<a
<x-a>0 = 1 si x>=a
<x-a>0dx = <x-a>1

x
<x-a>1= 0 si x<a
<x-a>1= (x-a) si x>=a
 <x-a> dx = <x-a> /2
1
2

<x-a>2
a
x
Parabola de Grado 2
x
<x-a>2 = 0 si x<a
<x-a>2 = (x-a)2 si x>=a
 <x-a> dx = <x-a> /3
2
a
x
3

5.11 Diagrama de Fuerzas Cortantes y de Momentos Flectores
Se denominan diagramas de fuerzas cortantes y de momentos flectores a los diagramas que
dan las fuerzas cortantes y momentos de flexión en cada sección de una barra prismática.
Fig. 5.8 Diagrama de Fuerzas Cortantes y de Momentos Flectores
PROBLEMAS RESUELTOS
5.1. Hallar la fuerza puntual equivalente y su ubicación de la carga distribuida cuya función
es p(x) = H(x/l)n.
l
Solución:
l ( n 1)
l
 x
Peq  W  H   dx  H
H
(n  1)
(n  1)l n
l
n

0
l
X eq 
 x
n
 H  l  xdx
0
l
H
(n  1)
H

l ( n  2)
(n  2)l n (n  1)l

l
(n  2)
H
(n  1)
5.2. Analizar los resultados del 5.1, para diferentes valores de n
Solución:
Cuando n = 0 carga constante
Cuando n = 1 carga triangular
Cuando n = 2 carga parabolica
Cuando 0<n<1 carga parabolica inv
5.3. Hallar el momento flector y la fuerza cortante de una carga triangular en una viga
simplemente apoyada.
Peq
H
A
B
l
Solución:
Peq = Área = Hl/2
xeq = CG = 2l/3
 MA = 0
Peq xeq – RB l = 0
RB = Hl/3
 MB = 0
RA l - Peq (l - xeq) = 0
RA = Hl/6
método de cortes
H
A
B
xeq
l
Peq
p=Hx/l
M
A
xeq
Q
x
La carga equivalente
Peq = Area = Hx2/2l
xeq = CG = 2x/3
 Mcorte = 0 RA x- Peq (x – xeq) – M = 0
M = (Hl/6)x – (Hx2/2l)(x/3)
M = Hlx(1- x2/l2)/6
 Fy = 0
(i
RA - Peq – Q = 0
Q = Hl/6 – Hx2/2l
Q = H (l/6 – x2/2l)
(ii
b) método de la doble integración
p = Hx/l
Integrando
Q = -Hx2/2l + c1
M = -Hx3/6l + c1 x + c2
Las condiciones de borde
x=0M=0
c2 = 0
x=lM=0
0 = -Hl2/6 +c1l
c1 = Hl/6
de donde
Q = - Hx2/2l + Hl/6
(iii
M = -Hx3/6l + Hlx/6
(iv
c) método de la doble integración de funciones singulares
p(x) = Ra <x>-1- (H/l)<x>1 + Rb<x-l>-1
p(x) = (Hl/6)<x>-1- (H/l)<x>1+(Hl/3)<x-l>-1
Integrando y aplicando las propiedades de las funciones de singularidad
Q = Hl/6<x>0- (H/2l)<x>2+(Hl/3)<x-l>0
M = (Hl/6)<x>1- (H/6l)<x>3+(Hl/3)<x-l>1
Cuando 0<x<l
<x>1 = x
<x>3 = x
<x-l>1 = 0
Q = Hl/6 - (Hx2/2l)
(v
M = Hlx/6 –Hx3/6l
(vi
Los resultados son los mismos por todos los métodos
5.4. Hallar las funciones de Momento Flector y Fuerza Cortante del sistema de la figura
p(x)=Hx2/l2
Peq
H
A
B
A
xeq
RA
L
Solución:
De 2
Peq = Hl/3
xeq = 3l/4
 Ma = 0
Peq xeq-Rb l = 0
Rb = (Hl/3)(3l/4)/l
Rb = Hl/4
 Mb = 0
Ra l - Peq (l - xeq) = 0
Ra = (Hl/3)(l-3l/4)/l
Ra = Hl/12
Prueba
Ra + Rb = Hl/4 + Hl/12 = 4HL/12 = Hl/3 = Peq
a) Método de cortes
Peq
M
A
RA
xeq
Q
x
La carga equivalente
p(x)=Hx2/l2
OK
x
2
x3
 x
Peq  W  H   dx  H 2
3l
l

0
X eq
 Fy = 0
2
4
 x
0 H  l  xdx H 4xl 2 3x



4
x3
x3
H 2
H 2
3l
3l
x
Ra - Peq - Q = 0
Q = Ra – Peq = Hl/12- Hx3/3l2
(i
 Mcorte = 0 Ra x - Peq (x-xeq) – M = 0
M = (Hl/12)x-(Hx3/3l2)(x/4)
M = Hlx/12 - (Hx4/12l2)
(ii
x=0
Q = Hl/12 = Ra
Ok
x=l
Q = Hl/12-Hl/3 = -3Hl/12 = -Hl/4 = -Rb
Ok
x=0
M=0
Ok
x=l
M = Hl2/12-(Hl/3)(l/4) = 0
Ok
Finalmente
M Hl Hx3

Q
x 12 3l2
Ok
Prueba:
b) Método de la doble integración
p = H(x/l)2
Integrando
Q = -Hx3/3l2 + c1
Integrando
M = -Hx4/12l2+c1x+c2
x=0M=0
0 = c2
x=lM=0
0 = -Hl2/12 + c1l
c1 = Hl/12
De donde
Q = -Hx3/3l2+Hl/12
M = -Hx4/12l2+Hl/12x
(iii
(iv
Idénticas expresiones a las halladas por el otro método.
5.5. Una viga simplemente apoyada tiene una carga distribuida cuya función p(x) = H(x/l)n.
a) Hallar la carga equivalente b) Hallar las reacciones y c) Hallar el momento flector y la
fuerza cortante
p(x)=H(x/l)n
Peq
H
A
B
A
RA
L
xeq
RB
Solución:
(n 1)
l  x n
l
l
Peq  W   H   dx  H
H
n
l
(
n
 1)
(
n

1
)
l


0
( n  2)
l  x n
l
 H   xdx H
n
( n  1)l
l
( n  2 )l
X eq  0  


l
l
( n  2)
H
H
( n  1)
( n  1)
 Ma = 0
Peq xeq-Rb l = 0
Rb = Hl/(n+2)
 Mb = 0
Ra l - Peq (l-xeq) = 0
Ra´ = Hl/(n+2)(n+1)
Prueba
Ra + Rb = Hl/(n+1) = Peq
OK
a) Método de cortes
Peq
M
A
xeq
RA
p(x)=H(x/l)n
Q
x
x
X eq 
 x
n
 H  l  xdx
0
H
x
( n 1)

H
(n  1)l n
x
H
x ( n  2)
(n  2)l n (n  1) x

(n  2)
x ( n 1)
(n  1)l n
x( n 1)
 x
Peq  W  H   dx  H
l
(n  1)l n
 

n
0
 Fy = 0
Ra - Peq - Q = 0
Q
H  l
x n 1 
 n 
(n  1)  n  2
l 
(i
 Mcorte = 0 Ra x - Peq (x-xeq) –M = 0
M
 x n 1 
Hx
l 

(n  2)(n  1) 
l n 
(ii
Verificación
x=0
Q = Hl/(n+1)(n+2) = Ra
Ok
x=l
Q = Hl/(n+1)(n+2)-Hl/(n+1) = -Hl/(n+2) = -Rb
Ok
x=0
M=0
Ok
x=l
M=0
Ok
Finalmente
M
Q
x
Ok
b) Método de la doble integración
p = H(x/l)n
Q
Integrando
Hx( n 1)
l n (n  1)
M 
 c1
(i
Hx( n  2)
l (n  2)(n  1)
n
 c1x  c2
(ii
Condiciones de borde
x=0M=0
0 = c2
x=lM=0
0 = -Hl2/(n+2)(n+1) + c1l
c1 = Hl/(n+2)(n+1)
Q
De donde
M
H  l
x n 1 
 n 

(n  1)  n  2
l 
(i
 x n 1 
Hx
l 

(n  2)(n  1) 
l n 
(ii
Idénticas expresiones a las halladas por el otro método. No se aplica el método de doble
integración de funciones de singularidad por ser muy similar.
5.6. Una viga simplemente apoyada tiene una carga cuya función p(x) = H(x/l)n. Hallar el
momento flector y la fuerza cortante máximos.
Peq
H
A
B
L
Solución: Del 5.anterior
Q
H  l
x n 1 

 n 
(n  1)  n  2 l 
A
RA
xeq
RB
cuando x = l Qmax = - Rb = - Hl/(n+2)
M
 x n 1 
Hx
 l  n 
(n  2)(n  1) 
l 
Máximo cuando Q = 0
Q
H  l
x n1 

 n   0
(n  1)  n  2 l 
l (n+1)/ (n+2) = x(n+1)
x = l/ (n+2)1/(n+1)
M max 
M max 
Hl 2
(n  2) ( n  2) /( n1) (n  2)
Hl 2
(n  2) ( 2 n 3) /( n 1)
5.7. Hallar el momento flector y la fuerza cortante de una viga simplemente apoyada con una
carga cuya función p(x) = H(1-x/l)n
H
p(x)=H(1-x/l)n
A
RA
B
l
RB
Solución: Este problema es el conjugado del problema anterior y basta reemplazar en los
resultados obtenidos x por su complemento l-x
Carga
p = H(l-x)/ln = H (1-x/l) n
(i
Fuerza Cortante
Q
H  l
(l  x)n 1 



(n  1)  n  2
ln

(ii
H (l  x)  (l  x)n 1 
l

(n  2)(n  1) 
ln

(iii
Momento Flector
M
5.8. Hallar el momento flector y la fuerza cortante de una carga triangular en una viga
simplemente empotrada.
Peq
H
M
o
l
xeq
R
R
Solución:
Peq = Area = Hl/2
xeq = CG = 2l/3
 Mo = 0
Peq (l-xeq )– Mr = 0
Mr = - Hl2 /6
 Fy = 0
R - Peq = 0
R = Hl/2
a) Método de cortes
Peq
M
xeq
x
p(x)=Hx/l
Q
La carga equivalente
Peq = Area = Hx2/2l
xeq = CG = 2x/3
 Mcorte = 0 Peq (x – xeq) + M = 0
M = – (Hx2/2l)(x/3)
M = – Hx3 /6l
 Fy = 0
- Peq – Q = 0
Q = – Hx2/2l
b) Método de la doble integración
p = Hx/l
Integrando
(I
Q = -Hx2/2l + c1
M = -Hx3/6l + c1 x + c2
Condiciones de borde
(ii
x=0M=0
c2 = 0
x=0Q=0
c1 = 0
De donde
Q = -Hx2/2l
(iii
M = -Hx3/6l
(iv
c) método de la doble integración de funciones singulares
p(x) = (H/l)<x>1 + R<x-l>-1
p(x) = (H/l)<x>1+(Hl/2)<x-l>-1
Integrando y aplicando las propiedades de funciones de singularidad
Q = - (H/2l)<x>2+(Hl/2)<x-l>0
M = - (H/6l)<x>3+(Hl/2)<x-l>1
Cuando 0<x<l <x>1 = x
<x>3 = x
<x-l>1 = 0
y
Q = - (Hx2/2l)
(v
M = – Hx3/6l
(vi
Los resultados son los mismos por todos los métodos
5.9. Hallar las funciones de Momento Flector y Fuerza Cortante del sistema de la figura
Peq
H
p(x)=H(x/l)2
M
p(x)=H(x/l)2
o
l
R
Solución:
Peq = Hl/3
xeq = 3l/4
 Mo = 0
Peq (l - xeq) = - Mr
Mr = Hl2 /12
 Fy = 0
R = (Hl/3)
a) Método de cortes
R - Peq = 0
xeq
Peq
p(x)=H(x/l)2
M
xeq
x
x
Q
2
x3
 x
Peq  W  H   dx  H 2
3l
l

0
x
X eq 
 Fy = 0
x
2
 H  l  xdx
0
x
H
3
H

x4
4l 2  3x
x
4
H
3
- Peq - Q = 0
Q = -Hx3/3l2
(i
 Mcorte = 0 - Peq (x-xeq) – M = 0
M = -(Hx3/3l2)(x/4) = - (Hx4/12l2)
(ii
x=0
Q=0
Ok
x=l
Q = -Hl/3 = -Rb
Ok
x=0
M=0
Ok
x=l
M = Hl2/12 = Mr
Ok
Finalmente
M
Hx 3
- 2 Q
x
3l
Ok
Verificación
b) Método de la doble integración
p = H(x/l)2
Integrando
Q = -Hx3/3l2 + c1
M = -Hx4/12l2+c1x+c2
x=0M=0
0 = c2
x=0Q=0
0 = c1
De donde
Q = -Hx3/3l2
(iii
M = -Hx4/12l2
(iv
Idénticas expresiones a las halladas por el método de cortes
5.10. Una viga simplemente empotrada tiene una carga cuya función es p(x) = H(x/l)n. Hallar
a) La carga equivalente b) Las reacciones y c) El momento flector y la fuerza cortante
Peq
H
p(x)=H(x/l)n
p(x)=H(x/l)n
M
o
l
xeq
R
Solución:
(n 1)
l  x n
l
l
Peq  W   H   dx  H
H
n
l
(
n
 1)
( n  1)l
0  
( n  2)
l  x n
l
 H   xdx H
n
( n  1)l
l
( n  2 )l
X eq  0  


l
l
( n  2)
H
H
( n  1)
( n  1)
 Mo = 0
Peq (l - xeq) = Mr
Mr = Hl2/(n+1)(n+2)
 Fy = 0
R - Peq = 0
R = Hl/(n+1)
a) Método de cortes
Peq
p(x)=H(x/l)n
M
xeq
x
x
Q
x( n 1)
 x
Peq  W  H   dx  H
(n  1)l n
l
n

0
x
X eq 

0
n
 x
H   xdx
l
H
 Fy = 0
x
( n 1)
H

(n  1)l n
H
x ( n  2)
(n  2)l n (n  1) x

(n  2)
x ( n 1)
(n  1)l n
- Peq - Q = 0
Q  H
x( n 1)
(n  1)l n
(i
 Mcorte = 0 - Peq (x-xeq) –M = 0
M 
Verificación
Hx( n  2)
(n  2)(n  1)l n
(ii
x=0
Q=0
Ok
x=l
Q = -Hl/(n+1) = -Rb
Ok
x=0
M=0
Ok
x=l
M = -Hl2/(n+2)(n+1) = Mr
Ok
Finalmente
M
Hx3
- 2 Q
x
3l
Ok
b) Método de la doble integración
p = H(x/l)n
Q
Integrando
Hx( n 1)
l n (n  1)
M 
l n (n  2)(n  1)
0 = c2
x=0Q=0
0 = c1
De donde
(i
Hx( n  2)
x=0M=0
Q
 c1
 c1x  c2
(ii
Hx( n 1)
l n (n  1)
M 
(i
Hx( n  2)
l (n  2)(n  1)
n
(ii
Idénticas expresiones a las halladas por el método de cortes. No se aplica el método de
doble integración de funciones de singularidad por ser muy similar.
5.11. Hallar los valores máximos de la fuerza cortante y del momento flector de la viga del
problema anterior.
Peq
H
p(x)=H(x/l)n
p(x)=H(x/l)n
M
o
l
R
xeq
Solución:
Q
De 5.10
M 
Hx( n 1)
l n (n  1)
(i
Hx( n  2)
l (n  2)(n  1)
n
Máximos en el empotramiento (x = l)
(ii
Qmax  
Hl
(n  1)
M max  
Hl 2
(n  2)(n  1)
5.12. Hallar las funciones de Momento Flector y Fuerza Cortante del sistema de la figura
x
H
x'
p(x)=H((l-x)/l)n
M
o
l
R
Solución:
Se reemplaza en 5.11 x por su complemento l - x
Carga
p = H(x/l)n
p = H(l-x)/ln = H (1-x/l) n
Q
Fuerza Corte
Q
(i
Hx( n 1)
l n (n  1)
(i
H (l  x)( n 1)
M 
Momento
M 
l n (n  1)
Hx( n  2)
l n (n  2)(n  1)
(ii
H (l  x)( n  2)
l (n  2)(n  1)
n
5.13. Hallar la fuerza cortante y momento flector del sistema de la figura
P
P
M1
a
l-a
Solución:
Ma = 0
P(a) - Rbl = 0
Rb = Pa/l
Mb = 0
Ral - P(l-a) = 0
Ra = P(l-a)/l
x
Q1
M2
a
x
Q2
Prueba
Ra + Rb = P
Ok
a) Método de los cortes
1er intervalo Ra x = M1
M1 = P(l-a)x/l
2do intervalo Ra x - P(x-a) - M2 = 0
M2 = P(l-a)x/l - P(x-a) = Pa (1-x/l)
b) Método de integración con funciones de singularidad
De derecha a izquierda
p(x) = Ra <x>-1 - P<x-a>-1 + Rb<x-l>-1
p(x) = P(l-a)/l<x>-1 - P<x-a>-1 + Pa/l<x-l>-1
Integrando y aplicando las propiedades de este tipo de funciones
Q = P(l-a)/l<x>0 - P<x-a>0 + Pa/l<x-l>0
M = P(l-a)/l<x>1 - P<x-a>1 + Pa/l<x-l>1
Cuando 0<x<a
<x>1 = x
<x-a>1 = 0
<x-l>1 = 0
y
M1 = P(l-a)x/l
Para a<x<l
<x>1 = x
<x-a>1 = x-a
<x-l>1 = 0
y
M2 = P(l-a)x/l - P(x-a) = Pa(1-x/l)
Idénticas expresiones a las halladas por el método de cortes.
5.14. Hallar la EC. de deformaciones, pendientes y valores máximos de estos en el sistema
de la figura usando funciones de singularidad
P
M
R
a
b
P
M1
M
R
x
M2
M
a
Q1
R
x
Solución:
 Fy = 0
R=P
M=0
Mr = P a
a) Método de los cortes
1er intervalo R x – M - M1 = 0
M1 = Px – Pa
2do intervalo R x – M - P(x-a) - M2 = 0
M2 = Px – Pa - P(x-a)
b) Método de integración con funciones de singularidad
Usando funciones de singularidad y de derecha a izquierda
p(x) = -Mr <x>-2 + R <x>-1- P<x-a>-1
p(x) = -Pa <x>-2 + P <x>-1 - P<x-a>-1
Integrando y aplicando las propiedades de este tipo de funciones
Q(x) = -Pa <x>-1 + P <x>0 - P<x-a>0
M(x) = -Pa <x>0 + P <x>1 - P<x-a>1
Para 0<x<a
<x>-1 = 0
<x>0 = 0
<x-a>0 = 0
<x-a>1 = 0
entonces
Q(x) = P
M(x) = -Pa x + P x
Para a<x<l
<x>-1 = 0
<x>0 = 0
<x-a>0 = 0
<x-a>1 = 0
entonces
Q(x) = 0
Q2
M(x) = 0
5.15. Hallar la fuerza cortante y momento flector del sistema de la figura
M
M
M1
a
l-a
x
Q1
M2
a
x
Q2
Solución:
Ma = 0
M - Rbl = 0
Rb = M/l
Mb = 0
Ral + M = 0
Ra = -M/l
Comprobación
Ra + Rb = 0
a) Método de los cortes
1er intervalo Ra x = M1
M1 = - Mx/l
2do intervalo Ra x + M - M2 = 0
M2 = -Mx/l +M
b) Método de integración con funciones de singularidad
De derecha a izquierda
p(x) = Ra <x>-1 + M<x-a>-2 + Rb<x-l>-1
p(x) = -M/l<x>-1 + M<x-a>-2 + M/l<x-l>-1
Integrando y aplicando las propiedades de este tipo de funciones
Q = -M/l<x>0 + M<x-a>-1 + M/l<x-l>0
M = -M/l<x>1 +M<x-a>0 + M/l<x-l>1
Para 0<x<a
<x>1 = x
<x-a>0 = 0
<x-l>1 = 0
y
M1 = -Mx/l
Para a<x<l
<x>1 = x
<x-a>0 = 1
Ok
<x-l>1 = 0
y
M2 = -Mx/l + M
Idénticas expresiones a las halladas por el método de cortes.
5.16. Hallar solo el momento flector de los sistemas de la figura. En todos los casos p(x) =
H(1+x/l)
2H
2H
H
H
2H
H
M
l
Ra
(a)
l/4
l
R
(b)
Rb
Ra
3l/4
(c)
Rb
Solución:
2l/3
Peq1
l/2
Peq2
2H
H
Peq1 = Hl/2
Peq2 = Hl
l
Se halla primero las reacciones en los apoyos de los tres casos
(a) Ma = 0
Peq1 xeq1 + Peq2 xq2-Rb l = 0
Rb l = (Hl/2)(2l/3) + (Hl)(l/2)
Rb = 5Hl/6
Mb = 0
Ral - Peq1 (l – xeq1) - Peq2(l - xeq2) = 0
Ra l = (Hl/2)(l - 2l/3) + (Hl)(l - l/2) = (Hl/2)(l/3) + (Hl)(l/2)
Ra = 4H/6 = 2Hl/3
Prueba
Ra + Rb = 5H/6 + 2H/3 = 9H/6 = 3H/2 = Peq1+Peq2
(b) Fy = 0
R = Peq1 + Peq2
R = ·3Hl/2
Mo = 0
M = Peq1 xeq1 + Peq2 xeq2
M = (Hl/2)(2l/3) + (Hl)(l/2) = 5Hl2/6
(c) Ma = 0
Peq1 (xeq1-l/4) + Peq2(xeq2-l/4) - Rb(3l/4) = 0
Rb(3l/4) = (Hl/2)(2l/3 - l/4) + (Hl)(l/2 - l/4) = (Hl/2)(5l/12) + (Hl)(l/4)
Rb = 11Hl/18
Ok
Mb = 0
Ra(3l/4) - Peq1 (l-xeq1) - Peq2(l-xeq2) = 0
Ral(3l/4) = (Hl/2)(l-2l/3) + (Hl)(l-l/2) = (Hl/2)(l/3) + (Hl)(l/2) = 2H/3
Ra = 8Hl/9
Prueba
Ra + Rb = 11H/18 + 8H/9 = 27H/18 = 3H/2 = Peq1 + Peq2
Ok
A continuación se hallan la Fuerza Cortante y el Momento Flector por integración
Integrando
Q = -H(x+x2/2l) + c1
M = - H(x2/2 + x3/6l) + c1x + c2
Las constantes dependen de las condiciones de borde en los tres casos
a) Si x = 0
M=0
c2 = 0
Si x = l
M = 0 0 = - H(l2/2 + l2/6) + c1l
c1 = 2Hl/3
M = - H(x2/2 + x3/6l - 2lx/3)
b) Si x = l
Q = 0 0 = -H(l+l/2)+c1
c1 = 3Hl/2
Si x = l
M = 0 0 = -H(l2/2+l3/6)+(3Hl/2)l+c2 c2 = -5Hl2/6
M = -H(x2/2+x3/6l)+3Hlx/2-5Hl2/6
c) En este caso hay dos intervalos pero como la carga es la misma en los dos intervalos la
variación se da solamente en las constantes. Entonces
Q1 = -H(x+x2/2l)+c1
valido 0<x<l/4
M1 = -H(x2/2+x3/6l)+c1x+c2
Q2 = -H(x+x2/2l)+c3
valido l/4<x<l
M2 = -H(x2/2+x3/6l)+c3x+c4
Y las condiciones de borde son
Si x = 0
Q1 = 0
c1 = 0
Si x = 0
M1 = 0
c2 = 0
Si x = l
Q2 = - Rb -H(l+l/2) + c3 = -11Hl/18 c3 = 8Hl/9
Si x = l
M2 = 0
0 = - H(l2/2+l3/6) + 19Hl/9 + c4
M1 = -H(x2/2+x3/6l)
M2 = -H(x2/2+x3/6l+8lx/9-2l2/9)
5.17. Hallar el momento flector del sistema de la figura
c4 = -2Hl2/9
2l/9
2l/9
l/6
H
P1
H
P2
l/3
l/3
2l/ 3
Ra
Rb
Ra
P3
2l/3
Rb
Solución:
La carga se descompone en formas más sencillas
P1 = Hl/6
x1 = 2l/9
P2 = Hl/3
x2 = l/6
P3 = 2Hl/3
x3 = l/3 + 2l/9 = 5l/9
Ma = 0
P1 x1+P2 x2 + P3x3 - Rbl = 0
Rb = (Hl/6)(2l/9) + (Hl/3)(l/6) + (2Hl/3)(5l/9)
Rb = 25Hl/54
Mb = 0
Ral – P1(l-x1) - P2(l-x2) - P3(l-x3) = 0
Ra = Hl/6(l-2l/9) + (Hl/3)(l-l/6) + (2Hl/3)(l-5l/9)
Ra = 38Hl/54
Prueba
Ra + Rb = 25Hl/54 + 38HL/54 = 7Hl/6 = Hl/6 + Hl/3 + 2Hl/3
Se analiza el sistema en dos intervalos
P1 = Hx/(l/3) + H
P2 = -3Hx/l + 3H
Integrando
Q1 = -3Hx2/2l – Hx + c1
M1 = -Hx3/2l - Hx2/2 + c1x + c2
Q2 = 3Hx2/2l - 3Hx + c3
M2 = Hx3/2l - 3Hx2/2 + c3x + c4
Las condiciones de borde son
x = 0 Q1 = Ra
c1 = 38Hl/54
Ok
De donde
x = 0 M1 = 0
c2 = 0
x = l Q2 = - Rb
- 25Hl/54 = 3Hl2/2l-3Hl+c3
x = l M2 = 0
0 = Hl3/2l - 3Hl2/2 + c3l + c4
c3 = 28Hl/27
c4 = Hl2 /27
M1 = - Hx3/2l – Hx2/2 + 19Hlx/27
M2 = Hx3/2l - 3Hx2/2 + 28Hlx/27 + Hl2/27
5.18. Hallar la fuerza cortante y momento flector del sistema de la figura
Hl/4
Hl/4
H
H
l/2
l/2
l/2
Ra
l/2
Ra
Rb
Rb
Solución:
Aplicando el método de doble integración y por simetría solo en la mitad izquierda
Ra = Rb = Hl/4
p1 = 2Hx/l
Q1(x) = - 2Hx2/(2l) + c1
M1(x) = - Hx3/(3l) + c1 x + c2
Condiciones de Borde
x=0M=0
c2 = 0
x = 0 Q = Ra
c1 = Ra = Hl/4
Q1(x) = - Hx2/l + Hl/4
M1(x) = - Hx3/(3l) + Hlx/4
Estas ecuaciones solo son válidas cuando 0<x<l/2
5.19. Hallar la fuerza cortante y momento flector del sistema de la figura
Peq
Peq  H
H
H
xeq 
a
a
l-a
Ra
l-a
Rb
( l  a)
2
( l  a)
3
Solución:
Ma = 0
Peq (l-xeq) - Rbl = 0
[H(l-a)/2][l-(l-a)/3] = Rbl
[H(l-a)/2][a/3+2l/3] = Rbl
Rb = H(l-a)(a+2l)/(6l)
Mb = 0
Ral - Peq(l-a)/3 = 0
Ral = [H(l-a)/2](l-a)/3
Ra = H(l-a)2/(6l)
Prueba
Ra + Rb = [H/(6l)](l - a)[(a + 2l) + (l - a)]
Ra + Rb = [H/(6l)](l - a)(3l) = H(l - a)/2 = Peq
Ok
a) Método de los cortes
Q1
Ra
peq
p
M2
M1
a
x
x a
l a
x a
 p
2
p  H
p eq
Q2
x
Ra
peq  H
xeq 
x  a 2
2( l  a )
x a
3
1er intervalo Ra x = M1
M1 = - H x (l-a)2/(6l)
2do intervalo Ra x – Peq xeq - M2 = 0
M2 = Hx(l-a)2/(6l)-H(x-a)3/[6(l-a)]
b) Método de integración con funciones de singularidad
H
Ra
a
la
Rb
De derecha a izquierda
p(x) = Ra <x>-1 + [H/(l-a)]<x-a>1 + Rb<x-l>-1
p(x) = H(l-a)2/(6l)<x>-1 + [H/(l-a)]<x-a>1 + H(l-a)(a+2l)/(6l)<x-l>-1
Integrando y aplicando las propiedades de este tipo de funciones
Q(x) = H(l-a)2/(6l)<x>0+H/[2(l-a)]<x-a>2+H(l-a)(a+2l)/(6l)<x-l>0
M(x) = H(l-a)2/(6l)<x>1+H/[6(l-a)]<x-a>3+H(l-a)(a+2l)/(6l)<x-l>1
Para 0<x<a
<x>1 = x
<x-a>1 = 0
<x-l>1 = 0
y
M1(x) = H(l-a)2/(6l) x
Para a<x<l
<x>1 = x
<x-a>1 = x-a
<x-l>1 = 0
M2(x) = Hx(l-a)2/(6l) – H(x-a)3/[6(l-a)]
Las expresiones obtenidas por los métodos de cortes e integración son idénticas.
PROBLEMAS PROPUESTOS
5.20. Hallar la fuerza puntual equivalente y su ubicación de la carga distribuida p(x) = H Sin
(x/2l).
5.21. Hallar la fuerza puntual equivalente y su ubicación de una carga distribuida de forma
semicircular
5.22. Hallar el momento flector y la fuerza cortante de una viga simplemente apoyada con
carga p(x) = H Sin (x/2l).
5.23. Hallar el momento flector y la fuerza cortante de una viga simplemente empotrada con
carga p(x) = H Sin (x/2l).
5.24. Hallar el momento flector y la fuerza cortante de una viga simplemente empotrada con
carga semicircular
5.25. Hallar el momento flector y la fuerza cortante de una viga simplemente empotrada con
carga semicircular.
5.26. En la viga de la figura se pide el momento flector y la fuerza cortante
H
l/2
l/2
Rb
Ra
5.27. En la viga de la figura se pide el momento flector y la fuerza cortante
H
M
l/2
R
l/2
5.28. En la viga de la figura se pide el momento flector y la fuerza cortante
H
l/2
Ra
l/2
Rb
5.29. En la viga de la figura se pide el momento flector y la fuerza cortante
H
M
l/2
R
l/2
5.30. Hallar la fuerza cortante y momento flector del sistema de la figura
H
M
H
Rx
l/3
Ry
l/4
5l/12
5.31. Hallar la fuerza cortante y momento flector del sistema de la figura
H
H
l/3
l/4
5l/1 2
Rb
5.32. Hallar el Momento Flector y Fuerza Cortante del sistema de la figura
H
M
l/2
l/2
R
5.33. Hallar solo el momento flector de los sistemas de la figura.
l/2
l/2
l/2
l/2
H
H
H
H
H
H
l/4
RA
l/2
3l/4
RB
5.34. Hallar el momento flector del sistema de la figura
RA
l/2
RB
H
H
l/3
l/3
l/3
RA
RB
5.35. Hallar la fuerza cortante y momento flector del sistema de la figura
P
H
l-a
a
RB
RA
5.36. Hallar la fuerza cortante y momento flector del sistema de la figura
2H
H
l-a
a
RB
RA
5.37. Hallar la fuerza cortante y momento flector del sistema de la figura
P
B
A
L/4
L
5.38. Hallar la fuerza cortante y momento flector del sistema de la figura
m0
B
A
L
5.39. Hallar la fuerza cortante y momento flector del sistema de la figura
La carga distribuida tiene una intensidad q = qo·sen(x/L)
q0
q=q0 sen(·x/L)
B
A
L
.
5.40. Hallar la fuerza cortante y momento flector del sistema de la figura
q ox
q( x)
L
B
2/3·L
L/3
A
5.41. Hallar la fuerza cortante y momento flector del sistema de la figura
La intensidad de carga varía según la onda senoidal, con valor q = qo·sen(x/L).
q0
q=q0 sen(·x/L)
B
2/3·L
L/3
A
5.42. Hallar la fuerza cortante y momento flector del sistema de la figura
P
q0=P·a
C
a
a
a
B
A
5.43. Hallar la fuerza cortante y momento flector del sistema de la figura
P
q( x)
q ox
q0=P·a
L
L/3
L
5.44. Hallar la fuerza cortante y momento flector del sistema de la figura
q0=P·a
q0=P·a
P
C
a
a
B
A
5.45. Hallar la fuerza cortante y momento flector del sistema de la figura
q0=P·l
q0=P·l
P
C
C
a
a
A
B
L
5.46. Hallar la fuerza cortante y momento flector del sistema de la figura
q0=P·l
C
L/3
L/3
A
B
L
5.47. Hallar la fuerza cortante y momento flector del sistema de la figura
q0=P·l
P
B
A
L
3L
5.48. Hallar la fuerza cortante y momento flector del sistema de la figura
q0=P·l
P
EI
l/4
l/4
l
5.49. Hallar la fuerza cortante y momento flector del sistema de la figura
q(x)=qo·x2/L2
EI
B
A
l
5.50. Hallar la fuerza cortante y momento flector del sistema de la figura
q0=P·l
q0=P·l/2
EI
l/2
l/2
5.51. Hallar la fuerza cortante y momento flector del sistema de la figura
q0=P·l
q(x)=qo·x2/L2
2P
EI
l/2
l
5.52. Hallar la fuerza cortante y momento flector del sistema de la figura
q0
l/2
l
B
A
5.53. Hallar la fuerza cortante y momento flector del sistema de la figura
q0=P·l
q0=P·l/2
EI
l/2
l/2
5.54. Hallar la fuerza cortante y momento flector del sistema de la figura
q0
l/3
l/3
l/3
5.55. Hallar la fuerza cortante y momento flector del sistema de la figura
Hl/4
Hl/4
H
l/2
Ra
l/2
Rb
6 Flexión – Tensiones Normales y Cortantes
6.1 Introducción
En este capítulo se desarrollarán las ecuaciones para calcular las tensiones que se
presentan en elementos sometidos a flexión. Las tensiones no deben exceder a los límites
de fluencia de los materiales empleados.
6.2 Tensiones Normales en Flexión
Considérese una viga sometida a un estado de flexión
Deflexion de la Viga
Fig. 6.1 Viga sometida a Flexión
Un elemento recto de pequeña longitud de la viga sin carga, se curvea por efecto de las
cargas y algunas fibras se acortan mientras que otras se alargan.
Fig. 6.2 Acortamiento y Alargamiento de las Fibras
El elemento diferencial curvo puede ser considerado como un arco de circulo con centro en
O y radio . La porción superior AB es de menor longitud a la inferior CD debido a que las
fibras superiores se comprimen y las inferiores se alargaron. Existe un plano llamado
“neutro” oo que no se alarga ni se acorta (no hay deformación y tampoco hay tensiones).
Fig. 6.3 Deformación de un Elemento Diferencial
Tomando el plano neutro como referencia, se observa que la deformada del elemento a una
distancia “y” es:
d = y d
(6.1
 = d/ds = y d/ds
(6.2
del Grafico
ds =  d
(6.3
de 6.2 y 6.3
=y/
(6.4
=E=Ey/
(6.5
De la ec 6.5 se aprecia que las tensiones normales en cualquier punto son proporcionales a
la distancia del mismo al eje neutro. Las tensiones son nulas en el eje neutro y máximas en
las fibras más alejadas.
Fig. 6.4 Distribución de Tensiones Normales
En la ec 6.5  es desconocido. De la estática
Fx = 0
 dF  N  0
A
(6.6
dF =  dA = (Ey/)dA
E

(6.7
 ydA  0
A
(6.8
En esta ecuación E/ no es cero por lo que
 ydA  0
A
(6.9
Entonces el origen del sistema de coordenadas empleado debe estar situado en el centro
geométrico de la sección transversal (que es equivalente al centro de gravedad en el caso
de vigas homogéneas). En otras palabras el eje neutro coincide con el eje centroidal de la
viga
La estática, además de requerir equilibrio de fuerzas requiere el equilibrio de momentos
M = 0
 dFy  M
A
(6.10
dF =  dA = (Ey/)dA
M 
y dA 

E
2
A
(6.11
EI

(6.12
El valor de “I” es el Momento de Inercia de la sección. Entonces de 6.5 y 6.12

Mc
I
 max 
(6.13
M max c
I
(6.14
El momento flector “M” depende únicamente del tipo de viga y carga, mientras que los
valores de “c” e “I” dependen exclusivamente de la sección transversal de la viga.
6.3 Tensiones Cortantes en Flexión
Considérese un elemento diferencial al que se realiza un corte en ab.
Fig. 6.5 Tensiones Cortantes en la Sección Superior
En las secciones laterales del elemento diferencial se aparecen tensiones normales
mientras que en la sección superior aparecen tensiones cortantes
De la estática
Fx = 0
 (  d )dA   dA  A
sup
Alat
Alat
0
(6.15
 ddA  A
sup
0
Alat
de 6.13
(6.16
 = M y / EI
(6.17
d = dM y / EI
(6.18
Asup = b dx
En 6.16
dMy
dA  bdx  0
EI
Alat
(6.19
dM
EI
(6.20

 ydA  bdx
Alat

Q y p Ap
dM

ydA 

Ibdx Alat
Ib
(6.21
La integral (yp y Ap) no son del área total sino del área parcial.

QS
Ib
(6.22
_
S

0
QyA
ydA 
Ib
 max 
(6.23
Qmax S max
Ib
(6.24
El valor de “Q” depende únicamente del tipo de viga y carga, mientras que los valores de
“S”, “I” y “b” dependen exclusivamente de la sección de la viga.
Las tensiones cortantes tienen una distribución parabólica y sus valores mínimos se
presentan en los extremos superior e inferior de la viga, mientras que su valor máximo se
presenta en el plano neutro, contrariamente a las tensiones normales que tienen una
distribución lineal y sus valores máximos se presentan en los extremos superior e inferior y
son nulos en el plano neutro
Fig. 6.6 Distribución Parabólica de las Tensiones Cortantes
6.4 Perfiles Comunes Usados en Vigas
Los perfiles más usados en vigas son los que tienen valores altos de Inercia, y por ello
generalmente se usan perfiles con secciones de mayor alto que ancho. En la figura se
muestran los perfiles preferidos para secciones transversales de vigas de los cuales se
hallarán las ecuaciones reducidas para calcular las tensiones de normales y cortantes.
Fig. 6.7 Perfiles Comunes Usados en vigas
PROBLEMAS RESUELTOS
6.1. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
un perfil rectangular.
ycg
h
b
Eje Neutro
h/2-y
Solución:
a) Tensiones Normales
ycg = h/2
c = +/- h/2
I = bh3/12

 
My My 12My
 3 
I
bh
bh3
12
My My 12My
 3 
I
bh
bh3
12
 max 
Mc M (h / 2) 6M

 2
I
bh3
bh
12
b) Tensiones Cortantes
La línea a-a divide el perfil en dos secciones: La superior 1 y la inferior 2.
Aparcial = b(h/2-y)
ycgparcial = y + (½)(h/2-y)
S = Apycgparcial = b(h/2-y)[y+(1/2)(h/2-y)] = b(h/2-y)(h/2+y)(1/2)
S = b(h2/4-y2)/2
En 1
Aparcial = b(h/2+y)
ycgparcial = (h/2+y)/2-y = (h/2-y)/2
S = b(h2/4-y2)/2
Entonces
S = b(h2/4-y2)/2
Smax y = 0 = bh2/8

QS

Ib
Qb(
2
h2
1 6Q( 1  y )
 y2 )
4 h2
4
2 
3
bh
bh
b
12
max = 1,5 Q/A
6.2. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
un perfil triangular.
h
LN
2h/3+y
h/3
h/3-y
b
Solución:
a) Tensiones Normales
ycg = h/3
c1 = h/3
c2 = 2h/3
I = bh3/36
 
My My 36My
 3 
I
bh
bh3
36
 max tracc 
Mc1 M (h / 3) 12M


I
bh3
bh2
36
 max comp 
Mc2 M (2h / 3) 24M


I
bh3
bh2
36
b) Tensiones Cortantes
De nuevo la línea a-a divide el perfil en dos secciones: La superior 1 y la inferior 2.
h/B = (2h/3+y)/b
b = (2h/3+y)B/h
A1 = b(2h/3+y)/2 = (2h/3+y)2(B/2h)
A2 = [B+b](1/2)(h2) = [B+(2h/3+y)B/h](1/2)(h/3-y)
ycg1 = (1/3)(2h/3+y)-y = (2h/9-2y/3)
ycg2 = (h/2+y)/2-y = (h/2-y)/2
S1 = A1ycg1 = (2h/3+y)2(B/2h)(2h/9-2y/3)
S2 = A2ycg2 = [B+(2h/3+y)B/h](1/2)(h/3-y) (h/2-y)/2
Smax = (4h2/9)(B/2h)(2h/9) = (4h2B/81)
2h
b
2h
Q(  y ) 3
Q(  y ) 2 6
QS
6h 
3
 sup 
 33
Ib
bh 2h
b
bh3
(  y)
36 3
h
2h
b
2h
Q(  y ) 3
Q(  y ) 2 6
QS
3
6h 
3
 sup 

b
Ib bh 3 2h
bh 3
(  y)
36 3
h
Cuando y = - 2h/3 se tiene  = 0 y cuando y = 0 se tiene
 max 
Q(
2h 2
4h 2 6
) 6 Q
3
9  Q8  4Q

3
3bh 3 A
bh
bh3
6.3. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
un perfil romboidal.
h/2
h
h
h
Solución:
a) Tensiones Normales
ycg = h/2
c = +/- h/2
I = 2h(h/2)3/36 + (h/2)(h/2)(h/6)2 = h4/48
 max 
Mc M (h / 2) 24M

 3
I
h4
h
48
b) Tensiones Cortantes
Aparcial = h(h/2)/2
ycgparcial = (h/2)/3
Smax = Aparcial ycgparcial = h3/24
 max
h3
)
QS
24  2Q


Ib
h4h
h2
48
Q(
6.4. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
un perfil rectangular hueco.
h
h/2
b
Solución:
a) Tensiones Normales
ycg = h/2
c = +/- h/2
I = [bh3 – (b-2e)(h-2e)3]/12
b
 max 
Mc
3Mh

2
I
e b 4e  6eh  3h2  2e  h 3



b) Tensiones Cortantes
Aparcial = b(h/2) – (b-2e)(h/2-e)
ycgparcial = [b(h/2)(H/2)(1/2) – (B-2E)(H/2-e)(h/2-e)(1/2)]Aparcial
Smax = [b(h/2)(H/2)(1/2) – (B-2E)(H/2-e)(h/2-e)(1/2)]
 max 


QS
 3Q 2b(e  h)  (2e  h)2

Ib
4e b(4e2  6eh  3h2 )  (2e  h)3


6.5. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
un perfil I.
h
h /2
b
b
Solución:
a) Tensiones Normales
ycg = h/2
c = +/- h/2
I = bh3/12-(b-e)(h-2e)3/12
 max 
Mc
M 6h

2
I
e 2b 4e  6eh  3h2  2e  h 3
 


b) Tensiones Cortantes
Aparcial = [bh – (b-e)(h- 2e)]/2
ycgparcial = e(h/2-e)(h/2-e)/2+be(h/2-e+e/2) Aparcial
Smax = e(h/2-e)(h/2-e)/2+be(h/2-e+e/2)
 max 


QS
 3Q 4be  h   2e  h 2

Ib
2e 2b 4e2  6eh  3h2  2e  h 3
 


6.6. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
un perfil H
h
h /2
b
b
Solución:
a) Tensiones Normales
ycg = h/2
c = +/- h/2
I = (b-2e)e3/12 + 2eh3/12
 max 
Mc
6Mh

I
(b  2e)e3  2eh3
b) Tensiones Cortantes
Aparcial = bh/2 – (b-2e)(h/2-e/2)
ycgparcial = (bh/2)(h/4)-(b-2e)(h/2-e/2){e/2+(h/2-e/2)/2} Aparcial
Smax = (bh2/8)-(b-2e)(h-e)h/8
 max 


QS 3Q bh2  (b  2e)(h  e)

Ib
2 (b  2e)e3  2eh3 e


6.7. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
un perfil T.
h
yc
g
b
Solución:
a) Tensiones Normales
ycg 
bh(h / 2)  (b  e)(h  e)(h  e)(1/ 2)
bh  (b  e)(h  e)
ycg  
b (e  2 h )  (e  h ) 2
2(b  e  h)
c1 = ycg
c2 = h-ycg
I


e be2  (h  e)(e2  2eh  4h2 ) eh2 (e  h)2

12
4(b  e  h)
 max 


Mc
 6 M b (e  2 h )  ( e  h ) 2

I
e b2e2  2b(e  h)(e2  eh  2h2 )  (e  h)2 (e2  2eh  h2 )


b) Tensiones Cortantes
Aparcial = [bh – (b-e)(h- 2e)]/2
ycgparcial = e(h/2-e)(h/2-e)/2+be(h/2-e+e/2) Aparcial
Smax = e ycg2/2
Smax 
 max

e be  2h   e  h 2

2
8(b  e  h)2


2
QS
3Q b(e  2h)  (e  h)2


Ib
2e b2e2  2be  h (e2  eh  2h2 )  (e  h)2 * (e2  2eh  h2 ) (b  e  h)



6.8. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
un perfil circular.
Solución:
a) Tensiones Normales
ycg = d/2
c = +/- d/2
I = d4/32
 max 
Mc M (d / 2) 32M


I
d 4
d 3
64
b) Tensiones Cortantes
Tomando un elemento diferencial
dA 
r (rd )
2

ycgparcial 

3
2r
2r 3
2r 3
Sin 
Sind  r (Cos  Cos 0)
3
2(3)
0
 3
 3
Aparcial
Aparcial
Aparcial
Aparcial
 dA
0
2r 3
4r
y cgparcial  3 
 2 3
r
2
S max  Aparcial ycgparcial 
 max 
QSmax
Ib
2r 3 d 3

3
12
d3
Qd 3
16Q 4Q
12  12



d 4
d 2 d 3 12 A 3 A
d
64
4 16
Q
6.9. Comparar la relación tensiones normales vs. peso y tensiones cortantes vs. peso para
los perfiles de la figura. Tomar Ancho = 6 cm, Alto = 12 cm y Espesor = 1 cm.
(a)
(b)
(d)
(e)
(c )
(f )
Solución:
 max 
Para a)
Mc M (h / 2) 6M

 2
I
bh3
bh
12
max = 1,5 Q/A
 max 
Para b)
Mc
M 6h

I
e 2b 4e2  6eh  3h2  2e  h 3
 




 max 
QS
 3Q 4be  h   2e  h 2

Ib
2e 2b 4e2  6eh  3h2  2e  h 3
 max 
Mc
6Mh

I
(b  2e)e3  2eh3
 max 
QS 3Q bh2  (b  2e)(h  e)

Ib
2 (b  2e)e3  2eh3 e
 max 
Mc
 6 M b (e  2 h )  ( e  h ) 2

2
2
I
e b e  2b(e  h)(e2  eh  2h2 )  (e  h)2 (e2  2eh  h2 )
Para c)
Para d)
 max
 












2
QS
3Q b(e  2h)  (e  h)2


Ib
2e b2e2  2be  h (e2  eh  2h2 )  (e  h)2 * (e2  2eh  h2 ) (b  e  h)

 max 
Mc
3Mh

2
I
e b 4e  6eh  3h2  2e  h 3
 max 
QS
 3Q 2b(e  h)  (2e  h)2

Ib
4e b(4e2  6eh  3h2 )  (2e  h)3
Para e)









6.10. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
un perfil trapezoidal.
9
12
9
12
15
Solución:
a) Tensiones Normales
ycg = (2A1 xcg1+A2 xcg2)/(2 A1+A2)
3
3
ycg = (2(3)(12/2)(4)+9(12)6)/(2(3)(12/2)+9(12)) =
ycg = [(B-b)(h2/6)+(bh2/2)]/[(B-b)(h/2)+(bh)]
ycg = (h2/3)(B/2+b)/[(h/2)(B+b)] = (2h/3)(B/2+b)/(B+b)
c1 = ycg = (2h/3)(B/2+b)/(B+b)
c2 = h - ycg = h - (2h/3)(B/2+b)/(B+b)
I = 2(Icg1+A1d12)+(Icg2+A2d22)
I = 2{[(B-b)/2]h3/36+[(B-b)/2](h/2)(Icg1+A1d12)+(Icg2+A2d22)
6.11. En la figura se muestra un eje de una transmisión. En los puntos A, C y E van
montados engranajes y en B y D los cojinetes de apoyo. Las fuerzas sobre los engranajes
son todas verticales, el eje es simétrico y las dimensiones están en centímetros. Se pide
calcular las tensiones normales de flexión y de corte máximos.
60[kg]
45[kg]
45[kg]
3
4.5
10
6
15
30
Solución:
Para una sección circular
 max 
M max c 16M max

I
d 3
 max 
QS 4Q

Ib 3 A
Por la simetría y de la Estática
Ra = Rb = (45+60+45)/2 = 75 Kg
En el eje de 3 Mmax = Ra 5 = 75(5) = 375 Kg cm
Qmax = Ra = 75 Kg
max = 70.73 Kg/cm²
max = 14.14 Kg/cm²
En el eje 4.5 Mmax = Ra 20 = 75(20) = 1500 Kg cm
Qmax = Ra = 75 Kg
max = 83.83 Kg/cm²
15
10
max = 6.2814 Kg/cm²
En el eje 6
Mmax = Ra 50 = 75(50) = 3750 Kg cm
Qmax = Ra = 75 Kg
max = 88.41 Kg/cm²
max = 3.53 Kg/cm²
PROBLEMAS PROPUESTOS
6.12. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
el perfil de la figura.
b
h
d
6.13. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
el perfil de la figura.
H
d
6.14. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
el perfil de la figura.
e
H
6.15. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
el perfil de la figura.
d
e
6.16. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
el perfil de la figura.
b
H
e
6.17. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
el perfil de la figura.
b
e
H
6.18. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
el perfil de la figura.
b
e
H
6.19. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
el perfil de la figura.
a
a
6.20. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
el perfil de la figura.
a
a
6.21. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
el perfil de la figura.
a
a
6.22. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
el perfil de la figura.
a
a
6.23. Hallar las expresiones para calcular las tensiones normales y cortantes máximos para
el perfil de la figura.
a
7 Deformaciones en Flexión
7.1 Introducción
En este capítulo se estudiarán tres métodos para hallar las deformaciones que se presentan
en vigas sometidas a flexión. Estos métodos son:a) Método de doble integración; b) Método
de superposición y c) Método del área del diagrama de momentos.
7.2 Línea Elástica
Se llama “Línea elástica” a la forma que adopta el eje de una viga al producirse la
deformación de la misma por acción de las cargas exteriores.
Fig. 7.1 Linea Elástica
7.3 Método de la Ecuación Diferencial de la Elástica o Doble Integración del Momento
Un elemento diferencial de la viga puede considerarse como un arco de círculo
Fig. 7.2 Deformación de un Elemento Diferencial
La ecuación 6.12 estableció que
M 
y dA 

E
2
A
EI

7.1
Por desarrollos se sabe que la curvatura de una curva plana está dada por la ec
1

Entonces
1



d2y
dx 2
  dy  2 
1    
  dx  
d2y
dx 2
  dy 
1   
  dx 
7.2
3/ 2
2 3/ 2




M
EI
7.3
La integración de esta ecuación es difícil pero para deformaciones pequeñas
dy/dx = tan (θ) = θ
7,4
y su valor al cuadrado se desprecia por lo que el denominador de 7.3 se iguala a la unidad
d2y M

dx 2 EI
7,5
d M

dx EI
7.6
7.4 Método de Superposición
Debido a que las ecuaciones de las deformadas son lineales se puede aplicar el principio de
superposición, que dice “Si el estado de carga en una viga puede descomponerse en n
cargas más sencillas, la deformada total de la viga es la superposición de las n deformadas
que producen cada una de las n cargas”.
Cuando se conoce la deformada de una viga empotrada bajo un estado de carga se puede
hallar la deformada otra viga con voladizo con el mismo estado de carga
Fig. 7.3 Deformada de una Viga con Voladizo
total =  +  b
(7.7
7.5 Método del Área del Diagrama de Momentos o Teoremas de Mohr
a) Primer Teorema de Mohr.- Permite calcular el ángulo θAB que forman entre sí dos
secciones A y B de una viga. Este ángulo es el mismo que el que forman las tangentes a la
elástica en los puntos A y B
Fig. 7.3 Angulo entre Secciones y entre Tangentes
La ecuación diferencial de la elástica es, según ecuación 6.6:
d M

dx EI
(7.8
Integrando entre los puntos A y B:
B
M
dx
EI
A
 ( AB )   ( A)   ( B)  
(7.9
Si EI es constante
 ( AB )   ( A)   ( B) 
B
1
Area ( M AB )
M dx 

EI A
EI
(7.10
"El ángulo θ (AB) que forman entre sí dos secciones de la viga flexionada, es igual al área
del diagrama de momentos flectores comprendida entre A y B: Area(MAB), dividido por el
módulo de rigidez de la viga EI"
b) Segundo Teorema de Mohr.- Permite calcular la distancia en vertical, δBA, que hay
desde un punto B de la elástica a la tangente en otro punto A de la elástica.
Fig. 7.4 Distancia Vertical entre Tangentes
Por dos puntos C y D muy próximos, situados en x y x+dx, se trazan sus tangentes, las
cuales intercectan a una línea vertical en B en B1 y B2. cuya longitud será:
B1B2 = B1B0 – B2B0 = (xB - x) tag θ - (xB - x) tag (θ - dθ)
(7.11
Para pequeñas deformaciones
B1B2 = (xB - x) θ - (xB - x) (θ - d θ) = (xB - x) dθ
(7.12
sumando las longitudes de los segmentos diferenciales B1B2 al mover los puntos C y D
desde A hasta B, tendremos la longitud total δBA deseada. Así:
B
 BA   ( xB  x)d
(7.13
A
y si finalmente se sustituye el valor absoluto de dθ obtenido en el primer teorema de Mohr:
M ( xB  x)
dx
EI
A
B
 BA  
(7.14
Si EI es constante
 BA
B
1
QBM ( AB )

M
(
x

x
)
dx

B
EI A
EI
(7.15
"La distancia en vertical: δBA que hay desde un punto B de la elástica a la tangente en otro
punto A de la misma, es igual al momento estático respecto del primer punto B del área del
diagrama de momentos flectores comprendida entre ambos puntos: QBAB, dividido por EI"
En el caso de que el diagrama tenga áreas positivas y negativas, se realizará el
procedimiento para cada área
M
d1
d2
CG1
T
x
A
B
CG2
EI() = Area AT – Area TB
(7.16
EI() = (Area AT)d1 – (Area TB) d2
(7.17
A continuación se muestran las áreas y centros de gravedad de figuras comunes :
b/2
b/3
h
h
b
3b/8
b
A=bh
b
A=bh/2
Rectangular
Triangular
b/4
b/5
h
b
A=bh/3
Parabolica
h
A=2bh/3
Parabolica
2b/
h
h
b
A=bh/4
Cubica
b
A=2bh/
Armonica
7.6 Método de la viga conjugada
Se basa en los mismos principios que el método área de momentos (teoremas de Mohr).
Con este método se genera una viga ficticia (conjugada) con las siguientes condiciones:
- Misma luz que la viga original.
- Mismas condiciones de apoyo que la viga original.
- Carga igual al diagrama de momento flector de la viga original dividido por EI
Recordando dos ecuaciones diferenciales ya conocidas:
2M
 p
y 2
(7.18
2 y
M

2
x
EI
(7.19
Llamando a M/EI el diagrama de momentos reducidos o diagrama de curvaturas y
tomándolo como un diagrama de cargas ficticias p* = M/(EI) aplicado sobre una viga también
ficticia y que se llama “viga conjugada”, de la identidad formal entre las dos ecuaciones
anteriores surge que la línea elástica de una viga coincide con el diagrama de momentos
ficticios M* producido en todas las secciones de su viga conjugada cargada con la carga p*.
En otras palabras:
y = M*
(7.20
VIGA REAL
Momento M
Angulo 
Flecha
y
VIGA FICTICIA
Carga M/EI
Cortante Q’
Momento M’
7.7 Sistemas Hiperestáticos.En algunas ocasiones las ecuaciones de la Estática ( F = 0 y  M = 0) son en número
menores al número de Cargas incógnitas que se desean hallar. Estos problemas se
conocen como estáticamente Indeterminados y en ellos se deben introducir ecuaciones
adicionales de deformaciones.
Deflexiones de vigas simplemente empotradas
M
P
r
Ry
l
M
P
r
Ry
a
b
M
l
Mb
M
r
Ry
p
l
EIymax 
Pl3
3
EI 
Px
( x  2l )
2
EI max 
Pl2
2
EIymax 
Pa2
(a  3l )
6
EI max 
Pl2
2
EIy 
Hx2
(4lx  x 2  6l 2 )
24
EIymax 
Hl4
8
EI 
Hx
(3lx  x 2  3l 2 )
6
EI max 
Hl3
6
EIy 
Mx2
2
EIymax 
Ml2
2
EI  Mx
R1 
M
r
Hl 2
x
(1  ) 3
6
l
Hl
x
Q
(1  ) 2
2
l
Hl
R1 
n  1 R2  0
EIy 
EI max  Ml
Hx 2 3
( x  5lx 2  10l 2 x  10l 3 )
120l
EIymax 
Hl4
30
Hx 3
( x  4 x 2 l  6 xl 2  4l 3 )
24l
EI max 
Hl3
24
EI 
M
l
x
p  H (1  ) n
l
M
Hl 2
M1 
(n  1)(n  2)
M2  0
r
Ry
R1 = 0 R2 = 0
M1 = Me M2 =
Me
M = Me
Q=0
Hl
2 R2  0
Hl 2
M1 
6
M2  0
Hx
l
Px2
( x  3l )
6
R1 = P R2 = 0
Px
Px2
M1 = Pa M2 = EIya  6 ( x  3a) EI a  2 ( x  2a)
;
;
0
0<x<a
Ma = P(x-a)
2
Pa2
Mb = 0
EIyb 
(a  3x) EI b  Pa
6
2
;
; a<x<l
Qa = P
Qb = 0
R1 = Hl R2 = 0
M1 = Hl2/2 M2
=0
M = (H/2)(x-l)2
Q = H(l-x)
r
Ry
R1 = P R2 = 0
M1 = Pl M2 = 0
M = P(x-l)
Q=P
EIy 
x
Hl 3 [(1  ) n  3  1]
l
Hl
x
2 
M
(1  EI)n 
(n  1)(n  2)(n  3)
(n  1)(n  2)
l
2
l
x
x
Hl 4[(1  ) n  4  (n  4)  1]
l
l
EIy  
(n  1)(n  2)(n  3)(n  4)
Q
Hl 
x
1  
(n  1) 
l
n 1
Hl 4
(n  1)(n  2)(n  4)
Hl 3

(n  1)(n  2)(n  3)
EIy max 
EI max
Deflexiones de vigas simplemente apoyadas
P
l/2
l/2
l
RB
RA
R1 = P/2
R2 = P/2
M = Px/2
Q = P/2
b
a
l
RA
RB
R1 = Pb/l
R2 = Pa/l
Ma = Pbx/l
Mb = Pa(l-x)/l
Qa = Pb/l
Qb = -Pa/l
M
b
a
RA
Px 3 2
( l  x2 )
12 4
EIy max 
EI 
P l2
(  x2 )
4 4
EI 1  EI 2 
EIy a 
P
l
RB
R1 = - M/l
R2 = M/l
Ma = - Mx/l
Mb = - M(l-x)/l
Qa = - M/l
Qb = - M/l
R1  R2  Hl / 2
Hxl
x
M
(1  )
2
l
l
Q  H (  x)
2
l
EIy b 
Pbx 2
(l  x 2  b 2 )
6l
Pb  l

( x  a) 3  (l 2  b 2 ) x  x 3 
6l  b

Pb
3x 2 b 2
(l 
 )
6
l
l
Pb  3l

2
EI b 
(
x

a
)
 (l 2  b 2 )  3x 2 
6l  b

EI a 
M
( x 3  6axl  3a 2 x  2l 2 x)
6l
M
EIy b 
( x 3  3x 2 l  3a 2 x  2l 2 x  3a 2 l )
6l
M
EI a 
(3x 2  6al  3a 2  2l 2 )
6
M
EIb 
(3x 2  6 xl  3a 2  2l 2 )
6
Hx 3
EIy 
(l  2lx 2  x 3 )
24
H
EI  (l 3  6lx 2  4 x 3 )
24
EIy a 
R1  Hl / 6
R2  Hl / 3
l
RA
RB
Hxl
x
(1  2 )
6
l
Hl
3x 2
Q
(1  2 )
6
l
M
R1  Hl /( n  2)(n  1)
R2  Hl /( n  2)
l
RA
RB
M 
x n 1
)
l n 1
(n  2)(n  1)
Hlx(1 
n 1
Q
Hl (
Hx
(7l 4  10l 2 x 2  3x 4 )
360l
H
EI 
(7l 3  30lx 2  15 x 4 )
360l
EIy 
2
1
x

)
n  2 l n 1
(n  1)
Pl 3
48
EIy 
 lx 2  l 3
Hx
l 3 n  x3 n 
EIy 



(n  2)(n  1)  6
(n  4)(n  3)l n 
EI 
 3lx 2  l 3 l 3 n  (n  4) x3 n 
H



(n  2)(n  1)  6
(n  4)(n  3)l n 
EIymax 
Pl 2
16
Pb(l 2  b 2 )3 / 2
9 3l
2
2
en x  (l  b ) / 3
Pb (l 2  b 2 )
6l
Pa (l 2  a 2 )
EI 2 
6l
EI1 
M
(6al  3a 2  2l 2 )
6l
M 2
EI 2 
(l  3a 2 )
6l
EI1 
EIy max 
5Hl 4
384
EI 1  EI 2 
Hl 3
24
5Hl 4
384
7 Hl 4
EI1 
360
8Hl 4
EI 2 
360
EIy max 

1
1
Hl 3 
 
(n  4)(n  3) 6 

EI1 
(n  2)(n  1)
1
1 
Hl 3  

3 (n  4) 

EI 2 
(n  2)(n  1)
PROBLEMAS RESUELTOS
Método de la doble integración
7.1. Hallar las ecuaciones de las pendientes y deformaciones del sistema de la figura
H
l
Ra
Rb
Solución:
De 5.2
M = (H/6)(lx-x3/l)
Integrando
EI y’ = (H/6)(lx2/2 – x4/4l) + c1
EI y = (H/6)(lx3/6 – x5/20l) + c1 x + c2
Condiciones de borde
x=0y=0
c2 = 0
x=ly=0
0 = (H/6)(l4/6 – l4/20) + c1 l
c1 = -(7H l3/360)
EIy ' 
H
(7l 3  30lx 2  15 x 4 )
360l
EIy 
Hx
(7l 4  10l 2 x 2  3x 4 )
360l
7.2. Hallar las ecuaciones de las pendientes y deformaciones del sistema de la figura
p (x)=H(x/l)2
A
B
l
RA
Solución:
De 5.4
M = (H/12)(lx-x4/l2)
Integrando
EI y’ = (H/12)(lx2/2 – x5/5l2 ) + c1
EI y = (H/12)(lx3/6 – x6/30l2 ) + c1 x + c2
Condiciones de borde
x=0
y=0
H
c2 = 0
RB
x=l
0 = (H/12)(l4/6 – l4/30) + c1 l
y=0
c1 = -(H l3/90)
EIy ' 
H lx 2 x 5 4l 3
(


)
12 2 5l 2 30
EIy 
H lx 5
x6
4l 3
(


)
2
12 6 30l
30
7.3. Hallar las ecuaciones de las pendientes y deformaciones del sistema de la figura
p(x)=H(x/l)n
A
H
B
l
RA
RB
Solución:
M
De 5.5
n2 

H
 xl  x


(n  2)(n  1) 
l n 
EIy' 
 lx2
H
x n 3 


 c1

(n  2)(n  1)  2 (n  3)l n 
EIy 
 lx3

H
xn 4

  c1x  c2

n
(n  2)(n  1)  6 (n  4)(n  3)l 
Integrando
Condiciones de borde
x=0y=0
c2 = 0
c1  
1

Hl3
1
 

(n  2)(n  1)  6 (n  4)(n  3) 
EIy' 
 lx2

H
x n 3
l3
l3





(n  2)(n  1)  2 (n  3)l n 6 (n  4)(n  3) 
EIy 
 lx3

H
xn 4
l 3x
l 3x





n

(n  2)(n  1)  6 (n  4)(n  3)l
6
(n  4)(n  3) 
x=ly=0
7.4. Hallar los valores de las pendientes en los extremos y la ubicación de la deformada
máxima del sistema de la figura
p(x)=H(x/l)n
A
H
B
RA
l
RB
Solución:
Del problema anterior
EIy' 
 lx2

H
x n 3
l3
l3





n

(n  2)(n  1)  2 (n  3)l
6 (n  4)(n  3) 
 izq 
 1

Hl3
1
 

(n  2)(n  1)  6 (n  4)(n  3) 
Para x = 0
 der 
Para x = l
1

Hl3
1
1
1
 

 
(n  2)(n  1)  2 (n  3) 6 (n  4)(n  3) 
La deformada máxima ocurre cuando y’ = 0
lx2
x n 3
l3
l3



0
2 (n  3)l n 6 (n  4)(n  3)
Ecuación de donde se despeja x
7.5. Hallar las ecuaciones de las pendientes y deformaciones del sistema de la figura
p(x)=H(1-x/l)n
H
A
B
RA
l
RB
Solución:
Se reemplaza en el problema anterior (l – x) por x
EIy' 
 l (l  x)2 (l  x)n 3 l 3

H
l3



 
n
(n  2)(n  1) 
2
6 (n  4)(n  3) 
(n  3)l
EIy 
 l (l  x)3
H
(l  x)n  4
l 3 (l  x)
l 3 (l  x) 




n

(n  2)(n  1) 
6
6
(n  4)(n  3) 
(n  4)(n  3)l
7.6. Hallar las ecuaciones de las pendientes, deformaciones y valores máximos de estos en
el sistema de la figura
H
A
B
RA
l
Solución:
Reemplazando n = 0 en los resultados del problema 7.3
RB
 lx 2
 H  lx 2 x 3 l 3
H
x n 3
l3
l3
l3 











(n  2)(n  1)  2 (n  3)l n 6 (n  4)(n  3)  2  2
3 6 4(3) 
EIy ' 

H
6lx2  4 x3  l 3
24
EIy' 
EIy 

 lx 3
 H  lx 3
H
xn 4
l3x
l3x
x4
l3x l3x 











(n  2)(n  1)  6 (n  4)(n  3)l n
6 (n  4)(n  3)  2  6 4(3) 6 4(3) 
EIy 

H
2lx 3  x 4  l 3 x
24

La deformada máxima ocurre en x = l/2 y la pendiente máxima ocurre en x = 0 y x = l
EIy max 
5Hl 4
384
EIy´max 
Hl 3
24
7.7. Hallar las ecuaciones de las pendientes y deformaciones del sistema de la figura
p(x)=H(x/l)
H
M
o
l
Solución:
M  H
x3
6l
EIy'   H
x4
 c1
24l
De 5.8
Integrando
EIy   H
x5
 c1x  c2
120l
Condiciones de Borde
x = l y’ = 0
x=ly=0
c1 
Hl 3
24
c2  
Hl 4
30
EIy '  
H  x4 3 
  l 
24  l

EIy  

H  x5 3
  l x5  l 4 4 
120  l

R
7.8. Hallar las ecuaciones de las pendientes y deformaciones del sistema de la figura
H
p(x)=H(x/l)2
M
o
l
R
Solución:
M  H
De 5.9
x4
12l 2
EIy'   H
Integrando
EIy   H
x5
60l 2
 c1
x6
360l 2
 c1x  c2
Condiciones de Borde
x = l y’ = 0
x=ly=0
c1  H
l3
60
l4
72
c2   H
EIy '  
H  x5 3 
  l 
60  l 2

EIy  

H  x6 3
 2  l x6  l 4 5 
360  l

7.9. Hallar las ecuaciones de las pendientes y deformaciones del sistema de la figura
H
p(x)=H(x/l)n
M
o
l
Solución:
M  H
De 5.10
x ( n  2)
(n  2)( n  1)l n
EIy '   H
Integrando
EIy   H
x ( n  3)
 c1
(n  3)( n  2)( n  1)l n
x ( n  4)
 c1 x  c2
(n  4)( n  3)( n  2)( n  1)l n
R
Condiciones de Borde
x = l y’ = 0
x=ly=0
l3
(n  3)(n  2)(n  1)
c1  H
l4
(n  4)( n  2)( n  1)
c2   H
EIy '  
 x n 3

H
 n  l 3 
(n  3)(n  2)(n  1)  l

 x n4 3

H

 l x(n  4)  l 4 (n  3) 
(n  4)(n  3)(n  2)(n  1)  l n

EIy  
7.10. Hallar los valores máximos de pendiente y deformación del sistema de la figura
H
p(x)=H(x/l)n
M
o
l
R
Solución:
Del problema anterior
EIy '  
 x n 3 3 
H

 l 
(n  3)(n  2)(n  1)  l n

EIy  
 x n 4 3

H

 l x(n  4)  l 4 (n  3) 
(n  4)(n  3)(n  2)(n  1)  l n

La pendiente y deformada máximas ocurren cuando x = 0
EI max 
Hl 3
(n  3)( n  2)( n  1)
EIy max  
Hl 4
(n  4)(n  2)(n  1)
7.11. Hallar las ecuaciones de las pendientes y deformaciones del sistema de la figura
H
p(x)=H(l-x/l)n
l
Solución: Se reemplaza en el problema 7.9 (l – x) por x
EIy '  
 (l  x) n3 3 
H

 l 
(n  3)(n  2)(n  1) 
ln

EIy  
 (l  x) n4 3

H

 l (l  x)(n  4)  l 4 (n  3) 
n
(n  4)(n  3)(n  2)(n  1) 
l

7.12. Hallar las ecuaciones de las pendientes, deformaciones y valores máximos de estos
en el sistema de la figura usando funciones de singularidad
P
M
R
a
b
Solución:
De 5.14
Q(x) = -Pa <x>-1 + P <x>0 - P<x-a>0
M(x) = -Pa <x>0 + P <x>1 - P<x-a>1
Integrando y aplicando las propiedades de funciones de singularidad
EIy´(x) = -Pa <x>1 + P <x>2/2 - P<x-a>2/2
EIy(x) = -Pa <x>2/2 + P <x>3/6 - P<x-a>3/6
Para 0<x<a
<x>n = xn
<x-a>n = 0
entonces
EIy´(x) = -Pa x + P x2/2
EIy(x) = -Pa x2/2 + P x3/6
Para a<x<l
EIy´
Px
( x  2a )
2
EIy 
Px2
( x  3a)
6
<x>n = xn
<x-a>n = (x-a)n
<x-l>n = 0
entonces
EIy´(x) = -Pa x + P x2/2 – P (x-a)2/2
EIy´(x) = -Pa x + P x2/2 – Px2/2 + Pxa - Pa2/2 = - Pa2/2
EIy(x) = -Pa x2/2 + P x3/6 – P (x-a)3/6
EIy(x) = -Pa x2/2 + P x3/6 – Px3/6 + Px2a/2 – Pxa2/2 + Pa3/6
EIy(x) = – Pxa2/2 + Pa3/6
EIy´ 
Pa 2
2
EIy 
Pa 2
(a  3 x)
6
Las deformadas máximas ocurren cuando x = l
EIy´max  
EIymax 
Pa 2
2
Pa2
(a  3l )
6
7.13. Hallar las ecuaciones de las pendientes, deformaciones y valores máximos de estos
en los sistemas de la figura
P
M
l
R
Solución:
Reemplazando en el problema anterior a = l y b = 0
EIy´
EIy 
Px
( x  2l )
2
Px2
( x  3l )
6
EIy 'max 
Pl 2
2
EIymax 
Pl3
3
7.14. Hallar las ecuaciones de las pendientes y deformaciones del sistema de la figura
P
a
Ra
Solución:
De 5.13
M1 = Px - Pxa/l
M2 = Pa- Pxa/l
b
Rb
Integrando
EIy '1 
Px 2 Px 2 a

 c1
2
2l
EIy1 
Px 3 Px 3 a

 c1 x  c 2
6
6l
EIy ' 2  Pax 
Px 2 a
 c3
2l
Pax 2 Px 3 a

 c3 x  c 4
2
6l
EIy 2 
Condiciones de Borde
x = 0 y1 = 0
C2 = 0
Pa 2 Pa 3
Pa 3

 c1  Pa 2 
 c3
2l
2l
x = a y1’ = y2’ 2
Pa 3 Pa 4
Pa 3 Pa 4

 c1 a  c 2 

 c3 a  c 4
6l
2
6l
x = a y1 = y2 6
0
x = l y2 = 0
De donde
Ml 3 Ml 2

 c3l  c4
6l
2
c1  P(
a 2 a 3 al

 )
2
6l
3
c3   P(
a 3 al
 )
6l
3
Pa 3
c4 
6
y
EIy a 
P
(lx 3  x 3 a  3a 2 lx  a 3 x  2al 2 x)
6l
EIy b 
P
(3ax 2 l  x 3 a  a 3 xl  2al 2 x  a 3 l )
6l
EI a 
P
(3lx 2  3x 2 a  3a 2 l  a 3  2al 2 )
6l
EI b 
P
(6axl  3x 2 a  a 3 l  2al 2 )
6l
7.15. Hallar las ecuaciones de las pendientes y deformaciones del sistema de la figura
P
a
b
Ra
Solución:
De 5.16
M1 = - Mx/l
M2 = -Mx/l +M
Integrando
EIy '1  
Mx 2
 c1
2l
EIy1  
Mx 3
 c1 x  c2
6l
EIy ' 2  
EIy 2  
Mx 2
 Mx  c3
2l
Mx 3 Mx 2

 c3 x  c4
6l
2
Condiciones de Borde
x = 0 y1 = 0
x = a y1’ = y2’
x = a y1 = y2
C2 = 0

Ma 2
Ma 2
 c1  
 Ma  c3
2l
2l

Ma 3
Ma 3 Ma 2
 c1a  c2  

 c3 a  c4
6l
6l
2
0
x = l y2 = 0
De donde
Ml 3 Ml 2

 c3l  c4
6l
2
c1  M (a 
c3   M (
c4 
y
a2 l
 )
2l 3
a2 l
 )
2l 3
Ma 2
2
EIy a 
M
( x 3  6axl  3a 2 x  2l 2 x)
6l
Rb
M
( x 3  3x 2 l  3a 2 x  2l 2 x  3a 2 l )
6l
EIy b 
EI a 
M
(3x 2  6al  3a 2  2l 2 )
6
EIb 
M
(3x 2  6 xl  3a 2  2l 2 )
6
7.16. Hallar las ecuaciones de las pendientes y deformaciones del sistema de la figura
Hl/4
Hl/4
H
H
l/2
l/2
l/2
Ra
l/2
Ra
Rb
Rb
Solución:
De 5.17
Q1(x) = - Hx2/l + Hl/4
M1(x) = - Hx3/(3l) + Hlx/4
Integrando
EI y1´ = - Hx4/(12l)+Hlx2/8+c1
EI y1 = - Hx5/(60l)+Hlx3/24+c1x+c2
Condiciones de Borde
x = 0 y1 = 0
c2 = 0
x = l/2 y1´ = 0 0 = - H(l/2)4/(12l) + (Hl/8)(l/2)2 + c3
c3 = - 5Hl3/192
 x 4 lx 2 5l 3 

EIy´ H  


 12l 8 192 
 x 5 lx 3 5l 3 x 
H
5
2 3
4
EIy  H  


  960l (16 x  40l x  25 xl )
60
l
24
192


Estas ecuaciones sólo son válidas cuando 0<x<l/2
7.17. Hallar por superposición la ecuación de la deformación del sistema de la figura
H
A
B
2H
H
RA
l
Ra
RB
H
Rb
A
B
RA
Solución: De las tablas
l
l
RB
Para 1
Para 2


EIy1 
Hx 3
l  2lx 2  x 3
24
EIy 2 
Hx
7l 4  10l 2 x 2  3x 4
360l
EIyTotal 

Hx  3
3x 4
 22l  40lx 2 
 15 x 3 
360 
l



7.18. Hallar por superposición la ecuación de la deformación del sistema de la figura
H
H
A
B
RA
RB
H
A
B
H
A
l
RA
RB
B
l
RA
RB
Solución:
Para 1
Para 2
Entonces


EIy1 
Hx 3
l  2lx 2  x 3
24
EIy 2 
Hx
25l 4  40l 2 x 2  16 x 4
960l

EIy tot 




Hx 3
Hx
l  2lx 2  x 3 
25l 4  40l 2 x 2  16 x 4
24
960l

Esta ec es válida solo en la mitad izquierda
7.19. Hallar por superposición la ecuación de la deformación del sistema de la figura
H
P
A
B
H
A
l
A
Solución: De tablas
Para 1
EIy1 

H 3
l  2lx 2  x 3
24
Para 2 de 7.15 con a = b = l/2
EIy 2 
P
B
Px 2
(3l  4 x 2 )
48

B
Entonces
EIy tot 


Hx 3
Px 2
l  2lx 2  x 3 
(3l  4 x 2 )
24
48
Ecuación valida solo en la mitad izquierda
7.20. Hallar por superposición la ecuación de la deformación del sistema de la figura
P
p(x)=H(x/l)n
A
B
P
A
B
RA
RB
H
A
B
Solución:
Para 1
EIy1 
Px 2
(3l  4 x 2 )
48
EIy 2 
 lx 3

H
x n4
l3x
l3x





n
(n  2)( n  1)  6 (n  4)( n  3)l
6 (n  4)( n  3) 
EIyTot 
 lx3
 Px 2
H
x n4
l3x
l3x
 
  (3l  4 x 2 )


n
(n  2)( n  1)  6 (n  4)( n  3)l
6 (n  4)( n  3)  48
Para 2
Ecuación valida solo en la mitad izquierda
7.21. Hallar por superposición la deformación máxima del sistema de la figura
P
P
P
(1
H
P
(2
l
(3
Solución:
Por la simetría, la deformación máxima se encuentra en l/2
La deformación en l/2 producida por la carga 2 se obtiene de
EIya 
con

Pbx 2
l  x 2  b2
6l

x = l/2; a = 2l/3 y b = l/3
l l
P( )( )
2
2
3
3
2  l 2  l  l   23Pl
EIy 2 


6l
4 9  1296

Por la simetría la deformación en l/2 producida por la carga 1 es la misma
EIy1 
23Pl 3
1296
La deformación en l/2 producida por la carga 3 se obtiene de
EIy 3 

Hx 3
l  2lx 2  x 3
24

con x = l/2
l
H( )
 3
l 2 l 3  5Hl 4
2
 l  2l   
EIy 3 
24 
4 8  384
Finalmente
EI max 
2(23) Pl 3 5Hl 4

1296
384
7.22. Hallar por superposición la deformada máxima del sistema de la figura
P
l /4
P
l /4
P
l /4
P
l /4
Solución:
1 
P(l / 4)3 P(l / 4) 2

(3l / 4)
3EI
2 EI
2 
( P)(l / 2)3 ( P)(l / 2) 2

(l / 2)
3EI
2 EI
3 
( P)(3l / 4)3 ( P)(3l / 4) 2

(l / 4)
3EI
2 EI
4 
( P)(l )3
3EI
Tot 
Pl 3  1
3
1
1
33
32
1  65Pl 3





 

EI  (64)3 (64)2 (8)3 (8)2 (64)3 (64)2 3  96 EI
7.23. Hallar por superposición la deformada máxima del sistema de la figura
2P
4P
3P
P
2P
P
3P
l/4
Solución:
l/4
l/4
l/4
4P
1 
P(l / 4)3 P(l / 4)2

(3l / 4)
3EI
2 EI
2 
(2 P)(l / 2) 3 (2 P)(l / 2) 2

(l / 2)
3EI
2 EI
3 
(3P)(3l / 4) 3 (3P)(3l / 4) 2

(l / 4)
3EI
2EI
4 
(4 P)(l ) 3
3EI
 Tot 
Pl 3
EI
 1
3
2
2
34
33
4  141Pl 3





 

64 EI
 (64)3 (64)2 (8)3 (8)2 (64)3 (64)2 3 
7.24. Hallar por superposición la deformada máxima del sistema de la figura
2P
4P
3P
P
2P
P
4P
3P
H
l/4
l/4
l/4
l/4
Solución:
1 
P(l / 4) 3 P(l / 4) 2

(3l / 4)
3EI
2 EI
2 
(2 P)(l / 2) 3 (2 P)(l / 2) 2

(l / 2)
3EI
2 EI
3 
(3P)(3l / 4) 3 (3P)(3l / 4) 2

(l / 4)
3EI
2 EI
4 
(4 P)(l ) 3
3EI
5 
( H )(l ) 4
8EI
 tot 
l3
108P  8Hl 
64 EI
7.25. Hallar por superposición la deformación en A y B del sistema de la figura
P
2H
2H
l /3
l /3
l /3
l /3
l /3
l /3
H
H
l/3
l/3
l/3
A
P
B
l /3
l /3
l /3
Solución:
Para 1
EI1 A 
EIy 
Para 2
(2 H )(2l / 3) 4 16 Hl 4

30
1215
Hx2
(4lx  x 2  6l 2 )
24
con x = 2l/3
EI 2 A 
EIy 
Para 3
Con x = 2l/3
( H )(2l / 3) 2
24
2l 2
17 Hl 4
 2l
2
4
l
(
)

(
)

6
l

 3

3
243
Px2
( x  3l )
6
EI 3 A 
3
P(2l / 3) 2  2l
 7 Pl
 3l  

6
3
 162
EI totA 
EI1B 
16 Hl 4 17 Hl 4 7 Pl 3


1215
243
162
(2 H )(2l / 3) 4 (2 H )(2l / 3) 3  l  26 Hl 4

 
30
24
 3  1215
EI 2 B 
( H )(l ) 4
8
EI 3 B 
P(l ) 3
3
EI totB 
26 Hl 4 Hl 4 Pl 3


1215
8
3
7.26. Hallar por superposición la deformación en A y B del sistema de la figura
P
P
H
l/2
EIy 
Para 1
Px2
( x  3l )
6
l/2
l/2
l/2
l/2
A
Solución:
l/2
B
H
Con x = l/2
P(l / 2) 2
6
EI 1 A 
EIy 
Para 2
3
l
 5Pl

3
l

 2

48
Hx 2 3
( x  5lx 2  10l 2 x  10l 3 )
120l
EI 2 A 
Con x = l/2
H (l / 2) 2
120l
2
 l  3
 49 Hl 4
l
2 l 
3
   5l    10l    10l  
3840
2
2
 2 

5Pl 3 49 Hl 4

48
3840
EI totA 
EI 1B 
Pl 3
3
EI 2 B 
Hl 4
30
EI totB 
Pl 3 Hl 4

3
30
7.27. Hallar por superposición la deformación en A y B del sistema de la figura
P
P
H
l/2
B
Con x = l/2
EIy 
Para 2
Px2
( x  3l )
6
EI 1 A 
3
P(l / 2) 2  l
 5Pl

3
l

 2

6
48
Hx2
(4lx  x 2  6l 2 )
24
EI 2 A 
Con x = l/2
H (l / 2) 2
24
l/2
l/2
H
Solución:
Para 1
l/2
l/2
A
EIy 
l/2
  l   l 2
 17 Hl 4
2
4l       6l  
384
  2   2 

EI totA 
5Pl 3 17 Hl 4

48
384
EI 1B 
Pl 3
3
EI 2 B 
Hl 4
8EI
EI totB 
Pl 3 Hl 4

3
8
7.28. Hallar por superposición la deformación en A y B del sistema de la figura
P
P
H
l/2
l/2
l/2
l/2
l/2
l/2
B
A
H
Solución:
EIy 
Para 1
Px2
( x  3l )
6
EI 1 A 
Con x = l/2
Para 2
EI 2 A
3
P(l / 2) 2  l
 5Pl

3
l

 2

6
48
l
H 
2
  
8
4
EI totA 
5Pl 3 Hl 4

48 128
EI 1B 
Pl 3
3
4
EI 2 B
3
l
l
H 
H 
2
2  l  7 Hl 4
       
8
6  2  512
EI totB 
Pl 3 7 Hl 4

3
512
7.29. Hallar por superposición la deformación en A y B del sistema de la figura
P
P
H
B
Px2
( x  3l )
6
Con x = l/2
EI 1 A 
Hx 2 3
( x  5lx 2  10l 2 x  10l 3 )
120l
EI 2 A 
H (l / 2) 2
120l
Con x = l/2
EIy 
Para 3
3
P(l / 2) 2  l
 5Pl
 3l  

6
48
2

EIy 
Para 2
2
 l  3
 49 Hl 4
l
2 l 
3
   5l    10l    10l  
2
2
2
3840
 
 
 

Hx2
(4lx  x 2  6l 2 )
24
EI 3 A 
Con x = l/2
H (l / 2) 2
24
  l   l 2
 17 Hl 4
2
4l       6l  
384
  2   2 

EI totA 
5Pl 3 49 Hl 4 17 Hl 4


48
3840
384
EI 1B 
Pl 3
3
EI 2 B 
Hl 4
30
EI 3 B 
Hl 4
8
EI totA 
l/2
l/2
l/2
H
Solución:
Para 1
l/2
l/2
A
EIy 
l/2
H
H
l/2
l/2
Pl 3 Hl 4 Hl 4


3
30
8
7.30. Hallar por superposición la deformación en A y B del sistema de la figura
6H
(-)
2l/3
l/3
A
2H
2H
2l/3
B
(+)
l/3
A
2l/3
B
l/3
A
4H
B
(+)
2l/3
l/3
A
B
Solución:
EIy 
Para 1
Con x = l/2
Hx 2 3
( x  5lx 2  10l 2 x  10l 3 )
120l
EI 1 A 
EIy 
Para 2
 6 H (2l / 3) 2
120lEI
2l 2
142 Hl 4
 2l 3
2 2l
3
(
)

5
l
(
)

10
l
(
)

10
l


 3

3
3
1215
Hx2
(4lx  x 2  6l 2 )
24
4
2 H 2l 2  2l 2
2l
 34 Hl
( )  ( )  4l ( )  6l 2  
24 3  3
3
243

EI 2 A 
Con x = l/2
4
Para 3
EI 3 A
 2l 
4H  
4
 3   32 Hl

30
1215
EI totA 
 142 Hl 4 347 Hl 4 32 Hl 4


1215
243
1215
EI1B  
(6 H )(l ) 4
30
EI 2 B 
(2 H )(l ) 4
8
EI 3 B 
(4 H )(2l / 3) 4 (4 H )(2l / 3) 3
52 Hl 4

(l / 3) 
30
24
1215
EI totB 
 6 Hl 4 Hl 4 52 Hl 4


30
4
1215
7.31. Hallar por superposición la Reacción en el apoyo derecho
Solución:
EI tot 
Ha 4 Ha 3b Rb l 3 M b l 2



0
30
24
3
2
(1
EI tot 
Ha 3 Rb a 2

 M bl  0
24
2
(2
Sumando 1 con 2 x l/2
Ha 4 Ha 3b Rb l 3 M b l 2 Ha 3l Rb a 2 l M b l 2






30
24
3
2
48
4
2
 a 4 a 3b a 3l 
 l 3 a 2l 
  Rb  

H 


4 
 30 24 48 
3
 16a 4  20a 3b  10a 3l 
 4l 3  3a 2 l 
  Rb 

H 
480
12




Rb 
H  16a 4  20a 3b  10a 3l 


40 
4l 3  3a 2 l

Método del Área del diagrama de Momentos
7.32. Hallar por el método del área del diagrama de momentos la deformada máxima del
sistema de la figura
A
A
B
H
tg A
tg B
l
Solución:
De 5.5 con n = 0
M
H
(lx  x 2 )
2
B
H
 AB
 BA
l/ 2
l/2
 2EI (lx  x ) xdx
 AB   max 
H
2
0
 AB   max 
l/2
 AB   max 
5Hl 4
384 EI
 2EI (lx  x )dx
H
2
0
 AB 
Hl 3
24 EI
7.33. Hallar por el método del área del diagrama de momentos la deformada máxima del
sistema de la figura
Hl/4
Hl/4
H
l/2
H
l/2
l/2
Ra
l/2
Ra
Rb
Rb
Solución:
De 5.17
Q1(x) = - Hx2/l + Hl/4
M1(x) = - Hx3/(3l) + Hlx/4
EI AB   max
EI AB   max 
EI AB   max
l/2
 x 5 lx 3 
x 3 lx

  H (  ) xdx  H  

3l 4
 15l 12  0
0
l/2
Hl 4
120
l/2
 x 4 lx 2 
x 3 lx

  H (  )dx  H  

3l 4
 12l 8  0
0
l/2
EI AB   max 
5Hl 3
192
7.34. Hallar por el método del área del diagrama de momentos la deformada máxima del
sistema de la figura. p = H (1 – x/l)n
tg B
 AB
M
M
Rx
A
Ry
Solución:
B
tg A
Rx
A
Ry
B
M 
De 5.12
H (l  x) ( n 2)
l n (n  2)(n  1)
EI BA   max
l
H (l  x) n2
 H (l  x) n4
 n
(l  x)dx  n
l (n  2)(n  1)
l (n  4)(n  2)(n  1) 0
0
l
EI BA   max 
Hl 4
(n  4)(n  2)(n  1)
l
H (l  x) n2
 H (l  x) n3
dx

l n (n  2)(n  1)
l n (n  3)(n  2)(n  1) 0
0
l
EI AB   max  
EI AB   max 
Hl 3
(n  3)(n  2)(n  1)
7.35. Hallar por el método del área del diagrama de momentos la deformada máxima del
sistema de la figura
A
C
B
A
B
H
tg C
tg A
 BA
l
tg B
Ra
Rb
Solución:
Hlx
x2
H
x3
(1  2 )  (lx  )
6
l
6
l
M 
De 5.3
l
EI AC  
0
H
x3
(lx  )(l  x)dx
6
l
H l 2 x 2 lx 3 lx 4 x 5
Hl 4
7 Hl 4
(


 )
(30  20  15  12) 
6 2
3 4l 5l
6(60)
360
EI AC 
Trigonometría Tg AB = AC/l
 AB 
7 Hl 3
360 EI
xb
2
4
x
H
x3
H  lx 2 x 4 
H lx
(lx  )dx  
   ( b  b )
6
l
6  2 4l  0
6 2
4l
0
xb
Además
Igualando
EI AB  
EI AB 
2
15xb  30lxb  7l 3  0
4
De donde
4
x
7 Hl 3 H lxb
 (
 b )
360
6 2
4l
xb = 0,519 l
2
 CA
EI max 
0, 519l

0
H
x3
2,5Hl 4
(lx  ) xdx 
6
l
384
Sistemas Hiperestáticos
7.36. Determinar la reacción del punto B de la viga mostrada en la figura.
l/2
H
l/2
A
l/2
B R
b
l/2
A
H
B
l/2
l/2
A
B
Solución:
 1B  Rb
 2B  
l3
3EI
7 H (l ) 4
384 EI
B = 1B + 2B = 0
de donde:
RB  
7Hl
128
7.37. Determinar la reacción en el punto medio de la viga mostrada de la figura
A
B
p(x)=H(x/l)n
H
RC
A
C
B
H
A
p(x)=H(x/l)n
C
B
Solución:
 B1  
 B2 
Rc l 3
48EI
 l4

H
l4
l4
l4
 



n4
EI (n  2)( n  1)  48 (n  4)( n  3)2
12 (n  4)( n  3) 
B = B1 + B2 = 0
R c 3  l  H 
 n2  7  n  16  (n  3)(  n 4)  n  48  (n  3)(  n 4)  4
(n  3)  n3  7  n2  14  n  8
7.38. Determinar la expresión para hallar la reacción en el punto B de la viga mostrada en la
figura
H
l/2
l/2
A
B
Rb
H
H
l/2
l/2
l/2
A
l/2
B
H
l/2
l/2
A
B
Solución:
 1B   Rb
l3
3EI
 2B 
( H )(l ) 4
30 EI
 3B 
( H )(l ) 4
8EI
B = 1B + 2B + 3B = 0
de donde:
RB 
19Hl
40
7.39. Determinar la reacción del apoyo B, de la viga mostrada en la figura.
l/2
H
l/2
B Rb
A
l/2
H
l/2
A
B
l/2
l/2
A
B
Solución:
 1B  
 2B 
Rb l 3
3EI
( H )(l ) 4
8EI
B = 1B + 2B = 0
de donde:
RB 
3Hl
8
7.40. Determinar la expresión para hallar la fuerza de reacción que ocurre en el punto B
2H
2l/3
2H
l/3
A
B
H
H
2l/3
2l/3
l/3
l/3
B
A
B
B
Solución:
 1B 
(2 H )( 2l / 3) 4 (2 H )( 2l / 3) 3

(l / 3)
30 EI
24 EI
 2B 
( H )(l ) 4
8EI
 3B  
Rb (l ) 3
3EI
por superposición
B = 1B + 2B + 3B = 0
RB 
de donde:
1343Hl
8Hl

3240
27(12)
7.41. Hallar la deformación máxima en una viga simplemente apoyada con carga uniforme
por el método de la Viga Conjugada
Solución:
PROBLEMAS PROPUESTOS
Método de la doble integración
7.42. Hallar las funciones de pendientes y deformadas del sistema de la figura
a
b
Rb
Ra
7.43. Hallar las funciones de pendientes y deformadas del sistema de la figura
p(x)=H(x/a)2
a
b
l
7.44. Hallar la posición de la deformación máxima, y la expresión para determinar esta, para
el sistema mostrado en la figura
p(x)=H(x/l)n
a
b
Rb
Ra
7.45. Hallar las funciones de deformación y pendiente de la figura
p(x)=H((l-x)/a)2
b
a
l
7.46. Hallar la expresión para determinar la deformación máxima y determinar la posición de
esta, en el sistema de la figura
p(x)=H((l-x)/a)2
b
a
l
7.47. Hallar la ec. de deformaciones, pendientes y valores máximos de estos en los
sistemas de la figura
P
H
b
a
l
7.48. Hallar las funciones de pendientes y deformadas del sistema de la figura
H
b
a
l
7.49. Hallar las funciones de pendientes y deformadas del sistema de la figura
p(x2)
b
H
a
l
7.50. Hallar las funciones de pendientes y deformadas del sistema de la figura
P
p(x)=H(x/l)n
H
b
a
l
7.51. Hallar la pendiente y deformada máximas del sistema de la figura
P
p(x)=H(b-x/b)n
H
M
o
b
a
R
l
7.52. Hallar las funciones de pendientes y deformadas del sistema de la figura
P
p(x)=H(b-x/b)n
H
M
o
R
b
a
l
7.53. Hallar la ec. de deformaciones, pendientes y valores máximos de estos en el sistema
de la figura usando funciones de singularidad
P
P
H
M
o
b
a
R
l
7.54. Hallar la ec. de deformaciones, pendientes y valores máximos de estos en los
sistemas de la figura
2P
P
H
M
o
b
a
R
l
7.55. Hallar la ec. de deformaciones, pendientes y valores máximos de estos en el sistema
de la figura por funciones de singularidad
2P
P
A
B
RA
l/3
l/3
RB
l/3
7.56. Hallar la ec. de deformaciones, pendientes y valores máximos de estos en los
sistemas de la figura
A
B
RA
l/2
RB
2l/3
l/2
Método de superposición
7.57. Hallar por superposición la ec. de deformación del sistema de la figura
b
a
l
7.58. Hallar por superposición la ec. de deformación del sistema de la figura
2H
H
l/2
l
7.59. Hallar por superposición la ec. de deformación del sistema de la figura
2H
H
l/2
l
7.60. Hallar por superposición la ec. de deformación del sistema de la figura
p(x)=H(x/l)n
a
b
l
7.61. Hallar por superposición la ec. de deformación del sistema de la figura
l/3
2l/3
Rb
Ra
7.62. Hallar por superposición la deformada máxima del sistema de la figura
P
l/4
2P
l/4
2P
l/4
P
l/4
7.63. Hallar por superposición la deformada máxima del sistema de la figura
4P
3P
2P
P
l /4
l /4
l /4
l /4
7.64. Hallar por superposición la deformada máxima del sistema de la figura
4P
3P
l /4
l /4
2P
l /4
l /4
7.65. Hallar por superposición la deformación en A y B del sistema de la figura
P
H
l/3
l/3
l/3
A
B
7.66. Hallar por superposición la deformación en A y B del sistema de la figura
H
l/3
l/3
l/3
A
B
7.67. Hallar por superposición la deformación en A y B del sistema de la figura
P
H
l/2
l/2
A
B
7.68. Hallar por superposición la deformación en A y B del sistema de la figura
P
H
2l/3
l/3
A
B
7.69. Hallar por superposición la deformación en A y B del sistema de la figura
P
H
2l/3
l/3
A
B
7.70. Hallar por superposición la deformación en A y B del sistema de la figura
P
H
2l/3
l/3
A
B
7.71. Hallar por el método de área de momentos la deformación del sistema de la figura, en
los punto A y B
H
2l/3
l/3
A
B
7.72. Hallar la ec. de deformaciones, pendientes y valores máximos de estos en los
sistemas de la figura
H
2l/3
l/3
A
B
7.73. Hallar por superposición la deformación en A y B del sistema de la figura siendo la
intensidad de carga máxima H
l/2
l/2
A
B
7.74. Hallar por superposición la ec. de deformación del sistema de la figura
P
H
l/2
l/2
A
B
7.75. Mediante el método de diagrama de momentos de terminar el valor de la deformación
máxima para la viga mostrada en la figura.
P
H
l/4
l/2
Sistemas Hiperestáticos
7.76. Determinar las reacciones que ocurre en los punto de apoyo de la viga mostrada en la
figura.
l/3
2l/3
Rb
Ra
7.77. Determinar la reacción en el punto medio de la viga mostrada de la figura
2H
H
l/2
l
7.78. Determinar la expresión para hallar la reacción en los punto de apoyo de la viga
mostrada en la figura
2H
H
l/2
l
7.79. Determinar la reacción de los puntos de apoyo de la viga mostrada en la figura.
H
H
H
l/2
l
7.80. Determinar la expresión para hallar la fuerza de reacción que ocurre en el punto de
apoyo
l/3
2l/3
7.81. Determinar las reacciones en los puntos de empotramiento de la viga mostrada en la
figura
p(x)=H(x/l)n
H
A
B
8 Solicitación Compuesta
8.1 Introducción
En los capítulos anteriores se estudiaron individualmente las Cargas de Tracción
Compresión, las Cargas de Corte, las Cargas de Torsión y las Cargas de Flexión. En este
capítulo se estudiaran la combinación de las anteriores cargas. Se analizaran las tensiones
y las se deformadas que presentan las piezas sometidas a cargas combinadas.
Torsion
a
Flexion a
Corte
Traccion
Fig. 8.1 Solicitación Compuesta
Ejemplos de elementos sometidos a cargas y tensiones combinados son: Los ejes y árboles
de máquinas con movimiento, que soportan cargas de flexión y de torsión; los pernos que en
el momento de su ajuste soportan cargas de torsión y de tracción; las cargas de tracción
cuando estas no están aplicadas en el centro de gravedad de la sección transversal y los
marcos rígidos.
Para la validez de las ecuaciones y resultados de este capítulo se asume la veracidad de las
siguientes condiciones:
1.- Los elementos son rectos
2.- Los elementos tienen secciones transversales uniformes
3.- Los materiales son homogéneos
4.- Los miembros no son tan esbeltos de modo que no se produce pandeo.
8.2 Combinación de Tensiones
a) Estado Tensional Simple
Ocurre cuando las tensiones son del mismo tipo, normales o cortantes, en este caso basta
realizar una suma vectorial de las tensiones parciales en un punto cualquiera (no solo se
deben considerar las magnitudes sino también las direcciones).
b) Estado Tensional Compuesto
Ocurre cuando tensiones normales () y tensiones cortantes ().actúan en un punto. Como
se vio anteriormente la magnitud de las tensiones cortantes es la misma.
y
y
y
y
x
x
x
x
y
x
x



y
x
x
y
y
y
x
y
y
x
Fig. 8.2 Estado de Tensión general en el Plano
Por trigonometría
l Cos  = dy
(8.1
l Sin  = dx
(8.2
 F1 = 0
 l dz+(xySin  - xCos )dydz+(xyCos  - ySin )dxdz = 0
(8.3
Se 1 y 2
 + (xySin  - xCos )Cos  + (xyCos  - ySin ) Sin  = 0
(8.4
 + 2xySin  Cos  - xCos2  - ySin2  = 0
(8.5
 + xySin 2 - x (1+Cos 2)/2 - y (1- Cos 2 )/2 = 0
(8.6
De la estática
  
x y
2

x y
2
cos(2  )   xy sen(2  )
(8.7
 F2 = 0
 l dz + (xyCos  + xSin )dydz + (-yxSin  - yCos )dxdz = 0
(8.8
De 1 y 4
 + (xyCos  + xSin )Cos  + (-xySin  - yCos ) Sin  = 0
(8.9
 + xyCos2  + xSin Cos  -xySin2  - yCos Sin  = 0
(8.10
 + xy (1+Cos2 )/2 + xSin 2/2 -yx(1- Cos 2)/2 - ySin 2/2 = 0
(8.11
   
 x  y
2
sen(2  )   xy cos(2  )
(8.12
Algunos casos especiales son:
Para  = 0
0 = x
0 = xy
(8.13
para  = 90
90 = y
90 = - xy
(8.14
c) Circulo de Mohr
La relación entre las tensiones normales y cortantes es la de un círculo conocido como el
Círculo de Mohr
De 3
 - (x + y)/2 = (x - y)Cos (2 )/2 + xySin 2
(8.15
(  
De 5
x  y
2
 x  y
2
)2 Cos2 2  2(
 x  y
2
)Cos2 xy Sin2  ( xy Sin2 )2
 = (y - x) Sin (2)/2 -xy Cos (2)/2
( )2  (
De 7 y 9
)2  (
(  
 x  y
2
x  y
2
)2 Sin2 2  2(
)2   2  (
 x  y
 x  y
2
2
(8.16
(8.17
) Sin2 xyCos2  ( xyCos2 )2
(8.18
)2   xy 2
(8.19
Comparando 8.19 con la ecuación de una circunferencia
(x – xo)2 + (y)2 = R2
(8.20
se ve que es la misma con las tensiones normales como abscisas () y las tensiones
cortantes como ordenadas (). Este es el Círculo de Mohr y tiene las siguientes
características:
- El centro del circulo tiene un desplazamiento en el eje horizontal de (y + x)/2
- No hay un desplazamiento en el eje vertical
- El radio de la circunferencia es de [(y + x)2 + xy2]1/2.

xy
max
xy
max

Fig. 8.3 Circulo de Mohr para el estado de Tensión en el Plano
d) Tensiones Principales
En esta sección se hallaran los valores máximos de las tensiones normales y cortantes y las
direcciones en la que estos se presentan. Como ya se vio anteriormente las tensiones
normales máximos se conocen como tensiones principales y las direcciones en las que
ocurren son las direcciones principales. En estas direcciones principales y en aquellas en las
que las tensiones cortantes son máximas la falla es la más probable.
Derivando 8.3 con respecto a  e igualando a cero
 

(
 x  y
2
)2Sin2   xy 2Cos2  0
(8.21
Tan2 
2 xy
 x  y
(8.22
De 8.13 y 8.4
1,2 
x  y
 (
2
 x  y
2
)2   xy 2
(8.23
Ecuación que da los valores de las tensiones normales máximas o principales
Derivando 8.5 con respecto a  e igualando a cero


(
 x  y
Tan2  
1,2   (
)2Cos2   xy 2Sin2  0
2
(8.24
 x  y
2 xy
 x  y
2
De 8.11 8.5
(8.25
)2   xy 2
(8.26
Ecuación que da los valores de las tensiones cortantes máximos
además
1,2 = 1 - 2
(8.27
8.3 Combinación de Deformaciones
a) Estado de Deformación Simple
Ocurre cuando las deformaciones son del mismo tipo, deformaciones y distorsiones, en este
caso basta realizar una suma vectorial de las deformaciones parciales en un punto
cualquiera (no solo se deben considerar las magnitudes sino también las direcciones).
b) Estado de Deformación Compuesto
Ocurre cuando deformaciones producidas por tensiones normales () y distorsiones
producidas por tensiones cortantes () aparecen en un punto. Como se vio anteriormente la
magnitud de las tensiones cortantes es la misma.
y
y
s(1+y)
s


s
x
s(1+x)
x
Fig. 8.4 Estado de Deformación General en el Plano
Las tensiones normales producen variación de las dimensiones mientras que las tensiones
cortantes producen una distorsión cuantificada por el ángulo .
Para hallar x’, y’ y ’ asociadas al marco x’ y y’ que forman un ángulo  con xy
y
y'
y
y'
s(1+y')
s
'
'
x'
s
x'

s(1+x')
x
x
Fig. 8.5 Deformaciones y Distorsiones
y
y
s(1
y
)
+ '


x(1+x)
x
x
x
Fig. 8.6 Relación entre Deformación y Distorsión
Del teorema del coseno
Pero
[s(1+)]2 = [x(1+x)]2+[y(1+y)]2-2x(1+x)y(1+y)Cos(/2+)
(8.28
x = s Cos 
(8.29
y = s Sin 
(8.30
y Como  es muy pequeño
Cos (/2 +  ) = - Sen (  ) = - 
(8.31
De 19, 20, 21 y 22
s2 (1  2   2 )  s2Cos2 (1  2 x   x2 )  s2Sin2 (1  2 y   y 2 )  2ssSinCos (1   x   y   x y )
(8.32
Despreciando términos de segundo orden de las deformaciones ( y )
(1  2 )  Cos2 (1  2 x )  Sin2 (1  2 y )  2SinCos (1   x   y )
(8.33
2  Cos2 2 x  Sin2 2 y  2SinCos
(8.34
 = x Cos2 + y Sin2 +  Sin  Cos 
(8.35
De las expresiones de ángulo doble
 x'   
x   y
Reemplazando  por  + 90
2

x   y
2
Cos2 

2
Sin2
(8.36
 y '   90 
x   y
2

x   y
2
Cos2 

2
Sin2
 x' y'  ( x   y )Sin2   xyCos2
(8.37
(8.38
d) Deformaciones Principales
Derivando 8.3 con respecto a  e igualando a cero
 
(

 x  y
Tan2 
2
)2Sin2   xy 2Cos2  0
(8.39
2 xy
 x  y
(8.40
De 8.13 y 8.4
1,2 
x  y
2
 (
 x  y
2
)2   xy 2
(8.41
Ecuación que da los valores de las tensiones normales máximas o principales
Derivando 8.5 con respecto a  e igualando a cero


(
 x  y
2
Tan2  
1,2   (
De 8.11 8.5
)2Cos2   xy 2Sin2  0
(8.42
 x  y
2 xy
 x  y
2
(8.43
)2   xy 2
(8.44
Ecuación que da los valores de las tensiones cortantes máximos
además
1,2 = 1 - 2
(8.45
8.4 Casos de Solicitación Compuesta
Los estados tensionales se obtienen como superposición de los correspondientes a cada
uno de los esfuerzos por separado. En la verificación de piezas deberá comprobarse que en
los puntos donde aparecen estados tensionales simples (Normal o corte puro), las tensiones
estén por debajo de los valores admisibles; y en aquellos lugares donde los estados sean
múltiples, deberá comprobarse las teoría de rotura.
a) Flexión Recta Compuesta
Esta situación se presenta cuando en una sección se presentan
Tracción/Compresión y Flexión. La combinación de tensiones normales da
cargas
de
 
N My

A
I
(8.46
Fig. 8.7 Tensiones Normales de Tracción Compresión y Flexión
La distribución de tensiones es lineal, pero el eje neutro deja de ser baricéntrico. Para
determinar la posición del eje neutro
 
N My

0
A
I
(8.47
La sección compuesta puede ser considerado como resultado de la acción de una fuerza
normal a la sección actuando en forme excéntrica con respecto al centro de gravedad.
Fig. 8.8 Fuerza Normal Excéntrica
Para que la flexión sea recta es necesario que la carga esté ubicada sobre alguno de los
ejes principales de inercia.
 
N My
N Ne

 
A
I
A
I
(8.48
La carga de Tracción / Compresión puede desplazarse sobre el eje “y”, de modo que el
diagrama de tensiones resulta triangular, y que el eje neutro coincida con la fibra superior o
inferior de la sección. Se llama “distancia nuclear” a la excentricidad de la carga con
respecto al baricentro que hace que el eje neutro coincida con la fibra superior o inferior de
la sección. El punto de aplicación de la carga se denomina “punto nuclear”. Si la carga se
ubica en cualquier punto dentro de los puntos nucleares, el diagrama de tensiones tendrá un
solo signo, es decir, el eje no cortará la sección.
Debido a que las cargas de tracción compresión no producen tensiones tangenciales, en la
flexión compuesta, las tensiones cortantes no varían a los de flexión simple.
b) Flexo - Torsión
Considérese por ejemplo una viga empotrada cargado con una Fuerza Transversal y un
Momento de Torsión en su extremo libre
Las tensiones cortantes máximas producidas por torsión ocurren en los puntos 1, 2, 3 y 4.
Su valor es
 max
d
Mr
2  16M t
 t 
4
d
Io
d 3
32
Mt
(8.48
Las tensiones normales máximas aparecen por flexión en el empotramiento en los puntos 1
y 3. Su valor es
 max
d
M y
2  32Ql
 max 
4
d
I
d 3
64
(Ql )
(8.48
Las tensiones cortantes máximas producidas por flexión aparecen en el empotramiento en
los puntos 2 y 4. Su valor es
 max 
QSmax 3 Q
Q

6 2
Ib
2A
d
(8.48
PROBLEMAS RESUELTOS
8.1. En una pieza se verifican los siguientes tensiones : x = 60 Kg/cm², y = 250 Kg/cm² y
xy = 50 Kg/cm². Hallar las tensiones en direcciones con ángulos de 0 hasta 360 con un
intervalo de 10.
Solución:


50.0
79.5
99.4
107.3
102.2
84.9
57.3
22.8
-14.5
-50.0
-79.5
-99.4
-107.3
-102.2
-84.9
-57.3
-22.8
14.5
50.0
79.5
99.4
107.3
102.2
84.9
57.3
22.8
-14.5
-50.0
-79.5
-99.4
-107.3
-102.2
-84.9
-57.3
-22.8
14.5
50.0
60.0
82.8
114.4
150.8
187.7
220.7
245.8
259.9
261.4
250.0
227.2
195.6
159.2
122.3
89.3
64.2
50.1
48.6
60.0
82.8
114.4
150.8
187.7
220.7
245.8
259.9
261.4
250.0
227.2
195.6
159.2
122.3
89.3
64.2
50.1
48.6
60.0
150,0
100,0
Esf Corte
(Gr) (Rad)
0
0.0
10
0.2
20
0.3
30
0.5
40
0.7
50
0.9
60
1.0
70
1.2
80
1.4
90
1.6
100
1.7
110
1.9
120
2.1
130
2.3
140
2.4
150
2.6
160
2.8
170
3.0
180
3.1
190
3.3
200
3.5
210
3.7
220
3.8
230
4.0
240
4.2
250
4.4
260
4.5
270
4.7
280
4.9
290
5.1
300
5.2
310
5.4
320
5.6
330
5.8
340
5.9
350
6.1
360
6.3
50,0
0,0
25,0
-50,0
75,0 125,0 175,0 225,0 275,0
-100,0
-150,0
Esf Normal
8.2. En el problema anterior, hallar las tensiones máximas y las direcciones en las que estos
ocurren.
Solución:
Para 
Tan2 
2 xy
 x  y

2(50)
60  250
 = -13.87
1,2 
x  y
2
 (
 x  y
2
1 = 262,35 Kg/cm²
2 = 47,64 Kg/cm²
)2   xy 2 
60  250
60  250 2
 (
)  502
2
2
Para 
Tan2  
 x  y
2 xy
 = 31.12
1,2   (
 x  y
2
)2   xy 2
1 = 107,35 Kg/cm²
2 = -107,35 Kg/cm²
además
1,2 = (1 - 2)/2
8.3. Hallar las ecuaciones y los valores máximos de las tensiones normales que aparecen
en una pieza con sección transversal rectangular cuando soporta una carga de compresión
en el medio de una de sus aristas.
P
b
a
Solución:
La carga puede reemplazarse por una carga de compresión aplicada en centro de gravedad
de la sección y un momento de flexión cuya magnitud es la del producto del valor de la
carga por el desplazamiento.
P
P
M = Pb/2
M = Pb/2
+
a) Compresión
a) Compresión
b) Flexión
Total
b  
a  
P
P

A
ab
My
P(b / 2) y
6 Py

 2
I
ab3 / 12
ab
 tot   a   b  
P 6 Py

ab ab2
b) flexión
A la izquierda y = +b/2
 totizq 
2P
ab
A la derecha y = -b/2
 totder  
4P
ab
El eje neutro por definición esta donde  = 0
 tot  
P 6 Py

0
ab ab2
y = + b/6
Es decir que el eje neutro se sitúa a b/6 a la izquierda del centro de gravedad
b/6
2P/ab
-4P/ab
8.4. Hallar las ecuaciones y los valores máximos de las tensiones normales que aparecen
en una pieza con sección transversal triangular cuando soporta una carga de compresión en
uno de sus vértices
P
c.g.
H
Solución:
Nuevamente se superponen una carga de compresión con otra de flexión
P
P
M = P2h/3
2h/3
M = P2h/3
+
a) Compresión
b) flexión
a  
a) Compresión
b) Flexión
Total
b  
P
2P

A
ab
My
P(2b / 3) y
24Py


3
I
ab / 36
ab2
 tot   a   b  
2 P 24Py

ab
ab2
A la izquierda y = +b/3
 totizq 
6P
ab
A la derecha y = -2b/3
 totder  
14P
ab
El eje neutro por definición esta donde  = 0
 tot  
2 P 24Py

0
ab
ab2
y = + b/12
Es decir a b/12 a la izquierda del centro
b/12
6P/ab
-14P/ab
8.5. Una pieza cilíndrica está sometida a torsión y corte como se ve en la figura. Hallar la
combinación de tensiones cortantes
Mt
P
P
Mt
Solución:
Las cargas de corte y torsión producen tensiones de corte
+
a)
Corte
a) Corte
b) Torsión
Arriba
Abajo
b)
Torsión
a 
P
4P

A d 2
b 
Mr M (d / 2) 16M


Io
d 4 / 32 d 3
 totarr 
 totarr 
4P
d 2
4P
d
 totarr  (
Lados
2


4P
d
2
16M
d 3
ambos son paralelos
16M
d 3
)2  (
ambos son paralelos
16M
d 3
)2
ambos son perpendiculares
El eje neutro por definición esta donde  = 0
 tot 
4P
d 2

M (r )
d 4 / 32
0
y = + Pd2/(8M)
Pd2/(8M)
8.6. Una manivela de sección circular y diámetro “d” soporta una carga puntual vertical en su
extremo, como se ve en la figura. Hallar las tensiones máximas
y
z
b
P
x
a
Solución:
La porción “a” se analiza como una viga empotrada con una carga puntual en su extremo y
la porción “b” se analiza como una viga empotrada con una carga puntual y un momento de
torsión en su extremo. Entonces la porción “a” está sometida a flexión mientras que la
porción “b” a torsión y flexión
P
P
a
b
Mt=Pa
En “a” solo flexión

Flexión
My
( Px)(r )

I
(d 4 / 64)
( Pa)(d / 2)
 max 

(d / 64)
4
32Pa
d 3
En “b” flexión y torsión

Flexión
My
( Pv)(r )

I
(d 4 / 64)
( Pb)(d / 2)
 max 

Torsión

(d 4 / 64)
32Pb
d 3
M t r ( Pa)(r )
 4
Io
d / 32
 max 
16Pa
d 3
Las tensiones son de diferente tipo por lo que se combinan por tensiones principales
Tomando
x 
32Pb
d 3
y = 0
 xy 
16Pa
1,2 
d 3
x  y
2
De 8.14
1,2 
16P
d
3
1,2   (
De 8.15
 1, 2 
 (
 x  y
2
)2   xy 2 
16Pb
16Pb
)2  (
d 3
 (
16Pb
d 3
)2  (
16Pa
d 3
)2
(b  a 2  b2 )
 x  y
2
)2   xy 2   (
d 3
16Pa
d 3
)2
16P
( a2  b2 )
3
d
8.7. La manivela de la figura tiene una sección circular de diámetro “d” y soporta una carga
distribuida vertical y una carga puntual horizontal. Hallar las tensiones máximas
y
z
b
P
x
H
a
Solución:
H
P=H*a
a
a/2
equivalente
La porción “a” se analiza como una viga empotrada con una carga distribuida en toda su
longitud y la porción “b” se analiza como una viga empotrada con una carga puntual y un
momento de torsión en su extremo. Entonces la porción “a” está sometida a flexión mientras
que la porción “b” a torsión y flexión en dos direcciones
Ha
H
P
b
Mt=Haa/2
En “a” solo flexión

Flexión
My ( Ha2 / 2)(r )

I
(d 4 / 64)
 max 
( Ha2 / 2)(d / 2)
(d / 64)
4

16Ha2
d 3
En “b” flexión y torsión

Flexión vert.
My ( Hav)(r )

I
(d 4 / 64)
 max 

Flexión hor
( Hab)(d / 2)
(d / 64)
4

32Hab
d 3
My
( Pv)(r )

I
(d 4 / 64)
 max 
( Pb)(d / 2)
(d / 64)
4

32Pb
d 3
a

Torsión
M t r ( Ha2 / 2)(r )

Io
d 4 / 32
 max 
Entonces
De 8.15
d 3
x 
32Hab
y 
32Pb
 xy 
De 8.14
8Ha2
d 3
d 3
8Ha2
1,2 
d 3
x  y
2
1,2   (
 (
x  y
2
 x  y
2
)2   xy 2 
) 2   xy 2   [
16
d
3
16
16
8Ha2
d
d
d 3
( Hab  Pb)  [
3
( Hab  Pb)]2  (
8Ha2
d 3
( Hab  Pb)]2  (
3
)2
)2
8.8. Hallar la deformación vertical del extremo libre de la manivela del problema 8.6
y
z
b
P
x
a
Solución:
P
P
a
b
Mt=Pa
a) La deformación vertical de la porción “a” originada por la carga vertical es
a 
Pa 3 Pa 3 64

3EI
3E d 4
b) La deformación vertical de la porción “b” originada por la carga vertical es
 b1
Pb 3 Pb 3 64


3EI
3E d 4
El momento de torsión origina un giro o deformada angular en la porción “b” de

M t b Pab 32

GI 0
G d 4
este giro produce una caída vertical del extremo libre de “a”
 b2
32 Pa 2 b
 a 
d 4
La deformada total del extremo libre es
 tot   a   b1   b 2 
64
d 4
 Pa 3 Pb 3 Pa 2 b 




3E
2G 
 3E
8.9. Hallar la deformación vertical del extremo libre de la manivela del problema 8.7
y
z
b
P
x
H
a
Solución:
La fuerza horizontal no produce una deformación vertical en el extremo libre
Ha
b
H
P
a
Mt=Haa/2
a) La deformación vertical de la porción “a” originada por la carga vertical distribuida es
a 
Ha 4 Ha 4 64

8EI
8E d 4
b) La deformación vertical de la porción “b” originada por la carga vertical es
 b1 
Hab3 Hab3 64

3EI
3E d 4
El momento de torsión origina un giro o deformada angular en la porción “b” de

M t b Ha 2 b 32

GI 0
2G d 4
este giro produce una caída vertical del extremo libre de “a”
 b 2  a 
16 Ha 3b
d 4
La deformada total del extremo libre es
 tot   a   b1   b 2 
64
d 4
 Ha 4 Hab3 Ha 3b 




3E
4G 
 8E
8.10. La viga de la figura tiene una sección transversal como se muestra Hallar las tensiones
en los puntos A y B, de la sección A-A.
Seccion A-A
P
l/2
2a
A
B
l
a
A
3/2 l

A
a
a
Solución.P
P
M1
R3
R3 l
N1
3/2 l

R1
Mo = 0
P(3l/2)-R2(3l/2+l cos ) = 0
R2 
3P
(3  2 cos  )
Las reacciones internas sobre la viga son:
M1 = 0
M1 + Px - R2(lcos  + x) = 0
Fy = 0
Q1 + R2 - P = 0
Fx = 0
N1 = 0
Para x = l
M1 
Q1 
Pl cos 
(3  2 cos  )
2 P cos 
(3  2 cos  )
N1 = 0
l
x
R1
R2
Las reacciones son
Q1

R2
Componentes de la tensión.
y
2a
y
B
a
x
A
a
a
Cargas de tracción. No hay cargas de tracción N1 = 0
Tensiones normales por Cargas de Flexión.-
A 
Mc A
I
Mc B
I
B 
Tensiones de corte por Cargas de Flexión.-
A 
Para A
QS A
Ib A
B 
QS B
IbB
cA = 5a/2
A parcial = 2 a a
y cg parcial = a
S max A = 2 a 3
bA = a
Para B
cB = a/2
A parcial = 0
y cg parcial = 0
S max B = 0
bB = a
I
La inercia
a(5a) 3
aa 3 127a 4
2

12
12
12
5a
a
a
a
Pl cos  5a
30 Pl cos 
(3  2 cos  ) 2
A 

4
127a
127(3  2 cos  )a 3
12
Remplazando
Pl cos  a
6 Pl cos 
(3  2 cos  ) 2
B  

4
127a
127(3  2 cos  )a 3
12
La tensión en el punto B es de compresión, por eso el signo negativo.
2 P cos 
2a 3
48P cos 
(3  2 cos  )
A 

4
127a
127(3  2 cos  )a 2
a
12
B  0
8.11. El bloque de la figura de peso despreciable se somete a dos fuerzas verticales, que se
aplican en diferentes esquinas. Determinar la distribución de la tensión normal que actúa en
la sección mostrada. (Las unidades geométricas están en [cm])
z
y
y
2
x
1000 [kg]
x
3
1.5
1
y
1000kg
1000*1.5=1500[kg-cm]
x
1000*0.9=900[kg-cm]
Solución.Tensiones normales:
P 1000 Kg
Kg

 222.22 2
2
A 45cm
cm
A 
La tensión de flexión
 fc
M c
I
siendo:
xo
xo
Ixx
Ixx
2 3 1  1.51 1.25
yo
2 3  1.51
0.9167cm
0.5  1.53
12
yo
 0.51.5

1.5  2
2


2 3 1.5  1.51 1.5
6  1.5
3
2
cm
1.513
12
4
2.3697cm
 123  21( 1  0.9167) 2   10.53  10.5 0.91 
12
 12


Iyy
2
Iyy
1.589cm
4
el tensión será en x será:
Tensión máximo de compresión de Mx con c = 3/2
 fc
 fc
Mxc
Ixx
949.487
kg
cm2
Tensión máximo de compresión de My con c = 0.916
 fc
 fc
 1.51 12
My c
Iyy
528.847
kg
cm2
0.5  2
2

Tensión debido a Mx Tensión debido a My
Tensión debido a P
8.12. Determinar el tensión máximo que ocurre en el Punto A de la columna mostrada en la
figura
z
P
y
a
A
a /2
x
a /2
Solución.Siendo la sección transversal de la columna, la que se muestra en la figura, tomaremos en
cuenta los datos indicados a continuación.
y
h
M
P
a
h
A
3
2
a h
2
a
a
x
A
1
4
a2  3
Las fuerzas trasladadas al centro de gravedad serán un momento y la respectiva carga:
M P h
2
3
M
1
3
P  3 a
Este momento está en la dirección x como se ve en la anterior figura.
La carga axial que actúa sobre la columna provocará la compresión de la misma y la tensión
que se suceda por este efecto será:
P
 c
A
la distribución de las tensiones en la sección transversal será el mostrado en la siguiente
figura:
z
y
P
c
A
x
Debido a que el punto A se encuentra por sobre el eje del centro de gravedad,
determinaremos la tensión de compresión debido al momento de flexión con:
M c
 fc
donde
I
c: la distancia de la línea del cg (eje neutro) al punto A en análisis.
I: Inercia respecto del eje xx de la sección transversal.
h
A
P
C
v
u
a
c u v
u
3
a
2 2
a
v
2
3
Remplazando las relaciones mostradas en la figura en la anterior ecuación:
 fc
8 P
3
2
 3
a
el diagrama de tensiones debido a la flexión es el mostrado en la siguiente figura:
y
z
M
fc
A
x
La tensión total que ocurre en el punto A es:
 A  c  fc
remplazando las anteriores expresiones, y simplificando, tenemos:
P
 A 4  3
a2
PROBLEMAS PROPUESTOS
8.13. En una pieza se verifican los siguientes tensiones : x = 90 Kg/cm², y = 350 Kg/cm² y
xy = 30 Kg/cm². Hallar las tensiones en direcciones con ángulos de 0 hasta 360 con un
intervalo de 10.
8.14. En el problema 8.13, hallar las tensiones máximas y las direcciones en las que estos
ocurren.
8.15. Hallar la combinación de tensiones normales del sistema de la figura
P
b
a
8.16. Hallar la combinación de tensiones normales del sistema de la figura, Cada lado del
triángulo l = 3 cm y la carga P = 800 Kg
P
8.17. Una perno en el momento de su apriete está sometida a cargas de torsión y a cargas
de tracción. Hallar la combinación de tensiones
8.18. Una manivela de sección circular y diámetro “d” soporta varias cargas puntuales como
se ve en la figura. Hallar las tensiones máximas
y
z
b
P
M
P
P
x
a
8.19. Una manivela de sección circular y diámetro “d” soporta varias cargas puntuales como
se ve en la figura. Hallar las tensiones máximas
y
z
b
M
P
x
P
a
P
P
8.20. Hallar las deformaciones horizontal y vertical del extremo libre del problema 8.18
8.21. Hallar las deformaciones horizontal y vertical del extremo libre del problema 8.19
8.22. Determinar los diagramas de tensión para cada una de las cargas, mostradas en la
figura:
8.23. Para el problema anterior determinar la tensión total en el punto donde se aplica la
carga de 500 Kg.
8.24. Determinar la tensión máxima de compresión de la columna mostrada en la figura.
z
3
y
x
1
800 [kg]
y
200 [kg]
3
x
1
8.25. Determinar la tensión máxima que soporta la columna mostrada en la figura
y
z
3
y
800 [kg]
x
x
5
1
1
8.26. Determinar la tensión máxima de compresión sobre la viga mostrada en la figura.
(Dimensiones en mm)
2000 [kg]
1500 [kg]
50
17
50
17
8.27. Hallar las tensiones para la columna mostrada en la figura.
1000 [kg]
800 [kg]
5
2
5
2
8.28. Hallar la tensión totales en los puntos indicados:
a
A
a/4
A
t
q
b/4 b
A
l
a=5 [cm]
b=7[cm]
t=1 [cm]
l
t
q=1200 [kg/m]
l=50[cm]
8.29. Determinar la tensión máxima en la sección indicada en la figura.
q=1500 [kg/m]
l=80[cm]
P=500 [kg]
A
l/2
P
l
A
l/2
45
a
t
b
a=8[cm]
b=8[cm]
t=2 [cm]
8.30. En el problema anterior determinar una fórmula genérica para determinar las tensiones
de compresión en el punto A.
8.31. Hallar las ecuaciones de las tensiones en cada una de las barras del sistema de la
figura.
z
y
x
a
A
Ø 5[cm]
B
a
a=50 [cm]
a
1000[kg]
1500[kg]
8.32. En el problema anterior, determinar la tensión máxima en el punto A.
9 Métodos Energéticos
9.1 Introducción
En la zona elástica (cuando las tensiones son inferiores a los límites de fluencia) los
materiales se comportan elásticamente y las deformaciones se almacenan como energía
potencial de deformación.
En esta capitulo primero se ve la relación que existe entre trabajo y energía potencial de
deformación, luego se deducen las expresiones de energía potencial de deformación para
elementos sometidos a cargas de tracción/compresión, corte, flexión y torsión y finalmente
se deducen las ecuaciones de Castigliano las que permiten hallar las deformaciones a partir
de las expresiones de energía potencial de deformación.
9.2 Trabajo de Desplazamiento
El trabajo, es el producto de una fuerza por la distancia que recorre y por el coseno del
ángulo que forman ambas magnitudes vectoriales entre sí. El trabajo se calcula mediante la
integral del producto escalar del vector fuerza por el vector desplazamiento.
d
F
FCos 
W = Area

d
Fig. 9.1 Trabajo de Desplazamiento
 
W   F  dr
(9.1
W = Fd Cos 
(9.2
El trabajo es el área bajo la curva Fuerza - Deformación
9.3 Trabajo y Energía Potencial de Deformación
Fig. 9.2 Trabajo y Energía de Deformación
Considere un resorte indeformado s = 0 antes de la aplicación de la fuerza externa Fe.
Cuando se aplica la fuerza Fe se produce un alargamiento del resorte s y aparece una
fuerza interior Fi = ks producida por la resistencia al alargamiento del resorte. El trabajo que
efectúa la fuerza Fi durante su desplazamiento es
dW = Fi ds = −k s ds
s
s
1
W   Fi ds   (ks)ds   ks2
2
0
0
Este trabajo es negativo pues se realiza en contra de la fuerza Fi del resorte,
El trabajo que efectúa la carga Fe, es
s
s
1
W   Fe ds   (ks)ds  ks2
2
0
0
Se puede decir que el trabajo de la fuerza externa (Fe) se gasta en deformar el resorte
(elemento interno) que acumula el trabajo en forma de una Energía Elástica Potencial de
Deformación (U). Si retiramos la fuerza Fe la partícula regresara a su posición original s = 0
y la Fi producirá un Trabajo positivo producto de la Energía acumulada.
9.4 Energía Potencial de Deformación parea los Diferentes Tipos de Carga
a) Energía Potencial de Tracción Compresión
 dWi  dU 


1
(A)(dl )
2

E
P
A
1 P 2 dl )
 dWi  dU 
2 EA
l
 Wi  U 
1 P 2 dl
2 0 EA
b) Energía Potencial de Cargas de Corte
 dWi  dU 


1
(bdy)(dl )
2

G
QS
Ib
2
1  QS 
 dWi  dU 

 bdydl
2G  Ib 
Llamando coeficiente de forma a (que depende del tipo de sección)

ys
 S 
   2 dy
A yi  I b 
 dWi  dU 
1 Q2

dl
2 GA
l
1
Q2
 Wi  U   
dl
2 0 GA
e) Energía Potencial de Cargas de Torsión
 dWi  dU 
d 
1
M t d
2
M t dl
GIo
2
1 M t dl
 dWi  dU 
2 GIo
l
2
1 M dl
 Wi  U   t
2 0 GIo
d) Energía Potencial de Cargas de Flexión
 dWi  dU 
d 
1
M f d
2
M f dl
EI
2
1 M f dl
 dWi  dU 
2 EI
l
2
1 M dl
 Wi  U   f
2 0 EI
9.5 Ecuaciones de la Energía
En la tabla se resume las expresiones de energía para los diferentes tipos de solicitaciones
Fuerza/Momento
Tracción
Compresión
Corte
Torsión
Flexión
P
Deformada
Pdx
 
EA
Qdx
GA
U
1
Q 2 dl (9.8

2
GA

1 M t dl (9.9
2  GI o
Q
  
Mt
 
Mtdx
GI o
 
M f dx
Mf
Energía
1 P 2 dl (9.7
U 
2 EA
EI
2
2
1 M dl (9.10
  f
2
EI
9.6 Teorema de Castigliano
Sea un cuerpo elástico, apoyado de tal forma que le sea imposible moverse y sobre él se
aplican gradualmente las fuerzas: Fi, F2, ..... F¡, ..... Fn. Considerando que el trabajo que
realizan las fuerzas externas se transforma todo en energía de deformación (campos
conservativos)
Los desplazamientos que sufren los puntos de aplicación de dichas fuerzas: Δ¡, se
descomponen en dos componentes, los desplazamientos δi que van en la misma dirección
que los vectores fuerza y los desplazamientos en direcciones perpendiculares a las
anteriores.
Esta descomposición se hace así para que en el cálculo del trabajo que realizan las fuerzas
exteriores tan sólo haya que tener en cuenta las componentes δi, que van en la misma
dirección que las fuerzas aplicadas, pues las otras componentes, al ser perpendiculares a
las direcciones de las fuerzas aplicadas, no realizan trabajo.
La energía de deformación del cuerpo será función de las fuerzas aplicadas sobre él:
U = U (Fi, F2, Fi,….,Fn)
(9.11
Si se diera un incremento infinitesimal a una cualquiera de las fuerzas aplicadas, por
ejemplo la F¡, la energía de deformación sería:
U
U
dFi
Fi
(9.12
Si se considerase ahora un segundo estado de cargas, en el que se invierta el orden de
aplicación de las fuerzas externas, así, se aplica en primer lugar dF¡ y a continuación las
restantes fuerzas: Fi, F2, ..... F¡, ..... Fn. La energía de deformación sería ahora:
Fig.9.8.c
1
dFi d i  U  dFi i
2
(9.13
En efecto:
- Al aplicar primero dFi, se realizará un trabajo de valor 1 dFi d i
2
- Al aplicar a continuación el resto de las fuerzas: Fi, F2, ..... F¡, ...., F„, se realizará un
trabajo: U  dFi i
en donde el término: dFj.5i es el trabajo indirecto que realiza dFi, que ya estaba aplicado, al
aplicar ahora el resto de las fuerzas y desplazarse su punto de aplicación δi.
Y como según se sabe, en el caso de campos conservativos: "el trabajo que realizan las
fuerzas externas es igual a la energía de deformación y su valor depende solamente de los
valores iniciales y finales de dichas fuerzas y no de su orden de aplicación". Como
consecuencia de ello serán iguales los dos valores obtenidos de la energía de deformación
para los dos estados de cargas considerados, ecuaciones: (8.12) y (8.13). Así pues se
verificará:
U
U
1
dFi  dFi d i  U  dFi i
Fi
2
(9.14
y despreciando infinitésimos de 2do orden frente a los de 1ro:
U
dFi  dFi i
Fi
(9.15
U
Fi
i 
(9.16
En el caso de que fuera un momento, en lugar de una fuerza, la carga que actuase sobre el
cuerpo, el giro producido se podría obtener de igual forma a través del Teorema de
Castigliano. Siguiendo un proceso análogo al anterior, la relación sería en este caso:
i 
U
M i
(9.17
- " El desplazamiento del punto de aplicación de una fuerza exterior que actúa sobre un
cuerpo, medido en dirección de la misma, es igual a la derivada parcial de la energía de
deformación respecto de dicha fuerza "
- " El desplazamiento angular del punto de aplicación de un momento exterior que actúa
sobre un cuerpo, medido en dirección de la misma, es igual a la derivada parcial de la
energía de deformación respecto de dicho momento"
Observaciones
- La energía de deformación U, es la suma de las energías parciales
2
2
1 P 2 dx 1
Q 2 dx 1 M t dx 1 M f dx
U 
 

 
2 EA
2
GA 2  GI o
2
EI
(9.18
- Si se quisiera calcular el desplazamiento de un punto donde no actuase ninguna fuerza
exterior, el Teorema de Castigliano se aplicaría de la siguiente forma: se supondría que
hubiese una fuerza F¡ actuando en dicho punto, a continuación se aplicaría el Teorema de
Castigliano y finalmente se haría que dicha fuerza fuese nula
9.7 Ecuaciones de Castigliano
Aplicando las ecuaciones de Castigliano a las ecuaciones de la Energía se obtiene
Tracción
U P l dx
 
Pn E 0 A
Torsión
U
1
 
M n G 0
n 
n 
n 
Flexión
n 
l
(9.19
M t
)dx
M n
Io
(9.20
M
)dx
Pn
I
(9.21
M
)dx
M n
I
(9.22
Mt (
M(
l
U 1
 
Pn E 0
U
1
 
M n E 0
l
M(
PROBLEMAS RESUELTOS
9.1. Hallar la deformada en el extremo libre de una viga simplemente empotrada tiene una
carga puntual.
P
P
Q
Mr
l
M
x
R
Solución:
M=0
M=Px
 max 
l

1 
M
M(
) dx

EI 
P
0

 max 
1
EI
 max 

l
 ( Px )xdx 
0
Px 3
3EI
Pl 3
3EI
9.2. Hallar la deformada angular en el extremo libre de una viga simplemente empotrada
tiene una carga puntual
P
P
Q
Mh
M
x
l
R
Mh
Solución:
Se introduce un momento ficticio Mh y ell momento:
M = P x + Mh
 max 
 max

l

1 

( Px  M h )(1)dx

EI 
0

 max 
Pero Mh = 0
l

1 
M
M(
)dx

EI 
M h
0


1 Px 2
(
 Mh)
EI
2
M1
 max 
Pl 2
2 EI
9.3. Hallar las deformadas lineal y angular en el extremo libre de una viga simplemente
empotrada con una carga puntual interna
P
a
H
H
Q
Mh
P
Q
Mh
M1
R
x
M1
x
Solución:
Se introducen una fuerza y un momento ficticio H y Mh:
Los momentos son:
ax0
M1 = H x + Mh
lxa
M2 = H x + P (x – a) + Mh
 max 
a
l

M 1
M 2
1 
M1 (
)dx   M 2 (
)dx 


EI 
H
H
 0
a
 
 max 
1
[ [ Hx  M h ]xdx   [ Hx  P( x  a)  M h ]xdx]
EI 0
a


a
l
Pero H = Mb = 0
 max 
P l 3  a 3 a(l 2  a 2 )
[

]
EI
3
2
 max 
a
l

M 1
M 2
1 
M1 (
)dx   M 2 (
)dx 


EI 
M h
M h
0

a


 max 
1
[ [ Hx  M h ](1)dx   [ Hx  P( x  a)  M h ](1)dx]
EI 0
a


a
l
Con H = Mh = 0
 max 
P l 2  a2
[
 a(l  a)]
EI
2
9.4. Hallar las deformadas lineal y angular en el extremo libre de una viga simplemente
empotrada con una distribuida p = H (x/l)n
H
F
Q
Mr
Mh
L
R
x
Solución:
Se introducen una fuerza y un momento ficticio F y Mh:
De 5.10 sin F ni Mb:
M 
Hx( n  2)
l n (n  2)(n  1)
con F y Mb:
M  Fx 
Hx( n  2)
 Mb
l n (n  2)(n  1)
 max 
l

1 
M
M(
)dx

EI 
F
0

 max 
1
EI

l
 [ Fx 
0
Hx( n  2)
 M b ]xdx
l (n  2)(n  1)
n
Pero H = Mb = 0
 max 
Hl 4
EI (n  4)(n  2)(n  1)
 max 
l

1 
M
M(
)dx

EI 
M b
0

 max 
1
EI

l
 [ Fx 
0
Hx( n  2)
 M b ](1)dx
l n (n  2)(n  1)
Con H = Mh = 0
 max 
Hl 3
EI (n  3)(n  2)(n  1)
9.5. Hallar las deformadas lineal y angular en el extremo libre de una viga simplemente
empotrada con una carga puntual
P
y=x2/b
P
Q
Mr
ds
b
M
R
dy
dx
b-x
x
Solución:
M = P (b - x)
 max
longitud

1 
M

M(
) ds

EI 
P


0



ds  dx2  dy2
dy = 2xdx/b
 max 
 max 
1
EI
b
 [ P(b  x)](b  x)
1  4( x / b) 2 dx
0

Pb 3
32  10 5  51ln( 2b  b 5 )  45 ln(b)
192 EI

9.6. Hallar la deformada lineal en el extremo libre de una viga simplemente empotrada con
una carga puntual en el extremo
P
P
P
Mr


x
l/2
M1
l/2
l/2
Solución:
Los momentos son:
M1 = - P Sin 45 x
lxa
M2 = - P (l/2 Sin 45 + v )
 max 
l/2
l / 2

M 1
M 2
1 
M1 (
)dx 
M2(
)dv

EI 
P
P
0
 0

 max 
l/2
l / 2

1 
P( xSin45) 2 dx 
P(l / 2Sin45  v) 2 dv

EI 
0
 0

 max 
((l / 2) Sin45  v) 3
P ( xSin45) 3
[

]
EI
3
3


M2
x
R
L/2  x  0
Q
Q


 max 
P (lSin 45) 3 [(l / 2) Sin 45  (l / 2)]3 [(l / 2) Sin 45]3
{


}
EI
24
3
3
 max 
Pl 3
4(sin 45) 2  3Sin 45  1
24 EI


9.7. Hallar el desplazamiento que tiene el apoyo móvil de una viga con forma parabólica y
carga puntual en su centro. Resolver para d = l/4
P
y-d=x2
Q
M1
y-d=x2
d
y
y
x

H
l
Ra
l/2-x
Ra
Rb
Solución:
Se introducen una fuerza ficticia H. Por simetría
Ra = Rb = P/2
l/2  x  0
M1 = Ra (l/2 -x) – H y
M1 = (P/2)(l/2 – x) – H (x2 + d)
Hay dos intervalos. Por simetría se duplica solo uno
 max 
l / 2

M 1
2 
M1 (
) ds

EI 
H
 0


ds  dx2  dy2
dy = 2 x dx
 max  
 max 
0
l/2

2 
P l
2
2
2
  [ (  x)  H ( x  d )]( x  d ) 1  4 x  dx
EI  0 2 2

0.02 Pl 3
EI
9.8. Hallar el desplazamiento que tiene el apoyo móvil de una viga con forma triangular y
carga puntual en su centro
P
l
Q
M1
30
x
H

Ra
Rb
Ra
Solución:
Se introducen una fuerza ficticia H.
Por simetría
Ra = Rb = P/2
l/2  x  0
M1 = Ra x Cos 30 – H x Sin 30
M1 
Px 3 Hx

4
2
Hay dos intervalos. Por simetría se duplica solo uno
 max 
l

M 1
2 
M1 (
) dx

EI 
H
0

 max 
l

2 
Px 3
Hx
x
[

]( ) dx
EI 
4
2
2 
0

 max 
2 P 3 x3
3Pl 3

EI 4
6
12 EI


9.9. En el sistema de la figura: a) Hallar el desplazamiento horizontal producido por la fuerza
P. b) El valor de , para que el desplazamiento sea nulo.
C
C
P
R
R
A

B
Rh
A
P

Rv
B
H
Fr
Solución:
a)  Ma = 0
Fr 2R – PR Sin  (1 + Cos ) + P Cos  R Sin  = 0
Fr = (P/2) Sin 
Se incluye una ficticia H en B para calcular la deformada horizontal de este punto
 BH 



1 
M
M 2
M1( 1 )dx  M 2 (
)dx

EI 
H
H

0



(I
C
M1
P
C
M2

B
P

H
B
H
Fr
0
Fr
M1 = Fr R (1 - Cos ) + HR Sin 
M1 = (P/2) R Sin (1 - Cos ) + HR Sin 

(ii
M2 = (½ Sin+3/2SinCos-CosSin-CosSin)RP+HRSin (iii
De i, ii y iii y simplificando
 BH 
PR3Sin( )
(3Cos  1  Cos2 )
3EI
b) Para que el desplazamiento sea nulo
(3 Cos  - 1 + Cos2  ) = 0
De donde:
 = 72.376
9.10. El bastidor A,B,C, articulado en uno de sus extremos y apoyado en el otro está
cargado, en uno de sus tramos con una carga uniformemente distribuida, como se muestra
en la figura. Hallar el desplazamiento horizontal de B (Considerar solamente efectos de
flexión)
C
C
dF
l
l
l


A

A
H
Rh
B
B
Fr
Rv
Solución:
De la estática :
 Ma = 0
2 Fr L Cos  - (qL2/2) Cos2  - (qL2/2) Sin2  = 0
C
x
M1
x
M2
H
H
B
B
Fr
Fr
Fr = (qL)/(4 Cos )
En el tramo derecho:
0xL
M1 = Fr x Cos  + H x Sin 
M1 = (qLx)/4 + H x Sin 
En el tramo izquierdo:
0xL
M2 = Fr (L Cos  + x Cos ) + H (L-x) Sin  - qx2/2
M2 = qL2/4 + qLx/4 + H Sin  - H x Sin  - qx2/2
remplazando en la ecuación de desplazamiento y simplificando:
 BH 
L
L

1 
M
M 2
M1( 1 )dx  M 2 (
)dx

EI 
H
H
0
0

 BH 
5
qL4 Sin
24EI


9.11. El bastidor ABC mostrado en la figura soporta una carga lineal en uno de sus tramos.
Hallar una expresión para calcular el desplazamiento horizontal del extremo derecho.
Solamente considerar tensiones de flexión.
q
q x  q (1 
B
A
B
Rh A
2L
L
2L
Rv


H
Solución:
M=0
Fr (2L + L Cos ) – (2/3)(qL2)(4/3) + HL Sin  = 0
Fr = (8qL – 9 H Sin )/(18 + 9 Cos )
q
M1
qx
x

M2
B
x

H
Fr
H
Fr
0xL
L
M1 = Fr L Cos  + H L Sin 
M1 = 2L( 4 qL Cos  + 9 H Sin )/(18 + 9 Cos )
0  x  2L
M2 = Fr (L Cos  + x) + H L Sin  - qx3/2 – (q – qx) x2/9
con
qx = q (1 – x/(2L))
Fr
x
)
2L
1 ( 8q L 9Hsin (  ) )  
1
1x
M2 
( L cos(  ) x ) Hsin(  ) L q  1  x2
9
2
2L
( 2 cos(  ) )
1
9
q
1 
1x
q 1  x2
9
2L
remplazando en la ecuación de desplazamiento y simplificando:
2L
L

1 
M1
M 2

M1 (
)dx  M 2 (
)dx

EI 
H
H
0
0


 BH

16
(27Cos  4)
qL4 Sin
135EI
4  4Cos  Cos2
 BH 
9.12. Una viga simple AB, con un voladizo BC Está sometida a una carga linealmente
variable en el tramo AB, como se ve en la figura. Determinar la expresión para calcular la
deflexión c del punto C
q
q
H=0
C
A
L
x
c
L/2
B
Solución:
Se aplica una carga ficticia H en el punto C
 Ma = 0
Rb = 3H/2 + qL/3
Ra = H/2 + qL/6
q
q
qx
q
q
H=0
M1
M2
A
C
A
x
x
RA
c
L
B
x
RA
x
B
RB
En el tramo izquierdo:
0xL
M1 = Ra x – qx x/2)(x/3)
qx = qx/L
M1  (
L  x  3L/2
qL H
q x2
 )x  x
6
2
6
M2  (
qL H
3H qL
qL
2L
 )x  (
 )( x  L) 
(x 
)
6
2
2
3
2
3
La deformación total en el extremo libre será dada por la expresión:
C 
3L / 2
L

1 
M
M 2
M1( 1 )dx  M 2 (
)dx

EI 
H
H
L
0



resolviendo
C 
 7qL4
360EI
9.13. En el 9.anterior, hallar el ángulo de deformación del punto B. (Úsese el momento M0 =
0 aplicado en el punto B. Ver figura).
q
q
M0=0
A
B
L
x
B
C
c
L/2
B
Solución:
Se aplica en B un momento ficticio Mo
 Ma = 0
Ra = qL/6 + Mo /L
Rb = qL/3 - Mo /L
0xL
M1 = (Ra x – qx x/2)(x/3)
qx = qx/L
M1 
L  x  3L/2
qx3 qx2
qL M

 (  o )x
3L
3
6
L
M2  (
qL M o
qL M

) x  (  o )( x  L)  M o
6
L
3
L
La deformación angular es
3L / 2
L

1 
M1
M 2
B 
M1 (
)dx  M 2 (
)dx

EI 
M o
M o
L
0


resolviendo:
B 

7qL3
180EI
ahora bien la deformación en C es
c = B L/2
C 
7qL4
360EI
9.14. Determinar el desplazamiento que se produce en el extremo libre de la viga mostrada
y cargada como se ve en la figura.
qx 
2q
2·q
L  x 
L
2q
q
q
B
B
L/2
l/2
L/2
l/2
x
x
Solución:
Se incluye una fuerza ficticia H
2q
2q
q
qx
q
q
H
M1
H
M2
B
l/
2
B
x
x
x
x
Para el tramo derecho:
0  x  L/2
con
M1  Hx 
q x x 2 ( 2q  q x ) 2 x

2
2
3
qx = 2q(l-x)/l
M1 
(3Hl  3qlx  qx2 ) x
3l
En el tramo izquierdo
L/2 x  L
M 2   Hx 
qLx qL2 qx2


4
24
2
La deformación total en el extremo libre será dada por la expresión:
resolviendo
B 
L
L / 2

1 
M
M 2
M1( 1 )dx  M 2 (
)dx

EI 
H
H
L/2
 0

B 
361qL4
1920EI


9.15. Hallar la deformación horizontal y vertical del punto B de la viga curva mostrada en la
figura, la carga aplicada en toda su longitud tiene dirección radial.
q
dF
q
Q
B

R
R
A
Solución:
Rh
Rv
H
Se incluyen las cargas ficticias H y Q




M1  QR(1  Cos )  HRSin  qR2Cos ( Sin  Sin )d  qR2 Sin (Cos  Cos )d
0
0
simplificando M1 = QR – QR Cos  + HR Sin  + qR2 ( 1 – Cos )
Las deformaciones
V 
 / 4

1 
M
M(
) Rd 

EI 
H
 0

H 
 / 4

1 
M
M(
) Rd 

EI 
Q
 0



(2 2  3) qR3
4 EI
V  
resolviendo:
H
3
1
 2  )qR3
8
4

EI
(
9.16. La viga curva semicircular, empotrada en el extremo A, está cargada en dos puntos
como se muestra en la figura, determinar la deformación horizontal y vertical que se produce
en el extremo libre de dicha barra.
P
P
P
R
R

A

A
H
Q
Solución:
Se incluyen dos cargas ficticias (H = 0 y Q = 0).
P
P
P
P
P
M
P
2
M1

A


AH
M
R

Q
3
H

Q
Los momentos son
0    /2
M1 = -QR(1-Cos )-HR Sin 
/2    3/4 M2 = PR Cos  - HR Sin  - QR (1 – Cos )
3/4    
R
A
M3 = PR 21/2/2 [(Cos  + 21/2/2)+(Sin  - 21/2/2)] +
H
Q
PR Cos  - HR Sin  - QR (1 – Cos )
Las deformaciones en el extremo libre son:
3 / 4

 / 2

1 
M1
M 2
M
h 
M1 (
) Rd  M 2 (
) Rd  M 3 ( 3 ) Rd 

EI 
H
H
H
 /2
3 / 4
 0




3 / 4

 / 2

1 
M
M 2
M
M1( 1 ) Rd 
M2(
) Rd 
M 3 ( 3 ) Rd 

EI 
Q
Q
Q
 /2
3 / 4
 0


v 


resolviendo y simplificando:
h  
h 
PR
(8  4 2  2 )
16EI
PR
(8 2  32  4  2 )
16EI
9.17. Determinar la fuerza de reacción que soporta el extremo apoyado B en la viga
mostrada en la figura.
P
P/l
B
A
l/2
Solución:
l/2
x
La deformada vertical en B es nula
 bv
l
l / 2

1 
M1
M 2

M1 (
)dx  M 2 (
)dx  0

EI 
Rb
Rb
l/2
0



Los momentos son
con
0  x  l/2
M1 = Rb x
l/2  x  l
M2 = Rb x – P (x-l/2) – qx (x – l/2)2 / 6
qx = (P/l)(2x/l-1)
M2 = (24 Rb x – 30 P x +13 P l – 8 P x3/l2 +12 Px2/l)/24
simplificando:
 bv 
l3
(640Rb  209P)  0
1920EI
Rb = (209/640)P
9.18. Una Barra curva delgada de forma semicircular está articulada en A y simplemente
apoyada en B, Como se muestra en la figura. En C actúa una carga vertical P. Determinar el
desplazamiento vertical v y el desplazamiento horizontal h en el extremo B, que se
encuentra apoyado en una superficie inclinada.
P
M1
P
C

H
R

H
Rh
R

B
A

Fr
Rv
Fr
Solución:
Ma = 0
Fr 2R Cos  - H 2R Sin  - PR = 0
Fr = (H Sin  + P/2)/ Cos 
Los momentos son
0    /2
M1 = R Sin(HCos + FrSin) + R(1 – Cos)(-HSin + Fr Cos)
/2    
M2 = R Sin(HCos + FrSin) + R(1 + Cos)(-HSin + Fr Cos)
- PR Cos 
=-
con
Simplificando M2 = (R/2)( P + P Cos  + 2 H Sin  / Cos  + P Tan  Sin )
La deformada
 

 / 2

1 
M
M 2
M1( 1 ) Rd  M 2 (
) Rd 

EI 
H
H
 /2
 0



Reemplazando y simplificando
 
PR3 (2Cos  Sin )
EI
4Cos2
9.19. Una barra curva delgada AB de forma semicircular está articulada en A y simplemente
apoyada en el extremo B una carga distribuida que actúa en dirección radial, como se
muestra en la figura, provoca que el extremo B se desplace horizontalmente, determinar una
expresión para calcular éste desplazamiento.
q
dF·cos

dF
dF

3
A

3
q

3
d

B
R
Rh A
B
Rv
Solución:
H
Rv
dF·sen
Considerando una fuerza ficticia H y de la estática
Rv 
1
2
2 / 3
 qRSind 
/3
qR
2
Los momentos son
0    /3
/3    /2
M1 = (q R2/2) ( 1- Cos ) – H R Sin 
3   2 1   2
1 2
2 1    2
qR
q R cos (  ) HRsin(  ) q R cos (  )
3 q R sin(  )
8
2
2
2
M2
 
La deformada
 /2
 / 3

1 
M
M 2
M1( 1 ) Rd  M 2 (
) Rd 

EI 
H
H
 /3
 0



Reemplazando y simplificando
 
qR4 (1  2 3 )
EI
24
9.20. La barra mostrada en la figura, se encuentra sometida a la acción de la carga uniforme
q en dirección vertical, determinar una expresión para calcular el desplazamiento del
extremo apoyado, considerando que el apoyo tiene una inclinación de /3.
q
q
H
Fr

R
Rh O

R
O
Rv
Solución:
De la estática Rh + H Cos  - Fr Sin  = 0
Rv – q R  + q R  + Fr Cos  + H Sin  = 0
de donde
Rh  
Rv 
qR  qR  qRSinCos  HSin
1  Cos
Fr 
qR  qR  qRSin  HSin
1  Cos
Rh
con  = /3
HCos  qRSin  qRSin  qR  qRCos2  H
1  Cos
H
2
9
3 q R 
Rv
4  
q R 
9
1
Fr
4  
q R 
9
1
6
3
1 
q R
2
3 q R
1 
H 3
3
3 q R
1 
H 3
3

q
dF
M

d

RhO

Rv
El momento


M  Rv R(1  Cos )  Rh RSin  qR2 (Cos  Cos )d
0
Simplificando y con H = 0
M  qR2[
 
La deformada
2 / 3

1 
M
M(
) Rd 

EI 
H
 0

 
Simplificando
4
1
2 3 1
(1  Cos )  ( 3  Cos )  Sin (
 )  Cos ]
9
6
9
2

qR4
(108  189 3  40 2 3 )
216EI
PROBLEMAS PROPUESTOS
9.21. Hallar las reacciones del sistema de la figura
H
l/2
l/2
9.22. Hallar las reacciones del sistema de la figura
P
P
l/4
P
P
l/4
l/4
l/4
9.23. Hallar las reacciones del sistema de la figura
H
l/2
l/2
Ra
Rb
A
B
C
9.24. Hallar la deformada lineal y angular del sistema de la figura
P
2P
l/2
l/2
R
9.25. Hallar la deformada lineal y angular del sistema de la figura
H
M
l/3
l/3
l/3
R
9.26. Hallar las reacciones del sistema de la figura
H
2l/3
Ra
9.27. Hallar las reacciones del sistema de la figura
H
l
9.28. Hallar las deformadas lineal y angular en el extremo libre de una viga simplemente
empotrada con una carga distribuida p = H Sin (x/2l)
H
M
L
R
9.29. Hallar las deformadas lineal y angular en el extremo libre de una viga simplemente
empotrada cargada con un momento uniformemente y constante m0
m0
B
A
L
9.30. Hallar la deformación máxima del sistema de la figura
q0=P·a
q0=P·a
P
C
a
a
B
A
9.31. Determinar la relación a/l para que la deformada en el centro sea nula.
q0=P·l
q0=P·l
P
C
C
a
a
A
B
L
9.32. Hallar la deformada en el centro y en los extremos del sistema de la figura.
q0=P·l
C
L/3
A
L/3
L
9.33. Hallar las reacciones en el sistema de la figura.
B
q0=P·L
L/2
L
9.34. Hallar las reacciones en el sistema de la figura.
q0=P·l
P
L/2
L/2
2L
9.35. Hallar las reacciones en el sistema de la figura
q0=P·l
A
C
B
b
L/2
L
9.36. Hallar las reacciones en el sistema de la figura.
q0
C
A
B
b
a
9.37. Hallar las reacciones en el sistema de la figura
q0=P·l
P
C
A
L
B
L
3L
9.38. Hallar las deformadas lineal y angular máximas en el sistema de la figura.
q(x)=qo·x2/L2
EI
B
A
l
9.39. Hallar el desplazamiento que tiene el apoyo móvil de una viga con forma cosenoidal y
carga puntual en su centro
P
d
y
x

l
Ra
Rb
9.40. Hallar el desplazamiento que tiene el apoyo móvil de una viga con forma cosenoidal y
carga puntual en su centro
y
x

l
Ra
Rb
9.41. Hallar las reacciones de la viga de forma cosenoidal de la figura
P
y
x
l
Ra
Rb
9.42. Hallar las reacciones de los empotramientos del pórtico de la figura
P
l/2
x
l
9.43. Hallar el desplazamiento del sistema de la figura
45
x

l
Ra
Rb
9.44. En el sistema de la figura: a) Hallar el desplazamiento horizontal producido por las
fuerzas P. b) El valor de, para que el desplazamiento sea nulo.
P
C
R
P

A
B
9.45. Un anillo de radio “R” de alambre de acero de radio “r” tiene una separación de h. Se
pide la fuerza P que cierra esta separación
r
P
P
h
9.46. Hallar las reacciones en el sistema de la figura
q0=P·l
q0=P·l/2
EI
l/2
l/2
10 Pandeo de Columnas
10.1 Introducción
En Tracción Compresión se estableció que la falla de una pieza ocurre cuando los esfuerzos
sobrepasan la fluencia, sin embargo cuando los elementos sometidos a compresión tienen
una longitud de varios diámetros, la pieza no falla cuando los esfuerzos superan la fluencia
sino que fallan por inestabilidad
10.2 Equilibrio Estable, Inestable e Indiferente
Una pieza está en equilibrio cuando se cumplen las ecuaciones de la estática. Ahora bien se
dice que el equilibrio es estable cuando frente a una perturbación el sistema no se aparta de
esta configuración, el equilibrio es inestable si frente a una causa perturbadora, el sistema
se aparta de esta configuración y ya no la vuelve a tomar y finalmente el equilibrio es
indiferente si frente a una causa perturbadora el sistema puede mantenerse en su
configuración o pasar a otras configuraciones muy próximas a la primera, deteniéndose en
alguna cualquiera de éstas.
Fig. 10.1 Equilibrio Estable, Inestable e indiferente
Una forma clásica de determinar si el equilibrio es estable consiste en desviar muy poco el
sistema de su configuración mediante una causa perturbadora cualquiera y ver qué sucede
cuando ésta cesa. Si el sistema retoma la configuración inicial el equilibrio es estable, si se
aleja aún más de ella el equilibrio es inestable; y por último, si el sistema permanece en la
posición final el equilibrio es indiferente.
Vamos a tratar de clarificar más aún estos conceptos estudiando el comportamiento de las
tres esferas del esquema de la figura 10.1. Si en el caso (a) hacemos mover la esfera sobre
la superficie y luego la soltamos, intuitivamente podemos reconocer que la esfera volverá a
su posición inicial. Este es un caso de equilibrio estable. Si en la situación (b) cambiamos
levemente a la esfera de posición, ésta ya no retomará la posición inicial sino que seguirá
rodando, ésta es entonces una situación de equilibrio inestable. Si en el caso (c) movemos
la esfera, ésta permanecerá en el nuevo lugar o próximo a éste, constituyendo entonces un
estado de equilibrio indiferente.
10.3 Tipos de apoyos y Columnas
Los apoyos de las columnas son los mismos de las vigas, es decir: a) Apoyo Móvil b) Apoyo
Fijo y c) Empotramiento
De la combinación de estos apoyos se obtienen los cuatro tipos de Columnas básicas
P
P
P
P
l
P
P
a)
a) Ambos extremos
articulados
b)
b) Ambos extremos
empotrados
P
c)
c) Un extremo empotrado
el otro libre
P
d)
d) Un extremo empotrado
el otro articulado
Fig. 10.2 Tipos de Columnas
10.4 Carga Crítica de Euler
Euler planteo el estudio teórico del Pandeo como un estudio de equilibrio. Así, si se tiene
una pieza sometida a una fuerza N de compresión y se encuentra en equilibrio, el mismo
ser: ESTABLE, INESTABLE o INDIFERENTE
Fig. 10.3 Equilibrio Estable, Inestable e Indiferente en Columnas
Equilibrio Estable: si al separarla un poco a la posición 2 y soltar, vuelve a la posición l.
Equilibrio Inestable: si al separarla un poco, a la posición 2 y soltar, se aleja de la posición l.
Equilibrio Indiferente: al separarla un poco, a la posición 2 y soltar, se queda en la posición 2
El que una pieza dada adopte uno u otro tipo de equilibrio, va a depender del valor de la
carga P de compresión a la que se le someta y se denomina: CARGA CRÍTICA (Pcr): "al
valor de la carga P de compresión que hace que se alcance el EQUILIBRIO INDIFERENTE"
Así pues se tendrá:
•
si P = Pcr —» Equilibrio Indiferente
(10.1
•
si P < Pcr —» Equilibrio Estable
(10.2
•
si P > Pcr —» Equilibrio Inestable
(10.3
Las piezas deberán trabajar con P < Pcr, para que se encuentren en equilibrio estable.
Para analizar el problema de estabilidad elástica relativo al pandeo de barras comprimidas
por Euler, se asumen las siguientes condiciones:
- La columna es homogéneo y elástica (No se supera la tensión de proporcionalidad)
- Su eje es idealmente recto.
- La carga está exactamente centrada.
- Los vínculos son ideales, sin rozamiento,
Considérese una columna con extremos articulados
Fig. 10.4 Fuerzas y Momento Internos en una Columna
Una sección a una distancia “x” del extremo presenta una deformada “y”
De la estática
M= - Py
(10.4
De la ecuación de doble integración en flexión
d2y/dx2= M/EI
(10.5
d2y/dx2= -Py/EI
(10.6
d2y/dx2+Py/EI = 0
(10.7
La Solución de esta ecuación es
y = C1 Sin C2x+C3Cos C4x
(10.8
dy/dx= C1C2Cos C2x - C3C4Sin C4x
(10.9
d2y/dx2= - C1C22Sin C2x-C3C42CosC4x
(10.10
Reemplazando 8.7 y 8.9 en 8.6
(-C1C22Sin C2x-C3C42CosC4x)+P(C1Sin C2x+C3Cos C4x)/EI=0
(10.11
Sin C2x(-C1C22+PC1/EI)+CosC4x(-C3C42+PC3/EI)=0
(10.12
-C1C22+PC1/EI=0
C2=(P/EI)1/2
(10.13
-C3C42+PC3/EI=0
C4=(P/EI)1/2
(10.14
y = C1 Sin (P/EI)1/2x +C3 Cos(P/EI)1/2x
(10.15
Para hallar c1 y c3 se ve que en los extremos de la columna no hay deformación.
Cuando x=0 y=0
0= C1 Sin (0)+C3 Cos(0)
(10.16
0 = C3
(10.17
Cuando x=l y=0
0 = C1 Sin (P/EI)1/2 l
(10.18
Hay dos posibilidades :
C1=0
descartada ya que anula toda Solución
(P/EI)1/2 l = n()
Entonces
Solución
Pcr= n2 2 EI/l2
Empleando la relación
(10.19
(10.20
I = A k2 donde A es el área y k es el radio de giro
Pcr/A= 2 E/(l/k)2
(10.21
donde l/k recibe el nombre de relación de esbeltez de la columna.
El mismo procedimiento puede ser aplicado para los cuatro tipos de columnas variando las
condiciones de borde.
La ecuación genérica de Euler es
Pcr= 2 EI/2
(10.21
cr = Pcr/A= 2 E/2
(10.22
Fig. 10.5 Valores de Lk para Diferentes Tipos de Columnas
Representando gráficamente, en unos ejes coordenados, la ecuación de la tensión crítica de
Euler en función de la esbeltez, se obtiene el siguiente diagrama
Fig. 10.6 Grafica de la Ecuación de Euler
10.5 Ecuación de la línea elástica:
Se vio que la solución de la ecuación diferencial de la elástica era de la forma: y = C1.sen
kz.x + C2.cos kz.x, sustituyendo los valores hallados de ci y c2 se obtiene
y = C1 Sin (nx/L)
(10.23
10.6 Límites de Aplicación de la Formula de Euler
El diagrama de la fig.10.15, que representa la curva de la tensión crítica de Euler, sólo va a
ser válida hasta un cierto punto P, que corresponde a una esbeltez llim, que es la esbeltez
para la cual: scr (tensión crítica) = fy (tensión del límite elástico). Ello es debido a que en la
deducción de la fórmula para la obtención de la carga crítica Ncr, se utiliza la ecuación
diferencial de la elástica y ésta sólo es aplicable para los casos en que E = cte o lo que es lo
mismo cuando s fy ( sección 3.5. diagrama tensiones deformaciones). Además, al
alcanzarse la tensión del límite elástico, el fallo se produciría por haberse alcanzado la
resistencia a la compresión de la sección. En la Fig. 10.18 se representa la curva de pandeo
de Euler y los modos de fallo
En piezas cortas sometidas a compresión la falla ocurre cuando los esfuerzos superan los
límites de fluencia. En piezas largas y esbeltas sometidas a compresión, la falla ocurre por
pandeo a pesar de que los esfuerzos son mucho menores al límite de fluencia
Gráficamente
Fig. 10.7 Fallo por Tensión y por Pandeo
En la gráfica se tiene la relación de esbeltez (l/k) como abscisa y la carga por unidad de área
(P/A) como ordenada. Entonces para elementos con relación de esbeltez bajos la falla
ocurre cuando la carga por unidad de área es mayor a la fluencia. Para elementos con
relación de esbeltez altos la falla se determina por la ecuación 8.22.
cr < Sy
Así pues tendremos que para poder utilizar la curva de Euler se habrá de verificar:
cr = Pcr/A= 2 E/2 < Sy

lim 
(10.24
 2E
(10.25
Sy
 2E
(10.26
Sy
• para esbelteces: λ mayores λlim SI se podrá aplicar la curva de Euler
• para esbelteces: λ menores λlim NO se podrá aplicar la curva de Euler
Los valores de llim para los aceros más utilizados en la construcción son:
Acero
S235
S275
S355
Sy
(N/mm2)
235
275
355
λlim
93,9
86,8
76,4
La curva de pandeo expresada en la fig.10.18 puede ser redibujada de forma adimensional,
dividiendo la tensión crítica de Euler entre el límite elástico: ( / Sy ) y la esbeltez entre la
esbeltez límite: (λ / λ lim), dando lugar a la siguiente curva de Pandeo adimensional
La ventaja de este gráfico es que puede aplicarse a barras de diferentes esbelteces y
resistencias
Fig. 10.8 Curva de Pandeo Adimensional
10.7 Columnas cargadas Excéntricamente – Formula de la Secante
La fórmula de Euler se obtuvo con base en las hipótesis de que la carga P se aplica en el
centroide de la sección transversal de la columna y de que ésta es perfectamente recta.
Esto es irreal, puesto que las columnas fabricadas nunca son perfectamente rectas, ni se
conoce con exactitud la posición de la carga aplicada. Por tanto, en realidad las columnas
nunca se pandean repentinamente, sino que comienzan a pandearse de modo ligero,
inmediatamente después de la aplicación de la carga.
Fig. 10.8 Columnas Cargadas Excéntricamente
El diseño entonces buscara no sobrepasar una deflexión especificada de la columna y a no
permitir que el esfuerzo máximo en la columna exceda un esfuerzo permisible. Considérese
una columna con una carga excéntrica
De la estática
M = - P (e + y)
(10.27
La ecuación diferencial para la curva de deflexión es. por tanto.
EI
2 y
  P (e  y )
x 2
(10.28
EI
2 y
 Py   Pe
x 2
(10.29
La solución homogénea es la misma que se vi anteriormente. Sin embargo debe incluirse
una solución particular
y  C1Sin
P
P
x  C2Cos
xe
EI
EI
(10.30
La solución homogénea es la misma que se vi anteriormente. Sin embargo debe incluirse
Cuando x = 0 y = 0
Entonces
c2 = e
Cuando x 0 L y = 0
(10.31
Entonces
0  C1 Sin
P
P
L  eCos
Le
EI
EI

P 
e1  Cos
L 
EI

C1  
P
Sin
L
EI
(10.32
(10.33
Usando ángulos dobles
1  Cos
Sin
 P L
P

L  2Sin 2 

EI
EI
2


 P L
 P L
P
Cos

L  2Sin

 EI 2 
EI
EI
2




(10.34
(10.35

P L

e 2Sin 2
EI 2 
P L

C1 
 eTan
EI 2
P L
P L
2Sin
Cos
EI 2
EI 2
(10.36


P L
P
P
y  e Tan
Sin
x  Cos
x  1
EI 2
EI
EI


(10.37
La deformada máxima ocurre en x = L/2 y es

P L 
y max  e Sec
 1
EI
2


(10.38
El esfuerzo máximo en la columna se determina teniendo en cuenta que es generado tanto
por la carga axial como por el momento.
El momento máximo ocurre a la mitad de la columna
M max  Pe  ymax   PeSec
P L
EI 2
(10.39
El esfuerzo máximo en la columna es de compresión, y su valor es:
 max 
P Mc

A I
(10.40
El esfuerzo máximo en la columna se determina teniendo en cuenta que es generado tanto
 max 
P Pec
P L

Sec
A
I
EI 2
(10.41
En vista que el radio de giro es r2 = I/A la ecuación anterior puede escribirse en una forma
conocida como fórmula de la secante:
 max 
P  ec
P L
1  2 Sec

A  r
EA 2r 
(10.42
Para un valor dado de ζmax. pueden trazarse gráficas de esta ecuación en función de Kl/r
vs P/A para diferentes valores de la razón de excentricidad ec/r2. En la figura se muestra la
gráfica para un acero A36. Nótese que cuando e → 0. o cuando ec/r2 → 0. la ecuación 10.42
da ζmax = P/A, donde P es la carga crítica en la columna, definida por la fórmula de Euler.
Fig. 10.9 Graficas de la ecuación de la Secante
Las curvas en la figura indican que diferencias en la razón de excentricidad tienen un
marcado efecto en la capacidad de carga de columnas con relaciones pequeñas de
esbeltez. Por otra parte, las columnas que tienen grandes relaciones de esbeltez, tienden a
fallar en o cerca de la carga crítica de Euler sin importar cuál sea la excentricidad. Cuando
se usa la ecuación 13-19 para fines de diseño, es importante por consiguiente contar con un
valor más o menos preciso de la razón de excentricidad en el caso de columnas cortas.
PROBLEMAS RESUELTOS
10.1. Se pide hallar la carga que provoca pandeo para los cuatro tipos de columnas. Material
acero; longitud 10 m y diámetro 1 cm.
Solución:
I = d4/64
Pcr =  2 E (d4/64)/l2
 = 1 Pcr= 1.01 Kg
 = 4 Pcr= 4.06 Kg
 = ¼ Pcr= 0.25 Kg
 = 2 Pcr= 2.03 Kg
10.2. Determinar la relación de esbeltez critica. Encima de la cual la falla se produce por
pandeo y debajo de la cual la falla se debe a esfuerzos que superan la fluencia. Tomar  =
1, Sy = 1800 Kg/cm².
Solución:
Falla por compresión
P/A = Sy
Falla por pandeo
Pcr/A=  2 E/(l/k)2
Igualando
 2 E/(l/k)2 = Sy
(l/k) = ( 2 E/Sy)1/2 = 107.3
10.3. En el anterior problema. Si el diámetro de la barra es 1 cm cual es la longitud que da la
relación de esbeltez calculada.
Solution:
I =  d4/64
A =  d2/4
k = (I/A)1/2 = d2/16 = 0.0625 cm²
l = k 107.3 = 6.7 cm
10.4. Hallar (P/A) para valores de (l/k) de 0 a 250 en la fórmula de Euler. Graficar los
resultados. Tomar  = 1, E = 2.1 E 06 y Sy= 1800 Kg/cm²
23
0
20
0
17
0
14
0
11
0
9000,0
8000,0
7000,0
6000,0
5000,0
4000,0
3000,0
2000,0
1000,0
0,0
80
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
220
230
240
250
Pcr /A=   2 E/(l/k)2
8290,5
5757,3
4229,8
3238,5
2558,8
2072,6
1712,9
1439,3
1226,4
1057,5
921,2
809,6
717,2
639,7
574,1
518,2
470,0
428,2
391,8
359,8
331,6
50
(l/k)
10.5. Hallar la carga máxima que puede soportar el sistema antes de sufrir Pandeo. Material
acero y diámetro 1 cm
P
100 cm
a
30
P
b
30
Ta
45
Tb
45
Solución :
Fx = 0
Ta Cos 30 = Tb Cos 45
(i
Fy = 0
Ta Sin 30 + Tb Sin 45 = P
(ii
DE i y ii
(Tb Cos 45/Cos 30) Sin 30 + Tb Sin 45 = P
(iii
Tb = 0.8965 P
Ta = 0.732 P
La Sin 30 = 100
la = 200 cm
Lb Sin 45 = 100
lb = 141.42 cm
Pcr=  2 EI/l2
Para A
0.732 P = 2 2.1 x 10 6  (1)4/64/2002
P = 34.74 Kg
Para B
0.8965 P = 2 2.1 x 10 6  (1)4/64/141.422
P
P
a
a
b
100 cm
30
30
Ta
Ta
Tb
30
P = 56.74 Kg
De donde
Pmax=34.74 Kg
10.6. Hallar la carga máxima que puede soportar el sistema antes de sufrir Pandeo. Material
acero y diámetro 1 cm
Solución :
Fx = 0
Ta Cos 30 = Ta Cos 30
No aporta
a O
a
O
30
O´
30
O`
Fy = 0
2 Ta Sin 30 + Tb = P
M = 0
Las fuerzas son concurrentes
(i
No aporta
El sistema es hiperestático por lo que se debe hallar la ec. de deformadas
b = OO´
a = OO´Sin 30
b = a /Sin 30
Tblb/EA=Tala/(EA Sin 30)
la Sin 30 = lb ;
la = 200 cm
Tbla Sin 30=Tala/Sin 30
Tb = Ta/Sin2 30
Tb = 4 Ta
De i y ii
(ii
2 (4 Tb) Sin 30 + Tb = P
Tb = 0.2 P
Ta = 0.8 P
Para A
0.2 P = 2 2.1 x 10 6  (1)4/64/2002
P = 127.17 Kg
Para B
0.8 P = 2 2.1 x 10 6  (1)4/64/1002
P = 127.17 Kg
P
P
100 cm
a
b a
Ta
Ta
Tb
Tc
30
c
Ra
De donde
Tc
Rb
Ra
Pmax=127.17 Kg
10.7. Si P = 1000 Kg hallar el diámetro de los elementos sometidos a compresión para evitar
el Pandeo. Material acero
A
TAC
20
30
B

60
B

C
2TBC Cos 
P
Vista Lateral
P
Solución :
Por simetría
Ra = Rb = P/2 = 500 Kg
En el apoyo izquierdo
Fx = 0
Ta Cos 30 + Tc = 0
(i
Fy = 0
Ta Sin 30 + Ra = 0
(ii
Ta = - Ra/Sin 30 = -1000 Kg (Compresión)
Ta  Pcr 
 EI
2
l2
 2 E(
d 4
)
64

(100 / Sin30) 2
Tc = - Ta Cos 30 = 866.2 Kg (Tracción)
De donde
d = 2.5 cm
10.8. Se pide hallar el diámetro de la barras BC. Material acero
Solución :
Del 10.12 del capítulo 1 :
TAC = 3163.09 Kg
Tracción
TBC = - 1546.56 Kg Compresión – Pandeo
LBC = (152+602)1/2
LBC = 61.84 cm
Pcr= 2 EI/l2 = 2 2.1 x 106 ( d4 /64) /l2 = 1546.56
dBC = 1.55 cm
Compárese con
dAC = 1.49 cm hallados en el capítulo 1
10.9. Graficar la relación fuerza sobre área P/A vs relación de esbeltez l/k utilizando la
fórmula de la secante. Tomar ec/k2 = 0, 0.1, 0.5 y 1. Sy = 1800 Kg/cm²
Solución :
P/A= Sy /(1+(ec/k2)Sec[(l/k)(P/4Ae)1/2]
En la ecuación no se puede despejar P/A pero si l/k
Graficando
P/A
100
200
300
400
500
600
700
800
900
1000
1100
1200
1300
1400
1500
1600
1700
455,3
321,9
262,8
227,6
203,6
185,9
172,1
161,0
151,8
144,0
137,3
131,4
126,3
121,7
117,5
113,8
110,4
453,6
319,4
259,5
223,5
198,6
179,9
165,1
152,8
142,1
132,5
123,5
114,6
105,1
94,0
78,4
46,6
0,0
446,7
309,1
246,1
206,9
178,5
156,0
136,6
118,8
101,2
82,1
58,3
0,0
438,2
296,2
229,2
185,6
152,4
123,9
96,5
65,9
0,0
2000
1500
0,1
0,5
1000
1
500
Euler
0
0,0
Nótese que la curva de Euler es la de la secante con ec/k2 = 0
200,0
400,0
600,0
PROBLEMAS PROPUESTOS
10.10. Que ancho debe tener una barra cuadrada para que no se produzca pandeo para los
cuatro tipos de columnas. Material acero, carga 100 Kg. y longitud 10 m
10.11. Determinar la relación de esbeltez critica para los cuatro tipos de columnas. Encima
de la cual la falla se produce por pandeo y debajo de la cual la falla se debe a esfuerzos que
superan la fluencia. Sy = 1800 Kg/cm².
10.12. Hallar el diámetro de una barra circular sólida que tiene la misma resistencia al
pandeo que otra hueca con diámetros externo e interno D y d respectivamente
10.13. Hallar (P/A) para valores de (l/k) de 0 a 250 para los cuatro tipos de columnas en la
fórmula de Euler. Graficar los resultados. Tomar E = 2.1 E 06 y Sy= 1800 Kg/cm²
10.14. Si P = 1000 Kg hallar el diámetro de los elementos sometidos a compresión para
evitar el Pandeo. Material acero
10.15. Hallar la carga máxima que puede soportar el sistema antes de sufrir Pandeo.
Material acero y diámetro 1 cm
10.16. Hallar la carga máxima que puede soportar el sistema antes de sufrir Pandeo.
Material acero y diámetro 1 cm
10.17. Hallar la carga máxima que puede soportar el sistema antes de sufrir Pandeo.
Material acero y diámetro 1 cm
10.18. Se pide hallar el diámetro de la barras BC. Material acero
10.19. Graficar la relación fuerza sobre área P/A vs relación de esbeltez l/k utilizando la
fórmula de la secante. Tomar ec/k2 = 0, 0.1, 0.5 y 1. Sy = 3000 Kg/cm²