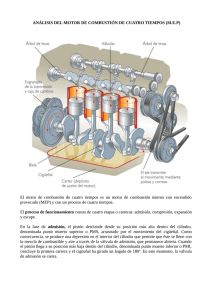
Cáp. IV CICLOS IDEALES DE LOS MCI 4.1. INTRODUCCIÓN Los

MAZ-222
Máquinas Térmicas
Cáp. IV
CICLOS IDEALES DE LOS MCI
4.1. INTRODUCCIÓN
Los ciclos ideales de los motores de combustión interna, la combustión juega un
rol sumamente importante en el caso de los diferentes ciclos termodinámicos, de
acuerdo que la sustancia de trabajo que participa en el proceso de combustión en
los MCI.
Dentro de los Motores de Combustión Interna, bajo la consideraciones de los
ciclos termodinámicos, donde en cada uno de los procesos fluye la sustancia de
trabajo, comportándose como GAS IDEAL al AIRE, el análisis termodinámico de
los MCI, bajo las consideraciones de un ciclo teórico, requiere de la
transformación del cambio químico, ocurrido con la sustancia de trabajo, durante
el proceso de combustión, esta suposición es admisible justificada por la relación
de:
Aire + Combustible = Gases de combustión.
Que determina las propiedades de la sustancia de trabajo.
Los ciclos ideales, han tomado como referencia el Ciclo de Carnot, este ciclo en
su estudio termodinámico, es un ciclo ideal más perfecto imaginable, donde se
obtiene la mayor cantidad de trabajo por calor agregado, pero en la práctica es
inviable, pero el estudio de los ciclos termodinámicos, exige progresivos grados de
aproximación en los parámetros termodinámicos próximos a los ciclos reales, es la
primera aproximación sobre el cual se estructurara el desarrollo y metodología
del análisis termodinámico.
En el estudio de los ciclos ideales de los Motores de Combustión Interna deberán
cumplir condiciones que son muy importantes en los diferentes procesos como:
 Como en cada uno de los procesos termodinámicos lo que fluye es la
Sustancia de Trabajo en todo el ciclo que será el aire comportándose como
gas ideal, sin esta sustancia de trabajo difícilmente podrá ser un ciclo ideal.
 El calor generado en la combustión se desarrollarse por la sustancia de
trabajo Aire + Combustible = Gases de combustión, por medio de la
reacción química exotérmica, además interviene el aporte calorífico de una
fuente caliente externa culata caliente, cuando el motor entre en régimen de
funcionamiento normal adquiriendo una temperatura normal.
 Las propiedades térmicas del aire como ser los calores específicos, el
exponente isentrópico, constante del aire, permanecerán constantes en los
diferentes procesos de los ciclos termodinámicos.
Página 1
MAZ-222
Máquinas Térmicas
 Las líneas descritas en los diferentes procesos, serán procesos a presión
constante, volumen constante, procesos isentrópicos, que no tendrán
ninguna variación descrita en los diagramas de presión y volumen en los
diferentes ciclos que estudiaremos posteriormente.
En los ciclos ideales no se tomarán en cuenta como ser:
 Las pérdidas de fricción en el sistema mecánico de los elementos que
compone un Motor de Combustión Interna.
 Si el Ciclo termodinámico es un motor convencional, motor multiválvular,
absolutamente no se consideraran por ser un ciclo ideal.
 Que la apertura y el cierre de las válvulas de admisión y escape, tomando
en cuenta que el pistón se desplaza del PMS al PMI en un proceso, es decir
no se tomaran en cuenta los grados de adelantos y retrasos.
 Que el sistema cilindro pistón es un sistema completamente hermético en
los procesos no fluyentes del ciclo.
 La resistencia hidráulica que fluye la sustancia de trabajo durante el
proceso de admisión, al llevar, filtro de aire, múltiple de admisión y otros
elementos que interviene en el proceso de admisión.
Tomando en cuenta estas condiciones estudiaremos los ciclos ideales de los
motores de combustión interna, tanto la parte teórica fundamentada y los cálculos
termodinámicos, en consideraciones tanto del altiplano como en el llano.



Ciclo Otto
Ciclo Diesel
Ciclo Dual o Mixto
4.2. CICLO OTTO
El ciclo Otto, es el ciclo ideal base para los motores a gasolina, la importancia de
este ciclo radica en que es un ciclo teórico de los motores de combustión interna
denominados como Ciclo Otto, encendido por chispa, que realiza la combustión a
volumen constante, en este proceso la sustancia de trabajo capta mejor la
naturaleza de la combustión, que prácticamente el desplazamiento del pistón es
despreciable entre el (PMS-PMI), que tal velozmente se desarrolla la combustión
en estos motores.
En el ciclo Otto la sustancia de trabajo se comporta como gas ideal, (aire +
combustible = mezcla gaseosa), lo que determina que para un estado cualquiera
del ciclo cumpla la condición de la ecuación de estado de los gases ideales como:
pV  RT
Página 2
MAZ-222
Máquinas Térmicas
El ciclo Otto, es un motor que está constituido por el sistema cilindro – pistón, en
el cual el pistón se mueve permanentemente en forma alternativa entre las
posiciones del PMS al PMI, el desplazamiento está regido por un mecanismo
llamado biela – manivela según el cual ese desplazamiento es llamado como
carrera del pistón (s), y el diámetro del pistón (D) es el área de la cabeza del
pistón.
En este acápite del ciclo Otto representamos los diagramas de:


Presión – volumen
Temperatura - entropía
Estos diagramas representan a un motor de combustión interna atmosférico de 4
tiempos motor gasolina.
p
T
3
3
qc  qa
qc  q a
2
W
4
0
qR
2
q
4
qR
1
1
Va
Ve
Vc
PMS
V
Vh
PMI
Diagramas de p-V ; T-S de un MCI 4 tiempos atmosféricos.
Página 3
S
MAZ-222
Máquinas Térmicas
4.2.1. PROCESOS DEL CICLO OTTO
Proceso de 0 – 1:
Proceso de admisión.
 Proceso a presión y temperatura atmosférica constante.
 El pistón se desplaza del PMS al PMI.
 Se admite la sustancia de trabajo (AIRE+COMBUSTIBLE)
Los parámetros a determinar son:
Vh 
mh 
 
Vc 
p0Vh
Kg 
RT0
m

4
D 2 s m3
 
 
Vh
m3
rk  1
V1  Vc  Vh m3
p0 ( Vh  Vc )
Kg 
RT0
mc 
mh
Kg 
ra
c
Podemos considerar parámetros como la presión atmosférica y temperatura
atmosférica, para los cálculos termodinámicos, considerando en sus condiciones
de alimentación, tanto en el altiplano como en el llano:
Altiplano
Llano
p1  p0  0 ,653bar   65300  N 2 
 m 
p1  p0  1bar   1x10 5  N 2 
 m 
T1  T0  10 0C  283 0 K
T1  T0  20 0C  293 0 K
 
Proceso de 1 – 2:
 
 
 
Proceso de compresión.
 Proceso isentrópico o adiabático a entropía constante.
 El pistón se desplaza del PMI al PMS.
 Se comprime la sustancia de trabajo.
Los parámetros a determinar son:
K
V 
p2  p1  1   N 2 
V2   m 
Proceso de 2 – 3:




V 
T2  T1  1 
V2 
K 1
( K )
W12 
p2V2  p1V1
J 
1 k
Proceso de combustión o explosión.
Proceso a volumen constante.
El desplazamiento del pistón es despreciable entre su inicio y final.
El pistón permanece en el PMS.
Se combustióna la mezcla de (AIRE+COMBUSTIBLE)
Los parámetros a determinar son:
Página 4
MAZ-222
Máquinas Térmicas
q23  qa  qc  mc HU J  T3 
Proceso de 3 – 4:
 
T
qc
pT N 
 T2 K  p3  2 3  2  S 23  mCv ln 3 J
T2 K
mCv
T2  m 
Proceso de expansión.
 Proceso isentrópico o adiabático a entropía constante.
 El pistón se desplaza del PMS al PMI.
 Se expanden los gases quemados lo cual producen trabajo.
Los parámetros a determinar son:
K
V 
p4  p3  3   N 2 
V4   m 
Proceso de 0 – 1:
V 
T4  T3  3 
V4 
K 1
W34 
( K )
p4V4  p3V3
J 
1 k
Proceso de calor rechazado.
 Proceso a volumen constante
 El pistón permanece en el PMI.
 En este proceso se expulsan los gases quemados.
Los parámetros a determinar son:
q41  qR  mCv( T1  T4 )J 
S 41  mCv ln
 
T1 J
T4 K
Cálculos finales
qT  qa  qR J  Wt  W1 2  W3  4 J  P 
Wt ni
Kw nt  Wt 100[% ] pm  Wt  N 2 
120000
qa
Vh  m 
4.2.2. ANÁLISIS TERMODINÁMICO DEL CICLO OTTO
4.3. CICLO DIESEL
En un MCI, un motor considerado encendido por la ignición del combustible, es
decir encendido por compresión, donde la inyección del combustible se desarrolla
desde una fuente exterior.
Página 5
MAZ-222
Máquinas Térmicas
Ese ciclo termodinámico Diesel se adecua a los motores de combustión interna de
cuatro tiempos, que utilizan combustibles (Diesel), que queman lentamente a
medida de que el pistón se va desplazando de manera que la combustión se va
consumiendo de manera progresiva, debido a la característica fundamental del
combustible, se asume que el fluido termodinámico es considerado al aire como un
gas ideal, de manera que los gases de combustión van empujando el émbolo del
pistón, expandiendo su volumen, mientras la presión en su interior queda la
misma.
Estos motores son considerados también, motores Diesel de inyección directa, lo
que da lugar que la combustión se desarrolla a presión constante.
p
T
qc  qa
2
qc  q a
3
4
0
Ve
Vc
q
2
W
Va
3
4
qR
qR
1
1
S
V
Vh
PMI
PMS
Diagramas de p-V; T-S de un Motor Diesel de 4 tiempos atmosféricos.
4.3.1. PROCESOS DEL CICLO DIESEL
Proceso de 0 – 1:
Proceso de admisión.
 Proceso a presión y temperatura atmosférica constante.
 El pistón se desplaza del PMS al PMI.
 Se admite la sustancia de trabajo (AIRE)
Los parámetros a determinar son:
Vh 
mh 
 
Vc 
p0Vh
Kg 
RT0
m

4
D 2 s m3
 
 
Vh
m3
rk  1
V1  Vc  Vh m3
p0 ( Vh  Vc )
Kg 
RT0
Página 6
mc 
mh
Kg 
ra
c
MAZ-222
Máquinas Térmicas
Podemos considerar parámetros como la presión atmosférica y temperatura
atmosférica, para los cálculos termodinámicos, considerando en sus condiciones
de alimentación, tanto en el altiplano como en el llano:
Altiplano
Llano
p1  p0  0 ,653bar   65300  N 2 
 m 
p1  p0  1bar   1x10 5  N 2 
 m 
T1  T0  10 0C  283 0 K
T1  T0  20 0C  293 0 K
 
Proceso de 1 – 2:
 
 
 
Proceso de compresión.
 Proceso isentrópico o adiabático a entropía constante.
 El pistón se desplaza del PMI al PMS.
 Se comprime la sustancia de trabajo.
Los parámetros a determinar son:
K
V 
p2  p1  1   N 2 
V2   m 
Proceso de 2 – 3:
V 
T2  T1  1 
V2 
K 1
W12 
( K )
p2V2  p1V1
J 
1 k
Proceso de combustión o explosión.
 Proceso a presión constante.
 Se inyecta el combustible se produce la (AUTOINFLAMACION), La
combustión se va consumiendo de manera progresiva a medida de que
pistón se desplaza.
 El pistón se desplaza de una condición inicial a una condición final.
Los parámetros a determinar son:
q23  qa  qc  mc HU J 
mc 
mh
Kg 
ra
S 23  mCp ln
c
Proceso de 3 – 4:
T3 
qc
 T2 K 
mCp
 
T3 J
T2 K
V3 
W23  p3 ( V3  V2 )J 
Proceso de expansión.
 Proceso isentrópico o adiabático a entropía constante.
 El pistón se desplaza del PMS al PMI.
 Se expanden los gases quemados lo cual producen trabajo.
Los parámetros a determinar son:
Página 7
 
V2T3 3
m
T2
MAZ-222
V 
T4  T3  3 
V4 
Máquinas Térmicas
K 1
K
( K )
Proceso de 0 – 1:
V 
p V  p3V3
J 
p4  p3  3   N 2  W34  4 4
m
1 k


V
 4
Proceso de calor rechazado.
 Proceso a volumen constante
 El pistón permanece en el PMI.
 En este proceso se expulsan los gases quemados.
Los parámetros a determinar son:
q41  qR  mCv( T1  T4 )J 
S 41  mCv ln
 
T1 J
T4 K
Cálculos finales
qt  qa  qR J  Wt  W1 2  W2  3  W3  4 J  P 
pm 
Wt ni
Kw n  Wt 100[% ]
qa
120000
Wt  N

Vh  m 2 
4.3.2. ANÁLISIS TERMODINÁMICO DEL CICLO DIESEL
4.4. CICLO DUAL
El ciclo dual, es un ciclo teórico Diesel que se aproxima a las actuaciones de un
ciclo real, de los motores modernos rápidos encendidos por compresión, gracias a
la inyección del combustible en un momento exacto que se produce la (auto
combustión o auto inflamación de la mezcla), por las elevada presión de
compresión.
Este ciclo Dual, es un ciclo que los suministros de calor se desarrollan en dos
procesos, uno a volumen constante y el otro a presión constante, significa que
tiene dos fases de combustión, una primera fase donde se inicializa la combustión
a V=Cte, que luego una segunda fase donde termina la combustión de manera
progresiva a p=Cte. Estos motores diesel tienen un sistema de alimentación de
inyección indirecta, esto implica que es un motor diesel que tiene una precámara
de combustión.
Página 8
MAZ-222
Máquinas Térmicas
Luego los otros procesos son procesos semejantes a las que se han considerado en
los ciclos Otto y Diesel.
q34
p
3
4
T
qc  qa  q23  q34
q34
q23
q23
2
3
W
2
5
qR
1
0
Va
Ve
4
Vc
5
qR
1
V
Vh
q
S
PMI
PMS
Diagramas de p-V; T-S de un ciclo dual de 4 tiempos atmosféricos.
4.4.1. PROCESOS DEL CICLO DUAL
Proceso de 0 - 1
Proceso de admisión
 Proceso a presión y temperatura atmosférica constante.
 El pistón se desplaza del PMS al PMI.
 Se admite la sustancia de trabajo (AIRE)
Los parámetros a determinar son:
Página 9
MAZ-222
Vh 
mh 
Máquinas Térmicas
 
Vc 
p0Vh
Kg 
RT0
m

4
D 2 s m3
 
 
Vh
m3
rk  1
V1  Vc  Vh m3
p0 ( Vh  Vc )
Kg 
RT0
mc 
mh
Kg 
ra
c
Podemos considerar parámetros como la presión atmosférica y temperatura
atmosférica, para los cálculos termodinámicos, considerando en sus condiciones
de alimentación, tanto en el altiplano como en el llano:
Altiplano
Llano
p1  p0  0 ,653bar   65300  N 2 
 m 
p1  p0  1bar   1x10 5  N 2 
 m 
T1  T0  10 0C  283 0 K
T1  T0  20 0C  293 0 K
 
Proceso de 1 – 2
 
 
 
Proceso de compresión
 Proceso isentrópico o adiabático a entropía constante.
 El pistón se desplaza del PMI al PMS.
 Se comprime la sustancia de trabajo.
Los parámetros a determinar son:
K
V 
p2  p1  1   N 2 
V2   m 
Proceso de 2 – 3






V 
T2  T1  1 
V2 
K 1
( K )
W12 
p2V2  p1V1
J 
1 k
Proceso primera fase de la combustión
Proceso a volumen constante.
Se inicializa la combustión a gracias a la inyección del combustible Diesel.
El desplazamiento del pistón es despreciable entre su inicio y final.
Permanece en el PMS.
Se inicializa la combustión a gracias a la inyección del combustible Diesel.
Considerar la relación de presión según M.S. Jovaj y Lukanin establecen:
  1,2  2,2
Los parámetros a determinar son:
pT
mh
Kgc 
qa  qc  mc HU J  p3  p2  N 2  T3  3 2 K  mc 
 m 
p2
ra
q23  mCv( T3  T2 )J 
Página 10
S 23  mCv ln
 
T3 J
T2 K
c
MAZ-222
Máquinas Térmicas
Proceso de 3 – 4
Proceso segunda fase de la combustión
 Proceso a presión constante.
 La combustión se va consumiendo de manera progresiva a medida de que
pistón se desplaza, lo cual completa la combustión.
 El pistón se desplaza.
Los parámetros a determinar son:
q3  4  qa  q2  3 J 
qa  q2  3  q3  4 J 
V4 
 
V3T4 3
m
T3
Proceso de 4 – 5
S 34  mCp ln
T4 
 
q34
 T3 K 
mCp
W34  p4 ( V4  V3 )J 
T4 J
T3 K
Proceso de expansión
 Proceso isentrópico o adiabático a entropía constante.
 El pistón se desplaza del PMS al PMI.
 Se expanden los gases quemados lo cual producen trabajo.
Los parámetros a determinar son:
K
V 
p5  p4  4   N 2 
V5   m 
Proceso de 5 – 1
V 
T5  T4  4 
V5 
K 1
W45 
( K )
p5V5  p4V4
J 
1 k
Proceso de calor rechazado
 Proceso a volumen constante
 El pistón permanece en el PMI.
 En este proceso se expulsan los gases quemados.
Los parámetros a determinar son:
q51  qR  mCv( T1  T5 )J 
S 51  mCv ln
 
T1 J
T5 K
Cálculos finales
qt  qa  qR J 
Wt  W1 2  W3  4  W4  5 J 
n
Wt
* 100%
qa
pm 
P
Wt ni
Kw
120000
Wt  N

Vh  m 2 
4.4.2. ANÁLISIS TERMODINÁMICO DEL CICLO DUAL
Página 11