ω ω ω ω ω ω ω ω π ω π π ω π ω π ω π ω π ω ω

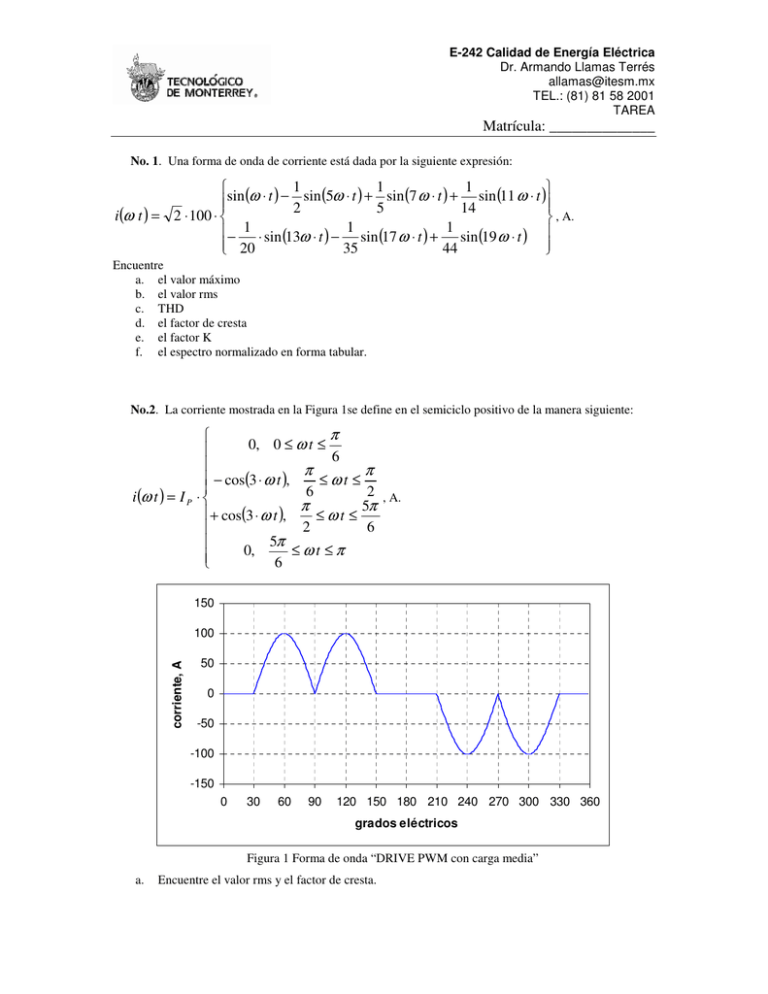
E-242 Calidad de Energía Eléctrica
Dr. Armando Llamas Terrés
allamas@itesm.mx
TEL.: (81) 81 58 2001
TAREA
Matrícula: ______________
No. 1. Una forma de onda de corriente está dada por la siguiente expresión:
1
1
1


sin (ω ⋅ t ) − 2 sin (5ω ⋅ t ) + 5 sin (7 ω ⋅ t ) + 14 sin (11 ω ⋅ t )
i (ω t ) = 2 ⋅ 100 ⋅ 
 , A.
1
1
1
−
⋅ sin (13ω ⋅ t ) − sin (17 ω ⋅ t ) + sin (19 ω ⋅ t ) 
 20

35
44
Encuentre
a. el valor máximo
b. el valor rms
c. THD
d. el factor de cresta
e. el factor K
f. el espectro normalizado en forma tabular.
No.2. La corriente mostrada en la Figura 1se define en el semiciclo positivo de la manera siguiente:
π

0, 0 ≤ ω t ≤

6

π
π
 − cos(3 ⋅ ω t ),
≤ωt ≤

6
2 , A.
i (ω t ) = I P ⋅ 
5π
π
+ cos(3 ⋅ ω t ),
≤ωt ≤
2
6

5π

0,
≤ωt ≤π

6
150
corriente, A
100
50
0
-50
-100
-150
0
30
60
90
120 150 180 210 240 270 300 330 360
grados eléctricos
Figura 1 Forma de onda “DRIVE PWM con carga media”
a.
Encuentre el valor rms y el factor de cresta.
E-242 Calidad de Energía Eléctrica
Dr. Armando Llamas Terrés
allamas@itesm.mx
TEL.: (81) 81 58 2001
TAREA
Matrícula: ______________
b.
c.
d.
Encuentre los coeficientes de la serie de Fourier correspondientes a la fundamental y a las
primeras cuatro armónicas con valor distinto de cero.
Encuentre el valor rms de la distorsión armónica empleando el valor rms total y el valor rms de la
fundamental.
Encuentre el factor K.