FISICA_2_BAC...s OPTICA
Anuncio
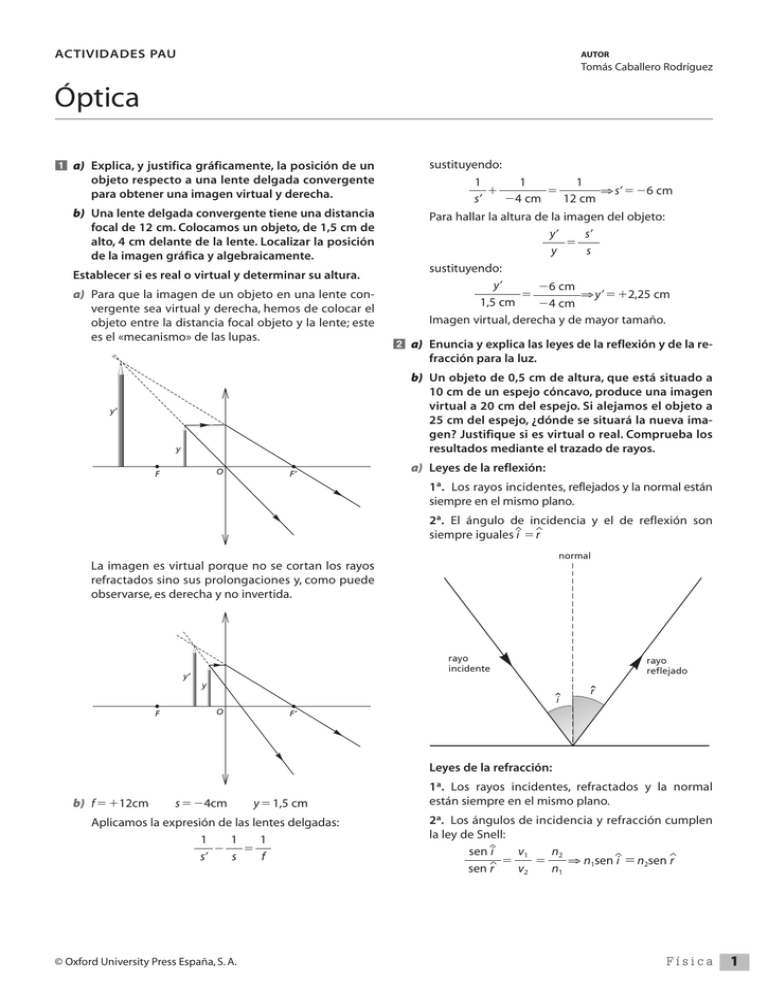
ACTIVIDADES PAU AUTOR Tomás Caballero Rodríguez Óptica a) Explica, y justifica gráficamente, la posición de un objeto respecto a una lente delgada convergente para obtener una imagen virtual y derecha. b) Una lente delgada convergente tiene una distancia focal de 12 cm. Colocamos un objeto, de 1,5 cm de alto, 4 cm delante de la lente. Localizar la posición de la imagen gráfica y algebraicamente. Establecer si es real o virtual y determinar su altura. a) Para que la imagen de un objeto en una lente convergente sea virtual y derecha, hemos de colocar el objeto entre la distancia focal objeto y la lente; este es el «mecanismo» de las lupas. sustituyendo: 1 1 1 ⇒s’ 6 cm s’ 4 cm 12 cm Para hallar la altura de la imagen del objeto: y’ s’ y s sustituyendo: y’ 6 cm ⇒y’ 2,25 cm 1,5 cm 4 cm Imagen virtual, derecha y de mayor tamaño. a) Enuncia y explica las leyes de la reflexión y de la refracción para la luz. b) Un objeto de 0,5 cm de altura, que está situado a 10 cm de un espejo cóncavo, produce una imagen virtual a 20 cm del espejo. Si alejamos el objeto a 25 cm del espejo, ¿dónde se situará la nueva imagen? Justifique si es virtual o real. Comprueba los resultados mediante el trazado de rayos. y’ y O F F’ a) Leyes de la reflexión: 1ª. Los rayos incidentes, reflejados y la normal están siempre en el mismo plano. 2ª. El ángulo de incidencia y el de reflexión son ^ ^ siempre iguales i r normal La imagen es virtual porque no se cortan los rayos refractados sino sus prolongaciones y, como puede observarse, es derecha y no invertida. rayo incidente y’ rayo reflejado y i F O r F’ Leyes de la refracción: b) f 12cm s 4cm y 1,5 cm Aplicamos la expresión de las lentes delgadas: 1 1 1 s’ s f © Oxford University Press España, S. A. 1ª. Los rayos incidentes, refractados y la normal están siempre en el mismo plano. 2ª. Los ángulos de incidencia y refracción cumplen la ley de Snell: ^ sen i v1 n2 ^ ^ ⇒ n1sen i n2sen r ^ sen r v2 n1 Física 1 ACTIVIDADES PAU Óptica (CONTINUACIÓN) Un rayo de luz blanca incide perpendicularmente sobre la superficie del agua. ¿Se observará el fenómeno de la dispersión cromática en la luz que se propaga por el agua? Razona tu respuesta. normal rayo incidente i medio 1 medio 2 r rayo refectado b) Si la imagen es virtual en el espejo cóncavo, s’ 20cm. Como el objeto se coloca delante del espejo, tomamos s 10cm. Con estos datos, sustituyéndolos en la expresión general, sacamos la distancia focal del espejo y el radio de curvatura del mismo. 1 1 1 1 1 1 ⇒ s’ s f 20 cm 10 cm f La dispersión de la luz blanca es la descomposición en sus colores más simples que experimenta un rayo de luz al cambiar de medio (prisma óptico, agua, etc.) siguiendo la ley de Snell de la refracción: ^ sen i v1 n2 ^ sen r v2 n1 Las distintas radiaciones que componen la luz blanca viajan a la misma velocidad en el aire, pero a distintas velocidades en los medios materiales; por esa razón experimentan distintos ángulos de refracción. Como el rayo de luz incide perpendicularmente sobre la ^ superficie del agua, el ángulo de incidencia es 0° ( i 0°) y, por lo tanto, el ángulo de refracción será también ^ 0° ( r 0°) y no se producirá la dispersión cromática. Operando: f20 cm y R2f40 cm. Ahora, colocamos el objeto a 25 cm del espejo, s 25cm, y calculamos dónde aparece la nueva imagen: 1 1 1 s’ 25 cm 20 cm Operando: s’ 100 cm. La imagen es real, ya que se cortan los propios rayos reflejados. El tamaño de la imagen es: s’ 100 cm y’ y’ ⇒ 4 s 25 cm y 0,5 cm Por lo tanto: y’2cm. rayo incidente v1, n1 aire agua v2, n2 rayo refractado Una onda luminosa viaja por un medio con velocidad c1 e incide sobre la frontera de separación con otro medio donde la velocidad de propagación es c2 ⴝ 2c1. Si el ángulo de incidencia es i ⴝ 10°: a) Calcula el ángulo de refracción. b) ¿A partir de que ángulo de incidencia se producirá reflexión total? y C y’ F O a) Aplicando la ley de Snell: ^ sen i v1 sen 10° c1 ⇒ 0,5 ^ ^ sen r v2 2c1 sen r ^ Operando sale: r 20,3° b) Para calcular con qué ángulo de incidencia se produce la reflexión total, volvemos a calcular la ley de Snell: ^ sen i límite v1 c1 ^ ⇒ sen i límite 0,5 sen 90° v2 2c1 ^ Por lo que: i límite 30°. A partir de un ángulo de incidencia límite de 30°, los rayos ya no se refractan porque no cambian de medio, sino que se quedan en el mismo medio. Este fenómeno se conoce como reflexión total. © Oxford University Press España, S. A. Física 2 ACTIVIDADES PAU Óptica (CONTINUACIÓN) ¿Qué se entiende por refracción de una onda y en qué condiciones se produce? Razona que características de la onda permanecen constantes y cuales se modifican cuando se produce el fenómeno de la refracción. y O F F’ La refracción de una onda es el cambio de dirección que experimenta la onda al pasar de un medio a otro distinto. La refracción se rige por dos leyes: 1.ª La dirección de incidencia de las ondas, la dirección de emergencia y la normal a la superficie de ambos medios está en un mismo plano. 2.ª Ley de Snell: el ángulo de incidencia y el de refracción están relacionados por: ^ sen i v1 ^ sen r v2 normal y’ Imagen real, invertida y de igual tamaño. b) Espejo plano situado a 2 cm: s’ = s (2 cm) 2 cm Sustituyendo los datos: y’ s’ 2 cm AL 1 y s (2 cm) La imagen que se obtiene es la siguiente: rayo incidente i medio 1 y medio 2 y’ r rayo refractado En la refracción, cambian la velocidad de propagación de la onda en los dos medios, la dirección de propagación de la onda y la longitud de onda en los dos medios, pero no se modifican ni el período ni la frecuencia. Como v , al ser la frecuencia independiente T del medio, cuando varía la velocidad ha de hacerlo la longitud de onda. Encontrar mediante un diagrama de rayos la imagen creada por: a) Una lente convergente de distancia focal 2 cm de un objeto situado a 4 cm. b) Un espejo plano de un objeto situado a 2 cm. Describir en ambos casos las características más importantes de la imagen (real o virtual, derecha o invertida). a) Lente convergente de f = 2 cm y s 4 cm 1 1 1 Sustituyendo en: s’ s f 1 1 1 cm ⇒ s’ = 4 cm s’ (4 cm) 2 y’ s’ 4 cm 1 AL y s (4 cm) La imagen que se crea es la siguiente: S S’ Imagen virtual, derecha y de igual tamaño que el objeto. Por medio de un espejo cóncavo se quiere proyectar un objeto de 1 cm sobre una pantalla plana, de modo que la imagen sea derecha y de 3 cm. La pantalla ha de estar colocada a 2 m del objeto. Calcular: a) El radio del espejo. b) Su distancia focal. c) Su potencia. d) Distancias del objeto e imagen al espejo. Analizando las características de la imagen: real, ya que podemos recogerla sobre una pantalla; invertida y mayor que el objeto, se llega a la conclusión de que el objeto ha de estar colocado entre el centro de curvatura del espejo cóncavo y el foco. De la expresión del aumento lateral sacamos la relación entre s’ y s: 3 cm s’ y’ s’ ⇒ ⇒ s’ 3s (1) 1 cm s y s Por otro lado, como la pantalla donde se recoge la imagen está colocada a 2 m del objeto, podemos escribir la ecuación: s’s2 (2) Igualando las ecuaciones (1) y (2): 3ss2 ⇒ s1 m y s’3 m (d) De acuerdo con el convenio de signos: s1 m y s’3 m © Oxford University Press España, S. A. Física 3 ACTIVIDADES PAU Óptica (CONTINUACIÓN) (b) Calculemos la distancia focal: 1 1 1 1 1 1 ⇒ s’ s f 3 m 1 m f operando: f 0,75 m (a) El radio de curvatura del espejo es: R2f1,5 m (c) La potencial del espejo es: 1 1 P 1,33 D f 0,75 m aire n21 agua n11,3 ilim reflexión total Cuando la luz pasa de un medio de n1 1,7 al aire n2 1, el ángulo límite es: n2 1 ^ i lim arcsen arcsen 36° n1 1,7 y C O F y’ Enuncia e ilustra mediante diagramas de rayos las leyes de la reflexión y la refracción de la luz. Leyes de la reflexión: 1.ª Los rayos incidentes, reflejados y la normal están siempre en el mismo plano. Una persona hipermétrope tiene el punto próximo a 0,60 m. ¿Qué tipo de lente correctora utilizará para poder leer con claridad un libro situado a 0, 30 m? Justifica tu respuesta. La hipermetropía es un trastorno de refracción del ojo con alteración de la visión debido a la falta de potencia en el cristalino, que hace que la imagen de los objetos lejanos se forme detrás de la retina. El hipermétrope se caracteriza por la visión borrosa de los objetos situados a cortas distancias, aunque puede ver con mayor claridad los situados a largas distancias. Se corrige con lentes convergentes, que hacen que la imagen se forme en la retina. Explica el fenómeno de la reflexión total. Calcula el ángulo límite cuando la luz pasa de un medio con índice de refracción de n ⴝ 1,7 al aire (n’ ⴝ 1). Cuando un rayo de luz pasa de un medio más refringente (con mayor índice de refracción), como el agua, a otro medio menos refringente (con menor índice de refracción), como el aire, se aleja de la normal a la superficie de separación, cumpliéndose la ley de Snell de la refracción: ^ 2.ª El ángulo de incidencia y el de reflexión son siempre ^ ^ iguales i r normal rayo incidente rayo reflejado r i Leyes de la refracción: 1.ª Los rayos incidentes, refractados y la normal están siempre en el mismo plano. 2.ª Los ángulos de incidencia y refracción cumplen la ley de Snell: ^ sen i v1 n2 ^ ^ ⇒ n1 sen i n2 sen r ^ sen r v2 n1 normal rayo incidente i medio 1 medio 2 r rayo refectado ^ n1 sen i n2 sen r Existe un ángulo de incidencia, llamado ángulo limite, al que le corresponde un ángulo de refracción de 90°. Por encima de ese ángulo límite los rayos ya no salen del primer medio, no se refractan, sino que se reflejan; a este fenómeno se le conoce como reflexión total. © Oxford University Press España, S. A. Física 4 ACTIVIDADES PAU Óptica (CONTINUACIÓN) En el banco óptico del laboratorio disponemos de una lente cuya distancia focal es ⴚ20 cm. a) Determina la posición y tamaño de la imagen de un objeto de 5 cm de altura cuando se coloca a 30 cm de la lente. y y’ b) Determina la posición y tamaño de la imagen de un objeto de 5 cm de altura cuando se coloca a 10 cm de la lente. F’ O F c) Calcula la potencia de la lente. a) Se trata de una lente divergente, ya que su distancia focal es negativa. Los datos son: f’ 20cm; s 30 cm; y 5 cm Utilizando la expresión general de las lentes y sustituyendo: 1 1 1 1 1 1 ⇒ s’ s f s’ 30 cm 20 cm que operando da: s’ 12 cm El tamaño de la imagen lo calculamos pendiente: y’ s’ y’ 12 cm AL ⇒ y s 5 cm 30 cm por lo que y’ 2 cm La imagen tiene las mismas características que la anterior. c) La potencia de una lente es la inversa de la distancia focal: 1 1 P 5 D f’ 0,2 m Un objeto luminoso se encuentra delante de un espejo esférico cóncavo. Realiza la construcción gráfica de la imagen ayudándote de diagramas si el objeto está situado a una distancia superior a la distancia focal del espejo. Tenemos que analizar tres posibilidades: a) R s f y y’ F’ y O F C F O y’ Imagen virtual, derecha y menor. b) Ahora s 10 cm. Procediendo como antes: 1 1 1 operando: s’ 20 cm s’ 10 cm 20 cm y’ 20 cm cuyo resultado es: y’ 10 cm 5 cm 10 cm © Oxford University Press España, S. A. Imagen real, invertida y mayor que el objeto. Física 5 ACTIVIDADES PAU Óptica (CONTINUACIÓN) b) R s y O F F’ y C F O y’ Como los rayos refractados son paralelos, no se cortarán nunca, por lo que la imagen se formará en el infinito. Imagen real, invertida y de igual tamaño que el objeto. c) Objeto colocado a menor distancia que la distancia focal (s f). c) R s y’ y y C y’ F O F O F’ Imagen real, invertida y menor. Características (tamaño y naturaleza) de la imagen obtenida en una lente convergente en función de la posición del objeto sobre el eje óptico. Ilustre gráficamente los diferentes casos. a) Objeto a una distancia mayor que la distancia focal (s f) y F O F’ y’ Es una imagen virtual, ya que no se cortan los rayos refractados sino sus prolongaciones por detrás, es derecha y mayor que el objeto. a) Determine la velocidad de la luz en el etanol teniendo en cuenta que su índice de refracción absoluto es n ⴝ 1,36. b) Un haz de luz roja cuya longitud de onda en el aire es de 695 nm penetra en dicho alcohol. Si el ángulo de incidencia es de 30°, ¿cuál es el ángulo de refracción? ¿Cuál es la longitud de onda y la frecuencia del haz de luz en el alcohol? c a) El índice de refracción se define como: n , así: v c c n 1,36 ⇒ v2 220 588 km/s v2 1,36 es la velocidad de la luz en el etanol. Imagen real, invertida y de mayor tamaño que el objeto, en este caso. Aunque el tamaño depende de la distancia al foco. b) Objeto colocado en el foco (s f) © Oxford University Press España, S. A. b) Aplicamos la ley de Snell para hallar el ángulo de refracción: ^ sen i v1 sen 30° c ⇒ 1,36 ^ ^ sen r v2 c sen r 1,36 Física 6 ACTIVIDADES PAU Óptica (CONTINUACIÓN) ^ sen r 0,5 ^ , por lo que r 21,6° 1,36 N rayo incidente aire n1, v1 = c 30o Ángulo de incidencia Ángulo de refracción Índice de refracción (nv) 1.ª 2.ª 3.ª 4.ª 20° 29° 40° 50° 14° 20° 26° 31° 1,41 1,42 1,47 1,49 La ley que hemos utilizado para calcular el índice de refracción del vidrio es la ley de Snell, que nos da la relación entre el ángulo de incidencia y el de refracción: ^ sen i n2 cte ^ sen r n1 etanol n2, v2 r rayo refractado Para hallar la longitud de onda en el etanol, hemos de tener en cuenta que: 1 v1 T 1 v2 2 2 T El medio 1 es el aire n1 1; por lo tanto, para hallar ^ sen i n2 ^ sen r sustituyendo en esta expresión se han obtenido los valores de n2 que figuran en la tabla. c Como v1 c y 1 695 nm, y además v2 , sus1,36 tituyendo: c 695 ⇒ 2 511 nm c 2 1,36 La frecuencia de las radiaciones luminosas es igual en el vacío que en los medios materiales; es independiente del medio, por lo que: 3 108 m/s v1 v2 1 2 ⇒ 4,31 1014 Hz 695 109 m 1 2 En el laboratorio del instituto se han medido los siguientes ángulos de refracción cuando un haz luminoso incide desde el aire (naire ⴝ 1) hacia una superficie de un vidrio cuyo índice de refracción pretendemos determinar. Calcula el índice de refracción de dicho vidrio. ¿Qué ley física has tenido en cuenta para calcular el índice de refracción? Experiencia Ángulo de incidencia Ángulo de refracción 1.ª 2.ª 3.ª 4.ª 20° 29° 40° 50° 14° 20° 26° 31° © Oxford University Press España, S. A. Experiencia Tomaremos como mejor valor, el afectado de menos error, la media aritmética de los valores: _ n2,i n2 1,45 0,01 4 i 冱 Explica el fenómeno de la dispersión de la luz, pon un ejemplo en el que se ponga de manifiesto. Si mediante una rendija se aísla un haz de rayos de luz solar y este se hace incidir en un prisma óptico, la imagen de la rendija que se recogerá en una pantalla después de que el haz haya atravesado el prisma estará formado por una serie de franjas coloreadas. Al realizar la experiencia con un rayo láser, por ejemplo, se obtiene una sola imagen de la rendija. La luz solar es compleja o policromática y la del láser es monocromática. A la descomposición de la luz blanca o de cualquier otra luz compleja en sus colores más simples se le denomina dispersión de la luz, y al conjunto de franjas coloreadas en la pantalla, espectro. Los colores aparecen siempre en el mismo orden y de menor a mayor desviación: rojo, amarillo, naranja, verde, azul, añil y violeta. El fenómeno conocido como arco iris es un ejemplo de dispersión cromática: las gotitas de agua presentes en la atmósfera hacen de prismas ópticos y descomponen la luz solar en sus colores más simples. Para explicar este fenómeno hay que admitir que en el vacío y en el aire la velocidad de la luz es la misma para todos los colores, pero no ocurre así en el vidrio, ya que cada color tiene distinta velocidad de propagación y, por lo tanto, de acuerdo con la ley de Snell, distinto ángulo de refracción. Física 7 ACTIVIDADES PAU Óptica (CONTINUACIÓN) Sabemos que: v1 1 y v2 2 ⇒ ^ v1 n2 sen i ⇒ 1 ^ v2 n1 sen r 2 El ángulo de incidencia es menor que el de refracción, como se aprecia en los datos numéricos de la experiencia. Las radiaciones de mayor son las de menor n, las menos desviadas (rojo) y viceversa (violeta). b) Ángulo límite o ángulo de incidencia límite es el valor que debe tener el ángulo de incidencia para que el ángulo de refracción sea de 90°. En nuestra ^ experiencia: i lim 44°. c) Para que se dé el fenómeno de la reflexión total, los rayos deben pasar de medios más refringentes a medios menos refringentes y el ángulo de incidencia debe ser superior al ángulo límite, en este caso, mayor que 44°. Luz blanca d) Si el ángulo es mayor que el ángulo límite, la luz no cambia de medio y se refleja totalmente; de ahí el nombre de reflexión total. En el laboratorio del instituto se han medido los siguientes ángulos de refracción cuando un haz luminoso incide desde un vidrio hacía el aire (naire ⴝ 1) para observar el fenómeno de la reflexión total. De acuerdo con los datos de la práctica responde a las siguientes cuestiones: a) Cuando un rayo luminoso pasa de un medio homogéneo como el vidrio, a otro medio, también homogéneo como el aire sufre una refracción de tal modo que el rayo refractado: ¿Se aleja o se acerca a la normal? b) ¿A qué llamamos ángulo límite? Determínalo en base a la tabla adjunta. c) ¿Qué condiciones deben cumplir los medios para que se produzca la reflexión total? d) Para ángulos de incidencia mayores que el ángulo límite, la luz: a) se refleja, b) se refracta, o c) se refleja y se refracta. Experiencia Ángulo de incidencia Ángulo de refracción 1.ª 2.ª 3.ª 4.ª 20° 30° 40° 44° 28° 45° 68° 90° a) Cuando un rayo de luz pasa de un medio más refringente (mayor n) a otro menos refringente, como ocurre aquí, el rayo refractado se aleja siempre de la normal ya que, de acuerdo con la ley de Snell: ^ sen i n2 cte ^ sen r n1 na=1 aire vidrio nv=1,44 ilin reflexión total ¿Qué es la potencia de una lente? ¿Cuál es la distancia focal de una lente de cuarzo que tiene una potencia de 8 dioptrías? La potencia de una lente es la inversa de la distancia focal imagen. Si esta distancia se expresa en metros (m), la potencia se mide en dioptrías (D) siendo 1 D 1 m1. 1 P f’ La potencia de las lentes convergentes es positiva, ya que f’ está a la derecha, y la potencia de las lentes divergentes es negativa, ya que f’ está a la izquierda. F O F’ F’ O F Si la lente de cuarzo tiene una potencia de 8 D, su distancia focal imagen es: 1 1 8 ⇒ f ’ 0,125 m f’ 8 Y como n2 naire n1 nvidrio ^ sen i ^ ^ ^ ^ ^ 1 ⇒ sen i sen r ⇒ i r sen r © Oxford University Press España, S. A. Física 8 ACTIVIDADES PAU Óptica (CONTINUACIÓN) Una lámina de vidrio (índice de refracción n ⴝ 1,52) de caras planas y paralelas y espesor d se encuentra entre el aire y el agua. Un rayo de luz monocromática de frecuencia 5 ⴢ 1014 Hz incide desde el agua en la lámina. Determine: 90o r1 i lim a) Las longitudes de onda del rayo en el agua y en el vidrio. b) El ángulo de incidencia en la primera cara de la lámina a partir del cual se produce reflexión total interna en la segunda cara. Datos: Índice de refracción de agua nagua ⴝ 1,33; Velocidad de la luz en el vacío c ⴝ 3 ⴢ 108 m/s a) c c c ⇒ agua vagua agua v nagua v 3 108 m/s 4,5 107 m 14 1,33 5 10 Hz c c c ⇒ vidrio nvidrio vvidrio vidrio v nvidrio v 3 108 m/s 4 107 m 1,52 5 1014 Hz Estas son las longitudes de onda del rayo en el agua y en el vidrio, teniendo presente que la frecuencia del rayo no varía al cambiar de medio. nagua b) i1 Un sistema óptico está formado por dos lentes: la primera es convergente y con distancia focal de 10 cm; la segunda, situada a 50 cm de distancia de la primera, es divergente y con 15 cm de distancia focal. Un objeto de tamaño 5 cm se coloca a una distancia de 20 cm delante de la lente convergente. a) Obtenga gráficamente mediante el trazado de rayos la imagen que produce el sistema óptico. b) Calcule la posición de la imagen producida por la primera lente. c) Calcule la posición de la imagen producida por el sistema óptico. d) ¿Cuál es el tamaño y la naturaleza de la imagen final formada por el sistema óptico? a) 90o aire n = 1 vidrio r1 ilim d y vidrio n2 = 1,52 agua n1 = 1,33 F i1 O F’ F’ y’’ O y’ Calculamos el ángulo de incidencia límite en la segunda cara: ^ ^ nvidrio sen i lim naire sen 90° ⇒ 1,52 sen i lim 1 1 ⇒ ^ ⇒ i lim 41,14° Si se supera este ángulo de incidencia en la segunda ^ cara ya se produce reflexión interna total. Este i lim es el ángulo de refracción en la primera cara ya que son ángulos alternos e internos: ^ ^ i lim r1 Para calcular el ángulo de incidencia en la primera cara volvemos a aplicar la ley de Snell a la entrada del rayo: ^ ^ ^ nagua sen i 1 nvidrio sen r1 ⇒ 1,33 sen i 1 1,52 sen 41,14° ^ Operando: i 1 48,75°. © Oxford University Press España, S. A. b) f 10 cm s 20 cm y 5 cm 1 1 1 1ª lente (convergente): s’ 20 cm 10 cm Operando: s’ 20 cm c) f 15 cm s 30 cm 1 1 1 2ª lente (divergente): s’’ 30 cm 15 cm Operando: s’’ 10 cm d) Tamaño de la imagen en la primera lente: y’ 20 cm ⇒ y’ 5 cm 5 cm 20 cm Física 9 ACTIVIDADES PAU Óptica (CONTINUACIÓN) Tamaño de la imagen en la segunda lente: y’’ 10 cm ⇒ y’’ 1,6 cm 5 cm 30 cm La imagen final formada por el sistema óptico es virtual, invertida y de menor tamaño que el objeto. Un microscopio consta de dos lentes convergentes (objetivo y ocular). a) Explique el papel que desempeña cada lente. b) Realice un diagrama de rayos que describa el funcionamiento del microscopio. a) El objetivo es la lente más próxima al objeto y tiene una distancia focal pequeña. El ocular es la más próxima al ojo y tiene mayor distancia focal. La imagen formada por la primera lente (objetivo) hace de objeto en la segunda lente (ocular) y la separación entre las dos lentes es tal que la imagen formada por la primera se sitúa entre la segunda y su foco. La imagen final es mayor, invertida y virtual. b) El diagrama de rayos es el siguiente: 쐌 Modelo corpuscular de Newton. Afirma que la luz es la proyección o emisión de pequeñas partículas o corpúsculos materiales a partir de un foco luminoso, las cuales se propagan a gran velocidad y rectilíneamente en todo medio transparente y homogéneo. Con esta teoría se podían explicar la propagación rectilínea de la luz, las leyes de la reflexión y la refracción y el color de los cuerpos, pero no fenómenos luminosos como la difracción o las interferencias. 쐌 Modelo ondulatorio de Huygens. La luz se propaga mediante ondas mecánicas semejantes a las sonoras, a través de un medio muy particular, el éter, que lo llena todo. Años más tarde, Maxwell dio un nuevo enfoque a la teoría ondulatoria postulando que la luz está compuesta por ondas electromagnéticas. A principios del siglo XX se imponía el modelo ondulatorio. Aunque el descubrimiento del efecto fotoeléctrico no podía explicarse con este modelo, sí era muy fácil entenderlo gracias a las ideas de Planck y Einstein acerca de la existencia de fotones (paquetes o granos de luz). Este dilema se ha resuelto hoy en día con la llamada dualidad onda-corpúsculo de la luz; así, se acepta que la luz tiene doble naturaleza: ondulatoria y corpuscular. Las ondas y las partículas se complementan entre sí para explicar completamente la naturaleza de la luz: «cuando la luz se propaga se comporta como onda, pero cuando interacciona con la materia presenta carácter corpuscular». Ocular Objetivo Leyes de la reflexión y la refracción. B Leyes de la reflexión: B’’ A F0b O F’0b B’ F0c F’0c 1.ª Los rayos incidentes, los reflejados y la normal están siempre en el mismo plano. 2.ª El ángulo de incidencia y el de reflexión son siempre ^ ^ iguales i r . A’ rayo incidente Imagen final normal rayo reflejado A’’ Naturaleza de la luz. La cuestión de la naturaleza de la luz ha preocupado a los científicos durante mucho tiempo y ha suscitado grandes controversias. i r Las teorías más importantes sobre la naturaleza de la luz han sido las siguientes: © Oxford University Press España, S. A. Física 10 ACTIVIDADES PAU Óptica (CONTINUACIÓN) Leyes de la refracción: 1.ª Los rayos incidentes, los refractados y la normal están siempre en el mismo plano. 2.ª Los ángulos de incidencia y refracción cumplen la ley de Snell: ^ sen i v1 ^ sen r v2 y F F’ O y’ Donde v1 y v2 son las velocidades de las ondas en los medios 1 y 2. normal rayo incidente De la lente de un proyector de cine se tienen los siguientes datos: es simétrica, está hecha de un vidrio de índice de refracción de 1,5, y tiene una distancia focal imagen de ⴙ10 cm. i medio 1 medio 2 a) Calcule la velocidad de la luz dentro de la lente. r rayo refractado Sea una lupa de 5 D. Situamos un objeto luminoso 40 cm por delante de la lente. Calcule la posición donde se forma la imagen. 1 1 Como P ⇒ 5 por lo que f 0,2 m 20 cm. f f Aplicando la expresión general y sustituyendo: 1 1 1 1 1 1 ⇒ ⇒ s’ 40 cm s’ s f s’ 40 cm 20 cm El aumento lateral es: AL s’ 40 1 s 40 Estos son los resultados numéricos que nos da el problema. Podemos ver que no se trata de una lupa, ya que las lupas son lentes convergentes en las que hay que colocar el objeto entre la lente y la distancia focal, es decir, s 20 cm. Las lupas nos dan imágenes virtuales, derechas y bastante más grandes, y en este caso el aumento lateral nos indica que la imagen es invertida y del mismo tamaño que el objeto. Conclusión: en la posición en que se coloca el objeto, esta lente convergente no hace de lupa. b) Determine los radios de curvatura de las dos superficies de la lente. c) ¿A qué distancia habrá que colocar la pantalla para proyectar la imagen de la película, si esta se sitúa a 10,05 cm por delante de la lente? a) El índice de refracción de un medio se define como: c c c 300 000 km/s n por lo que: v v n 1,5 1,5 200 000 km/s b) Como la lente es simétrica, los radios de curvatura de R las dos caras son iguales. Como f , sustituyendo: 2 R 2f 2 10 20 cm c) El objeto se sitúa a 10,05 cm por delante de la lente, por lo tanto: s 10,05 cm y la distancia focal imagen es f 10 cm. Sustituyendo en la expresión general de las lentes: 1 1 1 1 1 1 ⇒ s’ s f s’ 10,05 cm 10 cm Que operando nos da como resultado: s’ 5,012 cm 0,050 m Por lo tanto, hay que colocar la pantalla a 20,10 m de la lente para proyectar la imagen de la película. NOTA: No se hace la construcción geométrica porque se necesita mucho recorrido de los rayos para que se corten, pero es la construcción de la imagen en una lente convergente cuando s f. © Oxford University Press España, S. A. Física 11 ACTIVIDADES PAU Óptica (CONTINUACIÓN) Un espejo esférico convexo que actúa de retrovisor de un coche parado, proporciona una imagen virtual de un vehículo que se aproxima con velocidad constante. Cuando el vehículo se encuentra a 8 m del espejo, el tamaño de la imagen es 1/10 del tamaño real. A’ y y’ a) ¿Cuál es el radio de curvatura del espejo? b) ¿A que distancia del espejo se forma la imagen virtual? F O F’ c) Construir el diagrama de rayos. a) Calculamos en primer lugar a que distancia se forma la imagen del coche en el espejo convexo, teniendo en cuenta que s 8 m. Como el aumento lateral es: y’ s’ AL y s 1 s’ Sustituyendo: AL por lo que s’ 0,8 m 10 8 m b) El radio de curvatura del espejo puede calcularse con la expresión general de los espejos esféricos: 1 1 1 2 1 1 2 ⇒ s’ s f R 0,8 m 8 m R R Operando R 1,7 m y f 0,8 m 2 Es derecha y de mayor tamaño que el objeto. Colocando en esta zona el objeto (s f) la lente hace de lupa. a) Explique la formación de imágenes y sus características en una lente divergente. b) ¿Pueden formarse imágenes virtuales con lentes convergentes? Razone la respuesta. a) En las lentes divergentes las imágenes formadas son siempre virtuales, derechas y menores que el objeto, independientemente de la posición de este. c) En los espejos convexos la imagen formada es siempre virtual, derecha y menor. Haremos una muestra del trazado de rayos, aunque no trabajemos a escala. y y’ F’ y O y’ F F C Dada una lente convergente, obtener de forma gráfica la imagen de un objeto situado entre el foco y la lente. Indicar las características de dicha imagen. Al colocar el objeto entre el foco y la lente, la imagen obtenida es virtual, ya que no se cortan los rayos refractados sino sus prolongaciones. © Oxford University Press España, S. A. O Vemos que la lente divergente desvía los rayos paralelos al eje óptico y que los rayos que inciden sobre el centro óptico (O) no se refractan. b) Sí. En el caso de la lupa, que es una lente convergente en la que el objeto se sitúa entre la lente y el foco. La imagen formada es virtual, derecha y mayor que el objeto. Física 12 ACTIVIDADES PAU Óptica (CONTINUACIÓN) El aumento lateral se calcula: y’ s’ 1 1,5 m AL y s 2 3 m y Por lo tanto, la imagen es real, invertida y su tamaño es la mitad que el del objeto. y’ O F a) Explicar en qué consiste la hipermetropía. F’ b) ¿Con qué tipo de lentes se corrige? c) Una persona hipermétrope, ¿debe acercar mucho un libro a sus ojos para leerlo mejor? Razonar la respuesta. La imagen se denomina virtual porque los rayos emergen divergentes. Es una interpretación del cerebro, ya que los rayos parecen venir de allí. Un objeto se sitúa a 3 m de una lente delgada convergente cuya distancia focal es 1 m. a) Obtener la imagen del objeto mediante trazado de rayos. b) Indicar si la imagen es real o virtual, derecha o invertida, mayor o menor que el objeto. a) La hipermetropía es un trastorno de refracción del ojo con alteración de la visión debido a falta de potencia en el cristalino, lo que hace que la imagen de los objetos lejanos se forme detrás de la retina. b) Se corrige con lentes convergentes, que hacen que la imagen se forme en la retina. c) No. El hipermétrope se caracteriza por la visión borrosa de los objetos situados a cortas distancias, y puede ver con mayor claridad a distancias largas. Por lo tanto mientras más se acerque el libro peor lo verá. Nota: explicar el procedimiento seguido para trazar los rayos y razonar las respuestas. Lente Objeto Espejos esféricos: formación de imágenes y obtención de su fórmula general. F F’ 3m 1m Los espejos esféricos son superficies opacas, lisas y pulimentadas por su cara interior, espejos cóncavos o, por su cara exterior, espejos convexos y tienen la virtud de hacer converger en un punto los rayos reflejados próximos al eje óptico en su superficie. a) Para obtener la imagen de un objeto basta con sacar dos rayos de cada uno de sus extremos: a) Desde la parte superior del objeto se traza un rayo que irá paralelo al eje óptico y se reflejará pasando ^ ^ por el foco, ya que así se cumple que i r . y F O F’ y’ b) Otro rayo se traza desde la parte superior del objeto y pasara por el centro de curvatura y se reflejará ^ ^ sobre sí mismo, ya que así i r 0. c) Se traza desde la parte superior del objeto y pasa por el foco. El rayo reflejado sale paralelo al eje óptico. b) f 1; s 3 m. La posición de la imagen es: 1 1 1 ⇒ s’ 1,5 m s’ 3 m 1m © Oxford University Press España, S. A. Con dos es suficiente, donde se corten los rayos reflejados o sus prolongaciones, si estos no se cortan, tendremos la imagen de este punto, que será real si se cortan los rayos reflejados y virtual si se cortan sus prolongaciones. Además podemos observar gráficamente si la imagen esta derecha o invertida, aumentada o disminuida. Física 13 ACTIVIDADES PAU Óptica (CONTINUACIÓN) Enuncie las leyes de la reflexión de la luz. y’ y ^ F C 1.ª ley: los rayos incidentes, los rayos reflejados y la normal a la superficie de separación en el punto de incidencia están contenidos en un mismo plano. Lógicamente, este plano es perpendicular a la superficie en que se produce la reflexión. 2.ª ley: el ángulo de incidencia, i , es igual al ángulo de ^ reflexión, r . N Ri RR La fórmula general de los espejos esféricos la podemos obtener de los dioptrios esféricos haciendo n n’: El índice de refracción del segundo medio es igual al del primero, pero cambiando de signo. n’ n n’ n 2n’ n’ n ⇒ s’ s s’ s r r Dividiendo toda la expresión por n’ 1 1 2 1 s’ s r f La expresión del aumento lateral será: y’ ns’ s’ AL y n’s s Calcule las distancias focales de un dioptrio esférico convexo. El radio es 20 cm y los índices de refracción de los dos medio transparentes son n ⴝ 1 y n’ ⴝ 2. La distancia focal objeto en un dioptrio esférico viene dada por: n1r n2 n1 Como el dioptrio es convexo, r 0,2 m, n1 1 y n2 2 f Sustituyendo: 1(0,2) 0,2 m 21 La distancia focal imagen en un dioptrio esférico es: n2r 2(0,2) f’ 0,4 m n2 n1 21 f n1 F O i r Diga si la siguiente frase es cierta o falsa y razone la respuesta: «La imagen producida por dioptrio plano es real y de mayor tamaño que el objeto». FALSA. La imagen producida en los dioptrios planos es virtual, ya que no se cortan los rayos refractados, sino sus prolongaciones. La expresión general del dioptrio plano es: n’ n s’ s donde n y n’ son los índices de refracción de los dos medios y s y s’ las distancias a las que se encuentra el objeto y la imagen de la superficie de separación de los dos medios. La expresión del aumento lateral es: y’ ns’ AL 1 y n’s por lo tanto, las imágenes son del mismo tamaño que los objetos, y lo que varía es la distancia a la que aparece la imagen. NOTA: Hay que recordar que las expresiones utilizadas solo son válidas para rayos paraxiales, aquellos que forman con el eje óptico un ángulo de inclinación pequeño (6°). n2 C © Oxford University Press España, S. A. F’ Física 14 ACTIVIDADES PAU Óptica (CONTINUACIÓN) Supongamos una lente delgada, convergente y de distancia focal 8 cm. Calcula la posición de la imagen de un objeto situado a 6 cm de la lente y especifica sus características. AIRE n2 90o 90o AGUA n1 y’ ilim y s’ F s O F’ La fórmula general de las lentes es: 1 1 1 s’ s f Sustituimos s 6 cm y f 8 cm 1 1 1 1 1 ⇒ ⇒ s’ 24 cm s’ 6 cm 8 cm s’ 24 El aumento lateral: s’ 24 cm AL 4 s 6 cm La imagen es virtual, derecha y cuatro veces más grande que el objeto. ¿Qué ley física prevé la reflexión total y en qué condiciones se produce? Razona la respuesta. La reflexión total es una consecuencia de la refracción de la luz y se produce cuando los rayos de luz pasan de un medio de mayor índice de refracción a otro de menor, ya que en estas condiciones el rayo refractado se aleja de la normal. Si vamos aumentando el ángulo de incidencia, llegará un momento en que el ángulo de refracción valga 90°. A este valor del ángulo de incidencia que proporciona un ángulo de refracción de 90° se le llama ángulo de incidencia límite o, simplemente, ángulo límite. Si se supera el ángulo límite, el rayo refractado ya no cambiará de medio (no se refractará), sino que se reflejará dentro del mismo medio. Este fenómeno recibe el nombre de reflexión total. Para calcular el valor del ángulo límite aplicamos la ley de Snell: ^ sen i lim n2 n2 ^ ⇒ i lim arcsen sen 90° n1 n1 Indica los elementos ópticos que componen el ojo humano, en qué consiste la miopía y cómo se corrige. El globo ocular es un sistema óptico que está constituido por unos medios transparentes que forman imágenes reales, invertidas y más pequeñas. Está dividido en dos cámaras, separadas por una estructura elástica y transparente en forma de lente biconvexa, llamada cristalino, que está situada detrás del iris y sujeta por sus extremos al globo ocular mediante los músculos ciliares. En el centro del iris se encuentra la pupila, que es un orificio circular de diámetro variable que controla el paso de la luz. La retina es la capa más interna y profunda, y la pantalla en la que se forma la imagen de los objetos observados. La miopía se debe a un exceso de potencia. La imagen de los objetos lejanos se forma delante de la retina, por lo que no es nítida. Sus puntos remoto y próximo están más cerca de la normal, por lo que el ojo miope ve mejor de cerca y a distancias más próximas que el ojo normal. Se corrige con lentes divergentes. Un objeto se encuentra 10 cm a la izquierda del vértice de un espejo esférico cóncavo, cuyo radio de curvatura es 24 cm. Determina la posición de la imagen y su aumento. Como R 24 cm, la distancia focal será: R f 12 cm 2 y la distancia del objeto al espejo es s 10 cm. Aplicando la fórmula general de los espejos esféricos: 1 1 1 s’ s f Y sustituyendo: 1 1 1 s’ 10 12 operando nos da: s’ 60 cm. © Oxford University Press España, S. A. Física 15 ACTIVIDADES PAU Óptica (CONTINUACIÓN) El aumento lateral se calcula con la expresión: y’ s’ 60 AL 6 y s 10 Vemos que la imagen es virtual, derecha y seis veces mayor. y’ y s C © Oxford University Press España, S. A. F s’ O Física 16








