Pugnaloni-Ornela
Anuncio
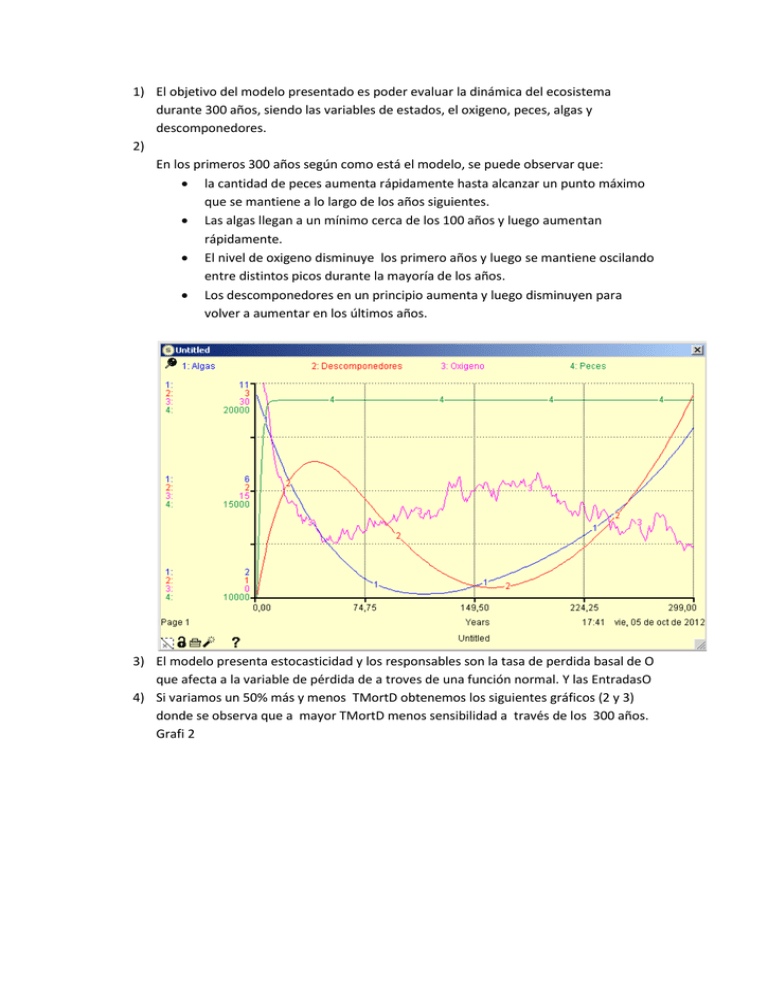
1) El objetivo del modelo presentado es poder evaluar la dinámica del ecosistema durante 300 años, siendo las variables de estados, el oxigeno, peces, algas y descomponedores. 2) En los primeros 300 años según como está el modelo, se puede observar que: la cantidad de peces aumenta rápidamente hasta alcanzar un punto máximo que se mantiene a lo largo de los años siguientes. Las algas llegan a un mínimo cerca de los 100 años y luego aumentan rápidamente. El nivel de oxigeno disminuye los primero años y luego se mantiene oscilando entre distintos picos durante la mayoría de los años. Los descomponedores en un principio aumenta y luego disminuyen para volver a aumentar en los últimos años. 3) El modelo presenta estocasticidad y los responsables son la tasa de perdida basal de O que afecta a la variable de pérdida de a troves de una función normal. Y las EntradasO 4) Si variamos un 50% más y menos TMortD obtenemos los siguientes gráficos (2 y 3) donde se observa que a mayor TMortD menos sensibilidad a través de los 300 años. Grafi 2 Grafico 3 Si variamos 50% mas o menos TMortA se observan los siguientes grafico (4 y 5) donde se observa que los descomponedores son menos sensibles a una TMortA de 0,02 (3era) y mas a una tasa de 0,01 (primera). Descomponedores: 1 - 2 - 3 - 4 - 5 1: 30 1: 15 1 2 1 1: 2 4 3 5 1 2 3 4 0 0,00 74,75 5 1 2 3 3 4 149,50 Page 4 5 224,25 Years 4 5 299,00 17:58 vie, 05 de oct de 2012 17:59 vie, 05 de oct de 2012 Grafico 4 Desco…nedores v. TMortA: 1 - 2 - 3 - 4 - 5 30 15 0 0 Page 5 0 TMortA 0 Grafico 5 Además comparando el efecto que le produce ambas tasas a los descomponedores se puede concluir que estos son menos sensibles al cambio de la TMortA que a la TMortD. Mal. A largo plazo es al revés. 5) Las conclusiones anteriores podrían a llegar a ser útiles a la hora de calibrar el modelo, ya que a partir de estas se puede centrar la atención en los parámetros que más afectan a la variable calibrada, ahorrando tiempo y costos para luego poderlo validar. 6) Uno de los parámetro que impacta indirectamente sobre la PerdidasO es la TMortA, ya que a mayor TMortA mayor Mortandad de algas y por ende mayor cantidad de Descomponedores (> crecimiento) lo que daría mayor PerdidaO. Por ende TmortA debería ser menor para que PerdidasO sea menor. Ojo que esto cambia a largo plazo Otro parámetro que afecta indirectamente a PerdidasO es la tasa de conversión de algas, ya que a mayor Tasa mayor descomponedores y por ende mayor perdidaO. 7) En el modelo para que la muerte de los peces consideré la cantidad de Oxigeno disponible hay que hacer una función Si, donde si la cantidad de oxigeno es menor a 5 la tasa de muerte será 1, si es mayor a 10 sera 0,1 entre medio de 5 y 10, la función se comportara linealmente decreciente. Para esto al modelo hubo que agregarle la tasa umbral máxima y min de oxigeno y afectar la tasa de muerte según detalle mas arriba. if (Oxigeno<O_umbral_min) then (1) else ( if (Oxigeno>O_umbral_min and Oxigeno<O_umbral_max) then (-0,18*oxigeno+1) else(0,1)) Mal 8) La dinámica de algas, oxigeno, descomponedores se mantiene relativamente igual, pero la de los peces cambia con respecto al modelo anterior. Ahora la cantidad de estos tienen distintos picos en años distintos años, ya que hay una mayor reproducción cuando el contenido de oxigeno es entre 0 y 5 y una menor cuanod el contenido de oxigeno es mayor a 10. 1: Peces 2: Oxigeno 1: 2: 3: 4: 20000 30 3 11 1: 2: 3: 4: 15000 15 2 6 3: Descomponedores 4: Algas 1 3 1 1 1 2 3 2 2 4 4 3 1: 2: 3: 4: 4 2 10000 0 1 2 3 4 0,00 74,75 149,50 Y ears Page 1 224,25 299,00 19:22 v ie, 05 de oct de 2012 Untitled 9) Los outouts del modelo serán: parámetros calculados (tasa de muerte, tperdbasalO, tasa de algas, falta tasa nacimiento ) todos los flujos que salen y entran a las variables de estados (Crecimiento y muerte de algas, crecimiento y muerte de descomponedores, crecimiento y muerte de peces y perdidas y entradas de oxigeno) además de las variables de estados, peces, algas, descomponedores y oxigeno. 10) A pesar de ser conciente de que hay algo que no esta funcionando bien el modelo, como esta funcionando podría decir que el máximo valor de Pamb que no pongan en peligro a los peces es de 0,01 ya que por ensima de este después de unos años los peces desaparecen. 1: Peces 1: 2: 2: P amb 20000 0 2 2 2 1 1 1: 2: 10000 0 2 1: 2: 0 0 0,00 250,00 Page 1 1 500,00 Y ears Untitled Años 317,00 318,00 319,00 320,00 321,00 322,00 Peces Pamb 19.996,22 0,02 19.998,11 0,02 19.999,05 0,02 19.999,53 0,02 19.999,76 0,02 19.999,88 0,02 1 750,00 1000,00 19:28 v ie, 05 de oct de 2012 323,00 324,00 325,00 326,00 327,00 328 329 330 331 332 333 334 335 336 19.999,94 19.999,97 19.999,99 19.999,99 20.000,00 0 0 0 0 0 0 0 0 0 0,02 0,02 0,02 0,02 0,02 0,02 0,02 0,02 0,02 0,02 0,02 0,02 0,02 0,02