TEMA 21 - Mural UV - Universitat de València

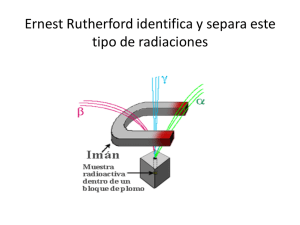
Tema 21. Segundo Cuatrimestre.
Física Nuclear. Física General.
TEMA 21. FÍSICA NUCLEAR.
1. Introducción.
Rutherford, en 1911 bombardeó los átomos con proyectiles de relativa
alta energía, constituidos por partículas cargadas (partículas α),
encontrando resultados sorprendentes: el modelo atómico aceptado hasta
este momento era el de Thompson, y de acuerdo con el mismo, los átomos
estaban formados a modo de esferas (cargadas positivamente), en cuyo
interior se encontraban embebidos los electrones (cargados negativamente),
como si de un pudding se tratara.
El resultado sorprendente del experimento de Rutherford era que la
mayor parte de los proyectiles atravesaban la materia atómica sin sufrir
reflexión apreciable, mientras que un número reducido de proyectiles
experimentaba reflexiones violentas hacia atrás, e incluso se encontraron
ángulos próximos a los 180º de deflexión.
Los estudios de Rutherford y los posteriores experimentos
condujeron a un modelo atómico constituido por un envoltorio de
electrones (carga negativa), que caracteriza el orden de magnitud del
tamaño del átomo, típicamente del Angstrom (10-10 m), y de un núcleo muy
masivo, constituido por protones (carga positiva) y neutrones, concentrado
en un espacio reducido, típicamente 1 Fermi (10-15 m) cinco órdenes de
magnitud más pequeño que el átomo.
El núcleo pasó a ser un objeto de estudio, aunque, como ha ocurrido
muchas veces en la física, los propios científicos y la opinión pública
dudaban de la posibilidad de aplicación práctica de dicha investigación.
Dudas disipadas en el siglo XX por las numerosas aplicaciones de la
física nuclear: a) en medicina (ej: RMN, gamma-grafías, técnicas PET para
diagnosis, tratamiento del cáncer mediante radio-isótopos o mediante
exposición controlada a un haz de iones C, b) aplicaciones tecnológicas,
como el estudio de las propiedades de los materiales, c) aplicaciones
industriales y producción de energía, d) datación radioactiva, e) la peor de
las aplicaciones: la militar, etc.
2. Constituyentes nucleares.
Las propiedades químicas de los elementos o átomos dependen del
número de electrones y de su estructura atómica, es decir, su distribución,
ya explicada mediante el modelo de capas: las capas incompletas son las
que juegan un papel en las combinaciones atómicas para formar moléculas.
1
Tema 21. Segundo Cuatrimestre.
Física Nuclear. Física General.
Los átomos son neutros, en su estado fundamental, y en consecuencia el
núcleo tiene una carga igual pero positiva, esta carga es transportada por
los protones: experimentalmente se ha demostrado que un protón transporta
una carga en valor absoluto igual a la del electrón, aunque su masa es
aproximadamente 2000 veces superior a la del electrón.
Se denomina número atómico Z al número de protones del núcleo, y
es este parámetro Z el que caracteriza al elemento. Por ejemplo, todos los
átomos de Fe tienen Z=26, es decir, 26 protones y 26 electrones en el
estado fundamental. El núcleo dispone de una carga +Ze, y la capa
electrónica –Ze.
2.1 El experimento de Rutherford.
Rutherford utilizó como blanco de la interacción, una capa muy fina
de átomos de Au. Ya sabía que las partículas α eran núcleos de 4He, con
una masa 8000 veces superior a la del electrón. Si el modelo de Thompson
era válido, las partículas α apenas deberían desviarse, pues al chocar contra
los electrones no sufren deflexión, por la diferencia de masa. Por otra parte,
atravesar los núcleos del modelo de Thompson, es prácticamente
equivalente a atravesar una fina lámina conductora cargada uniformemente,
con las cancelaciones características sobre la fuerza resultante de los
elementos simétricos.
La distribución del número de partículas difusas que
experimentalmente encontró Rutherford (sus colaboradores Geiger y
Mardsen, en realidad) era proporcional a Ec−2 sin −4 (θ/2) , lo que es
injustificable con el modelo de Thompson, por el gran número de partículas
desviadas hacia detrás.
En efecto, podemos hacer un cálculo aproximado del ángulo de
difusión θ de las partículas α, con momento P = m α v , al pasar por las
proximidades del núcleo, considerando que la interacción únicamente
ocurre durante el tiempo ∆t = R / v , que le cuesta a la partícula α atravesar
un radio nuclear, y que durante este tiempo actúa la fuerza repulsiva de
Coulomb, a una distancia promedio de R:
2Ze2
1
∆p
(Ze)(2e) R
∆p = F∆t =
→θ=
=
2
2
p 4πε0 m α v R
4πε0R v
lo que importa, en este cálculo muy elemental, es darse cuenta de que el
número de partículas difundidas, por ejemplo hacia atrás, depende
inversamente del tamaño nuclear R. Con el modelo de Thompson, las
partículas hacia atrás deberían ser muy pocas. Los resultados
experimentales apuntaban a que el núcleo era 10-5 veces más pequeño que
el átomo.
2
Tema 21. Segundo Cuatrimestre.
Física Nuclear. Física General.
2.2 Neutrones.
Puesto que la masa de los núcleos es aproximadamente dos veces
superior a la que podemos obtener considerando en su interior únicamente
los protones, Rutherford supuso que había en el interior de los núcleos otras
partículas neutras, de masa similar a los protones, y que se han denominado
neutrones. Esto nos permite definir el número másico A de un núcleo,
como la suma del número de protones Z y de neutrones N.
A = Z+ N
Número másico
En la década de los años 30, Chadwick demostró la existencia de los
neutrones bombardeando Li y B con partículas α. Los productos
producidos, neutros, los hizo colisionar con parafina (rica en H), y del
estudio de los protones difundidos, por colisión con los hipotéticos
neutrones, demostró que las partículas neutras producidas en el Li y B
tenían masa semejante a los protones, pero eran neutras.
2.3 La interacción fuerte.
Podemos calcular la fuerza repulsiva culombiana existente en el
interior de un núcleo de He (tamaño de 1 Fm) entre los dos protones. Para
contrarrestar esa enorme fuerza disgregadora, hace falta una fuerza muy
intensa que mantenga la estructura del núcleo unida. Esta fuerza se
denomina interacción fuerte o fuerza hadrónica, que actúa tanto sobre los
protones como sobre los neutrones, y es atractiva.
2.4 Isótopos.
Los elementos químicos en la Naturaleza, se caracterizan por su
número atómico Z, pero no todos los átomos están constituidos por el
mismo número N de neutrones. Así, por ejemplo el Uranio (elemento
químico) está en realidad constituido por núcleos, que teniendo siempre el
mismo número de protones y de electrones (Z=92), se puede encontrar con
diferente número de neutrones: N= 146, 144, 143, etc. Todos estos átomos
ocupan el mismo lugar en la tabla periódica de los elementos, y reciben el
nombre de isótopos (mismo lugar).
Los diferentes isótopos o núclidos, se representan por su símbolo
químico X, especificando usualmente el número másico A y el atómico Z,
de la forma:
A
ZX
235
4
3
→ Ejemplo: 238
92 U, 92 U, 2He, 2He,etc.
3
Tema 21. Segundo Cuatrimestre.
Física Nuclear. Física General.
El símbolo químico determina el número atómico unívocamente, por
lo que en la representación anterior se puede eliminar, sin ambigüedad. En
la figura 40.1 se representa el número de neutrones N de algunos núclidos
en función de su número de protones Z.
Figura 40.1. Número de neutrones en
función del número de protones, para los
núcleos estables. Se observa la existencia
de los isótopos. A medida que el número
de protones aumenta, la proporción de
neutrones es mayor, para asegurar la
estabilidad del núcleo.
La masa atómica que aparece en la tabla periódica es en realidad el
valor promedio de las masas de los isótopos, ponderado para las relativas
abundancias.
3. Masas nucleares y energías de enlace.
El espectrómetro de masas es un aparato que consiste en una fuente
de iones, un selector de velocidades y diferentes campos eléctricos y
magnéticos para acelerar los iones y hacerlos curvar en el campo
magnético. La finalidad del espectrómetro es la determinación de los
diferentes isótopos que componen un elemento, así como las abundancias
relativas de los diferentes isótopos. El radio de curvatura depende del
momento de los iones, y si hemos seleccionado un haz de partículas con la
misma velocidad, los radios dependen de la masa del isótopo1.
Figura
28.19.
Esquema
de
un
espectrómetro de masas. Una fuente ioniza
y extrae iones cargados, que al ser
acelerados por un campo eléctrico, son
curvados por un campo magnético
uniforme. Si los iones tienen la misma
velocidad, el radio de curvatura será
diferente para cada isótopo.
1
Ver Tipler página 918, 4ª Edición y Fishbane capítulo 29.
4
Tema 21. Segundo Cuatrimestre.
Física Nuclear. Física General.
Las masas de los isótopos, que usualmente aparecen en las tablas
atómicas hacen referencia a la masa del átomo, por lo que se ha restar la
masa de los electrones para obtener la masa del núcleo específico.
Habitualmente, las masas atómicas tienen precisiones de 1 frente a 108.
3.1. Unidad de masa atómica.
Se define como unidad de masa atómica (u.m.a.), la masa del átomo
de C, dividida por 12. El valor de la u.m.a. en kg o en MeV/c2 es:
12
1 u.m.a.= 1.66057x10−27kg = 931.494MeV/c2
1
Podemos expresar los valores de las masas de las partículas (p, n, e,
H) en función de estas unidades, en la forma:
m p = 1.00728 uma = 938.272MeV/c2
m n = 1.00866 uma = 939.566MeV/c2
m e = 5.48578x10−4 uma = 0.511MeV/c2
M(1 H)= 1.007825 uma = 938.783MeV/c2
donde debe observarse que las masas atómicas se suelen representar
por letras capitales2.
3.2 Energía de enlace.
Un núcleo, como el 12C, constituido por 6 protones y 6 neutrones, es
una estructura o configuración estable, y en consecuencia su energía debe
ser menor que la de sus componentes por separado.
Por otra parte, ya hemos visto, en la relatividad, la expresión de
Einstein de la equivalencia entre masa y energía: E=m·c2.
La conclusión de estas observaciones es que cabe esperar que la
masa de los núcleos en la Naturaleza, sea perceptiblemente3 menor que la
suma de las masas de sus componentes en p y n.
Esto es comprobable a partir del cuadro de masas de arriba, mediante
la ecuación:
2
Observad que la diferencia de masa entre el átomo de hidrógeno y el protón es la masa del electrón.
Aquí es perceptible, dada la intensidad de la interacción fuerte. El mismo razonamiento es aplicable a
todo sistema ligado, como el atómico, pero la intensidad de la fuerza coulombiana es muy débil y los
defectos de masa que aparecen en las estructuras atómicas y moleculares no son ponderables.
3
5
Tema 21. Segundo Cuatrimestre.
∆m =
Física Nuclear. Física General.
( )
∆E
= 6M 1 H +6m n − M
2
c
(12C)→ ∆m = 0.09891 uma
Es esta masa-energía, la que se desprende al formar el núcleo a partir
de sus componentes de p y n. Obsérvese que la contribución de los
electrones cancela, ya que el átomo de H tiene un electrón y el de C tiene 6.
Dada la intensidad de la interacción fuerte, resulta que las masas de
los núcleos son del orden de un 1% menor que la suma de las masas de sus
componentes en p y n. (Concepto de defecto de masa)
La energía de enlace Eb de los núcleos es pues, el defecto de masa
multiplicado por c2, como exige la relación de Einstein:
[ ( )
Eb = ZM 1 H + Nm n − M
(AZ X)] c2
es la energía de enlace del isótopo X, caracterizado por Z protones y A
nucleones4. La energía de enlace, como se ha definido antes, es positiva
para todos los núcleos (estables o inestables que forman estados ligados).
Un parámetro útil para discutir la estabilidad nuclear es la energía de
enlace promedio para cada nucleón Eb/A, que se muestra en la figura 40.3.
Figura 40.3. Energía de enlace por
nucleón, en función del número de
nucleones A. Obsérvese que las estructuras
nucleares más estables se encuentran
alrededor del Fe, es decir, los núcleos con
50 nucleones aproximadamente.
Conclusiones:
• Saturación de las fuerzas nucleares: el hecho de que la curva sea
prácticamente plana al lado derecho del máximo, indica que
existe una saturación de las fuerzas nucleares en el interior del
núcleo. Esto puede ocurrir si la fuerza nuclear fuerte es de corto
alcance, y cada nucleón únicamente interactúa con los vecinos.
Obsérvese que si cada nucleón interactuara con todos los
restantes, el número de parejas de interacciones debería crecer
según A(A-1) y la curva no podría ser plana.
4
Se denomina nucleón indistintamente a los p y n, dadas sus similitudes de comportamiento en la
interacción fuerte, misma masa, etc.
6
Tema 21. Segundo Cuatrimestre.
Física Nuclear. Física General.
• Dependencia con el número de vecinos: Se ve la importancia del
número de pares de interacciones en la parte izquierda del
máximo, donde la estabilidad crece extraordinariamente, debido
al aumento de pares de interacciones al ir añadiendo nucleones.
• Influencia de la interacción repulsiva de Coulomb: la interacción
culombiana no es tan intensa como la fuerte, pero es de largo
alcance, lo que hace que el número de interacciones repulsivas de
Coulomb en el núcleo crezca según Z(Z-1). Por eso, la interacción
culombiana para los núcleos grandes es muy importante, y
representa la causa más notoria de inestabilidad nuclear y del
decrecimiento parabólico de la curva a la derecha del máximo.
4. Tamaño y densidad nuclear.
Los núcleos han sido bombardeados, en experimentos realizados en
los aceleradores con proyectiles como electrones, protones, etc., y con
diferentes valores de energía. Los datos obtenidos nos dan información de
la distribución de carga y masa (nucleones) en el interior del núcleo.
Los experimentos son consistentes con una distribución uniforme
(constante) de los nucleones en el interior del volumen nuclear, sin
distinguir p y n, lo que corrobora el efecto de saturación de las fuerzas
nucleares comentado antes.
Distribución de carga y masa constante en el interior de esferas de
radio:
R A = r0 A1/3
donde RA representa el radio del núcleo con A nucleones, y r0 es el
parámetros de escala nuclear de valor 1.2 Fm.
Como el volumen de una esfera es proporcional a R3, la expresión
anterior indica que el volumen nuclear es proporcional al número de
nucleones acomodados en el núcleo, es decir, la densidad de materia
nuclear no depende de A, es prácticamente constante como hemos de
esperar debido a la saturación de la interacción nuclear.
Bordes difusos: Los núcleos no acaban abruptamente, sino que más allá del
radio RA, la densidad de materia nuclear decrece muy rápidamente en
función de r.
7
Tema 21. Segundo Cuatrimestre.
Física Nuclear. Física General.
5. Fuerzas nucleares.
Las fuerzas nucleares entre nucleones son de las más intensas en la
Naturaleza a pesar de su saturación, acabada de exponer, y a que cuando se
estudian desde el punto de vista de los constituyentes elementales de la
materia, resultan ser fuerzas residuales, de la misma forma que las fuerzas
de Van der Waals lo son entre las moléculas5.
En la figura 40.3, hemos visto que la energía promedio de los
nucleones del núcleo, es de 8 MeV; comparada con la energía de ionización
atómica, que es del orden de 10 eV, nos permite concluir que las energías
nucleares son del orden de 106 veces más intensas que las fuerzas atómicas.
Las fuerzas nucleares son de corto alcance y se saturan al interactuar
con los nucleones que tienen cerca.
Una representación cuantitativa simple de la interacción entre
nucleones, debida a Yukawa, tiene la forma siguiente:
2e
U(r) = −g
−r/R
r
donde U(r) representa la energía potencial en la interacción nucleón–
nucleón, en función de su distancia r. Los resultados experimentales son
reproducibles si el valor de R, que caracteriza el alcance de la interacción,
vale 2 x 10-15 m, es decir 2 Fm.
Compare el alumno la expresión anterior con la correspondiente
gravitatoria, y deduzca qué factor es el que origina el corto alcance.
Los numerosos experimentos de física nuclear realizados ponen de
manifiesto que las interacciones p-p, p-n y n-n son idénticas, si no
consideramos la influencia de la interacción electromagnética (Coulomb,
momentos magnéticos, espines, etc.).
6. Modelos nucleares.
La dificultad intrínseca en el estudio de los núcleos, tanto por la
propia fuerza nuclear, como por el elevado número de partículas que
implica un sistema nuclear, hace que el estudio se aborde mediante
modelos, cuya validez no se aplica a todos los núcleos.
5
Los nucleones se componen de partículas más elementales denominadas quarks, que son los que
soportan la interacción fuerte a través de la magnitud activa denominada color (“masa de la gravitatoria,
carga de la electromagnética”). Los nucleones son neutros en color, como las moléculas son neutras en
carga, lo que explica la afirmación de la parte superior.
8
Tema 21. Segundo Cuatrimestre.
Física Nuclear. Física General.
6.1 El modelo nuclear de capas.
¿Qué tiene en común la estructura nuclear con la estructura atómica
para que pueda aplicarse un cierto modelo de ocupación de niveles
nucleares en capas?.
A pesar de las fuertes diferencias que existen entre la interacción
culombiana (responsable de los átomos) y la fuerza fuerte, la descripción
de un núcleo tiene importantes semejanzas con el átomo:
• Los nucleones son fermiones, como los electrones, y se encuentran
confinados en un espacio reducido (cuantización de las energías
permitidas).
• A ambos sistemas se les aplica el principio de excusión de Pauli,
aunque en el caso del núcleo, neutrones y protones son dos partículas
distinguibles entre sí: protones y neutrones por tanto llenarán capas
diferentes (Figura 40.2).
• Los nucleones individualmente pueden considerarse sometidos a un
potencial externo en el interior del núcleo, promedio de todas las
interacciones que sufren con los nucleones de su entorno, y como
consecuencia creado por ellos mismos
Figura 40.2. a) Ocho neutrones en un pozo de potencial, b) cuatro protones y cuatro
neutrones en el mismo pozo. Observad que al ser los protones distinguibles de los
neutrones, el principio de exclusión hace que la configuración b) sea más estable, al
ocupar niveles más bajos de energía.
Estas semejanzas justifican que pueda aplicarse un modelo de capas
(nuclear) como buena aproximación al núcleo, aunque la idea clásica de
las órbitas sea, si cabe, más difícil de imaginar en el interior del núcleo6.
Figura 5.5. Potencial esférico (con simetría
esférica) realista para el modelo de capas.
R representa el tamaño del núcleo, que no
acaba abruptamente, sino de forma difusa.
6
Es difícil imaginar “órbitas estables” en el interior del núcleo. Pero el principio de exclusión de Pauli
juega un papel importante: los nucleones sólo podrán realizar transiciones a “otras órbitas” si al chocar
entre ellos disponen de suficiente energía para pasar a niveles vacíos, que son los de energía superior.
9
Tema 21. Segundo Cuatrimestre.
Física Nuclear. Física General.
El potencial que da buenos resultados es un potencial con simetría
esférica, intermedio entre un pozo cuadrado de potencial de radio R y el
oscilador armónico, como se ve en la figura 5.5.
El oscilador armónico en tres dimensiones dispone de niveles de
energía separados uniformemente de acuerdo con la expresión:
E = hω(2nr + ! + 3/2)
en la que, nr toma los valores nr=0,1,2,3, .., y ! , el número cuántico del
momento angular puede valer ! =0,1,2,3,...y que como sabemos representa
la existencia de 2(2 ! +1) estados ocupables para cada nucleón, si se
considera el espín. Así, la secuencia de llenado de los niveles energéticos
para los protones será:
E = (3 / 2 )h ω ; n r = 0 , ! =
E = (5 / 2 )hω; n r = 0, ! = 1;
E = (7 / 2 )hω; n r = 0, ! = 2;
E = (7 / 2 )hω; n r = 1, ! = 0;
E = (9 / 2 )hω; n r = 0, ! = 3;
E = (9 / 2 )hω; n r = 1, ! = 1;
Pr otones Totales
0;
2 protones
2
6 protones
8
10 protones
18
2 protones
20
14 protones
34
6 protones
40
La misma secuencia se aplica a los neutrones. Es de esperar que los
núcleos que tienen capas completas ocupadas por nucleones sean muy
estables, como ocurre en el átomo. Así, los números mágicos, que
corresponden a núcleos muy estables con capas completas corresponderían
en el potencial del oscilador a N =2, 8, 20, 40, etc., tanto para protones
como para neutrones.
Los nucleones, en el interior del núcleo, se encuentran sometidos al
potencial de la figura: ajustando correctamente la anchura R del pozo
(R=1.25 A1/3 ) y su profundidad –V0 (≈ 50 MeV), pueden describirse con
muy buena aproximación los niveles energéticos de los núcleos y su
secuencia de llenado ( Figura 5.6 izquierda).
Si introducimos ahora la interacción espín-órbita, semejante a la
atómica, pero mucho más intensa, reproducimos con mucha precisión la
secuencia en que los diferentes niveles atómicos se llenan y los números
mágicos (Figura 5.6 derecha). Se denomina números mágicos al número de
protones y/o neutrones que originan estructuras nucleares muy estables
(con gran energía de enlace), y que en el modelo atómico corresponderían a
capas completas. El concepto de capa no corresponde aquí al número
cuántico principal n, sino más bien a que haya un salto pronunciado de
10
Tema 21. Segundo Cuatrimestre.
Física Nuclear. Física General.
energía entre niveles energéticos próximos. Así, los números mágicos son:
2, 8, 20, 28, 50, 82 etc.
Figura 5.6: A la izquierda se observa la
secuencia
de
niveles
energéticos
cuantizados que se obtiene con el potencial
intermedio de la figura 5.5.. Los números
cuánticos que caracterizan los estados son
semejantes a los atómicos: n, l, ml. Este
último representa la cuantización angular
del momento angular. A la derecha, se ha
introducido el efecto de la interacción
espín-órbita, mucho más intenso que en el
átomo, y que justifica finalmente la
secuencia de los números mágicos (capas
completas) nucleares7.
6.2 El modelo de la gota líquida.
La saturación de las fuerzas nucleares, originada por las fuerzas de
corto alcance, y en consecuencia la densidad constante de la materia
nuclear (incomprensible), hicieron suponer que los núcleos deberían
comportarse como gotas de fluido incompresible.
La idea de este modelo, no es reproducir las características locales de
cada núcleo, sino más bien, la tendencia general de la energía de enlace de
los nucleones, puesta de manifiesto en la figura 40.7. Por esta razón, entra
en la categoría de modelos colectivos frente a los modelos de partícula
independiente del caso anterior.
El modelo parte de la suma de los constituyentes de los núcleos,
Z+N, para ir considerando los términos que aumentan o disminuyen su
estabilidad, es decir, su energía de enlace, tal y como se haría en una gota
esférica líquida, si bien las fuerzas a considerar aquí deben ser nucleares.
1) Término de orden cero: suma de les masas de los constituyentes:
ZM H + N m n = ZM H + (A − Z)m n
7
Observad que el signo de la interacción espín – órbita es aquí contrario al caso atómico, pues está
originado por partículas cargadas positivamente, lo que hace que los niveles de energía inferior sean los
de j superior.
11
Tema 21. Segundo Cuatrimestre.
Física Nuclear. Física General.
2) Energía de enlace proporcional al volumen nuclear. Justificado por la
saturación de las interacciones nucleares; fuerza estabilizadora con
signo negativo!!
− aV A
ésta energía de enlace reduce la masa del núcleo originando estabilidad.
3) Término de la tensión superficial (nuclear). Las gotas de lluvia en la
naturaleza tienen forma esférica porque es la configuración más estable,
al tener menor superficie. Mayor superficie significa realizar un trabajo
contra “la tensión superficial”, que incrementa la energía del sistema.
Este término es positivo, ya que incrementa la inestabilidad a mayor
superficie.
+ asA 2/3
4) La repulsión de Coulomb. La energía necesaria para acumular una carga
Ze desde el infinito, en un volumen de radio R=r0 A1/3, toma el valor:
3 Z2e2
Z2
0
.
72
MeV
=
5 4πε0r0 A1/3
A1/3
5) Término de simetría: favorece la igualdad entre el número de protones y
neutrones. Si los protones no estuvieran cargados, la secuencia de
niveles de protones y neutrones sería la misma, e irían llenándose
paralelamente con el mismo número de ellos. Sin embargo, al estar
cargados, los niveles del p son menos estables y se favorece que los
núcleos tengan ligeramente más neutrones.
+ aA
(A − 2Z)2
A
6) Término de energía de apareamiento ∆. Los núcleos muestran
preferencia en tener un número par de protones y también un número
par de neutrones, que forman estructuras muy estables. De hecho, el
número de núcleos con N y Z impares es muy pequeño. Este término se
representa por:
 − a p A −1/2, Para núcleos con Z,N pares.

0,
Para núcleos con A impar.
∆= 
−
1
/
2
+ a p A
Paranúcleoscon Z,Nimpares.

12
Tema 21. Segundo Cuatrimestre.
Física Nuclear. Física General.
6.2.1 Fórmula semiempírica de la masa.
La suma de todos los términos anteriores, conduce a una predicción
muy aproximada, si bien sin revelar estructuras locales, de la masa de los
núcleos o de su energía de enlace por nucleón. La fórmula es:
acZ2
(A − 2Z)2
M A = ZM H + (A − Z)m n − aV A + aSA + 1/3 + aA
+∆
A
A
Esta expresión supone, a pesar de su complicada apariencia8, realizar
un ajuste lineal por mínimos cuadrados sobre los parámetros aV, aS, aA, etc.,
que proporciona resultados muy buenos sobre la tendencia global de los
núcleos en el sistema periódico.
2/3
8
Ver el libro de R. Guardiola, E. Higon, J. Ros, “Métodos de cálculo numérico para la física” Universitat
de València, página 188.
13