φω φω ω ω φω ω ω ω - Red Creativa de Ciencia
Anuncio

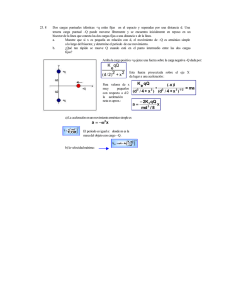
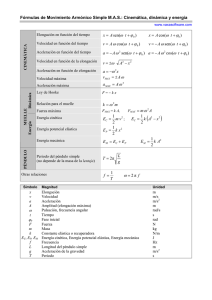
Problema 8. Oscilaciones. Movimiento armónico simple Un cuerpo está vibrando con movimiento armónico simple de amplitud 15 cm y frecuencia 4 Hz. Calcule: a) los valores máximos de aceleración y de velocidad, b) la aceleración y la velocidad cuando la coordenada es 9 cm, c) el tiempo requerido para moverse desde la posición de equilibrio hasta un punto distante 12 cm. Conocimientos previos necesarios Consideramos la función que da la posición del cuerpo en cualquier instante: x(t ) = A cos(ωt + φ ) . (1) v(t ) = − Aω sen (ωt + φ ) (2) La velocidad del cuerpo es: y su aceleración: a (t ) = − Aω 2 cos(ωt + φ ) a (t ) = −ω 2 x(t ) (3) A partir de estas funciones podemos resolver los puntos a) y b). Solución del problema a) El valor máximo de la velocidad es la amplitud de la función (2): v máx = Aω , (4) donde ω = 2πf . El valor máximo de la aceleración es la amplitud de la función (3): a máx = Aω 2 . (5) b) Para obtener la velocidad del cuerpo cuando está en cualquier posición x, usamos (2) y escribimos al seno en función del coseno: [ ] v(t ) = − Aω sen (ωt + φ ) = − Aω ± 1 − cos 2 (ωt + φ ) = ±ω A 2 − x 2 . (6) El doble signo da cuenta de los distintos sentidos del movimiento del cuerpo cuando esté pasando por la posición x. Para obtener la aceleración del cuerpo cuando está en cualquier posición x, usamos (3): a (t ) = −ω 2 x(t ) . (7) Para resolver el punto c) sugerimos representar gráficamente la función (1) y apoyar el razonamiento en el gráfico. c) Consideremos la gráfica de x(t) de la Figura 1. En la figura se ha marcado el intervalo de tiempo ∆t que se quiere calcular. Figura 1. Posición en función del tiempo Si desplazamos el origen de tiempo al punto A, la función que describe la posición del cuerpo a partir del instante tA es: x(t ) = Asen (ωt ) (8) Entonces, cuando el cuerpo esté en xB, alejado 12 cm de la posición de equilibrio, habrá transcurrido un tiempo desde que pasó por aquella posición dado por: ∆t = 1 ω arcsen( x B / A) . (9) Dejamos para el alumno el cálculo de los valores con los datos del problema y la búsqueda de otras posibilidades de solución.