Máximos y mínimos mediante el método de Lagrange:

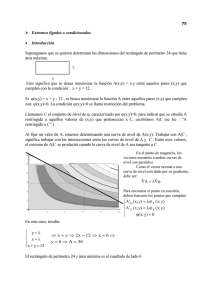
Máximos y mínimos mediante el método de Lagrange:
Sea una función continua y derivable de varias variables f ( x, y ) (“varias” variables, o sea , dos en
este ejemplo). Sabemos que para encontrar los extremos de la función (es decir, los puntos (x,y)
donde f alcanza su máximo o mínimo valor), debemos resolver las ecuaciones:
∂f ( x , y )
∂f ( x, y )
= 0;
=0
∂x
∂y
Esto es lo mismo que especificar el punto donde el gradiente de la función en el plano XY se
anula:
∇f ( x, y ) = 0.
Como usted sabe (!), el gradiente en este caso es un vector en el plano XY que indica la dirección
hacia donde hay que moverse para que la función aumente más bruscamente. El gradiente se anula
en los puntos donde la función es “horizontal” (donde la función no aumenta hacia ningún lado).
En la figura se muestra una función con un
máximo bien notorio. Las curvas de nivel indican
los puntos donde la función tiene un valor dado.
El gradiente de la función en un punto dado tiene
dirección perpendicular a la curva de nivel que
pasa por ese punto. En el máximo, la curva de
nivel degenera en un solo punto. En tal caso, el
gradiente es cero: a partir de ese punto no hay
ninguna dirección hacia donde la función
aumente.
_______________
A veces no queremos buscar el máximo de la función en todo el dominio (plano XY, en este caso),
sino sólo a lo largo de una curva en el plano XY (en el caso de una función de 3 variables, es decir
en el volumen XYZ, la restricción puede ser una curva o una superficie en el espacio XYZ).
Nuestro problema es entonces cómo encontrar los extremos de f si queremos limitarnos sólo a
puntos (x,y) que estén sobre una curva definida por:
g ( x, y ) = 0 .
La forma más directa (aunque no necesariamente la más simple de calcular) es usar la condición de
restricción g ( x, y ) = 0 para despejar y como función de x, y = y ( x ) , y luego reemplazar este valor
de y en la función f ( x, y ( x )) . De esta forma, tenemos una función de una variable menos (en este
caso una función que sólo depende de x) sin restricciones. Para encontrar los extremos,
simplemente buscamos los puntos x tales que
df ( x, y ( x))
=0
dx
Lo malo de este método es que en la práctica no siempre es posible despejar y = y ( x ) !!!
Alternativamente, podemos definir la curva g ( x, y ) = 0 en forma paramétrica, es decir, mediante
un par de funciones de un parámetro t: x = x (t ) e y = y (t ) tales que g ( x(t ), y (t )) = 0 . En este caso,
buscamos el extremo de la función f (t ) = f ( x (t ), y (t )) usando, como siempre, la condición:
df
=0
dt
En la práctica, esto a veces tampoco resulta fácil de hacer!!!
Veamos entonces la otra alternativa: el método de Lagrange.
Gráficamente, la función f ( x, y ) se puede representar por un mapa de curvas de nivel en el plano
XY, que en el ejemplo anterior son curvas circulares. Como sabemos, el punto máximo está en el
centro de las curvas de nivel.
Sobre este gráfico podemos dibujar la curva de restricción g ( x, y ) = 0 , que es la línea que
atraviesa la figura. Note que en esta
figura, hemos dibujado la curva con un
parámetro t, que avanza de izquierda a
derecha.
En el ejemplo, la función es mayor
mientras más nos movemos hacia el
centro de las curvas de nivel.
t
El máximo de f a lo largo de la curva
ocurre en el punto tal que al avanzar
sobre la curva no nos cambiamos de
nivel, es decir donde la curva es
tangente a la correspondiente curva de
nivel.
En otras palabras, el extremo de la
función f sobre la curva g = 0 ocurre
donde el gradiente de f es perpendicular
a la curva g = 0.
Hay otra forma de especificar esto más elegantemente: uno siempre puede definir el gradiente de la
función g, esto es ∇g , puesto que g ( x, y ) es simplemente otra función más en en plano XY,
donde la restricción g ( x, y ) = 0 simplemente corresponde a una de las curvas de nivel de g. Esto
significa que ∇g , para puntos sobre la curva g = 0, es un vector perpendicular a esta curva.
La condición del extremo es, por lo tanto, un punto donde el gradiente de f es paralelo al gradiente
de g:
Condición de extremo: ∇f = λ ∇g , donde λ es una constante de proporcionalidad.
Esta elegante condición corresponde exactamente al Método de Lagrange para encontrar máximos
y mínimos de una función f ( x, y ) sujeto a la restricción g ( x, y ) = 0 :
a) Construya una nueva función f ( x, y ) = f ( x, y ) − λ g ( x, y ) , donde λ es una cosntante
(multiplicador de Lagrange), hasta aquí desconocida.
b) Extremice esta nueva función, considerando las variables sin restricción, es decir:
∇f ( x, y ) = 0
Las ecuaciones obtenidas serán funciones de las coordenadas x, y y del parámetro λ .
c) Use la ecuación de restricción g ( x, y ) = 0 para determinar λ .
La belleza de este método es que es fácil de aplicar y fácil de generalizar a un número mayor de
variables y de restricciones.
En 3 dimensiones, con una restricción::
Queremos encontrar los extremos de f ( x, y , z ) , sujeto a g ( x, y , z ) = 0 .
Esto se generaliza en forma muy simple:
1) Ahora trabajamos en el espacio XYZ en vez del plano XY.
2) Ahora f ( x, y , z ) se puede representar en el espacio XYZ por superficies de nivel, donde
cada superficie es el lugar de puntos donde la función tiene un valor dado. Tal como las
curvas de nivel en dos dimensiones, las superficies de nivel resultan como hojas paralelas
en cada vecindad, y el gradiente de la función es un vector que apunta normalmente a las
hojas en la dirección en la que la función aumenta.
3) Ahora, la función de restricción g ( x, y , z ) = 0 es una superficie, que corresponde a una de
las superficies de nivel de la función g ( x, y , z ) .
4) Claramente, el extremo de la función f sujeta a la restricción g = 0 ocurre donde el
gradiente de f es perpendicular a la superficie g = 0, es decir, nuevamente los vectores
gradiente de f y g son paralelos!
En 3 dimensiones, con dos restricciones:
Qué pasa si hay dos ecuaciones de restricción? (en 3 dimensiones, eso puede ocurrir).
En tal caso, tenemos una función f ( x, y , z ) , de la cual buscamos los extremos, sujeto a las
condiciones conjuntas: g1 ( x, y, z ) = 0 y g 2 ( x, y, z ) = 0 .
Cada una de estas condiciones corresponde a una superficie en el espacio XYZ. La restricción
simultánea corresponde a los puntos que son comunes a ambas superficies, es decir, definen una
curva en el espacio XYZ, que es la intersección de las superficies (más vale que tal intersección
exista, pues de otro modo el problema es inconsistente!).
En tal caso, el extremo de la función, al igual que en el caso en dos dimensiones, ocurre donde la
curva de restricción es tangente a una superficie de nivel de la función f. Ahora, todo el problema
es expresar esa condición en término de los gradientes:
Sabemos que en cada punto, ∇f es un vector perpendicular a la superficie de nivel donde yace tal
punto. Por lo tanto, en el punto de extremo, ∇f es perpendicular a la curva de restricción.
La última pregunta que nos queda es:
cómo defino la dirección de la curva de
restricción?
∇g1
g1 = 0
∇g 2
g2 = 0
La respuesta es que, en vez de definir la
dirección de dicha curva, voy a identificar
el plano normal a la curva.
Cada superficie de restricción, en cada
punto, tiene definido un gradiente, que es
un vector normal a dicha superficie. Por lo
tanto, la curva de intersección de ambas
superficies es normal a ambos vectores
gradiente (ver figura). El plano normal a la curva, por lo tanto, es aquél que contiene a todos los
vectores que son combinación lineal de los dos gradientes, ∇g1 y ∇g 2 .
Como en el punto de extremo, ∇f debe ser normal a la curva, entonces dicho gradiente debe yacer
en el plano normal. Esto significa que ∇f es una combinación lineal de los dos vectores gradiente
∇g1 y ∇g 2 :
∇f = λ1 ∇g1 + λ2 ∇g 2 , para algún λ1 y λ2 .
Eso es nuevamente el método de Lagrange!
Generalicemos:
Para encontrar el extremo de la función multivariable f ( x1 , x2 , x3 ,...) para valores x1 , x2 , x3 ,...
restringidos a las condiciones g1 ( x1 , x2 , x3, ...) = 0 , g 2 ( x1 , x2 , x3, ...) = 0 , etc…
a) Construya la función f ( x , x , x ,...) = f ( x , x , x ,...) − λ g ( x , x , x ,...) − λ g ( x , x , x ,...) − ...
1
2
3
1
2
3
1
1
1
2
3
2
2
1
2
3
y extremice considerando como independientes a todas las variables y a todos los parámetros
λ1 , λ2 ,... es decir, imponga
∇f = 0
b) Use las ecuaciones de restricción g1 = 0,... para determinar los valores de los parámetros
λ1 , λ2 ,...
Problemas:
Encuentre el mínimo de la función f ( x, y ) = x 2 + y 2 para puntos x, y que yacen en la
curva ( x − 4) 2 + y 2 = 1 .
Haga un gráfico de la situación.
Solucione el problema haciendo un reemplazo de y en la función usando la restricción y encuentre
la solución al problema de minimización en una variable.
Alternativamente, use el método de Lagrange.