Currículo de matemáticas Cuaderno de ejercicios del
Anuncio

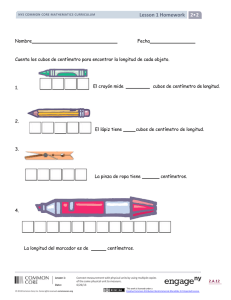
Currículo de matemáticas Cuaderno de ejercicios del estudiante Grado 3 Módulo 2 Valor posicional y solución de problemas con unidades de medida Nombre: NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 1 Problem Set 3•2 Nombre Fecha 1. Usa un cronómetro. ¿Cuánto tiempo te toma para chasquear los dedos 10 veces? Se tarda 3. para chasquear los dedos 10 veces. Usa un cronómetro. ¿Cuánto tiempo te toma nombrar 10 animales? Regístralos abajo. Se tarda para nombrar 10 animales. Lesson 1: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org 2. Usa un cronómetro. ¿Cuánto tiempo te toma en escribir todos los números del 0 a 25? Se tarda para escribir todos los números del 0 a 25. 4. Usa un cronómetro. ¿Cuánto tiempo se tarda en escribir, "7 × 8 = 56" 15 veces? Registra el tiempo abajo. Se tarda para escribir la ecuación 15 veces. Explore time as a continuous measurement using a stopwatch. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.9 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 1 Problem Set 3•2 5. Trabaja con tu grupo. Usa un cronómetro para medir el tiempo de cada una de las siguientes actividades. Actividad Tiempo Escribir tu nombre completo. segundos Hacer 20 saltos de tijera. Susurrar contando de a dos del 0 al 30. Dibujar 8 cuadrados. Contar en voz alta de cuatro en cuatro del 24 al 0. Decir los nombres de tus maestros desde el kindergarten al tercer grado. 6. 100 metros de relevo: Utiliza un cronómetro para medir y registrar tu tiempo. Nombre Tiempo Tiempo total: Lesson 1: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Explore time as a continuous measurement using a stopwatch. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.10 Lesson 1 Homework NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 3•2 Fecha 1. La tabla de abajo muestra el tiempo que le tomó a 5 estudiantes correr 100 metros. Samantha 19 segundos Melanie 22 segundos Chester 26 segundos Dominique 18 segundos Louie 24 segundos a. ¿Quién es el corredor más rápido? b. ¿Quién es el corredor más lento? c. ¿Cuantos segundos más rápido corre Samantha que Louie? 2. Enumera las actividades de la casa que toman los siguiente tiempos para completar. Si no tienes un cronometro, puedes utilizar la estrategia de contar “1 Mississippi, 2 Mississippi, 3 Mississippi….” Tiempo 30 segundos Actividades de la Casa Ejemplo: Amarrarse los cordones 45 segundos 60 segundos Lesson 1: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Explore time as a continuous measurement using a stopwatch. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.12 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 1 Homework 3•2 3. Parea el reloj analógico con el reloj digital correcto. Lesson 1: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Explore time as a continuous measurement using a stopwatch. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.13 Lesson 2 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 3•2 Fecha 1. Sigue las instrucciones para etiquetar la siguiente recta numérica. a. Ingrid se alista para ir a la escuela entre las 7:00 am y 8:00 am. Etiqueta la primera y la última marca de la recta numérica con 7:00 am y 8:00 am. b. Cada intervalo representa 5 minutos. Cuenta de cinco en cinco empezando de 0, o 7:00 am. Etiqueta 0, 5, y 10 debajo de la recta numérica hasta las 8:00 am. c. Ingrid comienza a vestirse a las 7:10 am. Marca con un punto en la recta numérica para representar esa hora. Encima de ese punto escribe la letra D. d. Ingrid desayuna a las 7:35 am. Marca con un punto en la recta numérica para representar esta hora. Encima de ese punto escribe la letra E. e. Ingrid empieza a cepillarse los dientes a las 7:40 am. Marca con un punto en la recta numérica para representar esta hora. Encima de ese punto escribe la letra T. f. Ingrid empieza a empacar su almuerzo a las 7:45 am. Marca con un punto en la recta numérica para representar esta hora. Encima de ese punto escribe la letra L. g. Ingrid empieza a esperar el autobús a las 7:55 am. Marca con un punto en la recta numérica para representar esta hora. Encima de ese punto escribe la letra W. Lesson 2: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Relate skip-counting by 5 on the clock and telling time to a continuous measurement model, the number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.21 Lesson 2 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM 3•2 2. Etiqueta cada 5 minutos en la siguiente recta numérica. Parea con una línea desde los relojes a los puntos sobre la recta numérica mostrando su hora. No todos los relojes coinciden con los puntos. 11 8:35 12 1 11 10 2 8 4 9 3 7 6 5 5:15 12 1 11 10 2 8 4 9 3 7 6 5 0 5:40 12 1 10 2 8 4 9 3 7 6 5 60 6:00 pm 5:00 pm 3. Noah usa la recta numérica para encontrar la hora 5:45 pm. Cada intervalo es de 5 minutos. La recta numérica muestra la hora de las 5 pm hasta las 6 pm. Etiqueta la siguiente recta numérica para mostrar su trabajo. 4. Tanner le dice a su hermano pequeño que 11:25 pm viene después de las 11:20 am. ¿ Estás de acuerdo con Tanner? ¿ Por qué si o por qué no? Lesson 2: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Relate skip-counting by 5 on the clock and telling time to a continuous measurement model, the number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.22 Lesson 2 Homework 3•2 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Fecha 1. Siga las instrucciones para etiquetar la siguiente recta numérica. a. El equipo de baloncesto practica entre las 4:00 pm y 5:00 pm. Etiqueta la primera y la última marca en la recta numérica como 4:00 pm y 5:00 pm. b. Cada intervalo representa 5 minutos. Cuenta de cinco en cinco empezando de 0, o 4:00 p.m. Etiqueta 0, 5 y 10 debajo de la recta numérica hasta las 5:00 pm. c. El equipo hace calentamientos a las 4:05 pm. Marca con un punto en la recta numérica para representar esta hora. Encima de este punto escribe la letra W. d. El equipo hace tiros libres a las 4:15 pm. Marca con un punto en la recta numérica para representar esta hora. Encima de ese punto escribe la letra F. e. El equipo hacen un juego de práctica a las 4:25 pm. Marca con un punto en la recta numérica para representar esta hora. Encima de ese punto escribe la letra G. f. El equipo tiene un descanso para tomar agua a las 4:50 pm. Marca con un punto en la recta numérica para representar esta hora. Encima de ese punto escribe la letra B. g. El equipo revisa sus jugadas a las 4:55 pm. Marca con un punto en la recta numérica para representar esta hora. Encima de ese punto escribe la letra P. Lesson 2: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Relate skip-counting by 5 on the clock and telling time to a continuous measurement model, the number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.24 Lesson 3 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 3•2 Fecha 1. Marca un punto en la recta numérica para las horas que se muestran en los siguientes relojes. Luego traza una línea para coincidir los relojes con los puntos. 11 12 1 11 10 2 8 4 9 3 7 1 8 4 9 3 7 6 12 11 2 5 6 12 10 1 10 2 8 4 9 3 5 7 6 5 8:00 pm 7:00 pm 20 10 0 2. Jessie se despertó esta mañana a las 6:48 am. Dibuja las manillas en el reloj para mostrar la hora a la que Jessie se despertó. 11 12 30 40 11 2 9 4 5 6 12 1 10 3 8 60 3. Mrs. Barnes empieza a enseñar matemáticas a las 8:23 am. Dibuja las manillas en el reloj para mostrar la hora a la que la Sra. Barnes empieza a enseñar matemáticas. 1 10 7 50 Lesson 3: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org 2 9 3 4 8 7 6 5 Count by fives and ones on the number line as a strategy to tell time to the nearest minute on the clock. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.34 3•2 Lesson 3 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM 4. El reloj muestra a qué hora Rebecca finalizó su tarea. ¿A qué hora finalizó su tarea Rebecca? 11 12 1 10 2 9 3 4 8 7 6 5 Rebecca finalizó su tarea a las _ . 5. El siguiente reloj muestra a qué hora la mamá de Mason le deja en la práctica. 11 a. ¿A qué hora deja a Mason su mamá en la práctica? 12 1 10 2 9 3 4 8 7 6 5 b. El entrenador de Mason llegó 11 minutos antes que Mason. ¿A qué hora llegó el entrenador de Mason? Lesson 3: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Count by fives and ones on the number line as a strategy to tell time to the nearest minute on the clock. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.35 3•2 Lesson 3 Homework 3•2 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Fecha 1. Marca los puntos en la recta numérica para cada hora que se demuestra en los siguientes relojes. Luego traza las líneas para coincidir los relojes con los puntos. 5:00 pm 4:00 pm 20 10 0 2. Julie cena a las 6:07 pm. Dibuja las manillas en el reloj para mostrar la hora a que Julie cena. 11 12 30 40 50 3. La clase de Educación Física empieza a las 1:32 pm. Dibuja las manillas en el reloj para mostrar la hora a que empieza la clase de Educación Física. 11 1 10 2 9 4 7 6 5 Lesson 3: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org 12 1 10 3 8 60 2 9 3 4 8 7 6 5 Count by fives and ones on the number line as a strategy to tell time to the nearest minute on the clock. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.37 Lesson 3 Homework NYS COMMON CORE MATHEMATICS CURRICULUM 4. El reloj muestra la hora a la que Zachary empieza a jugar con sus muñecos de acción. 3•2 INICIO a. ¿A qué hora empieza a jugar con sus muñecos de acción? b. Si juega con sus muñecos de acción por 23 minutos. ¿A qué hora él finaliza el juego? FIN c. Dibuja las manillas en el reloj a la derecha para mostrar la hora a la que Zachary finaliza el juego. d. Etiqueta la primera y última marca con un punto de las 2:00 pm y 3:00 pm. Luego marca con un punto la hora de inicio y de fin de juego de Zachary. Etiqueta su hora de inicio con la letra B y su hora final con la letra F. Lesson 3: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Count by fives and ones on the number line as a strategy to tell time to the nearest minute on the clock. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.38 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 3•2 Lesson 4 Problem Set Fecha Instrucciones: Utiliza la recta numérica para responder a los Problemas del 1 al 5. 1. Cole empezó a leer a las 6:23 pm. Paró a las 6:49 pm. ¿Cuántos minutos Cole estuvo leyendo? Cole leyó por _____________minutos. 2. Natalie terminó su práctica de piano a las 2:45 pm después de haber practicado por 37 minutos. ¿A qué hora empezó la práctica de Natalie? La práctica de Natalie empezó a las pm 3. Genevieve trabajó en su libro de recuerdos desde las 11:27 am hasta las 11:58 am. ¿Cuántos minutos trabajó en su libro de recuerdos? Genevieve trabajó en su libro de recuerdos por minutos. 4. Nate finaliza su tarea a las 4:47 pm después de dedicarse 38 minutos a la misma. ¿A qué hora Nate empezó su tarea? Nate empezó su tarea a las _________pm 5. Andrea va de pesca a las 9:03 am. Pescó por 49 minutos. ¿A qué hora Andrea terminó la pesca? Andrea terminó la pesca a las _________am Lesson 4: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve word problems involving time intervals within 1 hour by counting backward and forward using the number line and clock. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.47 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 4 Problem Set 3•2 6. Dion camina a la escuela. Los siguientes relojes muestran cuando él sale de su casa y cuando llega a la escuela. ¿Cuántos minutos Dion se demora en caminar hasta la escuela? Dion sale de su casa: 11 12 Dion llega a la escuela: 11 1 10 3 4 8 7 6 5 1 10 2 9 12 2 9 3 4 8 7 6 5 7. Sydney limpia su habitación por 45 minutos. Ella empieza a las 11:13 am. ¿A qué hora Sidney termina de limpiar su habitación? 8. El coro del tercer grado realizó un musical para la escuela. El musical tiene una duración de 42 minutos. Terminó a las 1:59 pm. ¿A qué hora comenzó el musical? Lesson 4: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve word problems involving time intervals within 1 hour by counting backward and forward using the number line and clock. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.48 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 4 Homework 3•2 Fecha Registra la hora de inicio de tu tarea en el reloj para el Problema 6. Instrucciones: Utiliza la recta numérica para responder a los Problemas del 1 al 4. 1. La mamá de Joy empezó a caminar a las 4:12 pm. Paró a las 4:43 pm. ¿Cuántos minutos ella caminó? La mamá de Joy caminó por __________ minutos. 2. Cassie finaliza la práctica de softbol a las 3:52 pm después de haber practicado por 30 minutos. ¿A qué hora Cassie empezó la práctica? Cassie empezó la práctica a las _. 3. Jordie construyó un modelo desde las 9:14 am hasta las 9:47 am. ¿Cuántos minutos Jordie pasó construyendo su modelo? Jordie construyó su modelo por __________ minutos. 4. Cara termina de leer a las 2:57 pm. Leyó un total de 46 minutos. ¿A qué hora Cara empezó a leer? Cara empezó a leer a las _________ pm. Lesson 4: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve word problems involving time intervals within 1 hour by counting backward and forward using the number line and clock. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.50 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 4 Homework 3•2 5. Jenna y su mamá fueron en autobús al centro comercial. Los relojes de abajo muestran cuando salieron de la casa y cuando llegaron al centro comercial. ¿Cuántos minutos les llevó llegar al centro comercial? Hora a la que salieron de la casa: 6. Registra la hora de inicio de tu tarea: Hora a la que llegaron al centro comercial: Registra la hora a la que terminas los Problemas 1–5: ¿Cuántos minutos dedicaste a los Problemas 1–5? Lesson 4: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve word problems involving time intervals within 1 hour by counting backward and forward using the number line and clock. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.51 3•2 Lesson 5 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Fecha 1. Cole leyó su libro durante 25 minutos ayer y durante 28 minutos hoy. ¿Cuántos minutos Cole estuvo leyendo en total? Muestra el problema en la recta numérica y escribe una ecuación para solucionar. 0 10 20 30 50 40 60 Cole leyó durante ________ minutos. 2. Tessa pasa 34 minutos bañando a su perro. Le toma 12 minutos enjabonarlo y enjuagarlo, y ¡el resto del tiempo los usa para meter al perro en la bañera! ¿Cuántos minutos le lleva a Tessa meter a su perro en la bañera? Dibuja una recta numérica para modelar el problema y escribe una ecuación para solucionar. 3. Tessa camina a su perro por 47 minutos. Jeremiah camina a su perro por 30 minutos. ¿Cuántos minutos más usa Tessa en caminar a su perro que Jeremiah? 4. A Austin le toma 4 minutos sacar la basura, 12 minutos para lavar los platos, y 13 minutos para trapear el piso de la cocina. ¿Cuánto tiempo se tarda Austin en hacer sus tareas domésticas? Lesson 5: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve word problems involving time intervals within 1 hour by adding and subtracting on the number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.60 NYS COMMON CORE MATHEMATICS CURRICULUM 4. Lesson 5 Problem Set 3•2 El transporte escolar de Austin llega a las 7:55 am. Sí él empieza sus tareas domésticas a las 7:30 am, ¿terminará a tiempo para alcanzar su transporte escolar? Explica tu razonamiento. 5. El gato de Gilberto duerme al sol por 23 minutos. El gato se despierta a la hora que muestra el reloj de abajo. ¿A qué hora empezó el gato a dormir? Lesson 5: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve word problems involving time intervals within 1 hour by adding and subtracting on the number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.61 Lesson 5 Homework NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 3•2 Fecha 1. Abby gastó ayer 22 minutos en su proyecto de ciencias y 34 minutos hoy. ¿Cuántos minutos gastó Abby trabajando en su proyecto de ciencias en total? Muestra el problema en la recta numérica y escribe una ecuación para solucionar. 0 10 20 30 50 40 60 Abby gastó ________ minutos. 2. Susanna gastó un total de 47 minutos trabajando en su proyecto. ¿Cuántos minutos más que Susanna gastó Abby trabajando en su proyecto? Dibuja una recta numérica para simular el problema y escribe una ecuación para solucionar. 3. Peter practica violín por un total de 55 minutos durante el fin de semana. Él practica 25 minutos el sábado. ¿Cuántos minutos practica el domingo? Lesson 5: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve word problems involving time intervals within 1 hour by adding and subtracting on the number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.63 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 5 Homework 3•2 4. a. A Marcus le gusta la jardinería. Él saca las malas hierbas durante 18 minutos, riega durante 13 minutos y planta por otros 16 minutos. ¿Cuántos minutos en total se dedica Marcus a la jardinería? 4. b. Marcus quiere mirar una película que empieza a las 2:55 pm. Le toma 10 minutos manejar al teatro. Sí Marcus empieza el trabajo de jardinería a las 2:00 pm, ¿podrá llegar a tiempo él para la película? Explica tu razonamiento. 5. Arelli duerme un poco la siesta después de la escuela. Cuando empieza a dormir la hora del reloj muestra 3:03 pm. Ella se despierta a la hora que se muestra en el reloj de abajo. ¿Cuánto tiempo Arelli durmió? Lesson 5: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve word problems involving time intervals within 1 hour by adding and subtracting on the number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.A.64 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 6 Problem Set 3•2 Fecha 1. Ilustra y describe el proceso de hacer un peso de 1 kilogramo. 2. Ilustra y describe el proceso de partición 1 kilogramos a 100 gramos. 3. Ilustra y describe el proceso de partición de 100 gramos a 10 gramos. Lesson 6: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Build and decompose a kilogram to reason about the size and weight of 1 kilogram, 100 grams, 10 grams, and 1 gram. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.8 Lesson 6 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM 3•2 4. Ilustra y describe el proceso de partición de 10 gramos a 1 gramo. 5. Compara las dos siguientes tablas de valor posicional. ¿Cómo la exploración de hoy utilizando kilogramos y gramos se relaciona con tu conocimiento de valor posicional? 1 kilogramo 100 gramos 10 gramos Miles Centenas Decenas Lesson 6: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org 1 gramo Unidades Build and decompose a kilogram to reason about the size and weight of 1 kilogram, 100 grams, 10 grams, and 1 gram. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.9 Lesson 6 Homework NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 3•2 Fecha 1. Utiliza la tabla para ayudarte a responder las siguientes preguntas: 1 kilogramo 100 gramos 10 gramos 1 gramo a. Isaiah pone un peso de 10 gramos en la bandeja de la balanza. ¿Cuántos pesos de 1 gramo necesita para balancear la balanza? b. Luego, Isaiah pone un peso de 100 gramos en la bandeja de la balanza. ¿Cuántos pesos de 10 gramos necesita para balancear la balanza? c. Isaiah luego pone un peso de kilogramo en la bandeja de la balanza. ¿Cuántos pesos de 100 gramos necesita para balancear la balanza? d. ¿Qué patrón notas en las Partes (a–c)? Lesson 6: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Build and decompose a kilogram to reason about the size and weight of 1 kilogram, 100 grams, 10 grams, and 1 gram. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.11 Lesson 6 Homework NYS COMMON CORE MATHEMATICS CURRICULUM 3•2 2. Lea cada balanza digital. Escribe cada peso utilizando la palabra kilogramo o gramo para cada medida. 3 kg 450 g 6 kg 1 kg 11 kg 907 g Lesson 6: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Build and decompose a kilogram to reason about the size and weight of 1 kilogram, 100 grams, 10 grams, and 1 gram. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.12 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 7 Problem Set 3•2 3•2 Fecha Trabaja con un compañero. Utiliza los pesos correspondientes para estimar el peso de los objetos en el salón de clases. Luego verifica tu cálculo pesándolos en la balanza. B. C. D. Los Objetos que Pesan Aproximadamente 1 Kilogramo Peso Real Los Objetos que Pesan Aproximadamente 100 Gramos Peso Real Los Objetos que Pesan Aproximadamente 10 Gramos Peso Real Los Objetos que Pesan Aproximadamente 1 Gramo Peso Real Lesson 7: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Develop estimation strategies by reasoning about the weight in kilograms of a series of familiar objects to establish mental benchmark measures. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.19 Lesson 7 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM 3•2 3•2 E. Encierra en un círculo la unidad de peso correcta para cada cálculo. 1. Una caja de cereal pesa aproximadamente 350 (gramos / kilogramos). 2. Una sandía pesa aproximadamente 3 (gramos / kilogramos). 3. Una tarjeta postal pesa aproximadamente 6 (gramos / kilogramos). 4. Un gato pesa aproximadamente 4 (gramos / kilogramos). 5. Una bicicleta pesa aproximadamente 15 (gramos / kilogramos). 6. Un limón pesa aproximadamente 58 (gramos / kilogramos). F. Durante el proceso de exploración, Derrick encuentra que su botella de agua pesa lo mismo que una bolsa de arroz de 1 kilogramo. Luego, él exclama, “¡La computadora portátil de nuestra clase pesa lo mismo que 2 botellas de agua! "¿Cuánto pesa la computadora portátil en Kilogramos? Explica tu razonamiento. G. Nessa le dice a su hermano que 1 kilogramo de arroz pesa lo mismo que 10 bolsas que contienen 100 gramos de frijoles cada uno. ¿Estás de acuerdo con ella? Explica porque o porque no. Lesson 7: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Develop estimation strategies by reasoning about the weight in kilograms of a series of familiar objects to establish mental benchmark measures. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.20 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 7 Homework 3•2 Fecha 1. Parea el objeto con su peso aproximado. 100 gramos 10 gramos 1 gramo 1 kilogramo 2. Alicia y Jeremy pesan un teléfono celular en una balanza digital. Ellos escriben 113 pero se olvidan de registrar la unidad de medida. ¿Cuál es la unidad de medida correcta? ¿Cómo lo sabes? Lesson 7: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Develop estimation strategies by reasoning about the weight in kilograms of a series of familiar objects to establish mental benchmark measures. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.22 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 7 Homework 3•2 3. Lee y escribe los siguientes pesos. Escribe la palabra kilogramo o gramo con la unidad de medida. Lesson 7: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Develop estimation strategies by reasoning about the weight in kilograms of a series of familiar objects to establish mental benchmark measures. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.23 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 8 Problem Set Nombre 3•2 Fecha 1. Tim va al Mercado a comprar frutas y vegetales. Pesa unas habichuelas y algunas uvas. Enumera los pesos para ambos las habichuelas y las uvas. Las habichuelas pesan Las uvas pesan gramos. ______________ gramos. 2. Utiliza el diagrama de cinta para simular los siguientes problemas. Keiko y su hermano Jiro fueron pesados en la oficina del doctor. Keiko pesa 35 kilogramos y Jiro pesa 43 kilogramos. a. ¿Cuál es el peso total de Keiko y Jiro? Keiko y Jiro pesan ____________ kilogramos. b. ¿Cuánto más pesado es Jiro que Keiko? Jiro es _____________ kilogramos más pesado que Keiko. Lesson 8: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve one-step word problems involving metric weights within 100 and estimate to reason about solutions. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.29 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 8 Problem Set 3•2 3. Jared calcula que su planta de interior es tan pesada como una bola de bolos de 5 kilogramos. Dibuja un diagrama de cinta para calcular el peso de 3 plantas de interior. 4. Jane y sus 8 amigos fueron a la recolección de manzanas. Ellos comparten igualmente lo que recogen. El peso total de las manzanas que ellos recogen se muestra a la derecha. a. ¿Cuántos kilogramos de manzanas aproximadamente llevará Jane a la casa? 27 kg b. Jane calcula que una calabaza pesa aproximadamente lo que pesan las manzanas que le comparten a ella. ¿Cuántos kilogramos aproximadamente pesan 7 calabazas juntas? Lesson 8: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve one-step word problems involving metric weights within 100 and estimate to reason about solutions. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.39 Lesson 8 Homework NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 3•2 Fecha 1. Los pesos de 3 canastas de frutas se muestran abajo. Canasta A 12kg Canasta B 8kg Canasta C 16kg a. La canasta es la más pesada. b. La canasta c. La canasta A es es la más liviana. kilogramos más pesada que la canasta B. d. ¿Cuál es el peso total de las tres canastas? 2. Cada periódico pesa aproximadamente 280 gramos. ¿Cuál es el peso total de los 3 periódicos? 3. La Sra. Ríos compra 453 gramos de fresas. A ella le quedan 23 gramos después de hacer unas batidas. ¿Cuántos gramos de fresas utilizó? Lesson 8: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve one-step word problems involving metric weights within 100 and estimate to reason about solutions. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.32 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 8 Homework 3•2 4. El papá de Andrea es 57 kilogramos más pesado que Andrea. Andrea pesa 34 kilogramos. a. ¿Cuánto pesa el papá de Andrea? b. ¿Cuánto pesan Andrea y su papá en total? 5. La abuela de Jennifer compra zanahorias del puesto de granja. Ella y sus 3 nietos comparten por igual las zanahorias. El peso total de las zanahorias que ella compra se muestra abajo. a. ¿Cuántos kilogramos de zanahorias Jennifer recibirá? 28 kg b. Jennifer utiliza 2 kilogramos de zanahorias para hornear unos panecillos. ¿Cuántos kilogramos de zanahorias le quedan? Lesson 8: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve one-step word problems involving metric weights within 100 and estimate to reason about solutions. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.33 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 9 Problem Set 3•2 Fecha Parte 1 a. Calcula si cada recipiente contiene menor que, mayor que, o igual que 1 litro. Recipiente 1 contiene menor que/ mayor que/ o igual que 1 litro. Real: Recipiente 2 contiene menor que/ mayor que/ o igual que 1 litro. Real: Recipiente 3 contiene menor que/ mayor que/ o igual que 1 litro. Real: Recipiente 4 contiene menor que/ mayor que/ o igual que 1 litro. Real: b. Después de la medición, ¿Qué te sorprendió? ¿Por qué? Parte 2 c. Ilustra y describe el proceso de partición de 1 litro de agua en 10 tazas. Lesson 9: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Decompose a liter to reason about the size of 1 liter, 100 milliliters, 20 milliliters, and 1 milliliter. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.39 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 9 Problem Set 3•2 d. Ilustra y describe el proceso de partición de la Taza K en 10 unidades más pequeñas. e. Ilustra y describe el proceso de partición de la Taza L en 10 unidades más pequeñas. f. ¿Qué es similar entre separar 1 litro en mililitros y separar 1 kilogramo en gramos? g. Un litro de agua pesa 1 kilogramo. ¿Cuánto pesa 1 mililitro de agua? Explica como lo sabes. Lesson 9: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Decompose a liter to reason about the size of 1 liter, 100 milliliters, 20 milliliters, and 1 milliliter. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.49 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 9 Homework 3•2 Fecha 1. Encuentra recipientes en tu casa que tengan una capacidad aproximada de 1 litro. Utiliza las etiquetas en los recipientes para ayudarte a identificarlos. a. Nombre del Recipiente Ejemplo: Cartón de Jugo de Naranja b. Dibuja los recipientes. ¿De qué manera el tamaño y forma se comparan? 2. El doctor receta a la Sra. Larson 5 mililitros de medicina cada día por 3 días. ¿Cuántos mililitros de medicina tomará en total? Lesson 9: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Decompose a liter to reason about the size of 1 liter, 100 milliliters, 20 milliliters, and 1 milliliter. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.42 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 9 Homework 3•2 3. La Sra. Goldstein vierte 3 cajas de jugo en un tazón para hacer ponche. Cada caja contiene 236 mililitros de jugo. ¿Cuánto jugo vierte la señora Goldstein en el tazón? 4. La pecera de Daniel contiene 24 litros de agua. Él utiliza un balde de 4-litros para llenar la pecera. ¿Cuántos baldes de agua se necesitan para llenar la pecera? 5. Sheila compra 15 litros de pintura para pintar su casa. Ella vierte la pintura igualmente en 3 baldes. ¿Cuántos litros de pintura hay en cada balde? Lesson 9: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Decompose a liter to reason about the size of 1 liter, 100 milliliters, 20 milliliters, and 1 milliliter. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.43 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 10 Problem Set 3•2 Fecha 1. Etiqueta la recta numérica vertical en el recipiente a la derecha. Responde las siguientes preguntas. a. ¿Qué has etiquetado en la marca del medio ¿Por qué? b. Explica como vertiendo cada taza de agua te ayudó a crear una recta numérica vertical. c. Sí derramas fuera 300 mL de agua, ¿cuántos mL quedan en el recipiente? 100 mL 2. ¿Cuánto líquido hay en cada recipiente? Lesson 10: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate and measure liquid volume in liters and milliliters using the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.50 Lesson 10 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM 3•2 3. Calcula la cantidad de líquido en cada recipiente al mililitro más cercano. 4. La siguiente tabla muestra la capacidad de 4 barriles. Barril A 75 litros Barril B 68 litros Barril C 96 litros Barril D 52 litros 100 L 90 L 80 L a. Etiqueta la recta numérica para mostrar la capacidad de cada barril. El Barril A ya se ha realizado. Barril A 75 L 70 L b. ¿Cuál de los barriles tiene la mayor capacidad? c. ¿Cuál de los barriles tiene la menor capacidad? 60 L d. Ben compra un barril que contiene aproximadamente 70 litros. ¿Cuál barril es más probable que Ben haya comprado? Explica porque. 50 L e. Utiliza la recta numérica para encontrar cuantos litros más el Barril C puede contener que el Barril B. Lesson 10: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org 40 L Estimate and measure liquid volume in liters and milliliters using the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.51 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 10 Homework Nombre 3•2 3•2 Fecha 1. ¿Cuánto líquido hay en cada recipiente? 2. Jon derrama los contenidos del Recipiente 1 dentro del Recipiente 3. ¿Cuánto líquido hay en el Recipiente 3 después que él derrama el líquido? 3. Calcula la cantidad de líquido en cada recipiente al litro más cercano. Lesson 10: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate and measure liquid volume in liters and milliliters using the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.53 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 10 Homework 4. Kristen está comparando la capacidad de los tanques de gasolina de los autos. Utiliza la siguiente tabla para responder a las preguntas. Tamaño del auto Grande 3•2 3•2 80 L Capacidad en litros 70 L 74 60 L Mediano Pequeño 57 Mediano 42 50 L a. Etiqueta la recta numérica para mostrar la capacidad de cada tanque de gasolina. El auto mediano ya está hecho para usted. 40 L b. ¿Cuál tanque de gasolina tiene la mayor capacidad? 30 L c. ¿Cuál tanque de gasolina tiene la menor capacidad? 20 L d. El auto de Kristen tiene el tanque con una capacidad aproximadamente de 60 litros. ¿Cuál de los autos de la tabla tiene aproximadamente la misma capacidad que el auto de Kristen? e. Utiliza la recta numérica para encontrar cuantos litros más el tanque del auto grande contiene que el tanque del auto pequeño. Lesson 10: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate and measure liquid volume in liters and milliliters using the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.54 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 11 Problem Set 3•2 Fecha 1. El peso total en gramos de una lata de tomates y un tarro de comida de bebé se muestra a la derecha. a. El tarro de comida de bebé pesa 113 gramos. ¿Cuánto pesa la lata de tomates? b. ¿Cuánto más pesa la lata de tomates que el tarro de comida de bebé? 2. El peso de un lapicero en gramos se muestra a la derecha. a. ¿Cuánto es el peso total de 10 lapiceros? b. Una caja vacía pesa 82 gramos. ¿Cuál es el peso total de una caja de 10 lapiceros? 3. El peso total de una manzana, un limón, y una banana en gramos se muestra a la derecha. a. Sí la manzana y el limón juntos pesan 317 gramos, ¿cuál es el peso de banana? b. Sí sabemos que el limón pesa 68 gramos menos que la banana, ¿cuánto pesa el limón? 508 c. ¿Cuál es el peso de la manzana? Lesson 11: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve mixed word problems involving all four operations with grams, kilograms, liters, and milliliters given in the same units. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.60 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 11 Problem Set 3•2 4. Un pavo congelado pesa aproximadamente 5 kilogramos. El cocinero hace pedidos de 45 Kilogramos de pavo. Utiliza un diagrama de cinta para encontrar aproximadamente cuantos pavos congelados él pide. 5. Una receta requiere 300 mililitros de leche. Sara decide triplicar la receta para la cena. ¿Cuántos mililitros de leche necesita para cocinar la cena? 6. Marian vierte un recipiente lleno de agua igualmente dentro de baldes. Cada balde tiene la capacidad de 4 litros. Después de llenar 3 baldes, a ella todavía le sobran 2 litros en su recipiente. ¿Cuál es la capacidad de su recipiente? Lesson 11: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve mixed word problems involving all four operations with grams, kilograms, liters, and milliliters given in the same units. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.61 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 11 Homework 3•2 Fecha 1. Karina va a una caminata. Ella trae un cuaderno, un lápiz y una cámara. El peso de cada artículo se muestra en la tabla. ¿Cuál es el peso total de los tres artículos? Artículo Peso Cuaderno 312 g Lápiz 10 g Cámara 365 g El peso total es de _________gramos . 2. Un caballo y su jinete pesan 729 Kilogramos. El caballo pesa 625 Kilogramos. ¿Cuánto pesa el jinete? El jinete pesa ____________kilogramos . Lesson 11: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve mixed word problems involving all four operations with grams, kilograms, liters, and milliliters given in the same units. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.63 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 11 Homework 3•2 3. El equipo de fútbol de Theresa llena 6 refrigeradores de agua antes del partido. Cada refrigerador de agua contiene 9 litros de agua. ¿Cuántos litros de agua tuvieron que llenar? 4. Dwight compró 48 kilogramos de fertilizante para su jardín. Él necesita 6 kilogramos de fertilizante para cada grupo de vegetales. ¿Cuántos grupos de vegetales puede fertilizar? 5. Nancy hornea 7 tortas para la venta de pasteles de la escuela. Cada torta requiere 5 mililitros de aceite. ¿Cuántos mililitros utiliza de aceite? Lesson 11: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Solve mixed word problems involving all four operations with grams, kilograms, liters, and milliliters given in the same units. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.B.64 Lesson 12 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 33•2 Fecha 1. Trabaja con un compañero. Utilice una regla y/o una regla de un metro para completar la siguiente tabla. Medición (en cm) Objeto El objeto mide entre (cuáles de las dos decenas)… 23 cm Ejemplo: Mi zapato 20 y 30 Longitud Redondeada al 10 cm más Cercano cm Lado largo de un escritorio y cm Un lápiz nuevo y cm Lado corto de un pedazo de papel y cm Lado largo de un pedazo de papel y cm 20 cm 2. Trabaja con un compañero. Utiliza una balanza digital para completar la siguiente tabla. Medición (en g) Bolsa 8g Ejemplo: Bolsa A La bolsa de arroz pesa entre (cuáles de las dos decenas)… 0 y 10 g Bolsa B y g Bolsa C y g Bolsa D y g Bolsa E y g Lesson 12: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Peso Redondeado al 10 g más Cercano 10 g Round two-digit measurements to the nearest ten on the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.C.8 33•2 Lesson 12 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM 3. Trabaja con un compañero. Utiliza un vaso de precipitados para completar la tabla de abajo. Recipiente Ejemplo: Recipiente A Medición El recipiente contiene entre (en mL) (cuáles de las dos decenas)… 33 mL 30 y 40 Volumen Liquido Redondeado al 10 mL más cercano mL 30 mL Recipiente B y Recipiente C y mL Recipiente D y mL Recipiente E y mL mL 4. Trabaja con un compañero. Utiliza un reloj para completar la siguiente tabla. Hora Real Actividad Ejemplo: La hora a la que empezamos matemáticas La hora a la que empecé los Problemas de Aplicación 10:03 La hora de la actividad entre (cuáles de las dos decenas)… 10:00 y y La hora a la que finalicé la Estación 2 y La hora a la que finalicé la Estación 3 y Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org 10:00 y La hora a la que finalicé la Estación 1 Lesson 12: 10:10 Hora Redondeada a los 10 Minutos más cercano Round two-digit measurements to the nearest ten on the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.C.9 Lesson 12 Homework NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 33•2 Fecha 1. Completa la tabla. Selecciona los objetos y usa una regla/una regla de un metro para completar con tus datos los dos últimos. Objeto Medida (en cm) El objeto mide entre, ¿cuáles de las dos decenas? Largo del escritorio 66 cm Ancho del escritorio 48 cm y cm Ancho de la puerta 81 cm y cm y cm y cm 2. La clase de gimnasia termina a las 10:27 am. Redondea la hora a los 10 minutos más cercano. _ y Longitud Redondeada al 10 cm más cercana cm 3. Mide el líquido en el vaso de precipitados a los 10 mililitros más cercano. 60 mL 50 mL 40 mL 30 mL 20 mL 10 mL La clase de gimnasia termina aproximadamente a las am. Lesson 12: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Hay aproximadamente precipitados. mililitros en el vaso de Round two-digit measurements to the nearest ten on the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.C.11 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 12 Homework 33•2 4. El peso de la Sra. Santos se muestra en la balanza. Redondea el peso a los 10 kilogramos más cercano. El peso de la Sra. Santos es La Sra. Santos pesa aproximadamente kilogramos. kilogramos. 5. Un cuidador del zoológico pesa a un chimpancé. Redondea el peso del chimpancé a los 10 kilogramos más cercano. El peso del chimpancé es de El chimpancé pesa aproximadamente Lesson 12: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org kilogramos. kilogramos. Round two-digit measurements to the nearest ten on the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.C.12 Lesson 13 Problem Set 33•2 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Fecha 1. Redondea a la decena más cercana. Usa la recta numérica para modelar tu pensamiento. a. 32 ≈ b. 36 ≈ 40 35 35 32 30 c. 62 ≈ d. 162 ≈ e. 278 ≈ f. Lesson 13: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org 405 ≈ Round two- and three- digit numbers to the nearest ten on the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.C.19 Lesson 13 Problem Set 33•2 NYS COMMON CORE MATHEMATICS CURRICULUM 2. Redondea el peso de cada articulo a los 10 gramos más cercano. Dibuja rectas numéricas para modelar tu pensamiento. Recta Numérica Redondea a los 10 gramos más cercano: 36 gramos 52 gramos 142 gramos 3. El juego de baloncesto de Carl empieza a las 3:03 pm y termina a las 3:51 pm. a. ¿Cuántos minutos en total es el juego de baloncesto de Carl? b. Redondea el número de minutos total a los 10 minutos más cercano. Lesson 13: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Round two- and three- digit numbers to the nearest ten on the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.C.29 Lesson 13 Homework 33•2 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Fecha 1. Redondea a la decena más cercana. Utiliza la recta numérica para modelar tu pensamiento. a. 43 ≈ b. 48 ≈ 50 45 43 40 c. 73 ≈ d. 173 ≈ e. 189 ≈ f. Lesson 13: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org 194 ≈ Round two- and three- digit numbers to the nearest ten on the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.C.22 Lesson 13 Homework 33•2 NYS COMMON CORE MATHEMATICS CURRICULUM 2. Redondea el peso de cada artículo a los 10 gramos más cercano. Dibuja rectas numéricas para modelar tu pensamiento. Recta Numérica Redondea a los 10 gramos más cercano: Barra de Cereal: 45 gramos Barra de pan: 673 gramos 3. El Club de Jardinería planta filas de zanahorias en el jardín. Un paquete de semillas pesa 28 gramos. Redondea el peso total de 2 paquetes de semillas a los 10 gramos más cercano. Muestra tu pensamiento utilizando una recta numérica. Lesson 13: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Round two- and three- digit numbers to the nearest ten on the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.C.23 Lesson 14 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 3•2 Fecha 1. Redondea a la centena más cercana. Utiliza la recta numérica para modelar tu pensamiento. a. 143 ≈ b. 286 ≈ 150 c. 320 ≈ d. 1,320 ≈ e. 1,572 ≈ f. Lesson 14: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org 1,250 ≈ Round to the nearest hundred on the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.C.31 Lesson 14 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM 2. 3•2 a. Shauna tiene 480 calcomanías. Redondea el número de calcomanías a la centena más cercana. b. Hay 525 páginas en un libro. Redondea el número de páginas a la centena más cercana. c. Un recipiente contiene 750 mL de agua. Redondea la capacidad a los 100 mL más cercano. d. Glen gasta $1,297 en un computador. Redondea el monto que Glen gasta a los $100 más cercano. e. La distancia entre dos ciudades es de 1,842 km. Redondea la distancia a los 100 km más cercano. 3. Encierra en un círculo los números que redondean a 600 cuando son redondeados a la centena más cercana. 527 550 639 681 713 603 4. El maestro pide a los estudiantes que redondeen 865 a la decena más cercana. Christian dice que es ochocientos setenta. Alexis no está de acuerdo y dice que es 87 decenas. ¿Quién está correcto? Explica tu pensamiento. Lesson 14: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Round to the nearest hundred on the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.C.32 Lesson 14 Homework NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 3•2 Fecha 1. Redondea a la centena más cercana. Utiliza la recta numérica para modelar tu pensamiento. b. 342 ≈ a. 156 ≈ 150 c. 685 ≈ d. 804 ≈ e. 260 ≈ f. Lesson 14: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org 1260 ≈ Round to the nearest hundred on the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.C.34 Lesson 14 Homework NYS COMMON CORE MATHEMATICS CURRICULUM 3•2 2. Completa la tabla. a. Luis tiene 217 tarjetas de béisbol. Redondea el número de tarjetas que Luis tiene a la centena más cercana. b. Habían 462 personas sentadas en la audiencia. Redondea el número de personas a la centena más cercana. c. Una botella de jugo contiene 386 mililitros. Redondea la capacidad al 100 mililitros más cercano. d. Un libro de matemáticas pesa 727 gramos. Redondea el peso a los 100 gramos más cercano. e. Los padres de Joanie gastaron $1,260 en 2 pasajes de avión. Redondea el total al $100 más cercano. 3. Encierra en un círculo los números que redondean a 400 cuando son redondeados a la centena más cercana. 368 342 420 492 449 464 5. Hay 525 páginas en un libro. Julia y Kim redondean el número de páginas a la decena más cercana. Julia dice que es 520. Kim dice que es 53 decenas. ¿Quién está correcto? Explica tu pensamiento. Lesson 14: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Round to the nearest hundred on the vertical number line. 7/4/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.C.35 Lesson 15 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 33•2 Fecha 1. Encuentra las siguientes sumas. a. 46 mL + 5 mL b. 46 mL + 25 mL c. 46 mL + 125 mL d. 59 cm + 30 cm e. 509 cm + 83 cm f. 597 cm + 30 cm 39 g + 63 g h. 345 g + 294 g i. 480 g + 476 g g. j. 1 L 245 mL + 2 L 412 mL = Lesson 15: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org k. 2 kg 509 g + 3 kg 367 g = Add measurements using the standard algorithm to compose larger units once. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.D.9 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 15 Problem Set 33•2 2. Nadine y Jen compran una bolsa pequeña de palomitas de maíz y un pretzel en el cine. El pretzel pesa 63 gramos más que las palomitas de maíz. ¿Cuál es el peso del pretzel? ? gramos 3. En la clase de matemáticas, Jason y Andrea encuentran el total del volumen líquido del agua en sus vasos de precipitados. Jason dice que el total es 782 mL, pero Andrea dice que es 792 mL. La cantidad de agua en cada vaso de precipitados se puede encontrar en la tabla a la derecha. Muestra de quién es el cálculo correcto. Explica el error del estudiante que está equivocado. Estudiante 44 gramos Volumen Líquido Jason 475 mL Andrea 317 mL 4. A Greg le toma 15 minutos para cortar el césped delantero. Le toma 17 minutos más para cortar el césped de atrás que el césped delantero. ¿Cuál es la cantidad total de tiempo que gasta Greg para cortar los céspedes? Lesson 15: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Add measurements using the standard algorithm to compose larger units once. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.D.10 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 15 Homework 33•2 Fecha 1. Encuentra las siguientes sumas. Puedes usar cálculo mental o un algoritmo. a. 75 cm + 7 cm b. 39 kg + 56 kg d. 283 g + 92 g c. 362 mL + 229 mL e. 451 mL + 339 mL f. 149 L + 331 L 2. El volumen líquido de cinco bebidas se muestran abajo. Drink Volumen Líquido Jugo de Manzana 125 mL Leche 236 mL Agua 248 mL Jugo de Naranja Ponche de Frutas a. Jen toma el jugo de manzana y el agua. ¿Cuántos mililitros toma ella en total? 174 mL 208 mL Jen toma b. Kevin toma la leche y el ponche de frutas. ¿Cuántos mililitros toma él en total? Kevin toma Lesson 15: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org mL. mL. Add measurements using the standard algorithm to compose larger units once. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.D.12 Lesson 15 Homework NYS COMMON CORE MATHEMATICS CURRICULUM 33•2 3. Hay 75 estudiantes en el Tercer Grado. Hay 44 estudiantes más en el Cuarto Grado que en el Tercer Grado. ¿Cuántos estudiantes hay en el Cuarto Grado? Utiliza un diagrama de cinta para modelar tu pensamiento. 4. El girasol del Sr. Green creció 29 centímetros en una semana. La semana pasada creció 5 centímetros más. ¿Cuánto es el número total de centímetros que creció el girasol en 2 semanas? 5. Kylie registra el peso de 3 objetos como se muestra abajo. ¿Cuáles de los 2 objetos puede poner ella en la bandeja de la balanza para igualar el peso de una bolsa de 460 gramos? Muestra como lo sabes. Libro de Tapa Blanda Banana 343 gramos 108 gramos Lesson 15: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Barra de Jabón 117 gramos Add measurements using the standard algorithm to compose larger units once. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.D.13 Lesson 16 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 33•2 Fecha 1. Encuentra las siguientes sumas. a. 52 mL + 68 mL b. 352 mL + 68 mL c. 352 mL + 468 mL d. 56 cm + 94 cm e. 506 cm + 94 cm f. 506 cm + 394 cm g. 697 g + 138 g h. 345 g + 597 g i. 486 g + 497 g j. 3 L 251 mL + 1 L 549 mL Lesson 16: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org k. 4 kg 384 g + 2kg 467 g Add measurements using the standard algorithm to compose larger units twice. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.D.21 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 16 Problem Set 33•2 2. Lane hace col agria. Él pesa la cantidad de col y de sal que utiliza. Dibuja y etiqueta un diagrama de cinta para encontrar el peso total de la col y de la sal que Lane utiliza. 907 g 93 g 3. Sue hornea tortitas para la venta de pasteles de la escuela. Después de envolver 86 tortitas, ella tiene todavía 58 tortitas que se están enfriando sobre la mesa. ¿Cuántas tortitas horneó en total? 4. La leche de cartón a la derecha contiene 183 mililitros más líquido que el jugo de cartón. ¿Cuál es la capacidad total del jugo de cartón y la leche de cartón? Lesson 16: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Jugo de cartón 279 mL Leche de cartón ? mL Add measurements using the standard algorithm to compose larger units twice. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.D.22 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 16 Homework 33•2 Fecha 1. Encuentra las siguientes sumas. a. 47 m + 8 m b. d. 63 mL + 9 mL 47 m + 38 m e. 463 mL + 79 mL g. 368 kg + 263 kg h. 508 kg + 293 kg j. 4 L 342 mL + 2 L 214 mL Lesson 16: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org c. 147 m + 383 m f. 463 mL + 179mL i. 103 kg + 799 kg k. 3 kg 296 g + 5kg 326g Add measurements using the standard algorithm to compose larger units twice. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.D.24 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 16 Homework 33•2 2. La Sra. Haley asa un pavo durante 55 minutos. Ella lo revisa, y decide asarlo por un período adicional de 36 minutos. Utiliza un diagrama de cinta para encontrar los minutos totales que la Sra. Haley asa el pavo. 3. Un caballito pesa 228 kilogramos menos que un Pony Shetland. Utiliza la tabla para encontrar el peso del Pony Shetland. Tipos de Caballos Peso en kg Pony Shetland Saddlebred Americano kg 543 kg Caballo Clydesdale Caballito kg 53 kg 4. Un caballo Clydesdale pesa tanto como un pony Shetland y un caballo de Saddlebred Americano combinado. ¿Cuánto pesa un caballo Clydesdale? Lesson 16: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Add measurements using the standard algorithm to compose larger units twice. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.D.25 Lesson 17 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 33•2 Fecha 1. a. Encuentra la suma real ya sea en una hoja o usando cálculo mental. Redondea cada sumando a la centena más cercana y encuentra las sumas estimadas. B C 451 + 253 = + = 356 + 161 = + = 652 + 158 = + = 451 + 249 = + = 356 + 148 = + = 647 + 158 = + = 448 + 249 = + = 347 + 149 = + = 647 + 146 = + = Encierra en un círculo la suma estimada que es la más cercana a la suma real. Encierra en un círculo la suma estimada que es la más cercana a la suma real. Encierra en un círculo la suma estimada que es la más cercana a la suma real. A b. Mira las sumas que te dieron los estimados más precisos. Explica abajo que tienen las mismas en común. Puedes utilizar una recta numérica para apoyar tu explicación. Lesson 17: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate sums by rounding and apply to solve measurement word problems. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.D.35 Lesson 17 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM 33•2 2. Janet miró una película que duró 94 minutos el viernes de noche. Miró una película que duró 151 minutos el sábado a la noche. a. Decide como redondear los minutos. Luego, estima el total de minutos de películas que Janet miró el viernes y sábado. b. ¿Cuánto tiempo realmente gastó Janet mirando películas? c. Explica si la suma estimada es cercana a la suma real. Redondea en una manera diferente y compara cual de los estimados es más cercano. 3. Sadie, una osa en el zoológico, pesa 182 kilogramos. Su cría pesa 74 kilogramos. a. Estima el peso total de Sadie y su cría utilizando el método que creas sea el mejor. b. ¿Cuál es el peso real de Sadie y su cría? Modela el problema con un diagrama de cinta. Lesson 17: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate sums by rounding and apply to solve measurement word problems. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.D.36 Lesson 17 Homework NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 33•2 Fecha 1. Cathy colecta la siguiente información sobre sus perros, Stella y Oliver. Stella Tiempo para Bañarse 36 minutos Oliver Peso 32 kg Tiempo para Bañarse 25 minutos Peso 7 kg Utiliza la información de las tablas para responder las preguntas de abajo. a. Estima el peso total de Stella y Oliver. b. ¿Cuál es el peso total de Stella y Oliver? c. Estima el tiempo total que gasta Cathy bañando a sus perros. d. ¿Cuál es el tiempo total real que gasta Cathy bañando a sus perros? e. Explica como la estimación te ayuda a verificar la razonabilidad de tus respuestas. Lesson 17: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate sums by rounding and apply to solve measurement word problems. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.D.38 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 17 Homework 33•2 2. Dena lee por 361 minutos durante la Semana 1 del evento de lectura “Read-A-Thon” de 2 semanas de su escuela. Ella lee por 212 minutos durante la Semana 2 del “Read-A-Thon”. a. Estima la cantidad total de tiempo que Dena lee durante el “Read-A-Thon” por redondeo. b. Estima la cantidad total de tiempo que Dena lee durante el “Read-A-Thon" por redondeo en una manera diferente. c. Calcula el número real de minutos que Dena lee durante el “Read-A-Thon”. ¿Cuál de los métodos de redondeo fue más preciso? ¿Por qué? Lesson 17: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate sums by rounding and apply to solve measurement word problems. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.D.39 Lesson 18 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 33•2 Fecha 1. Soluciona los siguientes problemas de resta. 360 mL – 24 mL c. 360 mL – 224 mL d. 518 cm – 21 cm e. 629 cm – 268 cm f. 938 cm – 440 cm g. 307 g – 130 g h. 307 g – 234 g i. 807 g – 732 g a. j. 60 mL – 24 mL 2 km 770 m – 1km 455 m Lesson 18: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org b. k. 3 kg 924 g – 1kg 893 g Decompose once to subtract measurements including three-digit minuends with zeros in the tens or ones place. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.9 Lesson 18 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM 33•2 2. El peso total de 3 libros se muestra a la derecha. Sí 2 libros pesan 233 gramos, ¿cuánto pesa el tercero? Utiliza un diagrama de cinta para modelar el problema. 405g 3. La tabla a la derecha muestra las duraciones de tres películas. a. La película Champions es 22 minutos más corta que The Lost Ship. ¿Cuánto tiempo dura Champions? The Lost Ship 117 minutos Magical Forests 145 minutos Champions ? minutos b. ¿Cuánto más largo es Magical Forests que Champions? 4. El largo total de una cuerda es de 208 cm. Scott, la corta en 3 pedazos. El primer pedazo es de 80 cm de largo. El segundo es de 94 cm de largo. ¿Cuál es el largo del tercer pedazo de cuerda? Lesson 18: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Decompose once to subtract measurements including three-digit minuends with zeros in the tens or ones place. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.10 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 18 Homework 33•2 Fecha 1. Soluciona los siguientes problemas de resta. a. 70 L − 46 L b. 370 L – 46 L c. 370 L – 146 L d. 607 cm − 32 cm e. 592 cm − 258 cm f. 918 cm − 553 cm g. 763 g − 82 g h. 803 g − 542 g i. 572 km − 266 km j. 837 km − 645 km Lesson 18: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Decompose once to subtract measurements including three-digit minuends with zeros in the tens or ones place. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.12 Lesson 18 Homework NYS COMMON CORE MATHEMATICS CURRICULUM 33•2 2. Una revista pesa 280 gramos menos que un periódico. El peso del periódico se muestra abajo. ¿Cuánto pesa la revista? Utiliza un diagrama de cinta para modelar tu pensamiento. 454 g 3. La tabla a la derecha muestra cuanto tiempo duran 3 partidos. a. El partido de baloncesto de Francesca es de 22 minutos menos que el partido de béisbol de Lucas. ¿Cuánto tiempo dura el partido de baloncesto de Francesca? Partido de Béisbol de Lucas 180 minutos Partido de Fútbol de Joey 139 minutos Partido de Baloncesto de Francesca minutos b. ¿Cuánto tiempo más dura el partido de baloncesto de Francesca que el partido de fútbol de Joey? Lesson 18: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Decompose once to subtract measurements including three-digit minuends with zeros in the tens or ones place. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.13 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 19 Problem Set 33•2 Fecha 1. Soluciona los siguientes problemas de resta. b. 340 cm – 260 cm a. 340 cm – 60 cm c. 513 g – 148 g d. 641 g – 387 g f. 700 mL – 452 mL e. 700 mL – 52 mL g. 6 km 802 m – 2 km 569 m Lesson 19: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org h. 5 L 920 mL – 3 L 869 mL Decompose twice to subtract measurements including three-digit minuends with zeros in the tens and ones places. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.20 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 19 Problem Set 33•2 2. David está manejando desde Los Angeles a San Francisco. La distancia total es de 617 kilómetros. Aún le quedan 468 kilómetros por manejar. ¿Cuántos kilómetros ha manejado hasta ahora? 3. El piano pesa 289 kilogramos más que la butaca del piano. ¿Cuánto pesa la butaca? Piano 297 kg Butaca ? kg 4. El tanque A contiene 165 litros menos de agua que el Tanque B. El Tanque B contiene 400 litros de agua. ¿Cuánta agua contiene el Tanque A? Lesson 19: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Decompose twice to subtract measurements including three-digit minuends with zeros in the tens and ones places. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.21 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 19 Homework 3•2 3 Fecha 1. Soluciona los siguientes problemas de resta. a. 280 g − 90 g b. 450 g − 284 g c. 423 cm − 136 cm d. 567 cm − 246 cm e. 900 g − 58 g f. 900 g − 358 g g. 4 L 710 mL − 2 L 690 mL h. 8 L 830 mL − 4 L 378 mL Lesson 19: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Decompose twice to subtract measurements including three-digit minuends with zeros in the tens and ones places. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.23 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 19 Homework 3•2 3 2. El peso total de una jirafa y su becerro es de 904 Kilogramos. ¿Cuánto pesa su becerro? Utiliza un diagrama de cinta para modelar tu pensamiento. Jirafa 829 kg Becerro ? Kg 3. El Canal Erie mide 584 kilómetros desde Albany a Buffalo. Salvador viaja por el canal desde Albany. Él debe viajar 396 kilómetros más antes de llegar a Buffalo. ¿Cuántos kilómetros ha viajado hasta ahora? 4. El Sr. Nguyen llena dos piscinas inflables. La piscina para niños contiene 185 litros de agua. La piscina más grande contiene 600 litros de agua. ¿Cuánta más agua contiene la piscina más grande que la piscina para niños? Lesson 19: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Decompose twice to subtract measurements including three-digit minuends with zeros in the tens and ones places. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.24 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 20 Problem Set 33•2 Fecha 1. a. Encuentra la diferencia real sea en una hoja o usando cálculo mental. Redondea cada parte y total a la centena más cercana y encuentra las restas estimadas. A B 448 − 153 = − = 747 − 261 = − = 451 − 153 = − = 756 − 261 = − = 448 − 149 = − = 747 − 249 = − = 451 − 149 = − = 756 − 248 = − = Encierra en un círculo las diferencias estimadas que sea la más cercana a las diferencias reales. Encierra en un círculo las diferencias estimadas que sea la más cercana a las diferencias reales. b. Mira las diferencias que te dieron los estimados más precisos. Explica abajo que tienen las mismas en común. Puedes utilizar una recta numérica para apoyar tu explicación. Lesson 20: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate differences by rounding and apply to solve measurement word problems. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.33 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 20 Problem Set 33•2 2. Camden utiliza un total de 372 litros de gasolina en dos meses. Él utiliza 184 litros de gasolina en el primer mes. ¿Cuántos litros de gasolina utiliza en el segundo mes? a. Estima la cantidad de gasolina que Camden utiliza en el segundo mes redondeando de la mejor manera que creas. b. ¿Cuántos litros de gasolina realmente utiliza Camden en el segundo mes? Muestra el problema con un diagrama de cinta. 3. El peso de una pera, una manzana, y un durazno se muestra a la derecha. La pera y la manzana juntas pesan 372 gramos. ¿Cuánto pesa el durazno? a. Estima el peso del durazno redondeando cada número de la mejor manera que creas. Explica tu opción. 500 g b. ¿Cuál es el peso actual del durazno? Muestra el problema con un diagrama de cinta. Lesson 20: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate differences by rounding and apply to solve measurement word problems. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.34 NYS COMMON CORE MATHEMATICS CURRICULUM Nombre Lesson 20 Homework 33•2 Fecha Estima, y luego soluciona cada problema. 1. Melissa y su mama van de viaje. Manejan 87 kilómetros antes del almuerzo y 59 kilómetros después del almuerzo. a. Estima cuántos kilómetros más ellas manejan antes del almuerzo que después redondeando a los 10 kilómetros más cercanos. b. Con precisión ¿cuánto más manejan ellas antes del almuerzo que después del almuerzo? c. Compara tu estimación de la parte (a) con tu respuesta de la parte (b). ¿Es razonable tu respuesta? Escribe una oración para explicar tu razonamiento. 2. Amy mide la cinta. Ella mide un total de 393 centímetros de la cinta y la corta en 2 piezas. La primera pieza es de 184 centímetros de largo. ¿Cuál es el largo de la segunda pieza de cinta? a. Estima la longitud de la segunda pieza de cinta redondeando en dos maneras diferentes. b. Con precisión ¿cuál es el largo de la segunda pieza de cinta? Explica porque una de la estimación era más cercana. Lesson 20: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate differences by rounding and apply to solve measurement word problems. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.36 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 20 Homework 33•2 3. El peso de la pierna de pollo, un bistec, y un jamón se muestra a la derecha. El pollo y el bistec juntos pesan 341 gramos. ¿Cuánto pesa el jamón? a. Estima el peso del jamón por redondeo. 989 gramos b. ¿Cuánto es el peso real del jamón? 4. Kate usa 506 litros de agua cada semana para regar las plantas. Usa 252 litros para regar las plantas en el invernadero. ¿Cuánta agua usa para regar las otras plantas? a. Estima la cantidad de agua que Kate usa para regar las otras plantas por redondeo. b. Estima la cantidad de agua que Kate usa para regar las otras plantas por redondeo de una manera diferente. c. ¿Cuánta agua usa Kate para regar las otras plantas? ¿Cuál estimación era más cercana? Explica porque. Lesson 20: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate differences by rounding and apply to solve measurement word problems. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.37 Lesson 21 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 33•2 Fecha 1. Pesa las bolsas de frijoles y arroz en la balanza. Luego escribe el peso en las balanzas de abajo. Frijoles Arroz a. Estima, y luego encuentra el peso total de los frijoles y arroz. Estimación: + Real: + ≈ + = = b. Estima, y luego encuentra la diferencia entre el peso de los frijoles y arroz. Estimación: - Real: - ≈ - = = c. ¿Son razonables tus respuestas? Explica porque. Lesson 21: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate sums and differences of measurements by rounding, and then solve mixed word problems. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.42 Lesson 21 Problem Set NYS COMMON CORE MATHEMATICS CURRICULUM 2. Mide las longitudes de 3 piezas de hilo. Hilo A a. Estima, y luego encuentra la longitud total del Hilo A y el Hilo C. Hilo B Hilo C 33•2 cm ≈ cm cm ≈ cm cm ≈ cm b. Estima, y luego resta la longitud del Hilo B de la longitud total del Hilo A y el Hilo C. Muestra el problema con un diagrama de cinta. 3. Marca la capacidad de 3 recipientes en las siguientes rectas numéricas. Luego redondea a los 10 mililitros más cercanos. Recipiente D Recipiente E Lesson 21: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Recipiente F Estimate sums and differences of measurements by rounding, and then solve mixed word problems. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.43 NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 21 Problem Set 33•2 a. Estima, y luego encuentra la cantidad total de líquido en los 3 recipientes. b. Estima, y luego encuentra la diferencia entre la cantidad de agua en el Recipiente D y el Recipiente E. Simula el problema con un diagrama de cinta. 4. Shane ve una película en el teatro que dura 115 minutos, incluyendo los avances. La tabla a la derecha muestra la duración en minutos de cada avance. a. Encuentra el número total de minutos para los 5 avances. Duración en minutos Avance 1 5 minutos Avance 2 4 minutos Avance 3 3 minutos Avance 4 5 minutos Avance 5 4 minutos Total b. Estima para encontrar la duración de la película sin avances. Luego encuentra la duración real de la película calculando la diferencia entre 115 minutos y el total de minutos de los avances. c. ¿Es razonable tu respuesta? Explica porque. Lesson 21: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate sums and differences of measurements by rounding, and then solve mixed word problems. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.44 Lesson 21 Homework NYS COMMON CORE MATHEMATICS CURRICULUM Nombre 33•2 Fecha 1. Hay 153 mililitros de jugo en 1 cartón. Un paquete de 3 cajas de jugo contiene un total de 459 mililitros. a. Estima, y luego encuentra la cantidad total de jugo en 1 cartón y un paquete de 3 cajas de jugo. 153 mL + 459 mL ≈ + = 153 mL + 459 mL = b. Estima, y luego encuentra la diferencia entre la cantidad de 1 cartón y un paquete de 3 cajas de jugo. 459 mL − 153 mL ≈ + = 459 mL − 153 mL = c. ¿Son razonables tus respuestas? ¿Por qué? 2. El Sr. Williams posee varias estaciones de servicio. Él vende 367 litros de gasolina por la mañana, 300 litros de gasolina por la tarde, y 219 litros de gasolina por la noche. a. Estima, y luego encuentra la cantidad total de gasolina que él vende en un día. b. Estima, y luego encuentra la diferencia entre la cantidad de gasolina que el Sr. Williams vende en la mañana y la cantidad que él vende en la noche. Lesson 21: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate sums and differences of measurements by rounding, and then solve mixed word problems. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.46 Lesson 21 Homework NYS COMMON CORE MATHEMATICS CURRICULUM 3. El Equipo Azul corre un relevo. La tabla muestra el tiempo en minutos que cada miembro del equipo pasó corriendo. Equipo Azul a. ¿Cuántos minutos le toma al Equipo Azul correr el relevo? 33•2 Tiempo en Minutos Jen 5 minutos Kristin 7 minutos Lester 6 minutos Evy 8 minutos Total b. Le toma al Equipo Rojo 37 minutos correr el relevo. Estima, y luego encuentra la diferencia de tiempo entre los 2 equipos. 4. Las longitudes de 3 pancartas se muestran a la derecha. a. Estima, y luego encuentra la longitud total de la Pancarta A y la Pancarta C. b. Pancarta A 437 cm Pancarta B 457 cm Pancarta C 332 cm Estima, y luego encuentra la diferencia en longitud entre la Pancarta B y la longitud total de la Pancarta A y la Pancarta C. Muestra el problema con un diagrama de cinta. Lesson 21: Date: © 2013 Common Core, Inc. Some rights reserved. commoncore.org Estimate sums and differences of measurements by rounding, and then solve mixed word problems. 7/5/13 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. 2.E.47