Tema 3.2 Circuitos combinacionales
Anuncio

Tema 3. 2
Sistemas Combinacionales
Índice
Circuitos combinacionales:
concepto, análisis y síntesis.
Métodos de simplificación de
funciones lógicas.
Estructuras combinacionales
básicas
Multiplexores
Demultiplexores
Decodificadores
Codificadores
Comparadores
Departamento de Automática
Universidad de Alcalá
Bibliografía
• Fundamentos de sistemas
digitales.
Thomas Floyd.
Prentice-Hall.
• Fundamentos de diseño lógico
y computadoras.
M. Morris Mano.
Prentice-Hall
Fundamentos de Tecnología de Computadores
Circuitos combinacionales (I)
Concepto: son aquellos circuitos cuyas salidas, en un determinado instante,
son función exclusivamente del valor de las entradas en ese instante.
Funciones
Análisis
Síntesis
Circuito
Lógico
Combinacional
Tablas de verdad
Análisis: Obtención de la función de salida de un circuito, para cada una de
las posibles combinaciones de las “n” variables de entrada.
Síntesis: Obtención del circuito que realiza la función especifícada.
2
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Circuitos combinacionales (II)
Los circuitos combinacionales pueden ser:
Sistemas unifuncionales: tienen una sola función de salida
Sistemas multifuncionales: tienen varias funciones de salida
Una función puede ser:
Completa. Su valor está determinado para todas las posibles
combinaciones de las variables de entrada.
Incompleta. Existen algunas combinaciones de entrada para las cuales el
valor de la función es indeterminado.
Causas:
Existencia de combinaciones de las variables que nunca se presentan.
Existencia de combinaciones de las variables para las que el valor que
tome la función sea indiferente.
3
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Síntesis de circuitos
combinacionales
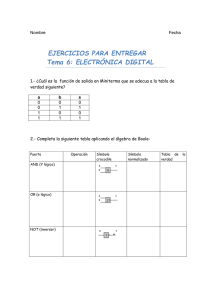
Proceso a seguir para obtener un circuito combinacional óptimo:
Establecer la tabla de verdad, desde el enunciado del problema.
Obtener la función canónica expresada en minterms o en
maxterms, a partir de la tabla de verdad.
Simplificar la función canónica, bien en forma algebraica
(aplicando teoremas y postulados del Álgebra de Boole), bien
mediante la aplicación de métodos gráficos sencillos (Karnaugh) o
con el método tabular numérico de Quine-McCluskey.
Realizar la función simplificada, mediante las oportunas puertas
lógicas.
4
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Métodos de simplificación de
funciones lógicas (I)
Método algebraico
Es el método básico de simplificación de funciones y consiste en aplicar
directamente la propiedad distributiva a los términos de la función,
eliminando variables. Por ejemplo:
f1(d,c,b,a) = d·c·b·a + d·c·b·a = d·c·b·(a+a) = d·c·b·1 = d·c·b
f2 (d,c,b,a) = (d+c+b+a)·(d+c+b+a) = (d+c+b·b+a) = (d+c+a)
Sin embargo, pocas veces viene expresada la función de forma que sea
fácilmente aplicable este método.
5
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Métodos de simplificación de
funciones lógicas (II)
Método de Karnaugh
Método tabular gráfico que se basa en los llamados “mapas de
Karnaugh”, consistentes en una tabla de cuadros, cada uno de los
cuales representa un término canónico.
Estos cuadros están distribuidos de tal modo que dos cualesquiera de
ellos, contiguos físicamente, corresponden a términos canónicos
adyacentes.
Términos canónicos adyacentes: son aquellos para los que sus
respectivas configuraciones binarias difieren entre sí en un único bit.
Se pueden definir también como aquellos términos a los que se les
puede aplicar la propiedad distributiva para simplificar una variable.
6
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Métodos de simplificación de
funciones lógicas (III)
Mapa de Karnaugh para funciones de dos variables
a
b
0
0
1
ba
1
0
1
2
3
0
Tres variables
ba
dc
ba
c
00 01 11 10
0
1
7
00 01 11 10
3
1
2
Cuatro variables
00 01 11 10
00
0
1
3
2
0
1
3
2
01
4
5
7
6
4
5
7
6
11
12
13
15
14
10
8
9
11
10
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Métodos de simplificación de
funciones lógicas (IV)
Procedimiento de simplificación mediante los mapas de Karnaugh
1.- Dibujar el mapa adecuado para la función a simplificar (2, 3 ó 4
variables).
2.- Marcar los cuadros correspondientes a los minterms o maxterms (“1”).
3.- Agrupar, mediante una curva cerrada, el máximo número posible de
elementos adyacentes (potencia de 2
2, 4, 8, 16). A continuación lo
mismo con los que queden y asi, sucesivamente, hasta que no reste
ningún elemento marcado (con adyacente también marcado) sin agrupar.
4.- Escribir la función mediante los términos simplificados obtenidos.
Criterio: en cada grupo desaparece la variable o variables cuyo valor es
“0” en la mitad de los cuadros del grupo, y “1” en la otra mitad. Las
variables que permanecen son tomadas como “no negadas” si su valor
es 1 en todo el grupo de cuadros, y como “negadas” si su valor es 0.
Si algún bit no tiene ningúno adyacente seguirá como término canónico
8
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Estructuras Combinacionales básicas (I)
Multiplexores
Un multiplexor es un circuito que tiene 2n entradas de información
(canales), una sola salida y un mecanismo de selección que determina
cuál de las entradas es la que se transfiere su información a la única
salida. Se comporta como un conmutador de entrada múltiple y salida
única, pero cuyo control no es mecánico, sino electrónico.
Selección
de datos
E6
E5
E4
E3
E2
E1
E0
9
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
{
C1
C0
E3
S
Entrada de
datos
E2
E1
Multiplexor
4a 1
Multiplexor
E7
S
Salida de
datos
E0
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Estructuras Combinacionales básicas (II)
Demultiplexores
Realizan la función inversa de un multiplexor, es decir, se comportan como
conmutadores de entrada única y salida múltiple, existiendo un mecanismo
de control que selecciona la salida hacia la que se envía la información de
entrada.
En general un demultiplexor tiene una única entrada de información, 2n
salidas y “n” entradas de control en las que se introduce el número binario
correspondiente a la salida seleccionada.
E
C0
10
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
Demultiplexor
1a4
C1
E
S3
S2
S1
S0
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Estructuras Combinacionales básicas (III)
Multiplexores /Demultiplexores
Aplicaciones básicas
Multiplexor
Esta entrada
controla la secuencia
de conmutación
11
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
Demultiplexor
Esta entrada
controla la secuencia
de conmutación
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Estructuras Combinacionales básicas (IV)
Decodificadores (1)
Son circuitos digitales que tienen como entrada (n bits) la información
codificada en binario, y tantas salidas como posibles configuraciones
binarias distintas de entrada (2 n), activándose en cada momento una sola
de ellas, la correspondiente a la combinación binaria aplicada a la entrada.
E1
E0
Dec odificador
2a 4
Decodificador 2 a 4
S3
S2
S1
S0
I
0
0
0
0
1
E1
0
0
1
1
X
E0
0
1
0
1
X
S3 S2 S1 S0
0 0 0 1
0 0 1 0
0 1 0 0
1 0 0 0
0 0 0 0
I
12
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Estructuras Combinacionales básicas (V)
Decodificadores (2)
Decodificador 3 a 8
E2
E1
E0
Dec odificador
3a 8
S7
S6
S5
S4
S3
S2
S1
S0
I
0
0
0
0
0
0
0
0
1
E2
0
0
0
0
1
1
1
1
X
E1
0
0
1
1
0
0
1
1
X
E0
0
1
0
1
0
1
0
1
X
S7 S6 S5 S4 S3 S2 S1 S0
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 1
1 1 1 1 1 0 1 1
1 1 1 1 0 1 1 1
1 1 1 0 1 1 1 1
1 1 0 1 1 1 1 1
1 0 1 1 1 1 1 1
0 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
I
13
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Estructuras Combinacionales básicas (VI)
Codificadores (1)
Realizan la función inversa de los decodificadores, es decir, poseen en
general N entradas y “n” salidas de código en las que aparece codificado
en binario el valor de la entrada que ha sido activada (N≤2 n).
Codificadores sin prioridad.
14
7
8
9
4
5
6
1
2
3
0
.
+/-
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
9
8
7
6
5
4
3
2
1
0
Codificador
Codificadores con prioridad.
Salida
Binaria
Codificada
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Estructuras Combinacionales básicas (VII)
Codificadores (2)
Codificador 8 a 3 con prioridad
I
E6
E5
E4
E3
Codific ador
8 a 3 con
prioridad
E7
S2
S1
S0
E2
E1
E0
I E7 E6
1 X X
0 1 1
0 X X
0 X X
0 X X
0 X X
0 X X
0 X X
0 X 0
0 0 1
E5
X
1
X
X
X
X
X
0
1
1
E4
X
1
X
X
X
X
0
1
1
1
E3
X
1
X
X
X
0
1
1
1
1
E2
X
1
X
X
0
1
1
1
1
1
E1
X
1
X
0
1
1
1
1
1
1
E0
X
1
0
1
1
1
1
1
1
1
S2 S1 S0
0 0 0
0 0 0
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
P1 P0
1 1
1 0
0 1
0 1
0 1
0 1
0 1
0 1
0 1
0 1
P1 P0
15
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Estructuras Combinacionales básicas (VIII)
Comparadores
Un comparador de “n” bits es un circuito combinacional que tiene por
entradas dos números binarios de “n” bits cada uno (A,B), determinando a
su salida si uno es mayor, menor o igual que el otro. Normalmente dispone
de tres salidas: A>B, A=B y A<B
A3
7485
A2
A1
Ay B
A0
0
C>
1
0
C=
C<
A> B
A= B
A< B
B3
C> C= C< A>B A=B A<B
A >B X
A <B X
A=B 0
A=B 0
A=B 1
X
X
0
1
0
X
X
1
0
0
1
0
0
0
1
0
0
0
1
0
0
1
1
0
0
B2
B1
B0
Comparador
de 4 bits
16
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Circuitos sumadores binarios (I)
Semisumador
Suma de dos únicos bits. Proporciona como salidas la suma y el acarreo.
Entradas
Sumando
a
0
0
1
1
Sumando
b
0
1
0
1
Salidas
Suma
S
0
1
1
0
Acarreo
Csalida
0
0
0
1
S= a
a
b
17
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
b
Csalida
= a·b
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Circuitos sumadores binarios (II)
Sumador completo
Suma de tres bits: 2 bits i-ésimos más el acarrreo
Entradas
Sumando
a
0
0
0
0
1
1
1
1
a
b
Sumando
b
0
0
1
1
0
0
1
1
a
Acarreo
Centrada
0
1
0
1
0
1
0
1
Suma
S
0
1
1
0
1
0
0
1
Acarreo
Csalida
0
0
0
1
0
1
1
1
b
C entrada
18
Salidas
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
S= (a
b)
C entrada
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Circuitos sumadores binarios (III)
Sumador completo
Circuito en función de semisumadores
a
b
a
b
C entrada
S= (a
(a
b)
C entrada
b)·C entrada
C
= a·b + (a
salida
b)·C
entrada
a·b
19
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Circuitos sumadores binarios (IV)
El acarreo en los circuitos sumadores
• Sumador paralelo con acarreo serie
Bn-1 An-1
Bn-2 An-2
B1 A1
B0 A 0 C -1
Sumador
completo
Sumador
completo
Sumador
completo
Sumador
completo
Cn-2
Cn-1
Sn-1
C1
Sn-2
C0
S1
S0
•Sumador paralelo con acarreo paralelo (acarreo anticipado)
C i = A i B i + (A i ⊕ B i) C i-1= G i + P i C i-1
• Generación de acarreo de la propia etapa G i = A i B i
• Propagación del acarreo de la etapa anterior P i = A i ⊕ B i
• Sumador en paralelo con acarreo mixto
20
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores
Circuitos sumadores/restadores
Operaciones con signo (Circuito Sumador/Restador)
• En complemento a uno
• En complemento a dos
Operando a
Operando b
Circuito
M
complementador
Suma/resta
a
Cn-1
a
n-1 n-2
... a
1
a
b
0
b
n-1 n-2
... b
1
b
Sumador completo de n bits
S
S
n-1 n-2
... S
1
0
C
-1
S
0
Resultado
21
Área de Arquitectura y Tecnología de Computadores
Departamento de Automática
Universidad de Alcalá
T3 Circuitos Combinacionales
Fundamentos de Tecnología de Computadores