xxviii reunión de estudios regionales
Anuncio

XXVIII REUNIÓN DE ESTUDIOS REGIONALES ESTIMACIÓN DE LA ELECCIÓN CONJUNTA DE TENENCIA Y DEMANDA DE VIVIENDA EN LA COMUNIDAD AUTÓNOMA DEL PAÍS VASCO Mijangos del Campo, Juan José E-mail: eipmidej@lg.ehu.es Departamento de Economía Industrial Escuela Universitaria de Estudios Empresariales de Bilbao Universidad del País Vasco (UPV/EHU) Palabras clave: Vivienda, Tenencia, Demanda, Elección Conjunta, Incentivos Fiscales Resumen En este trabajo se aplica el modelo de Lee y Trost (1978) para estimar la elección conjunta de tenencia y demanda de vivienda en la Comunidad Autónoma del País Vasco. El proceso de estimación se realiza en dos etapas; en la primera se estima la probabilidad de decantarse por la opción de la propiedad frente al alquiler como régimen de tenencia utilizando el modelo probit y, en la segunda, se estima la cantidad demanda de servicio vivienda como una elección realizada de forma conjunta con la elección de tenencia. En concreto, se confirma la simultaneidad entre la elección del régimen de tenencia en propiedad y la cantidad de servicio vivienda demandada; es decir, cuando una familia se decanta por la opción de comprar su vivienda, está decidiendo también qué cantidad desea adquirir. En el caso de estimar la función de demanda de servicio vivienda sin considerar la simultaneidad con la elección de tenencia, la estimación por mínimos cuadrados ordinarios daría lugar a estimadores sesgados. ESTIMACIÓN DE LA ELECCIÓN CONJUNTA DE TENENCIA Y DEMANDA DE VIVIENDA EN LA COMUNIDAD AUTÓNOMA DEL PAÍS VASCO 1.- INTRODUCCIÓN El punto de partida en el análisis estático de la demanda de vivienda fue la consideración de modelos que ignoraron las características específicas de ésta [Muth (1960), Olsen (1969), Fallis (1985)], partiendo de la hipótesis de que el objeto de transacción era un bien homogéneo (el servicio-vivienda) que no tiene en cuenta las características de la vivienda, su localización o el régimen de tenencia. Se trataba de modelos uniperiódicos en los que el individuo tenía un determinado volumen de renta que gastaba enteramente en el periodo corriente, consumiendo servicio-vivienda y otros bienes, de forma que la cantidad demandada se definía en función de la renta del individuo, el precio del servicio-vivienda y los precios de los otros bienes. La compra-venta de este producto homogéneo inobservable llamado serviciovivienda se puede realizar considerando dicho servicio como un promedio ponderado de espacio, calefacción, mantenimiento, cercanía al trabajo y otros usos suministrados por el activo de capital vivienda [De Leew y Ekanem (1971)]. De ahí que los servicios de vivienda se suelan medir utilizando variables proxy como el coste de uso de la vivienda y el valor actualizado neto de la vivienda principalmente1. En este trabajo se estima la demanda de servicio vivienda como un bien homogéneo en la Comunidad Autónoma del País Vasco. Para ello utilizaremos un modelo de elección conjunta de tenencia y demanda de vivienda en dos etapas [Lee y Trost (1978)]: en la primera etapa se estima la probabilidad de optar por la propiedad o el alquiler como régimen de tenencia y, en la segunda, se estima la cantidad demandada de servicio vivienda en propiedad y en alquiler realizada de forma conjunta con la elección de tenencia. De hecho comprobaremos cómo, cuando una familia se decanta por la tenencia en propiedad, está decidiendo al mismo tiempo cuánto quiere gastar en vivienda o, lo 1 Los trabajos en este sentido son ciertamente numerosos: Jorgenson (1967) -citado en McFadyen y Hobart (1978)-, Laidler (1969), Aaron (1972), McFadyen y Hobart (1978), Hendershott y Huh (1981), Hendershott y Shilling (1982), Dougherty y Van Order (1982), Poterba (1984 y 1992), Thion (1983), Rosen, Rosen y Holtz-Eakin (1984), Smith, Rosen y Fallis (1988), Mills (1990), González-Páramo y Onrubia (1992), López García (1996) (1997) y (1999), García-Montalvo y Mas (2000)]. 1 que es lo mismo, que existe simultaneidad entre las decisiones de elección de tenencia y demanda de vivienda en propiedad. En la siguiente sección se resumen los modelos teóricos y las variables utilizadas en este tipo de estudios. En el tercer epígrafe se desarrolla el modelo de Lee y Trost (1978), base del posterior análisis empírico. En el epígrafe cuarto precisamos el ámbito del estudio y las variables utilizadas. El quinto epígrafe contiene la estimación del modelo en dos etapas: la elección del régimen de tenencia mediante el modelo probit y, posteriormente, la estimación de la demanda de servicio vivienda en propiedad y en alquiler como una elección realizada de forma conjunta con la elección de tenencia. Finalmente, el trabajo concluye con un resumen de los principales resultados obtenidos. 2.- MODELOS TEÓRICOS Y VARIABLES En la mayoría de los casos, los investigadores han tratado de estimar la función de demanda de servicio-vivienda utilizando múltiples observaciones del comportamiento de los demandantes haciendo uso de modelos de regresión logarítmicolineal para obtener los mejores ajustes: Log H = b0 + b1 log Y + b2 log p1 + b3 log p2 + ∑α i +ω i Siendo H = cantidad de servicio-vivienda p1 = precio de una unidad de servicio-vivienda p2 = índice de precios de otros bienes Y = renta (actual o permanente) αi = factores demográficos b1 = elasticidad-renta de la demanda de servicio-vivienda b2 = elasticidad-precio de la demanda de servicio-vivienda b3 = elasticidad cruzada de la demanda de servicio-vivienda respecto del índice de precios de otros bienes. Los trabajos empíricos han planteado diversos problemas referidos a la definición y observación de las variables implicadas, empezando por la variable endógena. Dado que el servicio-vivienda no se puede medir por unidades, se optó por utilizar la variable gasto en servicio de vivienda igual al producto de la cantidad de servicio-vivienda consumida por su coste, hablándose genéricamente de valor de vivienda. 2 La opción más utilizada ha sido considerar el coste de uso de la vivienda. Así Maisel, Burham y Austin (1971) definen el gasto de vivienda como el pago de principal e intereses, mantenimiento y reparación, calefacción y otros gastos como agua, gas y electricidad. Polinsky y Ellwood (1979) definen el gasto en vivienda como el producto de la cantidad de servicio-vivienda consumida por el índice de precios de tales servicios, utilizando en la práctica los precios de venta. Friedman y Weinberg (1981) incluyen no sólo los servicios de la estructura, sino también la vecindad, accesibilidad y otros servicios de la localidad; también utilizan, en la práctica, el alquiler contratado por cada inquilino, dado que su análisis era para viviendas en alquiler. Rosen (1979) considera el valor de la vivienda, sin especificar más, dado que se trata de una magnitud proporcional al flujo de servicios que genera. Gillingham y Hagemann (1983) por su parte, consideran como variable que refleja el servicio de vivienda el alquiler de mercado estimado por el propietario. King (1980) elabora unos índices de consumo a partir de los valores tasados de las viviendas. Harmon (1988), Horioka (1988), Rapaport (1997) y Carliner (1973) utilizan el valor de la vivienda (en unos casos será valor de mercado, y en otros casos estimado) deflactado por índices de precios (que se elaboran en cada caso siguiendo distintos criterios). Si nos referimos ya a los trabajos existentes para el mercado español, se tiene que Jaén y Molina (1994) eligen el gasto anual en vivienda, valor proporcional al valor de la vivienda. Posteriormente, Colom y Molés (1998) también consideran como variable endógena el gasto anual en vivienda. Por otro lado, Blanco y Martínez Verdú (2000) consideran como servicio de vivienda los gastos en vivienda (no incluyen gastos en suministros tales como agua, electricidad,...) divididos entre un índice de precios de vivienda que refleje las diferencias espaciales. La segunda variable que podemos considerar es la renta, concepto quizá más confuso que en el estudio de otros bienes o servicios dadas las características propias de la vivienda (costes de construcción y larga duración del bien, importancia de los gastos en vivienda para las familias en relación a sus posibilidades económicas y el coste de cambiar la configuración de los servicios de vivienda recibidos). La larga duración de la vivienda y los altos costes de transacción implican que la noción relevante de renta sea una renta a largo plazo en oposición a una renta anual. Por eso, la mayoría de los estudios realizados utilizan la renta permanente, aunque en algunos casos se habla de renta actual (renta obtenida en el periodo), renta total, renta transitoria o renta efectiva. Así, Gillingham y Hagemann (1983) utilizan renta permanente antes de impuestos, 3 mientras que Horioka (1988) y Rapaport (1997) consideran como variable la renta permanente, pero estimada a partir de datos de sección cruzada. Para el caso español, se tiene que tanto Jaén y Molina (1994) como Colom y Molés (1998) utilizan renta disponible como una aproximación a la renta permanente. La elección de un concepto de renta u otro puede implicar sesgos en la estimación de las elasticidades aunque, si la varianza de la renta transitoria es pequeña en relación a la de la renta permanente, el sesgo será pequeño. Así, Carliner (1973) utilizó distintos cálculos para la renta permanente y estudió los efectos que dichas variaciones tienen sobre las elasticidades. La tercera variable a considerar sería el precio de la vivienda. En el mercado de la vivienda los precios no son nunca observables directamente. El problema se resuelve habitualmente utilizando índices de precios de vivienda como aproximación al verdadero precio, al igual que se utiliza como precio para los demás bienes el índice de precios al consumo general sin incluir la vivienda. En este sentido, se tiene que Rosen (1979), Gillingham y Hagemann (1983) y Horioka (1988) toman datos sobre precios y a partir de ellos elaboran un índice de precios que dependerá de la zona considerada. Realizan posteriormente las modificaciones necesarias para que quede recogida la implicación que la política fiscal tiene sobre los precios de la vivienda en propiedad. Por otro lado, King (1980) obtiene el precio dividiendo el gasto en vivienda entre un índice de consumo. Rapaport (1997) también realiza consideraciones fiscales sobre el precio de la vivienda en propiedad, pero estima el precio de la vivienda mediante regresiones hedónicas. En lo que se refiere al mercado español, Jaén y Molina (1994) utilizan un índice de precios sobre el que realizan consideraciones fiscales. Por otro lado, Blanco y Martínez Verdú (2000) toman datos del Ministerio de Obras Públicas, Transporte y Medio Ambiente (MOPTMA), separando por un lado entre precios por capital y ciudades de más de 100.000 habitantes y por otro lado resto de la provincia. Los precios de alquiler los estiman regresando el alquiler anual por metro cuadrado de las viviendas alquiladas después de 1984 en función de características de la vivienda y de su localización geográfica. Finalmente, Colom y Molés (1998) utilizan una aproximación hedónica similar a la utilizada por Rapaport (1997). La última clase de variables son las demográficas, considerándose que el sexo del cabeza de familia, su edad y el número de hijos de la familia (tamaño familiar) influyen en la demanda de vivienda. 4 3.- EL MODELO DE ELECCIÓN CONJUNTA DE LEE Y TROST El modelo que vamos a aplicar en este estudio es el propuesto por Lee y Trost (1978) y rediseñado por Olsen (1980). Se pretende especificar un modelo que permita determinar conjuntamente las decisiones de comprar o no una vivienda y de cuánto gastar en ella. En el caso en que exista simultaneidad entre ambas decisiones, si sólo se tiene en cuenta el gasto realizado en vivienda (y no la forma de tenencia), la estimación por mínimos cuadrados ordinarios daría lugar a estimadores sesgados. En caso de que no existiera simultaneidad los estimadores serían insesgados, pero para poder hablar de no simultaneidad habrá que contrastarlo. La especificación del modelo para la familia j adopta la siguiente forma: Qoj = xoj βo + εoj QRj = xRj βR + εRj I*j = zj α − εj donde: Qoj: cantidad de servicios de vivienda consumidos por la familia si compra. QRj: cantidad de servicios de vivienda consumidos por la familia si alquila. I*j: Indicador (no observable) que determina la elección de tenencia de la familia. xoj, xRj, zj: variables independientes. Los consumidores compran o alquilan, de tal modo que Qj = Qoj si y sólo si I*j > 0, es decir, si la utilidad de comprar es mayor que la de alquilar. En caso contrario, Qj = QRj. Existe por lo tanto una relación entre las ecuaciones de demanda y la de elección de tenencia, de tal modo que se considerará la primera ecuación (la de propiedad) condicionada a que I*j>0, es decir, a que zj α > εj, y se observará la otra ecuación (la de alquiler) condicionada a que zj α < εj. Para que los estimadores obtenidos para cada una de las ecuaciones por separado (alquiler y propiedad) fueran insesgados se precisaría que E(εoj) = E(εRj) = 0. Ahora bien, dada la condición que se establece sobre la ecuación de tenencia, lo que habría que comprobar es que: E(εoj | zj α > εj) = 0 E(εRj | zj α < εj) = 0 y esto sucederá únicamente si las variables εoj y εRj son independientes de εj. La elección de tenencia se representa mediante el modelo: I*j = zj α − εj, de este modo Ij = 1 si zj α > εj, o de otro modo, si I*j > 0. Ij = 0 en otro caso. Dado que 5 suponemos en este modelo que εj se distribuye normalmente, se trata de un modelo probit. Lo que hacemos a continuación es plantear el modelo sin presuponer la independencia entre las perturbaciones. Así, se recoge el caso más general y el caso en que haya independencia sería un caso particular. Esto permitirá, además, su contrastación. Supondremos, para ello, que εoj, εRj y εj siguen una distribución normal trivariante [Olsen (1980) relaja el supuesto de normalidad y lo exije sólo para εj, pero llega a los mismos resultados que nosotros] con media cero y matriz de covarianzas no singular común para todas las observaciones: σ o2 Σ = σ oR σ oε σ oε σ Rε 1 σ oR σ 2R σ Rε Nótese que suponemos que la varianza de εj es 1. Conviene, en este punto, recordar algunos resultados sobre distribuciones truncadas [Johnson y Kotz (1972)]. La función de densidad de una distribución N(m, σ2) es de la forma: f(x) = 1 σ 2π e - 1 2σ2 (x - m) 2 -∞<x < ∞ y su función de distribución se obtiene como: F(x) = 1 - 2 (t - m) 2 1 e dt ∫−∞ σ 2π 2σ x si truncamos inferiormente la distribución en el punto c1 (la variable sólo toma ahora valores entre c1 e ∞), la función de densidad de la distribución truncada pasa a ser: 1 f(x) truncada − 2 (x -m) 2 1 e 2σ f(x) = σ 2π = 1 - F(c1 ) P(x > c1 ) para c1 < x < ∞ Si truncamos superiormente en c2 (ahora la variable pasa a tomar valores sólo entre −∞ y c2), la función de densidad de la variable truncada pasará a ser: f(x) truncada = f(x) F(c 2 ) 6 para - ∞ < x < c 2 Finalmente, si acotamos inferior y superiormente en c1 y c2, la función de densidad de la variable truncada será: f (x) F(c 2 ) − F(c1 ) para x ∈ (c1 , c 2 ) Si consideramos el caso más general de truncamiento (doblemente truncada), se tiene que la esperanza matemática para dicha variable será: c2 E (x) = ∫ x f truncada (x) dx = m + c1 f(c1 ) − f (c 2 ) σ F(c 2 ) − F(c1 ) En el caso en que la variable sea N(0, 1) estas expresiones serán más sencillas, como de hecho ocurrirá en nuestro caso. Pasamos a referirnos a la normal tipificada, así tenemos que, si denotamos por ε a la variable N(0, 1), la esperanza matemática de dicha variable truncada en el caso más general (doblemente truncada en c1 y c2) sería: E (ε ) = m + f(c1 ) − f (c 2 ) f(c ) − f (c 2 ) f(c1 ) − f (c 2 ) σ = 0 +1 1 = F(c 2 ) − F(c1 ) F(c 2 ) − F(c1 ) F(c 2 ) − F(c1 ) Si consideramos ahora sólo truncamiento superior o inferior, en dichas expresiones tendríamos que, en el primer caso, c1→−∞ y en el segundo c2→∞, quedando como sigue; si el truncamiento es por la derecha, es decir, x<c2: E (ε) = - f(c 2 ) F(c 2 ) mientras que si el truncamiento es por la izquierda (x>c1): E (ε ) = f(c1 ) 1 − F(c1 ) Ahora, suponemos que tenemos una distribución normal trivariante con media 0 y matriz de covarianzas de la forma: σ12 Σ = σ 21 σ 31 σ12 σ 22 σ 32 σ13 σ 23 1 es decir, suponemos que ε3 tiene varianza 1 (será la que trunquemos). Ahora queremos conocer las propiedades de la distribución de ε1, ε2 condicionado a que la variable ε3 esté truncada. Partimos para ello de la distribución de ε1, ε2 condicionado a que la variable ε3 toma un valor determinado. En este caso, y suponiendo que la regresión de ε1 y ε2 sobre ε3 es lineal [Johnson y Kotz (1972)], se 7 tiene que (ε1, ε2) seguirá una distribución normal bivariante de medias respectivas ρ13⋅ε3⋅σ1, ρ23⋅ε3⋅σ2 , y de matriz de covarianzas 2 (1 − ρ13 ) σ12 2 ρ σ σ 12⋅3 1 2 2 ρ12 ⋅3 σ1 σ 2 2 2 (1 − ρ 23 ) σ 2 Lo que queremos calcular ahora es: − f(c 2 ) E(εi | ε3<c2) = ρi3⋅σi⋅E(ε3 | ε3<c2) = ρi3 σi F(c 2 ) f(c1 ) E(εi | ε3>c1) = ρi3⋅σi⋅E(ε3 | ε3>c1) = ρi3 σi 1 F(c ) 1 si tenemos en cuenta que ρ i3 = σ i3 , σi σ3 − f(c 2 ) E(εi | ε3<c2) = σi3 F(c 2 ) f(c1 ) E(εi | ε3>c1) = σi3 1 - F(c1 ) Si continuamos con nuestro modelo y utilizamos los resultados que acabamos de exponer sobre distribuciones truncadas podemos decir que: E(εoj | Ij = 1) = E(εoj | I*j > 0) = E(εoj | εj < zj α ). por lo tanto, la variable εj está truncada superiormente en el punto zj α , por lo que: E(εoj | Ij = 1) = − σoε f(z jα) F(z jα) donde f(zj α ) y F(zj α ) son respectivamente la función de densidad y de distribución de la N(0, 1) valoradas en el punto de truncamiento zj α . E(εRj | Ij = 0) = E(εRj | I*j < 0) = E(εRj | εj > zj α ) Es decir, se tiene que la distribución de εj está truncada por la izquierda, entonces: E(εRj | Ij = 0) = σRε f(z j α) 1 − F(z j α) Si tenemos en cuenta estas esperanzas matemáticas que ya no son nulas (seguirían siéndolo si las covarianzas entre εRj y εj, σRε, y εoj y εj, σoε, fuesen 0, es decir, si fuesen variables incorreladas), ahora sabemos que: E(Qoj | Ij = 1) = E(Qoj | εj < zj α ) = xoj βo + E(εoj | εj < zj α ) = 8 = xoj βo − σoε f(z j α) F(z j α) E(QRj | Ij = 0) = E(QRj | εj > zj α ) = xRj βR + E(εRj | εj > zj α ) = = xRj βR + σRε f(z j α) 1 − F(z j α) Por lo que pasaremos a especificar las ecuaciones de demanda como: Qoj = xoj βo − σoε QRj = xRj βR + σRε f(z jα) F(z jα) + ηoj f(z j α) 1 − F(z j α) + ηRj donde, ahora, E(ηoj | Ij = 1) = 0 E(ηRj | Ij = 0) = 0 A partir de aquí se puede proceder a la estimación en dos etapas. En la primera se estima el modelo de tenencia: P(Ij = 1) = F(zj α ) + uj, dado que suponemos normalidad para la perturbación, se tratará de un modelo probit. De esta manera obtenemos estimadores consistentes para α, α̂ . En la segunda etapa utilizamos este valor α̂ para estimar f(z j α) de demanda de vivienda en propiedad y 1 − F(z j α) f(z j α) F(z j α) en la función en la función de demanda de vivienda en alquiler. Pasamos así a tener las ecuaciones de demanda: Qoj = xoj βo − σoε f(z jαˆ ) + ηoj F(z jαˆ ) QRj = xRj βR + σRε f(z j αˆ ) + ηRj 1 − F(z j αˆ ) sustituyendo α por su estimación α̂ . A partir de aquí, en la ecuación de demanda en propiedad, se estiman los coeficientes βo y σoε, y en la de alquiler, βR y σRε por mínimos cuadrados ordinarios. Lee y Trost (1978) prueban que tales estimaciones son consistentes. 9 4.- ÁMBITO DE ESTUDIO Y VARIABLES UTILIZADAS El estudio que vamos a realizar se refiere a la Comunidad Autónoma del País Vasco. El motivo es que el mercado de la vivienda está profundamente segmentado, en realidad no hay un único mercado de la vivienda, como se desprende de la observación de las características del mercado de la vivienda en España desglosado por Comunidades Autónomas. De hecho, la desagregación podría ir incluso más allá de la propia Comunidad Autónoma, en concreto, en el presente estudio se plantean seis escenarios geográficos diferentes: las tres capitales vascas (Bilbao, San Sebastián y Vitoria) y el resto de cada provincia excluyendo la capital. Esta diferenciación de mercados de la vivienda la podemos justificar tanto si atendemos a consideraciones económicas que afectan al mercado de la vivienda como si analizamos la estructura dentro del mercado de la vivienda en cada comunidad. San Martín (1999) señala que el mercado inmobiliario ha evolucionado de manera diferente por regiones en función de variables entre las que destacan los factores demográficos, la coyuntura económica de las familias (referidas a empleo y salarios reales) y las condiciones de financiación y fiscalidad por el lado de la demanda, mientras que por el lado de la oferta se podría señalar también como factor importante, además de las condiciones de financiación (igual que para la demanda), la disponibilidad de factores necesarios para la producción y, entre ellos, especialmente, el suelo. La principal fuente de información utilizada ha sido la Encuesta de Presupuestos Familiares 1990/91 elaborada por el Instituto Nacional de Estadística y, en concreto, la información contenida en el capítulo referente a los Datos Generales del Hogar. Las variables utilizadas en el proceso de estimación son las siguientes. PRECIOS Los precios de compra y alquiler de la vivienda, deducidos de los precios que el Departamento de Ordenación del Territorio, Vivienda y Medio Ambiente del Gobierno Vasco ofrece en su publicación Oferta Inmobiliaria han de corregirse para considerar el especial tratamiento fiscal otorgado en nuestro país a la vivienda en propiedad. Para determinar cuál es el precio al que se enfrenta la familia, debe tenerse en cuenta en primer lugar el impuesto que grava la compra de la vivienda, esto es, 6% de IVA más 0.5% de impuesto sobre actos jurídicos documentados para vivienda nueva o 6% de Impuesto sobre Transmisiones Patrimoniales para vivienda de segunda mano, 10 conjunto al que denotaremos sin más t IVA (sea vivienda nueva o de segunda mano), así como los gastos notariales por escrituras de la vivienda, GN, que hacen que el precio pagado por el comprador, p o , no coincida con el dinero percibido por el vendedor, p v , en tanto que la relación entre ambos sería: po = (1 + t IVA + GN ) pv , dado que debemos asignar a cada zona un determinado precio con impuestos indirectos y gastos notariales ya incluidos. La realidad del mercado indica que la suma de los impuestos indirectos más el coste de escritura supone un porcentaje muy cercano al 9% del valor de la vivienda, con lo cual su coste final será un 109% sobre el valor inicial de la misma. Ahora bien, el sistema impositivo español, y en concreto el Impuesto sobre la Renta de las Personas Físicas, permitía la deducción en la base de los intereses del capital invertido en la compra de vivienda, así como la deducción en la cuota por adquisición de vivienda habitual, lo cual implica que, finalmente, el precio efectivo de la vivienda, p e , sea menor. Considerando primero la deducción en la cuota, podemos expresar p e como : pe = (1 − φ ) po , es decir, pe = (1 − φ ) po = (1 + t IVA + GN )(1 − φ ) pv , donde φ es la deducción correspondiente por adquisición de vivienda habitual. En el IRPF se establece que esta deducción en la cuota será de un 15% sobre el importe de vivienda pagado en dicho año, siendo la limitación para dicho importe el 30% de la base imponible de dicho ejercicio. Es evidente que habrá familias para las que el pago de la vivienda se produzca a lo largo de varios años, con lo cual deducirán una cantidad del valor de la vivienda mayor que otras familias que realicen el pago, por ejemplo, en un solo año. Es por ello que expresaremos esa deducción como una proporción, k, del 15%. Esto es, φ = 0.15k , donde k será algún valor comprendido entre 0 y 1. De hecho, para realizar las estimaciones vamos a considerar, a título orientativo, el punto medio, esto es, 0.5, dada la imposibilidad de determinar dicho coeficiente con los datos disponibles para las familias de la muestra, con lo cual consideraremos que la desgravación efectiva es 0.075. La consideración de otros valores cercanos para k no modifica de manera sustancial los resultados finalmente obtenidos en la estimación. Además de la deducción en la cuota, existen otras medidas fiscales que incentivan la compra de la vivienda, que hacen que el precio que el comprador paga (antes de considerar la deducción en la cuota) sea de hecho inferior a p o , y la denotaremos por p o ,i , dado que de hecho va a depender del tipo marginal de la familia en cuestión. 11 Para llegar a establecer la relación existente entre p o y po ,i , vamos a utilizar el método propuesto por Rosen (1979) y posteriormente utilizado, entre otros, por Jaén y Molina (1994) y Rapaport (1997). Según dicho procedimiento, se establece que el precio que debe pagar la familia i-ésima se obtiene como: Po , i = Po (1 − tiδ ) , donde t i es el tipo impositivo marginal de la familia i-ésima y δ es la proporción de cada peseta gastada en servicios de vivienda que es deducible (no gravada). Queda, pues, por determinar cuál es el valor de esta proporción, cuya deducción exponemos a continuación. Si los propietarios tuviesen un tratamiento fiscal similar al de otros inversores deberían computar como ingreso el rendimiento de su vivienda, GI. Si consideramos un propietario que alquila una vivienda del mismo valor, se le permitiría deducir de dicho rendimiento los gastos de depreciación, D, y mantenimiento, M, los impuestos sobre la propiedad, T, y los intereses ajenos necesarios para la obtención de dicha renta, MI. A partir de aquí se deduciría la renta neta, NI, como: NI = GI − M − D − T − MI Esta renta sería un ingreso que seguiría el mismo trato fiscal que si se tratara de cualquier otro tipo de inversión, de tal forma que, si el tipo impositivo marginal del propietario es t i , el pago por dicha renta imputada sería t i × NI (siempre que la inclusión de esta renta no suponga, de hecho, un salto al siguiente tramo impositivo). Sin embargo, el trato fiscal que se da al propietario es diferente. Así, no incluye el rendimiento de la vivienda como ingreso, aunque sí el 2% sobre su valor catastral (VC). Por otro lado, sí se le permite deducir los intereses hipotecarios pagados (MI), así como el pago del impuesto sobre bienes inmuebles (T). Vemos por lo tanto que el propietario va a beneficiarse de un ahorro impositivo que será tanto mayor cuanto mayor sea su tipo impositivo marginal. A continuación determinamos cuál va a ser dicho ahorro impositivo. El propietario pagará en impuestos, según lo que acabamos de ver: t i (0.02 × VC − MI − T ) . Si restamos esta cantidad a la que debería pagar con el otro tratamiento fiscal, t i × NI , se tiene que la diferencia es: t i × NI − t i (0.02 × VC − MI − T ) = t i (GI − M − D − T − MI) − t i (0.02 × VC − MI − T ) = = t i (GI − M − D − 0.02 × VC) 12 Dado que GI − M − D = NI + MI + T , el ahorro impositivo será: t i ( NI + MI + T − 0.02 × VC ) Si llamamos r al tipo de interés hipotecario, y L al préstamo solicitado para la compra de la vivienda, entonces, MI = rL. Por otro lado, si llamamos r* al rendimiento neto del capital, se tiene que NI = r*(V-L), donde V es el valor de la vivienda (precio con IVA (o impuesto equivalente) incluido). Si suponemos que el tipo de interés y el rendimiento del capital son iguales se tiene que: NI+MI = rL+r(V-L) = rV Este supuesto aparece en los artículos a los que hemos hecho referencia anteriormente. Se consigue con ello simplificar el análisis, ya que de este modo el valor de δ no dependerá de la proporción del préstamo sobre el valor de la vivienda. Por otro lado, dado que NI+MI = GI-M-D-T = rV, se tiene que GI = rV+M+D+T Se tendrá por otro lado que la parte del rendimiento no gravada (el ahorro sobre el rendimiento de la vivienda), que era NI+MI-0.02VC+T , es en realidad rV+T0.02VC. Por lo tanto, Entonces, δ = ti NI + MI + T − 0.02 × VC rV + T − 0.02 × VC = ti = ti × δ. GI rV + T + M + D rV + T − 0.02 × VC y el precio final para el propietario sin considerar las rV + T + M + D deducciones en la cuota se establece, como inicialmente habíamos propuesto, como Po ,i = Po (1 − t i δ ) . Por lo tanto, si incluimos las deducciones en la cuota se tiene que Pf ,i = Po (1 − 0.15k − tiδ ) = Pv (1 + t IVA + GN )(1 − 0.15k − tiδ ) . Para poder determinar cuál es el valor de δ , debemos establecer supuestos acerca de algunos de sus componentes. Consideraremos para ello los mismos valores que suelen utilizarse como aproximación en este tipo de estudios. No obstante, cabe comentar aquí que se han realizado los mismos análisis permitiendo variaciones sobre tales supuestos y los resultados obtenidos no difieren significativamente de los que finalmente exponemos. Como tipo de interés hipotecario, r, se tomará el que facilita el Banco de España como media de entidades para 1991, que era 16.04. Respecto de la tasa de depreciación y mantenimiento, utilizaremos el supuesto habitual que evidencia que, entre ambas, suponen en torno a un 3.5% del valor de la vivienda (2.25% por depreciación y 1.25 por mantenimiento) [Rapaport (1997), Jaén y Molina (1994), White y White (1977), Aaron (1972), Laidler (1969)]. López García (1999) utiliza el 4%, mientras que García- 13 Montalvo y Mas (2000) sugieren que el valor de la depreciación supone el 2% del valor de la vivienda, pero ya hemos comentado anteriormente que dicha modificación no alteraría prácticamente nuestros resultados. En cuanto al valor catastral de la vivienda, VC, existen distintas aproximaciones. Así Jaén y Molina (1994) suponen para el año 1981 que dicho valor equivale, aproximadamente, a la mitad del valor de la vivienda. Por otro lado, García-Montalvo y Mas (2000) en un estudio realizado para años posteriores (entre los que se incluye 1991) estiman que es aproximadamente el 24% del valor de la vivienda. Dada la mayor proximidad temporal de nuestro trabajo a este último, ése será el valor que nosotros aproximaremos. Finalmente, en lo que se refiere a la variable que hemos denotado por T, sería el impuesto sobre bienes inmuebles. Sobre este valor también tomamos como referencia el estudio de García-Montalvo y Mas (2000), en el que se considera que, a nivel de toda España, el Impuesto sobre Bienes Inmuebles (IBI) supone una proporción del 0.006 sobre el valor catastral de la vivienda. Señalan que no hay datos para el País Vasco y Navarra sobre este aspecto, y que por ello le aplican dicho valor. Nosotros utilizaremos ese mismo criterio. Dados los supuestos que hemos realizado sobre los parámetros que determinan el valor de δ llegamos a establecer que: δ = rV + T − 0.02 × VC (0.1604 + 0.006 × 0.24 − 0.02 × 0.24)V = = 0.798 rV + T + M + D (0.1604 + 0.006 × 0.24 + 0.035)V por lo que, si además tenemos en cuenta que la suma de impuestos indirectos más gastos notariales supone para 1991 el 9% y que, como ya hemos mencionado anteriormente, al hacer los cálculos vamos a suponer que las familias sólo consiguen deducir en la cuota la mitad del máximo que permitiría la normativa del IRPF, la variable que utilizaremos como precio de vivienda para el individuo i-ésimo es: Po ,i = Po (1 − 0.15k − 0.798 × ti ) = Pv (1 + 0.09)(1 − 0.075 − 0.798 × ti ) Las variables que vamos a utilizar como precio en la estimación van a ser, en realidad, los precios relativos respecto del precio de alquiler de una zona determinada (Bilbao). Es decir, construiremos un índice espacial de precios tomando como base ese precio concreto y, a partir de ahora, cuando hablemos de la variable precio nos referiremos a dicho precio relativo. Llamaremos PALQUI (en la regresión utilizaremos su logaritmo neperiano, LPALQUI) al precio relativo de alquiler de las distintas zonas 14 consideradas y PPROPI (en la regresión utilizaremos su logaritmo neperiano, LPPROPI) al precio relativo de compra de cada zona (nótese que este último será distinto para cada familia considerada). RENTA En lo que se refiere a la variable renta, lo ideal, dado que las decisiones tanto de tenencia como de demanda de vivienda son a más largo plazo, sería disponer de una medida de la renta permanente. Esta renta permanente se suele obtener promediando la renta familiar obtenida en los últimos años [Carliner (1973), Rosen (1979), Friedman y Weinberg (1981), Mayo (1981)]. En nuestro caso, dado que los datos son cross-section no hay posibilidad de utilizar este método. Existe otro método, utilizado en aquellos casos en que se quiere considerar la renta permanente a pesar de que únicamente se dispone de datos referidos a un periodo, que consiste en regresar la variable renta corriente familiar sobre características socioeconómicas de las familias y, posteriormente, utilizar en el análisis la estimación de la renta corriente como renta permanente a partir de los resultados de dicha regresión [Horioka (1988), Rapaport (1997)]. Nosotros hemos utilizado también este método, pero los resultados de la estimación empeoran sustancialmente respecto de los que finalmente hemos considerado. La variable renta utilizada es la obtenida a partir de la Encuesta de Presupuestos Familiares 1990-91 (EPF 90-91) en el apartado Ingresos Ordinarios de la familia. Preferimos los ingresos ordinarios que los ingresos totales, dado que en los totales entrarían ingresos que se han obtenido de forma esporádica en el periodo en curso pero con los que no se cuenta de forma habitual para el resto de periodos. Se han realizado las regresiones utilizando la renta ordinaria disponible, que hemos calculado utilizando las normas correspondientes al impuesto sobre la renta de las personas físicas correspondiente al año 1991. Se han tomado en consideración los tipos impositivos correspondientes para los distintos tramos suponiendo que se realiza una declaración conjunta. Por otro lado, no se han considerado las deducciones en la cuota obtenidas por la propiedad de la vivienda ya que, como señala Rapaport (1997), en ese caso tales deducciones serían endógenas en un modelo en que se está estudiando la demanda de vivienda. Además, si lo que queremos es emplear una renta disponible como aproximación a la renta permanente, no se deberían incluir tales deducciones que son 15 coyunturales; así, el hecho de que una familia decida amortizar un determinado año el doble que al año siguiente, modificará su renta disponible, pero no debiera afectar a la renta permanente. Es por ello que, como ya hemos señalado anteriormente, el efecto de las deducciones en la cuota de la inversión en vivienda habitual la recogemos a través del precio efectivo que la familia debe pagar por la vivienda. En el modelo de elección de tenencia se planteó la posibilidad de tratar la variable renta por tramos, mediante la utilización de variables dummies, pero los resultados empeoraban claramente respecto de los obtenidos en el modelo que finalmente hemos considerado, que es aquél en el que se recoge la variable renta en forma logarítmica (LINGORD) y además dicha variable elevada al cuadrado (LINGORD2). CANTIDAD DEMANDADA En lo que se refiere a la cantidad demandada, existen muchas alternativas en cuanto a cuál debe ser la variable a utilizar. Nosotros seguiremos aquí un criterio similar al utilizado por Rapaport (1997), Carliner (1973), Horioka (1988) y, ya para el caso español, por Blanco y Martínez Verdú (2000). Lo que se hará es utilizar una magnitud que represente el valor de la vivienda considerada dividido entre el precio correspondiente a dicho individuo. En nuestro caso, la magnitud que se considera es el dato que aparece en la EPF acerca de cuánto cree el encuestado que habría que pagar por una vivienda como la que ocupa en ese momento, cuando nos referimos a las viviendas en propiedad, y el dato referente a cuál es el alquiler que se paga por dicha vivienda, para vivienda en alquiler. En cada caso, dividimos entre el precio que corresponda y así obtenemos una unidad de vivienda homogénea (el gasto en vivienda se obtiene como precio por cantidad. Por ello, dado que los datos que nos dan se refieren a gasto, dividimos entre el precio para deducir la cantidad). En muchos estudios se recoge como variable cantidad el gasto efectuado en la vivienda, considerando distintas magnitudes a incluir en cada caso [Polinsky y Ellwood (1979), Gillingham y Hagemann (1983) y, en el caso español, Jaén y Molina (1994) y Colom y Molés (1998)]. Sin embargo, el efecto de una variación en los precios nunca quedaría claro. Así, un aumento considerable de precios podría provocar una caída en la cantidad, pero lo que podríamos ver reflejado es un aumento en el gasto (es lo que sucede en Colom y Molés (1998)). Es por ello que consideramos más apropiada nuestra variable, a la que denotaremos por QPROPI (su logaritmo neperiano será LQPROPI), 16 cuando nos refiramos a vivienda en propiedad y QALQUI (su logaritmo neperiano será LQALQUI), cuando nos refiramos a la vivienda en alquiler. TIPO DE MUNICIPIO En muchos estudios [Colom y Molés (2000), Blanco y Matínez Verdú (2000), Duce Tello (1995), Lee y Trost (1978)] se suele observar que, en determinados tipos de municipio, puede haber más propensión a alquilar o a comprar. Por ejemplo, en las ciudades grandes existe una mayor oferta de viviendas en alquiler, lo cual implicaría que este tipo de tenencia apareciera como mayoritariamente urbano. En este sentido, se consideran tres variables dummies que recogen el tamaño del municipio, que son TMUN1, TMUN2 y TMUN3. TMUN1 recoge los municipios con más de 50.000 habitantes, TMUN2 recoge los municipios con más de 5.000 y menos de 50.000 habitantes y TMUN3 los municipios con menos de 5.000 habitantes. NIVEL DE ESTUDIOS Se puede pensar que el nivel de estudios del cabeza de familia puede tener una incidencia en el régimen de tenencia de una vivienda. En los estudios realizados a este respecto [Colom y Molés (1998), Blanco y Martínez Verdú (2000), Duce Tello (1995)] se suele llegar siempre a la conclusión de que cuanto mayor es el nivel de estudios, el régimen de alquiler aumenta. La razón que se aporta para explicar dicho comportamiento se basa principalmente en las mayores expectativas de movilidad de dichas familias debido a la mayor cualificación profesional del cabeza de familia. Por ello, en nuestro análisis también se consideran variables que recogen el nivel de estudios. En concreto, ESTUD1, ESTUD2, ESTUD3 y ESTUD4, que indican: ESTUD1: Cabeza de familia analfabeto o sin estudios. ESTUD2: Cabeza de familia con estudios primarios, EGB o FP-1. ESTUD3: Cabeza de familia con BUP, COU, o FP-2. ESTUD4: Cabeza de familia diplomado, licenciado universitario o equivalente. MUJER Podría interesar conocer, además, si el hecho de que el cabeza de familia sea una mujer tiene alguna implicación en cuanto a las decisiones sobre vivienda aquí consideradas [Lee Trost (1978), Rosen (1979), Jaén y Molina (1994), Rapaport (1997) y Colom y Molés (1998) y (2000), entre otros]. Caso de que así fuera, podría estar 17 indicando algún tipo de discriminación socioeconómica asociada a la situación familiar de la mujer (divorcio, separación, viudedad, etc.). Es por ello que aparece la variable dummy MUJER que toma el valor 1 si el cabeza de familia es mujer y 0 en caso contrario. En muchos estudios se considera, además de ésta, la variable raza. Sin embargo, en una comunidad como la nuestra, en la que las personas de raza no blanca son tan minoritarias, no tendría sentido planteárselo. Por otro lado, en la EPF90-91 no aparece el dato sobre la raza del cabeza de familia. EDAD Una variable que puede tener un efecto considerable acerca de las decisiones sobre vivienda es la edad. En los trabajos realizados sobre vivienda suele apreciarse que, en lo que a la elección de tenencia se refiere, es más probable que la vivienda se tenga en propiedad para niveles medios de edad. En edad más temprana no es habitual, dado que la poca renta acumulada dificulta el acceso al mercado de vivienda en propiedad. Es por ello que se espera que la probabilidad de tener vivienda en propiedad aumente con la edad. Se suele argumentar, además, que dicha tendencia se invierte para valores altos de la variable. Es decir, llega un momento en que la probabilidad de tener vivienda en propiedad disminuye. Incluimos a este respecto cuatro variables dummies: EDAD1: Cabeza de familia con menos de 30 años. EDAD2: Cabeza de familia entre 30 y 44 años. EDAD3: Cabeza de familia entre 45 y 65 años. EDAD4: Cabeza de familia con más de 65 años. TAMAÑO DE LA FAMILIA Una variable que se debe considerar a la hora de estudiar las decisiones de la familia sobre vivienda es el tamaño de la familia. Lo que habitualmente sucede es que cuanto mayor es el tamaño de la familia, más renta se precisa destinar a fines distintos a la vivienda y, como consecuencia, la renta disponible para vivienda es menor. Esta es la razón de que cuando se considera el modelo de elección de tenencia, habitualmente el tamaño de la familia ejerza un efecto negativo sobre la probabilidad de disponer de vivienda en propiedad. Ahora bien, la política de ayudas públicas destinadas a las familias en situación precaria puede hacer que el efecto negativo del tamaño familiar sobre la probabilidad de tenencia en propiedad se vea, cuando menos, atenuado. 18 Si, por el contrario, nos referimos al modelo de demanda, cabe esperar que a medida que aumenta el tamaño de la familia el consumo aumente. Sin embargo, pasado un determinado nivel se observa que la disminución en el nivel de renta hace que el consumo de vivienda también disminuya. En este sentido, aparecen la siguientes variables: MIEM1: Familia con menos de 4 miembros. MIEM2: Familia entre 4 y 6 miembros (inclusive). MIEM3: Familia con más de 6 miembros. En la ecuación de demanda aparece NMIEM1, que es una variable dummy que toma el valor 1 si en la familia hay más de tres miembros y 0 en caso contrario. FECHA DE COMPRA O ALQUILER Aunque esta variable no suele utilizarse habitualmente en este tipo de trabajos, sí debemos considerarla en el caso del mercado de vivienda español dadas las especiales características del mercado de alquiler de vivienda. La razón es la legislación que ha habido en España sobre el régimen de alquiler. Tradicionalmente, dicho régimen se ha caracterizado por una congelación en el nivel de alquileres que hacía que durante muchos años los alquileres pagados apenas variaran. Esto hacía del alquiler una opción muy barata. Dado que esta situación se produjo hasta el año 1965, se ha incluido una variable dummy que recoge el hecho de que el alquiler se produjera antes de dicha fecha (ANTI1), ya que todos los alquileres incluidos en este grupo son de renta antigua. Posteriormente, en abril de 1985 se produjo el decreto Boyer. A partir de esta última fecha, se liberalizan los alquileres. Es por ello que, en el análisis empírico, se considerará una segunda variable dummy (ANTI2) para recoger los alquileres contratados entre 1965 y 1984. En los dos últimos periodos considerados (1965-1984 y posterior a 1985) se pueden encontrar mezcladas viviendas de “renta antigua” con viviendas de “renta libre” [Duce Tello (1995)]. Es la razón por la que, al utilizar tales variables dummies, si bien el efecto de la primera debiera ser claro (todas son rentas antiguas), el efecto de la segunda no lo será tanto, ya que se aplica a viviendas que pueden ser de los dos tipos. TIPO DE HOGAR Se incluye también en el análisis una variable que refleja cuál es el tipo de familia que se está tratando. La razón es que cabe la posibilidad de que familias de 19 idéntico tamaño adopten diferentes decisiones sobre vivienda dependiendo de que la composición familiar sea de uno u otro tipo. Por ejemplo, puede tener sentido considerar que la probabilidad de que una familia de cuatro miembros tenga una vivienda en propiedad, no sea la misma si la composición es de matrimonio con ascendientes, frente a matrimonio con dos hijos. Aunque en la EPF90-91 se hace una distinción más amplia, nosotros nos limitamos a distinguir aquellas familias en las que hay niños de aquéllas en las que no los hay, con la variable THOGAR2, que toma el valor 1 si en la familia hay niños y 0 en caso contrario. Esta opción de incluir una variable referida al tamaño de la familia y otra referida a la composición de la misma aparece, por ejemplo, en Blanco y Martínez Verdú (2000), aunque la variable tipo de hogar está más desagregada. Por otro lado, Duce Tello (1995) recoge en una variable el número de miembros de la familia y en otra el número de hijos de menos de 18 años, mientras que Rosen (1979) considera sólo el número de hijos de menos de 17 años. Encontramos, por tanto, argumentos para pensar que la existencia de niños en el hogar aporta una información relevante que complementa la obtenida por la variable tamaño de la familia. CATEGORÍA SOCIOPROFESIONAL Incluiremos una variable que recoja cuál es la categoría socio-profesional del cabeza de familia. Así, se tendrán las siguientes variables dummies: CATSP1: Trabajador manual de la industria y servicios. CATSP2: Trabajador no manual de la industria y servicios. CATSP3: Autónomo de la industria y servicios. CATSP4: Trabajador de la agricultura. CATSP5: Jubilado. CATSP6: Otros. Esta inclusión, también recogida en Colom y Molés (1998) y (2000), obedece a la consideración de que la percepción de familias que obtienen idénticos ingresos puede ser distinta dependiendo de la categoría socioprofesional del cabeza de familia; así el nivel de ingresos tendrá un carácter más permanente o estable para aquellas familias que trabajan por cuenta ajena que para aquéllas cuyo cabeza de familia es autónomo. 20 NÚMERO DE PERCEPTORES DE INGRESOS ORDINARIOS Consideramos que esta variable puede ser relevante, en tanto que no tienen el mismo nivel económico dos familias con el mismo volumen de ingresos si los mismos se perciben por el trabajo de tres personas (por ejemplo el cabeza de familia y dos hijos) o si sólo lo percibe el cabeza de familia. En muchos casos, la decisión sobre la vivienda familiar se hará únicamente en función de los ingresos del matrimonio y no de los ingresos de los hijos. Es por ello que en la ecuación de elección de tenencia se incluye la variable dummy NPERM2, que toma el valor 1 para aquellas familias en las que los ingresos hayan sido percibidos por más de dos miembros de las mismas y 0 en caso contrario, y en la ecuación de demanda la variable NPERMORD que recoge el número de perceptores de ingresos ordinarios. MOVILIDAD FAMILIAR Nos interesa recoger información referente a la movilidad familiar en tanto que puede ser relevante a la hora de optar por una vivienda en propiedad o en alquiler. De hecho, existen otros trabajos [Colom y Molés (1998), Blanco y Martínez Verdú (2000)] en los que se incluye este tipo de información y se llega a la conclusión esperada de que una mayor movilidad supone una menor probabilidad de tenencia en propiedad. En concreto, las variables utilizadas son CMUNI: variable dummy que toma el valor 1 si la familia cambió de municipio con posterioridad a 1986 y CPROVI: variable dummy que toma el valor 1 si la familia cambió de provincia con posterioridad a ese mismo año. 5.- RESULTADOS DE LA ESTIMACIÓN 5.1.- MODELO PROBIT DE ELECCIÓN DE TENENCIA La razón de decantarnos por el método probit de elección binaria es porque el modelo de tenencia y demanda de Lee y Trost (1978) supone que la perturbación aleatoria en la ecuación de elección discreta sigue una distribución normal. La tabla 1 muestra los resultados obtenidos mediante este tipo de estimación. 21 Tabla 1. Estimación de tenencia en propiedad por modelo Probit. Variable CONSTANTE LINGORD LINGORD2 TMUN2 TMUN3 ESTUD2 ESTUD3 ESTUD4 MUJER EDAD2 EDAD3 EDAD4 LPPROPI LPALQUI NPERM2 MIEM2 MIEM3 ANTI1 ANTI2 THOGAR2 CATSP1 CATSP2 CATSP3 CATSP4 CATSP5 CMUNI CPROVI N = 1302 Log-verosimilitud = −351.678 ICV = 0.247 Coeficiente −66.906 8.336 −0.248 0.227 −0.324 0.061 0.003 −0.216 0.036 0.113 0.686 0.755 −0.629 0.246 −0.448 −0.223 −1.074 −0.581 0.016 0.377 −0.660 −0.579 −0.780 −0.953 −0.534 −0.769 −0.932 Error Standard 24.779 3.529 0.126 0.167 0.226 0.201 0.251 0.275 0.163 0.236 0.256 0.303 0.338 0.317 0.170 0.149 0.329 0.199 0.165 0.162 0.236 0.234 0.271 0.494 0.209 0.192 0.406 Significatividad 0.0069 0.0182 0.0483 0.1748 0.1519 0.7614 0.9892 0.4337 0.8267 0.6326 0.0074 0.0127 0.0627 0.4379 0.0082 0.1345 0.0011 0.0036 0.9223 0.0199 0.0051 0.0131 0.0039 0.0537 0.0106 0.0001 0.0218 La variable que recoge los ingresos disponibles de la familia aparece en su forma logarítmica y en dicha forma logarítmica elevada al cuadrado. Ambas variables han obtenido coeficientes significativamente distintos de cero, la primera con signo positivo y la segunda con signo negativo. Se puede comprobar que, para los niveles de renta de la muestra, el efecto conjunto de ambas variables sobre la probabilidad de tenencia en propiedad es positivo. Dado que la derivada de la probabilidad de tenencia en propiedad respecto del los ingresos de la familia disminuye con el nivel de esta variable, puede hacerse negativa. Ahora bien, esta tendencia se producirá a partir de un nivel muy elevado de ingresos ordinarios disponibles y, además, la tasa de decrecimiento será muy pequeña, por lo que el comportamiento de la probabilidad de tenencia en propiedad respecto de la renta es creciente hasta un determinado nivel y a partir del mismo se 22 mantiene prácticamente constante. A modo ilustrativo, una familia con ingresos ordinarios disponibles de 20.000.000 de ptas. (nivel de renta para el cual empieza a verificarse dicha disminución en el modelo probit, y muy alejado del mayor nivel de renta de nuestra muestra, que no alcanza los 10.000.000 de ptas.) tendría una probabilidad de tenencia en propiedad de 0.9988, y una de 70.000.000 de ptas 0.996 (estos cálculos se han realizado para una familia media respecto de las demás variables). Si nos referimos a las variables que recogen el tipo de municipio, podemos observar que el signo de la primera variable dummy considerada (TMUN2) es positivo, mientras que el de la segunda (TMUN3) es negativo. En este tipo de modelos suele ser habitual que haya más probabilidad de tenencia en propiedad cuanto menor sea el municipio. Dado que la variable que recogemos por defecto es TMUN1, que corresponde a municipios con más de 50.000 habitantes, esta circunstancia sería cierta para la variable TMUN2 (municipios entre 5.000 y 50.000 habitantes), pero no para TMUN3, que tiene signo negativo. Hay que fijarse, sin embargo, en que los coeficientes obtenidos no son significativamente distintos de cero para los niveles de significación habituales. Es por ello que, a este respecto, no podemos extraer resultados concluyentes. En cuanto a las variables dummies que recogen el nivel de estudios del cabeza de familia, la variable por exclusión (la que denotamos ESTUD1) es la que se refiere a cabeza de familia sin estudios o analfabeto. Lo que se observa, por lo tanto, es que los coeficientes correspondientes a las tres variables dummies son no significativamente distintos de cero. Ahora bien, la pauta que es habitual encontrar en estudios similares también aparece aquí. Así, vemos que sí es cierto que para los dos siguientes niveles de estudios los coeficientes son positivos, lo que indicaría una mayor probabilidad de demanda de tenencia en propiedad. Ahora bien, para el cuarto nivel el coeficiente es negativo. La razón que se suele argumentar ante este resultado es la mayor movilidad que pueden presentar las familias cuyo cabeza de familia tiene una mayor formación académica. La variable MUJER, que es dummy (por defecto aparece cabeza de familia hombre) no es significativa para ninguno de los niveles de significación considerados. El coeficiente es positivo, pero dada su no significatividad, no podemos extraer conclusiones. El siguiente grupo de variables que aparecen son las dummies correspondientes a la edad. La variable por omisión sería la que recoge al cabeza de familia con edad inferior a 30 años, a partir de ahí, las edades aparecen en orden creciente. Si observamos 23 los resultados obtenidos, se tiene que las variables EDAD3 y EDAD4 son significativas para el nivel de significación 5%. La pauta que aparece reflejada en nuestros resultados es que cuanto mayor es la edad del cabeza de familia mayor es la probabilidad de tener la vivienda en propiedad. Este resultado suele ser habitual en estudios realizados en otros países y la razón aducida es que si el cabeza de familia es muy joven aún no ha podido acumular riqueza suficiente para acceder a la vivienda en propiedad, pero a menudo la tendencia se invierte al pasar a los mayores tramos de edad. En nuestros resultados no es eso lo que sucede, ya que observamos que la tendencia siempre es creciente. La razón de esta diferencia puede ser el comportamiento especial que tienen las familias en España, donde está profundamente arraigada la cultura de la propiedad de la vivienda, frente a otros muchos países de nuestro entorno en los que la tenencia en forma de alquiler está mucho más presente. Las siguientes variables recogen los precios de las dos alternativas que se le presentan al consumidor sobre tenencia de vivienda: el precio de la vivienda en propiedad y el precio de la vivienda en alquiler (hay más posibilidades pero no las consideramos). Los resultados que obtenemos tienen los signos esperados, esto es, la probabilidad de tenencia en propiedad aumenta cuando el precio del alquiler aumenta y disminuye cuando el que aumenta es el de propiedad. Ahora bien, mientras que el coeficiente del precio de la vivienda en propiedad es significativamente distinto de cero al nivel de significación 10%, el coeficiente del precio de la vivienda en alquiler no es significativamente distinto de cero. Cabe comentar aquí que los coeficientes obtenidos hacen que, para un determinado tipo de familia, la probabilidad en una de las zonas consideradas sea mayor (o menor) que en otra zona. En Li (1977) encontramos la estimación de un modelo logit en el que no se utiliza como variable explicativa el precio de la vivienda; se comenta el hecho de que, al realizar las estimaciones en diferentes zonas, aparecen diferencias en las constantes que recogerían peculiaridades de cada zona, y entre ellas podría haber una diferencia de coste de la vivienda. Si nosotros realizamos la misma regresión sin incluir los precios, pero considerando variables dummies para las zonas consideradas, se obtiene que la ciudad que destaca negativamente en cuanto a probabilidad de tenencia en propiedad es San Sebastián que, justamente, es la zona de mayor precio en propiedad de las seis consideradas. 24 Respecto de esta variable (precio de la vivienda en propiedad), tenemos que en Rosen (1979), Colom y Molés (1998) y en Blanco y Martínez Verdú (2000) aparece el signo esperado, aunque en estos dos últimos trabajos se considera como variable precio el cociente entre precio en propiedad y precio en alquiler. Por otro lado, Jaén y Molina (1994) obtienen coeficientes no significativamente distintos de cero y con los signos opuestos a los esperados. Duce Tello (1995) y Horioka (1988) no incluyen en la ecuación de tenencia los precios, argumentando este último que la exclusión se debe a que por la alta correlación existente entre los precios de alquiler y propiedad, uno o ambos coeficientes son no significativos. La siguiente variable explicativa que hemos considerado es NPERM2. Se trata de una variable dummy que recoge aquellas familias en las que los ingresos se han obtenido por más de dos perceptores. Si hay más de dos perceptores, es evidente que al menos uno de ellos no forma parte del matrimonio (se tratará de algún hijo, o de algún ascendiente). Es muy probable que las decisiones sobre vivienda se adopten en función de los ingresos que el matrimonio obtiene. Por lo tanto, el hecho de que esta variable tome el valor uno hace que, a la hora de decidir sobre la tenencia, se considera un volumen menor de ingresos que el que hemos computado. Cabe esperar, por lo tanto, un signo negativo para el coeficiente de esta variable, y esto es efectivamente lo que sucede. Se trata, además de un coeficiente significativamente distinto de cero. Nos referimos a continuación a las variables MIEM2 (familias con 4, 5 o 6 miembros) y MIEM3 (familias con más de 6 miembros). Por defecto se tendrán familias con menos de 4 miembros. En este caso se obtienen los signos esperados, esto es, negativos. Además, aparece muy clara la pauta que se repite en este tipo de trabajos y es que cuanto mayor es el tamaño de la familia, menor es la probabilidad de tenencia de vivienda en propiedad; así, se constata que el coeficiente es mayor (en valor absoluto) para la segunda de las variables. De hecho, se puede observar que el coeficiente correspondiente a la primera de las variables no es significativamente distinto de cero (aunque para un nivel de significación del 10% no estaría lejos de dicha significatividad). La razón que se argumenta es que un mayor tamaño familiar supone una menor renta disponible para poder acceder a la vivienda en propiedad. Las siguientes variables que aparecen recogidas son ANTI1 y ANTI2. Se trata de las variables dummies que pretenden recoger la especial situación del mercado del alquiler en España. El signo del coeficiente que obtenemos para ANTI1 es negativo y significativamente distinto de cero que es lo esperado dado que se recogerían aquellas 25 viviendas anteriores a 1965 que tienen rentas “congeladas”, por lo que la opción de alquiler para ellos es más barata que la de compra (por comparación con las viviendas correspondientes a otro periodo). Cuando nos referimos a la segunda variable, no está tan claro el resultado que se espera, y la razón es que tanto entre 1964 y 1985, como a partir de dicha fecha, las viviendas de renta “congelada” y renta libre se encuentran mezcladas. Tras realizar la estimación se observa que el signo obtenido para el coeficiente es positivo aunque muy próximo a cero (de hecho, no es significativamente distinto de cero). La siguiente variable que consideramos es la de tipo de hogar. La clasificación que se ha establecido es si en las familias hay niños o no (se entienden por niños los menores de 16 años). Por defecto, tendríamos familias en las que no hay niños. Al realizar la estimación se observa que el coeficiente es positivo y significativamente distinto de cero. Probablemente este comportamiento lo que refleja es que en las familias en las que ya hay niños hay una mayor estabilidad que conlleva también una mayor tendencia a tener la vivienda en propiedad. Llegamos a la consideración de las variables que recogen la categoría socioprofesional del cabeza de familia. Se observa que todas estas variables son significativas y que todos los coeficientes son negativos. La categoría que tenemos por defecto es la correspondiente a “Otros”. Lo que observamos en ambos modelos es que, de las cinco categorías socioprofesionales consideradas (exceptuamos la categoría “Otros” que es la de mayor probabilidad), las de menor probabilidad de vivienda en propiedad son la de agricultor (CATSP4) y la de autónomo de la industria y servicios (CATSP3), y la de mayor probabilidad el jubilado (CATSP5) seguida de trabajador manual y no manual de industria y servicios (CATSP1 y CATSP2). Los resultados obtenidos confirman nuestras expectativas dado que la mayor incertidumbre sobre el nivel de ingresos se dará en las familias clasificadas en las categorías CATSP3 y CATSP4. Finalmente nos referimos a las variables que reflejan la movilidad familiar (CMUNI y CPROVI). Se observa claramente que los coeficientes de ambas variables son, como esperábamos, negativos y significativamente distintos de cero, confirmando la menor tendencia a la opción de tenencia en propiedad para aquellas familias con mayor movilidad. 26 5.2.- MODELO DE ELECCIÓN CONJUNTA DE TENENCIA Y DEMANDA DE VIVIENDA En este apartado desarrollamos el modelo de tenencia bajo el supuesto de que la elección de demanda se realiza simultáneamente con la de tenencia. Para ello, seguiremos el modelo desarrollado por Lee y Trost (1978) e incluiremos en nuestra ecuación el término que permitirá, además, contrastar si se da o no la simultaneidad. El modelo que vamos a estimar es: LQPROPI i = α + β1 × ESTUD 2 i + β 2 × ESTUD3i + β 3 × ESTUD 4 i + β 4 × EDAD2 i + + β 5 × EDAD3i + β 6 × EDAD4 i + β 7 × NPERMORD i + β 8 × MUJER i + β 9 × CATSP1i + + β10 × CATSP 2 i + β11 × CATSP3i + β12 × CATSP 4 i +β13 × CATSP5 i + β14 × LINGORDi + + β15 × LINGORD2 i + β16 × NMIEM1i + β17 × LPPROPI i + β18 × SIMUPi para la demanda en propiedad, y LQALQUIi = α + β1 × ESTUD 2 i + β 2 × ESTUD3i + β 3 × ESTUD 4 i + β 4 × EDAD2 i + + β 5 × EDAD3i + β 6 × EDAD4 i + β 7 × NPERMORD i + β 8 × MUJER i + β 9 × CATSP1i + + β10 × CATSP 2 i + β11 × CATSP3i + β12 × CATSP 4 i +β13 × CATSP5 i + β14 × LINGORDi + + β15 × LINGORD2 i + β16 × NMIEM1i + β17 × LPALQUIi + β18 × SIMUA i para la demanda en alquiler, siendo SIMUPi = − f (z i αˆ ) f (z i αˆ ) y SIMUA i = , los F(z i αˆ ) 1 − F(z i αˆ ) términos que recogen la simultaneidad en ambas ecuaciones respectivamente (recordemos que f(⋅) y F(⋅) son, respectivamente, las funciones de densidad y de distribución de la normal tipificada). Es decir, recogemos la variable renta en forma logarítmica y esa misma variable elevada al cuadrado. La razón es que, con esta especificación, permitimos que la elasticidad renta varíe para los distintos niveles de la misma, mientras que si no introducimos el término cuadrático la elasticidad será constante para toda la población, lo cual parece menos acorde con la realidad. De hecho, se espera que la elasticidad aumente con la renta y eso es lo que de hecho se obtiene en nuestra estimación. En este sentido, Friedman y Weinberg (1981) señalan como explicación a las elasticidades tan bajas que obtienen en su trabajo, por comparación con el de Polinsky y Ellwood (1979) que la razón está en la selección de la muestra, ya que ellos consideran familias de ingresos bajos, mientras que Polinsky y Ellwood toman familias de ingresos medios. Añaden que esta circunstancia debería ser tenida en cuenta a la hora de decidir sobre política de vivienda, ya que si una determinada política va dirigida a familias con rentas 27 bajas, habrá que tomar en consideración la elasticidad del grupo de rentas bajas, y no la general de la población. Presentaremos inicialmente los resultados para la demanda de vivienda de aquellas familias que han optado por la propiedad y extraeremos conclusiones de los resultados. Posteriormente, presentaremos también los resultados para la estimación de la demanda de vivienda para las familias que han optado por el alquiler. Sin embargo, dado que el número de observaciones en este caso es pequeño, y teniendo en cuenta las especiales características del mercado de alquiler, seremos más cautos a la hora de extraer conclusiones de esta segunda ecuación. En ambos casos, se ha efectuado el contraste de Goldfeld y Quandt (1965) y se ha rechazado la hipótesis nula de homocedasticidad al nivel de significación del 5%. El modelo, por tanto, se estima por mínimos cuadrados ordinarios con un estimador consistente a la White de la matriz de varianzas y covarianzas de los parámetros estimados. A continuación (Tabla 2) exponemos los resultados para la estimación de la ecuación de demanda de vivienda de las familias propietarias. En dicha tabla no aparecen las tres variables referentes a la edad ni tampoco el sexo del cabeza de familia. La razón es que inicialmente se realizó la regresión utilizando todas las variables propuestas en la ecuación de demanda y se observó que estas cuatro variables eran no significativamente distintas de cero. Tras realizar un contraste de significación conjunta de las mismas se procedió a su exclusión del modelo. Variable CONSTANTE ESTUD2 ESTUD3 ESTUD4 NPERMORD CATSP1 CATSP2 CATSP3 CATSP4 CATSP5 LINGORD LINGORD2 NMIEM1 LPPROPI SIMUP N = 1151 R2 = 0,3 Tabla 2. Estimación de la ecuación de demanda en propiedad. Coeficiente Error Standard Significatividad 25.292 11.594 0.0291 0.116 0.064 0.0698 0.274 0.072 0.0001 0.389 0.083 0.0000 0.020 0.0000 −0.093 0.051 0.0004 −0.182 0.056 0.0082 −0.148 0.063 0.2584 −0.071 0.114 0.1420 −0.167 0.051 0.0584 −0.197 1.624 0.0582 −3.076 0.123 0.057 0.0305 0.102 0.030 0.0007 0.057 0.0000 −0.674 0.181 0.106 0.0863 28 Si nos fijamos en los coeficientes que corresponden a las variables referentes al nivel de estudios del cabeza de familia (ESTUD2, ESTUD3, ESTUD4), se puede comprobar que los tres coeficientes son significativamente distintos de cero para los niveles de significación habituales y, además, los valores indican que la demanda de servicios de vivienda aumenta con el nivel de estudios del cabeza de familia, resultado que es habitual en este tipo de trabajos. En lo que se refiere al número de perceptores de ingresos ordinarios (NPERMORD), su coeficiente es significativamente distinto de cero y tiene signo negativo, lo cual era de esperar dado el razonamiento que ya habíamos hecho al incluir esta variable en la ecuación de elección de tenencia. El siguiente grupo de variables que aparece en la tabla es el correspondiente a la categoría socioprofesional del cabeza de familia. Se puede observar que todos los coeficientes son negativos (algunos significativamente distintos de cero para el nivel 5%), por comparación con la categoría Otros. Si consideramos la variable que recoge el número de miembros de la familia, tras probar diferentes especificaciones, se ha comprobado que la que lograba un mejor ajuste era aquélla en que se tomaba como variable explicativa una dummy que toma el valor 1 cuando la familia tiene cuatro o más miembros, y 0 en caso contrario. Se puede comprobar que tiene un coeficiente significativo al nivel de significación 5% y positivo, lo que indica que cuanto mayor es el tamaño de la familia se demanda mayor servicio de vivienda. Aquellas familias cuyo número de miembros es superior a 3 tienen mayor demanda que las familias con un número de miembros menor o igual que 3. Llegamos así a la consideración de la variable renta. La forma en que se ha recogido esta variable en la regresión es doble, ya que aparece el logaritmo de la renta disponible y dicho logaritmo elevado al cuadrado. Esta especificación, que es la que mejor ajuste proporcionaba, es más flexible que aquélla que incluyese únicamente el logaritmo, ya que permite que la elasticidad renta varíe con el nivel de renta, lo cual parece razonable, en tanto que cuanto mayor sea el nivel de renta, esperamos que la elasticidad aumente. En este caso la elasticidad se calculará de la siguiente forma: −3.076 + (2 × 0.123 × LINGORD) función claramente creciente con el nivel de renta disponible. Si evaluamos esta expresión para la renta disponible media de la muestra (1.905.439 ptas.), se obtiene una elasticidad renta igual a 0.49. Si evaluásemos para un nivel más bajo de renta, por ejemplo 500.000 ptas., se obtiene una elasticidad renta igual 29 a 0.16, mientras que si la renta disponible es de 5.000.000 ptas., dicha elasticidad pasa a ser de 0.72. Si consideramos la misma regresión con un único término (LINGORD), se tiene que la elasticidad renta es igual a 0.48; podemos comprobar que, de hecho es un valor muy próximo al que se obtiene para la media en nuestra especificación. En lo que se refiere a la variable precio (LPPROPI), se obtiene un coeficiente significativamente distinto de cero para un nivel de significación del 5% e igual a –0.67. Además, dado que hemos planteado el modelo en forma logarítmica, se trata de la elasticidad precio de la demanda de servicios de vivienda. Finalmente, aparece la variable que reflejaría la posible simultaneidad entre las decisiones de tenencia y de demanda de vivienda en propiedad (SIMUP). Se observa que se trata de un coeficiente positivo y significativamente distinto de cero al nivel de significación del 10%. Es por ello que podemos concluir que sí existe simultaneidad entre ambas decisiones, por lo que, en el caso de que efectuemos la regresión sin tener en cuenta este último término, los coeficientes serían sesgados. En la tabla que aparece a continuación (Tabla 3) se recogen los resultados obtenidos para la ecuación de demanda de vivienda de las familias en alquiler. Variable CONSTANTE ANTI1 ANTI2 ESTUD2 ESTUD3 ESTUD4 EDAD2 EDAD3 EDAD4 NPERMORD MUJER CATSP1 CATSP2 CATSP3 CATSP4 CATSP5 LINGORD LINGORD2 NMIEM1 LPALQUI N = 150 R2 = 0,518 Tabla 3. Estimación de la ecuación de demanda en alquiler. Coeficiente Error Standard 8.505 0.457 0.384 −1.806 0.291 −0.290 0.303 0.274 0.148 0.386 0.561 0.495 0.170 0.267 0.375 −0.669 0.493 −0.696 0.100 −0.191 0.695 0.218 0.342 −0.110 0.346 −0.094 0.372 −0.300 0.757 −0.129 0.187 0.298 0.198 −0.904 0.061 0.015 0.254 −0.311 0.358 −0.556 30 Significatividad 0.0000 0.0000 0.3181 0.2694 0.7013 0.2568 0.5250 0.0743 0.1578 0.0579 0.0014 0.7478 0.7864 0.4211 0.8646 0.5305 0.0000 0.0000 0.2204 0.1209 En este caso, si planteamos la regresión añadiendo la variable que reflejaría la posible simultaneidad entre las decisiones de tenencia y demanda, se obtiene que su coeficiente no es significativamente distinto de cero y, además, si eliminamos esta variable de la regresión, se obtiene una mejora en el coeficiente de determinación corregido. Es por ello que la especificación que finalmente consideramos es aquélla en la que no aparece dicho término. En el caso de la demanda en propiedad sí concluíamos que se producía la simultaneidad. Tiene sentido que ésta sea la situación, ya que cuando una familia decide alquilar tiene menos costes si posteriormente quiere cambiar su nivel de consumo de vivienda ante variaciones en variables tales como renta, precio, tamaño de familia, etc. Por el contrario, para el propietario, el cambio en cantidad de servicios de vivienda tiene unos mayores costes, que harán que cuando decida comprar decida de manera más definitiva cuánto comprar. Los resultados obtenidos nos permiten ver cómo influye sobre la demanda de vivienda el año de alquiler de la vivienda. Así, el coeficiente que corresponde a la variable ANTI1, que toma el valor uno si la familia tiene alquilada la vivienda desde antes de 1965 y cero en caso contrario, es negativo y significativamente distinto de cero. Lo que indica claramente es que este tipo de familias tienen un consumo de servicios de vivienda muy inferior a las demás y la razón parece clara si tenemos en cuenta que se trata de viviendas sometidas a congelación de alquiler, y que la variable que nosotros recogemos para reflejar la demanda de servicio de vivienda es el alquiler pagado por la vivienda dividido entre el precio de alquiler de la zona correspondiente. Si nos fijamos en la otra variable que refleja el año de alquiler de la vivienda, ANTI2, se tiene que el coeficiente no es significativamente distinto de cero. La razón es que en este grupo se encuentran mezcladas viviendas de renta antigua con viviendas de alquiler libre, por lo que no cabría esperar claramente un efecto negativo. Si nos referimos ahora a las variables que recogen características del cabeza de familia, se puede comprobar cómo nivel de estudios y edad del cabeza de familia no son en general significativas (únicamente la variable EDAD3 tiene un coeficiente significativo para el nivel 10%). Sí tiene un coeficiente significativo la variable MUJER, lo que indicaría que hay una mayor demanda de servicios de vivienda cuando el cabeza de familia es mujer. Las variables que sí tienen coeficientes significativamente distintos de cero son las dos que recogen la variable renta (LINGORD y LINGORD2). La elasticidad renta sería también en esta ecuación de demanda creciente con la renta. Se estimará como: 31 −0.904 + (2 × 0.061 × LINGORD) Así, la elasticidad renta para una familia con ingresos disponibles medios (1.396.548 ptas.) es de 0.83. Si evaluamos ahora, al igual que hemos hecho en el caso de la demanda en propiedad, para una familia con unos ingresos de 500.000 ptas., la elasticidad pasa a ser 0.70 y finalmente, cuando evaluamos para una familia con 5.000.000 ptas., la elasticidad pasa a ser de 0.98. Vemos que en este caso las elasticidades renta son mayores que en el caso de las familias que tienen su vivienda en propiedad. Dados los menores costes de transacción que tienen las familias en alquiler en relación a las familias en propiedad para cambiar la cantidad demandada era de esperar este resultado. Si nos referimos a la variable que recoge el precio, aunque el coeficiente no es significativamente distinto de cero a los niveles habituales, estaría próximo a ser significativo para el nivel de 10%. El valor de su coeficiente, que es igual a la elasticidad precio, es –0.556, lo cual indicaría que se tiene una menor elasticidad precio que en el caso de la demanda en propiedad. Ahora bien, debemos ser conscientes de que en la muestra existe un grupo de familias a las que estamos asignando un precio de alquiler que no es el que les corresponde, dado que el que a ellas se les aplica está congelado por ley. Si excluyésemos de la muestra a las familias que tienen fecha de contrato de alquiler anterior a 1965 (es decir, eliminamos a todas aquellas familias que sabemos con certeza que tienen congelación contractual, aunque quedarán otras familias con contratos posteriores también con congelación contractual, pero desconocemos cuáles son), vemos que este resultado claramente cambia las elasticidades. En la tabla 4 aparecen los nuevos resultados (tras excluir a las familias con contrato anterior a 1965). Podemos concluir que, ahora, la elasticidad precio claramente ha aumentado, ya que ha pasado a ser –1.14 (indicaría que eran las familias con congelación contractual las que hacían disminuir la elasticidad precio). Por otra parte, la elasticidad renta pasa a ser ahora: −1.103 + (2× 0.078× LINGORD) Así, si de nuevo evaluamos para los niveles de renta disponible anteriores, se tiene que en el nivel medio (1.372.951 ptas.), la elasticidad renta es 1.10. Si evaluamos para una familia con 500.000 ptas. la elasticidad será de 0.94, y si pasamos a una familia con una renta disponible de 5.000.000 ptas., la elasticidad renta será de 1.30. 32 Tabla 4. Estimación de la ecuación de demanda en alquiler. Contratos posteriores a 1964. Variable Coeficiente Error Standard Significatividad CONSTANTE 7.728 0.524 0.0000 ESTUD2 0.641 0.398 0.1077 ESTUD3 0.291 0.467 0.5328 ESTUD4 0.678 0.551 0.2186 EDAD2 0.090 0.262 0.7311 EDAD3 0.281 0.0023 −0.857 EDAD4 0.431 0.0007 −1.454 NPERMORD 0.116 0.0230 −0.264 MUJER 0.689 0.256 0.0071 CATSP1 0.417 0.9166 −0.044 CATSP2 0.437 0.8173 −0.101 CATSP3 0.439 0.8004 −0.111 CATSP4 0.380 0.0074 −1.019 CATSP5 0.793 0.424 0.0617 LINGORD 0.250 0.0000 −1.103 LINGORD2 0.078 0.019 0.0000 NMIEM1 0.216 0.0171 −0.515 LPALQUI 0.270 0.0000 −1.141 N = 108 R2 = 0,392 Vemos, por lo tanto, que claramente la exclusión de las familias con rentas congeladas lleva a una obtención de elasticidades tanto renta como precio mayores que en el caso en que no se excluyen a dichas familias y claramente mayores que en el caso de la demanda en propiedad. 6.- CONCLUSIONES El modelo de Lee y Trost (1978) permite determinar conjuntamente las decisiones de comprar o alquilar una vivienda y de cuánto gastar en ella, considerando la simultaneidad entre ambas decisiones: si son simultáneas, considerar únicamente el gasto realizado en vivienda (y no la forma de tenencia) daría lugar a estimadores sesgados utilizando mínimos cuadrados ordinarios. En caso de que no hubiera simultaneidad, los estimadores sí serían insesgados, aunque sería preciso contrastar la no simultaneidad. La primera fase del análisis presenta los resultados correspondientes a la elección de tenencia bajo el modelo probit. Podemos afirmar que, en general, para las variables cuyos coeficientes resultaron significativamente distintos de cero, los resultados son los esperados. 33 Mayores niveles de renta implican una mayor probabilidad de optar por la propiedad frente al alquiler. Un mayor nivel de estudios se puede asociar a una menor probabilidad de tenencia en propiedad justificada por una mayor expectativa de movilidad de los individuos con mayor formación académica. Además, la probabilidad de tenencia en propiedad aumenta con la edad y, en nuestro caso, no decrece en los tramos de edad más elevados, al contrario de lo que ocurre en los estudios referidos a otros países. Por otro lado, si en la familia hay más de dos perceptores de renta (miembros del hogar adicionales al matrimonio) es de esperar que las decisiones sobre vivienda tengan en cuenta únicamente la renta del matrimonio. En ese caso, el volumen efectivo de ingresos computable sería menor, lo cual implicaría, a su vez, una menor probabilidad de tenencia, como ocurre en nuestro estudio. También confirmamos la pauta teórica de que cuanto mayor sea el número de miembros de la familia, menor es la opción por la propiedad, debido a la menor renta disponible de este tipo de familias, aunque ratificamos también el resultado de la mayor probabilidad de tenencia en propiedad en aquellos hogares en los que hay niños. Respecto de la categoría socioprofesional del cabeza de familia, es de destacar que la menor probabilidad de vivienda en propiedad es la de agricultor y la mayor la de los jubilados, seguida de los trabajadores manuales y no manuales de industria y servicios. Por otro lado, se constata que si la fecha de alquiler o compra de la vivienda es anterior a 1965 la probabilidad de tenencia en propiedad disminuye debido al especial tratamiento legislativo otorgado a la vivienda en alquiler en nuestro país. Respecto de la variable precio, la probabilidad de tenencia en propiedad aumenta cuando también lo hace el precio del alquiler y disminuye cuando el que aumenta es el de propiedad, lo que se traduce en diferentes probabilidades estimadas para las distintas zonas consideradas; ahora bien, las diferencias en dichas probabilidades se aminoran cuanto mayor es el nivel de renta de la familia. Finalmente, nuestros resultados confirman la teoría de que las familias con una mayor movilidad tienen una menor propensión a la tenencia de vivienda en propiedad. En la segunda fase de la estimación desarrollamos el modelo de tenencia bajo el supuesto de que la elección de demanda se realiza simultáneamente con la de tenencia. En esta etapa, la demanda de servicio-vivienda en propiedad aumenta con el nivel de estudios y disminuye con el número de perceptores de ingresos ordinarios. Además, cuanto mayor es el tamaño de la familia, más servicio-vivienda demanda. 34 La relación directa entre demanda de servicio-vivienda en propiedad y nivel de renta queda patente en el valor positivo y creciente con la renta de la elasticidad obtenida. La elasticidad renta correspondiente a la renta media de la muestra (1.905.439 ptas.) es 0.48, para un nivel de renta de 500.000 ptas. es de 0.16 y si consideramos una renta de 5.000.000 de ptas. el valor de la elasticidad renta sería 0.72. En el caso de la variable precio, se obtiene una elasticidad negativa y significativamente distinta de cero para un nivel de significación del 5%. En concreto, el valor obtenido es de −0.67, coincidente con el coeficiente estimado dada la especificación logarítmica del modelo para esta variable. Este valor, como ocurre con la elasticidad renta de la demanda, no está en absoluto alejado de los obtenidos en otros estudios a nivel nacional e internacional. Respecto de la variable que refleja la posible simultaneidad entre las decisiones de tenencia y demanda, podemos concluir que sí se da tal simultaneidad entre ambas decisiones, de forma que, en caso de no considerar ese término en la regresión, los coeficientes serían sesgados. Sobre este último resultado la literatura está mucho más dividida. Por el contrario, el coeficiente que refleja la simultaneidad entre las decisiones de tenencia y demanda en alquiler no es significativamente distinto de cero y, además, eliminar tal variable mejora el coeficiente de determinación corregido. Las variables respecto de las que se pueden extraer conclusiones más fidedignas en este caso, dada la significatividad de los coeficientes estimados, son las variables renta y precio, manteniendo las cautelas que exige la heterogeneidad contractual en el mercado español de la vivienda en alquiler. En concreto, la elasticidad renta es positiva y también aumenta con la renta, como ocurre en el caso de demanda de servicio-vivienda en propiedad: los valores de esta elasticidad para niveles bajo, medio y alto de renta son, respectivamente, 0.7, 0.83 y 0.98, mayores que en el caso de propiedad. La elasticidad precio es de −0.556, menor que la elasticidad precio de la demanda en propiedad, aunque habría que considerar el peso de los alquileres congelados, ya que, excluyendo los contratos con fechas anteriores a 1965, que se pueden considerar sin duda de renta congelada, la elasticidad precio pasaría a ser de −1.14. Algo similar ocurre con las elasticidades renta si excluimos de la estimación a las familias que se acogieron a ese tipo de contratos, ya 35 que en este caso las elasticidades renta pasarían a ser de 0.94, 1.10 y 1.30 para los tres niveles de renta (bajo, medio y alto respectivamente). BIBLIOGRAFÍA •AARON, H. (1972): “Shelter and subsidies”. The Brookings Institution, Washington D.C. •BLANCO, J.M. y MARTINEZ, R. (2000): “La demanda de servicios de vivienda en España: un análisis empírico”. XIV Reunión ASEPELT España. Oviedo. •CARLINER, G. (1973): “Income elasticity of housing demand”. Review of Economics and Statistics, 55; pp. 528-532. •COLOM, M.C. y MOLÉS, M.C. (1998): “Un análisis sobre el gasto en servicio de vivienda en España”. Estadística Española, 143; pp. 147-166. •COLOM, M.C. y MOLÉS, M.C. (2000): “Un análisis sobre el régimen de tenencia y el tipo de edificio en las ciudades españolas”. XIV Reunión ASEPELT. Oviedo. •DE LEEUW, F. y EKANEM, N. (1971): “The supply of rental housing”. The American Economic Review, 61; pp. 806-817. •DOUGHERTY, A. y VAN ORDER, R. (1982): “Inflation, housing costs and the consumer price index”. American Economic Review, vol. 72(1); pp. 154-164. •DUCE TELLO, R.M. (1995): “Un modelo de elección de tenencia para España”. Moneda y Crédito, 201; pp. 127-152. •FALLIS, G. (1985): “Housing economics”. Editorial Butterflows & Co. Toronto. •FRIEDMAN, J. y WEINBERG, D.H. (1981): “The demand for rental housing: evidence from housing allowance demand experiment”. Journal of Urban Economics, 9; pp. 311-331. •GARCIA-MONTALVO, J y MAS, M. (2000): “La vivienda y el sector de la construcción en España”. Instituto Valenciano de Investigaciones Económicas. Ed.: Caja de Ahorros del Mediterráneo (C.A.M.). •GILLINGHAM, R. y HAGEMANN, R. (1983): “Cross-sectional estimation of a simultaneous model of tenure choice and housing services demand”. Journal of Urban Economics, 14; pp. 16-39. •GOLDFELD, S.M. y QUANDT, R.E. (1965): “Some tests for homoskedasticity”. Journal or the American Statistical Association, 60; pp. 539-559. 36 •GONZALEZ-PARAMO, J.M. y ONRUBIA, J. (1992): “El gasto público en vivienda en España”. Hacienda Pública Española, 120-121: 1-2; pp. 189-231. •HARMON, O.R. (1988): “The income elasticity of demand for single family owneroccupied housing: an empirical reconciliation”. Journal of Urban Economics, vol 24; pp. 173-185. •HENDERSHOTT, P. y HU, S. (1981): “Inflation and extraordinary returns on owneroccupied housing”. Journal of Macroeconomics, 3; pp. 177-203. •HENDERSHOTT, P. y SHILLING, J. (1982): “The economic of tenure choice”, en C. Sirmans ed. “Research in Real State” Vo. 1 (Jai Press, Greenwich, CT); pp. 105-133. •HORIOKA, C.Y. (1988): “Tenure choice and housing demand in Japan”. Journal of Urban Economics, 24; pp. 289-309. •JAEN, M. y MOLINA, A. (1994): "Un análisis empírico de la tenencia y demanda de vivienda en Andalucía”. Investigaciones Económicas, vol. XVIII (1): pp. 143-164. •JOHNSON, N.L. y KOTZ, S. (1972): “Distributions in Statistics: Continuous multivariate distributions”. John Wiley & Sons. •KING, M. (1980): “An econometric model of tenure choice and demand for housing as a joint decision”. Journal of Public Economics, vol. 14; pp. 137-159. •LAIDLER, D. (1969): “Income tax incentives for owneroccupied housing” en “The taxation of income from capital”, A. C. Harberger y M. J. Bayley eds., The Brookings Institution, Washington D.C. •LEE, L.F. y TROST, R.P. (1978): “Estimation of some limited variable models with application to housing demand”. Journal of Econometrics, vol. 8; pp. 357-382. •LI, M.M. (1977): “A logit model of homeownership”. Econometrica, vol. 45, n. 5; pp. 1081-1097. •LOPEZ GARCIA, M.A. (1996): “Precio de la vivienda e incentivos fiscales a la vivienda en propiedad en España”. Revista de Economía Aplicada, v.4, n.21; pp. 37-74. •LOPEZ GARCIA, M.A. (1997): “La fiscalidad y la política de vivienda en España”. Hacienda Pública Española, 141/142; pp. 287 - 334. •LOPEZ GARCIA, M.A. (1999): “Efectos de la reforma del I.R.P.F. sobre la vivienda”. Revista de Economía Aplicada, v.7, n.21; pp. 95-120. •MAISEL, S., BURHAM, J. y AUSTIN, J. (1971): “The demand for housing: a comment”. Review of Economics and Statistics, vol. 53; pp. 410-415. 37 •MAYO, S.K. (1981): “Theory and estimation in the economics for housing demand”. Journal or Urban Economics, vol. 10; pp. 95-116. •McFADYEN, S. y HOBART, R. (1978): “An alternative measure of housing costs and the consumer price index”. Canadian Journal of Economics, 11; pp. 105-111. •MILLS, E.S. (1990): “Housing tenure choice”. Journal of Real State Finance and Economics, vol.3; pp. 323-331. •MUTH, R.F. (1960): “The demand for nonfarm housing” en “The demand for nondurable goods”. Ediciones A.C. Harberger, University of Chicago Press; pp. 29-96. Chicago. •OLSEN, E.O. (1969): “A competitive theory of the housing market”. American Economic Review, vol.59(4); pp. 612-622. •OLSEN, R. (1980): “A least square correction for selectivity bias”. Econometrica, 48; pp. 1815-1820. •POLINSKY, A.M. y ELLWOOD, D.T. (1979): “An empirical reconciliation of micro and grouped estimates of the demand for housing”. Review of Economics and Statistics, vol. 61, nº 2; 199-205. •POTERBA, J.M. (1984): “Tax subsidies to owner-occupied housing: an asset-market approach”. Quarterly Journal of Economics, vol. 94; pp. 729-752. •POTERBA, J.M. (1992): “Taxation and housing: old questions, new answers”. AEA Papers and Prodedings, Empirical Public Finance, vol. 82(2); 237-242. •RAPAPORT, C. (1997): “Housing demand and community choice: an empirical analysis”. Journal of Urban Economics, 42; pp. 243-260. •ROSEN, H.S. (1979): “Housing decisions and the U.S. income tax. An econometric analysis”. Journal of Public Economics, 11; pp. 1-23. •ROSEN, H., ROSEN, K. y HOLTZ-EAKIN, D. (1984): “Housing tenure, uncertainty and taxation”. The Review of Economics and Statistics, vol. 66, nº 3; pp. 405-416. •SAN MARTÍN, I., NIETO, E. y GUTIÉRREZ, F. (1999): “El mercado de la vivienda: diferencias regionales”. Argentaria Mercado Inmobiliario; pp. 37-52. •SMITH, L.B., ROSEN, K.T. y FALLIS, G. (1988): “Recent developments in economic models of housing markets”. Journal of Economic Literature, vol. 26; pp. 2964. •THION, B. (1983): “Le marché inmobilier: un marché rationnel?”. Banque, 432; pp. 1087-1094. 38 •WHITE, M.J. y WHITE, L.J. (1977): “The tax subsidy to owner occupied housing: Who benefits?”. Journal of Public Economics, 3; pp. 111-126. 39
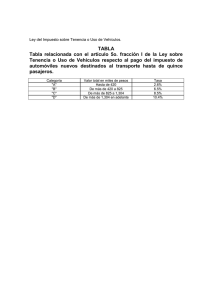


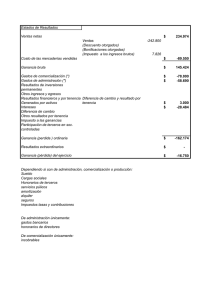

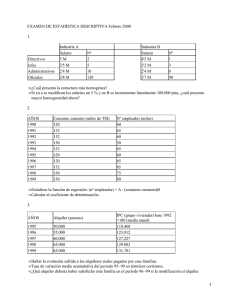
![Programa Taller Por politicas publicas de vivienda popular y seguridad de tenencia (S. Domingo, 19 de febrero de 2012).pdf [76,05 kB]](http://s2.studylib.es/store/data/002517871_1-105c5b4149d8fdce2c6ab1f5ad30ecb6-300x300.png)

