Trabajo Practico (Funciones de proporcionalidad)

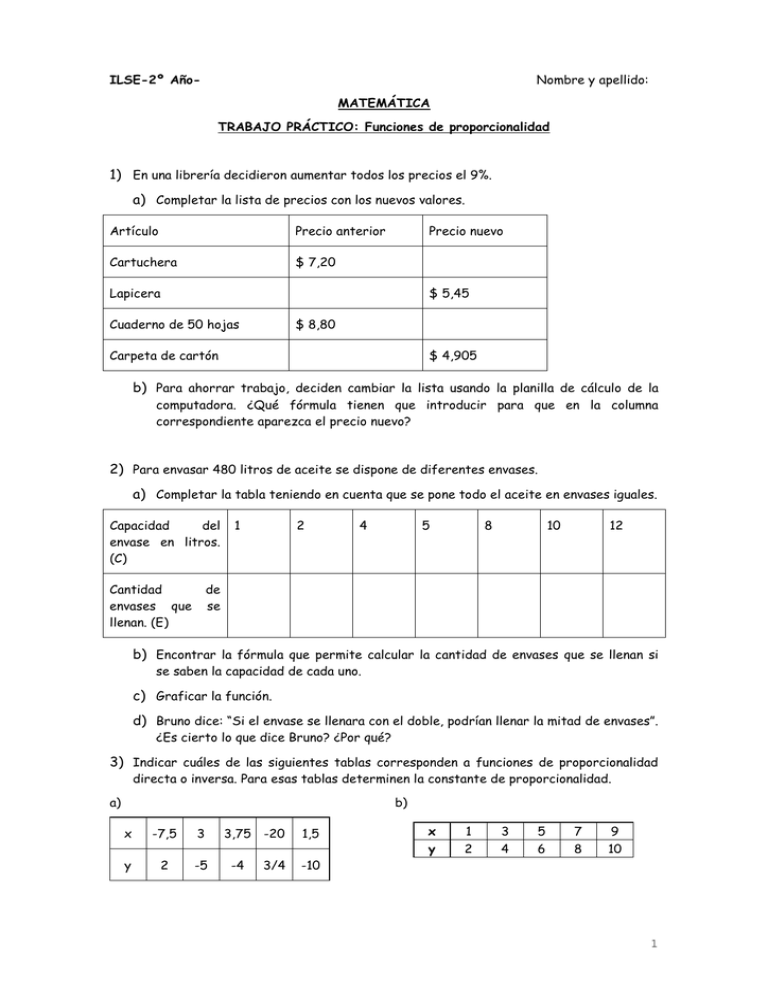
Nombre y apellido:
ILSE-2º AñoMATEMÁTICA
TRABAJO PRÁCTICO: Funciones de proporcionalidad
1) En una librería decidieron aumentar todos los precios el 9%.
a) Completar la lista de precios con los nuevos valores.
Artículo
Precio anterior
Cartuchera
$ 7,20
Precio nuevo
Lapicera
$ 5,45
Cuaderno de 50 hojas
$ 8,80
Carpeta de cartón
$ 4,905
b) Para ahorrar trabajo, deciden cambiar la lista usando la planilla de cálculo de la
computadora. ¿Qué fórmula tienen que introducir para que en la columna
correspondiente aparezca el precio nuevo?
2) Para envasar 480 litros de aceite se dispone de diferentes envases.
a) Completar la tabla teniendo en cuenta que se pone todo el aceite en envases iguales.
Capacidad
del
envase en litros.
(C)
Cantidad
envases que
llenan. (E)
1
2
4
5
8
10
12
de
se
b) Encontrar la fórmula que permite calcular la cantidad de envases que se llenan si
se saben la capacidad de cada uno.
c) Graficar la función.
d) Bruno dice: “Si el envase se llenara con el doble, podrían llenar la mitad de envases”.
¿Es cierto lo que dice Bruno? ¿Por qué?
3) Indicar cuáles de las siguientes tablas corresponden a funciones de proporcionalidad
directa o inversa. Para esas tablas determinen la constante de proporcionalidad.
a)
b)
x
-7,5
3
y
2
-5
3,75 -20
-4
3/4
1,5
x
y
1
2
3
4
5
6
7
8
9
10
-10
1
c)
d)
x
-1
1
-2/3 0,25 3/8
y
1
-1
3/2
4
x
y
-2
-2
-1
-4
-0.5
-8
0.5
8
1
4
-8/3
4) Indicar cuáles de los siguientes gráficos corresponden a funciones de proporcionalidad
directa o inversa. Determinar para esos gráficos, las respectivas constantes de
proporcionalidad.
a)
b)
c)
2
d)
e)
f)
− 1 ;4 


 2 3
3
5) Indicar
cuáles
de
las
siguientes
situaciones
corresponden
a
funciones
de
proporcionalidad directa, cuáles a funciones de proporcionalidad inversa y cuáles a
ninguna de las dos:
a) La cantidad de agua por minuto que arroja una bomba y el tiempo que tarda en
llenar una pileta determinada.
b) La altura de una pared de ancho constante y la cantidad de pintura necesaria
para pintarla.
c) El área de una pared y la cantidad de pintura necesaria para pintarla.
d) La cantidad de libros por estante y el número de estantes que se utilizan para
distribuir 200 libros en una biblioteca, colocando la misma cantidad de libros
por estante.
e) El peso y la altura de una persona.
f) El peso y la edad de una persona.
g) La cantidad de vasos que pueden llenarse con un litro de gaseosa y la capacidad
del vaso.
6) Considerar todos los rectángulos de perímetro 16 cm.
a) Construir la tabla de valores correspondiente a la altura “h” en función de la
base “b”.
b) Representar gráficamente.
c) Indicar si
Explicar.
se trata de una función de proporcionalidad directa o inversa.
7) Considerar todos los rectángulos de 16 cm2. de área.
a) Construir la tabla de valores correspondiente a la altura “h” en función de la base
“b”.
b) Representar gráficamente.
c) Indicar si se trata de una función de proporcionalidad directa o inversa. Explicar.
8) Considerar todos los triángulos equiláteros.
a) Construir la tabla de valores correspondiente a la altura “h” en función del lado
del triángulo “x”.
b) Expresar mediante una fórmula la relación entre la altura del triángulo y el lado
del mismo.
c) Representar gráficamente.
d) Indicar si se trata de una función de proporcionalidad directa o inversa.
Explicar.
4
9) Considerar todos los hexágonos regulares.
a) Construir la tabla de valores correspondiente al área “A” del hexágono en
función del lado del hexágono “x”.
b) Expresar mediante una fórmula la relación entre el área del hexágono y el lado
del mismo.
c) Representar gráficamente.
d) Indicar si se trata de una función de proporcionalidad directa o inversa.
Explicar.
10) Un rombo tiene la diagonal mayor igual al doble de la menor x, se pide:
a) Expresar:
i)
El lado del rombo en función de x.
ii) El perímetro del rombo en función de x.
iii) El área del rombo en función de x.
b) Representar gráficamente cada una de las funciones anteriores.
c) Indicar si alguna de las funciones del ítem a) es proporcionalidad directa o inversa.
11) Un cubo tiene la diagonal x.
a) Expresar, en función de la diagonal:
i)
La diagonal de una cara del cubo.
ii) La arista del cubo.
iii) El área total del cubo.
iv) El volumen del cubo
b) Representar gráficamente cada una de las funciones anteriores.
c) Indicar si alguna de las funciones del ítem a) es proporcionalidad directa o inversa.
12) Un prisma recto tiene 80 cm3. de volumen y altura x.
a) Expresar la superficie de la base en función de la altura x.
b) Calcular la superficie de la base si la altura es 5 cm.
c) ¿Qué valor debe tomar la altura para que la superficie de la base sea 12,50
cm2.?
d) Si la base del prisma es cuadrada y su altura es 20 cm, ¿cuál es su superficie
lateral?
e) Representar gráficamente la función obtenida en el ítem a) e indicar si la
misma es de proporcionalidad directa o inversa. Justificar.
13) Los gastos de un edificio de 6 departamentos se reparten en forma proporcional a la
superficie de cada uno. Los metros cuadrados de cada departamento se detallan en el
siguiente cuadro:
5
A
B
C
D
E
F
42m2
50 m2
65 m2
65 m2
80 m2
82 m2
Si los gastos del mes son de $960 ¿cuánto debe pagar el dueño de cada departamento?
14) Si a temperatura constante, el volumen V que ocupa un gas es inversamente proporcional a
la presión P que soporta, ¿qué sucede con el volumen V cuando la presión P
a) aumenta al doble?
b) disminuye a su tercera parte?
15) En una función de proporcionalidad directa definida de R en R se cumple que f(5)=3.
Hallar su fórmula y representar gráficamente.
16) En una función de proporcionalidad inversa, f(1/2)=4. Expresar la función y
representarla.
17) Un señor decide dejar sus bienes a sus tres hijos, un varón y dos mujeres. El
testamento dice que cada mujer recibirá una parte proporcional a su edad en el
momento de la muerte del padre y el varón una parte proporcional al doble de su edad
en el mismo momento. Cuando se hace el testamento, la edad del hijo varón es 20 y las
mujeres tienen 17 y 23 años respectivamente.
Si el padre muriese 10 años después de haber hecho el testamento y el monto de la
herencia es de $1.200.¿Cuánto recibiría cada hijo?
18) Un teatro reparte 2000 entradas entre 4 colegios proporcionalmente al número de
alumnos. El colegio A cuenta con 560 alumnos, el B con 640, C con 1210 y D con 790.
¿Cuántas entradas corresponden a cada uno?
19) Un hombre gana en un juego de azar y desea repartir el dinero entre sus tres hijos en
forma proporcional a las edades que son 10, 15 y 20 años. La cantidad correspondiente
al mayor y al menor suma 4.200 $. ¿Cuánto corresponde a cada uno?
6