Criterio de la segunda derivada
Anuncio
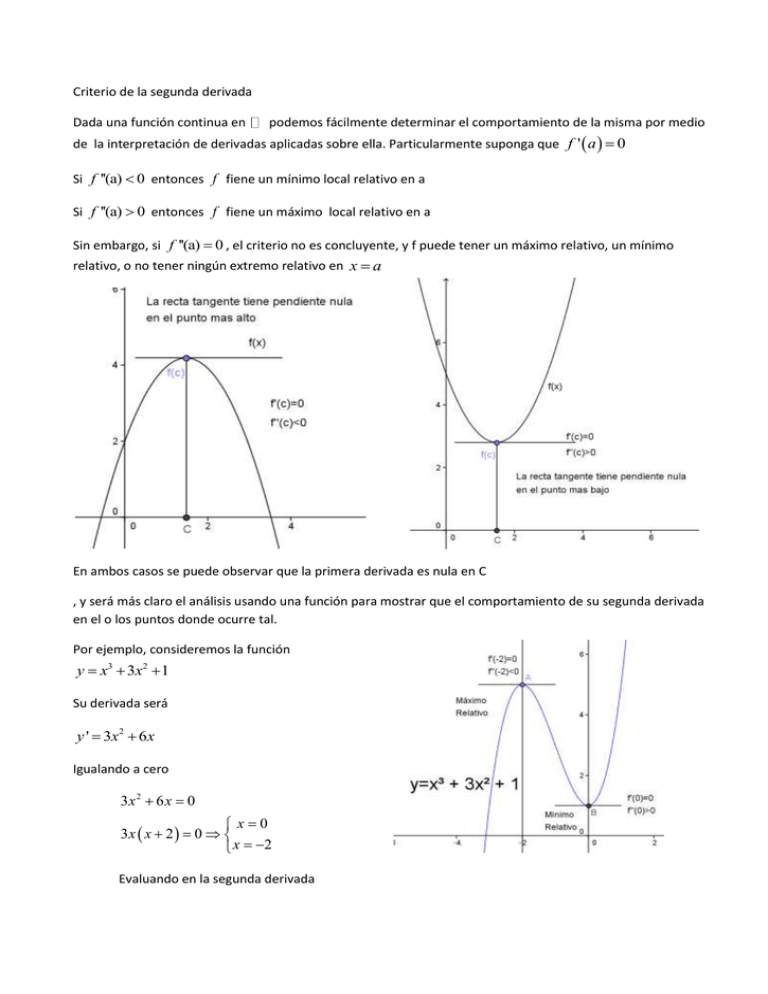
Criterio de la segunda derivada Dada una función continua en podemos fácilmente determinar el comportamiento de la misma por medio de la interpretación de derivadas aplicadas sobre ella. Particularmente suponga que f ' a 0 Si f ''(a) 0 entonces f fiene un mínimo local relativo en a Si f ''(a) 0 entonces f fiene un máximo local relativo en a Sin embargo, si f ''(a) 0 , el criterio no es concluyente, y f puede tener un máximo relativo, un mínimo relativo, o no tener ningún extremo relativo en x a En ambos casos se puede observar que la primera derivada es nula en C , y será más claro el análisis usando una función para mostrar que el comportamiento de su segunda derivada en el o los puntos donde ocurre tal. Por ejemplo, consideremos la función y x3 3x2 1 Su derivada será y ' 3x2 6x Igualando a cero 3x 2 6 x 0 x0 3x x 2 0 x 2 Evaluando en la segunda derivada y '' 6 x 6 y ''(0) 6 0 6 6 positivo mínimo y ''(2) 6 2 6 6 negativo máximo La idea básica de modelación parte en comprender el problema planteado y luego establecer una situación algebraica que describa tal. La clave está en contar con un adecuado manejo de lenguaje algebraico Ejercicios En los siguientes problemas determine el máximo y mínimo si e que existen de la función dada en el intervalo especificado f x x2 4x 5; 3 x 1 1 1 f x x ; x 3 x 2 f x x3 3x2 1; 3 x 2 f x 1 f x x ; x 0 x 1 3 x 9 x;0 x 2 3 f x 2x f x x5 5x4 1;0 x 5 32 ;x 0 x f x 1 ;x 0 x f x 1 ;x 0 x2 f x x 2 4 ; 3 x 2 f x 1 ;x 0 x 1 x2 1 f x ; 2 x x 1 2 f x f x 3x5 5x3 ; 2 x 0 f x 10x6 24x5 15x4 3; 1 x 1 5 1 x 1 2 ;x 0 En los siguientes problemas resuelva el problema de optimización y verifique usando el criterio de la segunda derivada para encontrar el punto de máximo o mínimo, según corresponda. 1. Suponga que x años después de su fundación en 1978, cierta asociación nacional de 3 2 consumidores tenía un total de f x 100 2 x 45 x 264 x integrantes. ¿En qué momento, entre 1978 y 1992, fue mayor el número de miembros de la asociación?¿cuántos eran los afiliados en ese momento? ¿En qué momento, entre 1978 y 1992, fue menor el número de miembros de la asociación?¿cuántos eran los afiliados en ese momento? 2. Una estación de radio que solo emite noticias ha realizado una encuesta sobre los hábitos de escucha de los residentes locales entre las 17.00 y la medianoche. La encuesta revela que el porcentaje de población adulta local que sintoniza la estación x horas después de las 5 pm es f ( x) = 1 -2x 3 + 27x 2 -108x + 240 ) ( 8 3. ¿ En que momento entre las 5:00 P.M. y la media noche escucha la emisora el mayor numero de personas? ¿Que porcentaje de la población escucha en ese momento? ¿ en que momento el menor número de personas? 4. Se tendera un cable desde una central eléctrica situada al lado de un rio de 900 metros de ancho hasta una fabrica situada al otro lado del rio, 3000 metros rio abajo. El costo por tender el cable bajo agua es de us$5 por metro y el costo sobre tierra es de US$4. Por metro . ¿cuál es la ruta mas económica? 5. Cada maquina de cierta fabrica puede producir 50 unidades por hora. El costo de puesta en marcha es de US$80 por maquina y el costo de operación es de US$5 por hora. ¿Cuantas maquinas deben emplearse para producir 8000 unidades el menor costo posible? ( recuerde que su respuesta debe ser un numero entero) 6. Se construirá un envase cilíndrico sin tapa para contener un volumen fijo de liquido. El costo del material usado para la parte inferior es de 3 centavos de dólar por pulgada cuadrada y el del lado curvado de 2 centavos de dólar por pulgada cuadrada. Determine una relación simple entre el radio y la altura del envase menos costoso. 7. Se estima que el costo de construcción de un edificio de oficinas que tiene n pisos d altura es C ( n ) = 2n2 + 500n + 600 miles de dólares. ¿cuántos pisos debería tener el edificio para minimizar el costo medio por piso? 8. Un impresor recibe un pedido para producir un cartel rectangular con 25 cm2 de impresión rodeados de márgenes de 2 cm a cada lado y 4 cm arriba y abajo. ¿cuáles son las dimensiones de la piza de papel mas pequeña que puede utilizarse par hacer el cartel? ( elija los valores apropiados para que los cálculos no sean tan complicados) 9.