tesis doctoral
Anuncio
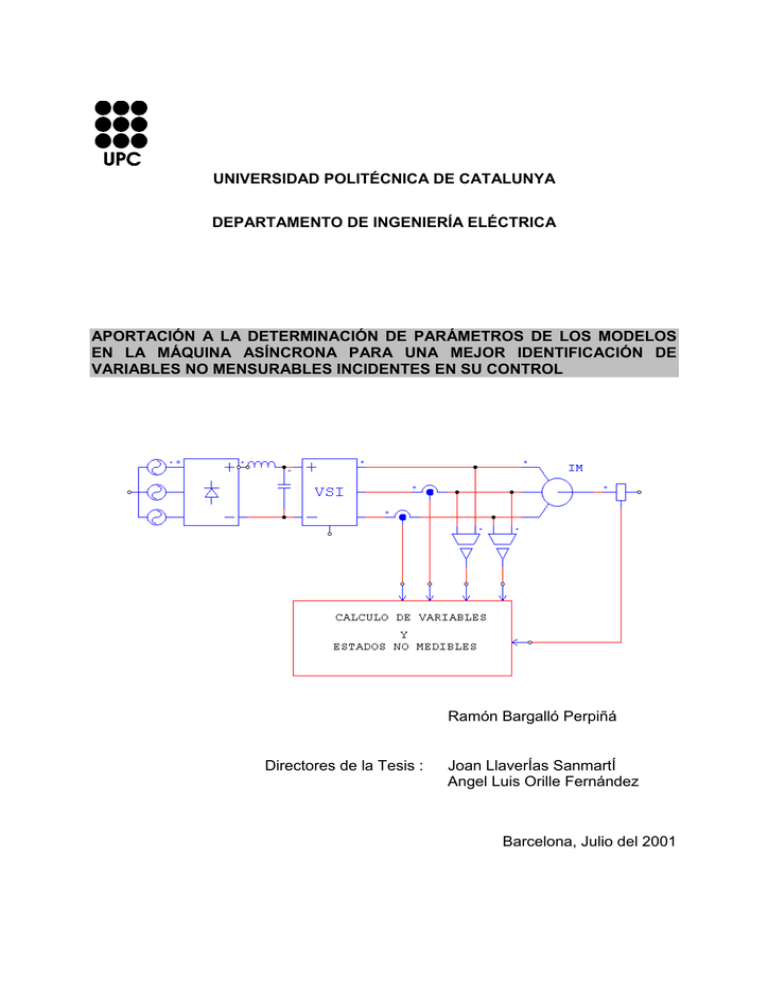
UNIVERSIDAD POLITÉCNICA DE CATALUNYA
DEPARTAMENTO DE INGENIERÍA ELÉCTRICA
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS
EN LA MÁQUINA ASÍNCRONA PARA UNA MEJOR IDENTIFICACIÓN DE
VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
Ramón Bargalló Perpiñá
Directores de la Tesis :
Joan LlaverÍas SanmartÍ
Angel Luis Orille Fernández
Barcelona, Julio del 2001
“En Física, como en las otras ciencias, puede demostrarse propter quid;
sin embargo el orden de la Ciencia quiere que se empiece por las cosas
más conocidas y fáciles y, por tanto, hay que proceder, en general, del
efecto a la causa: a posteriori, pues, conoceremos la materia, la forma y
la mayoria de las cosas, pues no podemos probarlo todo a priori”
Guillermo de Occam
Filósofo Inglés
(1295-1349/50)
........
Porque en la ciencia, como en la naturaleza, a menudo lo que funciona
es la solución más simple, la obvia.
Anónimo
INTRODUCCIÓN
INTRODUCCIÓN
1
INTRODUCCIÓN
A MODO DE INTRODUCCIÓN
Al analizar el funcionamiento de las máquinas eléctricas dudamos acerca de la
elección de, uno u otro, conjunto de variables, modelos, o conjunto de parámetros.
En este trabajo se han encontrado, frecuentemente, resultados que contradicen lo
medido experimentalmente, o tiempos de cálculo muy diversos según el modelo
adoptado o el tipo de simulación realizada; cosa por otra parte lógica en un ámbito
que admite aportaciones de mejora.
La necesidad de una buena modelización actualmente se plantea como una
premisa para obtener un mejor control y un adecuado dimensionado de los
accionamientos; con este fin se aborda este trabajo determinando la secuenciación
que sigue.
En primer lugar (Capítulo 1) se repasan los antecedentes y estado actual.
Seguidamente se ha planteado (Capítulo 2) el estudio de modelos de máquinas
asíncronas con caracterización de la saturación; existen diversos modelos que lo
posibilitan a costa de una mayor o menor dificultad de cálculo y resolución. La línea
escogida toma un modelo transformado que reduce el número de parámetros a
encontrar o estimar; en algunos de los modelos planteados se reduce la carga de
cálculo necesaria para su resolución. Asimismo se plantea el análisis de sensibilidad
de la respuesta (Capítulo 3) respecto a las variaciones de los parámetros; es
evidente que habrá parámetros que tendrán escasa influencia en la respuesta del
sistema, así como otros que influirán de forma directa e inmediata en la misma.
Una vez establecido el modelo, o modelos a utilizar, deben encontrarse los
parámetros de los mismos. Una primera parte se dedica a la determinación de
parámetros mediante ensayos fuera de línea (Capítulo 4), lo que permite
aproximarnos a la solución deseada. La determinación de parámetros mediante
ensayos en línea y técnicas de estimación en tiempo real (Capítulo 5), junto con la
consideración, en su caso, de observadores para variables auxiliares como el flujo,
permiten cerrar el capítulo de estimación de parámetros.
La determinación de variables auxiliares como los pares electromagnético y de carga
(Capítulo 6), es el objetivo final del trabajo. La aplicación de observadores y
estimadores permite la obtención de las variables deseadas, resultando un modelo
mas preciso y exacto.
A modo de aplicación se ha obtenido un medidor de par en régimen transitorio;
aspecto colateral del trabajo que resulta relevante dado que no se dispone,
actualmente, de un medidor de par con estas características. El equipo desarrollado
se basa en un conjunto que comprende máquina de corriente continua y sistema de
control.
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
INTRODUCCIÓN
2
Finalmente se aborda la modelización conjunta del sistema convertidor-máquinacarga (Capítulo 7). No se pretende analizar a fondo la modelización del convertidor,
ello podría ser objeto de un estudio más específico; no obstante la influencia que
tiene el tipo de señal aplicada a la máquina, aconseja su consideración con el fin de
obtener resultados más reales que una suposición de alimentación sinusoidal
permitirían.
Se finaliza con un capítulo final de discusiones (Capítulo 8) de los resultados
obtenidos, a los que siguen aquellas aplicaciones que se entienden como mejoradas
por este trabajo, así como las pertinentes conclusiones, tal como indica el gráfico
siguiente.
Cierra el documento una relación bibliográfica (Bibliografía) relevante y un apartado
de anexos donde se añaden deducciones matemáticas prolíficas tales como las de
las ecuaciones de sensibilidad (Anexo I), el cálculo de las ganancias del observador
(Anexo II) las características de las máquinas ensayadas (Anexo III) y .el método de
los mínimos cuadrados. Aplicaciones (Anexo IV).
Agradecimientos
Este trabajo ha sido parcialmente subvencionado por la CICYT TAP97-0969-C03-03.
Gracias a todos los compañeros que me han animado y criticado; recuerdo frases
del tipo:
“No entiendo nada pero esas ecuaciones tienen un aspecto formidable”
“¿Sirve para algo?”
“ Y esto, ¿qué te aporta?”
“Asegura el resultado porque no puede estar bien, es demasiado fácil”.
Gracias por el sarcasmo que ha servido para replantearme temas que,
evidentemente, no serian lo que son sin estos comentarios.
Gracias a los que me han ayudado a solucionar los inevitables problemas que suele
acarrear el desarrollo de equipos experimentales.
Finalmente, gracias a los que me rodean y que han soportado mi malhumor cuando
las cosas no salían como deseaba.
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
INTRODUCCIÓN
3
Modelos
para
máquinas
asíncronas
- Caracterización de la saturación
- Sensibilidad de los modelos a las
variaciones en los parámetros
Modelización del
convertidor
Estimación de parámetros
Ensayos fuera de línea
Identificación en tiempo real
Observadores para variables no
mensurables
- Flujo
- Par interno
- Par de carga
Aplicaciones. Discusión
de los resultados
Conclusiones
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ÍNDICE
ÍNDICE
1
ÍNDICE GENÉRICO
LISTA DE SÍMBOLOS
1. ANTECEDENTES Y ESTADO ACTUAL
1.1
2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA
SATURACIÓN
2.1
3. SENSIBILIDAD
3.1
4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS
FUERA DE LÍNEA
4.1
5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y
PARÁMETROS EN SERVICIO
5.1
6. APLICACIONES
6.1
7. MODELIZACIÓN DEL CONVERTIDOR
7.1
8. DISCUSIÓN DE LOS RESULTADOS.
CONCLUSIONES Y APORTACIONES
8.1
BIBLIOGRAFÍA
B.1
ANEXO I. EXPRESIONES PARA EL CÁLCULO DE LA SENSIBILIDAD
AI
ANEXO II. CALCULO DE LA GANANCIA DEL OBSERVADOR.
FÓRMULA DE ACKERMANN
AII
ANEXO III. MÁQUINAS ENSAYADAS
AIII
ANEXO IV. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS.
APLICACIONES
AIV
APORTACION A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ÍNDICE
1. ANTECEDENTES Y ESTADO ACTUAL
Modelos
Métodos. Observación y estimación de estados
Aplicaciones. Equipo para la medida del par en régimen Transitorio
PALABRAS CLAVE
2. MODELOS PARA LA MÁQUINA ASÍNCRONA CON
CONSIDERACIÓN DE LA SATURACIÓN
MODELIZACIÓN DE LOS EFECTOS DE LA SATURACIÓN
ECUACIONES DE LA MÁQUINA TENIENDO EN CUENTA LA SATURACIÓN.
CONSIDERACIÓN DE DIVERSOS CONJUNTOS DE VARIABLES DE ESTADO.
Variables de estado corrientes de estator y rotor. Modelo 1.
10
Variables de estado los flujos de estator y rotor. Modelo 2.
11
Variables de estado la corriente de estator y El flujo
magnetizante. Modelo 3.
Variables de estado las corrientes de estator y el flujo
del rotor. Modelo 4.
Variables de estado la corriente de estator y la
magnetizante. Modelo 5.
MODELOS SIMPLIFICADOS.
MODELOS CON SATURACIÓN DEPENDIENTE DE LAS
COMPONENTES DEL PROPIO EJE.
Variables de estado corrientes de estator y rotor. Modelo 6
Variables de estado los flujos de estator y rotor. Modelo 7.
Variables de estado la corriente del estator y el flujo
magnetizante. Modelo 8.
Variables de estado la corriente del estator y el flujo
del rotor. Modelo 9.
Variables de estado las corrientes del estator y
magnetizante. Modelo 10.
MODELOS EN T Y EN Γ
Variables de estado las corrientes de estator y rotor. Modelo 11.
Variables de estado los flujos de estator y rotor. Modelo 12.
Variables de estado la corriente de estator y el flujo
magnetizante. Modelo 13.
Variables de estado las corrientes de estator y el flujo
del rotor. Modelo 14.
Variables de estado las corrientes del estator y
magnetizante. Modelo 15.
Variables de estado las corrientes del estator y rotor. Modelo 16
Variables de estado los flujos del estator y rotor. Modelo 17.
Variables de estado la corriente de estator y el flujo
magnetizante. Modelo 18.
Variables de estado la corriente de estator y el flujo
de rotor. Modelo 19.
Variables de estado las corrientes del estator y
magnetizante. Modelo 20.
Variables de estado las corrientes del estator y rotor. Modelo 21.
Variables de estado los flujos del estator y rotor. Modelo 22.
Variables de estado la corriente del estator y el flujo
magnetizante. Modelo 23
Variables de estado la corriente del estator y el flujo
del rotor. Modelo 24.
Variables de estado las corrientes del estator y
magnetizante. Modelo 25.
Variables de estado las corrientes del estator y rotor. Modelo 26.
Variables de estado los flujos del estator y rotor. Modelo 27.
2
2
2
4
5
5
3
7
9
13
14
15
16
16
16
17
18
19
.
20
21
23
24
25
26
27
28
29
30
30
31
32
33
34
35
36
37
38
APORTACION A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ÍNDICE
Variables de estado la corriente del estator y el flujo
magnetizante. Modelo 28.
Variables de estado la corriente del estator y el flujo
de rotor. Modelo 29.
Variables de estado las corrientes del estator y
magnetizante. Modelo 30.
MODELOS BASADOS EN LA ORIENTACIÓN DEL CAMPO.
Variables de estado las corrientes del estator y rotor. Modelo 31.
Variables de estado los flujos del estator y rotor. Modelo 32.
Variables de estado la corriente del estator y el flujo
magnetizante. Modelo 33.
Variables de estado la corriente del estator y el flujo
del rotor. Modelo 34.
Variables de estado las corrientes del estator y
magnetizante. Modelo 35.
Variables de estado las corrientes del estator y rotor. Modelo 36.
Variables de estado los flujos del estator y rotor. Modelo 37.
Variables de estado la corriente del estator y el flujo
magnetizante. Modelo 38.
Variables de estado la corriente del estator y el flujo
del rotor. Modelo 39.
Variables de estado las corrientes del estator y
magnetizante. Modelo 40.
Variables de estado las corrientes del estator y rotor. Modelo 41.
Variables de estado los flujos del estator y rotor. Modelo 42.
Variables de estado la corriente del estator y el flujo
magnetizante. Modelo 43.
Variables de estado la corriente del estator y el flujo
de rotor. Modelo 44.
Variables de estado las corrientes del estator y
magnetizante. Modelo 45
RESUMEN COMPARATIVO DE LOS DISTINTOS MODELOS.
MODELOS BASADOS EN LA ORIENTACIÓN DEL CAMPO.
MODELOS BASADOS EN LA ORIENTACIÓN DEL CAMPO.MODELOS
TIPO Γ(I). CANCELACIÓN DE LSL.
MODELOS BASADOS EN LA ORIENTACIÓN DEL CAMPO. MODELOS
TIPO Γ (II). CANCELACIÓN DE LRL.
CONCLUSIONES.
3
39
39
40
41
41
42
43
43
44
45
45
46
47
47
48
48
49
49
49
50
52
52
53
53
3. SENSIBILIDAD
Ecuaciones de sensibilidad de un sistema dinámico.
Aplicación al caso de una bobina saturada.
Aplicación a las ecuaciones de la máquina asíncrona.
CONCLUSIONES.
2
2
4
10
31
4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
Ensayos a potencia útil nula
Modelización de la saturación.
Caracterización mediante polinomios [ Justus 91].
Aplicación a la caracterización de la curva de saturación de un transformador.
Aplicación a la modelización de características de saturación para
la máquina asíncrona.
Trabajo en vacío.
Trabajo a rotor frenado.
Resultados experimentales de contrastación.
CONCLUSIONES.
2
2
6
7
10
12
13
14
16
22
APORTACION A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ÍNDICE
4
5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
Observador para el flujo de la máquina asíncrona.
Modelo discreto para el observador.
Estimación de los parámetros(coeficientes) del modelo.
Parámetros(coeficientes) eléctricos.
Estimación del par electromagnético. Estimación de parámetros(coeficientes) mecánicos.
Contrastación experimental.
MODELO COMPLETO
Modelo reducido.
CONCLUSIONES.
Modelo completo:
Modelo reducido:
Parámetros mecánicos:
2
3
6
44
44
46
47
48
60
72
73
73
73
6. APLICACIONES.
Equipo para la determinación del par instantáneo.
Control por corriente de la máquina de corriente continua.
Estimación del par de carga.
Estimación del par electromagnético de la máquina asíncrona.
Resultados de simulación.
Contrastación experimental.
CONCLUSIONES.
2
2
3
4
7. MODELIZACIÓN DEL CONVERTIDOR
Función de conexión [Hautier 99].
Funciones de conversión.
Generalización de la modelización.
Conversión de tensiones.
Conversión de corrientes.
Aplicación a las estructuras convertidoras clásicas.
Convertidor 2/2.
Convertidor 3/2.
Convertidor 2/3.
Formulación del sistema completo de ecuaciones.
Aplicación a la modelización del transformador trifásico.
Aplicación al caso del conjunto convertidor+filtro de entrada+carga R+L+E.
Aplicación al caso del conjunto convertidor+filtro de entrada+máquina asíncrona+carga.
Aplicación al conjunto ondulador de corriente+filtro de salida +carga accionada.
Función generatriz de conversión.
Estructuras de control basadas en las funciones generatrices de modulación.
Aportación experimental: caso del conjunto máquina asíncrona+convertidor+carga.
CONCLUSIONES
2
2
3
7
9
10
11
11
12
13
14
16
18
20
27
31
36
37
40
5
8
10
APORTACION A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ÍNDICE
5
8. DISCUSIÓN DE RESULTADOS. CONCLUSIONES Y APORTACIONES
Modelos de máquinas asíncronas considerando la saturación.
Sensibilidad.
Obtención de los parámetros por ensayos fuera de línea.
Obtención de variables no medibles y parámetros en servicio.
Modelo completo:
Modelo reducido:
Parámetros mecánicos:
Modelización del convertidor.
Aplicaciones.
Futuros desarrollos.
2
2
3
4
4
6
7
7
8
8
9
BIBLIOGRAFIA
LIBROS
Máquinas Eléctricas. Teoria. Modelización. Control
Convertidores. Modelización. Control
Identificación de sistemas
Sensibilidad
Control no Lineal. Técnicas. Observadores.
TESIS DOCTORALES
ARTÍCULOS, PONENCIAS, COMUNICACIONES
Articulos sobre modelización de máquinas. Obtención de parámetros
y observación de variables no medibles y estados
Articulos sobre Control de Máquinas Asíncronas
Articulos històricos sobre modelización de máquinas y convertidores
PROYECTOS FINAL DE CARRERA
2
2
2
3
3
4
4
4
5
ANEXO I. EXPRESIONES PARA EL CÁLCULO DE LA SENSIBILIDAD
AI
ANEXO II. CALCULO DE LA GANANCIA DEL OBSERVADOR.
FÓRMULA DE ACKERMANN
AII
ANEXO III. MÁQUINAS ENSAYADAS
Características de las máquinas ensayadas.
Ensayos en vacío y cortocircuito a frecuencia nominal
Máquina nº1
Máquina nº2
Máquina nº3
ensayo a rotor frenado realizado a frecuencia de deslizamiento. máquina nº 2
ensayo en carga. máquina nº 2
Ficha del ensayo
AIII
2
2
2
3
4
5
7
9
ANEXO IV. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
Caracterización en línea.
Determinación de parámetros
Caso 1: N = np
Caso 2: N ≠ np
Método de los mínimos cuadrados
Estimación Recursiva de Mínimos Cuadrados.
RESTRICCIONES AL MÉTODO
Aplicación al caso de un transformador
resultados de simulación
Contrastación experimental. aplicación al caso de un transformador en vacío
CONCLUSIONES
2
2
3
3
3
4
5
7
8
9
29
34
5
7
7
8
APORTACION A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
LISTADO DE SIMBOLOS
LISTADO DE SÍMBOLOS
1
LISTADO DE SIMBOLOS
Variables
Tensiones
v, u
v
usA, usB, usC
urA, urB, urC
us
ur
u sg
tensión (V)
vector tensión (V) – en el sentido matricial del termino
tensión estatórica, fases a, b, c respectivamente (V)
tensión rotórica, fases a, b, c (V)
vector espacial de tensión estatórica; ref. fija (V)
vector espacial de tensión rotórica; ref. fija (V)
vector espacial de tensión estatórica; ref. genérica (V)
u rg
vector espacial de tensión rotórica;ref. genérica (V)
u s0
u s0 , u r 0
usx
usy
urx
ury
tensión homopolar (V)
tensión homopolar estatórica, rotórica (V)
tensión estatórica; componente real (V)
tensión estatórica; componente imaginaria (V)
tensión rotórica; componente real (V)
tensión rotórica; componente imaginaria (V)
Corrientes
i
isA, isB, isC
irA, irB, irC
is
ir
i sg
corriente (A)
corriente estatórica, fases a, b, c (A)
corriente rotórica, fases a, b, c (A)
vector espacial de corriente estatórica; referencia fija (A)
vector espacial de corriente rotórica; ref. fija (A)
vector espacial de corriente estatórica; ref. genérica (A)
i rg
vector espacial de corriente rotórica; ref. genérica (A)
is0
is0 , ir 0
i mg
corriente homopolar (A)
corriente homopolar estatórica, rotórica (A)
corriente magnetizante; ref. genérica (A)
i msg
corriente magnetizante estatórica; ref. genérica (A)
i mrg
corriente magnetizante rotórica; ref. genérica (A)
∆i
imx
imy
isx
isy
irx
iry
variación de corriente (A)
corriente magnetizante; componente real (A)
corriente magnetizante; componente imaginaria (A)
corriente estatórica; componente real (A)
corriente estatórica; componente imaginaria (A)
corriente rotórica; componente real (A)
corriente rotórica; componente imaginaria (A)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
LISTADO DE SÍMBOLOS
2
Flujos
ψ
ΨsA, ΨsB, ΨsC
ΨrA, ΨrB, ΨrC
Ψs
Ψr
Ψsg
flujo (Vs)
flujo estatórico, fases a, b, c (Vs)
flujo rotórico, fases a, b, c (Vs)
vector espacial de flujo estatórico;ref. fija (Vs)
vector espacial de flujo rotórico; ref. fija (Vs)
vector espacial de flujo estatórico;ref. genérica (Vs)
Ψrg
vector espacial de flujo rotórico; ref. genérica (Vs)
Ψs 0
Ψr 0
∆ψ
Ψmx
Ψmy
Ψm
Ψsx
Ψsy
Ψs
Ψrx
Ψry
Ψr
ΨN
vector espacial de flujo homopolar estatórico;ref. genérica (Vs)
vector espacial de flujo homopolar rotórico; ref. genérica (Vs)
variación de flujo (Vs)
flujo magnetizante; componente real (Vs)
flujo magnetizante; componente imaginaria (Vs)
flujo magnetizante (Vs)
flujo estatórico; componente real (Vs)
flujo estatórico; componente imaginaria (Vs)
flujo estatórico (Vs)
flujo rotórico; componente real (Vs)
flujo rotórico; componente imaginaria (Vs)
flujo rotórico (Vs)
flujo nominal (Vs)
Par, velocidad
Me
Mc
n
ωr
ωrm
ω, ωg
θr
θrm
par electromagnético, par interno (Nm)
par de carga (Nm)
velocidad de rotación (min-1)
velocidad de rotación (eléctrica) (rad/s)
velocidad mecánica de rotación (rad/s)
velocidad genérica del sistema de coordenadas (rad/s)
ángulo eléctrico (rad)
ángulo mecánico (rad)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
LISTADO DE SÍMBOLOS
3
Parámetros
Eléctricos
L
Lss, Ls
Lrr, Lr
Lm
Lddm
Lqqm
Ldq
Lsl
Lrl
L’sl
L’rl
L’m
L(i)
Lm(i)
Ls0, Ls0
[M]
[Ms], [Mr], [Msr]
Ms, Mr
Rs, rs
Rr, rr
Rs0, Rr0
coef. de autoinducción (H)
coeficiente de autoinducción estatórico (=Lsl+Lsm) (H)
coeficiente de autoinducción rotórico (=Lrl+Lrm) (H)
coef. de inducción mútua estator-rotor (H)
coef. de acoplamiento estator-rotor; eje directo (H)
coef. de acoplamiento estator-rotor; eje en cuadratura (H)
coef. de acoplamiento entre ejes
inductáncia de dispersión estatórica (H)
inductáncia de dispersión rotórica (H)
inductáncia de dispersión estatórica; modelo Γ(II) (H)
inductáncia de dispersión rotórica; modelo Γ(I) (H)
inductáncia mútua; modelos Γ(I), Γ(II) (H)
inductáncia dinámica (H)
inductáncia estática (H)
coef. autoinducción homopolar estatórico, rotórico (H)
matriz de acoplamiento
matriz de acoplamiento estatórico, rotórico, estator-rotor
coeficiente de inducción mútua estatórico, rotórico (H)
resisténcia estatórica (fase) (Ω)
resisténcia rotórica (fase) (Ω)
resistencia homopolar estatórica, rotórica (Ω)
Mecánicos
J
ρ
momento de inercia (kgm2)
coeficiente de rozamiento (Nm/rad/s)
Constructivos
D
l
Ns, Nr
P,p
δ
σsl, σrl
diámetro en el entrehierro (m)
longitud axial (m)
número de espiras equivalentes por fase de estator, rotor
pares de polos
espesor del entrehierro (m)
coef. de dispersión del estator, rotor
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
LISTADO DE SÍMBOLOS
4
Saturación
a
a1, a2, a3, a, b,
n, m
f(i)
g(Ψ)
I*
IN
iµc
iµsat
ka,kb, kc, kd, ke
ψr
ψsat
ψ*
relación de reducción estator-rotor
coeficientes característicos de la función de saturación
función de saturación
función de saturación
corriente en p.u.
corriente para la cual se obtiene el flujo nominal ΨN (A)
corriente coercitiva (A)
corriente de saturación (A)
parámetros característicos de la modelización del ciclo de
histéresis
flujo remanente (Vs)
flujo de saturación (Vs)
flujo en p.u.
Modelización del convertidor
fci
fg(k,t)
F
Fc(s)
F0
Fr
Ge
Gm
ici
ic
Is, Im
mg
mij
Mi
Mr
Mu
nj
Rcv
vc
vci
V0
Vs, Vm
función de conexión del interruptor i
función generatriz muestreada
matriz de funciones de conexión
función de transferéncia para la función generatriz de conversión
matriz de funciones de conexión en conducción discontinua
matriz reducida de funciones de conexión
vector de magnitudes a conmutar (Vs Is)T
vector de magnitudes conmutadas (Vm Im)T
corriente que atraviesa el interruptor i (A)
corriente a conmutar (A)
vectores de corrientes (V)
función generatriz de conversión
funciones compuestas de conversión
matriz reducida de funciones compuestas de conversión para
corrientes
matriz de conversión (generalizada)
matriz reducida de funciones compuestas de conversión para
tensiones
funciones simples de conversión
matriz relación de conversión entre funcion de conexión y
tensión a conmutar (V)
tensión entre bornes del interruptor i (V)
vector tensión en régimen discontinuo (V)
vectores de tensiones (V)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
LISTADO DE SÍMBOLOS
5
Ecuaciones de estado; observadores; identificación
A
B, Be, Bm
C,Cs
D, De, Dm
e(k)
F
G
h
K(k)
K
ksx, ksy, krx, kry
P(λ)
P(k)
Wo
X
Y
y(k)
^
δ
ϕ(k)
θ
γ
ε
matriz del sistema
matriz de entradas
matriz de observación
matriz de transferencia directa
error de medida
matriz del sistema (tiempo discreto)
matriz de entrada (tiempo discreto)
período de muestreo
ganancia del algoritmo de adaptación
ganancia del observador
ganancias del observador
polinomio característico
matriz de covariancias
matriz de observabilidad
vector de estados
vector de salidas
conjunto de medidas
todas las variables que llevan circunflejo son observadas
operador delta
conjunto de funciones consideradas para la identificación
vector de parámetros a estimar
ganancia del observador
error
Sensibilidad
γjk
σjk
p0
sensibilidad de la variable de estado k respecto del parámetro j
sensibilidad de la variable de salida k respecto del parámetro j
vector de parámetros
Varios
C
PFe
Pvacio
Qµ
RFe
Xµ
Zb
Zcc
α
ϕ
µ
capacidad (F)
perdidas en el hierro (W)
perdidas en vacío (W)
potencia magnetizante (var)
resistencia de pérdidas en el hierro (Ω)
reactancia magnetizante (Ω)
impedancia equivalente en vacio (Ω)
impedancia de cortocircuito (rotor frenado) (Ω)
relación entre pérdidas y potencia magnetizante
desfase tensión-corriente (º)
angulo formado por el vector corriente magnetizante respecto el
eje de referencia (º)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
LISTADO DE SÍMBOLOS
6
Constantes
a, a2
µ0
π
operadores vectoriales de giro 120º y 240º respectivamente
permeabilidad del vacio (= 4π10-7 H/m)
3.1415926535
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANTECEDENTES Y ESTADO
ACTUAL
CAPÍTULO 1. ANTECEDENTES Y ESTADO ACTUAL
1
1. ANTECEDENTES Y ESTADO ACTUAL
1. ANTECEDENTES Y ESTADO ACTUAL
Modelos
Métodos. Observación y estimación de estados
Aplicaciones. Equipo para la medida del par en régimen transitorio
PALABRAS CLAVE
2
2
4
5
5
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 1. ANTECEDENTES Y ESTADO ACTUAL
2
1. ANTECEDENTES Y ESTADO ACTUAL
En los últimos años el aumento de las aplicaciones con control de velocidad y/o
posición de las máquinas eléctricas, ha puesto de manifiesto la necesidad de
modelización del conjunto convertidor+máquina+carga accionada y del estudio en
detalle del algoritmo de control aplicado.
Actualmente las investigaciones apuntan a la minimización del número de sensores
para la realización del control de las máquinas eléctricas. La determinación de una o
más variables de estado no mensurables, incluye el tópico relacionado con la
determinación de los parámetros del modelo de máquina: resistencias, inductancias
y su nivel de saturación, presente en mayor o menor medida en todos los regímenes
de funcionamiento de la misma.
Por otra parte, los mejores conocimientos en teoría de control y la aplicación de
algoritmos y técnicas de control no lineal (adaptativo, optimo, etc.), requieren una
elevada exactitud en el conocimiento de los parámetros en juego para lograr una
convergencia adecuada a la solución correcta.
Modelos
La transformación de la energía en un convertidor electromecánico es un fenómeno
de estructura compleja que comprende aspectos electromagnéticos, mecánicos y
térmicos; la imbricación de los mismos introduce grandes dificultades tanto en su
concepción y calculo como en la predeterminación de su comportamiento. Para
describir el fenómeno físico se recurre a modelos.
El modelo es una estructura conceptual que sugiere un marco de ideas para
conjuntos de descripciones, de otro modo no estructuradas, que promueven la
inteligibilidad del fenómeno real. Explicar la realidad de un fenómeno físico puede
realizarse mediante modelos distintos, aunque siempre los resultados del modelo
diferirán del fenómeno real; ya que si no fueran diferentes la estructura original seria
observacionalmente obvia; esta diferencia se reduce con la utilización de técnicas
descriptivas más refinadas.
Podemos considerar dos clases de modelos en el ámbito de las máquinas eléctricas:
•
Modelos Físico – matemáticos, basados en
electromagnético a partir de las ecuaciones de
técnicas numéricas del tipo elemento finito o
principalmente en el cálculo y diseño así como en
de las máquinas eléctricas.
•
Modelos Paramétrico – físicos, basados en la formulación concentrada de los
parámetros electromagnéticos. Son utilizados principalmente para el estudio del
comportamiento de las máquinas y dispositivos eléctricos.
la formulación del campo
Maxwell y su resolución por
diferencia finita. Se utilizan
el estudio del comportamiento
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 1. ANTECEDENTES Y ESTADO ACTUAL
3
Además en cualquier máquina o dispositivo eléctrico existen unas variables externas
cuyas magnitudes son de fácil y económica medida (tensión, corriente, velocidad), y
otras internas no mensurables (flujo, par).
El estudio lleva a la determinación del modelo, o modelos, a utilizar en función del
control y/o método de determinación de los parámetros deseado, así como la
definición del conjunto de los mismos, sus valores nominales, las leyes de variación
que los afectan y el efecto sobre otras magnitudes de interés. Es evidente que,
dadas las aplicaciones a considerar, se tendrán en cuenta los modelos del segundo
tipo. Asimismo al considerar que todas las máquinas trabajan en régimen de
saturación ha de tenerse en cuenta el estudio y caracterización de la misma.
La consideración de funciones del tipo Ψ = ϕ (i ) - saturación (figura 1)- resulta de
interés para valorar los efectos de la saturación en la respuesta del sistema y la
variabilidad de los parámetros correspondientes a los modelos. En casos especiales,
un modelo linealizado de la máquina y un control más complejo pueden dar una
mejor solución al problema.
1 ,4
1 ,2
1
0 ,8
0 ,6
0 ,4
0 ,2
0
0
1 0
2 0
3 0
4 0
Figura 1 Ψ = ϕ (i )
En la literatura se encuentran dos tipos de modelos:
•
•
Basados en técnicas de orientación del campo, lo que limita la validez de dicho
modelo.
Basados en las expresiones generales pero asumiendo el conocimiento del resto
de variables del modelo y usualmente sin indicar como se han obtenido las
características, aspecto primordial de cara a su aplicación.
Ambas formulaciones dan solución en casos particulares (básicamente para
simulación de respuestas únicamente); los modelos que se plantearan
seguidamente no presentan ninguna limitación en cuanto a su aplicación, ya que se
han formulado de forma que el sistema resultante no necesite la resolución de una
restricción algebraica, hecho que invalida el modelo para su aplicación en tiempo
real.
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 1. ANTECEDENTES Y ESTADO ACTUAL
4
La modelización del comportamiento del elemento accionador (convertidor, red)
debe ser tratada con especial dedicación; la aplicación de señales con alto contenido
armónico y variaciones bruscas de valor conlleva la consideración de las no
linealidades en el comportamiento de la máquina.
Métodos. Observación y estimación de estados
La determinación de los parámetros puede realizarse mediante medidas externas
(modelos de función o matriz de transferencia), a partir de señales tipificadas, o del
estudio del servicio y comportamiento frente a variaciones de consigna; lo que lleva
a descripciones de tipo circuital para el comportamiento del sistema. También puede
hacerse a partir del estudio de la distribución del campo en la máquina (modelos en
elementos finitos - EF). En cada caso debe valorarse la aproximación realizada y las
limitaciones de cada método. En [Brule 00] se plantea la equivalencia de resultados
entre los modelos basados en EF y los resultantes de la formulación circuital sobre
la base de establecer el control de la máquina. Al ser el objetivo final el control del
sistema, este trabajo se basará exclusivamente en modelos de tipo circuital.
Una vez establecido el método, o métodos más adecuados para la determinación de
los parámetros, debe determinarse el conjunto, o conjuntos, de modelos
considerados para su aplicación a la estimación y/o observación de los estados o
magnitudes no mensurables del modelo y su viabilidad para la realización del control
de la máquina.
El deficiente conocimiento de los parámetros de la máquina y las soluciones
adoptadas, cuando existen, tiene unas implicaciones en el control evidentes que se
comprueba por el gran número de publicaciones actuales sobre el tema, así como
por la necesidad de complicar el algoritmo de control para obviar, o minimizar, los
efectos de las desviaciones respecto a los valores nominales supuestos de los
parámetros.
El conocimiento del modelo de funcionamiento del conjunto convertidor+máquina
accionada+carga, permitirá detectar, y/o prevenir, los funcionamientos anómalos del
sistema. El seguimiento de la evolución de las variables de estado de interés puede
permitir un mantenimiento preventivo del sistema accionado, así como la detección
de averías de funcionamiento, y de la modificación del algoritmo de control
resultante para la optimización del punto de trabajo del sistema según criterios a
determinar.
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 1. ANTECEDENTES Y ESTADO ACTUAL
5
Aplicaciones. Equipo para la medida del par en régimen transitorio
Un aspecto clave en la tesis ha sido la determinación del par. Pero,
¿ Cómo determinar que el par calculado mediante un observador es el
correcto?
Una solución es contrastar el par calculado con el medido mediante un medidor de
par en régimen transitorio; la no-disponibilidad del mismo junto con su elevado coste
hace que nos planteemos el cómo medir el par, lo cual nos lleva al desarrollo de un
equipo para la imposición del par de carga deseado, junto con su obtención a partir
de las medidas procedentes de una máquina de corriente continua controlada en
corriente. El resultado final es un equipo que permite ensayar cualquier
accionamiento con la posibilidad de imponer una ley de variación arbitraria del par
de carga aplicado, junto con la obtención por cálculo del par accionador en el eje del
sistema.
PALABRAS CLAVE
Máquina de inducción, Modelos con saturación, Sensibilidad de los modelos,
Determinación de parámetros, Mínimos cuadrados, Observadores adaptativos,
Observador del par, Medida del par en régimen transitorio, Modelización del
convertidor, Funciones de conexión, Funciones de conversión.
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
MODELOS DE MÁQUINAS
ASÍNCRONAS CON
CONSIDERACIÓN DE LA
SATURACIÓN
Inductáncia
θr
0
0,5
1
1,5
corriente
Lm
L
2
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
2. Modelos de máquinas asíncronas con consideración de
la saturación
2. MODELOS PARA LA MÁQUINA ASÍNCRONA CON CONSIDERACIÓN DE LA SATURACIÓN ........................................... 3
MODELIZACIÓN DE LOS EFECTOS DE LA SATURACIÓN ............................................................................................ 6
ECUACIONES DE LA MÁQUINA TENIENDO EN CUENTA LA SATURACIÓN. CONSIDERACIÓN DE DIVERSOS CONJUNTOS
DE VARIABLES DE ESTADO..................................................................................................................................... 8
Variables de estado corrientes de estator y rotor. Modelo 1......................................................................... 9
Variables de estado los flujos de estator y rotor. Modelo 2. ....................................................................... 10
Variables de estado la corriente de estator y el flujo magnetizante. Modelo 3........................................... 13
Variables de estado las corrientes de estator y el flujo del rotor. Modelo 4. .............................................. 14
Variables de estado la corriente de estator y la magnetizante. Modelo 5................................................... 15
MODELOS SIMPLIFICADOS. ................................................................................................................................. 16
MODELOS CON SATURACIÓN DEPENDIENTE DE LAS COMPONENTES DEL PROPIO EJE............................................. 16
Variables de estado corrientes de estator y rotor. Modelo 6....................................................................... 16
Variables de estado los flujos de estator y rotor. Modelo 7. ....................................................................... 17
Variables de estado la corriente del estator y el flujo magnetizante. Modelo 8.......................................... 18
Variables de estado la corriente del estator y el flujo del rotor. Modelo 9................................................ 19
Variables de estado las corrientes del estator y magnetizante. Modelo 10................................................. 20
MODELOS EN T Y EN Γ........................................................................................................................................ 21
Variables de estado las corrientes de estator y rotor. Modelo 11. .............................................................. 23
Variables de estado los flujos de estator y rotor. Modelo 12. ..................................................................... 24
Variables de estado la corriente de estator y el flujo magnetizante. Modelo 13......................................... 25
Variables de estado las corrientes de estator y el flujo del rotor. Modelo 14. ............................................ 26
Variables de estado las corrientes del estator y magnetizante. Modelo 15................................................. 27
Variables de estado las corrientes del estator y rotor. Modelo 16.............................................................. 28
Variables de estado los flujos del estator y rotor. Modelo 17. .................................................................... 29
Variables de estado la corriente de estator y el flujo magnetizante. Modelo 18......................................... 30
Variables de estado la corriente de estator y el flujo de rotor. Modelo 19. ................................................ 30
Variables de estado las corrientes del estator y magnetizante. Modelo 20................................................. 31
Variables de estado las corrientes del estator y rotor. Modelo 21.............................................................. 32
Variables de estado los flujos del estator y rotor. Modelo 22. .................................................................... 33
Variables de estado la corriente del estator y el flujo magnetizante. Modelo 23l....................................... 34
Variables de estado la corriente del estator y el flujo del rotor. Modelo 24............................................... 35
Variables de estado las corrientes del estator y magnetizante. Modelo 25................................................. 36
Variables de estado las corrientes del estator y rotor. Modelo 26.............................................................. 37
Variables de estado los flujos del estator y rotor. Modelo 27. .................................................................... 38
Variables de estado la corriente del estator y el flujo magnetizante. Modelo 28........................................ 39
Variables de estado la corriente del estator y el flujo de rotor. Modelo 29. ............................................... 39
Variables de estado las corrientes del estator y magnetizante. Modelo 30................................................. 40
MODELOS BASADOS EN LA ORIENTACIÓN DEL CAMPO. ......................................................................................... 41
Variables de estado las corrientes del estator y rotor. Modelo 31.............................................................. 41
Variables de estado los flujos del estator y rotor. Modelo 32. .................................................................... 42
Variables de estado la corriente del estator y el flujo magnetizante. Modelo 33........................................ 43
Variables de estado la corriente del estator y el flujo del rotor. Modelo 34............................................... 43
Variables de estado las corrientes del estator y magnetizante. Modelo 35................................................. 44
Variables de estado las corrientes del estator y rotor. Modelo 36.............................................................. 45
Variables de estado los flujos del estator y rotor. Modelo 37. .................................................................... 45
Variables de estado la corriente del estator y el flujo magnetizante. Modelo 38........................................ 46
Variables de estado la corriente del estator y el flujo del rotor. Modelo 39............................................... 47
Variables de estado las corrientes del estator y magnetizante. Modelo 40................................................. 47
Variables de estado las corrientes del estator y rotor. Modelo 41.............................................................. 48
Variables de estado los flujos del estator y rotor. Modelo 42. .................................................................... 48
Variables de estado la corriente del estator y el flujo magnetizante. Modelo 43........................................ 49
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
1
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
Variables de estado la corriente del estator y el flujo de rotor. Modelo 44. ............................................... 49
Variables de estado las corrientes del estator y magnetizante. Modelo 45................................................. 49
RESUMEN COMPARATIVO DE LOS DISTINTOS MODELOS. ....................................................................................... 50
MODELOS BASADOS EN LA ORIENTACIÓN DEL CAMPO. ......................................................................................... 52
MODELOS BASADOS EN LA ORIENTACIÓN DEL CAMPO. MODELOS TIPO Γ(I). CANCELACIÓN DE LSL........................ 52
MODELOS BASADOS EN LA ORIENTACIÓN DEL CAMPO. MODELOS TIPO Γ(II). CANCELACIÓN DE LRL. ..................... 53
CONCLUSIONES.................................................................................................................................................. 53
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
2
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
3
2. Modelos para la máquina asíncrona con consideración de la saturación
En el desarrollo de cualquier modelo debe partirse de unas hipótesis básicas que
limitan el alcance del mismo.
θr
Figura 1 Máquina eléctrica elemental
Las ecuaciones de la máquina asíncrona (figura 1) expresadas en la referencia
natural son las siguientes:
dΨsA
dt
dΨsB
= Rs ⋅ i sB +
dt
dΨsC
= Rs ⋅ i sC +
dt
usA = Rs ⋅ i sA +
usB
usC
dΨrA
dt
dΨrB
urB = Rr ⋅ irB +
dt
dΨrC
urC = Rr ⋅ irC +
dt
; urA = Rr ⋅ irA +
(1)
Si tomamos como punto de partida las siguientes consideraciones que, en su caso,
se verán alteradas o eliminadas:
- permeabilidad del hierro infinita
- no-existencia de armónicos de campo
- ancho del entrehierro despreciable
- construcción simétrica
estamos definiendo una determinada idealización de la máquina.
Si se considera la relación entre flujos y corrientes para el caso ideal anterior:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
[Ψ ] = [M ]⋅ [i ] ; [Ψ ] = [ΨsA
ΨsB
[i] = [isA
irC ]
i sB
isC
[M ] =
irB
ΨrA
ΨrB
ΨrC ]
t
t
M sr
M r
Ms
M rs
Ls
[M s ] = M s
M s
irA
ΨsC
4
Ms
Ms
Ls
Ms
Ms
Ls
[M sr ] = [M rs ]t
;
Lr
[M r ] = M r
M r
M sr ⋅ cos θ r
4⋅π
)
= M sr ⋅ cos(θ r +
3
M ⋅ cos(θ + 2 ⋅ π )
r
sr
3
Mr
Mr
Lr
Mr
Mr
Lr
2⋅π
M sr ⋅ cos(θ r +
)
3
M sr ⋅ cos θ r
4⋅π
M sr ⋅ cos(θ r +
)
3
3
2⋅π
)
M sr ⋅ cos(θ r +
3
M sr ⋅ cos θ r
M sr ⋅ cos(θ r +
4⋅π
)
(2)
juntamente con la ecuación del movimiento mecánico:
Me − Mc = J
donde:
L s = L sl + L sm ;
dω rm
;
dt
Lr = Lrl + Lrm ;
θ r = P ⋅ θ rm ;
ω rm =
M s = − L sm / 2 ;
dθ rm
dt
(3)
M r = − Lrm / 2 ;
M sr = L sm ⋅ Lrm
M c = M caga + ρ ⋅ ω rm
(4)
El modelo descrito es complejo y de difícil resolución: han de resolverse 8
ecuaciones diferenciales no lineales de coeficientes variables en el tiempo; además
debe invertirse una matriz [M] de orden 6 para cada incremento de tiempo.
A partir de la definición de vector espacial [Kovacs 84]:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
is =
(
2
isa + a ⋅ isb + a 2 ⋅ isc
3
)
5
(5)
se pueden obtener las siguientes expresiones para el estator y rotor, según una
referencia genérica:
u sg = Rs ⋅ isg +
d
Ψsg + j ⋅ ω g ⋅ Ψsg
dt
(6)
u rg = Rr ⋅ irg +
d
Ψrg + j ⋅ (ω g − ω r ) ⋅ Ψrg
dt
(7)
En el caso que exista componente homopolar, debe añadirse la siguiente ecuación:
Rs 0
d is0
L
= − s 0
dt ir 0
0
0
⋅ i s 0 + 1 0 ⋅ u s 0
Rr 0 i r 0 0 1 u r 0
Lr 0
(8)
u s0 =
u sA + u sB + u sC
3
ur 0 =
u rA + u rB + u rC
3
juntamente con las ecuaciones del par y de equilibrio mecánico:
3
M e = − ⋅ P ⋅ Ψrg × i rg
2
J⋅
dω rm
= Me − Mc;
dt
(9)
ω r = P ⋅ ω rm
(10)
El circuito equivalente correspondiente a las ecuaciones anteriores, es el siguiente;
Rs
j ω Ψsg
g
L
isg
u
sg
L
sl
img
L
rl
j(ω - ω ) Ψrg
g r
Rr
irg
m
u
rg
Figura 2 Esquema para el régimen transitorio.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
6
Los parámetros del modelo referidos al estator, partiendo de las simplificaciones
aceptadas, y de acuerdo con las dimensiones geométricas, son:
Lsm = N s2 ⋅
2 ⋅ µ0 ⋅ l ⋅ D
δ ⋅π
Lsm N s
=
Lrm N r
Lss = Lsl +
2
;
Lrm = N r2 ⋅
;
2 ⋅ µ0 ⋅ l ⋅ D
δ ⋅π
3 ⋅ µ0 ⋅ l ⋅ D
3
Lm = ⋅ M sr = N s ⋅ N r ⋅
2
δ ⋅π
3
⋅ Lsm = Lsl + Lm ;
2
Lrr = Lrl +
(11)
3
⋅ Lrm = Lrl + Lm
2
En caso de despreciar la saturación, se pueden plantear las siguientes
equivalencias:
Ψsg = Lss ⋅ i sg + Lm ⋅ irg
i mg = i sg + i rg
i msg =
Ψsg
Lm
;
;
Ψmg = Lm ⋅ (i sg + i rg )
= i rg + (1 + σ sl ) ⋅ i sg
;
imrg =
Ψrg = Lrr ⋅ irg + Lm ⋅ i sg
(12)
Ψs lg = Lsl ⋅ i sg
;
Ψrg
Lm
(13)
= i sg + (1 + σ rl ) ⋅ irg
El modelo, basado en la máquina idealizada, es válido siempre que no exista
saturación, o bien en el caso en que esta no tenga un efecto relevante en la
respuesta del sistema:
-
trabajo en régimen permanente
-
trabajo a flujo constante
Modelización de los efectos de la saturación
La consideración de la saturación del núcleo magnético conlleva la sustitución de la
relación lineal:
ψ = L⋅i
por otra que incluya la posibilidad de modificación de las inductancias con la
corriente, como puede verse en la expresión que sigue:
ψ = L(i ) ⋅ i
(14)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
7
En el desarrollo de las expresiones de la derivada del flujo, aparecerán dos
términos:
dψ d ( L(i ) ⋅ i )
dL(i ) di
di
= L(i ) ⋅ + i ⋅
⋅
=
dt
dt
dt
di dt
(15)
Al primer coeficiente se le denomina inductancia estática:
Lm (i ) =
ψ (i )
i
(16)
Al segundo se le llama inductancia dinámica:
L(i ) =
dΨ (i )
1
=
di (Ψ )
di
dΨ
(17)
Si se considera la característica de saturación de la figura 3, la inductancia estática,
para un punto cualquiera, corresponde a la pendiente de la recta que une el origen
con dicho punto, es decir:
Lm =
OB
OA
(18)
mientras que la dinámica se corresponde con:
L=
∆ψ
∆i
(19)
De las expresiones anteriores, se deduce que la inductancia estática es superior a la
dinámica, es decir Lm > L
B
1
∆Ψ
Flujo
∆i
A
0
corriente
Figura 3 Definición de inductancia dinámica y estática.
En la figura 4 se muestran ambas.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
8
Inductáncia
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
0
0 ,5
1
1 ,5
2
corriente
Lm
L
Figura 4 inductancia estática (Lm) y dinámica (L).
En este caso la relación (12) debe expresarse como sigue:
Ψsg = L sl ⋅ i sg + Ψm (i m )
Ψrg = Lrl ⋅ i rg + Ψm (i m )
;
Ψm (i m ) = f (i m )
(20)
relación fundamental ya que liga el flujo estatórico y rotórico con el flujo común en el
entrehierro de la máquina y con las corrientes que recorren los devanados (a partir
de la caracteristica de saturación Ψm (i m ) ).
Asimismo la relación (13) entre corrientes puede expresarse como:
is + ir = im
Ψ s − Ψm
L sl
+
Ψr − Ψm
Lrl
= i m = g ( Ψm )
(21)
Dado que el estado magnético de la máquina es global, solo pueden ser
relacionados el flujo total en el entrehierro (Ψm) mediante la corriente de
magnetización im que es proporcional a la capa de corriente en el entrehierro.
La ecuación (21) traduce la restricción algebraica más importante que aparecera en
la modelización que sigue. Para el caso lineal esta puede deshacerse y sustituirse
en las ecuaciones de estado que modelizan la máquina, sean cuales sean las
variables de estado consideradas. En los casos que consideraremos existen
conjuntos de variables de estado en los que esta simplificación no es posible; estos
modelos NO pueden ser considerados útiles a efectos de control ya que para cada
intervalo de cálculo debe resolverse una ecuación algebraica NO lineal, en la que no
es posible indicar a priori el tiempo de resolución de la misma.
Modelización de los efectos de la saturación. Consideración de
diversos conjuntos de variables de estado.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
9
La aplicación de las consideraciones anteriores al modelo de la máquina, lleva al
siguiente conjunto de ecuaciones para el estator y el rotor:
d
Ψsg + j ⋅ ω g ⋅ Ψsg
dt
(22)
d
Ψrg + j ⋅ (ω g − ω r ) ⋅ Ψrg
dt
(23)
u sg = Rs ⋅ isg +
u rg = Rr ⋅ irg +
juntamente con la ecuación mecánica:
3
M e = − ⋅ P ⋅ Ψrg × i rg
2
J⋅
dω rm
= Me − Mc;
dt
(24)
ω r = P ⋅ ω rm
(25)
Se introducen relaciones para la saturación de la forma:
Ψ = f (i ) = a1 ⋅ arctan(a 2 ⋅ i ) + a 3 ⋅ i
(26)
o bien:
Ψ
Ψ
+ b ⋅
= g (Ψ ) = a ⋅
IN
ΨN
ΨN
se obtienen expresiones para las inductancias, del tipo:
i
Lm =
a1 ⋅ arctan(a 2 ⋅ i )
+ a3
i
o bien:
Lm =
n
Ψ
Ψ
I N ⋅ a ⋅
ΨN
Ψ
+ b ⋅
ΨN
n
(27)
(28)
(29)
igualmente, para la inductancia dinámica:
L=
L=
a1 ⋅ a 2
+ a3
1 + (a 2 ⋅ i) 2
1
n −1
a
Ψ
+ b ⋅ n ⋅
IN ⋅
ΨN
Ψ N
Variables de estado corrientes de estator y rotor. Modelo 1.
(30)
(31)
Si se desarrollan las expresiones anteriores separando parte real e imaginaria, se
llega a:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
10
di
= M −1 ⋅ v − M −1 ⋅ A ⋅ i
dt
con
v = (u sx
Rs
ω g ⋅ ( Lm + L sl )
A=
0
(ω g − ω r ) ⋅ Lm
u sy
u ry )
i = (i sx
t
u rx
− ω g ⋅ ( Lm + L sl )
Rs
− (ω g − ω r ) ⋅ Lm
0
(32)
i sy
i ry )
t
i rx
(33)
− ω g ⋅ Lm
0
− (ω g − ω r ) ⋅ ( Lm + Lrl )
Rr
0
ω g ⋅ Lm
Rr
(ω g − ω r ) ⋅ ( Lm + Lrl )
(34)
Lsl + Lddm
Ldq
M =
Lddm
L
dq
Ldq
L sl + Lqqm
Ldq
Lqqm
Lddm = L ⋅ cos 2 µ + Lm ⋅ sin 2 µ
Lqqm = L ⋅ sin 2 µ + Lm ⋅ cos 2 µ
L=
(36)
Ldq = ( L − Lm ) ⋅ cos µ ⋅ sinµ
tanµ =
imy
Ψm = Ψmx + Ψmy
2
dΨm
di m
Ψm = f (i m )
(38)
i mx
Ldq
Lqqm
Ldq
Lrl + Lqqm
Lddm
Ldq
Lrl + Lddm
Ldq
2
;
i m = i mx + i my
i mx = i sx + i rx
2
2
;
Lm =
(35)
Ψm
im
(37)
(39)
(40)
i my = i sy + i ry
;
(41)
Ψmx = Lm ⋅ i mx
;
Ψmy = Lm ⋅ i my
En el modelo anterior, aparecen unos coeficientes de autoinducción Ldq que
representan el efecto de la saturación cruzada debido a la interacción entre
flujos de ejes. Si se desprecia la saturación L = Lm desaparece el termino
cruzado. Obsérvese que ello supone tener un termino adicional en las
ecuaciones de cada eje, debido a la corriente que circula por la bobina
correspondiente al otro eje. La dificultad del método estriba en que el conjunto
de ecuaciones algebraicas no lineales que definen el modelo debe resolverse
para cada incremento de tiempo ralentizando, de esta forma, el proceso de
cálculo.
Variables de estado los flujos de estator y rotor. Modelo 2.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
11
Eligiendo, como variables de estado, otro conjunto de variables puede simplificarse
la resolución del sistema anterior. En el caso de considerar como variables los flujos
de estator y rotor, se llega al siguiente conjunto de ecuaciones:
Ψ − Ψmx
d
Ψsx = u sx − Rs ⋅ sx
− ω g ⋅ Ψsy
dt
Lsl
Ψsy − Ψmy
d
Ψsy = u sy − Rs ⋅
+ ω g ⋅ Ψsx
dt
Lsl
(42)
Ψ − Ψmx
d
Ψrx = u rx − Rr ⋅ rx
− (ω g − ω r ) ⋅ Ψry
dt
Lrl
Ψry − Ψmy
d
Ψry = u ry − Rr ⋅
+ (ω g − ω r ) ⋅ Ψrx
dt
Lrl
(43)
Ecuaciones que, formalmente, son más sencillas que las obtenidas a partir del
conjunto de variables corrientes, pero a las que falta añadir una restricción
algebraica sobre los flujos:
Ψsg
Lsl
+
Ψrg
Lrl
1
1
= i m = g (Ψm )
− Ψm ⋅
+
Lsl Lrl
Ψ
im
= g (Ψm ) = a ⋅ m
IN
ΨN
Ψ
+ b ⋅ m
ΨN
(44)
n
(45)
conjunto de ecuaciones implícitas que se deben resolver para cada paso de
cálculo!.
Separando partes real e imaginaria, se llega a:
Ψsx Ψrx
+
− Ψmx
Lsl
Lrl
1
Ψ
Ψ
1
2
2
= i mx = g (Ψm ) ⋅ mx = g ( Ψmx
⋅
+
+ Ψmy
) ⋅ mx
Ψm
Ψm
Lsl Lrl
(46)
Ψsy
Ψ
Ψmy
1
1
2
2
= i my = g (Ψm ) ⋅ my = g ( Ψmx
⋅
+
)⋅
+ Ψmy
Ψm
Ψm
Lsl Lrl
(47)
Lsl
+
Ψrx
− Ψmy
Lrl
Si se intenta resolver el conjunto de ecuaciones resultante de otra forma, por
ejemplo, a partir de la consideración de la inductancia estática función del flujo, con:
Ψm = Lm (Ψm ) ⋅ i m
(48)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
12
se obtiene:
Ψsg
Ψm =
Lsl
+
Ψrg
Lrl
1
1
1
+
+
Lsl Lrl Lm (Ψm )
(49)
también se llega a una ecuación implícita que debe resolverse para cada paso
de cálculo.
Esto, actualmente, no es una gran limitación; existen poderosos programas de
cálculo y resolución de sistemas para el caso de un conjunto de ecuaciones
diferenciales sometidas a una restricción algebraica (MATLAB, SIMULINK, PSPICE,
VISSIM, etc.). El problema subyacente es la inaplicabilidad del método para realizar
el control de la máquina en tiempo real: no podemos definir el tiempo de cálculo del
algoritmo porque ignoramos el tiempo que invertirá el programa en resolver la
ecuación implícita anterior, peor aún, no sabemos si la solución encontrada será
correcta o única.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
13
Variables de estado la corriente de estator y el flujo magnetizante. Modelo 3.
Tras muchas transformaciones algebraicas, se llega al conjunto de ecuaciones
siguiente:
0
1
0
Lsl
isx u sx
0
1
Lsl
0
d isy u sy
∂g x
∂g x
(1 + Lrl ⋅
) − Lrl ⋅
=
+
⋅
− Lrl 0
∂
Ψ
∂Ψmy dt Ψmx u rx
mx
∂g y
∂g y
Ψ u
my
ry
(1 + Lrl ⋅
)
− Lrl − Lrl ⋅
0
∂
Ψ
∂
Ψ
mx
my
ω g ⋅ Lsl
ωg
0
isx
− rs
− rs
−ωg
0
isy
− ω g ⋅ Lsl
+
⋅
+
− rr
− (ω g − ω r ) ⋅ Lrl 0
− (ω g − ω r ) Ψmx
Ψ
(ω − ω ) ⋅ L − r
ω
−
ω
(
)
0
r
rl
r
g
r
my
g
(50)
0
0
+
− r ⋅ g + (ω g − ω r ) ⋅ Lrl ⋅ g y
r x
− r ⋅ g − (ω − ω ) ⋅ L ⋅ g
g
r
rl
x
r y
Donde:
Ψ
2
g x (Ψm ) = g (Ψm ) ⋅ mx = g ( Ψmx
Ψm
g y ( Ψm ) = g ( Ψ m ) ⋅
Ψmy
Ψm
2
= g ( Ψmx
2
(Ψmx
Ψ
Ψmx
2
mx
+b⋅
= I N ⋅ a ⋅
+ Ψmy ) ⋅
ΨN
Ψm
2
Ψ
(Ψmx
Ψmy
my
2
+b⋅
= I N ⋅ a ⋅
+ Ψmy ) ⋅
ΨN
Ψm
+Ψ )
2
my
n −1
2
Ψ Nn
+Ψ )
2
my
Ψ Nn
n −1
2
⋅ Ψmx
⋅ Ψmy
(51)
además, deben calcularse las derivadas siguientes:
∂g x
,
∂Ψmx
∂g x
,
∂Ψmy
∂g y
∂Ψmx
,
∂g y
∂Ψmy
(52)
obsérvese la complejidad del modelo resultante. En este caso, no debe
resolverse ninguna ecuación implícita para cada paso de cálculo; sin embargo
el modelo es muy complicado.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
14
Variables de estado las corrientes de estator y el flujo del rotor. Modelo 4.
Las ecuaciones resultantes son las que siguen:
L sl ⋅
d Ψr
dt
d is
dt
= u s − (rs + j ⋅ ω ⋅ Lsl ) ⋅ i s − (
= u r − (rr ⋅
Ψr − Ψm
Lrl
d Ψm
dt
+ j ⋅ ω ⋅ Ψm )
(53)
) − j ⋅ (ω − ω r ) ⋅ Ψr
sometidas a las siguientes restricciones:
Ψ − Ψm
Ψm = f (i m ) = f (i s + i r ) = f i s + r
Lrl
dΨ m d
=
f (i m )
dt
dt
(54)
aplicando como ejemplo al primer caso de aproximación por saturación:
Ψ − Ψm
Ψm = a1 ⋅ arctan(a 2 ⋅ i m ) + a 3 ⋅ i m = a1 ⋅ arctan a 2 ⋅ i s + r
+ a 3
L
rl
dΨm
=
dt
2
1 + a 2
a1 ⋅ a 2
Ψ − Ψm
⋅ i s + r
Lrl
2
1
di
+ a 3 ⋅ s +
dt Lrl
Ψ − Ψm
⋅ i s + r
L
rl
(55)
dΨ m
dΨ
⋅ r −
dt
dt
(56)
resulta una función y una ecuación diferencial implícitas que deben ser resueltas
para cada paso de cálculo.
Es un modelo realmente difícil de resolver.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
15
Variables de estado la corriente de estator y la magnetizante. Modelo 5.
Después de muchas transformaciones algebraicas, se obtiene:
Lsl
0
− L
rl
0
0
L sl
0
Lrl
∂L
∂L
di sx
⋅ i mx
−
⋅ i my
∂i m
∂i m
dt
∂L
∂L
di
⋅ i my
L+
⋅ i mx sy
∂i m
∂i m
⋅ dt
∂L
∂L
di mx
⋅ i mx + L
−
⋅ i my
Lrl +
dt
∂i m
∂i m
di my
∂L
∂L
⋅ i my
⋅ i mx + L
Lrl +
∂i m
∂i m
dt
L+
rs
ω ⋅ Lsl
−
− rr
− (ω − ω ) ⋅ L
r
rl
− ω ⋅ Lsl
rs
(ω − ω r ) ⋅ Lrl
− rr
u
sx
u sy
= u −
rx
u ry
−ω ⋅ L
i sx
0
i sy
⋅
− (ω − ω r ) ⋅ ( Lrl + L) i mx
rr
i
(ω − ω r ) ⋅ ( Lrl + L)
rr
my
(57)
0
ω⋅L
donde:
L = h(i m )
∂L ∂h(i m )
=
∂i m
∂i m
(58)
resulta un modelo complicado pero resoluble.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
16
Modelos simplificados.
La resolución de los modelos anteriores se puede simplificar considerando una série
de hipótesis adicionales:
•
Saturación dependiente únicamente de las componentes del propio eje, es decir:
Ψmx = f x (i mx );
Ψmy = f y (i my )
i mx = g x (Ψmx );
(59)
i my = g y (Ψmy )
Este método puede parecer poco ortodoxo, pero puede dar una solución a los
modelos anteriores en que era preciso resolver una ecuación algebraica para cada
paso de cálculo. Además, se puede plantear que las funciones representantes de la
saturación tengan coeficientes distintos para cada eje.
•
Consideración de un modelo de la máquina que tenga menos parámetros. Este
caso se verá en el apartado que sigue. El método, además, permite la valoración
experimental de los parámetros desconocidos.
Modelos con saturación dependiente de las componentes del propio eje.
Variables de estado corrientes de estator y rotor. Modelo 6
Tras muchas transformaciones algebraicas, se obtiene:
di
= M −1 ⋅ v + M −1 ⋅ ( A ⋅ i + Ω ⋅ Ψ )
dt
con
v = (u sx
u sy
u rx
u ry )
t
i = (i sx
i sy
Ψ = (Ψmx
− Rs
− ω g ⋅ sl
A=
0
0
ω g ⋅ L sl
− Rs
0
0
0
0
− Rr
− (ω g − ω r ) ⋅ Lrl
0
−ω
Ω=
0
(ω
− (ω − ω )
r
(60)
i ry )
t
i rx
Ψmy )
t
(61)
(62)
0
0
(ω g − ω r ) ⋅ Lrl
− Rr
(63)
ω
0
− ω r )
0
(64)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
Lsl + Lmx
0
M =
Lmx
0
0
L sl + Lmy
0
Lmy
Lmx =
Lmx
0
Lrl + Lmx
0
dΨmx
di mx
Ψmx = f x (i mx );
i mx = i sx + i rx
0
Lmy
0
Lrl + Lmy
Lmy =
dΨmy
di my
Ψmy = f y (i my )
;
i my = i sy + i ry
17
(65)
(66)
(67)
(68)
el cual resulta manejable.
Variables de estado los flujos de estator y rotor. Modelo 7.
Ψ − Ψmx
d
Ψsx = u sx − Rs ⋅ sx
− ω g ⋅ Ψsy
dt
Lsl
Ψsy − Ψmy
d
Ψsy = u sy − Rs ⋅
+ ω g ⋅ Ψsx
dt
Lsl
(69)
Ψ − Ψmx
d
Ψrx = u rx − Rr ⋅ rx
− (ω g − ω r ) ⋅ Ψry
dt
Lrl
Ψry − Ψmy
d
Ψry = u ry − Rr ⋅
+ (ω g − ω r ) ⋅ Ψrx
dt
Lrl
(70)
Ecuaciones que, formalmente, son más sencillas que las obtenidas a partir del
conjunto de las variables de estado corriente, pero a las que hace falta añadir una
restricción algebraica sobre los flujos:
Ψsx Ψrx
+
− Ψmx
Lsl
Lrl
Ψsy
1
1
= i mx = g (Ψmx )
⋅
+
L
L
rl
sl
1
Ψrx
1
= i my = g (Ψmy )
− Ψmy ⋅
+
L sl
Lrl
L
L
rl
sl
ecuaciones implícitas que se deben resolver para cada paso de cálculo.
+
(71)
(72)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
18
Variables de estado la corriente del estator y el flujo magnetizante. Modelo 8.
Después de varias transformaciones algebraicas, se llega al siguiente conjunto de
ecuaciones:
0
1
0
L sl
i sx u sx
0
1
L sl
0
d i sy u sy
∂g x
(1 + Lrl ⋅
) 0
⋅
− Lrl 0
= +
∂
Ψ
mx
dt Ψmx u rx
∂g y
Ψ u
my ry
0
0
(
1
)
L
L
−
+
⋅
rl
rl
∂
Ψ
my
ω g ⋅ L sl
ωg
0
i sx
− rs
− rs
−ωg
0
i sy
− ω g ⋅ L sl
+
⋅
+
− rr
− (ω g − ω r ) ⋅ Lrl 0
(ω g − ω r ) Ψmx
Ψ
(ω − ω ) ⋅ L
−
−
ω
−
ω
r
(
)
0
r
rl
r
g
r
my
g
0
0
+
− r ⋅ g + (ω g − ω r ) ⋅ Lrl ⋅ g y
r x
− r ⋅ g − (ω − ω ) ⋅ L ⋅ g
y
g
r
rl
x
r
(73)
Donde:
Ψmx
(Ψmx ) n
g x (Ψmx ) = a ⋅
+b⋅
ΨN
Ψn
g y (Ψmy ) = a ⋅
Ψmy
ΨN
+b⋅
2
(Ψmy
)n
(74)
Ψ Nn
además, deben calcularse las derivadas siguientes:
∂g x
,
∂Ψmx
∂g y
∂Ψmy
(75)
Obsérvese la complejidad del modelo resultante. En este caso no debe
resolverse ninguna ecuación implícita para cada paso de cálculo pero, sin
embargo, el modelo es muy complejo.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
19
Variables de estado la corriente del estator y el flujo del rotor. Modelo 9.
Las ecuaciones resultantes, son las que siguen:
df x
1 df x
⋅
di mx
Lrl di mx
L +
0
0
sl
1 df x
1 df x
1+
1+
⋅
⋅
i sx u sx
Lrl di mx
Lrl di mx
df y
1 df y d i sy u sy
⋅
=
+
⋅
di
L
di my dt Ψrx u rx
my
rl
0
0
L sl +
Ψ u
1 df y
1 df y
ry
ry
⋅
⋅
1+
1+
Lrl di my
Lrl di my
0
0
1
0
0
0
0
1
ω ⋅ Lsl
0
0
− rs
ω
0
i
sx
− rs
0
0
0
− ω ⋅ L sl
−ω
i sy rr
Ψ
r
0 ⋅ mx
− r
0
0
(ω − ω r ) ⋅
+ −
Ψ
Lrl
Lrl
Ψrx
my
r
rr Ψ
ry
− r
0
−
−
−
ω
ω
0
0
(
)
r
Lrl
Lrl
(76)
con:
Ψmx = f x (i mx );
Ψmy = f y (i my )
(77)
deben calcularse las siguientes derivadas:
df x
;
di mx
df y
di my
(78)
Es un modelo realmente difícil.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
20
Variables de estado las corrientes del estator y magnetizante. Modelo 10.
Tras varias transformaciones, se llega a:
Lsl
0
− Lrl
0
0
Lx +
L sl
0
∂L x
⋅ i mx
∂i mx
0
Lrl +
Lrl
rs
ω ⋅ Lsl
−
− rr
− (ω − ω ) ⋅ L
r
rl
∂L x
⋅ i mx + L x
∂i mx
0
− ω ⋅ Lsl
rs
(ω − ω r ) ⋅ Lrl
− rr
di sx
dt
di
∂L y
⋅ i my sy
Ly +
∂i my
⋅ dt
di mx
0
dt
∂L y
di my
⋅ i my + L y
Lrl +
dt
∂i my
0
ω ⋅ Lx
0
u
sx
u sy
= u −
rx
u ry
− ω ⋅ Ly
i sx
0
i sy
⋅
− (ω − ω r ) ⋅ ( Lrl + L y ) i mx
rr
i
(ω − ω r ) ⋅ ( Lrl + L x )
rr
my
(79)
donde:
L x = h x (i mx );
∂L x ∂h x (i mx )
=
;
∂i mx
∂i mx
L y = h y (i my )
∂L y
∂i my
=
∂h y (i my )
(80)
∂i my
resulta un modelo complicado pero resoluble.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
21
Modelos en T y en Γ.
Dada la imposibilidad práctica de separar la determinación de los fenómenos
inductivos de estatorl y rotor, resulta conveniente plantear un cambio de variables
que elimine una de las componentes del esquema equivalente (Lsl o Lrl). Designando
por a la relación de reducción de rotor a nuevo estator equivalente, se pueden
escribir las siguientes equivalencias:
irg' =
irg
a
; Ψrg' = a ⋅ Ψrg ; Rr' = a 2 ⋅ Rr
(81)
Este cambio de variable mantiene el balance de potencias [Bargalló 96].
Ψsg = Lsl ⋅ isg + Lm ⋅ (i sg + a ⋅ irg' )
= L'm ⋅ (isg + irg' )
con
(82)
L'm = a ⋅ Lm
Ψrg' = a 2 ⋅ Lrl ⋅ irg' + a ⋅ Lm ⋅ isg + a 2 ⋅ Lm ⋅ irg'
= L'rl ⋅ irg' +L'm ⋅ (isg + irg' )
L'rl = a ⋅ (a ⋅ ( Lr + Lm ) − Lm )
L'sl = (Lsl + Lm − a ⋅ Lm )
(83)
(84)
(85)
Eligiendo adecuadamente el valor de la relación a, se puede eliminar un parámetro.
L
Haciendo a = ss , se obtiene el esquema de la figura 5 en el que se ha eliminado la
Lm
inductancia de dispersión estatórica. A este modelo se le denominará tipo Γ(I).
Figura 5 Modelo en Γ(I).
Lm
se elimina la inductancia de dispersión rotórica (figura 6). A este
Lr
modelo se le denominará tipo Γ(II).
Para
a=
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
Figura 6 Modelo en Γ(II).
Mediante estos modelos, con un parámetro menos, es más sencillo resolver el
problema de la caracterización de la saturación.[P24], [P26].
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
22
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
23
Modelos tipo Γ(I). Cancelación de Lsl.
En este caso el flujo estatórico se identifica con el de magnetización:
Ψ s = Ψm
(86)
Variables de estado las corrientes de estator y rotor. Modelo 11.
di
= M −1 ⋅ v − M −1 ⋅ A ⋅ i
dt
con:
v = (u sx
u sy
Rs
ω g ⋅ Lm
A=
0
(ω − ω ) ⋅ L
r
m
g
u ry )
i = (i sx
t
u rx
− ω g ⋅ Lm
Rs
− (ω g − ω r ) ⋅ Lm
0
i sy
i rx
(87)
i ry )
0
ω g ⋅ Lm
Rr
(ω g − ω r ) ⋅ ( Lm + Lrl )
t
(88)
− ω g ⋅ Lm
0
− (ω g − ω r ) ⋅ ( Lm + Lrl )
Rr
(89)
Lddm
Ldq
M =
L
ddm
L
dq
Ldq
Lqqm
Ldq
Lqqm
Ldq
Lqqm
Ldq
Lrl + Lqqm
Lddm
Ldq
Lrl + Lddm
Ldq
Lddm = L ⋅ cos 2 µ + Lm ⋅ sin 2 µ
Lqqm = L ⋅ sin 2 µ + Lm ⋅ cos 2 µ
L=
(91)
Ldq = ( L − Lm ) ⋅ cos µ ⋅ sinµ
tanµ =
imy
2
2
;
Lm =
Ψm
im
Ψm = f (i m )
(93)
i mx
Ψm = Ψmx + Ψmy
dΨm
dim
(90)
i m = i mx + i my
i mx = i sx + i rx
Ψmx = Lm ⋅ i mx
2
2
(92)
(94)
(95)
i my = i sy + i ry
;
;
Ψmy = Lm ⋅ i my
(96)
El sistema sigue siendo de resolución complicada.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
24
Variables de estado los flujos de estator y rotor. Modelo 12.
Una vez simplificadas, las ecuaciones quedan de la siguiente forma:
d Ψs
Ψs − Ψr
= u s − rs ⋅
dt
Lrl
d Ψr
Ψr − Ψ s
= u r − rr ⋅
dt
Lrl
+ g (Ψs ) − j ⋅ ω ⋅ Ψs
− j ⋅ (ω − ω r ) ⋅ Ψr
(97)
que una vez desarrolladas se representan de la siguiente manera:
Ψ − Ψrx
⋅ sx
+ g x (Ψs ) + ω ⋅ Ψsy
Lrl
dΨsy
Ψsy − Ψry
= u sy − rs ⋅
+ g y (Ψs ) − ω ⋅ Ψsx
dt
Lrl
dΨsx
= u sx − rs
dt
Ψ − Ψsx
⋅ rx
Lrl
dΨry
Ψry − Ψsy
= u ry − rr ⋅
dt
Lrl
dΨrx
= u rx − rr
dt
+ (ω − ω r ) ⋅ Ψry
− (ω − ω r ) ⋅ Ψrx
(98)
con:
Ψsx 2 + Ψsy 2
Ψsx
Ψsx
+ b⋅
= I N ⋅ a ⋅
g x ( Ψs ) = g ( Ψs ) ⋅
n
Ψ
Ψs
ΨN
N
Ψsy 2 + Ψsy 2
Ψsy
Ψsy
+ b⋅
= I N ⋅ a ⋅
g y ( Ψs ) = g ( Ψs ) ⋅
n
Ψs
Ψ
ΨN
N
(
(
)
⋅ Ψsx
n −1
2
⋅ Ψsy
n −1
2
)
(99)
Si se compara con el modelo 2, este resulta mucho más sencillo ya que no es
necesaria la resolución de una ecuación algebraica para cada paso de
integración.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
25
Variables de estado la corriente de estator y el flujo magnetizante. Modelo 13.
Después de algunas operaciones algebraicas, se llega al conjunto de ecuaciones
que sigue:
0
0
−
Lrl
0
− rs
0
+
−r
r
(ω
g
i sx u sx
∂g x
∂g x
d i sy u sy
0
(1 + Lrl ⋅
) − Lrl ⋅
⋅
= +
∂Ψmx
∂Ψmy
dt Ψmx u rx
∂g y
∂g y
Ψ u
− Lrl − Lrl ⋅
(1 + Lrl ⋅
)
my ry
∂Ψmx
∂Ψmy
0
0
ωg
i sx
− rs
−ω g
0
i sy
+
⋅
− (ω g − ω r ) ⋅ Lrl 0
(ω g − ω r ) Ψmx
Ψ
− ω r ) ⋅ Lrl − rr
− (ω g − ω r ) 0
my
0
0
1
0
0
1
0
0
+
− r ⋅ g + (ω g − ω r ) ⋅ Lrl ⋅ g y
r x
− r ⋅ g − (ω − ω ) ⋅ L ⋅ g
g
r
rl
x
r y
(100)
Donde:
Ψ
2
g x (Ψm ) = g (Ψm ) ⋅ mx = g ( Ψmx
Ψm
g y ( Ψm ) = g ( Ψ m ) ⋅
Ψmy
Ψm
2
= g ( Ψmx
2
(Ψmx
Ψmx
Ψmx
2
+ Ψmy ) ⋅
= I N ⋅ a ⋅
+b⋅
Ψm
ΨN
2
Ψmy
(Ψmx
Ψmy
2
= I N ⋅ a ⋅
+b⋅
+ Ψmy ) ⋅
Ψm
ΨN
2
+ Ψmy
)
n −1
2
Ψ Nn
2
+ Ψmy
)
Ψ Nn
n −1
2
⋅ Ψmx
⋅ Ψmy
(101)
además, deben calcularse las derivadas:
∂g x
,
∂Ψmx
∂g x
,
∂Ψmy
∂g y
∂Ψmx
,
∂g y
∂Ψmy
(102)
En este caso, no debe resolverse ninguna ecuación implícita para cada paso
de cálculo pero, sin embargo, el modelo es de gran complejidad.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
26
Variables de estado las corrientes de estator y el flujo del rotor. Modelo 14.
Las ecuaciones resultantes, son las que siguen:
∂g x
∂g x
∂g x
∂g x
2
− 1 + Lrl ⋅
⋅ Lrl
1 + Lrl ⋅
− Lrl ⋅
Lrl ⋅
∂Ψsy
∂Ψsy
∂Ψsx
∂Ψsx
∂g y
∂g y
∂g y
∂g y
2
1 + Lrl ⋅
⋅ Lrl
− Lrl ⋅
− 1 + Lrl ⋅
Lrl ⋅
∂Ψsx
∂Ψsy
∂Ψsx
∂Ψsy
0
0
1
0
0
0
0
1
−ω
ω ⋅ Lrl
0
u sx − rr
i sx − ω ⋅ Lrl ⋅ g x
− rr
ω
0
u sy − ω ⋅ Lrl
i sy ω ⋅ Lrl ⋅ g y
+
⋅
u + − r
− (ω − ω r ) Ψrx rr ⋅ g x
0
0
rx
r
Ψ r ⋅ g
u
−
−
0
r
(
ω
ω
)
0
r
y
r
r
ry
ry
i sx
d i sy
⋅
=
dt Ψrx
Ψ
ry
(103)
donde:
Ψ
2
g x (Ψm ) = g (Ψm ) ⋅ mx = g ( Ψmx
Ψm
g y ( Ψm ) = g ( Ψ m ) ⋅
Ψmy
Ψm
2
= g ( Ψmx
2
(Ψmx
Ψ
Ψmx
2
mx
+ Ψmy ) ⋅
= I N ⋅ a ⋅
+b⋅
Ψm
ΨN
2
Ψ
(Ψmx
Ψmy
my
2
+b⋅
= I N ⋅ a ⋅
+ Ψmy ) ⋅
ΨN
Ψm
+Ψ )
2
my
n −1
2
Ψ Nn
+Ψ )
2
my
Ψ Nn
n −1
2
⋅ Ψmx
⋅ Ψmy
(104)
y deben calcularse las derivadas siguientes:
∂g x
,
∂Ψmx
∂g x
,
∂Ψmy
∂g y
∂Ψmx
,
∂g y
∂Ψmy
(105)
Es un modelo realmente complicado.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
27
Variables de estado las corrientes del estator y magnetizante. Modelo 15.
Después de transformaciones algebraicas, se llega a:
0
0
− L
rl
0
0
0
0
Lrl
∂L
∂L
di sx
⋅ i mx
−
⋅ i my
∂i m
∂i m
dt
∂L
∂L
di
L+
⋅ i my
⋅ i mx sy
∂i m
∂i m
⋅ dt
∂L
∂L
di mx
⋅ i mx + L
−
⋅ i my
Lrl +
dt
∂i m
∂i m
di my
∂L
∂L
⋅ i my
⋅ i mx + L
Lrl +
∂i m
∂i m
dt
L+
rs
0
−
− rr
− (ω − ω ) ⋅ L
r
rl
0
rs
(ω − ω r ) ⋅ Lrl
− rr
u
sx
u sy
= u −
rx
u ry
0
−ω ⋅ L
i sx
ω⋅L
0
i sy
⋅
rr
− (ω − ω r ) ⋅ ( Lrl + L) i mx
i
rr
(ω − ω r ) ⋅ ( Lrl + L)
my
(106)
donde:
L = h(i m )
∂L ∂h(i m )
=
∂i m
∂i m
(107)
resulta un modelo complicado pero resoluble.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
28
Modelos tipo Γ(II). Cancelación de Lrl.
En este caso, el flujo rotórico se identifica con el de magnetización:
Ψr = Ψm
(108)
Variables de estado las corrientes del estator y rotor. Modelo 16.
Después de varias transformaciones elementales se llega a:
di
= M −1 ⋅ v − M −1 ⋅ A ⋅ i
dt
con:
t
t
v = (u sx u sy u rx u ry )
i = (i sx i sy i rx i ry )
Rs
ω g ⋅ ( Lm + L sl )
A=
0
(ω − ω ) ⋅ L
r
m
g
− ω g ⋅ ( Lm + L sl )
Rs
− (ω g − ω r ) ⋅ Lm
0
Lsl + Lddm
Ldq
M =
Lddm
L
dq
Lddm
Ldq
Lddm
Ldq
Lddm = L ⋅ cos 2 µ + Lm ⋅ sin 2 µ
Lqqm = L ⋅ sin 2 µ + Lm ⋅ cos 2 µ
L=
(113)
Ldq = ( L − Lm ) ⋅ cos µ ⋅ sinµ
tanµ =
imy
Ψm = Ψmx + Ψmy
2
2
(111)
Ldq
Lqqm
Ldq
Lqqm
(112)
dΨm
dim
;
i m = i mx + i my
i mx = i sx + i rx
Ψmx = Lm ⋅ i mx
Lm =
Ψm = f (i m )
(115)
i mx
2
(110)
− ω g ⋅ Lm
0
− (ω g − ω r ) ⋅ ( Lm )
Rr
0
ω g ⋅ Lm
Rr
(ω g − ω r ) ⋅ ( Lm )
Ldq
L sl + Lqqm
Ldq
Lqqm
(109)
2
Ψm
im
(114)
(116)
(117)
i my = i sy + i ry
;
;
Ψmy = Lm ⋅ i my
(118)
Modelo de complejidad similar al nº 1.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
29
Variables de estado los flujos del estator y rotor. Modelo 17.
Una vez simplificadas, las ecuaciones quedan de la siguiente manera:
d Ψs
Ψ s − Ψr
= u s − rs ⋅
dt
L sl
d Ψr
Ψ s − Ψr
= u r − rr ⋅
dt
L sl
− j ⋅ ω ⋅ Ψs
− g (Ψr ) − j ⋅ (ω − ω r ) ⋅ Ψr
(119)
que una vez desarrolladas se representan como siguen:
Ψ − Ψrx
⋅ sx
Lsl
dΨsy
Ψsy − Ψry
= u sy − rs ⋅
dt
L sl
dΨsx
= u sx − rs
dt
+ ω ⋅ Ψsy
− ω ⋅ Ψsx
Ψ − Ψrx
⋅ sx
− g x (Ψrs ) + (ω − ω r ) ⋅ Ψry
L sl
dΨry
Ψsy − Ψry
= u ry − rr ⋅
− g y (Ψr ) − (ω − ω r ) ⋅ Ψrx
dt
L sl
dΨrx
= u rx − rr
dt
(120)
con:
Ψsx 2 + Ψsy 2
Ψsx
Ψsx
+ b⋅
= I N ⋅ a ⋅
g x ( Ψs ) = g ( Ψs ) ⋅
n
Ψ
Ψs
ΨN
N
Ψsy 2 + Ψsy 2
Ψsy
Ψsy
+ b⋅
= I N ⋅ a ⋅
g y ( Ψs ) = g ( Ψs ) ⋅
n
Ψs
Ψ
ΨN
N
(
(
)
⋅ Ψsx
n −1
2
⋅ Ψsy
n −1
2
)
(121)
Si se compara con el modelo 2, este resulta mucho más sencillo ya que no es
necesaria la resolución de una ecuación algebraica para cada paso de
integración.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
30
Variables de estado la corriente de estator y el flujo magnetizante. Modelo 18.
Variables de estado la corriente de estator y el flujo de rotor. Modelo 19.
Tras varias operaciones algebraicas, se llega al siguiente conjunto de ecuaciones:
L sl
0
0
0
0
L sl
0
0
1
0
1
0
− rs
− ω g ⋅ L sl
+
−r
r
0
i sx u sx
0
1 d i sy u sy
⋅
=
+
0 dt Ψmx u rx
Ψ u
1
my ry
ω ⋅ L sl
− rs
0
− rr
0
ω
0
− (ω − ω r )
(122)
−ω
0
i sx
0
0
i sy
⋅
+
(ω − ω r ) Ψmx − rr ⋅ g x
Ψ − r ⋅ g
0
y
my r
Donde:
2
(Ψmx
Ψmx
Ψmx
Ψmx
2
2
= g ( Ψmx + Ψmy ) ⋅
= I N ⋅ a ⋅
+b⋅
g x ( Ψm ) = g ( Ψm ) ⋅
Ψm
Ψm
ΨN
2
Ψmy
Ψmy
(Ψmx
Ψmy
2
2
+b⋅
= I N ⋅ a ⋅
= g ( Ψmx + Ψmy ) ⋅
g y ( Ψm ) = g ( Ψ m ) ⋅
ΨN
Ψm
Ψm
2
+ Ψmy
)
n −1
2
Ψ Nn
2
+ Ψmy
)
Ψ Nn
n −1
2
⋅ Ψmx
⋅ Ψmy
(123)
Obsérvese la relativa simplicidad del modelo resultante.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
31
Variables de estado las corrientes del estator y magnetizante. Modelo 20.
Después de varias transformaciones elementales, se llega a:
L sl
0
0
0
0
L sl
0
0
rs
ω ⋅ L sl
−
− rr
0
∂L
∂L
⋅ i mx
−
⋅ i my di sx
∂i m
∂i m
dt
u sx
∂L
∂L
di
⋅ i my
⋅ i mx sy
L+
u
∂i m
∂i m
⋅ dt = sy −
∂L
∂L
di
u
⋅ i mx + L −
⋅ i my mx rx
dt u
∂i m
∂i m
di my ry
∂L
∂L
⋅ i my
⋅ i mx + L
∂i m
∂i m
dt
− ω ⋅ L sl
−ω ⋅ L
0
i sx
rs
ω⋅L
0
i sy
⋅
− (ω − ω r ) ⋅ ( L) i mx
rr
0
i
− rr
rr
(ω − ω r ) ⋅ ( L)
my
L+
(124)
donde:
L = h(i m )
∂L ∂h(i m )
=
∂i m
∂i m
(125)
Resulta un modelo complicado pero resoluble.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
32
Modelos tipo Γ(I) (Lsl = 0) sin consideración de la saturación
cruzada.
En este caso, el flujo estatórico se identifica con el de magnetización:
Ψ s = Ψm
(126)
Variables de estado las corrientes del estator y rotor. Modelo 21.
Tras varias operaciones algebraicas se llega a:
di
= M −1 ⋅ v + M −1 ⋅ ( A ⋅ i + Ω ⋅ Ψ )
dt
con:
t
t
v = (u sx u sy u rx u ry )
i = (i sx i sy i rx i ry )
Ψ = (Ψmx
− Rs
0
A=
0
0
0
− Rs
0
0
0
0
− Rr
− (ω g − ω r ) ⋅ Lrl
0
−ω
Ω=
0
(ω
− (ω − ω )
r
Lmx
0
M =
L
mx
0
0
Lmy
0
Lmy
Lmx =
Lmx
0
Lrl + Lmx
0
dΨmx
di mx
Ψmx = f x (i mx );
i mx = i sx + i rx
t
0
0
(ω g − ω r ) ⋅ Lrl
− Rr
(129)
(130)
(131)
0
Lmy
0
Lrl + Lmy
(132)
dΨmy
di my
Ψmy = f y (i my )
;
(128)
ω
0
− ω r )
0
Lmy =
;
Ψmy )
(127)
i my = i sy + i ry
(133)
(134)
(135)
que resulta un modelo muy manejable.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
33
Variables de estado los flujos del estator y rotor. Modelo 22.
Una vez simplificadas las ecuaciones quedan:
d Ψs
Ψs − Ψr
= u s − rs ⋅
dt
Lrl
d Ψr
Ψr − Ψ s
= u r − rr ⋅
dt
Lrl
+ g (Ψs ) − j ⋅ ω ⋅ Ψs
− j ⋅ (ω − ω r ) ⋅ Ψr
(136)
que una vez desarrolladas se representan de la siguiente forma:
Ψ − Ψrx
⋅ sx
+ g x (Ψs ) + ω ⋅ Ψsy
Lrl
dΨsy
Ψsy − Ψry
= u sy − rs ⋅
+ g y (Ψs ) − ω ⋅ Ψsx
dt
Lrl
dΨsx
= u sx − rs
dt
Ψ − Ψsx
⋅ rx
Lrl
dΨry
Ψry − Ψsy
= u ry − rr ⋅
dt
Lrl
dΨrx
= u rx − rr
dt
+ (ω − ω r ) ⋅ Ψry
− (ω − ω r ) ⋅ Ψrx
(137)
con:
Ψsx
(Ψsx )n
g x (Ψsx ) = I N ⋅ a ⋅
+ b⋅
Ψ n
Ψ N
N
Ψsy
(Ψsy )n
+ b⋅
g y (Ψsy ) = I N ⋅ a ⋅
Ψ n
Ψ N
N
(138)
Este modelo resulta muy simple y sencillo de calcular.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
34
Variables de estado la corriente del estator y el flujo magnetizante. Modelo 23l
Después de algunas transformaciones algebraicas, se llega al siguiente conjunto de
ecuaciones:
0
0
− Lrl
0
− rs
0
+
−r
r
(ω
g
i sx u sx
∂g x
d i sy u sy
0
(1 + Lrl ⋅
) 0
⋅
= +
∂Ψmx
dt Ψmx u rx
∂g y
Ψ u
− Lrl 0
(1 + Lrl ⋅
)
my ry
∂Ψmy
0
0
ωg
i sx
− rs
−ω g
0
i sy
+
⋅
− (ω g − ω r ) ⋅ Lrl 0
(ω g − ω r ) Ψmx
Ψ
− ω r ) ⋅ Lrl − rr
− (ω g − ω r ) 0
my
0
0
1
0
0
1
0
0
+
− r ⋅ g + (ω g − ω r ) ⋅ Lrl ⋅ g y
r x
− r ⋅ g − (ω − ω ) ⋅ L ⋅ g
r
y
g
r
rl
x
(139)
Donde:
Ψ
(Ψ )n
g x (Ψsx ) = I N ⋅ a ⋅ sx + b ⋅ sx n
Ψ
N
Ψ N
Ψsy
(Ψsy )n
+ b⋅
g y (Ψsy ) = I N ⋅ a ⋅
Ψ n
Ψ N
N
(140)
además, deben calcularse las derivadas siguientes:
∂g x
,
∂Ψmx
∂g y
∂Ψmy
(141)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
35
Variables de estado la corriente del estator y el flujo del rotor. Modelo 24.
Las ecuaciones resultantes, son las que siguen:
∂g x
− 1 + Lrl ⋅
∂Ψsx
0
0
0
u sx − rr
u sy − ω ⋅ Lrl
u + − r
r
rx
u
0
ry
i sx
∂g y d i sy
∂g y
⋅
1 + Lrl ⋅
⋅ Lrl
=
− 1 + Lrl ⋅
0
dt Ψrx
∂
Ψ
∂
Ψ
sy
sy
Ψ
0
1
0
ry
0
0
1
−ω
ω ⋅ Lrl
0
i sx − ω ⋅ Lrl ⋅ g x
− rr
ω
0
i sy ω ⋅ Lrl ⋅ g y
+
⋅
− (ω − ω r ) Ψrx rr ⋅ g x
0
0
Ψ r ⋅ g
− rr
(ω − ω r )
0
ry
r
y
⋅ Lrl
∂g x
1 + Lrl ⋅
∂Ψsx
0
0
(142)
donde:
Ψ
(Ψ )n
g x (Ψsx ) = I N ⋅ a ⋅ sx + b ⋅ sx n
Ψ
Ψ N
N
Ψsy
(Ψsy )n
+ b⋅
g y (Ψsy ) = I N ⋅ a ⋅
Ψ n
Ψ N
N
(143)
y deben calcularse las derivadas siguientes:
∂g x
,
∂Ψmx
∂g y
∂Ψmy
(144)
Es un modelo complicado.
Además deben resolverse las siguientes ecuaciones implícitas:
Ψsx = Ψrx − Lrl ⋅ (g x (Ψsx ) − i sx )
Ψsy = Ψry − Lrl ⋅ (g y (Ψsy ) − i sy )
(145)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
36
Variables de estado las corrientes del estator y magnetizante. Modelo 25.
Después de muchas operaciones algebraicas, se llega a:
0
0
− Lrl
0
0
Lx +
0
0
∂L x
⋅ i mx
∂i mx
0
Lrl +
Lrl
rs
0
−
− rr
− (ω − ω ) ⋅ L
r
rl
∂L x
⋅ i mx + L x
∂i mx
0
0
rs
(ω − ω r ) ⋅ Lrl
− rr
di sx
dt
∂L y
⋅ i my di sy
Ly +
∂i my
⋅ dt
di mx
0
dt
∂L y
di my
⋅ i my + L y
Lrl +
dt
∂i my
0
ω ⋅ Lx
− (ω
rr
0
(ω − ω r ) ⋅ ( Lrl + L x )
u
sx
u sy
= u −
rx
u ry
− ω ⋅ Ly
i sx
0
i sy
⋅
− ω r ) ⋅ ( Lrl + L y ) i mx
i
rr
my
(146)
donde:
L x = h(i mx );
∂L x ∂h(i mx )
=
;
∂i mx
∂i mx
L y = h(i my )
∂L y
∂i my
=
∂h(i my )
(147)
∂i my
Resulta un modelo complicado pero resoluble.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
37
Modelos tipo Γ(II) (Lrl = 0) sin consideración de la saturación
cruzada.
En este caso, el flujo rotórico se identifica con el de magnetización:
Ψr = Ψm
(148)
Variables de estado las corrientes del estator y rotor. Modelo 26.
Después de varias transformaciones algebraicas, se llega a:
di
= M −1 ⋅ v + M −1 ⋅ ( A ⋅ i + Ω ⋅ Ψ )
dt
con:
v = (u sx
u sy
u rx
u ry )
i = (i sx
t
i sy
ω g ⋅ L sl
− Rs
0
0
− Rs
− ω g ⋅ sl
A=
0
0
i ry )
t
i rx
Ψ = (Ψmx
Ψmy )
t
− Rr
0
− Rr
0
ω
−ω
0
Ω=
0
(ω − ω r )
− (ω − ω )
0
r
Lsl + Lmx
0
M =
Lmx
0
Lmx =
0
0
0
Lsl + Lmy
0
Lmy
dΨmx
di mx
Ψmx = f x (i mx );
i mx = i sx + i rx
;
0
0
0
Lmx
0
Lmx
0
Lmy =
0
Lmy
0
Lmy
dΨmy
di my
Ψmy = f y (i my )
i my = i sy + i ry
(149)
(150)
(151)
(152)
(153)
(154)
(155)
(156)
(157)
que resulta un modelo manejable.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
38
Variables de estado los flujos del estator y rotor. Modelo 27.
Una vez simplificadas, las ecuaciones quedan de la siguiente manera:
d Ψs
Ψ s − Ψr
= u s − rs ⋅
dt
L sl
d Ψr
Ψ s − Ψr
= u r − rr ⋅
dt
L sl
− j ⋅ ω ⋅ Ψs
− g (Ψr ) − j ⋅ (ω − ω r ) ⋅ Ψr
(158)
que una vez desarrolladas se representan en la siguiente forma:
Ψ − Ψrx
⋅ sx
Lsl
dΨsy
Ψsy − Ψry
= u sy − rs ⋅
dt
L sl
dΨsx
= u sx − rs
dt
+ ω ⋅ Ψsy
− ω ⋅ Ψsx
Ψ − Ψrx
⋅ sx
− g x (Ψry ) + (ω − ω r ) ⋅ Ψry
L sl
dΨry
Ψsy − Ψry
= u ry − rr ⋅
− g y (Ψry ) − (ω − ω r ) ⋅ Ψrx
dt
L sl
dΨrx
= u rx − rr
dt
(159)
con:
Ψrx
(Ψrx )n
g x (Ψrx ) = I N ⋅ a ⋅
+ b⋅
Ψ n
Ψ N
N
Ψry
(Ψry )n
+ b⋅
g y (Ψry ) = I N ⋅ a ⋅
Ψ n
Ψ N
N
(160)
Si se compara con el modelo 2, este resulta mucho más sencillo ya que no es
necesaria la resolución de una ecuación algebraica para cada paso de
integración.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
39
Variables de estado la corriente del estator y el flujo magnetizante. Modelo 28.
Variables de estado la corriente del estator y el flujo de rotor. Modelo 29.
Tras muchas transformaciones algebraicas, se llega al siguiente conjunto de
ecuaciones:
L sl
0
0
0
0
L sl
0
0
1
0
1
0
− rs
− ω g ⋅ L sl
+
−r
r
0
i sx u sx
0
1 d i sy u sy
⋅
=
+
0 dt Ψmx u rx
Ψ u
1
my
ry
ω ⋅ L sl
− rs
0
− rr
0
ω
0
− (ω − ω r )
−ω
0
i sx
0
0
i sy
⋅
+
(ω − ω r ) Ψmx − rr ⋅ g x
Ψ − r ⋅ g
0
my
r
y
(161)
Donde:
Ψrx
(Ψrx )n
g x (Ψrx ) = I N ⋅ a ⋅
+ b⋅
Ψ n
Ψ
N
N
Ψry
(Ψry )n
+ b⋅
g y (Ψry ) = I N ⋅ a ⋅
Ψ n
Ψ
N
N
(162)
Obsérvese la relativa simplicidad del modelo resultante.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
40
Variables de estado las corrientes del estator y magnetizante. Modelo 30.
Después de muchas transformaciones algebraicas se llega a:
L sl
0
0
0
0
L sl
0
0
rs
ω ⋅ L sl
−
− rr
0
∂L x
⋅ i mx
∂i mx
di sx
dt
u
∂L y
sx
0
L+
⋅ i my di sy
u
∂i my
⋅ dt = sy −
di mx u rx
∂L x
0
⋅ i mx + L x
dt
∂i mx
u ry
di
my
∂L y
0
⋅ i my + L y
dt
∂i my
0
− ω ⋅ L sl
− ω ⋅ Ly
i sx
ω ⋅ Lx
0
rs
i sy
⋅
0
rr
− (ω − ω r ) ⋅ ( L y ) i mx
i
(ω − ω r ) ⋅ ( L x )
rr
− rr
my
Lx +
0
(163)
donde:
L x = h(i mx );
L y = h(i my )
∂L x ∂h(i mx )
=
;
∂i mx
∂i mx
∂L y
∂i my
=
∂h(i my )
(164)
∂i my
Resulta un modelo complicado pero resoluble.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
41
Modelos basados en la orientación del campo.
Si se considera el eje de rotación girando a velocidad ωg y concordante con el vector
representativo del flujo, o corriente magnetizante, este tendrá una componente
única:
i m = i sx + i rx ;
i m = imx + j ⋅ 0
(165)
0 = i sy + i ry
(166)
La ventaja de esta transformación es doble:
-
Reducción del sistema original de quinto orden a uno de cuarto orden
La saturación puede expresarse en función de una única componente:
Ψm = f (i m );
Lm = h(i m );
i m = g ( Ψm )
(167)
según el conjunto de variables elegidas.
Como contrapartida debe calcularse la velocidad para cada instante de tiempo
considerado y pued,en existir problemas de arranque de la simulación.
Variables de estado las corrientes del estator y rotor. Modelo 31.
Las ecuaciones de la máquina, expresadas en la nueva referencia vienen dadas por:
dL
dL
Lm + m ⋅ (i sx + i rx )
L sl + Lm + m ⋅ (i sx + i rx ) 0
i
u
d im
d im
d sx sx
⋅ i sy = u sy +
0
L sl
0
dt
dLm
dLm
i rx u rx
+
⋅
+
+
+
⋅
+
L
(
i
i
)
0
L
L
(
i
i
)
sx
rx
sx
rx
sl
m
m
d im
d im
− rs
ω ⋅ L sl
0 i sx
− ω ⋅ Lm ⋅ i sy
− ω ⋅ ( Lsl + Lm ) − rs
− (ω − ω ) ⋅ L
− rr i rx
0
r
rl
(168)
donde la velocidad de los ejes viene determinada a partir de la siguiente expresión:
u ry +
ω=
Lrl
L
L
⋅ u sy − rr + rl ⋅ rs ⋅ i sy + ω r ⋅ rl ⋅ (( Lrl + Lm ) ⋅ i rx + Lm ⋅ i sx )
L sl
Lsl
L sl
Lrl
⋅ [( Lsl + Lm ) ⋅ i sx + Lm ⋅ i rx ] + ( Lrl + Lm ) ⋅ i rx + Lm ⋅ i sx
Lsl
(169)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
42
Variables de estado los flujos del estator y rotor. Modelo 32.
Las ecuaciones transformadas quedan de la siguiente manera:
dΨsx
r
= u sx − s ⋅ (Ψsx − Ψmx ) + ω ⋅ Ψsy
dt
L sl
dΨsy
dt
= u sy −
rs
⋅ (Ψsy ) − ω ⋅ Ψsx
L sl
(170)
dΨrx
r
= u rx − r ⋅ (Ψrx − Ψmx ) + (ω − ω r ) ⋅ Ψry
dt
Lrl
conjuntamente con la siguiente restricción algebraica:
Ψsx Ψrx
+
− Ψmx
Lsl
Lrl
1
1
= i m = g (Ψm )
⋅
+
L
L
rl
sl
(171)
y la expresión para la determinación de la velocidad indicada a continuación:
u ry +
ω=
r
r L
⋅ r + s ⋅ rl + ω r ⋅ Ψrx
Lrl L sl Lsl
L
Ψrx + rl ⋅ Ψsx
L sl
Lrl
⋅ u sy − Ψry
L sl
(172)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
43
Variables de estado la corriente del estator y el flujo magnetizante. Modelo 33.
Después de algunas operaciones algebraicas, se llega a:
L
0
1
sl
Lsl
0
0
dg
− Lrl 0 1 + Lrl ⋅
dΨm
0
+ 0 ⋅ g ( Ψm )
r
r
i u − rs
d sx sx
⋅ i sy = u sy + − ω ⋅ L sl
dt
Ψm u rx rr
ω ⋅ Lsl
− rs
− (ω − ω r ) ⋅ Lrl
0 i sx
0 ⋅ i sy +
0 Ψm
(173)
junto con la expresión para el cálculo de la velocidad:
u ry +
ω=
L
Lrl
⋅ u sy − (rr + rl ⋅ rs ) ⋅ i sy + ω r ⋅ (Lrl ⋅ ( g (Ψm ) − i sx + Ψm )
L sl
L sl
Lrl ⋅ g (Ψm ) + Ψm
(174)
Variables de estado la corriente del estator y el flujo del rotor. Modelo 34.
df
1 df
⋅
di m
Lrl di m
L +
0
sl
1 df
1 df
⋅
⋅
1+
1+
i sx u sx
L
di
L
di m
rl
m
rl
d
0
Lsl
0
⋅ i sy = u sy +
dt Ψ u
0
0
1
rx rx
−r
i
⋅
ω
L
0
0
s
sl
sx
− ω ⋅ L sl
− rs
⋅ i sy + ω ⋅ f (i m )
r
r
− (ω − ω r ) ⋅ Lrl − r Ψrx r ⋅ f (i m )
0
Lrl
Lrl
(175)
junto con:
u ry +
ω=
Lrl
L
⋅ u sy + rr − rl ⋅ rs ⋅ i sy + ω r ⋅ Ψrx
L sl
L sl
L
Lrl ⋅ i sx + rl ⋅ f (i m ) + Ψrx
L sl
(176)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
44
Variables de estado las corrientes del estator y magnetizante. Modelo 35.
Lsl
0
− L
rl
0
Lsl
0
dLm
⋅ i m + Lm
i sx u sx − rs
di m
d
⋅ i = u + − ω ⋅ L
0
sl
dt sy sy
dLm
i m u rx rr
Lrl ⋅ 1 +
⋅ i m + Lm
di m
ω ⋅ Lsl
− rs
− (ω − ω r ) ⋅ Lrl
0 i sx
− ω ⋅ Lm ⋅ i sy
− rr i m
(177)
conjuntamente con:
u ry +
ω=
Lrl
L
⋅ u sy + rs ⋅ rl − rr ⋅ i sy + ω r ⋅ (( Lrl + Lm ) ⋅ i m − Lrl ⋅ i sx )
L sl
Lsl
Lrl
⋅ Lm + Lrl + Lm ⋅ i m + ( L sl − Lrl ) ⋅ i sx
Lsl
(178)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
45
Modelos de control por orientación del campo. Transformación tipo
Γ(I). Cancelación de Lsl.
Variables de estado las corrientes del estator y rotor. Modelo 36.
Después de alguna transformación, se llega a:
dLm
⋅ i m + Lm
di m
0
0
− rs
0
0
i sx u sx
d
dLm
⋅ i m + Lm ⋅ i rx = u rx +
Lrl
di m
dt i u
ry ry
Lrl
0
0
0
ω
i sx
− rr
(ω − ω r ) ⋅ Lrl ⋅ i rx +
0
− (ω − ω r ) ⋅ Lrl
− rr
i ry − (ω − ω r ) ⋅ Lm ⋅ i m
dLm
⋅ i m + Lm
di m
0
(179)
junto con:
ω=
u sy + rs ⋅ i ry
Lm ⋅ (i sx + i rx )
(180)
Resulta un modelo muy sencillo y conceptualmente claro.
Variables de estado los flujos del estator y rotor. Modelo 37.
Una vez simplificadas las ecuaciones, quedan:
Ψ − Ψrx
⋅ sx
Lrl
Ψ − Ψsx
dΨrx
= u rx − rr ⋅ rx
dt
Lrl
dΨsx
= u sx − rs
dt
+ g x (Ψs )
+ (ω − ω r ) ⋅ Ψry
(181)
dΨry
Ψry
− (ω − ω r ) ⋅ Ψrx
= u ry − rr ⋅
dt
Lrl
junto con:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
Ψry
u sy − rs ⋅ g (Ψm ) −
Lrl
ω=
Ψsx
46
(182)
Este modelo resulta muy simple y sencillo de calcular.
Variables de estado la corriente del estator y el flujo magnetizante. Modelo 38.
Después de algunas transformaciones, se llega a:
0
− L
rl
0
0
0
− Lrl
− rs
rr
(ω − ω ) ⋅ L
r
rl
1
dg
1 + Lrl ⋅
dΨm
0
i sx u sx
⋅ d i = u +
sy
rx
dt
Ψm u ry
0
(ω − ω r ) ⋅ Lrl
rr
(183)
0 i sx
0
0 ⋅ i sy + − rr ⋅ g (Ψm )
Ψ − (ω − ω ) ⋅ Ψ
r
m
m
Junto con:
ω=
u sy − rs ⋅ i sy
Ψm
(184)
que también resulta muy sencillo.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
47
Variables de estado la corriente del estator y el flujo del rotor. Modelo 39.
Se llega a:
df
di m
1 df
⋅
1+
L rl di m
0
0
r 0
r ⋅ f (i )
m
L
rl
0
1
L rl
1+
1
⋅
df
di m
df
⋅
L rl di m
1
0
0
d
0 ⋅
dt
1
i sx
Ψ rx
Ψ
ry
u sx
= u rx
u
ry
− r
s
+ 0
0
0
i sx
rr
−
(ω − ω r ) ⋅ Ψ rx
L rl
Ψ
r r ry
− (ω − ω r )
−
L rl
(185)
junto con:
ω=
u sy − rs ⋅ i sy
Ψm
(186)
Variables de estado las corrientes del estator y magnetizante. Modelo 40.
Se obtiene:
dLm
⋅ i m + Lm
0
0
di m
i sx u sx
d
dLm
⋅ i m + Lm ⋅ i sy = u rx +
Lrl +
0
− Lrl
di m
dt i u
m ry
− Lrl
0
0
− rs
0
0
i sx
− (ω − ω r ) ⋅ Lrl
− rr
rr
⋅ i sy +
(ω − ω ) ⋅ L
− (ω − ω r ) ⋅ Lrl + Lm i m
rr
r
rl
(187)
junto con:
ω=
u sy − rs ⋅ i sy
Lm ⋅ i m
(188)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
+
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
48
Modelos de control por orientación del campo. Transformación tipo
Γ(II). Cancelación de Lrl.
Variables de estado las corrientes del estator y rotor. Modelo 41.
Las ecuaciones transformadas conducen al siguiente sistema:
dL
dL
Lm + m ⋅ (i sx + i rx )
L sl + Lm + m ⋅ (i sx + i rx ) 0
i
u
d im
d im
d sx sx
⋅ i sy = u sy +
0
L sl
0
dt
dLm
dLm
i rx u rx
⋅ (i sx + i rx )
0 L sl + Lm +
⋅ (i sx + i rx )
Lm +
d im
d im
− rs
ω ⋅ L sl
0 i sx
− ω ⋅ Lm ⋅ i sy
− ω ⋅ ( Lsl + Lm ) − rs
− rr i rx
0
0
(189)
donde la velocidad de los ejes viene determinada a partir de la siguiente expresión:
ω=
u ry − rr ⋅ i sy
Lm ⋅ (i rx + i sx )
(190)
Variables de estado los flujos del estator y rotor. Modelo 42.
rs
−
Ψsx u sx Lsl
d
Ψsy = u sy + 0
dt
Ψr u rx rr
L
sl
junto con:
0
−
rs
Lsl
0
rs
L sl Ψ
0
sx
ω ⋅ Ψsy +
0
Ψ r ⋅ g (Ψ )
r
r rx r
− r
Lsl
u ry +
ω=
rr
⋅ Ψsy
L sl
+ ωr
Ψr
(191)
(192)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
49
Variables de estado la corriente del estator y el flujo magnetizante. Modelo 43.
Variables de estado la corriente del estator y el flujo de rotor. Modelo 44.
Después de algunas transformaciones algebraicas, se llega a:
L sl
0
0
0
L sl
0
1
i u − rs
d sx sx
0 ⋅ i sy = u sy + − ω ⋅ L sl
dt
1
Ψm u rx rr
ω ⋅ Lsl
− rs
0
0 i sx 0
0 ⋅ i sy + 0 ⋅ g (Ψm )
0 Ψm rr
(193)
juntamente con la expresión para el cálculo de la velocidad:
ω=
u ry − rr ⋅ i sy
Ψm
+ ωr
(194)
Variables de estado las corrientes del estator y magnetizante. Modelo 45
Finalmente, se obtienen las siguientes ecuaciones:
L sl
0
0
0
L sl
0
dLm
⋅ i m + Lm
− rs
i
u
di m
d sx sx
i sy = u sy + − ω ⋅ L sl
0
dt
dLm
⋅ i m + Lm i m u rx rr
di m
junto con:
ω=
u ry + rr ⋅ i sy
Lm ⋅ i m
ω ⋅ Lsl
− rs
+ ωr
0
0 i sx
− ω ⋅ Lm ⋅ i sy
− rr i m
(195)
(196)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
50
Resumen comparativo de los distintos modelos.
Modelo
0 (lineal)
Ecuaciones
implícitas o
algebraicas
NO
Derivadas de funciones
de la saturación
NO
Variables no mensurables
(Necesidad de observador de
estados)
SI (variable según el conjunto de
variables considerado)
Modelos con consideración de la saturación cruzada.
1
SI
2
SI
3
NO
4
SI
5
NO
L = h(i m );
∂g x
,
∂Ψmx
∂L ∂h(i m )
=
∂i m
∂i m
NO
∂g y
∂g x
,
∂Ψmy
∂Ψmx
i rx ;
Ψsx ;
∂g y
,
∂Ψmy
SI
∂L ∂h(i m )
=
∂i m
∂i m
L = h(i m );
i ry
Ψsy ;
Ψrx ;
Ψmx ;
Ψmy
Ψrx ;
Ψry
i mx ;
i my
i rx ;
i ry
Ψry
Modelos sin consideración de la saturación cruzada.
6
NO
7
SI
8
NO
9
10
NO
NO
Lmx =
dΨmx
di mx
Lmy =
dΨmy
di my
NO
∂g x
,
∂Ψmx
df x
;
di mx
∂Lx ∂hx (imx )
=
;
∂imx
∂imx
Ψsx ;
∂g y
∂Ψmy
df y
Ψsy ;
Ψrx ;
Ψmx ;
Ψmy
Ψrx ;
Ψry
i mx ;
i my
Ψry
di my
∂Ly
∂imy
=
∂hy (imy )
∂imy
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
51
Modelos tipo Γ(I). Cancelación de Lsl. Consideración de la saturación cruzada.
11
SI
12
NO
13
NO
14
15
NO
NO
L = h(i m );
∂L ∂h(i m )
=
∂i m
∂i m
NO
∂g x
,
∂Ψmx
∂g x
,
∂Ψmy
∂g x
,
∂Ψmx
∂g x
,
∂Ψmy
∂g y
∂Ψmx
∂g y
∂Ψmx
i rx ;
Ψsx ;
∂g y
,
∂Ψmy
∂g y
,
∂Ψmy
∂L ∂h(i m )
=
∂i m
∂i m
L = h(i m );
i ry
Ψsy ;
Ψrx ;
Ψmx ;
Ψmy
Ψrx ;
Ψry
i mx ;
i my
Ψry
Modelos tipo Γ(II). Cancelación de Lrl. Consideración de la saturación cruzada.
16
SI
17
NO
∂L ∂h(i m )
=
∂i m
∂i m
NO
18
NO
19
NO
20
NO
L = h(i m );
i rx ;
Ψsx ;
i ry
Ψsy ;
Ψrx ;
NO
Ψmx ;
Ψmy
NO
Ψrx ;
Ψry
i mx ;
i my
∂L ∂h(i m )
=
∂i m
∂i m
L = h(i m );
Ψry
Modelos tipo Γ(I). Cancelación de Lsl. Sin consideración de la saturación
cruzada.
21
NO
22
NO
23
NO
24
25
SI
NO
Lmx =
dΨmx
di mx
dΨmy
Lmy =
∂g x
,
∂Ψmx
L x = h(i mx );
∂L x ∂h(i mx )
=
;
∂i mx
∂i mx
Ψsx ;
∂g y
∂Ψmy
∂g y
∂Ψmy
L y = h(i my )
∂L y
∂i my
=
i ry
di my
NO
∂g x
,
∂Ψmx
i rx ;
Ψsy ;
Ψrx ;
Ψmx ;
Ψmy
Ψrx ;
Ψry
i mx ;
i my
Ψry
∂h(i my )
∂i my
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
52
Modelos tipo Γ(II). Cancelación de Lrl. Sin consideración de la saturación
cruzada.
26
NO
Lmx =
dΨmx
di mx
dΨmy
Lmy =
27
NO
NO
28
NO
29
NO
30
NO
L x = h(i mx );
i rx ;
i ry
di my
Ψsx ;
Ψsy ;
Ψrx ;
NO
Ψmx ;
Ψmy
NO
Ψrx ;
Ψry
i mx ;
i my
i rx ;
i ry
L y = h(i my )
∂L y
∂L x ∂h(i mx )
;
=
∂i mx
∂i mx
∂i my
=
Ψry
∂h(i my )
∂i my
Modelos basados en la orientación del campo.
31
SI
32
SI
33
SI
34
SI
35
SI
dLm
di m
NO
Ψsx ;
dg
dΨm
df
di m
L = h(i m );
∂L ∂h(i m )
=
∂i m
∂i m
Ψsy ;
Ψrx ;
Ψmx ;
Ψmy
Ψrx ;
Ψry
i mx ;
i my
Ψry
Modelos basados en la orientación del campo. Modelos tipo Γ(I). Cancelación
de Lsl.
36
SI
37
SI
38
SI
39
SI
40
SI
L = h(i m );
∂L ∂h(i m )
=
∂i m
∂i m
NO
dg
dΨm
df
di m
L = h(i m );
∂L ∂h(i m )
=
∂i m
∂i m
i rx ;
Ψsx ;
i ry
Ψsy ;
Ψrx ;
Ψmx ;
Ψmy
Ψrx ;
Ψry
i mx ;
i my
Ψry
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
53
Modelos basados en la orientación del campo. Modelos tipo Γ(II). Cancelación
de Lrl.
41
SI
42
SI
∂L ∂h(i m )
=
∂i m
∂i m
NO
43
SI
44
SI
45
SI
L = h(i m );
L = h(i m );
i rx ;
Ψsy ;
Ψrx ;
NO
Ψmx ;
Ψmy
NO
Ψrx ;
Ψry
i mx ;
i my
∂L ∂h(i m )
=
∂i m
∂i m
Ψsx ;
i ry
Ψry
Conclusiones.
A la vista de los resultados y debido a la necesidad de determinar los parámetros de
la forma más sencilla posible, se pueden deducir las siguientes consideraciones:
•
La ecuación (21) traduce la relación entre corriente de magnetización y flujo total
en el entrehierro. Para el caso lineal esta relación o RESTRICCIÓN
ALGEBRAICA puede deshacerse y sustituirse en las ecuaciones de estado que
modelizan la máquina, sean cuales sean las variables de estado consideradas.
En los casos que consideraremos existen conjuntos de variables de estado en
los que esta simplificación no es posible; estos modelos NO pueden ser
considerados útiles a efectos de control ya que para cada intervalo de cálculo
debe resolverse una ecuación algebraica NO lineal, en la que no es posible
indicar a priori el tiempo de resolución de la misma.
•
Los modelos que no consideran la saturación cruzada resultan más sencillos de
resolver y más prácticos para su inclusión dentro de algoritmos de determinación
de parámetros.
•
Los modelos simplificados (tipo Γ), resultan aún más sencillos de tratamiento.
•
En relación a la caracterización y determinación de los parámetros los modelos
tipo Γ (I) resultan mas interesantes ya que la caracterización de la saturación es
más sencilla
De las consideraciones anteriores, se deduce que los modelos más adecuados de
cara a los objetivos perseguidos, son los nº 21 a 25. Dentro de estos el modelo nº
24 no resulta adecuado debido a la restricción algebraica que presenta.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 2. MODELOS DE MÁQUINAS ASÍNCRONAS CON CONSIDERACIÓN DE LA SATURACIÓN
Los modelos nº 23 y nº 25, resultan complejos de resolución. Finalmente queda la
comparación entre los modelos nº 21 (con variables de estado las corrientes del
estator y rotor) y nº 22 (con variables de estado los flujos del estator y rotor). En los
capítulos que siguen, se detalla el uso de tales modelos para la determinación de los
parámetros, tanto en tiempo real como mediante ensayos fuera de línea.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
54
SENSIBILIDAD
∂f
dγ ∂f
= ⋅ γ +
dt ∂x p0
∂p p0
∂g
∂g
σ = ⋅ γ +
∂x p0
∂p p0
CAPÍTULO 3. SENSIBILIDAD.
1
3. SENSIBILIDAD
3. Sensibilidad ............................................................................................................................2
Ecuaciones de sensibilidad de un sistema dinámico [Eslami 94], [Rosenwasser 00]. .........2
Aplicación al caso de una bobina saturada. ...........................................................................4
Aplicación a las ecuaciones de la máquina asíncrona.............................................................10
Conclusiones. ........................................................................................................................31
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
2
3. Sensibilidad
Los modelos considerados en el capítulo anterior presentan ciertas características
que hacen que resulten muy afectados por las variaciones de los parámetros; de tal
manera que simulaciones sobre la misma máquina realizadas con diferentes
modelos pueden dar resultados discrepantes y tiempos de cálculo muy distintos.
Para analizar el problema, se debe evaluar la sensibilidad tanto estática (en régimen
permanente) como dinámica.
El análisis de las funciones de sensibilidad, permite estimar los errores en las salidas
ante variaciones de los parámetros, así como su influencia en la respuesta global del
sistema.
Un modelo menos sensible a las variaciones de los parámetros, será más útil para la
realización de algoritmos de control y, a su vez, se pondrá en evidencia que
parámetros son más delicados en su valoración posterior. En los capítulos que
siguen se realiza la identificación en tiempo real de los parámetros de los modelos;
si los parámetros en juego afectan poco a la respuesta del sistema, este resulta muy
robusto y, por tanto, se pueden admitir discrepancias en su valoración respecto el
valor nominal o exacto, según el caso.
Ecuaciones de sensibilidad
[Rosenwasser 00].
de
un
sistema
dinámico
[Eslami
94],
Dado un sistema cualquiera, descrito por el siguiente conjunto de ecuaciones
diferenciales:
dx
= f ( x, t , u , p o )
dt
y = g ( x, t , u , p )
;
x(t 0 ) = x 0
(1)
y el sistema, con parámetros desviados de su valor nominal:
dx
= f ( x, t , u , p )
dt
x(t 0 ) = x 0
(2)
El cambio de los valores del vector de estados debido a la variación de los
parámetros, viene dado por:
∂x
∆x(t , p ) = ⋅ ∆p = γ (t , p 0 ) ⋅ ∆p
∂p p0
(3)
Igualmente, para la función de salida:
∂y
∆y (t , p) = ⋅ ∆p = σ (t , p 0 ) ⋅ ∆p
∂p p0
(4)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
3
Las ecuaciones de sensibilidad del sistema, pueden plantearse como:
•
Funciones de sensibilidad de las variables de estado respecto a la variación de
los parámetros:
∂f
dγ ∂f
= ⋅ γ +
dt ∂x p0
∂p p0
•
(5)
Funciones de sensibilidad de las salidas respecto a la variación de los
parámetros:
∂g
∂g
σ = ⋅ γ +
∂x p0
∂p p0
(6)
Si el número de variables de estado es N, M el de salidas y P el de parámetros, la
∂f
matriz γ tiene dimensiones NxP, la matriz jacobiana NxN, la matriz jacobiana
∂x
∂f
∂g
∂g
NxP, la matriz σ MxP, el jacobiano MxN y el jacobiano MxP.
∂x p0
∂p p0
∂p p0
Valores de sensibilidad en régimen permanente
En régimen permanente, se cumplirá que:
dγ
=0
dt
(7)
entonces:
∂f
∂f
⋅ γ RP + = 0
∂x p0
∂p p0
γ RP
∂f
= −
∂x
−1
p0
∂f
⋅
∂p
p0
(8)
(9)
suponiendo que la matriz jacobiana no sea singular.
Los valores de la sensibilidad para las variables de salida se expresan como:
∂g
∂g
σ RP = ⋅ γ RP +
∂x p0
∂p p0
(10)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
4
Aplicación al caso de una bobina saturada.
Supongamos el caso de una bobina saturada alimentada a partir de una fuente de
tensión.
r
i
Ψ
u
Figura 1. Modelo de bobina saturada.
las ecuaciones que gobiernan el sistema, son las siguientes:
dΨ
=u − r ⋅i
dt
i
IN
Ψ
Ψ
=a⋅
+ b ⋅
ΨN
ΨN
(11)
n
que expresadas en formato normalizado conducen a:
Ψ
Ψ
⋅a ⋅
+ b ⋅
ΨN
ΨN
n
Ψ
Ψ
i = IN ⋅ a ⋅
+ b ⋅
ΨN
Ψ N
dΨ
= u − r ⋅ IN
dt
x=Ψ
y=i
p = (r
n
a b)
Ψ
Ψ
f ( x, t , u , p ) = u − r ⋅ I N ⋅ a ⋅
+ b ⋅
ΨN
ΨN
Ψ
Ψ
g ( x, t , u , p ) = I N ⋅ a ⋅
+ b ⋅
ΨN
ΨN
∂x
γ r ∂r
∂x ∂x
= γ a =
(14)
∂p ∂a
γ b ∂x
∂b
(12)
(13)
∂y
σ r ∂r
∂y ∂y
= σ a =
∂p ∂a
σ b ∂y
∂b
(15)
n
n
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
∂f
∂f
=
= −r ⋅ I N
∂x ∂Ψ
5
Ψ n −1
1
⋅ a ⋅
+ n ⋅ b ⋅ n
Ψ N
ΨN
− I ⋅ a ⋅ Ψ + b ⋅ Ψ
∂f N
Ψ
ΨN
N
r
∂
Ψ
∂f ∂f
=
=
− r ⋅ I N ⋅
∂p ∂a
Ψ N
∂f
Ψ n
− r ⋅ I N ⋅
∂b
Ψ
N
Ψ n −1
1
⋅ a ⋅
+ n ⋅ b ⋅ n
Ψ N
ΨN
(16)
∂g
0
r
∂
Ψ
∂g ∂g
(17)
=
= I N ⋅
∂p ∂a
Ψ N
∂g
Ψ n
∂b I N ⋅
Ψ
N
∂g ∂g
=
= IN
∂x ∂Ψ
n
El sistema a resolver, es el siguiente:
− I ⋅ a ⋅ Ψ + b ⋅ Ψ
Ψ
N Ψ
N
N
γ r 0
γ r
Ψ
Ψ n −1 γ a
d γ a 0
1
− r ⋅ I N ⋅
r
I
a
n
b
=
−
⋅
⋅
⋅
+
⋅
⋅
⋅
+
Ψ
N
n
Ψ N γ
Ψ
N
dt γ b 0
b
N
n
Ψ u
1
Ψ
− r ⋅ I N ⋅
Ψ N
0
σ r
γ r
Ψ n −1 γ a
1
σ a
σ = I N ⋅ a ⋅ Ψ + n ⋅ b ⋅ Ψ n N ⋅ γ +
b
N
b
i
0
IN
0
Ψ
I N ⋅
ΨN
Ψ n
I N ⋅
Ψ N
Ψ
Ψ
⋅ a ⋅
+ b ⋅
ΨN
ΨN
n
n
(18)
La resolución del sistema para U = 311 V; R = 0.942 Ω; a = 0.48; b = 0.52;
Ψ = 1.927Wb; I = 330 A ha dado los resultados reflejados en las figuras
N
N
siguientes:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
6
Figura 2. Corriente en la bobina.
Figura 3. Flujo.
Figura 4. γ a (t ) .
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
7
Figura 5. γ b (t ) .
Figura 6. γ r (t ) .
Figura 7. σ a (t ) .
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
8
Figura 8. σ b (t ) .
Figura 9. σ r (t ) .
De ellas se deduce lo siguiente:
-
El flujo resulta poco afectado por las variaciones de los parámetros. A
continuación se pueden observar los valores máximos de la sensibilidad del
mismo:
∂Ψ
= −0.02;
∂a max
∂Ψ
∂Ψ
= −0.52;
= −0.30
∂b max
∂r max
(19)
que referido al valor unitario, es decir:
Sαx =
∂x p N
⋅
∂p X N
(20)
lleva a los siguientes resultados:
S aΨ = −4.98 E − 3;
S bΨ = −0.140; S rΨ = −0.146
(21)
Los parámetros que afectan más al flujo son la resistencia y el factor b del polinomio
(lo cual era de esperar, dado que tiene más peso específico).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
-
9
La corriente es mucho más sensible a la variación de los parámetros. Tomando
como representativos los valores máximos, se llega a:
∂i
= 6.2;
∂a max
∂i
∂i
= 170; = −330
∂b max
∂r max
(22)
referidos al valor unitario:
S ai = 9.01E − 3;
S bi = 0.267; S ri = −0.942
(23)
Si se desean encontrar los valores en régimem permanente después de alguna
manipulación, se llega a:
−1
∂f ∂f
γ RP = − ⋅
(24)
∂x α 0 ∂p α
0
γ RP
σ RP
− I ⋅ a ⋅ Ψ + b ⋅ Ψ
Ψ
N Ψ
N
N
Ψ
1
=
⋅
− r ⋅ I N ⋅
n −1
Ψ N
1
Ψ
r ⋅ I N ⋅ a ⋅
+ n ⋅ b ⋅ n
Ψ n
Ψ
ΨN
N
− r ⋅ I N ⋅
Ψ
N
− I ⋅ a ⋅ Ψ + b ⋅ Ψ
N
Ψ
ΨN
N
Ψ
1
= ⋅
− r ⋅ I N ⋅
r
ΨN
Ψ n
− r ⋅ I N ⋅
Ψ N
n
n
− IN
0
r
Ψ
=
+ I N ⋅
Ψ
N
Ψ n
I N ⋅
Ψ N
Ψ
Ψ
⋅ a ⋅
+ b ⋅
ΨN
ΨN
0
0
(25)
n
(26)
obsérvese que los valores en régimen permanente coinciden con los calculados a
partir de la resolución del conjunto de ecuaciones diferenciales anteriores.
Atendiendo a lo anterior, resulta mucho más atractivo realizar el planteamiento en
función de las ecuaciones del flujo en vez que de las de corriente, ya que las
modificaciones en los parámetros suponen una menor variación de respuesta.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
10
Aplicación a las ecuaciones de la máquina asíncrona.
Se trata de considerar, para los diversos modelos descritos, las incidencias de las
variaciones de los parámetros y, dadas las limitaciones que presentan los modelos y
de acuerdo con los objetivos perseguidos, nos limitaremos a los casos tipo Γ(I) sin
consideración de la saturación cruzada (modelos 21 y 22).
Las variables de interés siempre serán las propias variables de estado, y el par
electromagnético será considerado como una salida del sistema. Adicionalmente, en
algunos casos, puede ser necesario considerar el flujo como una variable de salida
de interés.
Modelo nº 21.
Se puede expresar lo siguiente:
x = (i sx
i sy
u = (u sx
u sy
p = (R s
Rr
Lrl
y = (Ψsx
i rx
ω r )t
i ry
(27)
u rx
u ry
Mc )
(28)
ρ
a1
a2 )
(29)
J
t
t
Me)
Ψsy
t
(30)
definiendo las siguientes funciones de sensibilidad de las variables de estado:
γ irsxs
r
γ isys
∂x rs
= γ
∂p irrxs
γ i
rrys
γ ω
r
γ irsxr
γ irsyr
γ iLsxrl
γ iLsyrl
γ iJsx
γ iJsy
γ iρsx
γ iρsy
γ iasx1
γ iasy1
γ irrxr
γ irryr
γ iLrxrl
γ iLryrl
γ iJrx
γ iJry
γ iρrx
γ iρry
γ iarx1
γ iary1
γ ωrrr
γ ωLrlr
γ ωJ r
γ ωρr
γ ωa1r
γ iasx2
γ iasy2
γ iarx2
γ iary2
γ ωa2r
(31)
y la sensibilidad de las variables de salida:
σ Ψrs
∂y rs sx
= σ Ψ
∂p rssy
σ
Me
σ Ψrr sx
σ Ψrr sy
σ ΨLrlsx
σ ΨLrlsy
σ ΨJ sx
σ ΨJ sy
σ
σ
σ
rr
Me
Lrl
Me
J
Me
σ Ψρ sx
σ Ψρ sy
σ
ρ
Me
σ Ψa1sx
σ Ψa1sy
σ
a1
Me
σ Ψa2sx
σ Ψa2sy
σ Ma2e
(32)
Los gráficos que siguen, detallan los resultados para la máquina nº 2 (en el Anexo III
se recogen las características de las máquinas utilizadas en la tesis).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
11
Figura 10. i s (t );
ω r (t )
Figura 11.
γ irsxs (t );
γ irsxr (t )
Figura 12.
γ iLsxrl (t );
γ iJsx (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
12
Figura 13.
γ iρsx (t );
γ iasx1 (t )
Figura 14.
γ iasx2 (t );
γ irsys (t )
Figura 15.
γ irsyr (t );
γ iLsyrl (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
13
Figura 16.
γ iJsy (t );
γ iρsy (t )
Figura 17.
γ iasy1 (t );
γ iasy2 (t )
Figura 18.
γ irrxs (t );
γ irrxr (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
14
Figura 19.
γ iLrxrl (t );
γ iJrx (t )
Figura 20.
γ iρrx (t );
γ iarx1 (t )
Figura 21.
γ iarx2 (t );
γ irrys (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
15
Figura 22.
γ irryr (t );
γ iLryrl (t )
Figura 23.
γ iJry (t );
γ iρry (t )
Figura 24.
γ iary1 (t );
γ iary2 (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
16
Figura 25.
γ ωrsr (t );
γ ωrrr (t )
Figura 26.
γ ωLrlr (t );
γ ωJ r (t )
Figura 27.
γ ωρr (t );
γ ωa1r (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
17
Figura 28.
γ ωa2r (t );
σ Ψrssx (t )
Figura 29.
σ Ψrrsx (t );
σ ΨLrlsx (t )
Figura 30.
σ ΨJ sx (t );
σ Ψρ sx (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
18
Figura 31.
σ Ψa1sx (t );
σ Ψa2sx (t )
Figura 32.
σ Ψrssy (t );
σ Ψrrsy (t )
Figura 33.
σ ΨLrlsy (t );
σ ΨJ sy (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
19
Figura 34.
σ Ψρ sy (t );
σ Ψa1sy (t )
Figura 35.
σ Ψa2sy (t );
σ Mrs e (t )
Figura 36.
σ Mrr e (t );
σ MLrle (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
20
Figura 37.
σ MJ e (t );
σ Mρ e (t )
Figura 38.
σ Ma1e (t );
σ Ma2e (t )
Modelo nº 22.
En este caso:
x = (Ψsx
Ψsy
Ψrx
u = (u sx
u sy
u rx
u ry
p = (R s
Rr
Lrl
J
y = (i sx
i sy
ωr )
Ψry
t
(33)
Mc )
t
(34)
a b)
ρ
t
Me)
t
(35)
(36)
definiendo las siguientes funciones de sensibilidad de las variables de estado:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
γ Ψrssx
r
γ Ψssy
∂x rs
= γΨ
∂p rsrx
γ Ψ
rsry
γω
r
21
γ Ψrrsx
γ Ψrrsy
γ ΨLrlsx
γ ΨLrlsy
γ ΨJ sx
γ ΨJ sy
γ Ψρsx
γ Ψρsy
γ Ψa sx
γ Ψa sy
γ Ψrrrx
γ Ψrrry
γ ΨLrlrx
γ ΨLrlry
γ ΨJ rx
γ ΨJ ry
γ Ψρrx
γ Ψρry
γ Ψa rx
γ Ψa ry
γ ωrsr
γ ωLrlr
γ ωJr
γ ωρr
γ ωar
γ Ψb sx
b
γ Ψsy
γ Ψb rx
γ Ψb ry
γ ωb r
(37)
y la sensibilidad de las variables de salida:
σ irs
∂y rsxs
= σi
∂p rssy
σ M
e
σ irsxr
σ irsyr
σ iLsxrl
σ iLsyrl
σ iJsx
σ iJsy
σ
σ
σ
rr
Me
Lrl
Me
J
Me
σ iρsx
σ iρsy
σ
ρ
Me
σ iasx
σ iasy
σ
a
Me
σ ibsx
σ ibsy
σ Mb e
(38)
Los gráficos que siguen, detallan los resultados obtenidos para la máquina nº 2.
Figura 39. ω r (t );
Figura 40.
γ Ψrssx (t );
i s (t )
γ Ψrrsx (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
22
Figura 41.
γ ΨLrlsx (t );
γ ΨJ sx (t )
Figura 42.
γ Ψρ sx (t );
γ Ψa sx (t )
Figura 43.
γ Ψb sx (t );
γ Ψrssy (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
23
Figura 44.
γ Ψrr sy (t );
γ ΨLrlsy (t )
Figura 45.
γ ΨJ sy (t );
γ Ψρ sy (t )
Figura 46.
γ Ψa sy (t );
γ Ψb sy (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
24
Figura 47.
γ Ψrsrx (t );
γ Ψrrrx (t )
Figura 48.
γ ΨLrlrx (t );
γ ΨJ rx (t )
Figura 49.
γ Ψρ rx (t );
γ Ψa rx (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
25
Figura 50.
γ Ψb rx (t );
γ Ψrsry (t )
Figura 51.
γ Ψrrry (t );
γ ΨLrlry (t )
Figura 52.
γ ΨJ ry (t );
γ Ψρ ry (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
26
Figura 53.
γ Ψa ry (t );
γ Ψb ry (t )
Figura 54.
γ ωrsr (t );
γ ωrrr (t )
Figura 55.
γ ωLrrl (t );
γ ωJ r (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
27
Figura 56.
γ ωρr (t );
γ ωa r (t )
Figura 57.
γ ωb r (t );
σ irsxs (t )
σ irsxr (t );
σ iLsxrl (t )
Figura 58.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
28
Figura 59.
σ iJsx (t );
σ iρsx (t )
Figura 60.
σ iasx (t );
σ ibsx (t )
Figura 61.
σ irsys (t );
σ irsyr (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
29
Figura 62.
σ iLsyrl (t );
σ iJsy (t )
Figura 63.
σ iρsy (t );
σ iasy (t )
Figura 64.
σ ibsy (t );
σ Mrs e (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
30
Figura 65.
σ Mrr e (t );
σ MLrle (t )
Figura 66.
σ MJ e (t );
σ Mρ e (t )
Figura 67.
σ Ma e (t );
σ Mb e (t )
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
31
Conclusiones.
En el anexo II, se encuentran las ecuaciones desarrolladas obtenidas mediante la
utilización del programa MAPLE-V. A partir de las ecuaciones calculadas en MAPLE,
se genera un fichero compatible con FORTRAN 90, que enlaza con los programas
de simulación desarrollados en SIMNON v 2.0, lo que permite obtener las funciones
de sensibilidad deseadas.
Las tablas que siguen, resumen los valores máximos de las sensibilidades para cada
caso considerado, así como los valores unitarios de los mismos.
Tabla I.a. Sensibilidades máximas. Modelo nº21
isx
isy
irx
iry
ωr
Ψsx
Ψsy
Me
Rs
78
1120
-70
-80
-32
0.85
0.80
800
Rr
-64
100
65
-100
100
-0.15
0.12
-160
Lrl
-850
-1.05e6
800000
1.05e6
-1.05e6
-7500
8000
-3e6
J
-1010
710
1010
-700
1550
-2.2
2.2
-2900
ρ
-175
80
180
-80
200
-0.15
-0.2
-500
a1
10000
110000
-9800
11800
-10000
62
100
90000
a2
-30000
-115000
-30000
38000
-28000
390
380
-150000
Tabla I.b. Sensibilidades unitarias. Modelo nº21
isx
isy
irx
iry
ωr
Ψsx
Ψsy
Me
Rs
1.31
18.78
-1.17
-1.34
-0.04
0.25
0.23
6.18
Rr
-2.49
3.89
2.53
-3.89
0.28
-0.10
0.08
-2.87
Lrl
-0.39
-351
267
502
-25.7
-44.2
47.1
-463
J
-3.48
2.45
3.48
-2.42
0.39
-0.13
0.13
-4.6
ρ
-0.26
0.12
0.26
-0.12
0.02
-3.9e-3
-5.2e-6
-0.34
a1
414
4557
-406
489
-30.4
45.2
72.9
1720
a2
-311
-1193
-311
394
-21.3
71.2
69.4
-718
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
32
Tabla II.a. Sensibilidades máximas. Modelo nº22
Ψsx
Ψsy
Ψrx
Ψry
ωr
isx
isy
Me
Rs
0.70
0.70
0.56
-0.42
35
61
790
1000
Rr
-0.170
0.12
0.40
-0.81
65
-61
100
-180
Lrl
32
-40
-140
150
-25000
18000
-14900
-60000
J
2
1.6
-9
7
-1600
1200
-800
3300
ρ
0.09
0.17
-1.1
0.51
-140
140
-50
420
a
0.042
0.040
0.038
-0.042
4.5
12
-14
42
b
0.2
0.16
0.14
0.14
-13
17
-140
-250
Tabla II.b. Sensibilidades unitarias. Modelo nº22
Ψsx
Ψsy
Ψrx
Ψry
ωr
isx
isy
Me
Rs
0.21
0.21
0.16
-0.12
0.043
1.02
13.2
7.73
Rr
-0.12
0.08
0.27
-0.55
0.18
-1.02
3.89
-3.23
Lrl
0.18
-0.23
0.82
0.88
-0.61
6.02
-4.98
-9.26
J
0.12
0.09
-0.55
0.42
-0.41
4.14
-2.76
5.25
ρ
0.0023
0.0044
-0.028
0.013
-0.015
0.20
-0.07
0.28
a
8.6e-4
0.019
0.018
-0.021
9.15e-3
0.33
-0.39
0.53
b
0.097
0.049
0.043
0.043
-0.017
0.30
-2.48
-2.04
A partir de los resultados anteriores, se pueden extraer las siguientes
consideraciones:
•
Las corrientes resultan igualmente afectadas por las variaciones de rs y rr en
ambos modelos.
•
La sensibilidad de las mismas es mayor a las variaciones de Lrl; además el
modelo nº21 resulta mucho más sensible (observése la diferencia de escala entre
ambas gráficas).
•
Las variaciones en el momento de inercia J, y en el coeficiente de rozamiento ρ,
repercuten de forma similar en ambos modelos.
•
Las variaciones en los parámetros que definen las funciones de saturación (a1 y
a2 para el modelo nº 21; a y b para el modelo nº 22) influyen de forma mucho
más significativa en el primer modelo (nº 21).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 3. SENSIBILIDAD.
Respecto a la velocidad ωr :
•
Ambos modelos presentan un comportamiento similar; no obstante, el primer
modelo presenta discrepancias mayores para todos los parámetros
considerados, en especial los que caracterizan la saturación.
Respecto a los flujos:
•
El modelo nº 22, es mucho menos sensible a las variaciones de los parámetros
que el nº 21.
Respecto al par electromagnético:
•
Ambos modelos resultan muy sensibles a las modificaciones de Lrl (menos en el
modelo nº 22) y a las variaciones del momento de inercia (de nuevo, menor en el
modelo nº 22).
•
Respecto a los parámetros que caractgerizan la saturación, el modelo polinomial
considerado en el caso nº 22, resulta menos problemático que el modelo
arcotangente.
Como conclusión final, el modelo polinomial que caracteriza la saturación, resulta
menos influyente que el de Langevin y, por tanto, será el que se considerará para su
implementación en la determinación de los parámetros en tiempo real.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA
UNA MEJOR DETERMINACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
33
OBTENCIÓN DE LOS PARÁMETROS
POR ENSAYOS FUERA DE LÍNEA
A
W1
V
M
A
A
W2
n
Im
Isg
Usg
Irg
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
1
4. Obtención de los parámetros por ensayos fuera de línea
4. Obtención de los parámetros por ensayos fuera de línea ..................................................... 2
Ensayos a potencia útil nula .................................................................................................. 2
Modelización de la saturación. .............................................................................................. 6
Caracterización mediante polinomios [ Justus 91]. .............................................................. 7
Aplicación a la caracterización de la curva de saturación de un transformador. .............. 10
Aplicación a la modelización de características de saturación para la máquina asíncrona.
.............................................................................................................................................. 12
Trabajo en vacío................................................................................................................... 13
Trabajo a rotor frenado. ...................................................................................................... 14
Resultados experimentales de contrastación. ...................................................................... 16
Conclusiones. ....................................................................................................................... 22
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
2
4. Obtención de los parámetros por ensayos fuera de línea
Como paso previo a la obtención de los parámetros en tiempo real se plantea la
obtención de los mismos a partir de ensayos en régimen permanente. A partir de los
ensayos en vacío y cortocircuito puede plantearse la obtención de los parámetros
necesarios para la modelización de la máquina.
Los parámetros a obtener son los correspondientes al esquema equivalente en T:
resistencias e inductancias de dispersión, estatóricas y rotóricas, la inductancia de
magnetización, y la resistencia de pérdidas en el hierro.
Ensayos a potencia útil nula
A partir del esquema de la figura:
A
W1
V
M
A
A
W2
n
Figura 1. Esquema general para los ensayos.
válido para ambos ensayos, se obtienen los parámetros del circuito equivalente del
motor.
Im
Isg
Irg
Usg
Figura 2. Modelo en T (R.P.)
A partir del esquema equivalente para el ensayo en vacío, se puede considerar
para deslizamiento relativo d→0 que:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
Vs
I0
= Z b = Rs + j ⋅ X s + j ⋅
3
RFe ⋅ X µ
RFe + j ⋅ X µ
(1)
separando la parte real y la imaginaria, se obtiene
X µ2
Re( Z b ) = Rs + RFe ⋅
2
RFe
+ X µ2
= Rs + R p
(2)
Im ( Z b ) = X s + X µ ⋅
2
Fe
R
= Xs + X p
2
+ X µ2
RFe
resultando dos ecuaciones con tres incógnitas Xµ, RFe i Xs (Rs puede ser medida a
priori). Considerando la relación entre pérdidas magnéticas y potencia magnetizante,
se establece la siguiente restricción:
PFe =
k
RFe
Qµ =
k
Xµ
(3)
α=
Xµ
PFe
=
Qµ
RFe
El parámetro α, es típico para cada clase de material magnético y varia en función
del nivel de saturación alcanzado. El parámetro α tiene unos valores típicos que
oscilan entre α = 0.1 ÷ 0.5; se debe escoger iterativamente el que hace converger el
sistema a un resultado razonable.
Para una plancha de acero al silicio, (calidad 1,2 W/kg a Bˆ = 1T – excitación
sinusoidal 50 Hz) presentada como ejemplo, se obtienen los valores siguientes:
Tabla I. Pérdidas para plancha de acero al silicio
B (%)
30
40
50
60
70
80
90
100
P (W)
0,12
0,20
0,3
0,42
0,56
0,73
0,94
1,2
Q(var)
0,24
0,4
0,64
0,96
1,55
3
9,6
35
α
0,5
0,51
0,47
0,44
0,36
0,24
0,1
0,034
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
1,4
40
1,2
35
30
1
0,8
25
20
P
0,6
4
Q
15
10
0,4
0,2
5
0
0
30
40
50
60
70
80
90 100
30
40
50
60
70
80
90 100
0,6
0,5
0,4
0,3
alfa
0,2
0,1
0
30 40 50 60 70 80 90 100
Figura 3. Pérdidas (P), Potencia de magnetización (Q), parámetro α
Teniendo en cuenta la variabilidad de α con el punto de trabajo, se debería obtener
una combinación de parámetros Xs, RFe para cada régimen de funcionamiento.
Reordenando las ecuaciones anteriores, se llega a las dos ecuacuines siguientes:
α
1+α 2
tanϕ 0 =
=
Re( Z b )
α2
Rs + RFe ⋅
1+α 2
Im ( Z b )
X s + RFe ⋅
(4)
Pvacio = 3 ⋅ ( Rs + RFe ⋅
α
) ⋅ I o2
2
1+α
2
Ecuaciones que permiten obtener Xs, RFe y α.
Para el ensayo en cortocircuito (d = 1), se puede considerar el siguiente conjunto de
ecuaciones:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
Re( Z p ) = R Fe ⋅
α
= Rp
1+α 2
2
;
Im ( Z p ) = R Fe ⋅
5
α
= Xp
1+α 2
(5)
Z cc = R s + j ⋅ X s +
( R p + j ⋅ X p ) ⋅ ( RR + j ⋅ X r )
R p + j ⋅ X p + RR + j ⋅ X r
que unidas a las relativas al ensayo en vacío, permiten valorar el conjunto de
parámetros del modelo.
Las desventajas del método anterior se esperaban despues de analizar las
suposiciones que se han hecho, y que resultan:
-
Válidas si conocemos el tipo de material empleado en la construcción de la
máquina.
-
Válidas únicamente para el punto de trabajo nominal o en sus proximidades.
Una aportación interesante es que permite la valoración independiente de las
inductancias de dispersión estatórica y rotórica sin tener que realizar suposiciones
arriesgadas respecto a su valoración (del tipo Xs ≈ Xr ).
Para la máquina nº 2, se obtiene el siguiente conjunto de parámetros:
α = 0,151;
R Fe = 176.5Ω;
R s = 0.369Ω;
Rr = 0.86Ω;
X r = 1.24Ω;
X s = 1.30Ω;
X µ = 26.65Ω
que resultan validos para puntos de trabajo cercanos al nominal.
Si se considera el ensayo en carga de la misma se obtiene la siguiente tabla de
errores:
N(min
1
)
1498
1475
1461
1413
1373
1368
-
Tabla 2. Ensayo en carga.
I(calc)(A) I(exp)(A) ErrorI(%) P(calc)(W) P(exp.)(W)
ErrorP(%)
8.25
9.95
11.45
17.61
23.43
24.14
4.72
3.35
8.23
5.13
2.14
3.49
9.40
10.5
12.7
18.9
23.6
24.8
12.53
5.45
10.04
7.18
0.72
2.66
1117
3789
5359
10018
13936
14380
1172
3920
5840
10560
14240
14900
El método anterior, modeliza de forma sencilla la máquina. Los resultados obtenidos
aconsejan su utilización para la obtención de valores iniciales de los parámetros, o
para la modelización en estudios muy simplificados como, por ejemplo, el
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
6
comportamiento en régimen permanente y para zonas de trabajo próximas a la
nominal (zonas de saturación constante).
Con el fín de eliminar posibles variaciones debidas al efecto pelicular, se han
realizado los ensayos a rotor frenado de la máquina alimentada a frecuencia
reducida (5 Hz) obteniéndose un resultado similar al del ensayo a rotor frenado
realizado a 50 Hz.
Una dificultad del método recae en la forma de realizar las medidas: errores
pequeños en la determinación de la velocidad llevan a resultados totalmente
incongruentes. En nuestro caso se obtienen errores muy elevados si se realiza la
medida de velocidad medieante dinámo tacómetrica; realizando la medida con
medios más sofisticados, tales como una lampara estroboscópica, se obtienen
resultados mejores.
Modelización de la saturación.
La modelización de las características de saturación se puede realizar a partir de
dos puntos de vista distintos:
•
Consideración de modelos del tipo de Jiles-Atterton, complejos y difíciles de
caracterizar experimentalmente [Jiles 98].
•
Caracterización a partir de la aproximación funcional de curvas de saturación.
Para las aplicaciones de control como las que nos ocupan, el segundo punto de
vista resulta más adecuado ya que permite una aproximación suficiente.
Se consideran aproximaciones del tipo:
Ψ = f (i ) = a1 ⋅ arctan(a 2 ⋅ i ) + a 3 ⋅ i
(6)
o bien:
i
IN
Ψ
= g (Ψ ) = a ⋅
ΨN
Ψ
+ b ⋅
ΨN
n
(7)
donde n = 3,5, 7, 9, 11, ........
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
7
1,4
1,2
1
0,8
0,6
0,4
0,2
0
0
10
20
30
Figura 4. Característica de saturación
40
Ψ = f (i )
El primer tipo de aproximaciones, tiene su génesis en la teoría de Langevin sobre el
campo magnético en el interior de materiales magnéticos. El segundo tipo, es un
caso particular de la aproximación mediante polinomios.
Caracterización mediante polinomios [ Justus 91].
Si se considera el modelo anterior y una curva de saturación como la que se
representa en la figura 4, se encuentra que el parámetro a se puede obtener a partir
de la pendiente inicial de la curva:
I
di
dg (Ψ )
=
= N ⋅a
dΨ Ψ =0
dΨ Ψ =0 ΨN
(8)
Experimentalmente, se puede valorar a partir de medidas sobre la curva de
saturación o, en el caso de no disponer de ella, a partir de la respuesta al escalón
de la bobina en consideración. En efecto si se considera una bobina conectada a
una fuente de tensión de valor nominal, se cumple que:
dΨ
= UN − r ⋅i
dt
(9)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
8
Figura 5. Modelo bobina saturada
para t = 0:
dΨ
=UN
dt t =0
(10)
I
I
di
di
dΨ
⋅
= N ⋅ a ⋅ U N = N
=
dt t =0 dΨ t =0 dt t =0 ΨN
t1
ΨN
a=
U N ⋅ t1
(11)
1,2
In
1
0,8
0,6
0,4
0,2
t1
0
0
1
2
3
4
5
6
Figura 6. Representación de i(t)
1,2
ψN
1
0,8
0,6
0,4
0,2
t2
0
0
1
2
3
4
5
6
Figura 7. Representación de Ψ(t)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
9
Por otra parte de la gráfica del flujo en función del tiempo hallamos que:
Ψ
dΨ
=UN = N
dt t =0
t2
(12)
Para t →∞, i = IN; Ψ = ΨN = U N ⋅ t 2 , se cumple que:
a=
ΨN
t
= 2
U N ⋅ t1 t1
(13)
b = 1− a
(14)
además:
La principal dificultad del método anterior es la no disponibilidad de Ψ(t). A partir de
la característica de saturación, expresada en valores por unidad, y la construcción
gráfica de la figura 8, se obtienen los datos anteriores (a, b y m).
Ψ*
Figura 8. Construcción gráfica para caracterización de saturación
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
10
Además se cumple que:
I
d
1
IN
= a + n⋅b =
m
Ψ
d
ΨN Ψ = Ψ
(15)
1− m ⋅ a
m⋅b
(16)
N
n=
Aplicación a la caracterización de la curva de saturación de un transformador.
La caracterización de modelos que tengan en cuenta la saturación, puede realizarse
a partir del trabajo en vacío de un transformador. Si se supone la resistencia de la
bobina despreciable, una estimación del flujo Ψ puede obtenerse a partir de la
expresión:
Um
ω
Ψm =
(17)
con Um valor máximo de la tensión, Ψm valor máximo del flujo y ω = 2⋅π⋅f, válida en
régimen sinusoidal permanente. Una vez realizado el ensayo, la consideración de
relaciones entre el flujo Ψ y la corriente i, como las anteriores:
i * = a ⋅ψ * + b ⋅ψ *
donde:
i* =
i
IN
;
ψ* =
n
ψ
ψN
(18)
(19)
con IN, ΨN valores nominales respectivos, o:
ψ = a1 ⋅ arctan(a 2 ⋅ i )
(20)
consigue una caracterización a partir de ensayos realizados fuera de línea con
errores mínimos. El trabajo sigue la metodología explicada anteriormente para
determinar los coeficientes a, b y n según la construcción de la figura anterior y los
resultados experimentales de la Tabla 3.
•
Transformador monofásico 220/380 V, 1.3 kVA, 5.9/3.5 A, Pj = 40 W, Po = 18 W,
R1 = 0.942 Ω, R2 = 1.202 Ω ; Ψm = 0.99 Wb;
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
Ψ*
I*
11
Tabla 3. Ensayo en vacío
0.26 0.30 0.35 0.38 0.43 0.48 0.52 0.56 0.60 0.65 .70
0.16 0.17 0.18 0.19 0.21 0.23 0.25 0.27 0.29 0.31 0.33
0
0
Ψ* 0.73 0.78 0.82 0.86 0.92 0.95 1.00 1.03 1.08 1.13 1.16
I* 0.37 0.41 0.47 0.56 0.67 0.82 1.00 1.24 1.47 1.76 2.11
A partir de la construcción gráfica sobre la figura anterior, se obtienen los
parámetros buscados:
a = 0.48
;
n=
se elige:
b = 0.52
;
m = 0.22
1 − m ⋅ a 1 − 0.22 ⋅ 0.48
=
= 7.81
m ⋅b
0.22 ⋅ 0.52
(21)
n=7
i
IN
ψ
ψ
= 0.48 ⋅
+ 0.52 ⋅
ψN
ψ N
7
(22)
La aplicación de expresiones del tipo arctan() presenta la dificultad de determinación
de los parámetros, ya que estos se presentan como coeficientes de funciones en
una forma no afín con los parámetros desconocidos, lo que lleva a la consideración
de técnicas de mínimos cuadrados generalizados. Para el caso anterior, se obtiene
la siguiente función de Langevin:
ψ * = 0.805 ⋅ arctan(2.9258 ⋅ i * )
(23)
consiguiendo la tabla 4 de errores. Obsérvese que en la aproximación polinomial,
conseguida a partir del trazado gráfico sobre la figura, existen zonas con error
excesivo. En cambio la aproximación de Langevin, obtenida a partir del método de
mínimos cuadrados, logra una mejor aproximación si se exceptuan puntos
localizados.
Tabla 4. Errores calculados para cada punto experimental
Errp (%)
ErrLan (%)
-
21,97 15,23 6,48 3,69 1,04 -1,50 -1,98 -2,88
-35,64 -23,92 -11,56 -7,54 -3,20 0,60 2,18 3,83
Errp (%)
-10,23 -13,60 -11,33
ErrLan (%)
8,97 9,55 7,47
-6,02 -9,21 0,11 0,00 8,55 4,11
4,20 3,78 0,30 0,01 -1,80 -0,11
-4,33 -8,87
5,54 8,71
-14,80
11,64
-0,33 3,96
1,71 2,08
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
12
Figura 9. Comparación Polinomio y Langevin
Para cada caso y en función de las aplicaciones y el conjunto de variables
analizado, se considerará un conjunto u otro de funciones para la modelización de la
saturación.
Aplicación a la modelización de características de saturación para la máquina
asíncrona.
El modelo clásico en "T" del motor de inducción, se transforma en otro de la misma
forma con un parámetro menos; mediante ensayos en vacío y en cortocircuito y
mediciones auxiliares, son determinados los parámetros Rs, R'r, L'r y Lm,
localizándose en este último los efectos de saturación. A todos los efectos, se
considerará el elemento Rfe, representativo de las pérdidas en el hierro, como
añadido a las pérdidas fijas.
Ls
Rs
Uf
Is
Ψs
Lm
Lr
Im
Ψr
L'r
Rs
Ir
Rr/d
Uf
Is
'
Ψm = Ψs
I'r
L'm
R'r/d
'
Ψr
Figura 10. Modelos en T y Γ
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
13
Trabajo en vacío.
En el trabajo en vacío puede considerarse que el deslizamiento es nulo; y por lo
tanto, se obtiene un esquema equivalente como el de la figura que sigue.
Rs
Uf
Is
Ψs
L'm
Figura 11. Esquema equivalente en vacío
Si se realiza un ensayo a tensión sinusoidal de amplitud variable y frecuencia fija,
puede obtenerse el flujo a partir de la siguiente expresión, en la que se ha
despreciado la caída de tensión en la resistencia estatórica:
ˆ U ⋅ 2
ˆ' ≅ U = f
Ψ
ω1
ω1
(24)
Si se considera la relación entre flujo y corriente, se obtienen los resultados que
siguen:
Máquina nº1 (1.5 kW).
Ψ ' = 0.8550 ⋅ arctan(0.8649 ⋅ i )
i
IN
Ψ
Ψ
= 0.48 ⋅
+ 0.52 ⋅
ΨN
ΨN
7
∑ε
2
= 1.159
(25)
∑ε
2
= 0.032
(26)
∑ε
2
= 1.070
(27)
∑ε
2
= 0.0161
(28)
∑ε
2
= 1.0020
(29)
∑ε
2
= 0.0422
(30)
Máquina nº2 (7.5 kW).
Ψ ' = 0.9115 ⋅ arctan(0.2283 ⋅ i )
i
IN
Ψ
Ψ
= 0.61 ⋅
+ 0.39 ⋅
ΨN
ΨN
7
Máquina nº3 (22 kW).
Ψ ' = 1.0921 ⋅ arctan(0.0691 ⋅ i )
i
IN
Ψ
Ψ
= 0.8 ⋅
+ 0.2 ⋅
ΨN
ΨN
7
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
14
Téngase en cuenta que el flujo nominal se define para tensión nominal de
alimentación, y que la corriente nominal de la ecuación es la corriente
correspondiente al flujo nominal, y no la corriente nominal de la máquina.
Obsérvese que la aproximación polinomial logra menores errores que la función arco
tangente. Además la función potencial, para aplicaciones de control, resulta más
atractiva, ya que en su cálculo sólo intervienen sumas y productos.
Trabajo a rotor frenado.
A partir de la realización de un ensayo a rotor frenado con tensión variable, se
considera el esquema que sigue.
'
Ψσr
Rs
U f c c Is
I r'
L 'r
'
Ψs
L' m
I' m
R'r
Ψr
'
Figura 12. Esquema equivalente a rotor parado
Para la valoración de la corriente y el flujo rotórico debe resolverse el siguiente
conjunto de ecuaciones:
I m' =
U fcc − R s ⋅ I s
(31)
j ⋅ Xm
a1 ⋅ a 2
X m = ω ⋅ Lm = ω ⋅
1 + (a 2 ⋅ I m ) 2
I 'r = I 'm − I s
(32)
U σr = U fcc − R s ⋅ I s − R ' r ⋅I ' r
(34)
Ψ ' σr =
U ' σr
ω
(33)
(35)
si se tiene en cuenta la saturación a partir de la ecuación de Langevin.
En el caso de considerar el modelo polinomial, resulta más conveniente plantear el
siguiente sistema de ecuaciones:
U fcc − R s ⋅ I s
Ψs' =
(36)
ω
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
Xm =ω ⋅
15
1
(37)
a
Ψsn −1
IN ⋅
+ b ⋅ n
Ψ
ΨN
N
n
Ψ
Ψs
s
Im = a ⋅
+ b ⋅
ΨN
Ψ N
I 'r = I 'm − I s
(39)
U ' σr = U fcc − R s ⋅ I s − R' r ⋅I ' r
(40)
Ψ ' σr =
(38)
U ' σr
ω
(41)
La resisténcia rotórica se encuentra a partir de la atribución de la potencia
absorbida, en estas condiciones, y su distribución entre perdidas Joule en el estator
y rotor.
(
Pcc = 3 ⋅ U fcc ⋅ I s ⋅ cos ϕ cc = 3 ⋅ R s ⋅ I s2 + Rr ⋅ I r'2
)
(42)
En este caso, la relación obtenida para las máquinas consideradas resulta quasi
lineal dando los siguientes valores:
Máquina nº1 (1.5 kW).
Ψ ' σR = 0.0254 ⋅ i ' r
(43)
Ψ ' σR = 0.0037 ⋅ i ' r
(44)
Ψ ' σR = 0.0033 ⋅ i ' r
(45)
Máquina nº2 (7.5 kW).
Máquina nº3 (22 kW).
Mediante medición directa (puente de Thompson) en el caso de la resistencia
estatórica, y por balance de potencias en el caso de la resistencia rotórica, se
obtienen los siguientes valores para los elementos resistivos considerados
Tabla 5. Resistencias estatórica y rotórica
Rs (Ω)
R′r (Ω)
1)
4.83
7.907
2)
0.369
0.857
3)
0.173
0.272
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
16
Resultados experimentales de contrastación.
A partir de la contrastación de las pruebas realizadas para el conjunto de máquinas
considerado:
•
•
•
•
•
Arranque en vacío.
Arranque en carga, con par de variación lineal según la velocidad, y posterior
modificación a funcionamiento en vacío.
Alimentación a partir de red industrial 400 V-50 Hz.
Alimentación a partir de ondulador PWM con ma = 0.9 (factor de modulación en
amplitud, relación entre el valor máximo de la senoide de referencia y el máximo
de la portadora triangular); mf = 15 (factor de modulación en frecuencia, relación
entre frecuencia de portadora triangular y sinusoidal de referencia)
Simulación a partir de la consideración del modelo nº 21 con el siguiente
conjunto de parámetros: Rs = 0.369 Ω; Rr = 0.857 Ω; Ψ ' σR = 0.0037 ⋅ i ' r ;
Ψ ' = 0.9115 ⋅ arctan(0.2283 ⋅ i m ) ; J = 0.076 kgm2.
Se obtienen los resultados resumidos en las tablas siguientes.
Se han tabulado los siguientes valores:
n
n
n
n
n
n
n
Pico de corriente estatórica
Ismax (A)
Instante en que sucede el máximo
t1 (ms)
Velocidad angular final (plena carga)
nrf1 (min-1)
Corriente estatórica (valor final-plena carga)
Is1 (A)
Corriente estatórica (valor final- vacío)
Is2 (A)
Velocidad angular final (vacío)
nrf2 (min-1)
Tiempo de subida (10- 90 %)
Tr (ms)
El test mediante alimentación PWM no ha podido ser realizado para la máquina nº 3
debido a la limitación de potencia del equipo.
Tabla 6. Alimentación Sinusoidal
Ismax (A)
t1 (ms)
REAL SIMU
R
S
1)
25
26.6 17.5 21
2) 174.6 173.5 23 23.4
3) 400
411
12 12.5
-1
nrf (min )
R
S
1348 1381
1419 1418
1471 1414
Is1 (A)
Is2 (A)
R
S
R
S
5.5 6.3
4
3.9
27.4 30 13.6 12.4
88.9 93 26
28
-1
nrf2 (min )
Tr (ms)
R
S
R
S
1495 1485 79.1
82.4
1489 1496 128
121
1496 1498 238
235
Tabla 7. Alimentación PWM
1)
2)
Ismax (A)
R
S
25
27.4
170 171.5
-1
t1 (ms)
nrf1 (min )
R
S
R
S
10
10.4 1445 1363
22.8 23.7 1406 1408
Is1 (A)
R
S
6.5 7.82
26
28.5
Is2 (A)
R
S
4
3.6
12 10.9
-1
nrf2 (min )
R
S
1551 1548
1504 1498
Tr (ms)
R
S
150 98.6
100
128
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
17
Tabla 8. Errores
ε (%)
Sinusoidal
PWM
1)
6.40
9.6
Ismax
2)
0.63
0.88
3)
2.75
---
1)
20.0
4.00
t1
2)
1.74
3.95
3)
4.16
---
1)
3.22
5.67
nrf1
2)
0.07
0.14
3)
3.88
---
1)
4.17
34.2
Tr
2)
5.46
28.0
3)
1.26
---
Tabla 8 (continuación). Errores
ε (%)
Sinusoidal
PWM
1)
14.1
20.3
Is1
2)
9.50
9.61
3)
4.61
---
1)
2.50
10.0
Is2
2)
8.82
9.16
3)
7.69
---
1)
0.66
0.19
nrf2
2)
0.47
0.40
3)
0.14
---
A continuación se presentan los gráficos (experimental/simulación), obtenidos para
la máquina nº 2. Todos los gráficos tienen las escalas expresadas en unidades
coherentes.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
18
Figura 13. Corriente de estator simulada is(t) . Arranque en carga y posterior
descarga. Alimentación Sinusoidal
14.a: Arranque en carga
14.b: Cambio brusco de carga.
50 A/div, 50 ms/div
20 A/div, 50 ms/div
Figura 14. Corriente de estator real is(t) . Alimentación Sinusoidal.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
19
Figura 15. Velocidad en el eje simulada ωm(t). . Arranque en carga y posterior
descarga. Alimentación sinusoidal.
16.a: Arranque en carga
16.b: Cambio brusco de carga.
300 min-1/div, 50 ms/div
300 min-1/div, 50 ms/div
Figura 16. Velocidad en el eje ωm(t). Alimentación sinusoidal
Figura 17. Pares interno y de carga simulados Mi(ωm), Mc(ωm).
Alimentación Sinusoidal
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
20
Figura 18. Corriente de estator simulada is(t) . Arranque en carga y posterior
descarga. Alimentación PWM
Figura 19. Corriente real Is(t). Alimentación PWM
50 A/div, 50 ms/div
Figura 20. Velocidad en el eje simulada ωm(t). Alimentación PWM
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
21
Figura 21.Velocidad en el eje ωm(t). Alimentación PWM
300 min-1/div, 50 ms/div
Figura 22. Pares interno y de carga Mi(ωm), Mc(ωm). Alimentación PWM
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 4. OBTENCIÓN DE LOS PARÁMETROS POR ENSAYOS FUERA DE LÍNEA
22
Conclusiones.
•
La obtención de los parámetros mediante ensayos en régimen permanente
(vacío a tensión nominal y rotor frenado), proporcionan resultados correctos.
•
La comprobación de resultados en carga es coherente, estando limitada la
resolución del resultado por la precisión en la medida de la velocidad del eje.
•
Con el fín de eliminar posibles variaciones debidas al efecto pelicular, se han
realizado los ensayos a rotor frenado de la máquina alimentada a frecuencia
reducida (5 Hz) obteniéndose un resultado similar al del ensayo a rotor frenado
realizado a 50 Hz.
•
La consideración de un modelo con un elemento menos permite obviar la
dificultad de obtener los tres elementos inductivos del modelo clásico. A la vez
permite obtener, de una forma sencilla, los parámetros que caracterizan la
formulación de la saturación.
•
La modelización considerada, aplicada a una série de máquinas de potencias
diferentes (características en Anexo III), permite evaluar el modelo a partir del
análisis de los errores obtenidos mediante la consideración de las siguientes
variables:
-
•
pico de corriente
velocidad final (carga y vacío)
tiempo de subida
valores de corriente en régimen permanente (carga y vacío)
tipo de alimentación considerado (sinusoidal, PWM)
Los errores obtenidos (tabla 8) dan validez al modelo considerado.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
OBTENCIÓN DE VARIABLES NO
MEDIBLES Y PARÁMETROS EN
SERVICIO
-3.0m
200.0m
400.0m
600.0m
800.0m
20.00
20.00
0
0
-16.67
-16.67
-33.33
-33.33
-50.00
-50.00
-3.0m
200.0m
400.0m
600.0m
800.0m
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
5. Obtención de variables no medibles y parámetros en
servicio
5. Obtención de variables no medibles y parámetros en servicio ............................................. 2
Observador para el flujo de la máquina asíncrona. ............................................................. 3
Modelo discreto para el observador. ................................................................................ 6
Estimación de los parámetros(coeficientes) del modelo. ....................................................44
Parámetros(coeficientes) eléctricos. ...............................................................................44
Estimación del par electromagnético. Estimación de parámetros(coeficientes)
mecánicos. .......................................................................................................................46
Contrastación experimental. ...............................................................................................47
Modelo completo .................................................................................................................48
Modelo reducido..................................................................................................................60
Conclusiones........................................................................................................................72
Modelo completo: ............................................................................................................72
Modelo reducido: ............................................................................................................73
Parámetros mecánicos: ...................................................................................................73
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
1
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
2
5. Obtención de variables no medibles y parámetros en
servicio
Una modelización precisa conlleva una carga de cálculo poco compatible con los
requerimientos algorítmicos y de tiempo real que implica un sistema de control
complejo, como puede ser un control por orientación de campo. Los algoritmos
recursivos que mejoran la estimación de los parámetros buscados logran, si la
convergencia sigue un ritmo rápido, la correcta observación de dichos parámetros.
En la literatura se encuentran referencias sobre observación de variables no
mensurables; se puede citar un clásico [Verghese 88] que describe un observador
con parámetros variables con la velocidad y que ha sido ampliamente utilizado en
numerosas aplicaciones, aún hoy en día es uno de los esquemas de observación
preferidos para el caso de modelos lineales en los parámetros [Glumineau 99];
otros observadores tales como los descritos en [Atkinson 91], [Wijesundera 92] o
[Peterson 96] describen aplicaciones válidas solamente para casos particulares
como los que se presentan en el control por orientación del campo, estando
limitados, además, al caso de máquina sin saturación.
En los casos anteriores no se considera la identificación de los parámetros del
modelo; caso de precisarse la estimación de los mismos se acude a modelos de
función de transferencia, normalmente considerando la relación corriente-tensión
aplicada [Touhami 92], [Jarray 96] y la velocidad como un parámetro lentamente
variable; en otros [Kataota 93] se considera el problema conjunto de observación de
variables y parámetros a partir de la formulación de un filtro extendido de Kalman.
Todos los anteriores, no consideran la saturación del sistema y aplican los
resultados obtenidos a casos particulares como el comentado anteriormente.
En el capítulo que sigue, se desarrolla un observador adaptativo, junto con un
algoritmo recursivo que supera las limitaciones anteriores y puede ser aplicado en
tiempo real y a cualquier sistema susceptible de entrar en saturación.
u(t)
y(t)
SISTEMA EN
ESTUDIO
OBSERVADOR
ADAPTATIVO
ψ
MÍNIMOS
CUADRADOS
RECURSIVOS
aˆ , bˆ
Figura 1. Disposición identificador+Observador.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
3
Observador para el flujo de la máquina asíncrona.
A partir del modelo nº 22, reproducido aquí por comodidad:
rs
−
Lrl
Ψsx
−ω
d Ψsy
=
dt Ψrx rr
Ψ Lrl
ry
0
rs
rs Ψsx − rs
−
0
Lrl
Lrl Ψsy − rs
⋅
+
rr
Ψrx
ω − ωr
0
−
Ψ
Lrl
ry
rr
rr
− (ω − ω r ) −
Lrl
Lrl
Ψ
(Ψ )n
g (Ψsx ) = I N ⋅ a ⋅ sx + b ⋅ sx n
Ψ
Ψ N
N
Ψsy
(Ψsy )n
g (Ψsy ) = I N ⋅ a ⋅
+ b⋅
Ψ n
Ψ N
N
Ψ − Ψrx
i sx = sx
+ g (Ψsx )
Lrl
ω
rs
Lrl
0
i sy =
Ψsy − Ψry
Lrl
Ψ − Ψsx
i rx = rx
Lrl
i ry =
Ψry − Ψsy
⋅ g (Ψsx ) u sx
⋅ g (Ψsy ) u sy
+ 0
0
0
0
(1)
(2)
(3)
+ g (Ψsy )
(4)
Lrl
Se puede plantear el siguiente observador [Verghese 88], [Peterson 96], [Dawson
98], para los flujos estatórico y rotórico juntamente con la consideración de la
variable de salida, corriente estatórica, y su error de estimación como variable de
control del observador:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
rs
ω
−
Lrl
ˆ
Ψ
sx − ω − rs
ˆ sy
d Ψ
Lrl
=
ˆ
r
dt Ψrx r
0
Ψ
ˆ ry Lrl
rr
0
Lrl
k sx − k sy
k sx iˆsx − i sx
k sy
⋅
k
− k ry iˆsy − i sy
rx
k
k
sx
ry
ˆ sx − rs
rs Ψ
0
Ψ
ˆ
− r
Lrl
sy
⋅
+ s
ˆ
r
Ψ
ω − ω r rx
− r
ˆ
Lrl
Ψry
r
− (ω − ω r ) − r
Lrl
rs
Lrl
4
0
ˆ sx ) u sx
⋅ g (Ψ
ˆ sy ) u sy
⋅ g (Ψ
+ 0 +
0
0
0
ˆ sx − Ψ
ˆ rx
Ψ
ˆ sx )
+ g (Ψ
Lrl
ˆ sy − Ψ
ˆ ry
Ψ
ˆ sy )
=
+ g (Ψ
Lrl
ˆ −Ψ
ˆ sx
Ψ
= rx
Lrl
ˆ ry − Ψ
ˆ sy
Ψ
=
Lrl
(5)
iˆsx =
iˆsy
iˆrx
iˆry
donde:
k sx ;
k sy ;
k rx ;
(6)
(7)
k ry son las ganancias del observador.
Con el fin de simplificar posteriormente la síntesis del observador, se escoge una
referencia fija (ω = 0) , de forma que la estructura del observador, escrita en forma
vectorial, es la siguiente:
ˆ −Ψ
ˆ
Ψ
s
r
ˆ ) + K ⋅ iˆ − i
= u s − rs ⋅
+ g (Ψ
s
s
s
s
Lrl
dt
ˆ −Ψ
ˆ
ˆ
Ψ
dΨ
r
r
s
ˆ + K ⋅ iˆ − i
= u r − rr ⋅
+ j ⋅ωr ⋅ Ψ
r
r
s
s
Lrl
dt
K r 0 k sx + j ⋅ k sy
⋅
K = s = s
K r 0 rr k rx + k ry
d Ψs
(
)
(
iˆs =
ˆ −Ψ
ˆ
Ψ
s
r
Lrl
)
(8)
ˆ )
+ g (Ψ
s
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
5
El ajuste de la ganancia del observador es complicado debido a la no linealidad del
sistema, lo que inhabilita los métodos clásicos de cálculo. Como una aproximación
al ajuste de las mismas puede considerarse el modelo sin saturación. Bajo la
hipótesis de trabajo en la zona lineal puede aplicarse la fórmula de Ackermann para
la valoración de las ganancias. En este caso el modelo considerado es el siguiente:
rs
− rs ⋅ 1 + 1
L
ˆs
ˆ s us
d Ψ
L
L
⋅ Ψ
m
rl
rl
=
+ + K ⋅ (iˆs − i s )
u
Ψ
ˆ r
ˆ
rr
rr
dt Ψ
r
−
+ j ⋅ ω r r
(9)
Lrl
Lrl
ˆ
1
1
1 Ψ
s
−
iˆs =
+
⋅
ˆ r
Lrl Ψ
Lrl Lm
dxˆ
= A(ω r ) ⋅ xˆ + B ⋅ u + K ⋅ C ⋅ ( xˆ − x)
dt
(10)
donde:
ˆ
Ψ
x = s ;
ˆr
Ψ
1
B = ;
0
− rs
us
u = ; A(ω r ) =
ur
1
1
1
−
C =
+
L
Lrl
rl Lm
1
rs
1
⋅
+
Lrl
Lrl Lm
;
rr
rr
−
+ j ⋅ ω r
Lrl
Lrl
(11)
Si p1 y p2 són los polos complejos de una matriz 2x2, el polinomio característico del
observador anterior puede expresarse como:
P(λ ) = λ 2 + c1 ⋅ λ + c 2 = λ 2 − ( p1 + p 2 ) ⋅ λ + p1 ⋅ p 2
(12)
La valoración de las ganancias a través de la formula de Ackermann lleva a:
0
0
K = P( A(ω r )) ⋅ W0−1 ⋅ = A 2 − ( p1 + p 2 ) ⋅ A + p1 ⋅ p 2 ⋅ I ⋅ W0−1 ⋅
1
1
(
)
k sx + j ⋅ k sy rs
=
k =
k rx + j ⋅ k ry 0
(13)
−1
0
⋅K
rr
(14)
donde W 0 es la matriz de observabilidad:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
C
W0 =
C ⋅ A
6
(15)
La expresión obtenida para las ganancias resulta poco operativa para ser aplicada
directamente; en el anexo II se encuentra desarrollada a partir de las utilidades que
ofrece MAPLE. Si se toma como ejemplo la máquina nº 2 y los polos del observador
situados en s= - 1500 se obtienen los siguientes valores para las ganancias:
k sx + j ⋅ k sy − 0.369 + j ⋅ 0
=
k =
k
+
j
⋅
k
−
−
j
⋅
21
.
22
2
.
31
rx
ry
(16)
Modelo discreto para el observador.
La implementación digital del algoritmo para el observador, hace necesaria la
utilización del modelo discretizado del mismo. Usando frecuencias de muestreo
elevadas la utilización del operador δ [Middleton 90] para la discretización, garantiza
una mejor estabilidad numérica para el mismo y una mayor aproximación al modelo
continuo diseñado. El modelo discreto correspondiente puede expresarse como:
δx = F ⋅ x + G ⋅ u
donde:
δx =
x(t + h) − x(t )
h
(17)
(18)
Donde t denota el tiempo discretamente considerado: t = n ⋅ h (n = 0, 1, 2, ........).
Si, como es habitual, las señales externas son captadas a través de un convertidor
A/D junto con un bloqueador de orden cero, y se supone que la velocidad de
rotación se mantiene constante durante el intervalo de muestreo (hipótesis válida si
la frecuencia de muestreo es elevada), se pueden expresar las matrices del modelo
como:
e A⋅h − 1
e A⋅h − 1
⋅B
; G = A −1 ⋅
h
h
,asimismo, pueden expresarse como:
F=
k =∞
F=∑
k =1
A k ⋅ h k −1
;
k!
( A ⋅ h) k −1
⋅B
k!
k =1
(19)
k =∞
G=∑
(20)
En este caso si se considera una aproximación de primer orden se llega a:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
ˆs
δΨ
7
ˆ s (t ) − Ψ
ˆ r (t )
Ψ
ˆ s (t )) + K s ⋅ (iˆs (t ) − i s (t ) )
= u s (t ) − rs ⋅
+ g (Ψ
dt
h
Lrl
ˆr Ψ
ˆ r (t + h) − Ψ
ˆ r (t )
ˆ r (t ) − Ψ
ˆ s (t )
δΨ
Ψ
ˆ r (t ) + K r ⋅ (iˆs (t ) − i s (t ) )
+ j ⋅ωr ⋅ Ψ
=
= u r (t ) − rr ⋅
dt
h
L
rl
K r 0 k sx + j ⋅ k sy
⋅
K = s = s
K r 0 rr k rx + j ⋅ k ry
=
ˆ s (t + h) − Ψ
ˆ s (t )
Ψ
ˆ (t ) − Ψ
ˆ r (t )
Ψ
ˆ s (t ))
iˆs (t ) = s
+ g (Ψ
Lrl
(21)
La aplicación del método anterior, considerando una frecuencia de muestreo de 10
kHz (h=0.0001s), se presenta en los gráficos que siguen. Los resultados se
comparan con los obtenidos en la simulación del transitorio de arranque de la
máquina en carga, y una posterior modificación a régimen de vacío. Obsérvese la
correcta convergencia a los valores reales. En todos los gráficos se suponen
unidades coherentes y en los gráficos correspondientes a errores se representan
errores absolutos. Observése que el ajuste del observador se ha realizado
suponiendo un sistema de parámetros constantes (sin consideración de la
saturación); en cambio el observador realmente implementado es el
correspondiente al modelo nº 22, considerando la saturación. Se han realizado
varias series de simulaciones con diversos regímenes de carga y frecuencias de
alimentación diferentes.
Se han estudiado cuatro casos:
a) tensión y frecuencia nominal (220 V/ 50 Hz);
b) tensión y frecuencia reducida manteniendo constante la relación U/f ( U’ / 5Hz);
c) Tensión nominal y frecuencia aumentada un 50 % (220 V / 75 Hz) – zona de
debilitamiento del campo;
d) tensión nominal y frecuencia un 50 % inferior a la nominal ( 220 V / 25 Hz) –
zona extremadamente saturada.
Se han considerado además series de casos en los que los parámetros supuestos
varien en un +10 %, excepto en la resistencia rotórica que se ha considerado una
variación del + 70 %.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
125.0m
250.0m
375.0m
8
500.0m
2.000
2.000
1.500
1.500
1.000
1.000
0.500
0.500
0
0
0
125.0m
250.0m
375.0m
500.0m
Figura 2. Flujo estatórico calculado y observado. Alimentación a UN – 50 Hz.
0
0.333
0.667
1.000
1.333
1.600
1.600
1.600
1.333
1.333
1.000
1.000
0.667
0.667
0.333
0.333
0
0
0
0.333
0.667
1.000
1.333
1.600
Figura 3. Flujo estatórico calculado en función del flujo estatórico observado.
Alimentación a UN – 50 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
125.0m
250.0m
375.0m
9
500.0m
500.0n
500.0n
250.0n
250.0n
0
0
-250.0n
-250.0n
-500.0n
-500.0n
0
125.0m
250.0m
375.0m
500.0m
Figura 4. Error en flujo estatórico. Alimentación a UN – 50 Hz.
0
125.0m
250.0m
375.0m
500.0m
1000.0m
1000.0m
750.0m
750.0m
500.0m
500.0m
250.0m
250.0m
0
0
0
125.0m
250.0m
375.0m
500.0m
Figura 5. Flujo rotórico calculado y observado. Alimentación a UN – 50 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
800.0m
10
988.6m
1000.0m
1000.0m
750.0m
750.0m
500.0m
500.0m
250.0m
250.0m
0
0
0
200.0m
400.0m
600.0m
800.0m
988.6m
Figura 6. Flujo rotórico calculado en función del flujo rotórico observado.
Alimentación a UN – 50 Hz.
0
125.0m
250.0m
375.0m
500.0m
2.000u
2.000u
1.000u
1.000u
0
0
-1.000u
-1.000u
-2.000u
-2.000u
0
125.0m
250.0m
375.0m
500.0m
Figura 7. Error en flujo rotórico. Alimentación a UN – 50 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
125.0m
250.0m
375.0m
11
500.0m
300.0
300.0
250.0
250.0
200.0
200.0
150.0
150.0
100.0
100.0
50.0
50.0
0
0
0
125.0m
250.0m
375.0m
500.0m
Figura 8. Corriente estatórica calculada y observada. Alimentación a UN – 50 Hz.
0
50.0
100.0
150.0
200.0
250.0
300.0
300.0
300.0
250.0
250.0
200.0
200.0
150.0
150.0
100.0
100.0
50.0
50.0
0
0
0
50.0
100.0
150.0
200.0
250.0
300.0
Figura 9. Corriente estatórica calculada como función de la corriente estatórica
observada. Alimentación a UN – 50 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
125.0m
250.0m
375.0m
12
500.0m
50.00u
50.00u
25.00u
25.00u
0
0
-25.00u
-25.00u
-50.00u
-50.00u
0
125.0m
250.0m
375.0m
500.0m
Figura 10. Error en corriente. Alimentación a UN – 50 Hz.
0
250.0m
500.0m
750.0m
1000.0m
1.250
1.250
1.000
1.000
0.750
0.750
0.500
0.500
0.250
0.250
0
0
0
250.0m
500.0m
750.0m
1000.0m
Figura 11. Flujo estatórico calculado y observado. Alimentación a U’ – 5 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
0.250
0.500
0.750
1.000
13
1.250
1.250
1.250
1.000
1.000
0.750
0.750
0.500
0.500
0.250
0.250
0
0
0
0.250
0.500
0.750
1.000
1.250
Figura 12. Flujo estatórico calculado en función del flujo estatórico observado.
Alimentación a U’ – 5 Hz.
0
250.0m
500.0m
750.0m
1000.0m
250.0n
250.0n
125.0n
125.0n
0
0
-125.0n
-125.0n
-250.0n
-250.0n
0
250.0m
500.0m
750.0m
1000.0m
Figura 13. Error en flujo estatórico. Alimentación a U’ – 5 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
250.0m
500.0m
750.0m
14
1000.0m
1.250
1.250
1.000
1.000
0.750
0.750
0.500
0.500
0.250
0.250
0
0
0
250.0m
500.0m
750.0m
1000.0m
Figura 14. Flujo rotórico calculado y observado. Alimentación a U’ – 5 Hz.
0
0.250
0.500
0.750
1.000
1.250
1.250
1.250
1.000
1.000
0.750
0.750
0.500
0.500
0.250
0.250
0
0
0
0.250
0.500
0.750
1.000
1.250
Figura 15. Flujo rotórico calculado en función del flujo rotórico observado.
Alimentación a U’ – 5 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
250.0m
500.0m
750.0m
15
1000.0m
500.0n
500.0n
250.0n
250.0n
0
0
-250.0n
-250.0n
-500.0n
-500.0n
0
250.0m
500.0m
750.0m
1000.0m
Figura 16. Error en flujo rotórico. Alimentación a U’ – 5 Hz.
0
250.0m
500.0m
750.0m
1000.0m
50.00
50.00
37.50
37.50
25.00
25.00
12.50
12.50
0
0
0
250.0m
500.0m
750.0m
1000.0m
Figura 17. Corriente estatórica calculada y observada. Alimentación a U’ – 5 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
10.00
20.00
16
30.00
40.00
40.00
40.00
30.00
30.00
20.00
20.00
10.00
10.00
0
0
0
10.00
20.00
30.00
40.00
Figura 18. Corriente estatórica calculada como función de la corriente estatórica
observada. Alimentación a U’ – 5 Hz.
0
250.0m
500.0m
750.0m
1000.0m
50.00u
50.00u
25.00u
25.00u
0
0
-25.00u
-25.00u
-50.00u
-50.00u
0
250.0m
500.0m
750.0m
1000.0m
Figura 19. Error en corriente. Alimentación a U’ – 5 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
17
800.0m
1.200
1.200
1.000
1.000
0.750
0.750
0.500
0.500
0.250
0.250
0
0
0
200.0m
400.0m
600.0m
800.0m
Figura 20. Flujo estatórico calculado y observado. Alimentación a UN – 75 Hz.
0
0.250
0.500
0.750
1.000
1.200
1.200
1.200
1.000
1.000
0.750
0.750
0.500
0.500
0.250
0.250
0
0
0
0.250
0.500
0.750
1.000
1.200
Figura 21. Flujo estatórico calculado en función del flujo estatórico observado.
Alimentación a UN – 75 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
18
800.0m
500.0n
500.0n
250.0n
250.0n
0
0
-250.0n
-250.0n
-500.0n
-500.0n
0
200.0m
400.0m
600.0m
800.0m
Figura 22. Error en flujo estatórico. Alimentación a UN – 75 Hz.
0
200.0m
400.0m
600.0m
800.0m
800.0m
800.0m
600.0m
600.0m
400.0m
400.0m
200.0m
200.0m
0
0
0
200.0m
400.0m
600.0m
800.0m
Figura 23. Flujo rotórico calculado y observado. Alimentación a UN – 75 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
166.7m
333.3m
500.0m
19
700.0m
700.0m
700.0m
500.0m
500.0m
333.3m
333.3m
166.7m
166.7m
0
0
0
166.7m
333.3m
500.0m
700.0m
Figura 24. Flujo rotórico calculado en función del flujo rotórico observado.
Alimentación a UN – 75 Hz.
0
200.0m
400.0m
600.0m
800.0m
500.0n
500.0n
250.0n
250.0n
0
0
-250.0n
-250.0n
-500.0n
-500.0n
0
200.0m
400.0m
600.0m
800.0m
Figura 25. Error en flujo rotórico. Alimentación a UN – 75 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
20
800.0m
140.0
140.0
100.0
100.0
66.7
66.7
33.3
33.3
0
0
0
200.0m
400.0m
600.0m
800.0m
Figura 26. Corriente estatórica calculada y observada. Alimentación a UN – 75 Hz.
0
33.3
66.7
100.0
140.0
140.0
140.0
100.0
100.0
66.7
66.7
33.3
33.3
0
0
0
33.3
66.7
100.0
140.0
Figura 27. Corriente estatórica calculada como función de la corriente estatórica
observada. Alimentación a UN – 75 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
21
800.0m
20.00u
20.00u
10.00u
10.00u
0
0
-10.00u
-10.00u
-20.00u
-20.00u
0
200.0m
400.0m
600.0m
800.0m
Figura 28. Error en corriente estatórica. Alimentación a UN – 75 Hz.
0
200.0m
400.0m
600.0m
800.0m
2.258
2.258
2.000
2.000
1.500
1.500
1.000
1.000
0.500
0.500
-0.000
-0.000
0
200.0m
400.0m
600.0m
800.0m
Figura 29. Flujo estatórico calculado y observado. Alimentación a UN – 25 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
0.500
1.000
1.500
2.000
22
2.500
2.500
2.500
2.000
2.000
1.500
1.500
1.000
1.000
0.500
0.500
0
0
0
0.500
1.000
1.500
2.000
2.500
Figura 30. Flujo estatórico calculado en función del flujo estatórico observado.
Alimentación a UN – 25 Hz.
0
200.0m
400.0m
600.0m
800.0m
1000.0n
1000.0n
500.0n
500.0n
0
0
-500.0n
-500.0n
-1000.0n
-1000.0n
0
200.0m
400.0m
600.0m
800.0m
Figura 31. Error en flujo estatórico. Alimentación a UN – 25 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
23
600.0m
800.0m
2.000
2.000
1.500
1.500
1.000
1.000
0.500
0.500
0
0
0
200.0m
400.0m
600.0m
800.0m
Figura 32. Flujo rotórico calculado y observado. Alimentación a UN – 25 Hz.
0
0.333
0.667
1.000
1.333
1.667
1.900
1.900
1.900
1.667
1.667
1.333
1.333
1.000
1.000
0.667
0.667
0.333
0.333
0
0
0
0.333
0.667
1.000
1.333
1.667
1.900
Figura 33. Flujo rotórico calculado en función del flujo rotórico observado.
Alimentación a UN – 25 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
24
800.0m
10.000u
10.000u
5.000u
5.000u
0
0
-5.000u
-5.000u
-10.000u
-10.000u
0
200.0m
400.0m
600.0m
800.0m
Figura 34. Error en flujo rotórico. Alimentación a UN – 25 Hz.
0
200.0m
400.0m
600.0m
800.0m
701.7
701.7
500.0
500.0
333.3
333.3
166.7
166.7
-0.0
-0.0
0
200.0m
400.0m
600.0m
800.0m
Figura 35. Corriente estatórica calculada y observada. Alimentación a UN – 25 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
166.7
333.3
500.0
25
666.7 750.0
750.0
750.0
666.7
666.7
500.0
500.0
333.3
333.3
166.7
166.7
0
0
0
166.7
333.3
500.0
666.7 750.0
Figura 36. Corriente estatórica calculada como función de la corriente estatórica
observada. Alimentación a UN – 25 Hz.
0
200.0m
400.0m
600.0m
800.0m
500.0u
500.0u
250.0u
250.0u
0
0
-250.0u
-250.0u
-500.0u
-500.0u
0
200.0m
400.0m
600.0m
800.0m
Figura 37. Error en corriente. Alimentación a UN – 25 Hz.
La série que sigue considera una desviación máxima en los parámetros del modelo
considerado en un +10%, excepto en la resisténcia rotórica que se ha considerado
una variación del +70%.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
125.0m
250.0m
375.0m
26
500.0m
1.600
1.600
1.333
1.333
1.000
1.000
0.667
0.667
0.333
0.333
0
0
0
125.0m
250.0m
375.0m
500.0m
Figura 38. Flujo estatórico calculado y observado. Alimentación a UN – 50 Hz.
Parámetros modificados en + 10% (Rr 70%).
0
0.333
0.667
1.000
1.333
1.600
1.600
1.600
1.333
1.333
1.000
1.000
0.667
0.667
0.333
0.333
0
0
0
0.333
0.667
1.000
1.333
1.600
Figura 39. Flujo estatórico calculado en función del flujo estatórico observado.
Alimentación a UN – 50 Hz. Parámetros modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
125.0m
250.0m
375.0m
27
500.0m
5.000m
5.000m
2.500m
2.500m
0
0
-2.500m
-2.500m
-5.000m
-5.000m
0
125.0m
250.0m
375.0m
500.0m
Figura 40. Error en flujo estatórico. Alimentación a UN – 50 Hz. Parámetros
modificados en + 10% (Rr 70%).
0
125.0m
250.0m
375.0m
500.0m
1.250
1.250
1.000
1.000
0.750
0.750
0.500
0.500
0.250
0.250
0
0
0
125.0m
250.0m
375.0m
500.0m
Figura 41. Flujo rotórico calculado y observado. Alimentación a UN – 50 Hz.
Parámetros modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
250.0m
500.0m
750.0m
28
1000.0m
1000.0m
1000.0m
750.0m
750.0m
500.0m
500.0m
250.0m
250.0m
0
0
0
250.0m
500.0m
750.0m
1000.0m
Figura 42. Flujo rotórico calculado en función del flujo rotórico observado.
Alimentación a UN – 50 Hz. Parámetros modificados en + 10% (Rr 70%).
0
125.0m
250.0m
375.0m
500.0m
100.00m
100.00m
50.00m
50.00m
0
0
-50.00m
-50.00m
-100.00m
-100.00m
0
125.0m
250.0m
375.0m
500.0m
Figura 43. Error en flujo rotórico. Alimentación a UN – 50 Hz. Parámetros
modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
125.0m
250.0m
375.0m
29
500.0m
300.0
300.0
250.0
250.0
200.0
200.0
150.0
150.0
100.0
100.0
50.0
50.0
0
0
0
125.0m
250.0m
375.0m
500.0m
Figura 44. Corriente estatórica calculada y observada. Alimentación a UN – 50 Hz.
Parámetros modificados en + 10% (Rr 70%).
0
50.0
100.0
150.0
200.0
250.0
300.0
300.0
300.0
250.0
250.0
200.0
200.0
150.0
150.0
100.0
100.0
50.0
50.0
0
0
0
50.0
100.0
150.0
200.0
250.0
300.0
Figura 45. Corriente estatórica calculada como función de la corriente estatórica
observada. Alimentación a UN – 50 Hz. Parámetros modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
125.0m
250.0m
375.0m
30
500.0m
2.500
2.500
1.250
1.250
0
0
-1.250
-1.250
-2.500
-2.500
0
125.0m
250.0m
375.0m
500.0m
Figura 46. Error en corriente(eis). Alimentación a UN – 50 Hz. Parámetros
modificados en + 10% (Rr 70%).
0
0.250
0.500
0.750
1.000
1.244
1.250
1.250
1.000
1.000
0.750
0.750
0.500
0.500
0.250
0.250
0
0
0
0.250
0.500
0.750
1.000
1.244
Figura 47. Flujo estatórico calculado y observado. Alimentación a U’ – 5 Hz.
Parámetros modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
0.250
0.500
0.750
1.000
31
1.244
1.250
1.250
1.000
1.000
0.750
0.750
0.500
0.500
0.250
0.250
0
0
0
0.250
0.500
0.750
1.000
1.244
Figura 48. Flujo estatórico calculado en función del flujo estatórico observado.
Alimentación a U’ – 5 Hz. Parámetros modificados en + 10% (Rr 70%).
0
0.500
1.000
1.500
2.000
5.000m
5.000m
2.500m
2.500m
0
0
-2.500m
-2.500m
-5.000m
-5.000m
0
0.500
1.000
1.500
2.000
Figura 49. Error en flujo estatórico. Alimentación a U’ – 5 Hz. Parámetros
modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
0.500
1.000
1.500
32
2.000
2.000
2.000
1.500
1.500
1.000
1.000
0.500
0.500
0
0
0
0.500
1.000
1.500
2.000
Figura 49. Flujo rotórico calculado y observado. Alimentación a U’ – 5 Hz.
Parámetros modificados en + 10% (Rr 70%).
0
0.333
0.667
1.000
1.333 1.500
1.500
1.500
1.333
1.333
1.000
1.000
0.667
0.667
0.333
0.333
0
0
0
0.333
0.667
1.000
1.333 1.500
Figura 50. Flujo rotórico calculado en función del flujo rotórico observado.
Alimentación a U’ – 5 Hz. Parámetros modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
0.500
1.000
1.500
33
2.000
25.00m
25.00m
12.50m
12.50m
0
0
-12.50m
-12.50m
-25.00m
-25.00m
0
0.500
1.000
1.500
2.000
Figura 51. Error en flujo rotórico. Alimentación a U’ – 5 Hz. Parámetros modificados
en + 10% (Rr 70%).
0
250.0m
500.0m
750.0m
1000.0m
50.00
50.00
37.50
37.50
25.00
25.00
12.50
12.50
0
0
0
250.0m
500.0m
750.0m
1000.0m
Figura 52. Corriente estatórica calculada y observada. Alimentación a U’ – 5 Hz.
Parámetros modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
10.00
20.00
34
30.00
40.00
40.00
40.00
30.00
30.00
20.00
20.00
10.00
10.00
0
0
0
10.00
20.00
30.00
40.00
Figura 53. Corriente estatórica calculada como función de la corriente estatórica
observada. Alimentación a U’ – 5 Hz. Parámetros modificados en + 10% (Rr 70%).
0
250.0m
500.0m
750.0m
1000.0m
200.0m
200.0m
100.0m
100.0m
0
0
-100.0m
-100.0m
-200.0m
-200.0m
0
250.0m
500.0m
750.0m
1000.0m
Figura 54. Error en corriente. Alimentación a U’ – 5 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
35
800.0m
1.200
1.200
1.000
1.000
0.750
0.750
0.500
0.500
0.250
0.250
0
0
0
200.0m
400.0m
600.0m
800.0m
Figura 55. Flujo estatórico calculado y observado. Alimentación a UN – 75 Hz.
Parámetros modificados en + 10% (Rr 70%).
0
0.250
0.500
0.750
1.000
1.200
1.200
1.200
1.000
1.000
0.750
0.750
0.500
0.500
0.250
0.250
0
0
0
0.250
0.500
0.750
1.000
1.200
Figura 56. Flujo estatórico calculado en función del flujo estatórico observado.
Alimentación a UN – 75 Hz. Parámetros modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
36
800.0m
2.500m
2.500m
1.250m
1.250m
0
0
-1.250m
-1.250m
-2.500m
-2.500m
0
200.0m
400.0m
600.0m
800.0m
Figura 57. Error en flujo estatórico. Alimentación a UN – 75 Hz. Parámetros
modificados en + 10% (Rr 70%).
0
200.0m
400.0m
600.0m
800.0m
700.0m
700.0m
500.0m
500.0m
333.3m
333.3m
166.7m
166.7m
0
0
0
200.0m
400.0m
600.0m
800.0m
Figura 58. Flujo rotórico calculado y observado. Alimentación a UN – 75 Hz.
Parámetros modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
166.7m
333.3m
500.0m
37
700.0m
700.0m
700.0m
500.0m
500.0m
333.3m
333.3m
166.7m
166.7m
0
0
0
166.7m
333.3m
500.0m
700.0m
Figura 59. Flujo rotórico calculado en función del flujo rotórico observado.
Alimentación a UN – 75 Hz. Parámetros modificados en + 10% (Rr 70%).
0
200.0m
400.0m
600.0m
800.0m
100.00m
100.00m
50.00m
50.00m
0
0
-50.00m
-50.00m
-100.00m
-100.00m
0
200.0m
400.0m
600.0m
800.0m
Figura 60. Error en flujo rotórico. Alimentación a UN – 75 Hz. Parámetros
modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
38
800.0m
150.0
150.0
133.3
133.3
100.0
100.0
66.7
66.7
33.3
33.3
0
0
0
200.0m
400.0m
600.0m
800.0m
Figura 61. Corriente estatórica calculada y observada. Alimentación a UN – 75 Hz.
Parámetros modificados en + 10% (Rr 70%).
0
33.3
66.7
100.0
133.3 150.0
150.0
150.0
133.3
133.3
100.0
100.0
66.7
66.7
33.3
33.3
0
0
0
33.3
66.7
100.0
133.3 150.0
Figura 62. Corriente estatórica calculada como función de la corriente estatórica
observada. Alimentación a UN – 75 Hz. Parámetros modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
39
800.0m
1.250
1.250
1.000
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.250
-1.250
0
200.0m
400.0m
600.0m
800.0m
Figura 63. Error en corriente(eis). Alimentación a UN – 75 Hz. Parámetros
modificados en + 10% (Rr 70%).
0
200.0m
400.0m
600.0m
800.0m
2.258
2.258
2.000
2.000
1.500
1.500
1.000
1.000
0.500
0.500
-0.010
-0.010
0
200.0m
400.0m
600.0m
800.0m
Figura 64. Flujo estatórico calculado y observado. Alimentación a UN – 25 Hz.
Parámetros modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
0.500
1.000
1.500
40
2.000
2.300
2.300
2.300
2.000
2.000
1.500
1.500
1.000
1.000
0.500
0.500
0
0
0
0.500
1.000
1.500
2.000
2.300
Figura 65. Flujo estatórico calculado en función del flujo estatórico observado.
Alimentación a UN – 25 Hz. Parámetros modificados en + 10% (Rr 70%).
0
200.0m
400.0m
600.0m
800.0m
12.50m
12.50m
10.00m
10.00m
5.00m
5.00m
0
0
-5.00m
-5.00m
-10.00m
-10.00m
-12.50m
-12.50m
0
200.0m
400.0m
600.0m
800.0m
Figura 66. Error en flujo estatórico. Alimentación a UN – 25 Hz. Parámetros
modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
41
600.0m
800.0m
2.312
2.312
2.000
2.000
1.500
1.500
1.000
1.000
0.500
0.500
-0.070
-0.070
0
200.0m
400.0m
600.0m
800.0m
Figura 67. Flujo rotórico calculado y observado. Alimentación a UN – 25 Hz.
Parámetros modificados en + 10% (Rr 70%).
0
0.500
1.000
1.500
2.000
2.300
2.300
2.300
2.000
2.000
1.500
1.500
1.000
1.000
0.500
0.500
0
0
0
0.500
1.000
1.500
2.000
2.300
Figura 68. Flujo rotórico calculado en función del flujo rotórico observado.
Alimentación a UN – 25 Hz. Parámetros modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
42
800.0m
500.0m
500.0m
250.0m
250.0m
0
0
-250.0m
-250.0m
-500.0m
-500.0m
0
200.0m
400.0m
600.0m
800.0m
Figura 69. Error en flujo rotórico. Alimentación a UN – 25 Hz. Parámetros
modificados en + 10% (Rr 70%).
0
200.0m
400.0m
600.0m
800.0m
705.1
705.1
500.0
500.0
333.3
333.3
166.7
166.7
-2.5
-2.5
0
200.0m
400.0m
600.0m
800.0m
Figura 70. Corriente estatórica calculada y observada. Alimentación a UN – 25 Hz.
Parámetros modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
166.7
333.3
500.0
43
666.7 750.0
750.0
750.0
666.7
666.7
500.0
500.0
333.3
333.3
166.7
166.7
0
0
0
166.7
333.3
500.0
666.7 750.0
Figura 71. Corriente estatórica calculada como función de la corriente estatórica
observada. Alimentación a UN – 25 Hz. Parámetros modificados en + 10% (Rr 70%).
0
200.0m
400.0m
600.0m
800.0m
10.000
10.000
5.000
5.000
0
0
-5.000
-5.000
-10.000
-10.000
0
200.0m
400.0m
600.0m
800.0m
Figura 72. Error en corriente(eis). Alimentación a UN – 25 Hz. Parámetros
modificados en + 10% (Rr 70%).
Una vez contrastada la bondad del observador diseñado, se plantea la necesidad
de añadir el algoritmo de identificación de parámetros del modelo.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
44
Estimación de los parámetros(coeficientes) del modelo.
Parámetros(coeficientes) eléctricos.
Se parte de las expresiones del observador discreto (21):
rs
− ˆ
Lrl
ˆ sx (t + 1) Ψ
ˆ sx (t )
Ψ
− ω
ˆ sy (t + 1) Ψ
ˆ sy (t )
Ψ
h
=
+
⋅
r
Ψ
ˆ rx (t + 1) Ψ
ˆ rx (t )
ˆr
Ψ
ˆ
ˆ
Lˆ rl
ry (t + 1) Ψry (t )
0
k sx − k sy
k sx iˆsx − i sx
k sy
⋅
k
− k ry iˆsy − i sy
rx
k
k
ry
sx
ˆ sx − rs
rs Ψ
0
ˆ − r
Lˆ rl Ψ
sy
⋅
+ s
ˆ
rˆr
Ψ
ω − ω r rx
−
ˆ
Lrl
ˆ
Ψry
rˆ
− (ω − ω r ) − r
Lˆ rl
rs
Lˆ rl
ω
−
rs
Lˆ rl
0
rˆr
Lˆ rl
0
ˆ sx ) u sx
⋅ g (Ψ
ˆ sy ) u sy
⋅ g (Ψ
+ 0 +
0
0
0
(22)
y junto con las expresiones para las componentes de corriente estatórica
observada:
⋅ aˆ x
1
ˆ sy (t ) − Ψ
ˆ ry (t ) + I N ⋅ aˆ y
iˆsy (t ) =
⋅Ψ
Lˆ rl
1
ˆ sx (t ) − Ψ
ˆ rx (t )] + I N
iˆsx (t ) =
⋅ [Ψ
Lˆ rl
[
]
n
ˆ sy (t )
ˆ sy (t )
Ψ
Ψ
⋅
+ bˆ y ⋅
Φ
ΦN
N
ˆ (t )
Ψ
⋅ sx + bˆx
ΦN
ˆ (t )
Ψ
⋅ sx
ΦN
n
(23)
Nótese que se han considerado parámetros característicos de saturación distintos
( aˆ x ≠ aˆ y ; bx ≠ bˆ y ) para cada componente. Todos los parámetros del modelo de
máquina, excepto la resistencia estatórica que resulta de fácil medida, se
consideran desconocidos a efectos de formular el algoritmo de estimación. El flujo
rotórico puede expresarse a partir de la siguiente ecuación en tiempo discreto:
r
ˆ rx (t + 1) = Ψ
ˆ rx (t ) ⋅ 1 + h ⋅ ˆr
Ψ
Lˆ rl
r
ˆ ry (t + 1) = Ψ
ˆ ry (t ) ⋅ 1 + h ⋅ ˆr
Ψ
Lˆ rl
rˆ
ˆ sx (t ) − h ⋅ ω r ⋅ Ψ
ˆ ry (t )
+ h ⋅ r ⋅ Ψ
Lˆ rl
rˆ
ˆ sy (t ) + h ⋅ ω r ⋅ Ψ
ˆ rx (t )
+ h ⋅ r ⋅ Ψ
ˆ
L
rl
(24)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
45
avanzando un paso de muestreo el conjunto de ecuaciones (23), y sustituyendo en
ellas el (24) se llega a las siguientes expresiones:
I
r
r
ˆ sx (t + 1) ⋅ 1 + aˆ x ⋅ N − Ψ
ˆ sx (t ) ⋅ h ⋅ ˆr − Ψ
ˆ rx (t ) ⋅ 1 (1 − h ⋅ ˆr ) +
iˆsx (t + 1) = Ψ
2
Lˆ
ΦN
Lˆ rl
Lˆ rl
rl
Lˆ rl
ω
I
ˆ ry (t ) ⋅ h ⋅ r + [Ψ
ˆ sx (t + 1)]n N ⋅ bˆx
+Ψ
Lˆ rl
Φ nN
(25)
I
r
r
ˆ sy (t + 1) ⋅ 1 + aˆ y ⋅ N − Ψ
ˆ sy (t ) ⋅ h ⋅ ˆr − Ψ
ˆ ry (t ) ⋅ 1 (1 − h ⋅ ˆr ) +
iˆsy (t + 1) = Ψ
2
Lˆ
ΦN
Lˆ rl
Lˆ rl
rl
Lˆ rl
ω
I
ˆ rx (t ) ⋅ h ⋅ r + Ψ
ˆ sy (t + 1) n N ⋅ bˆ y
−Ψ
Lˆ rl
Φ nN
[
]
las cuales pueden ensamblarse como sigue:
iˆ (t + 1)
y = sx
iˆsy (t + 1)
Ψ
ˆ (t + 1)
ˆ (t )
0
−Ψ
sx
Φ T = sx
ˆ
ˆ
0
Ψsy (t + 1) − Ψsy (t )
1
I 1
I
θˆ T =
+ aˆ x ⋅ N
+ aˆ y ⋅ N
Lˆ
Φ N Lˆ rl
ΦN
rl
ˆ (t ) Ψ
ˆ (t ) ⋅ ω (t )
−Ψ
rx
ry
r
ˆ
ˆ
− Ψry (t ) − Ψrx (t ) ⋅ ω r (t )
rˆ
h⋅ r
Lˆ2rl
[Ψˆ
sx
(t + 1)
0
1
rˆ
(1 − h ⋅ r ) h ⋅ 1
Lˆ
Lˆ rl
Lˆ rl
rl
]
n
n
ˆ
Ψsy (t + 1)
[
IN ˆ
⋅ bx
Φ nN
0
]
I N ˆ
⋅ by
Φ nN
y = Φ T ⋅θˆ
(26)
Estas ecuaciones ya están en la forma canónica conveniente para su
implementación en un algoritmo de cálculo por mínimos cuadrados. El conjunto de
ecuaciones del observador (22), junto con la ecuación de identificación (26),
configuran las ecuaciones de un observador de tipo adaptativo que consigue
identificar a la vez los parámetros desconocidos y el flujo rotórico.
La ecuación (26) puede ser optimizada de cara a su implementación en tiempo real,
si se considera la siguiente relación entre los parámetros desconocidos:
θˆ
θˆ4 = 5 − θˆ3
h
(27)
donde:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
(θˆ
1
46
)
θˆ2 θˆ3 θˆ4 θˆ5 θˆ6 θˆ7 =
1
I
=
+ aˆ x ⋅ N
Lˆ
ΦN
rl
1
I
rˆ
ˆ y ⋅ N h ⋅ r2
+
a
Lˆ
Φ N
Lˆ rl
rl
1
rˆ
1
(1 − h ⋅ r ) h ⋅
Lˆ
Lˆ rl
Lˆ rl
rl
I N ˆ
⋅ by
Φ nN
IN ˆ
⋅ bx
Φ nN
(28)
Finalmente las ecuaciones de identificación quedan como sigue:
iˆ (t + 1)
y = sx
iˆsy (t + 1)
ˆ (t + 1)
Ψ
0
sx
T
Φ =
ˆ (t + 1)
0
Ψ
sy
θˆ T = θˆ1 θˆ2 θˆ3 θˆ5 θˆ6
(
[Ψˆ
ˆ
ˆ (t ) + Ψ
ˆ (t ) − Ψrx (t ) + Ψ
ˆ (t ) ⋅ ω (t )
−Ψ
sx
rx
ry
r
h
ˆ
ˆ (t ) + Ψ
ˆ (t ) − Ψrx (t ) − Ψ
ˆ (t ) ⋅ ω (t )
−Ψ
sy
ry
rx
r
h
θˆ
7
sx (t + 1)
0
)
]
n
n
ˆ (t + 1)
Ψ
sy
0
[
]
y = Φ T ⋅ θˆ
(29)
Para este caso las ecuaciones del algorítmo de identificación resultan como sigue:
θˆ(k ) = θˆ(k − 1) + K (k ) ⋅ ε (k )
ε (k ) = y (k ) − Φ (k ) ⋅ θˆ(k − 1)
P (k ) = P (k − 1) − K (k ) ⋅ Φ (k ) ⋅ P(k − 1)
(
K (k ) = P (k − 1) ⋅ Φ T (k ) ⋅ I + Φ (k ) ⋅ P(k − 1) ⋅ Φ T (k )
(30)
)
−1
Estimación del par electromagnético. Estimación de parámetros(coeficientes)
mecánicos.
Una vez obtenido el flujo, el par puede estimarse a partir de la siguiente expresión
3
ˆ sx ⋅ i sy − Ψ
ˆ sy ⋅ i sx )
Mˆ i = ⋅ p ⋅ (Ψ
2
(31)
nótese que para la estimación del par se utilizan variables observadas (flujo) y
medidas (corriente).
A partir de la medida de la velocidad y del par electromagnético calculado, se puede
plantear la resolución de la ecuación de equilibrio mecánico. En forma discreta:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
ω r (t + 1) − ω r (t ) 1
1
= ⋅ Mˆ i − ⋅ Mˆ c
h
Jˆ
Jˆ
47
(32)
que puede expresarse en la siguiente forma canónica para su implementación en el
algoritmo de identificación de parámetros:
(
ω r (t + 1) − ω r (t )
= Mˆ i
h
ω r (t + 1) − ω r (t )
h
Φ T = Mˆ i − 1
y=
(
)
1
ˆ
−1 ⋅ J
1 ⋅ Mˆ
ˆ
c
J
)
(33)
1
ˆ
θˆ = J
1 ⋅ Mˆ
ˆ
c
J
Obsérvese que se obtiene simultáneamente la inercia del conjunto ensayado y el
par de carga sobre el eje.
Contrastación experimental.
A continuación se representa el esquema del montaje utilizado (figura 73), el cual
está compuesto por los siguientes elementos:
•
•
•
•
•
•
•
•
Máquina asíncrona nº 2: 7.5 kW; 220/380 V; 27/15.6 A; cosϕ=0.85; 1450 min-1;
clase F; J = 0.076 kgm2; ∆
Posibilidad de alimentación sinusoidal (red 400 V / 50 Hz) o a través de
ondulador PWM (ley U/f = k; mf = 15)
Máquina de corriente continua 7.5 kW; 220 V; 20 A; Vex = 195 V; Iex = 1.64 A;
1480 min-1; class F; J = 0.076 kgm2
Control por corriente de la máquina de corriente continua. Imposición del par de
carga de evolución variable a voluntad (no detallado en la figura).
Captación de corriente a partir de sondas Hall.
Captación de tensión a partir de amplificadores de aislamiento.
Tarjeta de adquisición de datos de 12 bits de resolución. 8 canales diferenciales.
Frecuencia de muestreo ajustable; en este caso ajustada a 10 kHz.
Señales filtradas mediante un pasa-bajos con fc =5 kHz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
Figura 73. Montaje experimental.
Modelo completo
Las gráficas que siguen corresponden al caso de arranque en vacío (m0 ≈ 5 Nm,
correspondientes al par de pérdidas) de la máquina, y posterior aplicación súbita del
par nominal (≈ 50 Nm). La alimentación proviene de un ondulador PWM con las
características indicadas anteriormente (ma = 0.9; mf = 15). La prueba se realiza
aplicando tensión y frecuencia nominales, eliminendo la rampa de arranque que
suelen aplicar los onduladores en el arranque. Todas las magnitudes vienen
expresadas en sus unidades naturales; los errores son valores absolutos, no
relativos.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
48
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
49
800.0m
125.0
125.0
100.0
100.0
50.0
50.0
0
0
-50.0
-50.0
-100.0
-100.0
-125.0
-125.0
0
200.0m
400.0m
600.0m
800.0m
Figura 74. Isx(t). Variable medida y filtrada..
0
200.0m
400.0m
600.0m
800.0m
200.0
200.0
100.0
100.0
0
0
-100.0
-100.0
-200.0
-200.0
0
200.0m
400.0m
600.0m
800.0m
Figura 75. Isy(t). Variable medida y filtrada.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
50
800.0m
10.000
10.000
5.000
5.000
0
0
-5.000
-5.000
-10.000
-10.000
0
200.0m
400.0m
600.0m
800.0m
Figura 76. Error en corriente (Ex(t)).
0
200.0m
400.0m
600.0m
800.0m
12.00
10.00
12.00
10.00
5.00
5.00
0
0
-5.00
-5.00
-10.00
-12.00
-10.00
-12.00
0
200.0m
400.0m
600.0m
800.0m
Figura 77. Error en corriente (Ey(t)).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
51
800.0m
100.00
100.00
50.00
50.00
0
0
-50.00
-50.00
-100.00
-100.00
0
200.0m
400.0m
600.0m
800.0m
Figura 78. Irx(t). Variable observada.
0
200.0m
400.0m
600.0m
800.0m
100.00
100.00
50.00
50.00
0
0
-50.00
-50.00
-100.00
-100.00
0
200.0m
400.0m
600.0m
800.0m
Figura 79. Iry(t). Variable observada.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
52
800.0m
350.0
350.0
300.0
300.0
250.0
250.0
200.0
200.0
150.0
150.0
100.0
100.0
50.0
50.0
0
0
0
200.0m
400.0m
600.0m
800.0m
Figura 80. ω r (t ) . Variable medida y filtrada.
0
200.0m
400.0m
600.0m
800.0m
1.000
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.200
-1.000
-1.200
0
200.0m
400.0m
600.0m
800.0m
ˆ sx (t ) .
Figura 81. Ψ
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
53
800.0m
1.500
1.500
1.000
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.200
-1.200
0
200.0m
400.0m
600.0m
800.0m
600.0m
800.0m
ˆ (t ) .
Figura 82. Ψ
sy
0
200.0m
400.0m
1.500
1.500
1.000
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.200
-1.200
0
200.0m
400.0m
600.0m
800.0m
ˆ rx (t ) .
Figura 83. Ψ
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
54
800.0m
1.500
1.500
1.000
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.200
-1.200
0
200.0m
400.0m
600.0m
800.0m
600.0m
800.0m
ˆ ry (t ) .
Figura 84. Ψ
0
200.0m
400.0m
250.0
250.0
200.0
200.0
150.0
150.0
100.0
100.0
50.0
50.0
0
0
-50.0
-50.0
0
200.0m
400.0m
600.0m
800.0m
Figura 85. Mˆ i (t ) .
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
55
800.0m
50.00m
50.00m
37.50m
37.50m
25.00m
25.00m
12.50m
12.50m
0
0
0
200.0m
400.0m
600.0m
800.0m
600.0m
800.0m
Figura 86. Lˆ rl (t ) .
0
200.0m
400.0m
5.000
5.000
2.500
2.500
0
0
-2.500
-2.500
-5.000
-5.000
0
200.0m
400.0m
600.0m
800.0m
Figura 87. rˆr (t ) .
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
56
800.0m
10.000
10.000
7.500
7.500
5.000
5.000
2.500
2.500
0
0
0
200.0m
400.0m
600.0m
800.0m
600.0m
800.0m
Figura 88. aˆ x (t ) .
0
200.0m
400.0m
2.500
2.500
1.250
1.250
0
0
-1.250
-1.250
-2.500
-2.500
0
200.0m
400.0m
600.0m
800.0m
Figura 89. bˆx (t ) .
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
57
800.0m
10.000
10.000
7.500
7.500
5.000
5.000
2.500
2.500
0
0
0
200.0m
400.0m
600.0m
800.0m
600.0m
800.0m
Figura 90 aˆ y (t ) .
0
200.0m
400.0m
2.000
2.000
1.000
1.000
0
0
-1.000
-1.000
-2.000
-2.000
0
200.0m
400.0m
600.0m
800.0m
Figura 91. bˆ y (t ) .
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
58
800.0m
20.00
20.00
10.00
10.00
0
0
-10.00
-10.00
-20.00
-20.00
0
200.0m
400.0m
600.0m
800.0m
600.0m
800.0m
Figura 92. θˆ(t ) = 1 / Jˆ (t ) .
0
200.0m
400.0m
100.00
100.00
75.00
75.00
50.00
50.00
25.00
25.00
0
0
0
200.0m
400.0m
600.0m
800.0m
Figura 93. Mˆ c (t ) .
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
59
800.0m
50.00
50.00
37.50
37.50
25.00
25.00
12.50
12.50
0
0
0
200.0m
400.0m
600.0m
800.0m
Figura 94. I(t). Corriente por el inducido de la máquina de corriente continua.
La tabla que aparece a continuación resume el valor final de los parámetros
estimados en cada caso y su comparación respecto a los obtenidos en los ensayos
fuera de línea:
Tabla 1. Resultados de identificación. Modelo completo. Alimentación mediante
ondulador PWM
Fuera de
linea
Linea
Diferencia
(%)
lrl (mH)
rr (Ω
Ω)
ax
bx
ay
by
J
0.857
τr=lrl/rr
(ms)
8.52
7.3
0.61
0.39
0.61
0.39
0.076
10.68
46.3
1.15
34.1
9.28
9.00
0.76
24.2
0.78
100
0.726 -0.029 0.075
19.0
107
1.33
A la vista de los resultados las discrepancias en los parámetros son grandes y
podría cuestionar el resultado. Evidentemente, si lo que se pretende unicamente es
valorar los parámetros del modelo, este resultado es poco esperanzador.
En [Nelles 01, cap 2] se demuestra que para el caso no lineal, NO es posible
garantizar que el conjunto de parámetros obtenidos coincida con los verdaderos ( o
los que se consideran como tales). Los sistemas en que las ecuaciones son lineales
normalmente son identificables.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
60
Modelo reducido.
Ya que lo deseado realmente es la estimación del conjunto de parámetros, se
deben hacer suposiciones que lleven a un conjunto de ecuaciones en que las
funciones sean invertibles; a tal fín se propone en el epígrafe que sigue una
modelización reducida en que los únicos parámetros desconocidos son los
rotóricos. Los parámetros de estator (resistencia) y de saturación (a, b, n) se
consideran conocidos y constantes; Estos parámetros pueden encontrarse
mediante ensayos previos en vacío del sistema, tales como los que realizan los
equipos actuales de control de velocidad.
Se parte de las expresiones del observador discreto (22), repetidas aquí por
comodidad:
rs
− ˆ
L rl
ˆ sx (t + 1) Ψ
ˆ sx (t )
Ψ
− ω
ˆ
ˆ
Ψsy (t + 1) Ψsy (t )
=
+ h ⋅
Ψ
ˆ (t + 1)
ˆ (t )
r
Ψ
ˆr
rx
rx
Ψ
ˆ
ˆ
Lˆ rl
ry (t + 1) Ψry (t )
0
k sx − k sy
k sx iˆsx − i sx
k sy
⋅
k
− k ry iˆsy − i sy
rx
k
k sx
ry
ω
−
rs
Lˆ rl
0
rˆr
Lˆ rl
ˆ sx − rs
rs Ψ
0
ˆ − r
Lˆ rl Ψ
sy
⋅
+ s
ˆ
rˆr
Ψ
−
ω − ω r rx
Ψ
Lˆ rl
ˆ
ry
rˆ
− (ω − ω r ) − r
Lˆ rl
rs
Lˆ rl
0
ˆ sx ) u sx
⋅ g (Ψ
ˆ sy ) u sy
⋅ g (Ψ
+ 0 +
0
0
0
(34)
junto con las expresiones para las componentes de corriente estatórica observada:
⋅ aˆ x
1
ˆ
ˆ
iˆsy (t ) =
t
t
I
(
)
(
)
⋅ Ψsy − Ψry
+ N ⋅ aˆ y
ˆ
Lrl
iˆsx (t ) =
1
ˆ sx (t ) − Ψ
ˆ rx (t )] + I N
⋅ [Ψ
Lˆ rl
[
]
n
ˆ sy (t )
ˆ sy (t )
Ψ
Ψ
ˆ
b
⋅
+ y⋅
Φ
ΦN
N
ˆ (t )
Ψ
⋅ sx + bˆx
ΦN
ˆ (t )
Ψ
⋅ sx
ΦN
n
(35)
Para el caso que nos ocupa se considerarán conocidos los siguientes parámetros:
•
•
Resistencia estatórica rs
Parámetros característicos de la saturación a, b y n. Se consideran iguales
para cada componente.
. El flujo rotórico puede expresarse a partir de la siguiente ecuación en tiempo
discreto:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
r
ˆ rx (t + 1) = Ψ
ˆ rx (t ) ⋅ 1 + h ⋅ ˆr
Ψ
Lˆ rl
r
ˆ ry (t + 1) = Ψ
ˆ ry (t ) ⋅ 1 + h ⋅ ˆr
Ψ
Lˆ rl
rˆ
ˆ sx (t ) − h ⋅ ω r ⋅ Ψ
ˆ ry (t )
+ h ⋅ r ⋅ Ψ
Lˆ rl
rˆ
ˆ sy (t ) + h ⋅ ω r ⋅ Ψ
ˆ rx (t )
+ h ⋅ r ⋅ Ψ
ˆ
L
rl
61
(36)
avanzando un paso de muestreo el conjunto de ecuaciones (35), y sustituyendo en
ellas el (36) se llega a las siguientes expresiones:
I
r
r
ˆ sx (t + 1) ⋅ 1 + aˆ x ⋅ N − Ψ
ˆ sx (t ) ⋅ h ⋅ ˆr − Ψ
ˆ rx (t ) ⋅ 1 (1 − h ⋅ ˆr ) +
iˆsx (t + 1) = Ψ
Lˆ
Lˆ
Φ N
Lˆ2rl
Lˆ rl
rl
rl
ω
I
ˆ ry (t ) ⋅ h ⋅ r + [Ψ
ˆ sx (t + 1)]n N ⋅ bˆx
+Ψ
Lˆ rl
Φ nN
I
r
r
ˆ sy (t + 1) ⋅ 1 + aˆ y ⋅ N − Ψ
ˆ sy (t ) ⋅ h ⋅ ˆr − Ψ
ˆ ry (t ) ⋅ 1 (1 − h ⋅ ˆr ) +
iˆsy (t + 1) = Ψ
Lˆ
Lˆ
Φ N
Lˆ2rl
Lˆ rl
rl
rl
ω
I
ˆ rx (t ) ⋅ h ⋅ r + Ψ
ˆ sy (t + 1) n N ⋅ bˆ y
−Ψ
Lˆ rl
Φ nN
[
(37)
]
las cuales pueden ensamblarse como sigue:
[
[
]
]
ˆ
ˆ (t + 1) ⋅ a ⋅ I N − Ψ
ˆ (t + 1) n ⋅ I N ⋅ b
i sx (t + 1) − Ψ
sx
x
sx
x
y1
ΦN
Φ nN
y = =
n
I
I
y
N
N
ˆ
ˆ
2
iˆsy (t + 1) − Ψsy (t + 1) ⋅ a y ⋅ Φ − Ψsy (t + 1) ⋅ n ⋅ b y
ΦN
N
ˆ (t + 1) − Ψ
ˆ (t ) − Ψ
ˆ (t ) Ψ
ˆ (t ) ⋅ ω (t )
Ψ
sx
rx
ry
r
Φ T = sx
ˆ (t + 1) − Ψ
ˆ (t ) − Ψ
ˆ (t ) − Ψ
ˆ (t ) ⋅ ω (t )
Ψ
sy
ry
rx
r
sy
1
1
rˆ
rˆ
1
θˆ T =
h ⋅ r2
(1 − h ⋅ r ) h ⋅
Lˆ
Lˆ rl Lˆ rl
Lˆ rl
Lˆ rl
rl
y = Φ T ⋅ θˆ
(38)
Estas ecuaciones ya están en la forma canónica conveniente para su
implementación en un algoritmo de cálculo por mínimos cuadrados. El conjunto de
ecuaciones formado por el observador (34), junto con la ecuación de identificación
(38), configuran las expresiones de un observador de tipo adaptativo que consigue
a la vez identificar los parámetros desconocidos y el flujo rotórico.
La ecuación (38) puede ser optimizada de cara a su implementación en tiempo real
si se considera la siguiente relación entre los parámetros desconocidos:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
62
θˆ4 = h ⋅ θˆ1
θˆ3 = θˆ1 − θˆ2
(39)
donde:
(θˆ
1
1
θˆ2 θˆ3 θˆ4 =
Lˆ
rl
)
h⋅
rˆr
Lˆ2
rl
1
rˆ
1
(1 − h ⋅ r ) h ⋅
Lˆ
Lˆ rl
Lˆ rl
rl
(40)
Finalmente las ecuaciones de identificación quedan como sigue:
[Ψˆ (t + 1)] ⋅ ΦI ⋅ b
[Ψˆ (t + 1)] ⋅ ΦI ⋅ b
) (Ψˆ (t ) − Ψˆ (t ))
) (Ψˆ (t ) − Ψˆ (t ))
ˆ
ˆ (t + 1) ⋅ a ⋅ I N −
i sx (t + 1) − Ψ
sx
x
y1
ΦN
y = =
ˆ (t + 1) ⋅ a ⋅ I N −
y 2 iˆsy (t + 1) − Ψ
sy
y
ΦN
ˆ (t + 1) − Ψ
ˆ (t ) + h ⋅ Ψ
ˆ (t ) ⋅ ω (t )
Ψ
rx
ry
r
Φ T = sx
ˆ (t + 1) − Ψ
ˆ (t ) − h ⋅ Ψ
ˆ (t ) ⋅ ω (t )
Ψ
ry
rx
r
sy
1
rˆ
h ⋅ r2
θˆ T =
ˆ
Lˆ rl
Lrl
(
(
n
N
n
N
sx
n
N
n
N
sy
rx
sx
ry
sy
y
x
(41)
Para este caso las ecuaciones del algorítmo de identificación se escriben como
sigue:
θˆ(k ) 2 x1 = θˆ(k − 1) 2 x1 + K (k ) ⋅ ε (k ) 2 x1
ε (k ) = y (k ) − Φ (k ) ⋅ θˆ(k − 1)
2 x1
2 x1
2x2
P(k ) = P(k − 1) − K (k ) ⋅ Φ (k ) ⋅ P(k − 1)
(
(42)
2 x1
K (k ) 2 x 2 = P(k − 1) 2 x 2 ⋅ Φ T (k ) 2 x 2 ⋅ I 2 x 2 + Φ (k ) 2 x 2 ⋅ P(k − 1) 2 x 2 ⋅ Φ T (k ) 2 x 2
)
−1
que resulta muy compacto de cara a su implementación en tiempo real (inversión de
una matriz 2x2)
Las gráficas que siguen corresponden al caso de arranque en vacío (m0 ≈ 5 Nm,
relativas al par de pérdidas) de la máquina, y posterior aplicación súbita del par
nominal (≈ 50 Nm). La alimentación proviene de un ondulador PWM con las
características indicadas anteriormente (ma = 0.9; mf = 15). La prueba se realiza
aplicando tensión y frecuencia nominales, eliminendo la rampa de arranque que
suelen aplicar los onduladores en el arranque. Todas las magnitudes vienen
expresadas en sus unidades naturales; los errores son valores absolutos.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
63
800.0m
125.0
125.0
100.0
100.0
50.0
50.0
0
0
-50.0
-50.0
-100.0
-100.0
-125.0
-125.0
0
200.0m
400.0m
600.0m
800.0m
Figura 95. Isx(t). Variable medida y filtrada..
0
200.0m
400.0m
600.0m
800.0m
200.0
200.0
150.0
150.0
100.0
100.0
50.0
50.0
0
0
-50.0
-50.0
-125.0
-125.0
0
200.0m
400.0m
600.0m
800.0m
Figura 96. Isy(t). Variable medida y filtrada.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
64
800.0m
25.00
25.00
12.50
12.50
0
0
-12.50
-12.50
-25.00
-25.00
0
200.0m
400.0m
600.0m
800.0m
Figura 97. Error en corriente (Ex(t)).
0
200.0m
400.0m
600.0m
800.0m
25.00
25.00
12.50
12.50
0
0
-12.50
-12.50
-25.00
-25.00
0
200.0m
400.0m
600.0m
800.0m
Figura 98. Error en corriente (Ey(t)).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
65
800.0m
125.0
125.0
100.0
100.0
50.0
50.0
0
0
-50.0
-50.0
-100.0
-100.0
-125.0
-125.0
0
200.0m
400.0m
600.0m
800.0m
Figura 99. Irx(t). Variable observada.
0
200.0m
400.0m
600.0m
800.0m
125.0
100.0
125.0
100.0
50.0
50.0
0
0
-50.0
-50.0
-100.0
-100.0
-150.0
-150.0
0
200.0m
400.0m
600.0m
800.0m
Figura 100. Iry(t). Variable observada.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
66
800.0m
400.0
400.0
300.0
300.0
200.0
200.0
100.0
100.0
0
0
0
200.0m
400.0m
600.0m
800.0m
Figura 101. ω r (t ) . Variable medida y filtrada.
0
200.0m
400.0m
600.0m
800.0m
1.500
1.500
1.000
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.500
-1.500
0
200.0m
400.0m
600.0m
800.0m
ˆ sx (t ) .
Figura 102. Ψ
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
67
800.0m
1.500
1.500
1.000
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.500
-1.500
0
200.0m
400.0m
600.0m
800.0m
600.0m
800.0m
ˆ sy (t ) .
Figura 103. Ψ
0
200.0m
400.0m
1.500
1.500
1.000
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.500
-1.500
0
200.0m
400.0m
600.0m
800.0m
ˆ rx (t ) .
Figura 104. Ψ
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
68
800.0m
1.500
1.500
1.000
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.500
-1.500
0
200.0m
400.0m
600.0m
800.0m
600.0m
800.0m
ˆ ry (t ) .
Figura 105. Ψ
0
200.0m
400.0m
250.0
250.0
200.0
200.0
150.0
150.0
100.0
100.0
50.0
50.0
0
0
-50.0
-50.0
0
200.0m
400.0m
600.0m
800.0m
Figura 106. Mˆ i (t ) .
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
69
800.0m
25.00m
25.00m
12.50m
12.50m
0
0
-12.50m
-12.50m
-25.00m
-25.00m
0
200.0m
400.0m
600.0m
800.0m
600.0m
800.0m
Figura 107. Lˆ rl (t ) .
0
200.0m
400.0m
5.000
5.000
2.500
2.500
0
0
-2.500
-2.500
-5.000
-5.000
0
200.0m
400.0m
600.0m
800.0m
Figura 108. rˆr (t ) .
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
70
800.0m
100.00m
100.00m
50.00m
50.00m
0
0
-50.00m
-50.00m
-100.00m
-100.00m
0
200.0m
400.0m
600.0m
800.0m
600.0m
800.0m
Figura 109. τˆ r (t ) .
0
200.0m
400.0m
20.00
20.00
10.00
10.00
0
0
-10.00
-10.00
-20.00
-20.00
0
200.0m
400.0m
600.0m
800.0m
Figura 110. θˆ(t ) = 1 / Jˆ (t ) .
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
0
200.0m
400.0m
600.0m
71
800.0m
60.00
60.00
50.00
50.00
37.50
37.50
25.00
25.00
12.50
12.50
0
0
0
200.0m
400.0m
600.0m
800.0m
600.0m
800.0m
Figura 111. Mˆ c (t ) .
0
200.0m
400.0m
50.00
50.00
37.50
37.50
25.00
25.00
12.50
12.50
0
0
0
200.0m
400.0m
600.0m
800.0m
Figura 112. I(t). Corriente por el inducido de la máquina de corriente continua.
La tabla que aparece a continuación resume el valor final de los parámetros
estimados en cada caso y su comparación respecto a los obtenidos en los ensayos
fuera de línea:
Tabla 2. Resultados de identificación. Modelo reducido. Alimentación mediante
ondulador PWM
lrl (mH)
J
rr (Ω
Ω)
τr=lrl/rr (ms)
7.3
0.857
8.52
0.076
Fuera de linea
7.721
0.772
8.74
0.075
Linea
5.76
-9.92
2.58
1.33
Diferencia (%)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
Conclusiones.
•
Se han considerado dos formulaciones para el problema de la obtención de las
variables de estado desconocidas.
•
El observador desarrollado es robusto respecto a las variaciones en los
parámetros del mismo.
•
El observador desarrollado mantiene su robustez en la zona de debilitación de
campo.
•
Únicamente en el caso de fuerte saturación (UN; 25 Hz – ½ de la frecuencia
nominal, aproximadamente doble del flujo nominal) existen discrepancias
apreciables en alguna de las variables del observador (Flujo rotórico, corriente
estatórica); en todo caso las discrepancias son inferiores al 1%.
Modelo completo:
•
Para asegurar la convergencia del algoritmo de identificación hace falta arrancar
el algoritmo del observador con unos valores supuestos para los parámetros, y
después de un tiempo de rodaje no inferior a 40 ms puede iniciarse el algoritmo
de identificación de los mismos; tras múltiples ensayos y pruebas, y debido a la
no linealidad del conjunto observador+identificador, no se ha podido garantizar
la convergencia sin este proceso de inicialización.
•
El conjunto de parámetros obtenidos difiere del que se deduce de los ensayos
realizados fuera de línea (capítulo anterior); de cara a su implementación en los
algoritmos de control esto no es un inconveniente siempre que lo deseado sea
un modelo de “caja negra”, es decir que las variables externas sean las
correctas. En el caso que nos ocupa esto es así. No puede garantizarse en
ningún caso que las variables internas (flujo, par, corriente rotórica) sean las
correctas. Considérese el caso del modelo polinomial para la relación flujo
corriente:
Ψ
i
Ψ
=a⋅
+ b ⋅
In
ΨN
ΨN
n
si los parámetros a y b estimados no coinciden con los obtenidos en los ensayos
previos fuera de línea, no puede garantizarse que, aún obteniendo el mismo
valor para la corriente, el flujo sea el correcto.
•
La convergencia a valores constantes se produce únicamente para el caso de
alimentación PWM. En el caso de alimentación sinusoidal no es posible
garantizar la convergencia a valores correctos; la señal sinusoidal tiene un órden
2, insuficiente para resolver la identificación (6 parámetros).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
72
CAPÍTULO 5. OBTENCIÓN DE VARIABLES NO MEDIBLES Y PARÁMETROS EN SERVICIO
•
Se ha tenido en cuenta la posibilidad de considerar coeficientes de saturación
distintos para cada componente (ax, ay, bx, by). Con esta técnica puede obviarse
la utilización de los modelos con saturación cruzada.
•
La metodología empleada logra la convergencia de las variables observadas a
las reales en un tiempo inferior a los dos periodos de la onda (40 ms a 50 Hz –
una vez transcurrido el tiempo de inicialización).
Modelo reducido:
•
Es necesario el conocimiento completo de los parámetros de modelización del
estator (resistencia, saturación) para su desarrollo. Estos pueden ser obtenidos
anteriormente mediante el ensayo en vacío.
•
La convergencia del algorítmo es mucho menos crítica que en el caso anterior.
Es capaz de arrancar con valores iniciales cualesquiera, obteniéndose la
convergencia en un tiempo inferior a 120 ms (alimentando la máquina a 50 Hz).
Una vez arrancado el algorítmo se mantiene la convergencia ante variaciones
del sistema.
•
Los parámetros rotóricos obtenidos presentan una dispersión menor respecto a
los obtenidos en los ensayos fuera de línea.
Parámetros mecánicos:
•
El par de carga y el momento de inercia del conjunto presentan una
convergencia a valores correctos en un tiempo no superior a 100 ms. El
resultado de los parámetros mecánicos es independiente del modelo de
identificación considerado.
•
Para ambos modelos el error en la estimación de la constante de tiempo rotórica
és suficientemente pequeño como para ser útil en el planteo de algorítmos de
control que precisen de la misma (control por orientación del campo).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
73
APLICACIONES
0
33.3m
66.7m
100.0m
133.3m
166.7m
195.0m
123.9
123.9
100.0
100.0
66.7
66.7
33.3
33.3
0
0
-16.8
-16.8
0
33.3m
66.7m
100.0m
133.3m
166.7m
195.0m
CAPÍTULO 6. APLICACIONES
1
6. Aplicaciones
6. Aplicaciones............................................................................................................................2
Equipo para la determinación del par instantáneo................................................................2
Control por corriente de la máquina de corriente continua. .................................................3
Estimación del par de carga...................................................................................................4
Estimación del par electromagnético de la máquina asíncrona. Resultados de simulación. 5
Contrastación experimental. ..................................................................................................8
Conclusiones.........................................................................................................................10
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 6. APLICACIONES
2
6. Aplicaciones.
Equipo para la determinación del par instantáneo.
Como complemento al trabajo realizado y con el fin de disponer de un medidor
calibrado del par instantáneo, se ha desarrollado y construido un equipo para el
ensayo de accionamentos eléctricos.
Dicho equipo permite trabajar en cada uno de los cuatro cuadrantes del plano Par Velocidad. La solución del sistema de potencia es a base del conjunto Rectificador Troceador - Sistema de frenado.
Figura 1. Equipo para la generación y estimación del par.
Figura 2. Etapa de potencia desarrollada.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 6. APLICACIONES
3
Las características del equipo son las siguientes:
•
•
•
•
•
Máquina de corriente continua: 7.5 kW; 220 V; 20 A; Vex = 195 V; Iex = 1.64 A;
1480 min-1; clase F; J = 0.076 kgm2.
Troceador a base de IGBT; corriente máxima: 75 A; frecuencia de conmutación
nominal: 10 kHz.
Tensión del circuito de continua: 540 V.
Posibilidad de control del par siguiendo cualquier ley de variación temporal.
Medida de corriente y velocidad para la observación del par en el eje.
Control por corriente de la máquina de corriente continua.
A partir del sistema descriptor del accionamiento en c.c.:
di r
−
dt = l
dω k
dt J
k
− i 1
0
l ⋅ + ⋅u + 1 ⋅ M
l
− c
0 ω 0
J
(1)
se plantea el control por banda de histéresis de la corriente en el inducido de la
máquina, es decir:
dσ
=0
dt
di ref
r
k
1
− ⋅ i − ⋅ ω + ⋅ u eq −
=0
l
l
l
dt
di ref
r
k
1
= −l ⋅ − ⋅ i − ⋅ ω + ⋅ u eq −
l
l
l
dt
σ = i − i ref = 0;
u eq
(2)
(3)
Para que exista este modo de funcionamiento debe cumplirse que u eq ≤ U max , donde
Umax es la máxima tensión aplicable a la máquina. Este tipo de control es muy
robusto respecto a la variación de los parámetros del sistema y de respuesta rápida.
Si se admite que el par y la corriente son proporcionales, este controlador logra que
el par de la máquina siga la referencia deseada. En la figura 3 se puede ver la
respuesta ante una variación del tipo IN hasta –IN; obsérvese que el tiempo de
respuesta es inferior a 2 ms.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 6. APLICACIONES
4
Figura 3 .Corriente por el inducido de la máquina de corriente continua.1div= 20 A; 1
div= 2 ms.
Estimación del par de carga.
Si se admite la separación de modos eléctrico y mecánico, es posible plantear un
observador para el subsistema mecánico, donde el par electromagnético se
considera la entrada y el par de carga la perturbación desconocida:
J⋅
dω
= k ⋅i − Mc
dt
(4)
El sistema es gobernable y observable. Considerando la corriente por el inducido de
la máquina de corriente continua como la entrada del sistema, se puede plantear el
siguiente observador para el par M̂ c :
dm aux
= −γ ⋅ m aux + γ ⋅ (k ⋅ i − γ ⋅ J ⋅ ω r )
dt
Mˆ c = m aux + γ ⋅ J ⋅ ω r
(5)
donde γ es la ganancia del observador y maux una variable auxiliar. Este observador
sólo precisa la medida de la corriente y la velocidad en el eje de la máquina de
corriente continua, y el conocimiento de los valores nominales, o asignados como
tales, de la constante de par (k) y el momento de inercia (J) del sistema. Mediante el
ajuste de la ganancia del observador puede lograrse que el resultado sea insensible
a las variaciones en los parámetros de la máquina de c.c. utilizada (Boldea 99).
Mediante la adecuada elección de la ganancia, el observador se hace estable y
convergente a los valores deseados con dinámica impuesta. La elección para la
ecuación del par de carga depende de su ley de variación; el caso expuesto supone
un par constante a tramos; en el caso de leyes de variación complejas se pueden
elegir expresiones para el observador más elaboradas.
Obsérvese que (figura 1) el par de carga de la máquina de corriente continua es el
par creado por el accionamiento acoplado a su eje.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 6. APLICACIONES
5
Estimación del par electromagnético de la máquina asíncrona. Resultados de
simulación.
De forma idéntica al capítulo anterior, mediante la expresión:
3
ˆ sx ⋅ i sy − Ψ
ˆ sy ⋅ i sx )
Mˆ i = ⋅ p ⋅ (Ψ
2
(27)
puede estimarse el par a partir de las variables observadas (flujo) y medidas
(corriente).
En las figuras que aparecen a continuación se representa, para los casos
considerados en dicho capítulo, el par calculado, el observado y el de carga. Para
este caso, el par de carga presenta una variación lineal con la velocidad y un cambio
posterior a régimen de vacío.
0
125.0m
250.0m
375.0m
500.0m
345.6
345.6
300.0
300.0
200.0
200.0
100.0
100.0
0
0
-57.3
-57.3
0
125.0m
250.0m
375.0m
500.0m
Figura 4. Par interno, par estimado y par de carga. Alimentación a UN – 50 Hz.
0
125.0m
250.0m
375.0m
500.0m
10.000
10.000
5.000
5.000
0
0
-5.000
-5.000
-10.000
-10.000
0
125.0m
250.0m
375.0m
500.0m
Figura 5. Error de par (%). Alimentación a UN – 50 Hz.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 6. APLICACIONES
0
6
250.0m
500.0m
750.0m
1000.0m
25.00
25.00
20.00
20.00
10.00
10.00
0
0
-10.00
-10.00
-15.00
-15.00
0
250.0m
500.0m
750.0m
1000.0m
Figura 6. Par interno, par estimado y par de carga. Alimentación a U’ – 5 Hz.
0
250.0m
500.0m
750.0m
1000.0m
1000.0m
1000.0m
500.0m
500.0m
0
0
-500.0m
-500.0m
-1000.0m
-1000.0m
0
250.0m
500.0m
750.0m
1000.0m
Figura 7. Error de par (%). Alimentación a U’ – 5 Hz.
0
125.0m
250.0m
375.0m
500.0m
345.7
345.7
300.0
300.0
200.0
200.0
100.0
100.0
0
0
-56.3
-56.3
0
125.0m
250.0m
375.0m
500.0m
Figura 8. Par interno, par estimado y par de carga. Alimentación a UN – 50 Hz.
Parámetros modificados en + 10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 6. APLICACIONES
0
7
125.0m
250.0m
375.0m
500.0m
10.000
10.000
5.000
5.000
0
0
-5.000
-5.000
-10.000
-10.000
0
125.0m
250.0m
375.0m
500.0m
Figura 9. Error de par (%). Alimentación a UN – 50 Hz. Parámetros modificados en +
10% (Rr 70%).
0
0.500
1.000
1.500
2.000
21.94
20.00
21.94
20.00
15.00
15.00
10.00
10.00
5.00
5.00
0
0
-5.00
-5.00
-8.00
-8.00
0
0.500
1.000
1.500
2.000
Figura 10. Par interno, par estimado y par de carga. Alimentación a U’ – 5 Hz.
Parámetros modificados en + 10% (Rr 70%).
0
0.500
1.000
1.500
2.000
1000.0m
1000.0m
500.0m
500.0m
0
0
-500.0m
-500.0m
-1000.0m
-1000.0m
0
0.500
1.000
1.500
2.000
Figura 11. Error de par (%). Alimentación a U’ – 5 Hz. Parámetros modificados en +
10% (Rr 70%).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 6. APLICACIONES
8
Contrastación experimental.
Montaje experimental (figura 12) basado en:
-
Máquina asíncrona nº 2: 7.5 kW; 220/380 V; 27/15.6 A; cosϕ=0.85; 1450 min-1;
clase F; J = 0.076 kgm2; ∆.
Máquina de corriente continua 7.5 kW; 220 V; 20 A; Vex = 195 V; Iex = 1.64 A;
1480 min-1; clase F; J = 0.076 kgm2.
Medida de corriente a partir de sonda de efecto Hall.
Medida de velocidad a partir de dinamo tacométrica.
Sistema de adquisición de datos formado por una tarjeta con una precisión de 12
bits conectada a un ordenador.
Figura 12. Montaje experimental.
En las figuras 13,14, 15 y 16 se representa el par estimado a partir de la medida de
la velocidad y la corriente de la máquina de continua, y el calculado por simulación
de la máquina asíncrona en las siguientes condiciones:
•
•
•
Arranque a media carga.
Variación lineal de carga desde media a plena carga, a partir del punto de trabajo
una vez finalizado el transitorio de arranque.
Parámetros de la máquina obtenidos aplicando el algoritmo de identificación
desarrollado en el capítulo anterior.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 6. APLICACIONES
0
9
33.3m
66.7m
100.0m
133.3m
166.7m
195.0m
123.9
123.9
100.0
100.0
66.7
66.7
33.3
33.3
0
0
-16.8
-16.8
0
33.3m
66.7m
100.0m
133.3m
166.7m
195.0m
Figura 13.Par estimado. Transitorio de arranque.
0
50.0m
100.0m
150.0m
200.0m
500.0
500.0
375.0
375.0
250.0
250.0
125.0
125.0
0
0
-50.0
-50.0
0
50.0m
100.0m
150.0m
200.0m
Figura 14. Par calculado. Transitorio de arranque.
0
33.3m
66.7m
100.0m
133.3m
166.7m
197.9m
82.77
75.00
82.77
75.00
50.00
50.00
25.00
25.00
0
0
-28.31
-28.31
0
33.3m
66.7m
100.0m
133.3m
166.7m
197.9m
Figura 15. Par estimado. Variación de carga lineal.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 6. APLICACIONES
600.0m
10
700.0m
800.0m
900.0m
1000.0m
82.60
82.60
60.00
60.00
40.00
40.00
20.00
20.00
-2.70
-2.70
600.0m
700.0m
800.0m
900.0m
1000.0m
Figura 16. Par calculado. Variación de carga lineal.
Conclusiones.
A partir de los resultados obtenidos caben las siguientes consideraciones:
•
La obtención del valor del par instantáneo de cualquier accionamiento justifica la
complejidad inherente al desarrollo de un observador.
•
El observador planteado es muy robusto respecto a variaciones en los
parámetros de la carga.
•
En los instantes iniciales existe mayor error debido al tiempo de convergencia del
observador y, sobre todo, debido a los errores de medida de la velocidad
(dinamo tacometrica) y a los juegos del eje no modelizados.
•
A partir de dos períodos de onda (40 ms) el error resulta inferior al 5 %.
•
Una vez transcurrido el período de arranque los resultados tienen errores
menores, lo que condiciona el uso del método a sistemas ya en funcionamiento.
•
Los resultados experimentales sobre el sistema real permiten asegurar la
obtención de un equipo de medida del par económico, fiable y de inmediata
aplicación docente e industrial.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
MODELIZACIÓN DEL
CONVERTIDOR
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
1
7. Modelización del convertidor
7. Modelización del convertidor .................................................................................................2
Función de conexión [Hautier 99]. ........................................................................................2
Funciones de conversión. .......................................................................................................3
Generalización de la modelización. .......................................................................................7
Conversión de tensiones. ........................................................................................................9
Conversión de corrientes......................................................................................................10
Aplicación a las estructuras convertidoras clásicas. ...........................................................11
Convertidor 2/2.................................................................................................................11
Convertidor 3/2.................................................................................................................12
Convertidor 2/3.................................................................................................................13
Formulación del sistema completo de ecuaciones. ..............................................................14
Aplicación a la modelización del transformador trifásico...................................................16
Aplicación al caso del conjunto convertidor+filtro de entrada+carga R+L+E..................18
Aplicación al caso del conjunto convertidor+filtro de entrada+máquina asíncrona+carga.
..............................................................................................................................................20
Aplicación al conjunto ondulador de corriente+filtro de salida + carga accionada..........27
Función generatriz de conversión. .......................................................................................31
Estructuras de control basadas en las funciones generatrices de modulación....................36
Aportación experimental: caso del conjunto máquina asíncrona+convertidor+carga.......37
Conclusiones.........................................................................................................................40
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
2
7. Modelización del convertidor
En el desarrollo de cualquier modelo debe partirse de unas hipótesis básicas que
limitan el alcance del mismo. Para el caso que nos ocupa se toma como punto de
partida las siguientes [Labrique 95], [Labrique 98], [Hautier 99]:
-
conducción continua
pérdidas en los interruptores nulas
bidireccionalidad en corriente
control de cierre y apertura
Estas hipótesis definen un convertidor idealizado. A partir de las consideraciones
anteriores se pueden escribir las ecuaciones eléctricas de funcionamiento del
convertidor.
Una vez establecidas las mismas se puede realizar el enlace con el resto del
sistema; finalmente se obtiene un conjunto de relaciones entre el estado del
convertidor y el estado del sistema alimentado (máquina, carga pasiva, filtro, etc.),
que permite plantear de forma cómoda la simulación del sistema y la definición de
su ley de control.
Función de conexión [Hautier 99].
Figura 1. Definición de tensiones y corrientes.
Se asimila cada uno de los interruptores elementales del convertidor a un interruptor
ideal, tal como se muestra en la figura 2.
Figura 2. Interruptor real versus ideal.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
3
Cada interruptor supone la consideración de una función de conexión fci de
manera que la corriente que lo atraviesa ici y la tensión vci en sus bornes, se pueden
expresar como:
ici = f ci ⋅ ic
vci = (1 − f ci ) ⋅ vc
(1)
fci = 0; Interruptor abierto, fci = 1: interruptor cerrado,
ic :corriente a conmutar, vc :tensión a conmutar.
Para la figura 1, ic se corresponde con las corrientes de carga i1, i2, i3, y vc a la
tensión del circuito de continua E obtenida, por ejemplo, a partir de un puente
rectificador asociado a un filtro.
En cada instante sólo puede estar cerrado uno de los interruptores de cada sección;
esto añade una restricción entre las funciones de conversión asociadas a cada
interruptor:
f c1 + f c 2 = 1
(2)
Funciones de conversión.
A partir de las notaciones de la figura anterior, se puede expresar lo siguiente:
u12 = v21 − v11
u 23 = v31 − v21
(3)
u31 = v11 − v31
u12
1 − 1 0 f 11
m12
u 23 = E ⋅ 0 1 − 1 ⋅ f 21 = E ⋅ m23
u
−1 0 1 f
m
31
31
31
(4)
donde m12, m23, m31, representan respectivamente las funciones compuestas de
conversión de las magnitudes de salida respectivas. Se cumple que:
u12 = v sa − vsb
u 23 = v sb − vsc
(5)
u31 = vsc − v sa
En el caso de considerar que las tensiones simples forman un sistema equilibrado,
se pueden utilizar las funciones simples de conversión nj:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
4
v sa
na
2 − 1 − 1 f 11
1
v sb = E ⋅ nb = ⋅ E ⋅ − 1 2 − 1 ⋅ f 21
v
n 3
−1 −1 2 f
sc
c
31
(6)
La corriente que circula por el tramo de continua puede ser calculada a partir de la
siguiente expresión:
idc = (i sa
i sb
f 11
i sc ) ⋅ f 21
f
31
(7)
Las funciones de conexión fci deben ser calculadas a partir del conocimiento de las
funciones de conversión deseadas, simples o compuestas. Desgraciadamente el
cálculo directo de las funciones fci a partir de las funciones de conversión mij o nj, no
es posible al ser singulares las matrices que las relacionan. Existen infinitas
soluciones para la resolución del sistema pudiéndose recurrir a criterios intuitivos o
transcendentes, basados en las propiedades de los sistemas trifásicos. Para el caso
de alimentación de una máquina, las funciones de conversión deben ser
sinusoidales y equilibradas.
A modo de ejemplo, se consideran las funciones de conexión resultantes de la
comparación entre una señal sinusoidal de referencia con la triangular de frecuencia
superior, obteniéndose el caso de ondas moduladas en amplitud de forma
asíncrona. La simulación de un caso con los datos que figuran a continuación, avala
la modelización: Vma = 0.8 V-50 Hz, Vtri = 1 V-1500 Hz.
Figura 3. Señal de referencia y portadora.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
5
Figura 4. Función compuesta de conversión.
Figura 5. Análisis armónico de la función de conversión.
Figura 6. Tensión simple de salida.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
6
Figura 7. Análisis armónico de la tensión simple de salida.
Figura 8. Corriente de fase.
Figura 9. Corriente por el circuito de continua.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
7
Generalización de la modelización.
vm1
vm2
vmn
Im1
Im2
imq
ick
vck
fck
Figura 10. Convertidor generalizado.
Sea:
f 11
f
21
F=
...
f n1
f 12
f 22
...
f n2
...
...
...
...
f 1q
f 2 q
...
f nq
(8)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
[
= [i
= [v
]
Vm = [vm1 vm 2 ... vmn ]
Vs = vs1 vs 2 ... vsq ;
Is
V0
t
]
t
is 2 ... isq ;
s1
m10
vm 2 0
8
t
[
I m = im1 im 2 ... imq
... vmn0
]
]
t
(9)
t
Vm = F ⋅ Vs + F0 ⋅ V0
(10)
Im = F t ⋅ Is
donde V0 es el vector de tensiones que aparecen en conducción discontinua.
Además:
q
∏ (1 − f1k )
k =1
0
F0 =
0
0
q
Restricciones:
∑f
ck
q
(1 − f 2 k )
0
0
∏
k =1
0
.......
0
q
0
0 ∏ (1 − f nk )
k =1
0
0
0
(11)
= 1 . Sólo puede conducir un elemento de cada sección de
k =1
conmutación.
En la hipótesis de conducción continua F0 = 0:
n
∑ isc = 0
c =1
q
∑i
mk
=0
(12)
k =1
Sólo resultan independientes n-1 corrientes de fuente y q-1 corrientes moduladas.
Se puede elegir una de las líneas como referencia para las mismas, así se
considera el esquema de la figura donde existen q-1 y n-1 potenciales
independientes.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
9
Um1
Um2
isn
us1
Im2
Im1
us2
im
Figura 11. Convertidor generalizado. Convención de corrientes y tensiones.
Conversión de tensiones.
(k = {1,2,..., q − 1 })
u sk = v sk − v sq
u mc = v mc − v mn
(13)
(c = {1,2,..., n − 1 })
De las anteriores:
q
v mc = ∑ f ck ⋅ v sk
k =1
q
v mn = ∑ f nk ⋅ v sk
k =1
q −1
v mc = ∑ f ck ⋅ v sk + f cq ⋅ v sq
k =1
q −1
f cq = 1 − ∑ f ck
k =1
(14)
q −1
v mn = ∑ f nk ⋅ v sk + f nq ⋅ v sq
k =1
q −1
f nq = 1 − ∑ f nk
(15)
k =1
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
10
q −1
q −1
k =1
k =1
u mc = v mc − v mn = ∑ ( f ck − f nk ) ⋅ (v sk − v sq ) = ∑ mck ⋅ u sk
(16)
mck = f ck − f nk
[
]
U s = u s1 us 2 ... u sq −1 ;
t
m11
m
21
Mu =
...
mn −1,1
(17)
U m = [um1 um 2 ... umn −1 ]
(18)
U m = M u ⋅U s
(19)
... m1,q −1
... m2,q −1
...
...
... mn −1,q −1
(20)
t
m12
m22
...
mn −1, 2
Conversión de corrientes.
n
n −1
c =1
c =1
imk = ∑ f ck ⋅ i sc = ∑ f ck ⋅ i sc + f nk ⋅ i sn
(21)
n −1
i sn = −∑ i sc
c =1
n
n −1
c =1
c =1
(22)
imk = ∑ ( f ck − f nk ) ⋅ i sc = ∑ mck ⋅ i sc
[
I s = [is1 is 2 ... isn −1 ] ;
I m = im1 im 2 ... imq −1
t
Im = M i ⋅ Is
m11
m
21
Mi =
...
m1,q −1
m12
m22
...
m2,q −1
... mn−1,1
... mn −1, 2
...
...
... mn−1, q −1
M i = M ut = M
f 11 − f n1
f − f
21
n1
M =
...
f n −1,1 − f n1
f 12 − f n 2
f 22 − f n 2
...
f n −1, 2 − f n 2
...
...
...
...
f 1, q −1 − f n , q −1
f 2,q −1 − f n , q −1
...
f n −1, q −1 − f n ,q −1
]
t
(23)
(24)
(25)
(26)
27)
que se puede escribir de la siguiente manera:
M = Rcv ⋅ Fr
(28)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
f11
f
21
Fr =
...
f n1
f12
f 22
...
fn2
...
...
...
...
0
0
1
0
1
0
Rcv = 0
0
1
...... ...... ......
0
0
0
f1, q −1
f 2, q −1
...
f n , q −1
11
...... − 1
....... − 1
...... − 1
...... ......
1
− 1
(29)
dim ensión( Rcv ) = (n − 1) xn
La matriz Rcv define la relación de conversión, permite el paso entre las funciones
de conexión y las funciones de conversión; esta operación no es biyectiva.
La matriz Fr designa la matriz de conexión reducida, obtenida a partir de F tras la
q
supresión de la columna q teniendo en cuenta la restricción ∑ f ck = 1 .
k =1
Aplicación a las estructuras convertidoras clásicas.
Convertidor 2/2.
La figura muestra la parte operativa de la estructura 2/2 que permite la transferencia
energética entre una fuente de tensión y una fuente de corriente. Esta estructura es
común para los variadores de alterna, los troceadores, los onduladores y
rectificadores monofásicos.
Im
Um
Figura 12. Convertidor 2/2.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
12
En este caso n = 2; q = 2.
-
Matrices de conexión:
f 11
F =
f 21
-
f 12
;
f 22
f 11
Fr =
f 21
(30)
Relación de conversión y matriz de conversión:
Rcv = (1 − 1);
M = ( f 11 − f 21 )
(31)
En este caso, la matriz se reduce a un escalar igual a la función de conversión
única, m, del montaje:
um = m ⋅ us ;
im = m ⋅ is
(32)
m = f 11 − f 21
Convertidor 3/2.
Corresponde a la estructura de ondulador de tensión trifásico así como para los
rectificadores de corriente.
Im
Um1
Um2
Figura 13. Convertidor 3/2.
En este caso n = 3; q = 2.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
13
- Matrices de conexión:
-
f 11 f 12
f 11
F = f 21 f 22 ;
Fr = f 21
f
f
31 f 32
31
Relación de conversión y matriz de conversión:
1 0 − 1
;
Rcv =
0 1 − 1
f − f 31 m1
=
M = 11
f 21 − f 31 m 2
u m1 m1
= ⋅ u s ;
u m2 m2
i m = (m1
(33)
(34)
finalmente:
i
m 2 ) ⋅ s1
is2
(35)
Convertidor 2/3.
Corresponde a la estructura de ondulador de corriente y a la estructura de
rectificador en funcionamiento continuo.
Um
Im1
Im2
Figura 14. Convertidor 2/3.
En este caso n = 2, q = 3.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
-
14
Matrices de conexión:
f 11
F =
f 21
f 12
f 22
f 13
;
f 23
f 11
Fr =
f 21
f 12
f 22
(36)
- Relación de conversión y matriz de conversión:
Rcv = (1 − 1);
M = ( f 11 − f 21
f 12 − f 22 ) = (m1
m2 )
(37)
finalmente:
i m1 m1
= ⋅ i s ;
im 2 m2
u m = (m1
u 1
m 2 ) ⋅ s
us2
(38)
Formulación del sistema completo de ecuaciones.
Figura 15. Sistema completo.
Para una estructura dada se puede escribir lo siguiente:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
U m = M u ⋅U s
Im = Mi ⋅ Is
;
15
U
M
G m = m ; M r = u
Im
0
0
;
M i
U
G s = s
Is
Gm = M r ⋅ Gs
R ⋅ F
M r = cv r
0
0
t
Fr ⋅ Rcv
t
(39)
(40)
(41)
además el vector de magnitudes conmutadas esta formado, normalmente, por
componentes del vector de estado, de tal forma que dichas magnitudes pueden ser
expresadas de la siguiente forma:
Gm = M r ⋅ C s ⋅ X
(42)
donde Cs es una matriz de observación particular que define el vector de
magnitudes conmutadas en función de las variables de estado.
El modelo de la parte operativa se describe a partir de un conjunto de ecuaciones de
estado como el siguiente:
dX
= A ⋅ X + Be ⋅ Ge + Bm ⋅ G m
dt
(43)
sustituyendo la anterior se llega a:
dX
= ( A + B m ⋅ M r ⋅ C s ) ⋅ X + Be ⋅ G e
dt
44)
Completando la definición mediante la ecuación de observación de la salida:
Y = C ⋅ X + De ⋅ G e + D m ⋅ G m
Y = (C + Dm ⋅ M r ⋅ C s ) ⋅ X + De ⋅ Ge
(45)
(46)
Las expresiones anteriores, definen el conjunto de ecuaciones no lineales de control
características de todo convertidor estático.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
16
Aplicación a la modelización del transformador trifásico.
Figura 16. Modelización del transformador trifásico
Sea:
u1 = (u11 u12 u13 ) ; vector de tensiones primarias.
ψ = (ψ 1 ψ 2 ψ 3 ) ; vector de flujo en cada núcleo.
i1 = (i11 i12 i13 ) ; vector de corrientes primarias.
u 2 = (u 21 u 22 u 23 ) ; vector de tensiones secundarias.
i 2 = (i 21 i 22 i 23 ) ; vector de corrientes secundarias.
i1µ = (i1µ1 i1µ 2 i1µ 3 ) ; vector de corrientes magnetizantes primarias.
u1m = (u1m1 u1m 2 u1m 3 ) ; vector de tensiones primarias moduladas.
i 2 m = (i 2 m1 i 2 m 2 i 2 m 3 ) ; vector de corrientes secundarias moduladas.
I; matriz identidad 3x3.
n
m = 2 ⋅ I ; matriz de modulación. Obsérvese que en este caso la matriz de
n1
modulación no depende del tiempo como ocurre en el caso de modelizar un
convertidor estático.
n1, n2, número de espiras primarias y secundarias, respectivamente.
L2, inductancia de fugas totalizada en el secundario. Se adopta como modelo para
cada fase del transformador el de la figura siguiente.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
17
I1
I2
I1µ
U2
U1
Figura 17. Modelo equivalente para cada fase del transformador.
Se pueden plantear las siguientes ecuaciones:
u1m = m ⋅ u1 ;
i2 m = mt ⋅ i2
iiµ = f (ψ )
(47)
(48)
di 2
1
=
⋅ I ⋅ (u1m − u 2 )
dt L2
i1 = i 2 m + i1µ
(49)
(50)
faltan añadir las ecuaciones de acoplamiento con las respectivas redes:
u1 = C p ⋅ v ABC ;
vabc = Cs ⋅ u2 ;
con:
i ABC = C tp ⋅ i1
i2 = Cst ⋅ iabc
v ABC = (v AN v BN v CN )
i ABC = (i A i B iC )
v abv = (v an v bn v cn )
i abc = (i a i b i c )
(51)
(52)
(53)
Las matrices Cp y Cs dependen del tipo de conexión del transformador.
Globalmente se puede expresar lo siguiente:
mc = C s ⋅ m ⋅ C p
(54)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
v abc = mc ⋅ v ABC ;
18
i ABC = mct ⋅ i abc
(55)
Para el caso de un transformador tipo Dy11, las matrices de acoplamiento y
conexión son las siguientes:
1 −1 0
Cp = 0
1 − 1;
−1 0
1
1 0 0
C s = 0 1 0 ;
0 0 1
n
mc = 2
n1
1 0 0
n2
m=
⋅ 0 1 0
n1
0 0 1
1 −1 0
⋅ 0
1 − 1
−1 0
1
(56)
(57)
Aplicación al caso del conjunto convertidor+filtro de entrada+carga R+L+E.
Figura 18. Conjunto convertidor+filtro de entrada + carga R+L+E.
En este caso, convertidor:
u m1 m1
= ⋅ u s ;
u
m2 m2
i m = (m1
i 1
m 2 ) ⋅ s
is2
(58)
Filtro:
du s
= ie − i m
dt
di
L f ⋅ e = ur − us
dt
C⋅
(59)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
19
Carga:
di s1
di
+ L ⋅ s 2 + r ⋅ (2 ⋅ i s1 + i s 2 ) + e ac
dt
dt
di
di
= 2 ⋅ L ⋅ s 2 + L ⋅ s1 + r ⋅ (2 ⋅ i s 2 + i s1 ) + ebc
dt
dt
U m1 = 2 ⋅ L ⋅
U m2
(60)
que reordenadas quedan de la siguiente manera:
1
0
0
0
0
C
us 1
us − 1
0
0
0
Lf
ie
d ie L f
=
⋅
+
R i s1 0
4⋅R
dt i s1
0
0
−
i
i
L
L
3
⋅
3
⋅
s2
s2
R
4⋅R
0
0
−
0
3⋅ L
3⋅ L
1
0
−
0
C
0
0 u m1
0
2
1
+
⋅ u
0 m2
−
3⋅ L 3⋅ L
i
1
m
2
−
0
3⋅ L
3⋅ L
0
0
2
3⋅ L
1
3⋅ L
−
0
u
r
1 ⋅ e ac +
3 ⋅ L ebc
2
−
3⋅ L
0
(61)
Para este caso:
m1
M r = m2
0
0
0
m1
0 us
0 ⋅ i s1
m 2 i s 2
us
i
X = e ;
i
s1
i
s2
0
1
L
A= f
0
0
(62)
1
C
0
0
0
0
0
4⋅R
−
3⋅ L
R
3⋅ L
0
;
R
3⋅ L
4⋅R
−
3⋅ L
0
1 0 0 0
Cs = 0 0 1 0
0 0 0 1
0
1
−
Lf
Be =
0
0
0
0
2
3⋅ L
1
3⋅ L
−
(63)
0
1
3⋅ L
2
−
3⋅ L
0
(64)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
ur
Ge = e ac ;
e
bc
0
0
2
Bm =
−
3⋅ L
1
3⋅ L
20
0
0
1
3⋅ L
2
−
3⋅ L
−
1
C
0
;
0
0
u m1
Gm = u m2
i
m
(65)
finalmente:
0
us 1
d ie L f
=
dt i s1 2 ⋅ m1
−
i 3 ⋅ L
s2
m1
3⋅ L
1
C
−
m1
C
0
0
m2
3⋅ L
2 ⋅ m2
−
3⋅ L
4⋅R
−
3⋅ L
R
3⋅ L
m2
0
C
us − 1
0
ie L f
+
⋅
R i s1 0
3 ⋅ L i s 2
0
4⋅R
−
3⋅ L
−
0
0
2
3⋅ L
1
3⋅ L
−
0
u
r
1 ⋅ e ac
3 ⋅ L ebc
2
−
3⋅ L
0
(66)
Este mismo modelo puede servir para el caso de máquina síncrona de polos lisos.
Aplicación al caso del conjunto convertidor+filtro de entrada+máquina
asíncrona+carga.
Figura 19. Convertidor+Filtro de entrada+máquina asíncrona+carga.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
21
Filtro:
du s
= ie − i m
dt
di
L f ⋅ e = ur − us
dt
C⋅
(67)
Convertidor:
u m1 m1
= ⋅ u s ;
u m2 m2
i m = (m1
i
m 2 ) ⋅ s1
is2
(68)
Acoplamiento convertidor y máquina. Suponiendo conexión estrella en la máquina
se pueden plantear las ecuaciones que siguen:
Figura 20. Asignación de tensiones y corrientes.
v an
v an
v m1 1 0 − 1
=
⋅ v bn = C u ⋅ v bn
v m 2 0 1 − 1 v
v
cn
cn
v an
2 − 1
1
v m1
v
= C v ⋅ m1
v bn = ⋅ − 1 2 ⋅
vm 2
v 3 − 1 − 1 v m 2
cn
0
i an 1
i s1
1 ⋅ = C s
ibn = 0
i − 1 − 1 i s 2
cn
i
⋅ s1
is2
(69)
(70)
(71)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
i an
i s1 1 0 0
=
⋅ ibn = C i
is2 0 1 0 i
cn
1
u sx
2
u sy = ⋅ 0
u 3
1
s0
2
22
i an
⋅ ibn
i
cn
1
1
−
1 −
2
2 v an
u sx
v an
2
3
3
−
⋅ v bn = P ⋅ v bn
u sy = ⋅ 0
2
2
u 3
v
1
1
1 v cn
s0
cn
2
2 2
1
1
−
−
2
2
2 − 1
v m1
v m1
3
3 1
P
C
−
⋅
⋅
−
1
2
⋅
=
⋅
⋅
v
v
v
2
2 3
2
2
m
m
1
1
− 1 − 1
2
2
(72)
(73)
(74)
2
0
3
i an
3 1
3
ibn = ⋅ −
2
i 2 3
cn
1
3
−
−
2
3
2
3 i sx
i sx
2
−1
i
P
⋅
=
⋅
(75)
i sy
sy
3
is0
2 i s 0
3
2
2
0
3 i sx
3
i an
i sx
i s1 1 0 0 1 0 0 3 1
3
2
−1
=
⋅ ibn =
⋅ ⋅ −
i
C
P
⋅
=
⋅
⋅
i sy
sy
i
2
3
is2 0 1 0 i 0 1 0 2 3
i
is0
cn
s0
1
3
2
−
−
2 3
3
(76)
se añaden las ecuaciones de la máquina que completan el conjunto:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
23
dΨsx
= u sx − R s ⋅ i sx + ω ⋅ Ψsy
dt
dΨsy
= u sy − R s ⋅ i sy − ω ⋅ Ψsx
dt
dΨrx
= u rx − Rr ⋅ i rx − (ω − ω r ) ⋅ Ψry
dt
dΨry
= u ry − Rr ⋅ i ry + (ω − ω r ) ⋅ Ψrx
dt
dΨs 0
= u s 0 − Rs 0 ⋅ i s 0
dt
dΨr 0
= u r 0 − Rr 0 ⋅ i r 0
dt
i sx L s
i sy 0
i = L
rx m
i 0
ry
i s 0 Ls 0
=
ir 0 0
Lr
i sx A
i sy = 0
i
s0
0
−1
0 Ψsx
0 Lm Ψsy
1
⋅
=
Ψ
0 Lr
0
L s ⋅ Lr − L2m
rx
Lm 0 Lr Ψry
1
0
−1
0 Ψs 0 L s 0
⋅ Ψs 0
⋅
=
1 Ψr 0
L r 0 Ψr 0 0
Lr 0
0
Ls
Lm
0
0
L
− m
A
Lr
A
0
0
0
1
Ls 0
0
J⋅
0
−
Lm
A
0
Lr
0
⋅
− Lm
0
0
Lr
0
− Lm
(77)
− Lm
0
Ls
0
0 Ψsx
− Lm Ψsy
⋅
0 Ψrx
Ls Ψry
Ψ
Ψsx
sx
0 Ψsy
Ψsy
Ψs 0 = L−1 ⋅ Ψs 0
0 ⋅
Ψ
Ψrx
rx
Ψ
0 Ψry
ry
Ψ
Ψ
r0
r0
dω r
3
= − ρ ⋅ ω r + ⋅ p ⋅ (Ψsx ⋅ i sy − Ψsy ⋅ i sx ) − M c
dt
2
(78)
(79)
Reordenando, se llega a:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
24
1/ C
0
0
0
0
0
0
0
0
− 1/ L f
− R s ⋅ Lr
us
ω
0
0
0
A
ie
− R s ⋅ Lr
Ψ 0
−ω
0
0
sx
A
− Rs 0
d Ψsy
0
0
0
Ψ = 0
dt s 0
Ls 0
R r ⋅ Lm
Ψrx
0
0
0
0
A
Ψ
ry
R r ⋅ Lm
Ψ 0
0
0
0
r0
A
0
0
0
0
0
0 0 0
0
0 0 0 − 1/ C
0
1 / L f 0 0 0
0 0 0
0
0 0 0 ur 1 0 0
0 u sx
0 0 0 u rx 0 1 0
0 u sy
0
⋅u +
⋅ u
0
0
0
0
0
0
1
0
ry
s0
0
1 0 0 ur0 0 0 0
0 i m
0 1 0
0
0
0 0 0
0
0 0 0
0 0 1
0
0
0
Rs ⋅ Lm
A
0
0
0
0
Rs ⋅ Lm
A
0
0
Rr ⋅ Ls
A
ω − ωr
− (ω − ω r )
− Rr ⋅ Ls
A
0
0
u
0 s
ie
0 Ψsx
Ψsy
0 ⋅
+
Ψs 0
0 Ψrx
Ψry
0 Ψr 0
− Rr 0
Lr 0
0
0
(80)
Añadiendo las relaciones entre las tensiones y corriente moduladas como función de
las variables de estado, se llega a:
u sx
u sy P
u = 0
s0 3x3
i
m
P
0 3x3
P
0 3x3
u an
01x1 u bn P
⋅
=
I u cn 0 3 x 3
i
m
01x1 C v
⋅
I 01 X 2
uM1
03X1
⋅ u m 2 =
i
im
01 x1 C v
⋅
I 01 X 2
m1
03 X 1
⋅ m2
i
0
0
0
m1
0 us
0 ⋅ i s1 =
m2 i s 2
01 x1 C v
⋅
I 01 X 2
m1
03 X 1
⋅ m2
i
0
0
0
m1
0
I
0 ⋅
0
m2 2 x1
(81)
us
01 x 3 i sx
⋅
C i ⋅ P −1 i sy
i
s0
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
u sx
u sy P
u = 0
s0 3x3
i
m
01 x1 C v
⋅
I 01 X 2
m1
03X1
⋅ m2
i
0
25
0
0
m1
0
I
0 ⋅
0
m 2 2 x1
us
ie
Ψ
sx
0 1x 3 0 Ψsy
⋅ ⋅
C i ⋅ P −1 L−1 Ψs 0
Ψrx
Ψry
Ψ
r0
(82)
La aplicación del conjunto anterior lleva a los resultados que siguen, mostrando la
operatividad de la modelización propuesta.
Figura 21. Tensiones aplicadas Um1 y Um2.
Figura 22. Variables de estado del filtro. Us, I(Lf).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
26
Figura 23. Corrientes Is1, Is2 por la máquina.
Figura 24. Par electromagnético, de carga y velocidad.
Figura 25. Análisis armónico Um1 e Is1.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
27
Aplicación al conjunto ondulador de corriente+filtro de salida + carga
accionada.
Figura 26. Convertidor de corriente+filtro de salida+máquina asíncrona+carga.
Ecuaciones del filtro:
V s1 R ⋅ C
=
Vs 2 0
0 d u c1 u c1
⋅ +
R ⋅ C dt u c 2 u c 2
(83)
Ecuaciones de la máquina:
Rs ⋅ Lr
ω
0
−
A
R ⋅L
− s r
0
Ψsx − ω
A
Ψsy
R
− s0
0
0
Ψ
d s0
Ls 0
=
R
L
⋅
dt Ψrx r m
0
0
Ψ
A
ry
Rr ⋅ Lm
Ψ
0
0
r0
A
0
0
0
0 0 0
1 0 0
0 0 0
0 1 0
0 0 0 u rx 0 0 1 u sx
⋅ u ry +
⋅ u sy
+
1 0 0 0 0 0
ur0
us0
0 1 0
0 0 0
0 0 1
0 0 0
dΨ
= As ⋅ Ψ + Br ⋅ u r + Bs ⋅ u s
dt
Rs ⋅ Lm
A
0
0
Rs ⋅ Lm
A
0
0
Rr ⋅ Ls
A
ω − ωr
− (ω − ω r ) −
0
Rr ⋅ Ls
A
0
0
0 Ψsx
Ψsy
0
Ψ
⋅ s0 +
0 Ψrx
Ψry
0 Ψr 0
Rr 0
−
Lr 0
(84)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
28
Teniendo en cuenta las relaciones entre tensiones aplicadas y transformadas:
dΨ
= As ⋅ Ψ + Br ⋅ u r + B s ⋅ u s = As ⋅ Ψ + Br ⋅ u r + B s ⋅ P ⋅ C v
dt
V
⋅ s1
V s 2
(85)
Sustituyendo:
dΨ
= As ⋅ Ψ + Br ⋅ u r + B s ⋅ u s = As ⋅ Ψ + Br ⋅ u r + Bs ⋅ P ⋅ C v
dt
R ⋅ C
⋅
0
0 d u c1 u c1
⋅ +
R ⋅ C dt u c 2 u c 2
(86)
dΨ
= As ⋅ Ψ + Br ⋅ u r + B s ⋅ u s = As ⋅ Ψ + Br ⋅ u r + Bs ⋅ P ⋅ C v
dt
y teniendo en cuenta que:
du
⋅ Rc ⋅ c + u c
dt
du
I m1 C 0 d u c1 I s1
=
⋅ + = C c ⋅ c + C i ⋅ P −1 ⋅ L−1 ⋅ Ψ
dt
I m 2 0 C dt u c 2 I s 2
(87)
(88)
se llega a:
As
I − B s ⋅ P ⋅ C v ⋅ Rc d Ψ
⋅ =
−1
−1
Cc
0
dt u c − C i ⋅ P ⋅ L
Bs ⋅ P ⋅ C v Ψ Br
0 m
⋅ + ⋅ u r + ⋅ 1 I s
0
I m2
uc 0
(89)
Los resultados que siguen confirman la correcta solución de las ecuaciones.
Figura 27. Corrientes por el motor.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
29
Figura 28. Tensiones aplicadas al motor.
Figura 29. Corriente por el filtro.
Figura 30. Corriente de salida del ondulador.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
30
Figura 31. Corrientes hacia el filtro.
Figra 32. Corrientes por el motor.
Figura 33. Velocidad, Par electromagnético.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
31
Función generatriz de conversión.
A partir de las definiciones anteriores y de los posibles estados de las células de
conmutación, es evidente que los elementos mij sólo pueden tomar los valores 1, 0 y
–1. Caso de desear una representación continua de los mismos, se puede definir
una función generatriz de conversión tal que su valor para un instante de tiempo,
sea equivalente al “valor medio instantáneo” de la función durante el período T:
mg =
1 ( k +1)⋅T
m(τ ) ⋅ dτ
∫
⋅
k
T
T
T →0
(90)
En la práctica, la función generatriz siempre es muestreada ya que el período T es
finito; la figura muestra como se obtiene m a partir de mg. Así, mg(k,t) es la función
muestreada de mg(t) para k ∈ {0,1,2,..., q, q + 1,...}. Si el bloqueo se produce al inicio del
período comprendido entre los instantes qT y (q+1)T, mg(q) representa, durante
este intervalo, la amplitud de mg(k,t) y por tanto el valor medio de la función de
conversión m.
Figura 34. Función generatriz.
Si la carga accionada presenta un comportamiento paso-bajo, la señal de salida del
convertidor puede ser asimilada a su valor medio para cada intervalo de muestreo
considerado, con el añadido de un retardo TD entre la señal mg(t) y su equivalente
continuo mg(t-TD), representativo del valor medio de mg(k,t). Normalmente, se
asimila este retardo al valor medio del período de muestreo resultando una función
de transferencia para el convertidor como la siguiente:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
32
T
T
− ⋅s
u ( s ) − 2 ⋅s
Fc ( s ) =
⋅e
= K ⋅e 2
mg (s)
(91)
El inconveniente que presenta esta función de transferencia se puede eliminar
realizando una aproximación de la exponencial según Pade, adoptando la forma
canónica siguiente:
(2 ⋅ n − i )!⋅n!
n
e
T
− •s
2
=
∑ (2 ⋅ n)!⋅i!⋅(n − i)! ⋅ (−s ⋅ T
D
i =0
n
)i
(2 ⋅ n − i )!⋅n!
⋅ ( s ⋅ TD ) i
∑
n
i
n
i
⋅
⋅
⋅
−
(
2
)!
!
(
)!
i =0
(92)
que presenta una constelación de polos estables y ceros inestables que mantienen
las características desestabilizantes del retardo.
Por ejemplo, para el caso de T=0.2 ms y considerando n=1 (aproximación de primer
orden):
Fc ( s ) = K ⋅ e
T
− ⋅s
2
1 − 50 ⋅10 −6 ⋅ s
≈K⋅
1 + 50 ⋅10 −6 ⋅ s
(93)
Aplicando el método anterior a las funciones de conexión fij se puede definir la
función fg(k,t), función generatriz muestreada, correspondiente a la resultante del
muestreo de la función generatriz de conexión fg(t):
1 q⋅T
f g (τ ) ⋅ dτ = δ 1 (q − 1)
T ∫( q −1)⋅T
(94)
El valor medio relativo a cada intervalo de muestreo fg(q), se corresponde con el
tiempo de conexión relativo a cada intervalo considerado, es decir:
f g (q) =
t on (q )
⇒ t on (q) = f g (q) ⋅ T
T
(95)
Esto permite calcular el tiempo de conexión de cada interruptor, una vez fijado el
período de muestreo para el convertidor.
Generalizando para el caso de un convertidor complejo, se puede plantear:
1
M rg = Rcv ⋅ Frg = Rcv ⋅
T
∫
( q +1)⋅T
q ⋅T
Fr (τ ) ⋅ dτ
T →0
(96)
finalmente:
G m = M rg ⋅ C s ⋅ X
(97)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
33
La aplicación al caso anterior (filtro+convertidor+máquina accionada+carga) lleva a
los siguientes resultados.
Figura 35. Tensiones aplicadas a la máquina.
Figura 36. Variables de estado del filtro. Us, I(Lf).
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
34
Figura 37. Corrientes por el motor.
Figura 38. Par electromagnético, de carga y velocidad.
Figura 39. Análisis armónico tensión aplicada, corriente por la máquina.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
35
Que coinciden en la aproximación de primer armónico con los calculados mediante
el modelo exacto. A efectos de control se puede sustituir el modelo exacto mediante
el modelo promediado. Si se comparan los resultados se observa un retardo medio
no superior a ½ del período de muestreo considerado; como se puede ver en la
gráfica que sigue.
Figura 40. Comparación del cálculo exacto y el promediado.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
36
Estructuras de control basadas en las funciones generatrices de modulación.
Una vez formulada la modelización, puede plantearse el cálculo de las funciones
generatrices de modulación para realizar cualquier estructura de control. Por
ejemplo, en la figura que sigue se plantea la obtención de las funciones de control a
partir del conocimiento de la corriente y de la velocidad y a partir de la inversión del
modelo de la máquina.
Us
Relaciones de
conversión
m1
Um1
m2
Um2
MÁQUINA
ondulador
Is1
Is2
Estructura de control
P-1
F
θ
GENERADOR
DE FUNCIONES
DE CONEXIÓN
M1ref
Isy
ω
msxref
P
M2ref
Isx
msyref
MODELO INVERSO
OBSERVADORES
CONTROL
Referencias de par y
corriente
Figura 41. Estructura de control basada en las funciones generatrices de conexión.
Aplicación al control de la máquina asíncrona.
Esta estructura es general para cualquier algoritmo de control que se plantee, ya
que permite el cálculo de la señal a aplicar en función de las variables de control
consideradas.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
Aportación
experimental:
asíncrona+convertidor+carga.
37
caso
del
conjunto
máquina
Aplicación de la metodología anterior a un sistema formado por los siguientes
componentes:
-
Ondulador PWM, con señal portadora triangular de 1000 Hz, VN = 220 V, 1.8
kVA, ley V/f = K de 0 a 50 Hz; V = k = VN para f> 50 Hz. Prueba realizada para
salida a frecuencia nominal (50 Hz; mf = 20; ma = 0.9).
-
Máquina asíncrona de 1.5 kW, 220 V/380 V, 1470 min-1.
-
Parámetros de la máquina obtenidos a partir de ensayos normalizados: Rs = 5.18
Ω; Rr = 5.31 Ω; Lsl = 0.01375 H; Lrl = 0.01435 H; M = 0.3675 H; J = 0.003375
kgm2.
-
Par de carga aplicado = 1.8 Nm, correspondiente al servicio de la máquina en
vacío y atribuible al par de rozamientos mecánicos.
Obteniéndose los siguientes resultados de contrastación:
V1L
I1L
Vfp
Nf
Experimental
282 V
3.7 A
69.2 V
1490 min-1
Simulación
270 V
4.2 A
80 V
1480 min-1
Error
4.25%
13.5%
15.60%
0.67%
La tabla recoge los resultados relativos al valor eficaz de la componente
fundamental de tensión V1L, de primer armónico de corriente I1L, y del armónico de
tensión de primer orden ( f p = m f ⋅ f1 ± f1 , 950 Hz) y valor final de velocidad nf.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
38
Figura 42. Tensión aplicada. 1 div = 100 V ; 1 div = 5 ms.
Figura 43. Tensión calculada.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
39
Figura 44. Corriente real. 1 div = 2 A; 1div = 5 ms.
Figura 45. Corriente calculada.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 7 . MODELIZACIÓN DEL CONVERTIDOR
40
Conclusiones
El método de modelización considerado permite la formulación del conjunto de
ecuaciones correspondientes al motor y su alimentación, resultando una forma
natural y relativamente, sencilla.
Es obvio que las funciones de conexión ya han sido utilizadas ampliamente en el
caso de modelización de convertidores, pero no es así en el supuesto de considerar
como carga del mismo una máquina.
Asimismo la consideración del conjunto permite obtener leyes directas de control
para el convertidor, partiendo de variables de interés electrotécnico: corriente,
velocidad o par.
A partir de los resultados obtenidos caben las siguientes consideraciones:
•
El modelo completo permite obtener resultados de forma exacta.
•
La consideración de modelos promediados lleva a resultados correctos en el
caso de índices de modulación elevados.
•
A efectos de sintetizar el control se puede sustituir la función exacta por la
promediada.
•
El conjunto completo de ecuaciones es de una gran belleza conceptual y
aplicada.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
DISCUSIÓN DE LOS RESULTADOS.
CONCLUSIONES Y APORTACIONES
CAPÍTULO 8. DISCUSIÓN DE LOS RESULTADOS. CONCLUSIONES Y APORTACIONES
1
8. DISCUSIÓN DE RESULTADOS. CONCLUSIONES Y
APORTACIONES
8. DISCUSIÓN DE RESULTADOS. CONCLUSIONES Y APORTACIONES ...........................2
Modelos de máquinas asíncronas considerando la saturación. .............................................2
Sensibilidad. ............................................................................................................................3
Obtención de los parámetros por ensayos fuera de línea.......................................................4
Obtención de variables no medibles y parámetros en servicio...............................................5
Modelo completo: ................................................................................................................6
Modelo reducido:.................................................................................................................7
Parámetros mecánicos: .......................................................................................................7
Modelización del convertidor..................................................................................................8
Aplicaciones. ...........................................................................................................................8
Futuros desarrollos. ................................................................................................................9
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 8. DISCUSIÓN DE LOS RESULTADOS. CONCLUSIONES Y APORTACIONES
2
8. DISCUSIÓN DE RESULTADOS. CONCLUSIONES Y
APORTACIONES
Modelos de máquinas asíncronas considerando la saturación.
a) Se han desarrollado y discutido diversos modelos para máquinas asíncronas
considerando la saturación.
b) Desde el punto de vista de simulación todos los modelos aportan la misma
información y los mismos resultados.
c) Si se tienen en cuenta las restricciones de control, los modelos que en su
formulación incluyan ecuaciones algebraicas, no han de considerarse para su
aplicación en algoritmos de control, debido a la posibilidad de retardo en el
cálculo de variables.
d) La utilización de modelos con un parámetro menos, Lsl o Lrl según el caso,
conlleva una formulación más sencilla y a la vez, posibilita la estimación de los
parámetros sin tener que aventurar hipótesis poco contrastadas (del tipo Lsl = Lrl).
e) La utilización de modelos con saturación cruzada introduce una restricción
algebraica que invalida totalmente su aplicación en tiempo real.
f) Los modelos basados en orientación del campo resultan muy sencillos en su
formulación, a costa de necesitar el cálculo de la velocidad y posición de los ejes
de referencia para cada instante de tiempo; por tratarse de un caso particular,
aunque de mucha aplicación, no se han considerado para el desarrollo de
modelos de identificación en tiempo real.
g) Los modelos nº 21 y 22 resultan los más interesantes:
•
Están formulados con un parámetro menos (Lsl), por lo que resultan
de resolución sencilla.
•
No presentan ninguna restricción algebraica para su resolución.
•
Se diferencian en la formulación de la función de saturación.
•
A efectos de formulación para su implementación en algoritmos de
identificación de parámetros en tiempo real, el modelo nº 21 resulta
menos interesante ya que los parámetros desconocidos aparecen
como coeficientes dentro de la función de saturación:
Ψ = a1 ⋅ atan(a 2 ⋅ i )
Lo cual representa un obstáculo en su implementación.
(1)
h) Ambos modelos se consideran para su implementación en la modelización.
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 8. DISCUSIÓN DE LOS RESULTADOS. CONCLUSIONES Y APORTACIONES
3
Sensibilidad.
a) El análisis de las funciones de sensibilidad permite estimar los errores que se
producen en las salidas ocasionados por las variaciones de los parámetros, así
como su influencia en la respuesta global del sistema.
b) El modelo que resulte menos sensible a las variaciones de los parámetros será
mas útil para la realización de algoritmos de control y, a su vez, se pondrán en
evidencia que parámetros son más delicados para su valoración posterior.
c) El análisis de los modelos anteriores, (21 y 22), conduce a las siguientes
conclusiones:
•
Las corrientes resultan igualmente afectadas por las variaciones de rs y rr en
ambos modelos.
•
La sensibilidad de las mismas es mayor a las variaciones de Lrl; además, el
modelo nº21 resulta mucho más sensible.
•
Las variaciones en el momento de inercia J, y en el coeficiente de rozamiento
ρ, repercuten de forma similar en ambos modelos.
•
Las variaciones en los parámetros que definen las funciones de saturación (a1
y a2 para el modelo nº 21; a y b para el modelo nº 22), influyen de forma
mucho más significativa en el primer modelo (nº 21).
•
Respecto a la velocidad ωr:
-
•
Ambos modelos presentan un comportamiento similar; no obstante, el
primer modelo presenta discrepancias mayores para todos los parámetros
considerados, en especial los que definen la caracterización de la
saturación.
Respecto a los flujos:
-El modelo nº 22 es mucho menos sensible a las variaciones de los
parámetros que el nº 21.
•
Respecto al par electromagnético:
-
En ambos modelos resulta muy sensible a las modificaciones de Lrl
(menos en el modelo nº 22), y a las variaciones del momento de inercia
(de nuevo, menor en el modelo nº 22).
-
Respecto a los parámetros que caracterizan la saturación, el modelo
polinomial considerado en el caso nº 22, resulta menos problemático que
el modelo arcotangente.
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 8. DISCUSIÓN DE LOS RESULTADOS. CONCLUSIONES Y APORTACIONES
4
d) Como conclusión final, el modelo polinomial para caracterizar la saturación
resulta menos influyente que el de Langevin y, por lo tanto será el considerado
para su implementación en la determinación de los parámetros en tiempo real.
Tabla 1. Sensibilidades unitarias. Modelo nº21
isx
isy
irx
iry
ωr
Ψsx
Ψsy
Me
Rs
1.31
18.78
-1.17
-1.34
-0.04
0.25
0.23
6.18
Rr
-2.49
3.89
2.53
-3.89
0.28
-0.10
0.08
-2.87
Lrl
-0.39
-351
267
502
-25.7
-44.2
47.1
-463
J
-3.48
2.45
3.48
-2.42
0.39
-0.13
0.13
-4.6
ρ
-0.26
0.12
0.26
-0.12
0.02
-3.9e-3
-5.2e-6
-0.34
a1
414
4557
-406
489
-30.4
45.2
72.9
1720
a2
-311
-1193
-311
394
-21.3
71.2
69.4
-718
a
8.6e-4
0.019
0.018
-0.021
9.15e-3
0.33
-0.39
0.53
b
0.097
0.049
0.043
0.043
-0.017
0.30
-2.48
-2.04
Tabla 2. Sensibilidades unitarias. Modelo nº22
Ψsx
Ψsy
Ψrx
Ψry
ωr
isx
isy
Me
Rs
0.21
0.21
0.16
-0.12
0.043
1.02
13.2
7.73
Rr
-0.12
0.08
0.27
-0.55
0.18
-1.02
3.89
-3.23
Lrl
0.18
-0.23
0.82
0.88
-0.61
6.02
-4.98
-9.26
J
0.12
0.09
-0.55
0.42
-0.41
4.14
-2.76
5.25
ρ
0.0023
0.0044
-0.028
0.013
-0.015
0.20
-0.07
0.28
Obtención de los parámetros por ensayos fuera de línea.
a) Como paso previo a la obtención de los parámetros en tiempo real, se plantea la
obtención de los mismos a partir de ensayos en régimen permanente.
b) A partir de los ensayos en vacío y cortocircuito puede plantearse la obtención de
los parámetros necesarios para la modelización de la máquina.
c) El algóritmo presentado permite la valoración independiente de las reactancias
de dispersión estatórica y rotórica, y de la resistencia equivalente de pérdidas en
el hierro, a partir del conocimiento de la calidad de la plancha magnética.
d) La obtención de los parámetros mediante ensayos en régimen permanente
(vacío a tensión nominal y rotor frenado), proporcionan resultados correctos. La
comprobación de resultados en carga es coherente, estando limitada la
resolución del resultado por la precisión en la medida de la velocidad del eje.
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 8. DISCUSIÓN DE LOS RESULTADOS. CONCLUSIONES Y APORTACIONES
5
e) Se han utilizado dos formulaciones distintas para aproximar las características de
saturación:
•
Polinomial
•
Arco tangente
Ψ
i
Ψ
=a⋅
+ b ⋅
In
ΨN
ΨN
Ψ = a1 ⋅ atan(a 2 ⋅ i )
n
Ambas logran aproximaciones suficientemente exactas, la consideración de una
u otra dependerá de la aplicación final.
Tabla 3. Parámetros obtenidos en la modelización de la saturación.
Máquina 1
Máquina 2
Máquina 3
Polinomial
a
0.48
0.61
0.8
b
0.52
0.39
0.2
2
0.032
0.0161
0.0422
∑ε
Langevin
a1
a2
∑ ε2
0.8550
0.8649
1.159
0.9115
0.2283
1.070
1.0921
0.0691
1.0020
f) Se han contrastado los modelos obtenidos para tres grupos de máquinas de
potencias crecientes (1.5, 7.5, 22 kW), a las que se ha aplicado una alimentación
sinusoidal o PWM proveniente de un ondulador, y un ciclo de carga consistente
en arranques en vacío y carga, con posterior variación de la misma. En todos los
casos se han obtenido errores aceptables lo que valida el modelo considerado.
Obtención de variables no medibles y parámetros en servicio.
a) El observador desarrollado es robusto respecto a las variaciones en los
parámetros (coeficientes) del mismo.
b) El observador desarrollado mantiene su robustez en la zona de debilitación de
campo. Únicamente en el caso de fuerte saturación (UN; 25 Hz – ½ de la
frecuencia nominal, aproximadamente doble del flujo nominal) existen
discrepancias apreciables en alguna de las variables del observador (Flujo
rotórico, corriente estatórica); en todo caso las discrepancias son inferiores al
1%.
c) Se han considerado dos formulaciones para el problema de la obtención de las
variables de estado desconocidas.
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 8. DISCUSIÓN DE LOS RESULTADOS. CONCLUSIONES Y APORTACIONES
6
Modelo completo:
d) Para asegurar la convergencia del algoritmo de identificación hace falta arrancar
el algoritmo del observador con unos valores supuestos para los parámetros, y
después de un tiempo de rodaje no inferior a 40 ms puede iniciarse el algoritmo
de identificación de los mismos; tras múltiples ensayos y pruebas, y debido a la
no linealidad del conjunto observador+identificador, no se ha podido garantizar la
convergencia sin este proceso de inicialización.
e) El conjunto de parámetros obtenidos difiere del que se deduce de los ensayos
realizados fuera de línea (capítulo anterior); de cara a su implementación en los
algoritmos de control esto no es un inconveniente siempre que lo deseado sea un
modelo de “caja negra”, es decir que las variables externas sean las correctas.
En el caso que nos ocupa esto es así. No puede garantizarse en ningún caso
que las variables internas (flujo, par, corriente rotórica) sean las correctas.
Considérese el caso del modelo polinomial para la relación flujo corriente:
Ψ
Ψ
i
=a⋅
+ b ⋅
In
ΨN
ΨN
n
si los parámetros a y b estimados no coinciden con los obtenidos en los ensayos
previos fuera de línea, no puede garantizarse que, aún obteniendo el mismo valor
para la corriente, el flujo sea el correcto.
Tabla 4. Resultados de identificación. Modelo completo. Alimentación
mediante ondulador PWM
Fuera de
linea
Linea
Diferencia
(%)
lrl (mH)
rr (Ω
Ω)
ax
bx
ay
by
J
0.857
τr=lrl/rr
(ms)
8.52
7.3
0.61
0.39
0.61
0.39
0.076
10.68
46.3
1.15
34.1
9.28
9.00
0.76
24.2
0.78
100
0.726 -0.029 0.075
19.0
107
1.33
f) La convergencia a valores constantes se produce únicamente para el caso de
alimentación PWM. En el caso de alimentación sinusoidal no es posible
garantizar la convergencia a valores correctos; la señal sinusoidal tiene un órden
2, insuficiente para resolver la identificación (6 parámetros).
g) Se ha tenido en cuenta la posibilidad de considerar coeficientes de saturación
distintos para cada componente (ax, ay, bx, by). Con esta técnica puede obviarse
la utilización de los modelos con saturación cruzada.
h) La metodología empleada logra la convergencia de las variables observadas a
las reales en un tiempo inferior a los dos períodos de la onda (40 ms a 50 Hz –
una vez transcurrido el tiempo de inicialización).
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 8. DISCUSIÓN DE LOS RESULTADOS. CONCLUSIONES Y APORTACIONES
7
Modelo reducido:
i) Es necesario el conocimiento completo de los parámetros de modelización del
estator (resistencia, saturación) para su desarrollo. Estos pueden ser obtenidos
anteriormente mediante el ensayo en vacío.
j) La convergencia del algorítmo es mucho menos crítica que en el caso anterior.
Es capaz de arrancar con valores iniciales cualesquiera, obteniéndose la
convergencia en un tiempo inferior a 120 ms (alimentando la máquina a 50 Hz)..
k) Una vez arrancado el algorítmo se mantiene la convergencia ante variaciones del
sistema (convergencia en menos de 10 ms – ½ periodo a 50 Hz)
l) Los parámetros rotóricos obtenidos presentan una dispersión menor respecto a
los obtenidos en los ensayos fuera de línea.
Tabla 5. Resultados de identificación. Modelo reducido. Alimentación mediante
ondulador PWM
lrl (mH)
J
rr (Ω
Ω)
τr=lrl/rr (ms)
Fuera de linea
7.3
0.857
8.52
0.076
Linea
7.721
0.772
8.74
0.075
Diferencia (%)
5.76
-9.92
2.58
1.33
Parámetros mecánicos:
m) El par de carga y el momento de inercia del conjunto presentan una convergencia
a valores correctos en un tiempo no superior a 100 ms. El resultado de los
parámetros mecánicos es independiente del modelo de identificación
considerado.
n) Para ambos modelos el error en la estimación de la constante de tiempo rotórica
és suficientemente pequeño como para ser útil en el planteo de algorítmos de
control que precisen de la misma (control por orientación del campo).
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 8. DISCUSIÓN DE LOS RESULTADOS. CONCLUSIONES Y APORTACIONES
8
Modelización del convertidor.
La consideración de las funciones de conexión aplicadas a los convertidores
alimentando cargas pasivas, ha sido ampliamente desarrollada en la literatura
técnica. Su aplicación a las cargas activas, como las máquinas eléctricas, es una
laguna que se ha llenado. El modelo desarrollado permite:
a) La consideración, de forma natural y sencilla, del conjunto de ecuaciones
correspondientes al motor accionado y a su alimentación.
b) Obtener leyes de control de una forma natural a partir de la inversión del modelo
del sistema.
c) Contrastar experimentalmente el desarrollo obtenido.
Aplicaciones.
a) Se ha desarrollado y construido un equipo para el ensayo de accionamientos
eléctricos.
b) Permite trabajar en los cuatro cuadrantes del plano par-velocidad así como el
control del par de carga presente en el eje, siguiendo una ley arbitraria.
c) Se ha desarrollado e implementado un algoritmo observador para el par en el eje,
que permite a partir de las medidas de corriente y velocidad de la máquina de
corriente continua, valorar el par electromagnético de la máquina ensayada.
d) El error resulta inferior al 5% a partir de dos períodos de onda (40 ms a 50 Hz).
e) El equipo desarrollado, tiene un evidente interés para su aplicación docente e
industrial
f) El equipo, como se puede apreciar a continuación, tiene un coste económico más
reducido que otros de similares características:
•
•
•
•
•
•
Máquina de c.c. 7.5 kW
Dinamo tacométrica+acopl.
Equipo de potencia
Tarjeta de control+obs.
Ingenieria+mano de obra
Beneficio/Comercialización
•
•
Total
Freno comercial similar
220.000 ptas.
50.000 ptas.
200.000 ptas.
60.000 ptas.
470.000 ptas
500.000 ptas
1.530.000 ptas.
4.000.000 ptas.
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
CAPÍTULO 8. DISCUSIÓN DE LOS RESULTADOS. CONCLUSIONES Y APORTACIONES
9
Aportaciones.
•
Estudio sistemático de modelos con saturación a fin de determinar cual o cuales
de los mismos són adecuados para la implementación de técnicas de control y de
identificación en tiempo real.
•
Estudio de la sensibilidad de los modelos escogidos ante variaciones de los
parámetros. Hasta donde alcanzan mis conocimientos el tema es una laguna
poco explorada.
•
Comparación de diversos métodos de obtención de parámetros (con
consideración de la saturación) tanto en régimen permanente (ensayos fuera de
línea) como en transitorio (identificación en tiempo real).
•
Comparación en la identificación en tiempo real de diversos modelos. Influencia
del número de parámetros y del tipo de señal aplicada en la identificabilidad del
sistema.
•
Aportación a la obtención del par electromagnético y a su validación mediante
medidas externas.
•
Construcción de un equipo para el ensayo de accionamientos en régimen
dinámico. Esto consiste, en opinión del autor, un “subproducto” de la tesis que
posiblemente tenga mayor aplicación docente e industrial.
Futuros desarrollos.
La línea iniciada abre diversas áreas de interés:
a) Extender la modelización a otros tipos de máquinas eléctricas.
b) Desarrollar equipos para el control del par basados en máquinas de alterna.
c) Desarrollar algoritmos de control basados en una correcta identificación de los
parámetros del sistema, que puedan llevar a una optimización, o minimización,
de tránsitos energéticos en el convertidor.
d) Contrastación de los métodos de obtención de parámetros en línea mediante
algoritmos basados en la resolución del campo electromagnético en la máquina
(Elementos finitos). Actualmente, empiezan a circular programas que permiten la
resolución de transitorios eléctricos conjuntamente con la formulación de la
máquina a partir de modelos basados en elementos finitos (SIMPLORER +
FLUX2D); estos permitirán la contrastación de los algoritmos en tiempo real a
partir de los modelos distribuidos de la máquina. En nuestro caso no se ha
podido desarrollar el tema por no disponer de los programas adecuados.
Barcelona, Julio del 2001
APORTACIÓN A LA DETERMINACIÓN DE PARAMETROS EN LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
BIBLIOGRAFÍA
BIBLIOGRAFIA.
1
BIBLIOGRAFIA
BIBLIOGRAFIA ...................................................................................................................................1
Libros ...............................................................................................................................................2
Máquinas Eléctricas. Teoria. Modelización. Control..................................................................2
Convertidores. Modelización. Control.........................................................................................3
Identificación de sistemas ............................................................................................................3
Sensibilidad ..................................................................................................................................4
Control no Lineal. Técnicas. Observadores.................................................................................4
Tesis Doctorales ...............................................................................................................................4
Artículos, Ponencias, Comunicaciones ............................................................................................5
Articulos sobre modelización de máquinas. Obtención de parámetros y observación de
variables no medibles y estados ...................................................................................................5
Articulos sobre Control de Máquinas Asíncronas .......................................................................7
Articulos històricos sobre modelización de máquinas y convertidores .......................................7
Proyectos Final de Carrera .............................................................................................................8
Normas .............................................................................................................................................8
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA MEJOR
IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
BIBLIOGRAFIA.
2
Libros
Máquinas Eléctricas. Teoria. Modelización. Control
[Serrano 79] L. Serrano Iribarnegaray. “Máquinas de alterna en régimen dinámico. Una
formulación físico-matemàtica a partir de la teoría de los vectores espaciales”. UPM
Madrid, 1979
[Kovacs 84] P.K. Kovacs. “Transient Phenomena in Electrical Machines”. Elsevier,
Amsterdam, 1984
[Leonhard 96] W. LEONHARD. “Control of electrical drives”. Springer- Verlag. 1990
[Justus 91] Justus. Dynamisches Verhalten Elektrischer Maschinen. Vieweg Publishing,
Braunschweig/Wiesbaden, 1991
[Vas 92] P.VAS. “Electrical machines and drives. A Space-Vector Theory Approach”.
Oxford University Press,, 1992.
[Vas 93] P.Vas.” Parameter estimation,Condition monitoring and diagnosis of electrical
machines” Oxford University Press, Oxford, 1993
[Caron 95] J.P.Caron,J.P.Hautier. “ Modelisation et commande de la machine
asynchrone”. Ed.Technip,1995
[Roboam 95] X. ROBOAM. “ De la modelisation a la commande des machines
electriques.” ENSEEIHT. 1995
[Jiles 98] D.Jiles. “Introducction to magnetism and magnetic materials”. Ed. Chapman and
Hall, 1998
[Ong 98] C. Ong. “Dynamic simulation of electric machinery”. Ed. Prentice Hall, 1998
[Vas 98] P. Vas. “Sensorless vector and direct torque control”. Ed. Oxford University
Press, 1998
[Dawson 98] D.M.Dawson, J. Hu, T.C.Burg. “Nonlinear control of electric machinery”. Ed.
Marcel Decker, 1998
[Vas 99] P. Vas. “Artificial intelligence based electrical machines and drives. Application of
fuzzy, neural, fuzzy-neural, and genetic algorithm based techniques”. Ed. Oxford
University Press, 1999
[Boldea 99] I. Boldea, S.A. Nasar. “Electric Drives”. CRC Press, 1999
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA MEJOR
IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
BIBLIOGRAFIA.
3
Convertidores. Modelización. Control
[Buhler 91] H. Bühler. “Convertisseurs statiques”. Ed. PPUR, 1991
[Labrique 95] F.Labrique, G.Seguier,R.Bausiere. “Les convertisseurs de l’électronique de
puissance. T4. La conversion continu-alternatif”.Ed. Lavoisier. 1995
[Bose 97] B.K.Bose.” Power Electronics and Variable Frequency Drives.”. IEEE Press,
New York, 1997.
[Labrique 98] F.Labrique, H. Buyse G.Seguier,R.Bausiere. “Les convertisseurs de
l’électronique de puissance. T5. Commande et comportement dynamique”.Ed. Lavoisier.
1998
[Hautier 99] J.P. Hautier, J.P. Caron. “Convertisseus statiques: Methodologie causale de
modelisation et de commande”. Ed. Technip, 1999
Identificación de sistemas
[Ljung 87] L.Ljung. “Theory and practice of recursive identification”. MIT Press, Boston,
1987
[Ljung 87] L.Ljung. “System identification:theory for the user”. Prentice Hall International,
London, 1987
[Soderstrom 89] T.Soderstrom,P.Stoica.
International,London, 1989
“System
identification”.
Prentice
Hall
[Middleton 90] R.H.Middleton, G.C. Goodwin. “Digital control and estimation”. Ed. Prentice
Hall, NewJersey, 1990.
[Borne 92] P.Borne, et. al. ” Modelisation et identification del processus, tome 1 et 2”. Ed.
Technip, Paris, 1992
[Juang 94] J.N. Juang. “Applied System Identification”. Ed. Prentice Hall, 1994
[Johansson 94] R. Johansson. “System modeling and Identification”. Ed. Prentice Hall,
1994
[Kulhavy 96] R. Kulhavý. “Recursive Nonlinear Estimation”. Ed. Springer, 1996
[Walter 97] E.Walter, L. Pronzato. “Identification of parametric models from experimental
data”. Ed. Springer Verlag, 1997
[Bendat 98] J.S.Bendat. “Nonlinear systems techniques and applications”. Ed. John
Wiley&Sons. 1998.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA MEJOR
IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
BIBLIOGRAFIA.
4
[Tong 99] H.Tong. “Non linear time series: a dynamical system approach”. Ed. Oxford
University Press. 1999
[Nelles 01] O. Nelles. “Nonlinear System Identification”. Springer- Verlag. 2001
Sensibilidad
[Eslami 94] M. Eslami. “Theory of sensitivity in dynamic systems”. Ed. Springer-Verlsg.
1994
[Rosenwasser 00] E. Rosenwasser, R. Yusupov. “Sensitivity of automatic control
systems”. Ed. CRC-Press. 2000
Control no Lineal. Técnicas. Observadores.
[Marino 94] R.Marino,P.Tomei. “ Nonlinear control design.Geometric, Adaptive and
Robust”. Ed. Prentice Hall, 1994
[Krstic 95] M. Krstic, I. Kanellakopoulos, P. Kokotovic “Nonlinear and adaptive control
design”, Ed. Wiley Interscience, 1995
[Ioannou 96] P.A.Ioannou, J.Sun. “Robust adaptive control”. Ed. Prentice Hall, 1996
[Schroder 99] D. Schröder (Ed.). “Intelligent observer and control design for nonlinear
systems”. Ed. Springer Verlsg. 1999
[ Sastry 99] S. Sastry. “Nonlinear systems. Analysis, stability and control”. Ed. Springer
Verlag, 1999.
Tesis Doctorales
[Peterson 96] Bo Peterson. “Induction machine Speed Estimation. Observations on
Observers”. Industrial Electrical Engineering and Automation. Lund Institute of
Technology. 1996
[Corcoles 98] Felipe Corcoles López. “Estudio y caracterización de la máquina de
inducción. Aplicación de métodos analíticos y aproximados para el análisis transitorio”.
Departament d’Enginyeria Eléctrica. ETSEIB-UPC, 1998.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA MEJOR
IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
BIBLIOGRAFIA.
5
Artículos, Ponencias, Comunicaciones
Articulos sobre modelización de máquinas. Obtención de parámetros y observación
de variables no medibles y estados
[Verghesse 88] G.C.Verghese, S.R. Sanders. “Observers for flux estimation in induction
machines”. IEEE-IE, vol 35, 85-94.
[Atkinson 91] D.J.Atkinson,P.A.Acarnley,J.W.Finch.” Observers for induction motor state
and parameter estimation”. IEEE-IA, vol 27, 1119-1127, 1991
[Holtz 91] J.Holtz,T.Thimm.”Identification of the machine parameters in a vector controlled
induction motor drive”. IEEE-IA, vol 27, 1111-1118, 1991
[Wijesundera 92] D.S.Wijesundera,R.D.Jackson.”Observers for field oriented control of
induction motor drives”. IEE, vol 139, 381-386, 1992
[Chai 92] H.Chai,P.P.Acarnley.” Induction motor parameter estimation algorithm using
spectral analysis”. IEE, vol 139, 165-174, 1992
[Moreira 92] J.C.Moreira,T.A.Lipo.” Modeling of saturated AC machines including air gap
flux harmonic components”. IEEE-IA, vol 28,343-349, 1992
[Bottura 93] C.P.Bottura,J.L.Silvino,P. de Resende.” A flux observer for induction
machines based on a time variant discrete model” : IEEE-IA, vol 29, 349-354, 1993
[Klaes 93] N.R.Klaes.” Parameter identification of an induction machine with regard to
dependences on saturation”. IEEE-IA, vol 29, 1135-1140, 1993
[Du 93] T.Du,M.A.Brdys.” Implementation of extended Luenberger observers for jont state
and parameter estimation of PWM induction motor drive”. EPE-93, 439-444, 1993
[Katakoa 94] T.Kataoka,S.Toda,Y.Sato.” On line estimation of induction motor parameters
by extended Kalman filter”. EPE-93, 325-329, 1993
[Dell’Aquila 94] A.Dell'Aquila,V.Giliberti,F.S.Lovecchio,L.Salvatore.” Real time estimation
of induction motor parameters by LSE”. IEEE, 2127-2131, 1994
[Jacobina 94] C.B.Jacobina,A.M.N.Lima.” Parameter estimation models for induction
machines”. IEEE, 726-733, 1994
[Levi 94] E.Levi.” Applications of the current state space model in analysis of saturated
induction machines”. Electric power systems research, 31, 203-216, 1994
[Kubota 94] H.Kubota,K.Matsuse.” Speed sensorless field oriented control of induction
motor with rotor resistance adaptation”. IEEE-IA, vol 30, 1219-1224, 1994
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA MEJOR
IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
BIBLIOGRAFIA.
6
[Moon 94] S-I.Moon,A.Keyhani.” Estimation of induction machine parameters from
standstill time domain data”. IEEE-IA, vol 30, 1609-1615, 1994
[Bunte 95] A.Bunte,H.Grotstollen.” Off line parameter identification of an inverter fed
induction motor at standstill”. EPE-95, 3492-3496, 1995
[Borsting 95] H.Borsting,M.Knudsen,P.Vadstrup.” Standstill estimation of electrical
parameters in induction motor using an optimal input signal”. EPE-95, 1814-1819, 1995
[Sullivan 96] C.R.Sullivan,C.Kao,B.M.Acker,S.R.Sanders.” Control systems for induction
machines with magnetic saturation”. IEEE-IE, vol43, 142-151, 1996
[Nuscleler 96] R.Nuscheler.” Problems and failure sources with the parameter
identification of asynchronous machines and their dependence on the identification
method”. ICEM-96, 130-135, 1996
[Ferrah 96] A.Ferrah,K.J.Bradley,M.S.Woolfson,G.M.Asper.” Modern spectral methods
and induction motor design for real time speed estimation in sensorless vector drives”.
ICEM-96, 476-481, 1996
[Dolimar 96] Dolimar,G.Steuenberger,R.Belmans.” Determination of the induction motor
model parameters using finite elements”. ICEM-96, 153-158, 1996
[Demeter 96] E.Demeter,F.Hantilla,J.Tegopoulos.” Sensitivies calculation for electrical
machines”. ICEM-96, 101-106, 1996
[Jarray
96]
K.Jarray,M.Gossa,A.Chaari,M.Jemli,M.Boussak.”
Induction
machine
parameters and flux on line estimation using recursive least squares algorithm”. ICEM-96,
66.69, 1996
[Bargallo 96] R.Bargallo, J.Llaverias.” Induction machines modelling
saturation.Parameters estimation and validation”. ICEM-96, 29-33, 1996
with
[Jaddynsky 96] W.Jazdynsky.” Nonstationary models of induction motors and their
identification with the help of multicriterion optimisation”. ICEM-96, 40-45, 1996
[Bargallo 98] R.Bargallo, J.Llaverias, E. Martin. "Contribution to parameter validation of
the induction motor with saturation. Transient behavior and PWM supply”. ICEM-98, 1998
[Bargallo 99] R. Bargallo, J. Llaverias, E. Martin. “Determinación de parámetros en la
modelización de sistemas con saturación. Identificación en tiempo real”. 5as JHLIE, 1999
[Bargallo 00] R. Bargalló, J. Llaverías, E. Martin. “Transient torque determination in
controlled drives. Contribution to the development of an equipment for dynamic operation
test”. ICEM-2000, Helsinki, Agosto 2000
[Brule 00] S. Brule, A. Tounzi. “Comparison between FEM and the Park’s model to study
the control of an induction machine”. ICEM 2000, Helsinki, Agosto 2000
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA MEJOR
IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
BIBLIOGRAFIA.
7
Articulos sobre Control de Máquinas Asíncronas
[Tajima 93]H.Tajima,Y.Hori.” Speed sersorless field orientation control of the induction
machine”. IEEE-IA, vol 29, 175-180, 1993
[Frick 94] A.Frick,E.von Westerholt,B de Fornel.” Non linear control of induction motors via
inpùt output decoupling”. ETEP, vol 4, 261-268, 1994
[Peng 94] F-Z.Peng,T.Fukao.” Robust speed identification for speed sensorless vector
control of induction motors”. IEEE-IA, vol 30, 1234-1240, 1994
[Kim 94] Y-R.Kim,S-K.Sul,M-H.Park.” Speed sensorless vector control of induction motor
using extended Kalman filter”. IEEE-IA, vol 30, 1225-1233, 1994
[Ho 95] E.Ho,P.C.Sen.” High performance decoupling control techniques for various
rotating field machines”. IEEE-Ie, vol 42, 40-49, 1995
[Ide 96] K.Ide.” Simple adaptive speed control with exact linearization for CSI fed Ac
motors”. ICEM-96, 184-189, 1996.
[Kumin 96] L.Kumin,D.Dolimar,P.Cafuta,P.Grcar.” Comparison of the field oriented and
the input output linearizing control scheme for the induction motor”. ICEM-96, 141-146,
1996
Articulos històricos sobre modelización de máquinas y convertidores
[Krause 69] P.C.Krause, T.A. Lipo. “Analysis and simplified representation of a rectifierinverter induction motor drive”. IEEE-PAS-88, 588-596, 1969
[Lipo 69] T.A.Lipo, P.C.Krause. “Stability analysis of a rectifier-inverter induction motor
drive”.IEEE-PAS-88, 55-66, 1969
[Blaschke 72] F.Blaschke. “The principle of field orientation as applied to the new
TRANSVEKTOR closed loop control system for rotating field machines”. Siemens Review,
vol 34, 217-220, 1972
[Lipo 75] T.A.Lipo,E.P.Cornell. “State variable steady state analysis of a controlled current
induction motor drive”. IEEE-IA, vol 11, 704-712, 1975
[Cornell 77] E.P.Cornell, T.A.Lipo. “Modeling and design of controlled current induction
motor drive system”. IEEE-IA, vol 13, 321-330, 1977
[MacDonald 78] M.L.MacDonald, P.C.Sen.”Control loop study of induction motor drives
using DQ model”. IEEE-IAS-78 Anual meeting, 897-903, 1978
[Lipo 78] T.A.Lipo.”Analysis and control of torque pulsations in current fed induction motor
drives” IEEE-Power Elec. Spec. Conf., 89-96, 1978
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA MEJOR
IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
BIBLIOGRAFIA.
8
[Gabriel 80] R.Gabriel,W.Leonhard,C.Nordby.”Microprocessor control of the converter fed
induction motor” Process Automation, 35-41, 1980
[Pfaff 83] G.Pfaff, A.Wick.” Direct current control of AC drives with pulsed frequency
converters”. Process Automation, 83-88, 1983
[Slemon 83] G.R.Slemon.”Circuits models for polyphase induction machines”. Electric
Machines and Power Systems,8, 369-379, 1983
[Kerkman 85] R.L.Kerkman. “Steady-State and transient analyses of an induction machine
with saturation of the magnetizing branch”. IEEE, IA-21, 226-234, 1985
Proyectos Final de Carrera
[Sallent 94] Jordi Sallent i Salomó. “Modelat i simulació d’un conjunt convertidor+màquina
d’inducció. Aplicació a l’anàlisi de sensibilitat dinàmica de la màquina”. PFC. 1994.
[Garcia 97] Xavier Garcia i Barrachina. “Identificación en tiempo real de los parámetros
eléctricos y mecánics de máquinas de inducción mediante un DSP”. PFC. 1997
[Rovira 99] Jordi Rovira Carrera. “Modelització de Màquines Asíncrones”. PFC. 1999
[Conesa 99] David Conesa Lopez. ”Desarrollo de un sistema de medidas de magnitudes
electromecánicas. Sistema para la variación y el control de par desarrollado por una
máquina de corriente continua”. PFC. 1999.
[Escoda 99] Ignasi Escoda Escriva. “Desenvolupament d’un sistema de mesura i/o
observació de magnituts electromecàniques”. PFC. 1999
Normas
[IEEE112] “IEEE Standard Test Procedure for Poliphase Induction Motors and
Generators”. IEEE Std 112-1996. IEEE. New York. 1997
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA MEJOR
IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO I. EXPRESIONES PARA EL
CÁLCULO DE LA SENSIBILIDAD
γ irsxs
r
γ isys
∂x rs
= γ irx
∂p
γ irs
rrys
γ ω
r
γ irsxr
γ irsyr
γ iLsxrl
γ iLsyrl
γ iJsx
γ iJsy
γ iρsx
γ iρsy
γ iasx1
γ iasy1
γ irrxr
γ irryr
γ iLrxrl
γ iLryrl
γ iJrx
γ iJry
γ iρrx
γ iρry
γ iarx1
γ iary1
γ ωrrr
γ ωLrrl
γ ωJr
γ ωρr
γ ωa1r
γ iasx2
a2
γ isy
γ iarx2
γ iary2
a2
γ ωr
ANEXO I. CÁLCULO DE FUNCIONES DE SENSIBILIDAD
MODELO Nº 21
AI
Formulación general
x = (i sx
i sy
u = (u sx
u sy
p = (R s
Rr
Lrl
y = (Ψsx
i rx
ωr )
t
i ry
(1)
u rx
u ry
Mc )
(2)
ρ
a1
a2 )
(3)
J
t
t
Me)
Ψsy
t
(4)
definiendo las siguientes funciones de sensibilidad de las variables de estado:
γ irsxs
r
γ isys
∂x rs
= γi
∂p rrxs
γ i
rrys
γ ω
r
γ irsxr
γ irsyr
γ iLsxrl
γ iLsyrl
γ iJsx
γ iJsy
γ iρsx
γ iρsy
γ iasx1
γ iasy1
γ irrxr
γ irryr
γ iLrxrl
γ iLryrl
γ iJrx
γ iJry
γ iρrx
γ iρry
γ iarx1
γ iary1
γ ωrrr
γ ωLrlr
γ ωJ r
γ ωρr
γ ωa1r
γ iasx2
a2
γ isy
γ iarx2
γ iary2
γ ωa2r
(5)
y de la sensibilidad de las variables de salida
σ Ψrs
∂y rs sx
= σ Ψ
∂p rssy
σ M
e
σ Ψrr sx
σ Ψrr sy
σ ΨLrlsx
σ ΨLrlsy
σ ΨJ sx
σ ΨJ sy
σ
σ
σ
rr
Me
Lrl
Me
J
Me
σ Ψρ sx
σ Ψρ sy
σ
ρ
Me
σ Ψa1sx
σ Ψa1sy
σ
a1
Me
σ Ψa2sx
σ Ψa2sy
σ Ma2e
(6)
en las páginas que siguen se encuentran los cálculos desarrollados a partir de las
utilidades que ofrece el programa MAPLE RV.0 para la manipulación algebraica y su
posterior volcado en codigo FORTRAN 90 para su aplicación en los algorítmos
utilizados en la tesis.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
> with(linalg):
Warning, new definition for norm
Warning, new definition for trace
> imx:=isx+irx;imy:=isy+iry;fluxsx:=a1*arctan(a2*imx);fluxsy:=a1*a
rctan(a2*imy);
> Flux:=array(1..2,[fluxsx,fluxsy]);Lmx:=a1*a2/(1+(a2*imx)^2);Lmy:
=a1*a2/(1+(a2*imy)^2);
> M:=matrix(5,5,[[Lmx,0,Lmx,0,0],[0,Lmy,0,Lmy,0],[Lmx,0,Lrl+Lmx,0,
0],[0,Lmy,0,Lrl+Lmy,0],[0,0,0,0,J]]);
imx := isx + irx
imy := isy + iry
fluxsx := a1 arctan( a2 ( isx + irx ) )
fluxsy := a1 arctan( a2 ( isy + iry ) )
Flux := [ a1 arctan( a2 ( isx + irx ) ), a1 arctan( a2 ( isy + iry ) ) ]
Lmx :=
Lmy :=
a1 a2
1 + a22 ( isx + irx )2
a1 a2
1 + a22 ( isy + iry )2
a1 a2
a1 a2
0
,
,
, 0, 0
2
2
2
2
1 + a2 ( isx + irx )
1
+
a2
(
isx
+
irx
)
a1 a2
a1 a2
0
,
,
, 0
0 ,
2
2
2
2
1
+
a2
(
isy
+
iry
)
1
+
a2
(
isy
+
iry
)
M :=
a1 a2
a1 a2
,
0
,
Lrl
+
,0 ,0
1 + a22 ( isx + irx )2
1 + a22 ( isx + irx )2
a1 a2
a1 a2
0 ,
,
0
,
Lrl
+
,0
2
2
1 + a22 ( isy + iry )2
1
+
a2
(
isy
+
iry
)
0 ,
0,
0,
0,
J
>
> A:=matrix(5,5,[[-Rs,0,0,0,0],[0,-Rs,0,0,0],[0,0,-Rr,(w-wr)*Lrl,0
],[0,0,-(w-wr)*Lrl,-Rr,0],[-(3/2)*P*fluxsy,(3/2)*P*fluxsx,0,0,-r
ho]]);
−Rs ,
0,
0,
0,
0
0 ,
−Rs ,
0,
0,
0
0 ,
0,
−Rr ,
( w − wr ) Lrl ,
0
A :=
0,
0,
−( w − wr ) Lrl ,
−Rr ,
0
3
3
− P a1 arctan( a2 ( isy + iry ) ) , P a1 arctan( a2 ( isx + irx ) ) ,0 ,0 ,−ρ
2
2
> OM:=matrix(5,2,[[0,w],[-w,0],[0,w-wr],[-(w-wr),0],[0,0]]);
Page 1
0
w
−w
0
OM := 0
w − wr
−w + wr
0
0
0
> v:=vector([usx,usy,urx,ury,-Mc]);
v := [ usx, usy, urx, ury, −Mc ]
> x:=vector([isx,isy,irx,iry,wr]);
x := [ isx, isy, irx, iry, wr ]
> M1:=inverse(M);
Lrl + Lrl a22 isx2 + 2 Lrl a22 isx irx + Lrl a22 irx2 + a1 a2
1
0
−
0
0
,
,
,
,
Lrl a1 a2
Lrl
2
2
2
2
2
1
Lrl + Lrl a2 isy + 2 Lrl a2 isy iry + Lrl a2 iry + a1 a2
0 ,
,0 ,−
,0
Lrl a1 a2
Lrl
1
1
M1 := −
,
,
0,
0,
0
Lrl
Lrl
1
1
0 ,
0,
0
−
,
,
Lrl
Lrl
1
0 ,
0,
0,
0,
J
> parc1:=multiply(M1,v):parc2:=multiply(A,x):parc3:=multiply(OM,Fl
ux):parc4:=matadd(parc3,parc2):parc5:=multiply(M1,parc4):Final:=
matadd(parc1,parc5);
( Lrl + Lrl a22 isx2 + 2 Lrl a22 isx irx + Lrl a22 irx2 + a1 a2 ) usx urx
−
Final :=
Lrl a1 a2
Lrl
+
−
( Lrl + Lrl a22 isx2 + 2 Lrl a22 isx irx + Lrl a22 irx2 + a1 a2 ) ( w a1 %2 − Rs isx )
Lrl a1 a2
( w − wr ) a1 %2 − Rr irx + ( w − wr ) Lrl iry
Lrl
,
( Lrl + Lrl a22 isy2 + 2 Lrl a22 isy iry + Lrl a22 iry2 + a1 a2 ) usy
Lrl a1 a2
+
−
−
−
ury
Lrl
( Lrl + Lrl a22 isy2 + 2 Lrl a22 isy iry + Lrl a22 iry2 + a1 a2 ) ( −w a1 %1 − Rs isy )
Lrl a1 a2
( −w + wr ) a1 %1 − ( w − wr ) Lrl irx − Rr iry
Lrl
usx
Lrl
+
urx
Lrl
−
w a1 %2 − Rs isx
Lrl
+
,
( w − wr ) a1 %2 − Rr irx + ( w − wr ) Lrl iry
Lrl
Page 2
,
−
−
usy
Lrl
Mc
J
+
ury
Lrl
−
+
3
2
−
−w a1 %1 − Rs isy
Lrl
P a1 %2 isx +
+
( −w + wr ) a1 %1 − ( w − wr ) Lrl irx − Rr iry
Lrl
,
P a1 %1 isy − ρ wr
2
J
3
%1 := arctan( a2 ( isx + irx ) )
%2 := arctan( a2 ( isy + iry ) )
>
parc4 := w a1 arctan( a2 ( isy + iry ) ) − Rs isx, −w a1 arctan( a2 ( isx + irx ) ) − Rs isy,
( w − wr ) a1 arctan( a2 ( isy + iry ) ) − Rr irx + ( w − wr ) Lrl iry,
( −w + wr ) a1 arctan( a2 ( isx + irx ) ) − ( w − wr ) Lrl irx − Rr iry,
−
3
2
P Fluxsy isx +
P Fluxsx isy − ρ wr
2
3
>
( Lrl + Lrl a22 isx2 + 2 Lrl a22 isx irx + Lrl a22 irx2 + a1 a2 ) ( w a1 %2 − Rs isx )
parc5 :=
Lrl a1 a2
−
( w − wr ) a1 %2 − Rr irx + ( w − wr ) Lrl iry
Lrl
,
( Lrl + Lrl a22 isy2 + 2 Lrl a22 isy iry + Lrl a22 iry2 + a1 a2 ) ( −w a1 %1 − Rs isy )
Lrl a1 a2
−
−
−
−
( −w + wr ) a1 %1 − ( w − wr ) Lrl irx − Rr iry
Lrl
w a1 %2 − Rs isx
Lrl
+
−w a1 %1 − Rs isy
Lrl
3
2
P Fluxsy isx +
,
( w − wr ) a1 %2 − Rr irx + ( w − wr ) Lrl iry
Lrl
+
,
( −w + wr ) a1 %1 − ( w − wr ) Lrl irx − Rr iry
Lrl
,
P Fluxsx isy − ρ wr
2
J
3
%1 := arctan( a2 ( isx + irx ) )
%2 := arctan( a2 ( isy + iry ) )
>
( Lrl + Lrl a22 isx2 + 2 Lrl a22 isx irx + Lrl a22 irx2 + a1 a2 ) usx urx
Final :=
−
Lrl a1 a2
Lrl
Page 3
+
−
( Lrl + Lrl a22 isx2 + 2 Lrl a22 isx irx + Lrl a22 irx2 + a1 a2 ) ( w a1 %2 − Rs isx )
Lrl a1 a2
( w − wr ) a1 %2 − Rr irx + ( w − wr ) Lrl iry
Lrl
,
( Lrl + Lrl a22 isy2 + 2 Lrl a22 isy iry + Lrl a22 iry2 + a1 a2 ) usy
Lrl a1 a2
+
−
−
−
−
−
ury
Lrl
( Lrl + Lrl a22 isy2 + 2 Lrl a22 isy iry + Lrl a22 iry2 + a1 a2 ) ( −w a1 %1 − Rs isy )
Lrl a1 a2
( −w + wr ) a1 %1 − ( w − wr ) Lrl irx − Rr iry
Lrl
usx
Lrl
usy
Lrl
Mc
J
+
+
urx
Lrl
ury
Lrl
−
+
3
2
−
−
w a1 %2 − Rs isx
Lrl
+
−w a1 %1 − Rs isy
Lrl
P Fluxsy isx +
,
( w − wr ) a1 %2 − Rr irx + ( w − wr ) Lrl iry
Lrl
+
,
( −w + wr ) a1 %1 − ( w − wr ) Lrl irx − Rr iry
Lrl
P Fluxsx isy − ρ wr
2
J
3
%1 := arctan( a2 ( isx + irx ) )
%2 := arctan( a2 ( isy + iry ) )
> param:=vector([Rs,Rr,Lrl,J,rho,a1,a2]);
param := [ Rs, Rr, Lrl, J, ρ, a1, a2 ]
> Pare:=(3/2)*P*(fluxsx*isy-fluxsy*isx);
3
Pare := P ( a1 arctan( a2 ( isx + irx ) ) isy − a1 arctan( a2 ( isy + iry ) ) isx )
2
> salidas:=vector([fluxsx,fluxsy,Pare]);
salidas := a1 arctan( a2 ( isx + irx ) ), a1 arctan( a2 ( isy + iry ) ),
P ( a1 arctan( a2 ( isx + irx ) ) isy − a1 arctan( a2 ( isy + iry ) ) isx )
2
> dfx:=jacobian(Final,x);
3
dfx :=
%3 usx
%3 ( w a1 %2 − Rs isx )
%1 Rs
+
−
,
Lrl a1 a2
Lrl a1 a2
Lrl a1 a2
%1 w
Lrl ( 1 + a2 ( isy + iry ) )
2
2
−
( w − wr ) a1 a2
Lrl ( 1 + a22 ( isy + iry )2 )
Page 4
,
,
%3 usx
Lrl a1 a2
+
%3 ( w a1 %2 − Rs isx )
Lrl a1 a2
+
Rr
Lrl
,
( w − wr ) a1 a2
1 + a2 ( isy + iry )
2
%1 w
Lrl ( 1 + a22 ( isy + iry )2 )
−
2
+ ( w − wr ) Lrl
Lrl
−a1 %2 − Lrl iry
,−
Lrl
%4 w
( −w + wr ) a1 a2
−
,
−
Lrl ( 1 + a22 ( isx + irx )2 ) Lrl ( 1 + a22 ( isx + irx )2 )
%6 usy
Lrl a1 a2
+
%6 ( −w a1 %5 − Rs isy )
Lrl a1 a2
−
%4 Rs
Lrl a1 a2
( −w + wr ) a1 a2
−
%4 w
Lrl ( 1 + a22 ( isx + irx )2 )
−
1 + a22 ( isx + irx )2
,
− ( w − wr ) Lrl
,
Lrl
%6 usy
%6 ( −w a1 %5 − Rs isy ) Rr
a1 %5 + Lrl irx
,−
+
+
Lrl a1 a2
Lrl a1 a2
Lrl
Lrl
Rs
w a1 a2
( w − wr ) a1 a2
Rr
,−
,
,
+
−
Lrl
Lrl
Lrl ( 1 + a22 ( isy + iry )2 ) Lrl ( 1 + a22 ( isy + iry )2 )
( w − wr ) a1 a2
−
w a1 a2
Lrl ( 1 + a22 ( isy + iry )2 )
+
1 + a22 ( isy + iry )2
+ ( w − wr ) Lrl
Lrl
−a1 %2 − Lrl iry
,
Lrl
w a1 a2
( −w + wr ) a1 a2
Rs
+
,
,
Lrl ( 1 + a22 ( isx + irx )2 ) Lrl ( 1 + a22 ( isx + irx )2 ) Lrl
( −w + wr ) a1 a2
w a1 a2
Lrl ( 1 + a22 ( isx + irx )2 )
+
1 + a22 ( isx + irx )2
− ( w − wr ) Lrl
Lrl
Rr a1 %5 + Lrl irx
,−
,
Lrl
Lrl
3
P a1 a2 isy
3
P a1 a2 isx
3
3
− P a1 %2 +
−
+ P a1 %5
2
2
2
2
2
2 1 + a2 ( isx + irx )
2 1 + a2 ( isy + iry )
2
,
,
J
J
3
P a1 a2 isy
3
P a1 a2 isx
ρ
,−
, −
2 J ( 1 + a22 ( isx + irx )2 )
2 J ( 1 + a22 ( isy + iry )2 )
J
%1 := Lrl + Lrl a22 isx2 + 2 Lrl a22 isx irx + Lrl a22 irx2 + a1 a2
Page 5
%2 := arctan( a2 ( isy + iry ) )
%3 := 2 Lrl a22 isx + 2 Lrl a22 irx
%4 := Lrl + Lrl a22 isy2 + 2 Lrl a22 isy iry + Lrl a22 iry2 + a1 a2
%5 := arctan( a2 ( isx + irx ) )
%6 := 2 Lrl a22 isy + 2 Lrl a22 iry
> dfparam:=jacobian(Final,param);
dfparam :=
%1 isx
irx
%1 usx
( 1 + a22 isx2 + 2 a22 isx irx + a22 irx2 ) usx urx
−
,
,−
+
+
Lrl a1 a2
Lrl a1 a2 Lrl
Lrl2 a1 a2
Lrl2
−
+
−
+
+
+
%1 ( w a1 %2 − Rs isx )
Lrl2 a1 a2
+
( 1 + a22 isx2 + 2 a22 isx irx + a22 irx2 ) ( w a1 %2 − Rs isx )
Lrl a1 a2
( w − wr ) a1 %2 − Rr irx + ( w − wr ) Lrl iry
Lrl2
%1 ( w a1 %2 − Rs isx )
Lrl a12 a2
+
w a1 %2 − Rs isx
Lrl a1
( w − wr ) iry
−
Lrl
+
%1 w %2
Lrl a1 a2
( 2 Lrl a2 isx2 + 4 Lrl a2 isx irx + 2 Lrl a2 irx2 + a1 ) usx
Lrl a1 a2
%1 usx
Lrl a12 a2
( w − wr ) %2
−
−
,0,0,−
Lrl
,−
usx
+
Lrl a1
%1 usx
Lrl a1 a22
%1 ( w a1 %2 − Rs isx )
Lrl a1 a22
( 2 Lrl a2 isx2 + 4 Lrl a2 isx irx + 2 Lrl a2 irx2 + a1 ) ( w a1 %2 − Rs isx )
Lrl a1 a2
%1 w ( isy + iry )
Lrl a2 ( 1 + a22 ( isy + iry )2 )
−
( w − wr ) a1 ( isy + iry )
Lrl ( 1 + a22 ( isy + iry )2 )
%3 isy
iry
%3 usy
( 1 + a22 isy2 + 2 a22 isy iry + a22 iry2 ) usy ury
−
,
,−
+
+
Lrl a1 a2
Lrl a1 a2 Lrl
Lrl2 a1 a2
Lrl2
−
+
−
+
+
−
%3 ( −w a1 %4 − Rs isy )
Lrl2 a1 a2
+
( 1 + a22 isy2 + 2 a22 isy iry + a22 iry2 ) ( −w a1 %4 − Rs isy )
Lrl a1 a2
( −w + wr ) a1 %4 − ( w − wr ) Lrl irx − Rr iry
Lrl2
%3 ( −w a1 %4 − Rs isy )
Lrl a12 a2
+
−w a1 %4 − Rs isy
Lrl a1
( w − wr ) irx
+
Lrl
−
%3 w %4
Lrl a1 a2
( 2 Lrl a2 isy2 + 4 Lrl a2 isy iry + 2 Lrl a2 iry2 + a1 ) usy
Lrl a1 a2
−
−
,0,0,−
%3 usy
Lrl a12 a2
( −w + wr ) %4
Lrl
Lrl a1 a22
%3 w ( isx + irx )
Lrl a2 ( 1 + a22 ( isx + irx )2 )
−
( −w + wr ) a1 ( isx + irx )
2
2
Lrl ( 1 + a2 ( isx + irx ) )
Page 6
usy
Lrl a1
%3 usy
Lrl a1 a22
%3 ( −w a1 %4 − Rs isy )
( 2 Lrl a2 isy2 + 4 Lrl a2 isy iry + 2 Lrl a2 iry2 + a1 ) ( −w a1 %4 − Rs isy )
Lrl a1 a2
,−
+
isx
irx
,−
,
Lrl
Lrl
usx
Lrl2
−
urx
Lrl2
,0,0,−
+
w a1 %2 − Rs isx
Lrl2
w %2
Lrl
+
( w − wr ) %2
Lrl
−
( w − wr ) a1 %2 − Rr irx + ( w − wr ) Lrl iry
,−
Lrl2
w a1 ( isy + iry )
Lrl ( 1 + a22 ( isy + iry )2 )
+
+
( w − wr ) iry
Lrl
( w − wr ) a1 ( isy + iry )
Lrl ( 1 + a22 ( isy + iry )2 )
isy
iry usy
ury −w a1 %4 − Rs isy
,−
,
−
+
Lrl Lrl2 Lrl2
Lrl
Lrl2
( −w + wr ) a1 %4 − ( w − wr ) Lrl irx − Rr iry
−
Lrl2
w %4
Lrl
+
( −w + wr ) %4
Lrl
,
−
( w − wr ) irx
w a1 ( isx + irx )
Lrl ( 1 + a22 ( isx + irx )2 )
Lrl
+
,0,0,
( −w + wr ) a1 ( isx + irx )
Lrl ( 1 + a22 ( isx + irx )2 )
3
3
3
3
−
P
a1
%2
isx
+
P
a1
%4
isy
−
ρ
wr
−
P
%2
isx
+
P %4 isy
Mc
2
2
wr
2
2
,−
,
,
0 , 0 , 0 , 2 −
J
J
J2
J
3 P a1 ( isy + iry ) isx
3 P a1 ( isx + irx ) isy
2 1 + a22 ( isy + iry )2 2 1 + a22 ( isx + irx )2
J
−
+
%1 := Lrl + Lrl a22 isx2 + 2 Lrl a22 isx irx + Lrl a22 irx2 + a1 a2
%2 := arctan( a2 ( isy + iry ) )
%3 := Lrl + Lrl a22 isy2 + 2 Lrl a22 isy iry + Lrl a22 iry2 + a1 a2
%4 := arctan( a2 ( isx + irx ) )
> dgx:=jacobian(salidas,x);
dgx :=
a1 a2
a1 a2
,0,
, 0 , 0
2
2
2
2
1 + a2 ( isx + irx )
1 + a2 ( isx + irx )
a1 a2
a1 a2
0 ,
,0,
, 0
2
2
2
2
1 + a2 ( isy + iry )
1 + a2 ( isy + iry )
3
a1 a2 isy
P
− a1 arctan( a2 ( isy + iry ) ) ,
2
2
2 1 + a2 ( isx + irx )
a1 a2 isx
3
P a1 a2 isy
,
P a1 arctan( a2 ( isx + irx ) ) −
,
2
2
2
1 + a2 ( isy + iry ) 2 1 + a22 ( isx + irx )2
3
,
0
2 1 + a22 ( isy + iry )2
> dgparam:=jacobian(salidas,param);
−
3
P a1 a2 isx
dgparam :=
Page 7
a1 ( isx + irx )
0 , 0 , 0 , 0 , 0 , arctan( a2 ( isx + irx ) ) ,
1 + a22 ( isx + irx )2
a1 ( isy + iry )
0 , 0 , 0 , 0 , 0 , arctan( a2 ( isy + iry ) ) ,
1 + a22 ( isy + iry )2
3
0 , 0 , 0 , 0 , 0 , P ( arctan( a2 ( isx + irx ) ) isy − arctan( a2 ( isy + iry ) ) isx ) ,
2
a1 ( isx + irx ) isy
a1 ( isy + iry ) isx
P
−
2 1 + a22 ( isx + irx )2 1 + a22 ( isy + iry )2
> gamm:=matrix(5,7,[[gamma11,gamma12,gamma13,gamma14,gamma15,gamma
16,gamma17],[gamma21,gamma22,gamma23,gamma24,gamma25,gamma26,gam
ma27],[gamma31,gamma32,gamma33,gamma34,gamma35,gamma36,gamma37],
[gamma41,gamma42,gamma43,gamma44,gamma45,gamma46,gamma47],[gamma
51,gamma52,gamma53,gamma54,gamma55,gamma56,gamma57]]);
3
γ11
γ21
gamm := γ31
γ41
γ51
> p1:=multiply(dfx,gamm);
γ12
γ22
γ32
γ42
γ52
γ13
γ23
γ33
γ43
γ53
γ14
γ24
γ34
γ44
γ54
γ15
γ25
γ35
γ45
γ55
γ16
γ26
γ36
γ46
γ56
γ17
γ27
γ37
γ47
γ57
p1 :=
( −a1 %1 − Lrl iry ) γ51
%9 γ11 + ( %4 − %8 ) γ21 + %7 γ31 + ( %4 − %2 ) γ41 −
,
Lrl
%9 γ12 + ( %4 − %8 ) γ22 + %7 γ32 + ( %4 − %2 ) γ42 −
%9 γ13 + ( %4 − %8 ) γ23 + %7 γ33 + ( %4 − %2 ) γ43 −
%9 γ14 + ( %4 − %8 ) γ24 + %7 γ34 + ( %4 − %2 ) γ44 −
%9 γ15 + ( %4 − %8 ) γ25 + %7 γ35 + ( %4 − %2 ) γ45 −
%9 γ16 + ( %4 − %8 ) γ26 + %7 γ36 + ( %4 − %2 ) γ46 −
%9 γ17 + ( %4 − %8 ) γ27 + %7 γ37 + ( %4 − %2 ) γ47 −
( −a1 %1 − Lrl iry ) γ52
Lrl
( −a1 %1 − Lrl iry ) γ53
Lrl
( −a1 %1 − Lrl iry ) γ54
Lrl
( −a1 %1 − Lrl iry ) γ55
Lrl
( −a1 %1 − Lrl iry ) γ56
Lrl
,
,
,
,
,
( −a1 %1 − Lrl iry ) γ57
Lrl
( a1 %10 + Lrl irx ) γ51
( −%16 − %18 ) γ11 + %17 γ21 + ( −%16 − %14 ) γ31 + %13 γ41 −
,
Lrl
( −%16 − %18 ) γ12 + %17 γ22 + ( −%16 − %14 ) γ32 + %13 γ42 −
Page 8
( a1 %10 + Lrl irx ) γ52
Lrl
,
( −%16 − %18 ) γ13 + %17 γ23 + ( −%16 − %14 ) γ33 + %13 γ43 −
( −%16 − %18 ) γ14 + %17 γ24 + ( −%16 − %14 ) γ34 + %13 γ44 −
( −%16 − %18 ) γ15 + %17 γ25 + ( −%16 − %14 ) γ35 + %13 γ45 −
( −%16 − %18 ) γ16 + %17 γ26 + ( −%16 − %14 ) γ36 + %13 γ46 −
( −%16 − %18 ) γ17 + %17 γ27 + ( −%16 − %14 ) γ37 + %13 γ47 −
( a1 %10 + Lrl irx ) γ53
Lrl
( a1 %10 + Lrl irx ) γ54
Lrl
( a1 %10 + Lrl irx ) γ55
Lrl
( a1 %10 + Lrl irx ) γ56
Lrl
Lrl
Rs γ13
Lrl
Rs γ14
Lrl
Rs γ15
Lrl
Rs γ16
Lrl
Rs γ17
Lrl
+ ( −%19 + %8 ) γ22 −
+ ( −%19 + %8 ) γ23 −
+ ( −%19 + %8 ) γ24 −
+ ( −%19 + %8 ) γ25 −
+ ( −%19 + %8 ) γ26 −
+ ( −%19 + %8 ) γ27 −
Rr γ32
Lrl
Rr γ33
Lrl
Rr γ34
Lrl
Rr γ35
Lrl
Rr γ36
Lrl
Rr γ37
Lrl
+ ( −%19 + %2 ) γ42 +
+ ( −%19 + %2 ) γ43 +
+ ( −%19 + %2 ) γ44 +
+ ( −%19 + %2 ) γ45 +
+ ( −%19 + %2 ) γ46 +
+ ( −%19 + %2 ) γ47 +
( −a1 %1 − Lrl iry ) γ52
Lrl
( −a1 %1 − Lrl iry ) γ53
Lrl
( −a1 %1 − Lrl iry ) γ54
Lrl
( −a1 %1 − Lrl iry ) γ55
Lrl
( −a1 %1 − Lrl iry ) γ56
Lrl
,
,
,
,
,
( −a1 %1 − Lrl iry ) γ57
Lrl
Rs γ21
Rr γ41 ( a1 %10 + Lrl irx ) γ51
( %20 + %18 ) γ11 +
,
+ ( %20 + %14 ) γ31 −
+
Lrl
Lrl
Lrl
( %20 + %18 ) γ12 +
( %20 + %18 ) γ13 +
( %20 + %18 ) γ14 +
( %20 + %18 ) γ15 +
( %20 + %18 ) γ16 +
Rs γ22
Lrl
Rs γ23
Lrl
Rs γ24
Lrl
Rs γ25
Lrl
Rs γ26
Lrl
+ ( %20 + %14 ) γ32 −
+ ( %20 + %14 ) γ33 −
+ ( %20 + %14 ) γ34 −
+ ( %20 + %14 ) γ35 −
+ ( %20 + %14 ) γ36 −
Page 9
Rr γ42
Lrl
Rr γ43
Lrl
Rr γ44
Lrl
Rr γ45
Lrl
Rr γ46
Lrl
+
+
+
+
+
,
,
,
( a1 %10 + Lrl irx ) γ57
Lrl
Rs γ11
Rr γ31
( −a1 %1 − Lrl iry ) γ51
+ ( −%19 + %8 ) γ21 −
+ ( −%19 + %2 ) γ41 +
,
Lrl
Lrl
Lrl
Rs γ12
,
( a1 %10 + Lrl irx ) γ52
Lrl
( a1 %10 + Lrl irx ) γ53
Lrl
( a1 %10 + Lrl irx ) γ54
Lrl
( a1 %10 + Lrl irx ) γ55
Lrl
( a1 %10 + Lrl irx ) γ56
Lrl
,
,
,
,
,
( %20 + %18 ) γ17 +
Rs γ27
Lrl
+ ( %20 + %14 ) γ37 −
Rr γ47
Lrl
+
( a1 %10 + Lrl irx ) γ57
Lrl
%22 γ11 %21 γ21 3
P a1 a2 isy γ31
3
P a1 a2 isx γ41
ρ γ51
,
+
+
−
−
2
2
2
2
J
J
2 J ( 1 + a2 ( isx + irx ) ) 2 J ( 1 + a2 ( isy + iry ) )
J
%22 γ12
J
%22 γ13
J
%22 γ14
J
%22 γ15
J
%22 γ16
J
%22 γ17
J
+
+
+
+
+
+
%21 γ22
J
%21 γ23
J
%21 γ24
J
%21 γ25
J
%21 γ26
J
%21 γ27
J
+
+
+
+
+
+
P a1 a2 isy γ32
3
2 J ( 1 + a2 ( isx + irx ) )
2
2
P a1 a2 isy γ33
3
2 J ( 1 + a2 ( isx + irx ) )
2
2
P a1 a2 isy γ34
3
2 J ( 1 + a22 ( isx + irx )2 )
P a1 a2 isy γ35
3
2 J ( 1 + a22 ( isx + irx )2 )
P a1 a2 isy γ36
3
2 J ( 1 + a22 ( isx + irx )2 )
P a1 a2 isy γ37
3
2 J ( 1 + a22 ( isx + irx )2 )
−
−
−
−
−
−
3
P a1 a2 isx γ42
2 J ( 1 + a2 ( isy + iry ) )
2
3
P a1 a2 isx γ43
2 J ( 1 + a2 ( isy + iry ) )
2
3
2 J ( 1 + a22 ( isy + iry )2 )
3
P a1 a2 isx γ45
2 J ( 1 + a22 ( isy + iry )2 )
3
P a1 a2 isx γ46
2 J ( 1 + a22 ( isy + iry )2 )
3
P a1 a2 isx γ47
2 J ( 1 + a22 ( isy + iry )2 )
%2 :=
+ ( w − wr ) Lrl
1 + a22 ( isy + iry )2
Lrl
%3 := Lrl + Lrl a22 isx2 + 2 Lrl a22 isx irx + Lrl a22 irx2 + a1 a2
%4 :=
%3 w
Lrl ( 1 + a22 ( isy + iry )2 )
%5 := 2 Lrl a22 isx + 2 Lrl a22 irx
%6 :=
%7 :=
%8 :=
%9 :=
%5 ( w a1 %1 − Rs isx )
Lrl a1 a2
%5 usx
Lrl a1 a2
+ %6 +
Rr
Lrl
( w − wr ) a1 a2
Lrl ( 1 + a22 ( isy + iry )2 )
%5 usx
Lrl a1 a2
+ %6 −
%3 Rs
Lrl a1 a2
%10 := arctan( a2 ( isx + irx ) )
%11 := 2 Lrl a22 isy + 2 Lrl a22 iry
%12 :=
%11 ( −w a1 %10 − Rs isy )
Lrl a1 a2
Page 10
2
P a1 a2 isx γ44
%1 := arctan( a2 ( isy + iry ) )
( w − wr ) a1 a2
2
−
−
−
−
−
−
ρ γ52
J
ρ γ53
J
ρ γ54
J
ρ γ55
J
ρ γ56
J
,
,
,
,
,
ρ γ57
J
%13 :=
%11 usy
Lrl a1 a2
Rr
+ %12 +
Lrl
( −w + wr ) a1 a2
%14 :=
1 + a22 ( isx + irx )2
− ( w − wr ) Lrl
Lrl
%15 := Lrl + Lrl a2 isy + 2 Lrl a22 isy iry + Lrl a22 iry2 + a1 a2
2
%16 :=
%17 :=
%18 :=
%19 :=
%20 :=
2
%15 w
Lrl ( 1 + a22 ( isx + irx )2 )
%11 usy
Lrl a1 a2
+ %12 −
%15 Rs
Lrl a1 a2
( −w + wr ) a1 a2
Lrl ( 1 + a22 ( isx + irx )2 )
w a1 a2
Lrl ( 1 + a22 ( isy + iry )2 )
w a1 a2
Lrl ( 1 + a22 ( isx + irx )2 )
%21 := −
%22 := −
3
P a1 a2 isx
2 1 + a22 ( isy + iry )2
3
P a1 %1 +
3
+
3
2
P a1 %10
P a1 a2 isy
2
2 1 + a22 ( isx + irx )2
> dsens:=matadd(p1,dfparam);
dsens :=
( −a1 %2 − Lrl iry ) γ51
%1 isx
%9 γ11 + ( %4 − %8 ) γ21 + %7 γ31 + ( %4 − %3 ) γ41 −
−
Lrl
Lrl a1 a2
, %9 γ12 + ( %4 − %8 ) γ22 + %7 γ32 + ( %4 − %3 ) γ42 −
%9 γ13 + ( %4 − %8 ) γ23 + %7 γ33 + ( %4 − %3 ) γ43 −
+
+
+
( 1 + a22 isx2 + 2 a22 isx irx + a22 irx2 ) usx
Lrl a1 a2
+
urx
Lrl2
−
( −a1 %2 − Lrl iry ) γ52
Lrl
( −a1 %2 − Lrl iry ) γ53
Lrl
−
%1 ( w a1 %2 − Rs isx )
Lrl2 a1 a2
( 1 + a22 isx2 + 2 a22 isx irx + a22 irx2 ) ( w a1 %2 − Rs isx )
Lrl a1 a2
( w − wr ) a1 %2 − Rr irx + ( w − wr ) Lrl iry
Lrl
2
−
( w − wr ) iry
Lrl
%9 γ14 + ( %4 − %8 ) γ24 + %7 γ34 + ( %4 − %3 ) γ44 −
Page 11
,
( −a1 %2 − Lrl iry ) γ54
Lrl
+
,
irx
Lrl
,
%1 usx
Lrl2 a1 a2
%9 γ15 + ( %4 − %8 ) γ25 + %7 γ35 + ( %4 − %3 ) γ45 −
usx
−
Lrl a1
%1 ( w a1 %2 − Rs isx )
2
Lrl a1 a2
+
Lrl
w a1 %2 − Rs isx
Lrl a1
+
+
+
%1 w %2
Lrl a1 a2
−
Lrl
( 2 Lrl a2 isx2 + 4 Lrl a2 isx irx + 2 Lrl a2 irx2 + a1 ) usx
Lrl a1 a2
−
−
, %9 γ16
%1 usx
Lrl a12 a2
( w − wr ) %2
( −a1 %2 − Lrl iry ) γ57
+ ( %4 − %8 ) γ27 + %7 γ37 + ( %4 − %3 ) γ47 −
+
Lrl
( −a1 %2 − Lrl iry ) γ56
+ ( %4 − %8 ) γ26 + %7 γ36 + ( %4 − %3 ) γ46 −
+
( −a1 %2 − Lrl iry ) γ55
Lrl
−
, %9 γ17
%1 usx
Lrl a1 a22
%1 ( w a1 %2 − Rs isx )
Lrl a1 a22
( 2 Lrl a2 isx2 + 4 Lrl a2 isx irx + 2 Lrl a2 irx2 + a1 ) ( w a1 %2 − Rs isx )
Lrl a1 a2
%1 w ( isy + iry )
Lrl a2 ( 1 + a22 ( isy + iry )2 )
−
( w − wr ) a1 ( isy + iry )
Lrl ( 1 + a22 ( isy + iry )2 )
( a1 %11 + Lrl irx ) γ51
( −%16 − %18 ) γ11 + %17 γ21 + ( −%16 − %15 ) γ31 + %14 γ41 −
Lrl
−
−
%10 isy
, ( −%16 − %18 ) γ12 + %17 γ22 + ( −%16 − %15 ) γ32 + %14 γ42
Lrl a1 a2
( a1 %11 + Lrl irx ) γ52
Lrl
+ %14 γ43 −
+
+
+
+
iry
Lrl
, ( −%16 − %18 ) γ13 + %17 γ23 + ( −%16 − %15 ) γ33
( a1 %11 + Lrl irx ) γ53
Lrl
−
%10 usy
Lrl2 a1 a2
( 1 + a22 isy2 + 2 a22 isy iry + a22 iry2 ) usy
Lrl a1 a2
+
ury
Lrl2
−
%10 ( −w a1 %11 − Rs isy )
Lrl2 a1 a2
( 1 + a22 isy2 + 2 a22 isy iry + a22 iry2 ) ( −w a1 %11 − Rs isy )
Lrl a1 a2
( −w + wr ) a1 %11 − ( w − wr ) Lrl irx − Rr iry
Lrl2
+
( w − wr ) irx
Lrl
,
( −%16 − %18 ) γ14 + %17 γ24 + ( −%16 − %15 ) γ34 + %14 γ44 −
( −%16 − %18 ) γ15 + %17 γ25 + ( −%16 − %15 ) γ35 + %14 γ45 −
( −%16 − %18 ) γ16 + %17 γ26 + ( −%16 − %15 ) γ36 + %14 γ46 −
−
%10 usy
2
Lrl a1 a2
+
usy
Lrl a1
−
%10 ( −w a1 %11 − Rs isy )
2
Lrl a1 a2
Page 12
+
( a1 %11 + Lrl irx ) γ54
Lrl
( a1 %11 + Lrl irx ) γ55
Lrl
,
,
( a1 %11 + Lrl irx ) γ56
−w a1 %11 − Rs isy
Lrl a1
Lrl
−
%10 w %11
Lrl a1 a2
−
−
+
+
−
( −w + wr ) %11
Lrl
, ( −%16 − %18 ) γ17 + %17 γ27 + ( −%16 − %15 ) γ37 + %14 γ47
( a1 %11 + Lrl irx ) γ57
Lrl
−
%10 usy
Lrl a1 a22
( 2 Lrl a2 isy2 + 4 Lrl a2 isy iry + 2 Lrl a2 iry2 + a1 ) usy
Lrl a1 a2
−
%10 ( −w a1 %11 − Rs isy )
Lrl a1 a22
( 2 Lrl a2 isy2 + 4 Lrl a2 isy iry + 2 Lrl a2 iry2 + a1 ) ( −w a1 %11 − Rs isy )
Lrl a1 a2
%10 w ( isx + irx )
Lrl a2 ( 1 + a22 ( isx + irx )2 )
−
( −w + wr ) a1 ( isx + irx )
2
2
Lrl ( 1 + a2 ( isx + irx ) )
Rs γ11
Rr γ31
( −a1 %2 − Lrl iry ) γ51 isx
+ ( −%19 + %8 ) γ21 −
+ ( −%19 + %3 ) γ41 +
+
,
Lrl
Lrl
Lrl
Lrl
Rs γ12
Lrl
Rs γ13
Lrl
−
urx
Lrl2
Rs γ14
Lrl
Rs γ15
Lrl
+ ( −%19 + %8 ) γ22 −
+ ( −%19 + %8 ) γ23 −
+
w a1 %2 − Rs isx
Lrl2
+ ( −%19 + %8 ) γ24 −
+ ( −%19 + %8 ) γ25 −
+ ( −%19 + %8 ) γ26 −
+
+
−
Rr γ36
Lrl
Rr γ32
Lrl
Rr γ33
Lrl
+ ( −%19 + %3 ) γ42 +
+ ( −%19 + %3 ) γ43 +
( −a1 %2 − Lrl iry ) γ52
Lrl
( −a1 %2 − Lrl iry ) γ53
Lrl
( w − wr ) a1 %2 − Rr irx + ( w − wr ) Lrl iry
Lrl2
Rr γ34
Lrl
Rr γ35
Lrl
+ ( −%19 + %3 ) γ44 +
+ ( −%19 + %3 ) γ45 +
+
+
irx
usx
Lrl2
Lrl
( −a1 %2 − Lrl iry ) γ54
Lrl
,
Lrl
( w − wr ) iry
,
,
( −a1 %2 − Lrl iry ) γ55 Rs γ16
,
Lrl
Lrl
( −a1 %2 − Lrl iry ) γ56
+ ( −%19 + %3 ) γ46 +
−
Lrl
−
w %2
Lrl
( w − wr ) %2 Rs γ17
Rr γ37
,
+ ( −%19 + %8 ) γ27 −
+ ( −%19 + %3 ) γ47
Lrl
Lrl
Lrl
( −a1 %2 − Lrl iry ) γ57
Lrl
−
w a1 ( isy + iry )
Lrl ( 1 + a22 ( isy + iry )2 )
+
( w − wr ) a1 ( isy + iry )
Lrl ( 1 + a22 ( isy + iry )2 )
Rs γ21
Rr γ41 ( a1 %11 + Lrl irx ) γ51 isy
( %20 + %18 ) γ11 +
+ ( %20 + %15 ) γ31 −
+
+
,
Lrl
Lrl
Lrl
Lrl
( %20 + %18 ) γ12 +
( %20 + %18 ) γ13 +
−
ury
Lrl2
+
Rs γ22
Lrl
Rs γ23
Lrl
+ ( %20 + %15 ) γ32 −
+ ( %20 + %15 ) γ33 −
−w a1 %11 − Rs isy
Lrl2
−
Rr γ42
Lrl
Rr γ43
Lrl
+
+
( a1 %11 + Lrl irx ) γ52
Lrl
( a1 %11 + Lrl irx ) γ53
Lrl
( −w + wr ) a1 %11 − ( w − wr ) Lrl irx − Rr iry
Lrl2
Page 13
−
+
iry
Lrl
usy
Lrl2
,
−
( w − wr ) irx
Lrl
,
( %20 + %18 ) γ14 +
( %20 + %18 ) γ15 +
( %20 + %18 ) γ16 +
+
+
w %11
Lrl
+
Rs γ24
Lrl
Rs γ25
Lrl
Rs γ26
Lrl
+ ( %20 + %15 ) γ34 −
+ ( %20 + %15 ) γ35 −
+ ( %20 + %15 ) γ36 −
( −w + wr ) %11
Lrl
( a1 %11 + Lrl irx ) γ57
Lrl
+
, ( %20 + %18 ) γ17 +
Rr γ44
Lrl
Rr γ45
Lrl
Rr γ46
Lrl
Rs γ27
Lrl
w a1 ( isx + irx )
Lrl ( 1 + a22 ( isx + irx )2 )
+
+
+
+
( a1 %11 + Lrl irx ) γ54
Lrl
( a1 %11 + Lrl irx ) γ55
Lrl
,
,
( a1 %11 + Lrl irx ) γ56
Lrl
+ ( %20 + %15 ) γ37 −
Rr γ47
Lrl
( −w + wr ) a1 ( isx + irx )
Lrl ( 1 + a22 ( isx + irx )2 )
%22 γ11 %21 γ21 3
P a1 a2 isy γ31
3
P a1 a2 isx γ41
ρ γ51
+
+
−
−
,
J
J
2 J ( 1 + a22 ( isx + irx )2 ) 2 J ( 1 + a22 ( isy + iry )2 )
J
%22 γ12
J
%22 γ13
J
%22 γ14
J
−
−
3
2
+
+
%21 γ22
J
%21 γ23
J
%21 γ24
J
P a1 %2 isx +
+
3
2 J ( 1 + a22 ( isx + irx )2 )
+
3
+
3
3
2
P a1 a2 isy γ32
P a1 a2 isy γ33
2 J ( 1 + a22 ( isx + irx )2 )
P a1 a2 isy γ34
2 J ( 1 + a22 ( isx + irx )2 )
J
%22 γ16
J
−
+
3
2
+
+
%21 γ25
J
%21 γ26
J
P %2 isx +
3
2
P a1 a2 isx γ42
3
2 J ( 1 + a22 ( isy + iry )2 )
−
3
−
3
P a1 a2 isx γ43
2 J ( 1 + a22 ( isy + iry )2 )
P a1 a2 isx γ44
2 J ( 1 + a22 ( isy + iry )2 )
−
−
−
ρ γ52
J
ρ γ53
J
ρ γ54
J
,
,
+
Mc
J2
,
+
+
3
P a1 a2 isy γ35
2 J ( 1 + a22 ( isx + irx )2 )
3
P a1 a2 isy γ36
2 J ( 1 + a22 ( isx + irx )2 )
P %11 isy
,
J
3
−
P a1 %11 isy − ρ wr
J2
%22 γ15
−
+
P a1 a2 isx γ47
2 J ( 1 + a22 ( isy + iry )2 )
−
%22 γ17
J
ρ γ57
J
−
+
+
−
−
2 J ( 1 + a22 ( isy + iry )2 )
P a1 a2 isx γ46
3
2 J ( 1 + a22 ( isy + iry )2 )
%21 γ27
J
P a1 a2 isx γ45
3
+
3
−
−
ρ γ55
J
−
ρ γ56
J
P a1 a2 isy γ37
2 J ( 1 + a22 ( isx + irx )2 )
3 P a1 ( isy + iry ) isx
3 P a1 ( isx + irx ) isy
2 1 + a22 ( isy + iry )2 2 1 + a22 ( isx + irx )2
J
%1 := Lrl + Lrl a22 isx2 + 2 Lrl a22 isx irx + Lrl a22 irx2 + a1 a2
%2 := arctan( a2 ( isy + iry ) )
Page 14
+
wr
J
,
( w − wr ) a1 a2
%3 :=
%4 :=
+ ( w − wr ) Lrl
1 + a22 ( isy + iry )2
Lrl
%1 w
Lrl ( 1 + a22 ( isy + iry )2 )
%5 := 2 Lrl a22 isx + 2 Lrl a22 irx
%6 :=
%7 :=
%8 :=
%9 :=
%5 ( w a1 %2 − Rs isx )
Lrl a1 a2
%5 usx
+ %6 +
Lrl a1 a2
Rr
Lrl
( w − wr ) a1 a2
Lrl ( 1 + a22 ( isy + iry )2 )
%5 usx
+ %6 −
Lrl a1 a2
%1 Rs
Lrl a1 a2
%10 := Lrl + Lrl a22 isy2 + 2 Lrl a22 isy iry + Lrl a22 iry2 + a1 a2
%11 := arctan( a2 ( isx + irx ) )
%12 := 2 Lrl a22 isy + 2 Lrl a22 iry
%13 :=
%14 :=
%12 ( −w a1 %11 − Rs isy )
Lrl a1 a2
%12 usy
Lrl a1 a2
+ %13 +
( −w + wr ) a1 a2
%15 :=
%16 :=
%17 :=
%18 :=
%19 :=
%20 :=
1 + a22 ( isx + irx )2
Rr
Lrl
− ( w − wr ) Lrl
Lrl
%10 w
Lrl ( 1 + a22 ( isx + irx )2 )
%12 usy
Lrl a1 a2
+ %13 −
%10 Rs
Lrl a1 a2
( −w + wr ) a1 a2
Lrl ( 1 + a22 ( isx + irx )2 )
w a1 a2
Lrl ( 1 + a22 ( isy + iry )2 )
w a1 a2
Lrl ( 1 + a22 ( isx + irx )2 )
%21 := −
3
P a1 a2 isx
2 1 + a22 ( isy + iry )2
+
3
2
P a1 %11
Page 15
%22 := −
3
P a1 %2 +
3
P a1 a2 isy
2
2 1 + a22 ( isx + irx )2
> p2:=multiply(dgx,gamm);
p2 :=
a1 a2 γ11
a1 a2 γ31
a1 a2 γ12
a1 a2 γ32
+
+
,
,
2
2
2
2
2
2
1 + a2 ( isx + irx ) 1 + a2 ( isx + irx )
1 + a22 ( isx + irx )2
1 + a2 ( isx + irx )
a1 a2 γ13
1 + a2 ( isx + irx )
2
2
a1 a2 γ15
1 + a2 ( isx + irx )
2
2
a1 a2 γ17
1 + a22 ( isx + irx )2
+
+
+
a1 a2 γ33
1 + a2 ( isx + irx )
2
2
a1 a2 γ35
1 + a2 ( isx + irx )
2
2
,
,
a1 a2 γ14
1 + a2 ( isx + irx )
2
2
+
2
+
a1 a2 γ16
1 + a2 ( isx + irx )
2
a1 a2 γ34
1 + a22 ( isx + irx )2
a1 a2 γ36
1 + a22 ( isx + irx )2
,
,
a1 a2 γ37
2
2
1 + a2 ( isx + irx )
a1 a2 γ21
a1 a2 γ41
a1 a2 γ22
a1 a2 γ42
+
,
+
,
1 + a22 ( isy + iry )2 1 + a22 ( isy + iry )2 1 + a22 ( isy + iry )2 1 + a22 ( isy + iry )2
a1 a2 γ23
1 + a22 ( isy + iry )2
a1 a2 γ25
1 + a22 ( isy + iry )2
a1 a2 γ27
1 + a22 ( isy + iry )2
+
+
+
a1 a2 γ43
1 + a22 ( isy + iry )2
a1 a2 γ45
1 + a22 ( isy + iry )2
,
,
a1 a2 γ24
1 + a22 ( isy + iry )2
a1 a2 γ26
1 + a22 ( isy + iry )2
+
+
a1 a2 γ44
1 + a22 ( isy + iry )2
a1 a2 γ46
1 + a22 ( isy + iry )2
a1 a2 γ47
2
2
1 + a2 ( isy + iry )
3
3 P a1 a2 isy γ31
3 P a1 a2 isx γ41
3
P %2 γ11 + P %1 γ21 +
−
,
2
2 1 + a22 ( isx + irx )2 2 1 + a22 ( isy + iry )2
2
3
2
3
2
3
2
3
2
3
2
3
2
P %2 γ12 +
3
2
P %2 γ13 +
3
P %2 γ14 +
3
P %2 γ15 +
3
P %2 γ16 +
3
P %2 γ17 +
2
2
2
2
3
2
P %1 γ22 +
3
2 1 + a22 ( isx + irx )2
P %1 γ23 +
3
P %1 γ24 +
3
P %1 γ25 +
3
P %1 γ26 +
3
P %1 γ27 +
P a1 a2 isy γ32
P a1 a2 isy γ33
2 1 + a22 ( isx + irx )2
P a1 a2 isy γ34
2 1 + a22 ( isx + irx )2
P a1 a2 isy γ35
2 1 + a22 ( isx + irx )2
P a1 a2 isy γ36
2 1 + a22 ( isx + irx )2
3
P a1 a2 isy γ37
2 1 + a22 ( isx + irx )2
%1 := a1 arctan( a2 ( isx + irx ) ) −
−
3
2 1 + a22 ( isy + iry )2
−
3
−
3
−
3
−
3
−
P a1 a2 isx γ43
2 1 + a22 ( isy + iry )2
P a1 a2 isx γ44
2 1 + a22 ( isy + iry )2
P a1 a2 isx γ45
2 1 + a22 ( isy + iry )2
P a1 a2 isx γ46
2 1 + a22 ( isy + iry )2
1 + a22 ( isy + iry )2
P a1 a2 isx γ47
,
,
,
,
,
2 1 + a22 ( isy + iry )2
3
a1 a2 isx
Page 16
P a1 a2 isx γ42
,
,
a1 a2 isy
− a1 arctan( a2 ( isy + iry ) )
1 + a22 ( isx + irx )2
> senssali:=matadd(p2,dgparam);
%2 :=
senssali :=
a1 a2 γ11
a1 a2 γ31
a1 a2 γ12
a1 a2 γ32
+
+
,
,
2
2
2
2
2
2
1 + a2 ( isx + irx ) 1 + a2 ( isx + irx )
1 + a22 ( isx + irx )2
1 + a2 ( isx + irx )
a1 a2 γ13
1 + a2 ( isx + irx )
2
2
a1 a2 γ15
1 + a2 ( isx + irx )
2
2
a1 a2 γ17
1 + a22 ( isx + irx )2
+
+
+
a1 a2 γ33
1 + a2 ( isx + irx )
2
2
a1 a2 γ35
1 + a2 ( isx + irx )
2
2
a1 a2 γ37
1 + a22 ( isx + irx )2
,
,
+
a1 a2 γ14
1 + a2 ( isx + irx )
2
2
+
2
+
a1 a2 γ16
1 + a2 ( isx + irx )
2
a1 a2 γ34
1 + a22 ( isx + irx )2
a1 a2 γ36
1 + a22 ( isx + irx )2
,
+ %1 ,
a1 ( isx + irx )
2
2
1 + a2 ( isx + irx )
a1 a2 γ21
a1 a2 γ41
a1 a2 γ22
a1 a2 γ42
+
,
+
,
1 + a22 ( isy + iry )2 1 + a22 ( isy + iry )2 1 + a22 ( isy + iry )2 1 + a22 ( isy + iry )2
a1 a2 γ23
1 + a22 ( isy + iry )2
a1 a2 γ25
1 + a22 ( isy + iry )2
a1 a2 γ27
1 + a22 ( isy + iry )2
+
+
+
a1 a2 γ43
1 + a22 ( isy + iry )2
a1 a2 γ45
1 + a22 ( isy + iry )2
a1 a2 γ47
1 + a22 ( isy + iry )2
,
,
+
a1 a2 γ24
1 + a22 ( isy + iry )2
a1 a2 γ26
1 + a22 ( isy + iry )2
+
+
a1 a2 γ44
1 + a22 ( isy + iry )2
a1 a2 γ46
1 + a22 ( isy + iry )2
,
+ %2 ,
a1 ( isy + iry )
2
2
1 + a2 ( isy + iry )
3
3 P a1 a2 isy γ31
3 P a1 a2 isx γ41
3
P %4 γ11 + P %3 γ21 +
−
,
2
2 1 + a22 ( isx + irx )2 2 1 + a22 ( isy + iry )2
2
3
2
3
2
3
2
3
2
P %4 γ12 +
2
2
P %4 γ13 +
3
P %4 γ14 +
3
P %4 γ15 +
3
+
3
3
3
2
2
2
3
2
3
3
P %3 γ24 +
3
P %3 γ25 +
3
3
P a1 a2 isy γ32
2 1 + a22 ( isx + irx )2
P %3 γ23 +
P %3 γ26 +
P %4 γ17 +
+
2
P %3 γ22 +
P a1 a2 isy γ33
2 1 + a22 ( isx + irx )2
P a1 a2 isy γ34
2 1 + a22 ( isx + irx )2
P a1 a2 isy γ35
2 1 + a22 ( isx + irx )2
P a1 a2 isy γ36
2 1 + a22 ( isx + irx )2
P %3 γ27 +
3
−
3
−
3
P a1 a2 isx γ42
2 1 + a22 ( isy + iry )2
−
3
−
3
−
3
P a1 a2 isx γ43
2 1 + a22 ( isy + iry )2
P a1 a2 isx γ44
2 1 + a22 ( isy + iry )2
P a1 a2 isx γ45
2 1 + a22 ( isy + iry )2
2 1 + a22 ( isx + irx )2
−
3
Page 17
+
3
2
,
,
3
P %4 γ16
P ( %1 isy − %2 isx ) ,
P a1 a2 isx γ47
2 1 + a22 ( isy + iry )2
a1 ( isx + irx ) isy
a1 ( isy + iry ) isx
P
−
2 1 + a22 ( isx + irx )2 1 + a22 ( isy + iry )2
3
,
2 1 + a22 ( isy + iry )2 2
P a1 a2 isx γ46
P a1 a2 isy γ37
,
%1 := arctan( a2 ( isx + irx ) )
%2 := arctan( a2 ( isy + iry ) )
%3 := a1 %1 −
a1 a2 isx
1 + a22 ( isy + iry )2
a1 a2 isy
− a1 %2
1 + a22 ( isx + irx )2
> fortran(dsens,optimized,filename=dsens21);
> fortran(senssali,optimized,filename=dsens21);
>
%4 :=
Page 18
ANEXO I. CÁLCULO DE FUNCIONES DE SENSIBILIDAD
MODELO Nº 22
AI
Formulación general
En este caso
x = (Ψsx
Ψsy
Ψrx
ω r )t
Ψry
u = (u sx
u sy
u rx
u ry
p = (R s
Rr
Lrl
J
y = (i sx
i sy
Me)
(7)
Mc )
t
(8)
a b)
ρ
t
t
(9)
(10)
definiendo las siguientes funciones de sensibilidad de las variables de estado:
γ Ψrssx
r
γ Ψssy
∂x rs
= γΨ
∂p rsrx
γ Ψ
rsry
γω
r
γ Ψrr sx
γ Ψrrsy
γ ΨLrlsx
γ ΨLrlsy
γ ΨJ sx
γ ΨJ sy
γ Ψρsx
γ Ψρsy
γ Ψa sx
γ Ψa sy
γ Ψrrrx
γ Ψrrry
γ ΨLrlrx
γ ΨLrlry
γ ΨJ rx
γ ΨJ ry
γ Ψρrx
γ Ψρry
γ Ψa rx
γ Ψa ry
γ ωrrr
γ ωLrlr
γ ωJr
γ ωρr
γ ωar
γ Ψb sx
γ Ψb sy
γ Ψb rx
γ Ψb ry
γ ωb r
(11)
y de la sensibilidad de las variables de salida
σ irs
∂y rsxs
= σi
∂p rssy
σ M
e
σ irsxr
σ irsyr
σ iLsxrl
σ iLsyrl
σ iJsx
σ iJsy
σ
σ
σ
rr
Me
Lrl
Me
J
Me
σ iρsx
σ iρsy
σ
ρ
Me
σ iasx
σ iasy
σ
a
Me
σ ibsx
σ ibsy
σ Mb e
(12)
en las páginas que siguen se encuentran los cálculos desarrollados a partir de las
utilidades que ofrece el programa MAPLE RV.0 para la manipulación algebraica y su
posterior volcado en codigo FORTRAN 90 para su aplicación en los algorítmos
utilizados en la tesis.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
> with(linalg):
> gx:=In*(a*(fluxsx/Fn)+b*(fluxsx/Fn)^n);gy:=In*(a*(fluxsy/Fn)+b*(
fluxsy/Fn)^n);irx:=(fluxrx-fluxsx)/Lrl;iry:=(fluxry-fluxsy)/Lrl;
isx:=gx-irx;isy:=gy-iry;
Warning, new definition for stack
a fluxsx
fluxsx n
gx := In
+ b
Fn
Fn
a fluxsy
fluxsy n
gy := In
+ b
Fn
Fn
irx :=
iry :=
fluxrx − fluxsx
Lrl
fluxry − fluxsy
Lrl
a fluxsx
fluxsx n fluxrx − fluxsx
−
isx := In
+ b
Fn
Fn
Lrl
fluxsy n fluxry − fluxsy
a fluxsy
−
isy := In
+ b
Fn
Lrl
Fn
> dfsx:=usx-Rs*(((fluxsx-fluxrx)/Lrl)+gx)+w*fluxsy;
fluxsx − fluxrx
a fluxsx
fluxsx n
+ w fluxsy
+ b
dfsx := usx − Rs
+ In
Lrl
Fn
Fn
> dfsy:=usy-Rs*(((fluxsy-fluxry)/Lrl)+gy)-w*fluxsx;
fluxsy − fluxry
a fluxsy
fluxsy n
− w fluxsx
+ b
dfsy := usy − Rs
+ In
Lrl
Fn
Fn
> dfrx:=urx-Rr*(((fluxrx-fluxsx)/Lrl))+(w-wr)*fluxry;
Rr ( fluxrx − fluxsx )
+ ( w − wr ) fluxry
Lrl
> dfry:=ury-Rr*(((fluxry-fluxsy)/Lrl))-(w-wr)*fluxrx;
dfrx := urx −
dfry := ury −
Rr ( fluxry − fluxsy )
− ( w − wr ) fluxrx
Lrl
> dwr:=(1/J)*((3/2)*P*(fluxsx*isy-fluxsy*isx)-rho*wr-Mc);
3
a fluxsy
fluxsy n fluxry − fluxsy
−
dwr := P fluxsx In
+ b
2
Fn
Fn
Lrl
a fluxsx
fluxsx n fluxrx − fluxsx
−
− ρ wr − Mc / J
− fluxsy In
+ b
Fn
Fn
Lrl
> Par:=(3/2)*P*(fluxsx*isy-fluxsy*isx);
a fluxsy
fluxsy n fluxry − fluxsy
−
Par := P fluxsx In
+ b
2
Fn
Fn
Lrl
3
a fluxsx
fluxsx n fluxrx − fluxsx
−
− fluxsy In
+ b
Fn
Fn
Lrl
Page 1
> ff:=vector([dfsx,dfsy,dfrx,dfry,dwr]);
a fluxsx
fluxsx − fluxrx
fluxsx n
+ w fluxsy,
ff := usx − Rs
+ In
+ b
Lrl
Fn
Fn
a fluxsy
fluxsy n
fluxsy − fluxry
− w fluxsx,
usy − Rs
+ In
+ b
Lrl
Fn
Fn
urx −
Rr ( fluxrx − fluxsx )
Lrl
+ ( w − wr ) fluxry, ury −
Rr ( fluxry − fluxsy )
Lrl
3
− ( w − wr ) fluxrx,
2
a fluxsy
fluxsy n fluxry − fluxsy
−
P fluxsx In
+ b
Fn
Fn
Lrl
a fluxsx
fluxsx n fluxrx − fluxsx
−
− ρ wr − Mc / J
− fluxsy In
+ b
Fn
Fn
Lrl
> x:=vector([fluxsx,fluxsy,fluxrx,fluxry,wr]);
x := [ fluxsx, fluxsy, fluxrx, fluxry, wr ]
> param:=vector([Rs,Rr,Lrl,J,rho,a,b]);
param := [ Rs, Rr, Lrl, J, ρ, a, b ]
> salidas:=vector([isx,isy,Par]);
a fluxsx
fluxsx n fluxrx − fluxsx
−
,
salidas := In
+ b
Fn
Fn
Lrl
a fluxsy
fluxsy n fluxry − fluxsy 3
−
, P
In
+ b
Fn
Lrl
2
Fn
a fluxsy
fluxsy n fluxry − fluxsy
−
fluxsx In
+ b
Fn
Fn
Lrl
a fluxsx
fluxsx n fluxrx − fluxsx
−
− fluxsy In
+ b
Fn
Fn
Lrl
> dfx:=jacobian(ff,x);
dfx :=
fluxsx n
n
b
a
1
Fn
Rs
, w ,
−Rs
+ In
+
, 0 , 0
Lrl
Fn
fluxsx
Lrl
fluxsy n
n
b
1
a
Fn
Rs
−w , −Rs
, 0 ,
+
,
In
+
0
Lrl
Fn
Lrl
fluxsy
Rr
Rr
,0,−
, w − wr , −fluxry
Lrl
Lrl
Rr
Rr
0 ,
, −w + wr , −
, fluxrx
Lrl
Lrl
Page 2
3
2
fluxsx n
n
b
n
1
a
a fluxsy
fluxsy
fluxry
−
fluxsy
Fn
−
+ In
+
P In
+ b
− fluxsy
Fn
Lrl
Lrl
Fn
Fn
fluxsx
J
,
3
2
fluxsy n
n
b
n
a
1
a
fluxsx
fluxsx
fluxrx
−
fluxsx
Fn
− In
+
P fluxsx
+ In
+
+ b
Lrl
Fn
Fn
Lrl
fluxsy
Fn
J
3 P fluxsy
3 P fluxsx
ρ
,
,−
, −
2 J Lrl
2 J Lrl
J
> dfparam:=jacobian(ff,param);
dfparam :=
fluxsx − fluxrx
a fluxsx
fluxsx n
Rs ( fluxsx − fluxrx )
−
, 0 ,
,0,0,
− In
+ b
Lrl
Fn
Fn
Lrl2
−
Rs In fluxsx
Fn
fluxsx n
, −Rs In
Fn
fluxsy − fluxry
a fluxsy
fluxsy n
Rs ( fluxsy − fluxry )
−
, 0 ,
− In
+ b
,0,0,
Lrl
Fn
Fn
Lrl2
−
Rs In fluxsy
Fn
fluxsy n
, −Rs In
Fn
fluxrx − fluxsx Rr ( fluxrx − fluxsx )
0 , −
,
,
0
,
0
,
0
,
0
2
Lrl
Lrl
fluxry − fluxsy Rr ( fluxry − fluxsy )
0 , −
0
0
0
0
,
,
,
,
,
2
Lrl
Lrl
fluxsx ( fluxry − fluxsy ) fluxsy ( fluxrx − fluxsx )
P
−
2
2
3
Lrl
Lrl
3
, − P
0 , 0 ,
2
J
2
a fluxsy
fluxsy n fluxry − fluxsy
−
fluxsx In
+ b
Fn
Fn
Lrl
Page 3
a fluxsx
fluxsx n fluxrx − fluxsx
−
− ρ wr − Mc
+ b
− fluxsy In
Fn
Fn
Lrl
J2 , −
wr
J
,0,
fluxsy n
fluxsx n
− fluxsy In
P fluxsx In
3
Fn
Fn
2
J
> dgx:=jacobian(salidas,x);
dgx :=
fluxsx n
n
b
a
1
1
Fn
,0,−
0
0
,
,
In
+
+
Lrl
Fn
Lrl
fluxsx
fluxsy n
n
b
a
1
1
Fn
0 ,
, 0
+ In
+
,0,−
Lrl
fluxsy
Fn
Lrl
3
2
fluxsx n
n
b
n
a fluxsy
1
a
Fn
fluxsy
fluxry
−
fluxsy
−
P In
+ b
+
− fluxsy
+ In
,
Fn
Fn
Lrl
Lrl
Fn
fluxsx
3
2
fluxsy n
n
b
n
1
a
Fn
a
fluxsx
fluxsx
fluxrx
−
fluxsx
− In
,
+
P fluxsx
+ In
+ b
+
Lrl
Fn
fluxsy
Fn
Fn
Lrl
3 P fluxsy
3 P fluxsx
,−
, 0
2 Lrl
2 Lrl
> dgparam:=jacobian(salidas,param);
dgparam :=
fluxrx − fluxsx
In fluxsx
fluxsx n
0 , 0 ,
0
0
,
,
,
,
In
Fn
Fn
Lrl2
fluxry − fluxsy
In fluxsy
fluxsy n
0 , 0 ,
,
0
,
0
,
,
In
Fn
Fn
Lrl2
3 fluxsx ( fluxry − fluxsy ) fluxsy ( fluxrx − fluxsx )
0 , 0 , P
, 0 , 0 , 0 ,
−
2
Lrl2
Lrl2
fluxsy n
fluxsx n
− fluxsy In
P fluxsx In
2
Fn
Fn
3
Page 4
> gamm:=matrix(5,7,[[gamma11,gamma12,gamma13,gamma14,gamma15,gamma
16,gamma17],[gamma21,gamma22,gamma23,gamma24,gamma25,gamma26,gam
ma27],[gamma31,gamma32,gamma33,gamma34,gamma35,gamma36,gamma37],
[gamma41,gamma42,gamma43,gamma44,gamma45,gamma46,gamma47],[gamma
51,gamma52,gamma53,gamma54,gamma55,gamma56,gamma57]]);
γ11 γ12
γ21 γ22
gamm := γ31 γ32
γ41 γ42
γ51 γ52
> aux1:=multiply(dfx,gamm);
γ13
γ23
γ33
γ43
γ53
γ14
γ24
γ34
γ44
γ54
γ15
γ25
γ35
γ45
γ55
γ16
γ26
γ36
γ46
γ56
γ17
γ27
γ37
γ47
γ57
aux1 :=
Rs γ31
Rs γ32
−Rs %1 γ11 + w γ21 +
, −Rs %1 γ12 + w γ22 +
,
Lrl
Lrl
−Rs %1 γ13 + w γ23 +
Rs γ33
Lrl
, −Rs %1 γ16 + w γ26 +
, −Rs %1 γ14 + w γ24 +
Rs γ36
Lrl
Rs γ34
Lrl
, −Rs %1 γ17 + w γ27 +
, −Rs %1 γ15 + w γ25 +
Rs γ35
Lrl
Rs γ37
Lrl
Rs γ41
Rs γ42
−w γ11 − Rs %2 γ21 +
, −w γ12 − Rs %2 γ22 +
,
Lrl
Lrl
−w γ13 − Rs %2 γ23 +
Rs γ43
, −w γ16 − Rs %2 γ26 +
Lrl
, −w γ14 − Rs %2 γ24 +
Rs γ46
Lrl
Rs γ44
, −w γ17 − Rs %2 γ27 +
Lrl
, −w γ15 − Rs %2 γ25 +
Rs γ45
Lrl
Rs γ47
Lrl
Rr γ11 Rr γ31
Rr γ12 Rr γ32
−
+ ( w − wr ) γ41 − fluxry γ51 ,
−
+ ( w − wr ) γ42 − fluxry γ52
Lrl
Lrl
Lrl
Lrl
,
,
,
Rr γ13
Lrl
Rr γ15
Lrl
Rr γ17
Lrl
−
−
−
Rr γ33
Lrl
Rr γ35
Lrl
Rr γ37
Lrl
+ ( w − wr ) γ43 − fluxry γ53 ,
+ ( w − wr ) γ45 − fluxry γ55 ,
Rr γ14
Lrl
Rr γ16
Lrl
+ ( w − wr ) γ47 − fluxry γ57
Rr γ21
Rr γ41
+ ( −w + wr ) γ31 −
+ fluxrx γ51 ,
Lrl
Lrl
Rr γ22
Lrl
Rr γ23
Lrl
+ ( −w + wr ) γ32 −
+ ( −w + wr ) γ33 −
Rr γ42
Lrl
Rr γ43
Lrl
+ fluxrx γ52 ,
+ fluxrx γ53 ,
Page 5
−
−
Rr γ34
Lrl
Rr γ36
Lrl
+ ( w − wr ) γ44 − fluxry γ54
+ ( w − wr ) γ46 − fluxry γ56
Rr γ24
Lrl
Rr γ25
Lrl
Rr γ26
Lrl
Rr γ27
Lrl
+ ( −w + wr ) γ34 −
+ ( −w + wr ) γ35 −
+ ( −w + wr ) γ36 −
+ ( −w + wr ) γ37 −
Rr γ44
Lrl
Rr γ45
Lrl
Rr γ46
Lrl
Rr γ47
Lrl
+ fluxrx γ54 ,
+ fluxrx γ55 ,
+ fluxrx γ56 ,
+ fluxrx γ57
3 P %4 γ11 3 P %3 γ21 3 P fluxsy γ31 3 P fluxsx γ41 ρ γ51
,
+
+
−
−
2
J
2
J
2
J Lrl
2
J Lrl
J
3 P %4 γ12
2
J
3 P %4 γ13
2
J
3 P %4 γ14
2
J
3 P %4 γ15
2
J
3 P %4 γ16
2
J
3 P %4 γ17
2
J
+
+
+
+
+
+
3 P %3 γ22
2
J
3 P %3 γ23
2
J
3 P %3 γ24
2
J
3 P %3 γ25
2
J
3 P %3 γ26
2
J
3 P %3 γ27
2
J
+
+
+
+
+
+
3 P fluxsy γ32
2
J Lrl
3 P fluxsy γ33
2
J Lrl
3 P fluxsy γ34
2
J Lrl
3 P fluxsy γ35
2
J Lrl
3 P fluxsy γ36
2
J Lrl
3 P fluxsy γ37
2
J Lrl
−
−
−
−
−
−
3 P fluxsx γ42
2
J Lrl
3 P fluxsx γ43
2
J Lrl
3 P fluxsx γ44
2
J Lrl
3 P fluxsx γ45
2
J Lrl
3 P fluxsx γ46
2
J Lrl
3 P fluxsx γ47
2
J Lrl
−
−
−
−
−
−
ρ γ52
J
ρ γ53
J
ρ γ54
J
ρ γ55
J
ρ γ56
J
,
,
,
,
,
ρ γ57
J
fluxsx n
n
b
a
1
Fn
%1 :=
+ In
+
Lrl
Fn
fluxsx
fluxsy n
n
b
a
1
Fn
%2 :=
+ In
+
Lrl
Fn
fluxsy
a fluxsx
fluxsx n fluxrx − fluxsx
+
%3 := fluxsx %2 − In
+ b
Fn
Fn
Lrl
a fluxsy
fluxsy n fluxry − fluxsy
−
%4 := In
+ b
− fluxsy %1
Fn
Fn
Lrl
> dga:=matadd(aux1,dfparam);
dga :=
Rs γ31 fluxsx − fluxrx
Rs γ32
−Rs %2 γ11 + w γ21 +
−
− %1 , −Rs %2 γ12 + w γ22 +
,
Lrl
Lrl
Lrl
Page 6
−Rs %2 γ13 + w γ23 +
−Rs %2 γ15 + w γ25 +
−Rs %2 γ17 + w γ27 +
Rs γ33
Lrl
Rs γ35
Lrl
Rs γ37
Lrl
+
Rs ( fluxsx − fluxrx )
Lrl2
, −Rs %2 γ14 + w γ24 +
, −Rs %2 γ16 + w γ26 +
Rs γ36
Lrl
−
Rs In fluxsx
Fn
Rs γ34
Lrl
,
,
fluxsx n
− Rs In
Fn
Rs γ41 fluxsy − fluxry
Rs γ42
−w γ11 − Rs %4 γ21 +
−
− %3 , −w γ12 − Rs %4 γ22 +
,
Lrl
Lrl
Lrl
−w γ13 − Rs %4 γ23 +
−w γ15 − Rs %4 γ25 +
−w γ17 − Rs %4 γ27 +
Rs γ43
Lrl
Rs γ45
Lrl
Rs γ47
Lrl
+
Rs ( fluxsy − fluxry )
Lrl2
, −w γ14 − Rs %4 γ24 +
, −w γ16 − Rs %4 γ26 +
Rs γ46
Lrl
−
Rs In fluxsy
Fn
Rs γ44
Lrl
,
,
fluxsy n
− Rs In
Fn
Rr γ11 Rr γ31
−
+ ( w − wr ) γ41 − fluxry γ51 ,
Lrl
Lrl
Rr γ12
Lrl
Rr γ13
Lrl
Rr γ14
Lrl
Rr γ16
Lrl
−
−
−
−
Rr γ32
Lrl
Rr γ33
Lrl
Rr γ34
Lrl
Rr γ36
Lrl
fluxrx − fluxsx
+ ( w − wr ) γ42 − fluxry γ52 −
Lrl
Rr ( fluxrx − fluxsx )
+ ( w − wr ) γ43 − fluxry γ53 +
+ ( w − wr ) γ44 − fluxry γ54 ,
+ ( w − wr ) γ46 − fluxry γ56 ,
,
Lrl2
Rr γ15
Lrl
Rr γ17
Lrl
−
−
Rr γ35
Lrl
Rr γ37
Lrl
,
+ ( w − wr ) γ45 − fluxry γ55 ,
+ ( w − wr ) γ47 − fluxry γ57
Rr γ21
Rr γ41
+ ( −w + wr ) γ31 −
+ fluxrx γ51 ,
Lrl
Lrl
Rr γ22
Lrl
Rr γ23
Lrl
Rr γ24
Lrl
Rr γ25
Lrl
Rr γ26
Lrl
+ ( −w + wr ) γ32 −
+ ( −w + wr ) γ33 −
+ ( −w + wr ) γ34 −
+ ( −w + wr ) γ35 −
+ ( −w + wr ) γ36 −
Rr γ42
Lrl
Rr γ43
Lrl
Rr γ44
Lrl
Rr γ45
Lrl
Rr γ46
Lrl
+ fluxrx γ52 −
+ fluxrx γ53 +
fluxry − fluxsy
Lrl
,
Rr ( fluxry − fluxsy )
+ fluxrx γ54 ,
+ fluxrx γ55 ,
+ fluxrx γ56 ,
Page 7
Lrl2
,
Rr γ27
Lrl
+ ( −w + wr ) γ37 −
Rr γ47
Lrl
+ fluxrx γ57
3 P %6 γ11 3 P %5 γ21 3 P fluxsy γ31 3 P fluxsx γ41 ρ γ51
+
+
−
−
,
J
2
J
2
J Lrl
2
J Lrl
J
2
3 P %6 γ12
2
+
J
+
3 P %5 γ23
2
J
3 P %5 γ22
2
+
J
+
3 P fluxsy γ32
2
3 P fluxsy γ33
2
J Lrl
J Lrl
−
−
3 P fluxsx γ42
2
3 P fluxsx γ43
2
J Lrl
J Lrl
−
−
ρ γ52 3 P %6 γ13
,
J
2
J
ρ γ53
J
fluxsx ( fluxry − fluxsy ) fluxsy ( fluxrx − fluxsx )
P
−
3
Lrl2
Lrl2
3 P %6 γ14 3 P %5 γ24
+
,
+
2
J
2
J
2
J
+
3 P fluxsy γ34
2
J Lrl
−
3 P fluxsx γ44
2
J Lrl
−
ρ γ54
J
fluxry − fluxsy
fluxrx − fluxsx
− fluxsy %1 −
− ρ wr − Mc
P fluxsx %3 −
2
Lrl
Lrl
3
−
J2
3 P %6 γ15
2
J
3 P %6 γ16
2
+
J
+
+
3 P %5 γ27
2
J
3 P %5 γ25
2
J
3 P %5 γ26
2
+
J
+
+
3 P fluxsy γ35
2
3 P fluxsy γ36
2
3 P fluxsy γ37
2
J Lrl
J Lrl
J Lrl
−
−
−
3 P fluxsx γ45
2
3 P fluxsx γ46
2
3 P fluxsx γ47
2
J Lrl
J Lrl
J Lrl
−
fluxsy n
fluxsx n
P fluxsx In
− fluxsy In
3
Fn
Fn
+
2
J
fluxsx n
a fluxsx
%1 := In
+ b
Fn
Fn
fluxsx n
n
b
a
1
Fn
%2 :=
+ In
+
Lrl
Fn
fluxsx
a fluxsy
fluxsy n
%3 := In
+ b
Fn
Fn
fluxsy n
n
b
a
1
Fn
%4 :=
+ In
+
Lrl
Fn
fluxsy
Page 8
ρ γ57
J
−
−
ρ γ55
J
−
wr
J
,
ρ γ56 3 P %6 γ17
,
J
2
J
,
%5 := fluxsx %4 − %1 +
%6 := %3 −
fluxrx − fluxsx
Lrl
fluxry − fluxsy
− fluxsy %2
Lrl
> aux2:=multiply(dgx,gamm);
aux2 :=
γ31
γ32
γ33
γ34
γ35
%1 γ11 −
, %1 γ12 −
, %1 γ13 −
, %1 γ14 −
, %1 γ15 −
,
Lrl
Lrl
Lrl
Lrl
Lrl
%1 γ16 −
γ36
Lrl
, %1 γ17 −
γ37
Lrl
γ41
γ42
γ43
γ44
γ45
%2 γ21 −
, %2 γ22 −
, %2 γ23 −
, %2 γ24 −
, %2 γ25 −
,
Lrl
Lrl
Lrl
Lrl
Lrl
%2 γ26 −
γ46
Lrl
, %2 γ27 −
γ47
Lrl
3
3
3 P fluxsy γ31 3 P fluxsx γ41
P %4 γ11 + P %3 γ21 +
−
,
2
2
2
Lrl
2
Lrl
3
2
3
2
3
2
3
2
3
2
3
2
P %4 γ12 +
P %4 γ13 +
P %4 γ14 +
3
2
3
2
3
2
P %4 γ15 +
3
P %4 γ16 +
3
P %4 γ17 +
3
2
2
2
P %3 γ22 +
P %3 γ23 +
P %3 γ24 +
P %3 γ25 +
P %3 γ26 +
P %3 γ27 +
3 P fluxsy γ32
2
Lrl
3 P fluxsy γ33
2
Lrl
3 P fluxsy γ34
2
Lrl
3 P fluxsy γ35
2
Lrl
3 P fluxsy γ36
2
Lrl
3 P fluxsy γ37
2
Lrl
−
−
−
−
−
−
3 P fluxsx γ42
2
Lrl
3 P fluxsx γ43
2
Lrl
3 P fluxsx γ44
2
Lrl
3 P fluxsx γ45
2
Lrl
3 P fluxsx γ46
2
Lrl
,
,
,
,
,
3 P fluxsx γ47
2
Lrl
fluxsx n
n
b
a
1
Fn
%1 :=
+ In
+
Lrl
Fn
fluxsx
fluxsy n
n
b
a
1
Fn
%2 :=
+ In
+
Lrl
Fn
fluxsy
fluxsx n fluxrx − fluxsx
a fluxsx
+
%3 := fluxsx %2 − In
+ b
Fn
Fn
Lrl
Page 9
a fluxsy
fluxsy n fluxry − fluxsy
−
%4 := In
+ b
− fluxsy %1
Fn
Fn
Lrl
> senssali:=matadd(aux2,dgparam);
senssali :=
γ31
γ32
γ33 fluxrx − fluxsx
γ34
%1 γ11 −
, %1 γ12 −
, %1 γ13 −
+
,
%1
γ14
−
,
Lrl
Lrl
Lrl
Lrl
Lrl2
%1 γ15 −
γ35
Lrl
, %1 γ16 −
γ36
Lrl
+
In fluxsx
Fn
γ37
fluxsx n
, %1 γ17 −
+ In
Lrl
Fn
γ41
γ42
γ43 fluxry − fluxsy
γ44
%2 γ21 −
%2
γ24
−
, %2 γ22 −
, %2 γ23 −
+
,
,
Lrl
Lrl
Lrl
Lrl
Lrl2
%2 γ25 −
γ45
Lrl
, %2 γ26 −
γ46
Lrl
+
In fluxsy
Fn
γ47
fluxsy n
, %2 γ27 −
+ In
Lrl
Fn
3
3
3 P fluxsy γ31 3 P fluxsx γ41
P %4 γ11 + P %3 γ21 +
,
−
2
2
Lrl
2
Lrl
2
3
2
P %4 γ12 +
+
3
2
3
2
3
2
2
P %3 γ22 +
3 P fluxsy γ33
2
Lrl
P %4 γ14 +
P %4 γ15 +
P %4 γ16 +
+
3
3
2
3
2
3
2
Lrl
2
Lrl
P %3 γ25 +
P %3 γ26 +
−
2
3 P fluxsx γ43
P %3 γ24 +
3 P fluxsy γ37
2
−
3 P fluxsy γ32
+
2
fluxsx ( fluxry − fluxsy ) fluxsy ( fluxrx − fluxsx )
,
P
−
2
2
2
Lrl
Lrl
Lrl
3 P fluxsy γ35
2
Lrl
3 P fluxsy γ36
2
Lrl
3 P fluxsx γ42 3
3
, P %4 γ13 + P %3 γ23
2
Lrl
2
2
3
3 P fluxsy γ34
3 P fluxsx γ47
2
Lrl
−
Lrl
−
−
−
3 P fluxsx γ44
2
Lrl
3 P fluxsx γ45
2
Lrl
,
,
3 P fluxsx γ46 3
3
, P %4 γ17 + P %3 γ27
2
Lrl
2
2
fluxsy n
fluxsx n
+ P fluxsx In
− fluxsy In
2
Fn
Fn
3
fluxsx n
n
b
a
1
Fn
%1 :=
+ In
+
Lrl
Fn
fluxsx
fluxsy n
n
b
a
1
Fn
%2 :=
+ In
+
Lrl
fluxsy
Fn
a fluxsx
fluxsx n fluxrx − fluxsx
+
%3 := fluxsx %2 − In
+ b
Lrl
Fn
Fn
a fluxsy
fluxsy n fluxry − fluxsy
−
%4 := In
+ b
− fluxsy %1
Fn
Fn
Lrl
> fortran(dga,optimized,filename=dsens22);
Page 10
> fortran(senssali,optimized,filename=dsens22);
>
Page 11
ANEXO II. CALCULO DE LA
GANANCIA DEL OBSERVADOR.
FÓRMULA DE ACKERMANN
0
0
K = P ( A(ω r )) ⋅ W0−1 ⋅ = (A 2 − ( p1 + p 2 ) ⋅ A + p1 ⋅ p 2 ⋅ I )⋅ W0−1 ⋅
1
1
−1
k sx + j ⋅ k sy rs 0
=
⋅ K
k =
+
⋅
k
j
k
0
r
ry
r
rx
C
W0 =
C ⋅ A
ANEXO II. CÁLCULO DE GANANCIAS DEL OBSERVADOR
AII
ANEXO II. CÁLCULO DE LA GANANCIA DEL OBSERVADOR.
FÓRMULA DE ACKERMANN
Relaciones básicas
0
0
K = P( A(ω r )) ⋅ W0−1 ⋅ = A 2 − ( p1 + p 2 ) ⋅ A + p1 ⋅ p 2 ⋅ I ⋅ W0−1 ⋅
1
1
(
)
k sx + j ⋅ k sy rs
=
k =
k
k
+
rx
ry
0
−1
0
⋅K
rr
C
W0 =
C
A
⋅
(1)
(2)
(3)
en las páginas que siguen se encuentran los cálculos desarrollados a partir de las
utilidades que ofrece el programa MAPLE RV.0 para la manipulación algebraica
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
> with(linalg):Rs:=0.369;Rr:=0.857;Lrl:=0.00736;Lm:=0.0207;c1:=300
0;c2:=2250000;omegar:=314;
Rs := .369
Rr := .857
Lrl := .00736
Lm := .0207
c1 := 3000
c2 := 2250000
omegar := 314
>
> A:=matrix(2,2,[[-Rs*((1/Lrl)+(1/Lm)),Rs/Lrl],[Rr/Lrl,(-Rr/Lrl)+I
*omegar]]);
-67.96195650
50.13586957
A :=
116.4402174 −116.4402174 + 314. I
> C:=matrix(1,2,[[(1/Lrl)+(1/Lm),-1/Lrl]]);
C := [184.1787439
-135.8695652]
>
> aux1:=multiply(C,A);
aux1 := [-28337.82949 25054.64319 − 42663.04347 I]
> Wo:=matrix(2,2,[[(1/Lrl)+(1/Lm),-1/Lrl],[-(1/Lrl+1/Lm)^2*Rs-1/Lr
l^2*Rr, (1/Lrl+1/Lm)*Rs/Lrl-1/Lrl*(-Rr/Lrl+I*omegar)]]);
-135.8695652
184.1787439
Wo :=
-28337.82949 25054.64319 − 42663.04347 I
>
> Woinv:=inverse(Wo);
.005685857406 + .002635533073 I .1666114720 10-5 + .00001712937016 I
Woinv :=
.0003474955909 + .003572611498 I .2258511064 10-5 + .00002321981288 I
> aux2:=matrix(2,1,[[0],[1]]);
0
aux2 :=
1
> aux3:=multiply(Woinv,aux2);
.1666114720 10-5 + .00001712937016 I
aux3 :=
.2258511064 10-5 + .00002321981288 I
>
> aux5:=multiply(A,A);
10456.65908
−9245.163339 + 15742.66304 I
aux5 :=
−21471.82922 + 36562.22826 I −79199.84422 − 73124.45653 I
> aux6:=scalarmul(A,c1);
Page 1
-203885.8695
150407.6087
aux6 :=
349320.6522 −349320.6522 + 942000. I
> aux7:=scalarmul([[1,0],[0,1]],c2);
2250000
aux7 :=
0
> aux8:=matadd(aux5,aux6,aux7);
0
2250000
-193429.2104
141162.4454 + 15742.66304 I
aux8 :=
327848.8230 + 36562.22826 I −428520.4964 + 868875.5435 I
> K:=multiply(aux8,aux3);
−.3690000000 + .2 10-8 I
K :=
−21.22300001 − 2.311040001 I
>
>
Page 2
ANEXO III. MÁQUINAS ENSAYADAS
ANEXO III. CONJUNTO DE MÁQUINAS ENSAYADAS
1
ANEXO III. MÁQUINAS ENSAYADAS
Características de las máquinas ensayadas.
Ensayos en vacío y cortocircuito a frecuencia nominal
Máquina nº1
Máquina nº2
Máquina nº3
Ensayo a rotor frenado realizado a frecuencia de deslizamiento. Máquina nº2.
Ensayo en carga. Máquina nº2
Ficha del ensayo
2
2
2
3
4
5
7
9
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO III. CONJUNTO DE MÁQUINAS ENSAYADAS
2
Características de las máquinas ensayadas.
1) 1.5 kW; 220 / 380 V; 6.4 / 3.7 A; cosϕ = 0.85; 1420 min-1; clase F; J = 0.0105 kgm2; ∆
2) 7.5 kW; 220 / 380 V; 27 / 15.6 A; cosϕ = 0.85; 1450 min-1 ; clase F; J = 0.076 kgm2; ∆
3) 22 kW; 220 / 380 V; 74 / 43 A; cosϕ = 0.85 ; 1450 min-1 ; clase F; J = 0.251 kgm2; Y
Ensayos en vacío y cortocircuito a frecuencia nominal.
Determinación del flujo estatórico a partir del ensayo en vacío y del flujo rotórico a partir
del ensayo en cortocircuito
Máquina nº1
Tabla 1. Ensayo en vacío. Máquina nº1
Us
Is
Us
Is
50
1.03
190
2.80
60
0.99
200
3.30
70
1.01
210
3.97
80
1.06
220
4.76
90
1.14
230
5.86
100
1.23
240
7.25
110
1.33
250
8.61
120
1.46
260
10.3
130
1.58
140
1.71
150
1.84
160
2.00
170
2.19
180
2.40
1,4
1,2
1
0,8
0,6
0,4
0,2
0
0
2
4
6
8
10
12
Figura 1. Flujo estatórico como función de la corriente estatórica. Máquina nº1
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO III. CONJUNTO DE MÁQUINAS ENSAYADAS
3
Tabla 2. Ensayo a rotor frenado. Máquina nº1
Us
Is
10
1.22
20
2.24
30
3.42
40
4.95
50
6.26
60
7.36
70
8.63
80
9.91
90
10.9
100
11.7
110
12.6
0,4
0,3
0,2
0,1
0
0
2
4
6
8
10
12
14
Figura 2. Flujo estatórico como función de la corriente estatórica. Máquina nº1
Máquina nº2
Tabla 3. Ensayo en vacío. Máquina nº2
Us
Is
Us
Is
79
4.00
220
14.4
89
4.30
232
17.5
100
4.64
240
20.1
111
5.00
250
23.7
120
5.30
262
28.9
129
5.60
141
6.19
151
6.65
160
7.17
168
7.58
180
8.40
191
9.30
200
10.4
211
12.3
1,4
1,2
1
0,8
0,6
0,4
0,2
0
0
10
20
30
40
Figura 3. Flujo estatórico como función de la corriente estatórica. Máquina nº2
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO III. CONJUNTO DE MÁQUINAS ENSAYADAS
4
Tabla 4. Ensayo a rotor frenado. Máquina nº2
Us
Is
22.6
10.5
30.5
16.9
40.5
25.4
50.8
34.7
61.9
45.0
71.0
53.5
81.1
62.5
0,3
0,25
0,2
0,15
0,1
0,05
0
0
20
40
60
80
Figura .4. Flujo estatórico como función de la corriente estatórica. Máquina nº2
Máquina nº3
Tabla 5. Ensayo en vacío. Máquina nº3
Us
Is
Us
Is
119
5.20
377
16.9
149
6.00
390
18.1
171
6.80
401
19.2
192
7.60
414
20.8
217
8.60
429
23.1
231
9.20
440
25.2
252
10.1
450
27.8
269
10.8
458
29.2
286
11.7
470
32.0
300
12.3
480
34.0
318
13.2
335
14.2
348
14.9
363
15.8
1 ,4
1 ,2
1
0 ,8
0 ,6
0 ,4
0 ,2
0
0
1 0
2 0
3 0
4 0
Figura 5. Flujo estatórico como función de la corriente estatórica. Máquina nº3
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO III. CONJUNTO DE MÁQUINAS ENSAYADAS
5
Tabla 6. Ensayo a rotor frenado. Máquina nº3
Us
Is
44.1
17.5
54.1
23.5
64.6
30.2
75.0
36.8
87.9
45.3
95.7
50.5
107
58.2
117
65.2
129
74.0
139
80.7
150
88.4
0,6
0,5
0,4
0,3
0,2
0,1
0
0
20
40
60
80
100
Figura 6. Flujo estatórico como función de la corriente estatórica. Máquina nº3
Ensayo a rotor frenado realizado a frecuencia de deslizamiento. Máquina nº2.
Tabla 7. Ensayo a rotor frenado. Máquina nº3. Frecuencia de deslizamiento
Us
Is
5.66
7.07
6.36
7.42
15.56 19.80 21.92
16.97 22.63 22.98
0,25
0,2
0,15
0,1
0,05
0
0
5
10
15
20
25
Figura 7. Flujo estatórico como función de la corriente estatórica. Máquina nº2
Las gráficas que siguen muestran la tensión aplicada y la corriente que circula por una
fase del estator. Obsérvese que es prácticamente sinusoidal.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO III. CONJUNTO DE MÁQUINAS ENSAYADAS
6
Figura 7. Ensayo a rotor frenado. Registro oscilográfico de Tensión aplicada y corriente
estatórica. Escalas de izquierda a derecha y de arriba abajo:
5V/div; 5 A/div; 50 ms/div
5V/div; 10 A/div; 50 ms/div
10V/div; 10 A/div; 20 ms/div
10V/div; 10 A/div; 20 ms/div
10V/div; 25 A/div; 20 ms/div
.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO III. CONJUNTO DE MÁQUINAS ENSAYADAS
7
Ensayo en carga. Máquina nº2
Tabla 8. Ensayo en carga. Máquina nº2. Método de los 3 vatimetros.
Nº
Van
Vbn
Vcn
Ia
Ib
Ic
W1
W2
W3
1
2
3
4
5
6
7
238.7
237.6
235.6
233.5
232.8
232.6
(V)
241
240.5
238
235.9
235
235.1
(V)
238.4
237.4
235.4
233.6
232.8
232.8
(V)
4.58
5.14
3.14
4.78
5.9
2.41
(A)
4.87
5.45
3.26
4.83
6.01
2.5
(A)
4.66
5.18
3.13
4.62
5.79
2.44
(A)
28.5
66
49
89
119
50
(div)
18
67
51
90
119
51
(div)
12.5
63
46
85
118
48
(div)
N
Factor
T.I.
1498
2
1475
2
1461
4
1413
4
1373
4
1368
10
-1
(min ) ---
Escala
vatimetro
10
10
10
10
10
10
(W/div)
Figura 8. Tensión fase neutro con y sin conexión del neutro de la máquina al neutro de la
red. 200 V/div; 2 ms/div. Obsérvese que el valor máximo de la onda no varia
Las gráficas que siguen muestran la tensión aplicada (fase-neutro) y la corriente que
circula por la fase correspondiente del estator.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO III. CONJUNTO DE MÁQUINAS ENSAYADAS
8
Figura 9. Tensión fase neutro y corriente de fase estatórica. Cada fila corresponde a un
punto de las medidas de la tabla 8. De izquierda a derecha se muestran las
representaciones para los valores correspondientes a las fases a, b, c respectivamente.
Escalas: 200V/div; 20 A/div; 2 ms/div
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO III. CONJUNTO DE MÁQUINAS ENSAYADAS
9
Ficha del ensayo
•
•
•
•
•
•
•
•
Temperatura ambiente: 21 ºC
VatÍmetros Kainos 24-60-120-240 V / 1 – 5 A clase 0.5
Transformadores de intensidad Norma; 5-10-20-50-100 A/5 A clase 0.2
VoltÍmetros Kainos 120-240-360 V clase 0.5
AmperÍmetros Kainos 1-2.5-5 A clase 0.5
Puente de Thompson-Wheatstone clase 0.2
Fuente de alterna ajustable: regulador de inducción 4.4 – 440 V /80 A
Medida de velocidad a partir de lámpara estroboscópica.
•
El ensayo a frecuencia de deslizamiento se ha realizado a partir de la tensión
generada mediante una máquina síncrona de 25 kVA; 220 /380 V arrastrada a partir
de una máquina asíncrona alimentada mediante un ondulador PWM con control de
velocidad en lazo cerrado.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO IV. EL MÉTODO DE LOS
MÍNIMOS CUADRADOS
RECURSIVOS. APLICACIONES
u(t)
y(t)
SISTEMA EN
ESTUDIO
ψ
OBSERVADOR
ADAPTATIVO
MÍNIMOS
CUADRADOS
RECURSIVOS
aˆ , bˆ
[
θˆ( N + 1) = θˆ( N ) + K ( N ) ⋅ y ( N + 1) − ϕ ( N + 1) ⋅ θˆ( N )
[
]
K ( N ) = P ( N ) ⋅ ϕ T ( N + 1) ⋅ I + ϕ ( N + 1) ⋅ P ( N ) ⋅ ϕ T ( N + 1)
P ( N + 1) = P ( N ) − K ( N ) ⋅ ϕ ( N + 1) ⋅ P ( N )
]
−1
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
AIV-1
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS
RECURSIVOS. APLICACIONES
EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES .............. 2
Caracterización en línea. ...................................................................................................... 2
Determinación de parámetros ............................................................................................... 3
Caso 1: N = np ................................................................................................................... 3
Caso 2: N ≠ np ................................................................................................................... 3
Método de los mínimos cuadrados ........................................................................................ 4
Estimación Recursiva de Mínimos Cuadrados...................................................................... 5
Restricciones al método..................................................................................................... 7
Aplicación al caso de un transformador ............................................................................... 8
Resultados de simulación. ..................................................................................................... 9
Contrastación experimental. Aplicación al caso de transformador en vacío .....................29
Conclusiones....................................................................................................................34
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
AIV-2
EL MÉTODO DE LOS MÍNIMOS CUADRADOS
RECURSIVOS. APLICACIONES
Caracterización en línea.
La obtención de parámetros en servicio de un sistema dinámico puede ser
planteada a partir de la consideración de un observador adaptativo, junto con un
estimador recursivo de los parámetros considerados.
Si se considera un sistema definido a partir del siguiente conjunto de ecuaciones:
dx
= f ( x, u , θ , t )
dt
y = h( x, u , θ , t )
(1)
donde u es la entrada (o entradas) aplicada, x el conjunto de variables de estado, y
el conjunto de variables de salida y θ el conjunto de parámetros a encontrar, la
solución adaptativa del problema lleva a la formulación de un algoritmo como el
indicado en la figura que sigue, formado a partir de la consideración de un
observador adaptativo para el sistema:
u(t)
y(t)
SISTEMA EN
ESTUDIO
OBSERVADOR
ADAPTATIVO
ψ
MÍNIMOS
CUADRADOS
RECURSIVOS
aˆ , bˆ
Figura 1. Disposición identificador+Observador.
dxˆ
= f ( xˆ, u , θˆ, t )
dt
yˆ = h( xˆ , u , θˆ, t )
(2)
donde las variables con “^” indican valores observados. El algoritmo de adaptación
de los parámetros desconocidos sigue una ley proporcional al error de medida:
∆θ ∝ y − yˆ
(3)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
AIV-3
y bajo ciertas condiciones el algoritmo converge a un conjunto de valores correctos,
resultando un error nulo o muy pequeño [Ljung 87], [Kulhavy 96], [Walter 97].
Determinación de parámetros
Se estudia el problema de la determinación de un vector θ de np parámetros (que a
priori deben considerarse constantes en el tiempo) utilizando una serie N de
medidas y T = ( y1 , y 2 ,...., y n ) sobre la salida del sistema lineal:
y = Φ ⋅θ
siendo Φ una matriz de N filas y np columnas.
(4)
El problema se resuelve de diversas formas dependiento de si el número N de
medidas es igual, menor, o mayor, que el número de parámetros.
Caso 1: N = np
Suponiendo que Φ tenga rango completo el problema se resuelve de forma
inmediata mediante:
θˆ = Φ −1 ⋅ y
(5)
Caso 2: N ≠ np
En este caso no existe inversa, con lo cual la ecuación (2) no puede emplearse.
Cabe distinguir dos situaciones:
a) N < np
Existen más incógnitas que ecuaciones. Por consiguiente existen infinitas
soluciones. Sin embargo, seleccionando la estimación:
θ 0 = Φ* ⋅ y
(6)
siendo Φ* la denominada “matriz inversa generalizada”, la solución obtenida es la
de la mínima norma; es decir, verifica la relación:
θ 0 ≤ θ1
(7)
siendo θ1 cualquier otra solución.
La matriz inversa generalizada Φ* es la única que verifica las ecuaciones siguientes:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
Φ ⋅ Φ * ⋅Φ = Φ
Φ * ⋅Φ ⋅ Φ* = Φ *
(Φ ⋅ Φ*) t = Φ ⋅ Φ *
AIV-4
(8)
(Φ * ⋅Φ ) t = Φ * ⋅Φ
Se demuestra también que, si las N filas ( N<np) de Φ son linealmente
independientes, la estimación se reduce a:
θ 0 = Φ *D ⋅ y = Φ T ⋅ (Φ ⋅ Φ T ) −1 ⋅ y
(9)
La matriz Φ*D se denomina inversa generalizada por la derecha, ya que verifica:
Φ ⋅ Φ *D = I
(10)
b) N = np
En este caso se tienen más ecuaciones que incógnitas. En general no existe
solución. Sin embargo, se puede demostrar que si Φ es de rango máximo, el
método de los mínimos cuadrados conduce a la solución:
θ 0 = Φ *I ⋅ y = (Φ ⋅ Φ T ) −1 ⋅ Φ T ⋅ y
(11)
que establece una relación lineal entre estimación y medidas. La matriz:
Φ *I = (Φ ⋅ Φ T ) −1 ⋅ Φ T
(12)
se denomina inversa generalizada por la izquierda y verifica la ecuación:
Φ *I ⋅ Φ = I
(13)
En la sección que sigue se muestra que la estimación anterior (11) es la que
proporciona el método de los mínimos cuadrados.
Método de los mínimos cuadrados
Se trata de obtener la estimación del conjunto de parámetros θˆ que minimiza el
índice:
J = Φ ⋅θ − y
2
(14)
Derivando respecto a los parámetros e igualando a cero:
∂J
= 2 ⋅ (Φ ⋅ θ − y ) T ⋅ Φ = 0
∂θ
(15)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
AIV-5
despejando el vector incógnita se llega a:
θˆ = (Φ T ⋅ Φ ) −1 ⋅ Φ T ⋅ y
(16)
Estimación Recursiva de Mínimos Cuadrados.
Habitualmente las medidas se toman de forma secuencial, resultando interesante el
cálculo del vector de parámetros en función de diferentes valores del número de
observaciones. Obviamente si se dispone de una estimación θˆ( N ) después de
utilizar N observaciones, y se pretende conocer la estimación θˆ( N + 1) utilizando
una observación más, en vez de tener que resolver nuevamente el problema
aplicando (16), resulta conveniente emplear una estimación recurrente que corrija
θˆ( N ) en función de la nueva observación.
Considérese la ecuación (4) después de N observaciones. Utilizando N como
argumento se puede escribir:
Y ( N ) = Φ ( N ) ⋅ θˆ( N )
(17)
Siendo:
ϕ (1)
ϕ (2)
Φ( N ) =
;
.....
ϕ ( N )
y (1)
y (2)
Y (N ) =
.....
y( N )
(18)
La estimación en este instante puede expresarse como:
θˆ( N ) = (Φ T ( N ) ⋅ Φ ( N )) −1 ⋅ Φ T ( N ) ⋅ y ( N )
(19)
Si se plantea que en el instante actual se ha obtenido una medida más:
Y ( N + 1) = Φ( N + 1) ⋅ θˆ( N + 1)
(20)
Φ( N )
;
Φ( N + 1) =
ϕ ( N + 1)
(21)
Y (N )
Y ( N + 1) =
y ( N + 1)
La estimación resultante es:
θˆ( N + 1) = (Φ T ( N + 1) ⋅ Φ ( N + 1)) −1 ⋅ Φ T ( N + 1) ⋅ y ( N + 1)
(22)
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
AIV-6
que reordenada puede escribirse como sigue:
[
]
−1
θˆ( N + 1) = Φ T ( N ) ⋅ Φ ( N ) + ϕ T ( N + 1) ⋅ ϕ ( N + 1) ⋅ Φ T ( N + 1) ⋅ Y ( N + 1)
(23)
Se define, por conveniencia, la matriz P(N) y P(N+1):
P( N ) = (Φ T ( N ) ⋅ Φ ( N )) −1
(24)
P( N + 1) = (Φ T ( N + 1) ⋅ Φ( N + 1)) −1
Se puede escribir la siguiente relación para su inversa:
P −1 ( N + 1) = P −1 ( N ) + ϕ T ( N + 1) ⋅ ϕ ( N + 1)
(25)
Finalmente:
θˆ( N + 1) = P( N + 1) ⋅ (Φ T ( N ) ⋅ Y ( N ) + ϕ T ( N + 1) ⋅ y ( N + 1) )
(26)
Resulta conveniente el siguiente lema de inversión de matrices:
(A + B ⋅ C ⋅ D )−1 = A −1 − A −1 ⋅ B ⋅ (C −1 + D ⋅ A −1 ⋅ B )−1 ⋅ D ⋅ A −1
(27)
donde A, C y (C −1 + D ⋅ A −1 ⋅ B) son matrices cuadradas no singulares. Identificando:
A = P −1 ( N );
B = ϕ T ( N + 1);
C = I;
D = ϕ ( N + 1)
(28)
la expresión (22) se convierte en:
(
P( N + 1) = P( N ) − P ( N ) ⋅ ϕ T ( N + 1) ⋅ I + ϕ ( N + 1) ⋅ P ( N ) ⋅ ϕ T ( N + 1)
)
−1
⋅ ϕ ( N + 1) ⋅ P( N )
(29)
Sustituyendo la ecuación (29) en la (26) se llega a:
[
θˆ( N + 1) = θˆ( N ) + K ( N ) ⋅ y ( N + 1) − ϕ ( N + 1) ⋅ θˆ( N )
[
]
K ( N ) = P( N ) ⋅ ϕ T ( N + 1) ⋅ I + ϕ ( N + 1) ⋅ P( N ) ⋅ ϕ T ( N + 1)
P( N + 1) = P( N ) − K ( N ) ⋅ ϕ ( N + 1) ⋅ P( N )
]
−1
(30)
Resultando un conjunto de ecuaciones recursivo que actualiza el vector de
parámetros, según un término proporcional a la diferencia entre la medida y(N+1) y
la predicción ϕ ( N + 1) ⋅ θˆ( N ) calculada mediante los parámetros obtenidos en la
medida anterior. Obsérvese también que para aplicar (30) hace falta invertir una
matriz. Esto no representa, en la mayoria de los casos, ningún problema ya que la
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
AIV-7
matriz a invertir tiene como dimensión el número de salidas del sistema (en el caso
monovariable, dimensión 1: un escalar).
Para el caso escalar las ecuaciones anteriores se reducen a las siguientes:
ϑˆ ( N ) = ϑˆ ( N − 1) + K ( N ) ⋅ ( y ( N ) − ϕ T ( N ) ⋅ ϑˆ ( N − 1))
K ( N ) = P( N ) ⋅ ϕ ( N )
(31)
con:
P( N − 1) ⋅ ϕ ( N ) ⋅ ϕ T ( N ) ⋅ P( N − 1)
P( N ) = P( N − 1) −
1 + ϕ T ( N ) ⋅ P ( N − 1) ⋅ ϕ ( N )
(32)
Restricciones al método
•
Necesidad de que los parámetros desconocidos han de ser coeficientes de las
funciones consideradas.
•
Necesidad de que la señal de excitación u(t) sea lo suficientemente rica (en el
sentido estadístico) para excitar todos los modos del sistema. Esto se garantiza
con una señal que sea una excitación persistente de orden n; es decir, que
cumpla los siguientes requisitos:
1 L
⋅ ∑ u( t + τ) ⋅ u T ( t )
L→∞ L
t =1
•
Exista el límite
ru ( τ) = lim
•
1 L
La matriz R u ( n) = lim ⋅ ∑ ϕ( t ) ⋅ ϕ T ( t )
L→∞ L
t =1
sea definida positiva.
Lo anterior se cumple si el desarrollo armónico de la señal aplicada contiene como
mínimo n/2 armónicos.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
AIV-8
Aplicación al caso de un transformador
La aplicación del método anterior al caso de modelización de un transformador
monofásico susceptible de entrar en saturación ilustrará el algoritmo que se
propone.
Figura 2. Modelo de transformador y su carga.
Las ecuaciones de definición del sistema son las siguientes:
dΨm
= u − r1 ⋅ i1
dt
dΨm
di
N2 ⋅
= (Lc arg a + L2 disp )⋅ 2 + (Rc arg a + R2 )⋅ i2
dt
dt
i1 = i mag + i ' 2
N1 ⋅
imag
Ψ
Ψ
= I N ⋅ a ⋅ m + b ⋅ m
ΨN
ΨN
n
(33)
donse se ha considerado el efecto de dispersión concentrado en el secundario. De
esta forma el sistema resulta resoluble en tiempo real ya que no aparece ninguna
ecuación implícita que deba resolverse (es evidente que las ecuaciones del
transformador son equivalentes a las de la máquina asíncrona – o a la inversa,
como se desee; por lo tanto la discusión desarrollada en el capítulo 2 es
perfectamente válida para este caso).
Se considera el modelo de saturación representado por:
y (k ) = ϕ T (k ) ⋅ θ
(34)
y la aplicación del método de los mínimos cuadrados recursivos (RLS. En el caso
de las funciones representativas de la saturación consideradas el exponente n
puede obtenerse mediante ensayos o tanteos previos como n = (5, 7 o 9), se trata
de determinar sólo los coeficientes a y b, los cuales pueden expresarse según la
forma canónica:
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
y (k ) = i(k )
ˆ (k )
Ψ
ϕ (k ) = I N ⋅ m
ΨN
T
ˆ (k )
Ψ
IN ⋅ m
Ψ
N
n
AIV-9
θ T ( k ) = a ( k ) b ( k )
(
)
(35)
Resultados de simulación.
Las figuras que siguen indican los resultados obtenidos en la simulación del
transitorio de conexión en carga del transformador de características que siguen:
•
•
•
•
•
Transformador monofásico 220/380 V, 1.3 kVA, 5.9/3.5 A, Pj = 40 W, Po = 18
W, R1 = 0.942 Ω, R2 = 1.202 Ω ; Ψm = 0.99 Wb; n = 7.
Carga R = 20 Ω; L = 100 mH (corresponde aproximadamente al caso nominal)
Caso 1: Alimentación sinusoidal coincidente con el inicio de la onda. Existe
sobrecorriente de conexión.
Caso 2. Alimentación sinusoidal retardada 90º. Prácticamente sin sobrecorriente
de conexión.
Caso 3. Alimentación PWM; mf = 15; ma = 0.85. Señal aplicada súbitamente (sin
rampa de arranque en el ondulador).
0
50.0m
100.0m
150.0m
200.0m
400.0
400.0
200.0
200.0
0
0
-200.0
-200.0
-400.0
-400.0
0
50.0m
100.0m
150.0m
200.0m
Figura 3. Tensión aplicada. Alimentación sinusoidal .Caso 1.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
50.0m
100.0m
150.0m
AIV-10
200.0m
50.0
50.0
0
0
-50.0
-50.0
-100.0
-100.0
-150.0
-150.0
0
50.0m
100.0m
150.0m
200.0m
Figura 4. Corriente por el primario. Alimentación sinusoidal .Caso 1.
0
50.0m
100.0m
150.0m
200.0m
10.000
10.000
5.000
5.000
0
0
-5.000
-5.000
-10.000
-10.000
0
50.0m
100.0m
150.0m
200.0m
Figura 5. Corriente secundaria reducida al primario. Alimentación sinusoidal .Caso
1.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
50.0m
100.0m
150.0m
200.0m
250.0m
AIV-11
300.0m
10.0
0
10.0
0
-25.0
-25.0
-50.0
-50.0
-75.0
-75.0
-100.0
-100.0
-120.0
-120.0
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 6. Corriente magnetizante calculada y estimada. Alimentación sinusoidal.
Caso 1.
-125.0
-100.0
-66.7
-33.3
0 10.0
10.0
10.0
-33.3
-33.3
-66.7
-66.7
-100.0
-100.0
-125.0
-125.0
-125.0
-100.0
-66.7
-33.3
0 10.0
Figura 7. Corriente magnetizante estimada como función de la corriente
magnetizante estimada. Alimentación sinusoidal. Caso 1.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
50.0m
100.0m
150.0m
200.0m
250.0m
AIV-12
300.0m
10.000
10.000
5.000
5.000
0
0
-5.000
-5.000
-10.000
-10.000
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 8. Error de estimación en corriente de magnetización. Alimentación
sinusoidal .Caso 1.
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
1.000
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.500
-1.500
-2.000
-2.000
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 9. Flujo común calculado y estimado. Alimentación sinusoidal .Caso 1.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
-1.700
-1.000
-0.500
0
0.500
AIV-13
1.000
1.000
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.700
-1.700
-1.700
-1.000
-0.500
0
0.500
1.000
Figura 10. Flujo común estimado como función del flujo común calculado.
Alimentación sinusoidal. Caso 1.
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
100.00m
100.00m
50.00m
50.00m
0
0
-50.00m
-50.00m
-100.00m
-100.00m
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 11. Error de estimación en flujo común. Alimentación sinusoidal .Caso 1.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
-24.80
-20.00
-15.00
-10.00
-5.00
AIV-14
0
5.50
0.993
0.993
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.405
-1.405
-24.80
-20.00
-15.00
-10.00
-5.00
0
5.50
Figura 12. Característica de saturación calculada. Alimentación sinusoidal. Caso 1.
-24.80
-20.00
-15.00
-10.00
-5.00
0
5.50
1.073
1.073
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.485
-1.485
-24.80
-20.00
-15.00
-10.00
-5.00
0
5.50
Figura 13. Característica de saturación estimada. Alimentación sinusoidal. Caso 1.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
25.00m
50.00m
75.00m
AIV-15
100.00m
700.0m
700.0m
500.0m
500.0m
333.3m
333.3m
166.7m
166.7m
0
0
0
25.00m
50.00m
75.00m
100.00m
Figura 14. Parámetro aˆ (k ) . Alimentación sinusoidal. Caso 1.
0
25.00m
50.00m
75.00m
100.00m
700.0m
700.0m
500.0m
500.0m
333.3m
333.3m
166.7m
166.7m
0
0
0
25.00m
50.00m
75.00m
100.00m
Figura 15. Parámetro bˆ(k ) . Alimentación sinusoidal. Caso 1.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
50.0m
100.0m
150.0m
200.0m
250.0m
AIV-16
300.0m
400.0
400.0
200.0
200.0
0
0
-200.0
-200.0
-400.0
-400.0
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 16. Tensión aplicada. Alimentación sinusoidal .Caso 2.
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
20.00
20.00
10.00
10.00
0
0
-10.00
-10.00
-20.00
-20.00
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 17. Corriente por el primario. Alimentación sinusoidal .Caso 2.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
50.0m
100.0m
150.0m
200.0m
250.0m
AIV-17
300.0m
10.000
10.000
5.000
5.000
0
0
-5.000
-5.000
-10.000
-10.000
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 18. Corriente secundaria reducida al primario. Alimentación sinusoidal .Caso
2.
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
6.000
5.000
6.000
5.000
2.500
2.500
0
0
-2.500
-2.500
-5.000
-6.000
-5.000
-6.000
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 19. Corriente magnetizante calculada y estimada. Alimentación sinusoidal.
Caso 2.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
-6.000
-2.500
0
2.500
AIV-18
6.000
6.000
5.000
6.000
5.000
2.500
2.500
0
0
-2.500
-2.500
-5.000
-6.000
-5.000
-6.000
-6.000
-2.500
0
2.500
6.000
Figura 20. Corriente magnetizante estimada como función de la corriente
magnetizante estimada. Alimentación sinusoidal. Caso 2.
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
2.000
2.000
1.000
1.000
0
0
-1.000
-1.000
-2.000
-2.000
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 21. Error de estimación en corriente de magnetización. Alimentación
sinusoidal .Caso 2.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
50.0m
100.0m
150.0m
200.0m
250.0m
AIV-19
300.0m
1.400
1.400
1.000
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.400
-1.400
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 22. Flujo común calculado y estimado. Alimentación sinusoidal .Caso 2.
-1.200
-0.500
0
0.500
1.200
1.200
1.000
1.200
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.200
-1.000
-1.200
-1.200
-0.500
0
0.500
1.200
Figura 23. Flujo común estimado como función del flujo común calculado.
Alimentación sinusoidal. Caso 2.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
50.0m
100.0m
150.0m
200.0m
250.0m
AIV-20
300.0m
100.00m
100.00m
50.00m
50.00m
0
0
-50.00m
-50.00m
-100.00m
-100.00m
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 24. Error de estimación en flujo común. Alimentación sinusoidal .Caso 2.
-6.000
-2.500
0
2.500
6.000
1000.0m
1000.0m
500.0m
500.0m
0
0
-500.0m
-500.0m
-1000.0m
-1000.0m
-6.000
-2.500
0
2.500
6.000
Figura 25. Característica de saturación calculada. Alimentación sinusoidal. Caso 2.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
-6.000
-2.500
0
2.500
AIV-21
6.000
1000.0m
1000.0m
500.0m
500.0m
0
0
-500.0m
-500.0m
-1000.0m
-1000.0m
-6.000
-2.500
0
2.500
6.000
Figura 26. Característica de saturación estimada. Alimentación sinusoidal. Caso 2.
0
25.00m
50.00m
75.00m
100.00m
539.0m
539.0m
375.0m
375.0m
250.0m
250.0m
125.0m
125.0m
0
0
0
25.00m
50.00m
75.00m
100.00m
Figura 27. Parámetro aˆ (k ) . Alimentación sinusoidal. Caso 2.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
25.00m
50.00m
75.00m
AIV-22
100.00m
539.0m
539.0m
375.0m
375.0m
250.0m
250.0m
125.0m
125.0m
0
0
0
25.00m
50.00m
75.00m
100.00m
Figura 28. Parámetro bˆ(k ) . Alimentación sinusoidal. Caso 2.
0
25.00m
50.00m
75.00m
100.00m
400.0
400.0
200.0
200.0
0
0
-200.0
-200.0
-400.0
-400.0
0
25.00m
50.00m
75.00m
100.00m
Figura 16. Tensión aplicada. Alimentación PWM. Caso 3.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
50.0m
100.0m
150.0m
AIV-23
200.0m
20.0
20.0
0
0
-33.3
-33.3
-66.7
-66.7
-100.0
-100.0
-133.3
-133.3
-160.0
-160.0
0
50.0m
100.0m
150.0m
200.0m
Figura 17. Corriente por el primario. Alimentación PWM. Caso 3.
0
50.0m
100.0m
150.0m
200.0m
10.000
10.000
5.000
5.000
0
0
-5.000
-5.000
-10.000
-10.000
0
50.0m
100.0m
150.0m
200.0m
Figura 18. Corriente secundaria reducida al primario. Alimentación PWM. Caso 3.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
50.0m
100.0m
150.0m
200.0m
250.0m
AIV-24
300.0m
10.0
10.0
-33.3
-33.3
-66.7
-66.7
-100.0
-100.0
-133.3
-133.3
-150.0
-150.0
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 19. Corriente magnetizante calculada y estimada. Alimentación PWM.
Caso 3.
-150.0 -133.3
-100.0
-66.7
-33.3
0 10.0
10.0
10.0
-33.3
-33.3
-66.7
-66.7
-100.0
-100.0
-133.3
-133.3
-150.0
-150.0
-150.0 -133.3
-100.0
-66.7
-33.3
0 10.0
Figura 20. Corriente magnetizante estimada como función de la corriente
magnetizante estimada. Alimentación PWM. Caso 3.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
50.0m
100.0m
150.0m
AIV-25
200.0m
20.00
20.00
10.00
10.00
0
0
-10.00
-10.00
-20.00
-20.00
0
50.0m
100.0m
150.0m
200.0m
Figura 21. Error de estimación en corriente de magnetización. Alimentación PWM.
Caso 3.
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
1.800
1.500
1.800
1.500
1.000
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.500
-1.800
-1.500
-1.800
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 22. Flujo común calculado y estimado. Alimentación PWM. Caso 3.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
-1.800 -1.500
-1.000
-0.500
0
0.500
AIV-26
1.200
1.200
1.200
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.500
-1.500
-2.000
-2.000
-1.800 -1.500
-1.000
-0.500
0
0.500
1.200
Figura 23. Flujo común estimado como función del flujo común calculado.
Alimentación PWM. Caso 3.
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
200.0m
200.0m
100.0m
100.0m
0
0
-100.0m
-100.0m
-200.0m
-200.0m
0
50.0m
100.0m
150.0m
200.0m
250.0m
300.0m
Figura 24. Error de estimación en flujo común. Alimentación PWM. Caso 3.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
-33.10
-25.00
-20.00
-15.00
-10.00
-5.00
AIV-27
0
6.50
1.232
1.000
1.232
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.498
-1.498
-33.10
-25.00
-20.00
-15.00
-10.00
-5.00
0
6.50
Figura 25. Característica de saturación calculada. Alimentación PWM. Caso 3.
-33.10
-25.00
-20.00
-15.00
-10.00
-5.00
0
6.50
1.232
1.000
1.232
1.000
0.500
0.500
0
0
-0.500
-0.500
-1.000
-1.000
-1.498
-1.498
-33.10
-25.00
-20.00
-15.00
-10.00
-5.00
0
6.50
Figura 26. Característica de saturación estimada. Alimentación PWM. Caso 3.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
25.00m
50.00m
75.00m
AIV-28
100.00m
1000.0m
1000.0m
750.0m
750.0m
500.0m
500.0m
250.0m
250.0m
0
0
0
25.00m
50.00m
75.00m
100.00m
Figura 27. Parámetro aˆ (k ) . Alimentación PWM. Caso 3.
0
25.00m
50.00m
75.00m
100.00m
1000.0m
1000.0m
750.0m
750.0m
500.0m
500.0m
250.0m
250.0m
0
0
0
25.00m
50.00m
75.00m
100.00m
Figura 28. Parámetro bˆ(k ) . Alimentación PWM. Caso 3.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
AIV-29
Contrastación experimental. Aplicación al caso de transformador en vacío
Figura 29. Disposición ensayos.
Se ha realizado el montaje de la figura 29 que representa un transformador
monofásico en vacío, alimentado desde la red industrial (220 V, 50 Hz), y
posteriormente a partir de una fuente proveniente de un ondulador PWM con las
características siguientes :
Tensión de salida : 0 - 400 V
frecuencia de salida :
0 - 120 Hz
mf = 15
Ensayo realizado para valores nominales de tensión y frecuencia.
Equipo de medida formado por :
• Sonda de corriente por efecto Hall.
• Osciloscopio digital de 20 MHz.
•Tarjeta de adquisición de datos (8 bits) conectada al osciloscopio y a un ordenador
personal no representado.
• Transformador monofásico 220/380 V, 1.3 kVA, 5.9/3.5 A, Pj = 40 W, Po = 18 W,
R1 = 0.942 Ω, R2 = 1.202 Ω ; Ψm = 0.99 Wb; n = 7 (es el transformador ensayado
anteriormente).
En la figura 30 se representa la evolución de la corriente real y la corriente estimada
para el caso de alimentación sinusoidal. Se observa la convergencia de la última al
valor real en un tiempo no superior a 40 ms (2 periodos de la onda), lo que
garantiza la identificación de los coeficientes buscados. En la figura 31, se
representa el error de observación. Las figuras 32 y 33 representan la evolución de
los parámetros identificados en función del tiempo.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
20.00m
40.00m
60.00m
AIV-30
80.00m
160.0
160.0
133.3
133.3
100.0
100.0
66.7
66.7
33.3
33.3
0
0
-20.0
-20.0
0
20.00m
40.00m
60.00m
80.00m
Figura 30. Comparación corriente real y estimada. Alimentación sinusoidal.
0
20.00m
40.00m
60.00m
80.00m
20.00
20.00
10.00
10.00
0
0
-10.00
-10.00
-20.00
-20.00
0
20.00m
40.00m
60.00m
80.00m
Figura 31. Error de estimación. Alimentación sinusoidal.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
20.00m
40.00m
60.00m
AIV-31
80.00m
10.000
10.000
5.000
5.000
0
0
-5.000
-5.000
-10.000
-10.000
0
20.00m
40.00m
60.00m
80.00m
Figura 32. Parámetro â(t). Alimentación sinusoidal.
0
20.00m
40.00m
60.00m
80.00m
10.000
10.000
7.500
7.500
5.000
5.000
2.500
2.500
0
-1.000
0
-1.000
0
20.00m
40.00m
60.00m
80.00m
Figura 33. Parámetro bˆ(t ) . Alimentación sinusoidal.
En la figura 34 se representa la evolución de la corriente real y la corriente estimada
para el caso de alimentación PWM. Se observa la convergencia de la última al valor
real en un tiempo no superior a 15 ms (1 periodo de la onda). En la figura 35, se
representa el error de observación. Las figuras 36 y 37 representan la evolución de
los parámetros identificados en función del tiempo.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
10.00m
20.00m
30.00m
40.00m
AIV-32
49.51m
34.36
34.36
20.00
20.00
0
0
-20.00
-20.00
-40.00
-40.00
-57.04
-57.04
0
10.00m
20.00m
30.00m
40.00m
49.51m
Figura 34. Comparación corriente real y estimada. Alimentación PWM.
0
10.00m
20.00m
30.00m
40.00m
49.51m
50.00
50.00
25.00
25.00
0
0
-25.00
-25.00
-50.00
-50.00
0
10.00m
20.00m
30.00m
40.00m
49.51m
Figura 35. Error de observación. Alimentación PWM.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
0
10.00m
20.00m
30.00m
40.00m
AIV-33
49.51m
2.000
2.000
1.000
1.000
0
0
-1.000
-1.000
-2.000
-2.000
0
10.00m
20.00m
30.00m
40.00m
49.51m
Figura 36. Parámetro â(t). Alimentación PWM.
0
10.00m
20.00m
30.00m
40.00m
49.51m
2.500
2.500
1.250
1.250
0
0
-1.250
-1.250
-2.600
-2.600
0
10.00m
20.00m
30.00m
40.00m
49.51m
Figura 37. Parámetro bˆ(t ) . Alimentación PWM.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL
ANEXO 4. EL MÉTODO DE LOS MÍNIMOS CUADRADOS RECURSIVOS. APLICACIONES
AIV-34
Conclusiones
•
El método presentado, permite la caracterización de sistemas magnéticos
saturados a partir de medidas realizadas en línea.
-
Simulación
•
En todos los casos se llega a resultados correctos en la estimación del flujo y de
la corriente de magnetización.
•
En el segundo caso (alimentación sinusoidal sin apenas corriente de conexión)
existe una desviación en el valor final de los parámetros estimados; ello puede
ser debido a las relativamente pobres condiciones de la señal sinusoidal para
discernir la identificación de dos parámetros (máximo teórico posible con este
tipo de señal).
•
En el caso de alimentación PWM se logra la convergencia a valores correctos.
-
Contrastación experimental
•
Los parámetros estimados difieren de los obtenidos en ensayos previos fuera de
línea y de los obtenidos por simulación. Caben diversas fuentes de discrepancia:
• Fenómenos no modelados : histéresis.
•
•
Error de cuantización. La resolución con la que se
discretizan las señales es pobre (8 bits) para
representar todo el rango de valores posibles en el
transitorio de conexión (255 valores para un rango de
corrientes que varia aproximadamente entre ± 140 A y
para un rango de tensiones que varia entre ± 400 V).
Los parámetros obtenidos por ensayos fuera de línea son hallados a partir de
medidas en régimen permanente y considerando valores eficaces de tensión y
corriente; en la identificación en línea se consideran valores instantaneos de
tensión y corriente lo que puede llevar a una interpretación diferente para los
parámetros obtenidos por el algoritmo.
APORTACIÓN A LA DETERMINACIÓN DE PARÁMETROS DE LOS MODELOS EN LA MÁQUINA ASÍNCRONA PARA UNA
MEJOR IDENTIFICACIÓN DE VARIABLES NO MENSURABLES INCIDENTES EN SU CONTROL