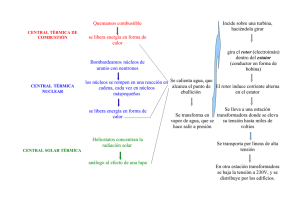
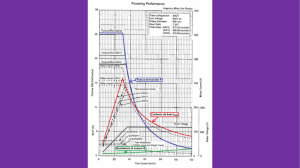
Modelo de la maquina de induccion considerando la saturacion

UNIVERSIDAD SIMÓN BOLÍVAR
DECANATO DE ESTUDIOS PROFESIONALES
COORDINACIÓN DE TECNOLOGÍA E INGENIERÍA ELÉCTRICA
MODELO DE LA MÁQUINA DE INDUCCIÓN CONSIDERANDO LA
SATURACIÓN
Por:
Daniel Andrés Delgado Palacios
PROYECTO DE GRADO
Presentado ante la Ilustre Universidad Simón Bolívar
como requisito parcial para optar al título de
Ingeniero Electricista
Sartenejas, Noviembre de 2012
UNIVERSIDAD SIMÓN BOLÍVAR
DECANATO DE ESTUDIOS PROFESIONALES
COORDINACIÓN DE TECNOLOGÍA E INGENIERÍA ELÉCTRICA
MODELO DE LA MÁQUINA DE INDUCCIÓN CONSIDERANDO LA
SATURACIÓN
Por:
Daniel Andrés Delgado Palacios
Realizado con la asesoría de:
Prof. José Manuel Aller
PROYECTO DE GRADO
Presentado ante la Ilustre Universidad Simón Bolívar
como requisito parcial para optar al título de
Ingeniero Electricista
Sartenejas, Noviembre de 2012
Modelación de la Máquina de Inducción Considerando la
Saturación
Realizado por:
Daniel Delgado
La máquina de inducción opera sin entrar en saturación en su condición nominal, a diferencia de la máquina síncrona cuyos puntos de operación están por encima del codo de
saturación en la característica magnética de la máquina. Sin embargo, si se pretende operar
una máquina asíncrona con puentes convertidores de tipo asimétrico es necesario que el
modelo de la máquina considere la saturación en vista de que dicho puente convertidor es
capaz de inyectar corriente de secuencia cero e incluso niveles DC a la máquina, la cual
puede saturar el núcleo ferromagnético. En este trabajo, se utiliza el modelo de la máquina
de inducción en coordenadas primitivas definiendo los flujos en cada fase del estator y rotor
como variables de estado. Se hace uso del concepto de grados de saturación como la relación entre la corriente saturada necesaria para producir el enlace de flujo existente en una
bobina determinada, y la corriente lineal, correspondiente a la corriente asociada al flujo de
operación cuando la característica magnética es una línea recta que parte del origen. Los
grados de saturación definidos de esta manera son mayores a la unidad y permiten considerar las variaciones de las permeanzas en el camino magnético de acuerdo a lo establecido
por la característica de vacío del convertidor. Así, las matrices de inductancias del modelo
de la máquina en coordenadas primitivas se ven modificadas por los grados de saturación.
Como cada fase se satura de manera diferente en el tiempo, esto de acuerdo a la posición
del campo magnético rotatorio, cada una de las fases del estator y rotor tendrán un grado
de saturación diferente en cada instante, el cual debe ser calculado para determinar la modificación de cada término de la matriz de inductancia. El modelo, simulado de esta forma
permite obtener los valores instantáneos de las corrientes distorsionadas cuando se aumenta
el flujo (tensión del estator) a niveles por encima del nominal y se tiene una característica
magnética saturada.
iv
Al profesor José Manuel Aller, por haberme guiado
continuamente durante el desarrollo de este trabajo y
por haberme enseñado cosas nuevas en el área de máquinas eléctricas.
Al profesor Alexander Bueno, por habernos acompañado en los ensayos experimentales realizados como parte
del desarrollo del trabajo.
A mi madre, Iraida Palacios por alentarme constantemente a seguir adelante durante toda mi etapa académica y aún más en estos últimos meses.
A mi padre, Manuel Delgado por ser apoyo en los
momentos de dificultad.
A mis hermanos, Joan Delgado, Judely Delgado y Erwuin Delgado por estar siempre atentos a mi desenvolvimiento y desarrollo académico.
A mis apreciados amigos, a quienes respeto y admiro
por la sublime combinación de cualidades y defectos que
los hacen ser especiales en mi vida. A ellos que me han
acompañado durante mi carrera, dándome ánimos y
apoyándome constantemente. A ellos porque han sido
parte fundamental para llegar hasta aquí. A ustedes,
porque sé que siempre estarán allí.
Daniel Delgado, Junio 2012
v
Índice general
Índice general
vi
Índice de tablas
ix
Índice de figuras
x
Lista de símbolos
xii
Lista de abreviaturas
xvi
INTRODUCCIÓN
1
1 HISTÉRESIS
1.1. Descripción del comportamiento . . .
1.2. Pérdidas por histéresis . . . . . . . .
1.2.1. Pérdidas por histéresis rotatoria[8] .
1.3. Histéresis en los transformadores . .
.
.
.
.
4
4
5
6
7
.
.
.
.
10
10
11
12
13
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 LA SATURACIÓN
2.1. Saturación en los convertidores electromecánicos
2.2. Determinación de la curva de saturación . . . .
2.3. Modificación de las inductancias . . . . . . . . .
2.3.1. Grados de saturación . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 MODELOS DE SATURACIÓN EN VECTORES ESPACIALES
15
3.1. Modelo de enlaces de flujos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
3.2. Modelo en corrientes [5] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
4 MODELO DE SATURACIÓN EN COORDENADAS αβ
19
4.1. El modelo en coordenadas αβ . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
4.2. Consideración de la saturación . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
5 MODELO DE SATURACIÓN EN COORDENADAS PRIMITIVAS
23
5.1. La máquina de inducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
5.2. Modificación de las ecuaciones de la máquina . . . . . . . . . . . . . . . . . . . 24
6 ENSAYOS EXPERIMENTALES
28
vi
6.1. Características del convertidor . . . . . . . . .
6.2. Parámetros . . . . . . . . . . . . . . . . . . .
6.2.1. Resistencias . . . . . . . . . . . . . . . . . .
6.2.2. Corrección de la resistencia por temperatura
6.2.3. Pruebas de vacío y rotor bloqueado . . . . .
6.2.3.1.Prueba de vacío . . . . . . . . . . . . . . . .
6.2.3.2.Prueba de rotor bloqueado . . . . . . . . . .
6.2.4. Cálculo optimizado de los parámetros[1] . .
6.3. Determinación de la curva de magnetización .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
28
29
29
30
32
32
34
37
39
7 RESULTADOS
43
7.1. Curva de saturación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
7.2. Comparación de los modelos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
CONCLUSIONES Y RECOMENDACIONES
53
REFERENCIAS BIBLIOGRÁFICAS
55
A VECTORES ESPACIALES
56
A.1. Definición . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
A.2. Potencia Activa y Reactiva Instantánea . . . . . . . . . . . . . . . . . . . . . . . 57
A.3. Interpretación Física . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
B MÉTODO DE EULER
60
B.1. Modo Matricial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
C PROGRAMA COMPUTACIONAL PARA EL MODELO DE LOS ENLACES DE FLUJOS
62
D PROGRAMA COMPUTACIONAL PARA EL MODELO EN CORRIENTES
67
E PROGRAMA COMPUTACIONAL PARA EL MODELO EN COORDENADAS αβ
73
F PROGRAMA COMPUTACIONAL PARA EL MODELO EN COORDENADAS PRIMITIVAS
79
G PUENTE ASIMÉTRICO
85
G.1. Puente convencional y puente asimétrico . . . . . . . . . . . . . . . . . . 85
G.2. Operación del puente asimétrico . . . . . . . . . . . . . . . . . . . . . . . . 86
vii
G.3. Aplicaciones del puente asimétrico . . . . . . . . . . . . . . . . . . . . . .
viii
86
Índice de tablas
6.1. Datos nominales de la máquina de inducción . . . . . . .
6.2. Bases del sistema . . . . . . . . . . . . . . . . . . . . . .
6.3. Resistencias entre dos terminales del rotor . . . . . . . .
6.5. Relación de transformación entre el estator y el rotor . .
6.6. Resistencias en el estator . . . . . . . . . . . . . . . . . .
6.4. Resistencia del rotor . . . . . . . . . . . . . . . . . . . .
6.7. Resistencias en el estator de la máquina una vez operada
6.8. Resistencias del estator y rotor en por unidad . . . . . .
6.9. Variables de la operación en vacío . . . . . . . . . . . . .
6.10. Variables de la operación a rotor bloqueado . . . . . . .
6.11. Parámetros de la máquina. . . . . . . . . . . . . . . . . .
6.12. Ecuaciones de los polinomios. . . . . . . . . . . . . . . .
ix
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
28
29
29
30
30
30
31
32
34
36
39
41
Índice de figuras
1.1.
1.2.
1.3.
1.4.
Curva de primera imanación [8]. . . . . . . . . . . . . . . . . . . . . . . . . . . .
Energía en un ciclo de histéresis [8]. . . . . . . . . . . . . . . . . . . . . . . . .
Corriente de excitación de un transformador (oscilograma)[8] . . . . . . . . . . .
Terceros armónicos en las corrientes de excitación de un transformador trifásico
en conexión delta [8]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.5. Corriente de línea en un trasformador trifásico conectado en delta [8]. . . . . . .
5
6
7
2.1. Curva de saturación del Hierro [3] . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2. Curva de histéresis de un núcleo ferromagnético [3] . . . . . . . . . . . . . . . .
2.3. Determinación de los grados de saturación en la máquina sincrónica [1] . . . . .
11
12
14
3.1. Diagrama de flujo para el modelo de los enlaces de flujo . . . . . . . . . . . . . .
3.2. Diagrama de Flujo para el modelo en corrientes . . . . . . . . . . . . . . . . . .
17
18
4.1. Máquina en coordenadas αβ. [1] . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2. Diagrama de flujo para el modelo en coordenadas αβ. . . . . . . . . . . . . . . .
4.3. Diagrama de flujo para el cálculo de los grados de saturación. . . . . . . . . . .
20
22
22
5.1. Diagrama de flujo para el modelo en coordenadas primitivas . . . . . . . . . . .
5.2. Diagrama de flujo para el cálculo de los grados de saturación de la máquina . .
26
27
6.1. Efecto de la temperatura sobre la resistencia del cobre.[4] . . . .
6.2. Tensión en vacío . . . . . . . . . . . . . . . . . . . . . . . . . .
6.3. Corriente en vacío . . . . . . . . . . . . . . . . . . . . . . . . . .
6.4. Potencia instantánea . . . . . . . . . . . . . . . . . . . . . . . .
6.5. Tensión a rotor bloqueado . . . . . . . . . . . . . . . . . . . . .
6.6. Corriente a rotor bloqueado . . . . . . . . . . . . . . . . . . . .
6.7. Potencia instantánea . . . . . . . . . . . . . . . . . . . . . . . .
6.8. Circuito equivalente durante la prueba de rotor bloqueado [3] .
6.9. Circuito equivalente de la máquina de inducción.[1] . . . . . . .
6.10. Curvas de histéresis . . . . . . . . . . . . . . . . . . . . . . . . .
6.11. Determinación de los puntos extremos en el ciclo de histéresis .
6.12. Curva de saturación resultante . . . . . . . . . . . . . . . . . . .
6.13. Aproximación polinómica por mínimos cuadrados de la curva de
.
.
.
.
.
.
.
.
.
.
.
.
.
31
32
32
33
34
35
36
37
38
40
40
41
42
7.1. Curva de saturación simplificada . . . . . . . . . . . . . . . . . . . . . . . . . .
43
x
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
saturación
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
8
9
7.2.
7.3.
7.4.
7.5.
7.6.
7.7.
7.8.
7.9.
Flujos en el estator de la máquina . . . . . . . . .
Corrientes en el estator . . . . . . . . . . . . . . .
Corrientes en el estator (detalle) . . . . . . . . . .
Espectro armónico de las corrientes del modelo en
Corrientes absorbidas por la máquina . . . . . . .
Par eléctrico . . . . . . . . . . . . . . . . . . . . .
Velocidad . . . . . . . . . . . . . . . . . . . . . .
Corriente en el estator. Máquina cargada s = 0,04
.
.
.
.
.
.
.
.
44
46
47
48
49
50
51
52
A.1. Representación gráfica del vector espacial de un sistema trifásico [1]. . . . . . . .
57
G.1. Inversor trifásico convencional. [2] . . . . . . . . . . . . . . . . . . . . . . . . . .
G.2. Inversor trifásico con puente asimétrico.[7] . . . . . . . . . . . . . . . . . . . . .
85
86
xi
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
coordenadas primitivas.
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Lista de símbolos
[Ler ] es la matriz de inductancias mútuas de acoplamiento estator-rotor
[Lme ] es la matriz de inductancia de magnetización del estator
[Lmr ] es la matriz de inductancia de magnetización del rotor
[Lre ] es la matriz de inductancias mútuas de acoplamiento rotor-estator
λs
es el enlace de flujo magnético en el estator
λae
es el enlace de flujo del estator en la fase a
λar
es el enlace de flujo del rotor en la fase a
λbe
es el enlace de flujo del estator en la fase b
λbr
es el enlace de flujo del rotor en la fase b
λce
es el enlace de flujo del estator en la fase c
λcr
es el enlace de flujo del rotor en la fase c
λeα
es el enlace de flujo en la bobina α del estator
λeβ
es el enlace de flujo en la bobina β del estator
λrα
es el enlace de flujo en la bobina α del rotor
λrβ
es el enlace de flujo en la bobina β del rotor
ωr
es la velocidad del rotor
−
→
λm
es el vector espacial de enlaces de flujos de magnetización
<
es la reluctancia de la máquina
λ~r
es el vector espacial de enlaces de flujos en el rotor
λ~s
es el vector espacial de enlaces de flujos en el estator
i~s
es el vector espacial de las corrientes por el estator
v~s
es el vector espacial tensiones en el estator
℘
es la permenza del camino magnético
xii
is
es la corriente por las bobinas del estator
I0
es la corriente de la prueba de vacío
iae
es la corriente del estator en la fase a
iar
es la corriente del rotor en la fase a
ibe
es la corriente del estator en la fase b
ibr
es la corriente del rotor en la fase b
ice
es la corriente del estator en la fase c
icr
es la corriente del rotor en la fase c
ieα
es la corriente en la bobina α del estator
ieβ
es la tensión en la bobina β del estator
if aselineal es la corriente de fase lineal de la máquina
if asesat es la corriente de fase saturada de la máquina
irα
es la corriente en la bobina α del rotor
irβ
es la tensión en la bobina β del rotor
IRB
es la potencia corriente a rotor bloqueado
Lm
es la inductancia de magnetización de la máquina
Lr
es la inductancia de dispersión del rotor
Ls
es la inductancia de dispersión del estator
L0
es la inductancia promedio de las inductancias transitorias y en régimen permanente
(Lms y Lmt )
L2
es la semi diferencia de las inductancias transitorias y en régimen permanente (Lms
y Lmt )
Lσe
es la inductancia de dispersión del estator
Lσr
es la inductancia de dispersión del rotor
Ler
es la inductancia mútua de acoplamiento estator-rotor
xiii
Llin
es la inductancia lineal de la máquina
Lme
es la inductancia de magnetización del estator
Lmr
es la inductancia de magnetización del rotor
Lms
es la inductancia de magnetización en estado estacionario
Lmt
es la inductancia de magnetización en estado transitorio
Lre
es la inductancia mútua de acoplamiento rotor-estator
Lsat
es la inductancia saturada de la máquina
P0
es la potencia activa de la prueba de vacío
Q0
es la potencia reactiva de la prueba de vacío
QRB
es la potencia reactiva a rotor bloqueado
Rs
es la resistencia del estator
Rm
es la resistencia de la rama magnetizante de la máquina (circuito equivalente de la
máquina)
S
es el grado de saturación
Sαe
es el grado de saturación de la bobina α del estator
Sαr
es el grado de saturación de la bobina α del rotor
Sβe
es el grado de saturación de la bobina β del estator
Sβr
es el grado de saturación de la bobina β del rotor
Sae
es el grado de saturación de la fase a del estator
Sar
es el grado de saturación de la fase a del rotor
Sbe
es el grado de saturación de la fase b del estator
Sbr
es el grado de saturación de la fase b del rotor
Sce
es el grado de saturación de la fase c del estator
Scr
es el grado de saturación de la fase c del rotor
xiv
vs
es la tensión en el estator
V0
es la tensión de la prueba de vacío
vae
es la tensión del estator en la fase a
var
es la tensión del rotor en la fase a
vbe
es la tensión del estator en la fase b
vbr
es la tensión del rotor en la fase b
vce
es la tensión del estator en la fase c
vcr
es la tensión del rotor en la fase c
veα
es la tensión en la bobina α del estator
veβ
es la tensión en la bobina β del estator
vrα
es la tensión en la bobina α del rotor
vrβ
es la tensión en la bobina β del rotor
X1
es la reactancia del estator (circuito equivalente de la máquina)
X1
es la reactancia del rotor (circuito equivalente de la máquina)
Xm
es la reactancia de la rama magnetizante de la máquina (circuito equivalente de la
máquina)
xv
Lista de abreviaturas
AC
Corriente Alterna (del inglés Alternating Current).
DC
Corriente Directa o Continúa (del inglés Direct Current).
Fmm
Fuerza Magnetomotriz
xvi
1
INTRODUCCIÓN
El fenómeno de la magnetización conlleva a hacer consideraciones atómicas y subatómicas
a la hora de explicar su mecanismo. En este sentido, se definen las corrientes atómicas sin
transporte de carga y son producidas por los electrones ligados al núcleo del átomo, son éstas
las fuentes del magnetismo [11]. Bajo esta concepción, la magnetización queda determinada
por la naturaleza dipolar del material. Un electrón circulando alrededor de un núcleo (como
lo establece la física clásica) es equivalente a una corriente eléctrica circulando alrededor de
la órbita. Los dos tipos de movimientos del electrón son el orbital y el espín. En consecuencia
posee dos momentos magnéticos asociados a estos tipos de movimientos. El electrón posee
así un momento magnético que es el resultado de sumar ambos momentos magnéticos[11]:
m
~t = m
~s+m
~0=−
e
e~ps
−
p~0
me
2me
(1)
Con p~s y p~0 los momentos magnéticos de espín y orbital respectivamente.
Sin embargo, considerar el modelo del átomo clásico no es correcto ya que la velocidad del
electrón moviéndose alrededor del núcleo es muy alta, por lo tanto, su comportamiento debe
ser descrito por la mecánica cuántica. De esta manera, los momentos magnéticos orbital y
de espín quedan definidos por los números cuánticos correspondientes. A continuación se
definen las expresiones para los momentos angulares según la mecánica cuántica:
p~0 = ~l~
(2)
p~s = ~s~
(3)
Donde ~l y ~s son el número cuántico del momento angular orbital y de espín, ~ es la constante modificada de Planck. Una vez definidos los momentos angulares, se pueden determinar
los momentos magnéticos.
Lo anterior constituye la base elemental del magnetismo, lo que permite visualizar cuáles
son los elementos que intervienen a nivel atómico en el proceso de magnetización.
De esta manera conviene hacer referencia a los materiales ferromagnéticos los cuales, como
ya se sabe poseen espines orientados en paralelo. En estos materiales se da una magnetización espontánea como resultado del momento magnético de cada espín. Sin embargo estos
elementos suelen estar en un estado desmagnetizado, esto gracias a que internamente existen
divisiones denominadas dominios, los cuales se encuentran orientados de tal manera que la
magnetización resultante es nula.
2
Bajo esta configuración interna del material, cuando el mismo es sometido a un campo
magnético, los dominios tienden a orientarse con éste y es de esta manera como se da el
fenómeno de la magnetización. El fenómeno de la histéresis (tema que se desarrolla en el
capítulo 1) es un efecto macroscópico, debido a la rotación o variación de tamaño de los
dominios magnéticos [11].
Los dominios se forman gracias a un balance energético entre cuatro energías diferentes:
Energía de intercambio, energía magnetoestática, energía anisotrópica magnetocristalina y
energía anisotrópica magnetoelástica. A continuación una breve descripción de estas energías:
1. La energía de intercambio permite la orientación en paralelo o antiparalelo de los
espines, lo que permite la formación del dominio como tal.
2. La energía magnetoestática es debida a la interacción entre los momentos del material
y el campo aplicado [11].
3. La energía de anisotropía es la que de alguna manera regula la la deformación espontánea de un material. Tiende a hacer disminuir las paredes de los dominios [11].
Todas estás energías en equilibrio permiten que los dominios coexistan en condiciones de
mínima energía. Las paredes de los dominios no son más que una zona de transición entre
un dominio y otro.
Todo lo descrito hasta este momento define las bases fundamentales en el proceso de la
magnetización de un material ferromagnético al estar en presencia de un campo, lo que a
su vez permite el estudio de la saturación del núcleo de las máquinas eléctricas, las cuales
de acuerdo al tipo de máquina se ven más o menos afectadas por este fenómeno.
Las máquinas de inducción por lo general operan por debajo del codo de saturación, lo
que garantiza que las inductancias de la máquina en los modelos se mantengan constantes
independientemente del punto de operación. Sin embargo, existen casos en los que la consideración de característica magnética lineal no es válida, en [12] se mencionan varios casos en
los que la autora considera que es indispensable considerar la saturación del convertidor: al
trabajar con niveles de flujo inferiores o superiores al nominal, generadores de inducción en
los que la característica magnética es de suma importancia al dimensionar el banco de condensadores, en regímenes transitorios en los que se encuentran envueltas corrientes elevadas,
en este último caso el modelo saturado proporciona valores más reducidos de par gracias
a que la inductancia magnetizante se reduce. La motivación de este trabajo radica en la
posibilidad de alimentar la máquina de inducción, de manera controlada, con un puente
asimétrico, el cual como se puede ver en [7], puede inyectar corrientes de secuencia cero o
3
incluso niveles de corriente continua no nulo en el núcleo del transformador, lo que puede
ocasionar la saturación del núcleo.
En este sentido, el modelo que se desarrollará en este trabajo permite que se pueda
controlar la saturación de la máquina de inducción cuando es alimentada con un convertidor
asimétrico.
CAPÍTULO 1
HISTÉRESIS
El fenómeno de la magnetización es empleado ampliamente hoy día en distintas tecnologías, valga citar los discos duros que consisten de dos platos de material ferromagnético
girando a muy alta velocidad, un cabezal se encarga de modificar la magnetización de cada
zona de los platos (escritura) y de medir su polarización (lectura). Cada pico en los polos
magnéticos simboliza un 1 binario mientras que donde no se registran picos se interpreta
un 0. Para estos efectos no solo importa la inducción magnética a la que es sometido el
material sino que además es de gran relevancia las magnetizaciones pasadas, los materiales
ferromagnéticos presentan una cierta memoria.
El fenómeno de la magnetización va de la mano con el de histéresis que consiste en la
capacidad que tiene el material ferromagnético que fue sometido a un campo de mantener
cierto magnetismo en ausencia de dicho campo.
1.1.
Descripción del comportamiento
Para describir el fenómeno de la histéresis es necesario tener la configuración que permita
controlar la intensidad de campo magnético, esto se logra, por ejemplo, mediante un toroide
por el que se hace circular a voluntad la corriente deseada.
Se supone que el material no se encuentra inicialmente magnetizado si se aumenta la
intensidad de campo hasta un valor +Hmáx (figura 1.1), la característica sigue la curva oab
que lleva por nombre curva de primera imanación. Al disminuir el valor de H, se sigue la
ruta bc, en el punto c se tiene lo que es conocido como magnetismo remanente, el cual está
caracterizado por la existencia de magnetización a pesar de haberse anulado la causante del
fenómeno. Dicha magnetización solo se anula cuando se está en presencia de una intensidad
de campo magnético igual a od. Al continuar disminuyendo la intensidad se alcanza el punto
0
0 0 0
b , al volver aumentar H se siguen los puntos b c d e, hasta este punto se ha completado un
ciclo completo (+Hmáx −Hmáx ) pero aún este ciclo es abierto. Luego de varios ciclos se llega
a tener una curva cerrada la cual es conocida comúnmente como ciclo de histéresis.
5
Figura 1.1: Curva de primera imanación [8].
1.2.
Pérdidas por histéresis
La histéresis es la propiedad que tiene el material de oponerse a cambios magnéticos [8],
esta oposición implica un gasto de energía cuando el material se encuentra sometido a un
campo magnético cíclico, este gasto de energía se refleja en calentamiento del material.
Para definir las pérdidas, es conveniente recordar que la densidad volumétrica de energía
absorbida por un material que pasa de una inducción magnética B1 a B2 se puede determinar
mediante la ecuación 1.1.
ˆ
B2
HdB
w=
(1.1)
B1
Conocida la curva de imanación B(H) se puede entonces determinar la energía que maneja
un ciclo completo de histéresis a partir de la ecuación 1.1. Como se ha podido observar de
la figura 1.1, en un ciclo de histéresis, la inducción magnética es menor cuando el campo
magnético aumenta que cuando éste disminuye (esta es la razón principal del nombre que
se le asigna a este fenómeno, ya que se presenta una oposición); por lo tanto, al calcular la
energía, ésta será mayor cuando aumenta H y bastante menor cuando disminuya, este hecho
puede observarse en la figura 1.2 donde al pasar desde a hasta b se consume una energía
igual al área sombreada en el apartado a de la figura, cuando se pasa desde b hasta c la
energía es cedida a la excitación con lo cual el área encerrada tiene signo contrario al caso
anterior, con lo cual en el intervalo H ≥ 0 la energía neta es consumida por el material y
6
es igual al valor del área encerrada por en ciclo de histéresis, como dicho ciclo es simétrico,
ocurre lo mismo para el intervalo H ≤ 0.
Figura 1.2: Energía en un ciclo de histéresis [8].
1.2.1.
Pérdidas por histéresis rotatoria[8]
Aún cuando el campo magnético no varíe en el tiempo si el volumen imantado varía su
posición al rotar alrededor de un eje produce un fenómeno conocido como pérdidas por
histéresis rotatoria. En una máquina eléctrica por tanto se da la histéresis alterna y la
histéresis rotatoria, las cuales generan pérdidas de manera independiente.
La histéresis rotatoria es debida a que el elemento inductor (polo) produce un campo en
una dirección determinada y el inducido, influenciado por dicho campo, rota en su propio
eje y la zona del inducido que inicialmente estaba recibiendo el campo en una dirección
posteriormente estará en presencia del polo opuesto y en consecuencia de un campo en
dirección contraria, esto produce que cíclicamente, el inducido reciba un campo alterno
debido a la rotación del mismo.
7
Las pérdidas de este tipo son esencialmente varias veces mayor que las producidas por
la histéresis alterna bajo un campo magnético de las mismas características. Sin embargo,
un material sometido a ambos fenómenos (histéresis alterna e histéresis rotatoria) presenta
menores pérdidas a que si estuviese sometida exclusivamente a la histéresis rotatoria.
1.3.
Histéresis en los transformadores
Cuando un transformador es alimentado en vacío con tensión sinusoidal, las corrientes
en el lado de baja presenta contenidos armónicos que pueden tener importantes influencias
en las líneas de potencia adyacentes al provocar interferencia inductiva, además pueden
exagerarse ante efectos de resonancia con las capacitancias de las líneas o cables. En la
figura 1.3 se puede observar un oscilograma con la forma de onda de un transformador
de 60 Hz alimentado a 200V efectivos, nótese que la forma de la corriente al aumentar es
distinta que al disminuir lo cual es debido a lo asimétrico del ciclo de histéresis al aumentar
y disminuir el campo magnético H.
Figura 1.3: Corriente de excitación de un transformador (oscilograma)[8]
Las corrientes de Foucault se oponen a la variación de flujo, por lo tanto, si se añade esta
componente, el ciclo de histéresis será más ancho, en consecuencia, el área de este ciclo será
8
proporcional a la pérdida total en el núcleo y no solo a las pérdidas por histéresis[8].
Si se considera un transformador trifásico en conexión delta cuya alimentación es senoidal,
la forma de onda de las corrientes por cada fase sigue siendo la observada en la figura 1.3 con
un desfase de 120º. La distorsión de la onda que se observa es característica de la presencia
de terceros armónicos. Supóngase conocida las corrientes de excitación de cada fase (AB,
BC, CA), como ya se dijo el desfase entre ellas es de 120º o un tercio del periodo de la onda,
por lo tanto el tercer armónico de cada fase estará desfasado en tres tercios del periodo,
es decir un periodo completo, lo que se traduce en un desfase nulo entre las tres formas
de onda del tercer armónico de las corrientes de excitación. Lo mismo ocurre con todos los
armónicos de orden superior múltiplos de tres.
Figura 1.4: Terceros armónicos en las corrientes de excitación de un transformador
trifásico en conexión delta [8].
En consecuencia, si se determina o se mide la corriente de línea del transformador, los
terceros armónicos se anularán y la forma de onda de dicha corriente no presentará el pico
característico que se ha descrito de la corriente de excitación. A continuación se observa la
forma de onda de la corriente de línea.
9
Figura 1.5: Corriente de línea en un trasformador trifásico conectado en delta [8].
CAPÍTULO 2
LA SATURACIÓN
2.1.
Saturación en los convertidores electromecánicos
Cuando un convertidor electromecánico es alimentado con corriente alterna, las variaciones
en el flujo son función directa de la tensión (en magnitud y frecuencia) aplicada [3].
dλs
= vs − Rs is
dt
(2.1)
En general, la caída de tensión en la resistencia es despreciable y la relación 2.1 permite
obtener el enlace de flujo λe directamente una vez conocida la tensión ve . Conocido el enlace
de flujo, la fuerza magnetomotriz también queda definida como el flujo neto (Φ = Nλ , con
N el número de vueltas) dividido por la permeanza del camino magnético.
F mm =
Φ
℘
Asimismo, la fuerza magnetomotriz está definida como el número de vueltas por la corriente inyectada al convertidor.
F mm = N i
Las variaciones en el flujo causan variaciones en la corriente. Para un cierto rango de
tensiones ve , la permeanza permanece invariable, por lo que la relación entre el flujo y
la corriente es lineal. Sin embargo, al alcanzar un cierto nivel de tensión, la permeanza
disminuye y las corrientes aumentan de forma no-lineal con el flujo. Es así como queda
definida una curva de saturación para un convertidor electromecánico, en la cual se tiene
una zona lineal donde la relación flujo-corriente es proporcional y una zona no-lineal donde
para una pequeña variación de flujo (tensión) las corrientes se incrementan en una proporción
mayor y se produce distorsión armónica en ellas.
11
Figura 2.1: Curva de saturación del Hierro [3]
Observese la figura 2.1 donde se muestra la evolución de los dominios o dipolos magnéticos
de un material ferromagnético sometido a un campo HA , si este campo es de magnitud muy
pequeña se produce un crecimiento reversible caracterizado por el ensanchamiento de los
dipolos que están orientados en paralelo a la dirección del campo, bajo estás condiciones, si
se elimina el campo HA , la densidad de flujo B también desaparece. En la medida en que
se aumenta el campo los dipolos se reorientan en la dirección del mismo lo cual produce un
campo magnético adicional e interno que refuerza al campo externo que ha modificado los
dipolos, esta zona de la curva es irreversible y si se elimina el campo externo, los dipolos
quedan orientados y se tiene un magnetismo remanente dado por la nueva posición de
los dipolos. El estado final del material (si se continúa aumentando el campo HA ) es la
saturación, momento en el cual los dipolos se encuentran completamente alineados [3]. Este
proceso permite comprender el desarrollo de la saturación a nivel atómico.
Por lo general, la curva de saturación se expresa como la relación entre el flujo magnético
(Φ = SB, con S igual al área transversal que atraviesa la densidad de flujo B) y la corriente
¸
(i = H dl) en vista de que dichas variables son proporcionales a B y H es valido utilizarlas
en el análisis de la saturación de los convertidores electromecánicos.
2.2.
Determinación de la curva de saturación
Para determinar la curva de saturación de un convertidor electromecánico es necesario
hacerlo operar en vacío ya que en esta condición no existe contrafuerza magnetomotriz que
12
contrarreste la saturación, de esta manera se debe incrementar progresivamente la tensión
en el estator midiendo en cada paso la forma de onda de las corrientes y las tensiones en los
bornes. Con estás variables se pueden determinar los flujos en el estator según la ecuación
2.1.
Conocidos los flujos y las corrientes se pueden obtener las curvas de histéresis del convertidor para cada nivel de tensión en la figura 2.2 se puede observar dicha curva, la cual
representa el comportamiento del material ferromagnético. De esta manera, la curva de magnetización se puede determinar a partir de los puntos extremos de cada una de las curvas
de histéresis determinadas a distintos niveles de tensión.
Figura 2.2: Curva de histéresis de un núcleo ferromagnético [3]
2.3.
Modificación de las inductancias
La característica de magnetización de la figura 2.1 representa la relación entre el flujo
magnético que es directamente proporcional a la densidad de flujo magnético B y la corriente
es proporcional a la intensidad de flujo magnético H según la ley de Ampere. Estas dos
B
variables están relacionadas entre sí mediante la permeabilidad del material (µ = H
). La
característica de magnetización de un convertidor representa la variación de la permeanza
del camino magnético que recorre el flujo[1], debido a que este parámetro es directamente
proporcional a la permeabilidad del medio.
℘=
µS
l
(2.2)
En la ecuación 2.2, S representa la sección transversal por donde circula el flujo y l la
longitud de recorrido de dicho flujo. De esta manera la inductancia de la máquina queda
13
determinada como sigue.
(2.3)
L = N1 N2 ℘
Con N1 y N2 el número de vueltas de la bobina 1 y 2 respectivamente.
Cuando se trabaja con el convertidor saturado, las inductancias de magnetización dejan
de ser constantes y pasan a depender del punto de operación en que se encuentre en un
determinado momento. Esto es debido a que la permeanza del camino magnético cambia
como consecuencia de la variación de la permeabilidad con la curva de saturación. Bajo
esta consideración, las inductancias de la máquina se ven modificadas por los grados de
saturación como se vio en la sección 2.1.
Si se desea determinar la inductancia de magnetización entre dos bobinas, se debe considerar que el circuito magnético asociado está constituido por dos permeanzas en serie, como
cada una posee 2l de camino magnético, dichas permeanzas tienen un valor igual al doble
= 2℘).
de la permeanza utilizada para el cálculo de la inductancia propia (℘1 = 2µS
l
℘12 =
1
℘1
1
+
1
℘2
=
1
2℘
1
+
1
2℘
=
4℘℘
=℘
2℘ + 2℘
(2.4)
Como las bobinas se consideran exactamente iguales y se desprecia el fenómeno de la
saturación, la permeanza de la ecuación 2.4 es igual a la permeanza propia de la bobina.
2.3.1.
Grados de saturación
El estudio de la saturación en las máquinas sincrónicas es de suma importancia porque
este convertidor mantiene sus puntos de operación por encima del codo de saturación. Así,
en [1] se desarrolla la relación que hay entre las permeanzas no saturadas y las permeanzas
saturadas. Se necesitará un determinado valor de corriente en la máquina no saturada y
una magnitud mayor en la máquina saturada siempre que dichas corrientes induzcan un
flujo que sea capaz de generar la fuerza electromotriz en el convertidor. Partiendo de este
principio se establece que la permenza en operación lineal está relacionada con la permeanza
en saturación mediante la relación entre las corrientes anteriormente mencionadas, dicha
relación recibe el nombre de grado de saturación, el cual es un valor que puede ser fácilmente
determinado a partir del estudio gráfico de la curva de magnetización.
En la figura 2.3 se muestra el procedimiento que permite determinar los grados de saturación en la máquina sincrónica, en ella se usa la relación gráfica entre la tensión y la
corriente de campo. En este trabajo se extiende el uso de dichos grados de saturación a las
14
Figura 2.3: Determinación de los grados de saturación en la máquina sincrónica [1]
máquinas de inducción para modificar las permeanzas de los caminos magnéticos entre fase
por lo cual la curva de saturación será la relación entre el flujo y la corriente por fase.
S=
if asesat
if aselineal
⇒ Lsat =
Llin
℘
⇒ Lsat = N1 N2
s
s
(2.5)
Redefinido los grados de saturación de esta manera, si se desea determinar la permeanza
entre dos caminos magnéticos susceptibles a la saturación se hará según la ecuación 2.6. Se
puede apreciar que la permeanza del camino magnético saturado es menor que la permeanza
no saturada, lo cual es consistente porque de esta manera se limita el flujo en la medida en
que se trabaja cerca de la zona de mayor saturación de la curva de magnetización.
<1 =
℘12sat =
s1
2℘
1
<
1
<
=
<2 = =
2
2℘
2
2℘
1
+
s2
2℘
=
4℘℘
=
2s1 ℘ + 2s2 ℘
℘
s1 +s2
2
(2.6)
CAPÍTULO 3
MODELOS DE SATURACIÓN EN VECTORES ESPACIALES
Como bien es sabido las ecuaciones de la máquina pueden ser transformadas a vectores
espaciales, lo que facilita y simplifica su análisis. Los modelos presentados en este capítulo
se basan en las ecuaciones de la máquina en esta transformación.
En investigaciones anteriores se han hecho estudios sobre la saturación de la máquina de
inducción creándose modelos matemáticos donde se deja de considerar que la inductancia
Lm , del circuito tradicional de la máquina en vectores espaciales, es constante. En estos
modelos dicha inductancia varía de acuerdo a la curva de saturación del convertidor.
3.1.
Modelo de enlaces de flujos
Este modelo, desarrollado por Jie Dang, está basado en las ecuaciones de la máquina
considerando como variables de estado los enlaces de flujo del estator y del rotor en vectores
espaciales.
dλ~s
= v~s − Rs i~s
dt
(3.1)
dλ~r
= v~r − Rr i~r + jωr λ~r
dt
(3.2)
Las corrientes pueden ser determinadas mediante las ecuaciones 3.3 y 3.4.
→
−
→
−
→
−
λs = Ls is + Lm ir
(3.3)
→
−
→
−
→
−
λr = Lr ir + Lm is
(3.4)
→
−
→
−
Lr λs − Lm λr
→
−
is =
Ls Lr − L2m
(3.5)
16
→
−
→
−
Ls λr − Lm λs
→
−
ir =
Ls Lr − L2m
(3.6)
Conocidas las corrientes en el estator y el rotor se determina el flujo de magnetización
~λm = Lm (i~s + i~r ). En cada iteración de la resolución numérica se corrige la inductancia Lm
considerando la curva de magnetización como im = f (λm ). Al determinar la inductancia
Lm = λm/im se está tomando en consideración los distintos puntos de saturación en los que
se puede ubicar el convertidor al ser operado.
3.2.
Modelo en corrientes [5]
Este modelo utiliza las corrientes como variables de estado y además considera dos inductancias, una transitoria y una en estado estacionario, la primera mide el incremental,
la pendiente en cada punto de la curva de magnetización y la segunda mide la inductancia
para una reta que va desde el origen hasta el punto de operación de la máquina (inductancia
lineal) y en la zona por debajo del codo de saturación ambas inductancias son iguales. El
modelo es un poco más complejo matemáticamente y se basa en las ecuaciones 3.9 y 3.10
Lms =
λm
im
(3.7)
Lmt =
dλm
dim
(3.8)
di~s
di~r
di~∗
di~∗
v~s = Rs i~s + (Lσs + L0 )
+ L0
+ L2 ej2θ s + L2 ej2θ r
dt
dt
dt
dt
v~r = Rr i~r +(Lσr +L0 )
(3.9)
di~r
di~r
di~∗
di~∗
+L0 +L2 ej2θ s +L2 ej2θ r −jωr (Lσr +Lms )i~r −jωr Lms i~s (3.10)
dt
dt
dt
dt
Donde L0 es el promedio de las inductancias transitorias y en régimen permanente, L2 es
la semi diferencia de esas inductancias y θ el ángulo de la corriente de magnetización.
De esta manera queda considerada la saturación al determinar las inductancias anteriores
a partir de la curva de saturación de la máquina.
En la figura 3.2 se presenta el diagrama de flujo para el modelo en corrientes explicado.
17
Inicio
~λe , ~λr , Lm
Cálculo de las
i
h i
h corrientes:
~i = [L]−1 ~λ
Integración numérica:
dλ~e
~e − Re i~e
dt = v
dλ~r
~
~
dt = v~r − Rr ir+ jωr λr
∗
Te = 32 Lm =mag i~e + i~r
λ~e ,λ~r
Rama magnetizante:
~λm = Lm (i~s + i~r )
~ ilin = L−1
mo λm isat = f ~λm No
Lm =
|isat − ilin | ≤ 10−4
|~λm |
Sí
Lm = Lm0
isat
Lm
Lm
Figura 3.1: Diagrama de flujo para el modelo de los enlaces de flujo
18
Inicio
i~s , i~r
Cálculo del enlace de flujo de
magnetización:
~ ~ ~ im = is + ir , λm = f ~im Corrientes de magnetización:
isat = f (λm ) , ilin = L−1
m0 λm
Sí
No
|isat − ilin | ≤ 10−4
Inductancia en estado
estacionario:
Lms = Lm0
Inductancia transitoria:
m
Lmt = dλ
dim
Inductancia en estado
estacionario:
m
Lms = λim
Inductancia transitoria:
m
Lmt = dλ
dim
mt
L0 = Lms +L
2
Lmt −Lms
L2 =
2
Integración numérica:
~∗
~∗
~
~
~
v~s = Rs is + (Lσs + L0 ) ddtis + L0 ddtir + L2 ej2θ ddtis + L2 ej2θ ddtir
v~r =
~
Rr i~r + (Lσr + L0 ) ddtir
~∗
j2θ di~∗r
~
~
+ L2 ej2θ ddtis + L
2 e dt∗ − jωr (Lσr + Lms )ir − jωr Lms is
Te = 32 Lms =mag i~e + i~r
~
+ L0 ddtir
Figura 3.2: Diagrama de Flujo para el modelo en corrientes
i~s , i~r
CAPÍTULO 4
MODELO DE SATURACIÓN EN COORDENADAS αβ
El modelo que se presenta en este capítulo se basa en la representación de la máquina
de inducción trfásica en un convertidor bifásico equivalente que considera la saturación de
cada eje ortogonal entre sí, mediante la inclusión de los grados de saturación.
Como es de esperarse la máquina debe ser alimentada con el vector espacial de tensiones
que contiene toda la información del sistema trifásico. Se modifican de las inductancias
de magnetización propias y mútuas para lograr la equivalencia de los sistemas bifásicos y
trifásicos.
4.1.
El modelo en coordenadas αβ
La matriz de resistencia que permite modelar el comportamiento de la máquina de inducción solo contiene términos en la diagonal principal ya que no existen resistencias mútuas
entre las bobinas del estator y del rotor. Por otra parte, la matriz de inductancias tiene en
la diagonal principal las inductancias propias del estator y el rotor respectivamente; como
las bobinas están en cuadratura no existe inductancia mútua entre las bobinas del estator.
Cuando la bobina α del estator y α del rotor se encuntran alineadas (θ = 0), la inductancia
mútua entre ellas es máxima, es por ello que el termino de la matriz asociado (elemento
1-3) se encuentra multiplicado por un cos θ, ocurre lo mismo en el caso de la bobina β del
estator y β del rotor. La inductancia asociada a la bobina α del rotor y β del estator es
máxima cuando θ = π2 por lo tanto este término de la matriz puede ser represntado con un
senθ. En el caso de la inductancia entre el devanado β del rotor y α del estator el máximo
ocurre cuando el ángulo es − π2 , por lo que el termino de la matriz está múltiplicado por un
−senθ. Así, queda definida la matriz de inductancias, si se considera que dicha matriz es
simétrica[1].
[v] = [R][i] + p[λ] = [R][i] + θ̇[τ (θ)][i] + [L(θ)]p[i]
(4.1)
20
Figura 4.1: Máquina en coordenadas αβ. [1]
1
Te = [i]t [τ (θ)][i]
2
"
[v] =
ve
vr
 h
#
= h
veα veβ
vrα vrβ
"
[λ] =



[R] = 




[τ (θ)] = 


"
it ; [i] =
 h
#
= h

ie
ir
#
λeα λeβ
λrα λrβ
 h
= h
ieα ieβ
irα irβ
it 
it ;
it 
it 

Le
0
Ler cosθ −Ler senθ






0
L
L
senθ
L
cosθ
e
er
er
; [L] = 
;

 L cosθ L senθ

L
0
er
er
r



−Ler senθ Ler cosθ
0
Lr

0
0
−Ler senθ −Ler cosθ

0
0
Ler cosθ −Ler senθ 


−Ler senθ Ler cosθ
0
0

−Ler cosθ −Ler senθ
0
0
Reα 0
0
0
0 Reβ 0
0
0
0 Rrα 0
0
0
0 Rrβ


λe
λr
it 
(4.2)
21
4.2.
Consideración de la saturación
En el modelo definido en la sección anterior se desprecia la saturación ya que las inductancias de magnetización se asumen constantes y las matrices sólo dependen de parámetros
geométricos. Un análisis análogo al llevado a cabo en el Capítulo 2 permite corregir las
matrices con los grados de saturación. Recordar además que las inductacias propias Le y Lr
pueden ser descompuestas en una inductancia de dispersión y una de magnetización.





[L] = 




Lm
Sαe
Lσe +
0
Ler
Sαe +Sαr
2
Ler
er
− SαeL+S
senθ
Sαe +Sαr cosθ
βr
0
2
Lm
Sβe
Lσe +
cosθ
er
− SαeL+S
senθ
βr
2
Ler
Sβe +Sαr
2
Ler
Sβe +Sβr
2
0
2



cosθ
Sβe +Sβr

2
;

0


m
Lσr + SLβr
Ler
Ler
Sβe +Sαr senθ
2
senθ
Lσr +
cosθ
0
Lm
Sαr
er
er
− SαeL+S
− SαeL+S
cosθ
αr senθ
βr
0



0
0

[τ (θ)] = 
Ler
er
 − SαeL+S
Sβe +Sαr cosθ
αr senθ

2
2

Ler
er
cosθ
−
− SαeL+S
Sβe +Sβr senθ
βr
2

2

2
Ler
Sβe +Sαr
2
cosθ
0
0


− Sβe +Sβr senθ 

2


0


0
Ler
2
Para modelar la máquina de inducción trifásica en este sistema de coordenadas es necesario
pasar del sistema de tres tensiones a dos, mediante la transformación a vectores espaciales
se puede lograr.
va =
√
√
2V cos(ωt); vb = 2V cos(ωt −
vαβ =
h
1 α α
2
ih
2π
);
3
va vb vc
vc =
√
2V cos(ωt +
it
√
=
2π
)
3
3V ejωt
(4.3)
De donde, vα y vβ son la parte real e imaginaria de vαβ , respectivamente.
En las figura 4.2 y 4.3 se muestra el diagrama de flujo correspondiente al modelo en coordenadas y el diagrama de flujo para el cálculo de los grados de saturación, respectivamente.
22
Inicio
[λe ]
[λ] =
[λr ]
Grados de saturación:
sαe , sβe , sαr , sβr
Matriz de inductancias:
[L(θ, Sf e , Sf r )]
Cálculo de corrientes:
[i] = [L(θ, Sf e , Sf r )]−1 [λ]
Integración numérica:
p [λ] = [v] − [R] [i]
Te = 21 [i]t [τ (θ)][i]
Figura 4.2: Diagrama de flujo para el modelo en coordenadas αβ.
Inicio
λ
Corriente linealizada y
saturada:
ilin = L−1
mo λ
isat = f (λ)
|isat − ilin | ≤ 10−3
No
s=
isat
ilin
Sí
s=1
Salida = s
Figura 4.3: Diagrama de flujo para el cálculo de los grados de saturación.
CAPÍTULO 5
MODELO DE SATURACIÓN EN COORDENADAS
PRIMITIVAS
El campo magnético rotatorio de una máquina satura de manera diferente cada bobina de
la misma de acuerdo a la ubicación en que este campo se encuentre en un instante de tiempo
determinado. Tanto la ubicación espacial como la magnitud determinan la saturación de
cada fase del convertidor, permitiendo observar las armónicas en las corrientes al momento
de hacer trabajar la máquina en vacío o con niveles de tensión por encima del nominal.
Las armónicas en las corrientes permiten verificar que el fenómeno de saturación afecta
principalmente las corrientes de la máquina mientras que los flujos se mantienen senoidales
(cuando se alimenta el estator con un sistema senoidal de tensiones) ya que estos últimos
son el resultado de la integración de las tensiones inyectadas.
5.1.
La máquina de inducción
La máquina de inducción por lo general trabaja en la zona lineal de la curva de magnetización, es por ello que en las ecuaciones 5.1 y 5.2 las inductacias Lme , Lmr y Ler son
consideradas invariables y pueden salir de las matrices correspondientes que únicamente dependen de la geometría del convertidor y son independientes de la característica magnética
del mismo.
[v] = [R][i] + p[λ] = [R][i] + θ̇[τ (θ)][i] + [L(θ)]p[i]
(5.1)
1
Te = [i]t [τ (θ)][i]
2
(5.2)
donde:
"
[v] =
ve
vr
#
 h
= h
vae vbe vce
var vbr vcr
it 
it ; [i] =
"
ie
ir
#
 h
= h
iae ibe ice
iar ibr icr
it 
it ;
24
"
[λ] =
"
[R] =
= h
λae λbe λce
λar λbr λcr
it 
it 
# "
#
[Lee ] [Ler ]
Lσe [I] + Lme [S]
Ler [C(θ)]
; [L(θ)] =
=
;
[Lre ] [Lrr ]
Ler [C(θ)]t
Lσr [I] + Lmr [S]
# "
#
"
d
d
d
[0]
L
[L
]
[L
]
[C(θ)]
er dθ
ee
er
dθ
=
;
[τ (θ)] = dθ
t
d
d
d
[L
]
[L
]
[C(θ)]
[0]
L
re
rr
er
dθ
dθ

 dθ




1 0 0
1 − 12 − 12
0 0 0






[I] =  0 1 0 ; [S] =  − 21 1 − 12 ; [0] =  0 0 0 ;
0 0 1
− 21 − 12 1
0 0 0


4π
)
cos(θ
+
)
cos(θ)
cos(θ + 2π
3
3

2π 
[C(θ)] =  cos(θ + 4π
)
cos(θ)
cos(θ
+
) ;
3
3
Re [I] [0]
[0] Rr [I]
#
[λe ]
[λr ]
 h
#
"
) cos(θ + 4π
)
cos(θ)
cos(θ + 2π
3
3


4π
sen(θ)
sen(θ + 2π
)
sen(θ
+
)
3
3

d
4π
2π 
[C(θ)]
=
−
sen(θ
+
)
sen(θ)
sen(θ
+
) 

dθ
3
3
4π
2π
sen(θ)
sen(θ + 3 ) sen(θ + 3 )
5.2.
Modificación de las ecuaciones de la máquina
Al considerar la saturación, las ecuaciones 5.1 y 5.2 se modifican por los grados de saturación como en el caso de la máquina en coordenadas αβ. Al igual que en ese caso, las únicas
inductancias modificadas por los grados de saturación son las de magnetización Ler , Lre ,
Lme y Lmr , con esta consideración, resultan matrices que dependen tanto de la geometría
de la máquina como del punto de operación en la curva de magnetización.

Lme
Sae


L
[Lme ] =  − 2 Sbeme
+Sae
2

Lme
− 2 Sce
+Sae
2
−
Lme
S +S
2 ae 2 be
Lme
Sbe
−
2
Lme
Sce +Sbe
2
Lme
− 2 Sae
+Sce
2
−
Lme
S +S
2 be 2 ce
Lme
Sce





 = Lme 

1
Sae
1
− Sbe +S
ae
1
− Sce +S
ae
1
1
− Sae +S
− Sae +S
ce
be
1
Sbe
1
− Sce +S
be


1
− Sbe +S
;
ce
1
Sce
25


[Lmr ] = Lmr 



[Ler ] = Ler 


1
Sar
1
− Sbr +S
ar
1
− Scr +S
ar
cos(θ)
Sae +Sar
2
cos(θ+ 4π
)
3
Sbe +Sar
2
cos(θ+ 2π
)
3
Sce +Sar
2
1
1
− Sar +S
− Sar +S
cr
br
1
Sbr
1
− Scr +S
br
cos(θ+ 2π
)
3
Sae +Sbr
2
cos(θ)
Sbe +Sbr
2
cos(θ+ 4π
)
3
Sce +Sbr
2


1
− Sbr +S
;
cr
1
Scr
cos(θ+ 4π
)
3
Sae +Scr
2
cos(θ+ 2π
)
3
Sbe +Scr
2
cos(θ)






Sce +Scr
2
Bajo estás modificaciones, la matriz [L(θ, Sf e , Sf r )] (con f = a, b, c) se hace muy sensible y
el cálculo de su inversa no permite la correcta resolución numérica de las ecuaciones cuando
se tiene como variables de estado las corrientes de la máquina. Por el contrario, si se toman
los enlaces de flujo como variables de estado, la resolución del problema numérico es posible
con menos dificultad en vista de que la inversa de la matriz de inductancias solo afecta en
la pequeña caída de tensión Ri = R[L(θ, Sf e , Sf r )]−1 λ de la ecuación 5.1.
El cálculo del par es realiza según la ecuación 5.2.
En la figura 5.1 se muestra el diagrama de flujo que permite determinar el comportamiento
de la máquina de inducción bajo condiciones de saturación.
En la figura 5.2 se presenta el diagrama de flujo que permite calcular los grados de saturación del convertidor.
26
Inicio
[λe ]
[λ] =
[λr ]
Grados de saturación:
sae , sbe , sce , sar , sbr , scr
Matriz de inductancias:
[L(θ, Sf e , Sf r )]
Cálculo de corrientes:
[i] = [L(θ, Sf e , Sf r )]−1 [λ]
Integración numérica:
p [λ] = [v] − [R] [i]
Te = 21 [i]t [τ (θ)][i]
Figura 5.1: Diagrama de flujo para el modelo en coordenadas primitivas
27
Inicio
λ
Corriente linealizada y
saturada:
ilin = L−1
mo λ
isat = f (λ)
|isat − ilin | ≤ 10−3
No
s=
isat
ilin
Sí
s=1
Salida = s
Figura 5.2: Diagrama de flujo para el cálculo de los grados de saturación de la máquina
CAPÍTULO 6
ENSAYOS EXPERIMENTALES
Se utilizó una máquina de inducción del Laboratorio de Conversión y Transporte de
Energía de la Universidad Simón Bolívar. Se le realizaron pruebas de vacío en régimen
permanente donde se le aumentó la tensión progresivamente, en cada paso se adquirieron
las tensiones y corrientes instantáneas en el estator. Estas mediciones permiten determinar la
curva de magnetización de la máquina. También se realizaron registros de estás variables en
régimen transitorio y las pruebas básicas de vacío, rotor bloqueado y carga para comparar la
respuesta del modelo planteado en este trabajo y las adquisiciones hechas en el laboratorio.
6.1.
Características del convertidor
En el laboratorio de Conversión de Energía Eléctrica de la Universidad Simón Bolívar, se
utilizó una máquina de inducción de rotor bobinado para hacerle las mediciones de tensiones
y corrientes en el estator.
Se utilizó un transformador variable para ajustar progresivamente los valores de tensión
en el estator de la máquina. Las corrientes fueron medidas a través de dos transformadores
de corrientes conectados en las fases a y c. También se midieron las tensiones de línea ab y
bc.
Tabla 6.1: Datos nominales de la máquina de inducción
Vn
In
Pn
f pn
fn
ηn
240/416 V (4 − Y )
16/9.2 A
4 kW
0.8
60 Hz
1710 rpm
29
Tabla 6.2: Bases del sistema
Vbase
Sbase
Ibase
Zbase
240V
4kV A
5,56A
43,2ohm
Se miden las variables en régimen permanente para distintos niveles de tensión efectiva
a la entrada del convertidor, en pasos de 10 V hasta alcanzar 280 V. Adicionalmente se
registran las variables estatóricas durante los arranques de la máquina.
Para procesar los datos adquiridos se eligen y determinan las bases que se van a utilizar
para tener un sistema adimensional de unidades. En este caso se han seleccionado la base
de tensión monofásica, como la bobina ha de ver 240V como tensión nominal en cualquier
conexión, se elige ese número como la base de tensión. La potencia base se elige como la
potencia en el eje 4kW. Así, la corriente y la impedancia base quedan determinadas como
valores monofásicos.
6.2.
Parámetros
6.2.1.
Resistencias
La máquina utilizada es de rotor bobinado conectado en Y por lo que se tiene acceso
a los tres terminales de las bobinas, con la ayuda de un ohmetro se midió la resistencia
equivalente entre un par de terminales a una temperatura de 23 ◦ C.
Tabla 6.3: Resistencias entre dos terminales del rotor
R12
470,6mΩ
R23
479,5mΩ
R31
502,4mΩ
Las resistencias medidas anteriormente corresponden a la medición en serie de las resistencias de dos bobinas por lo que la resistencia de la bobina se puede aproximar a la mitad
de cada bobina medida.
30
Tabla 6.5: Relación de transformación entre el estator y el rotor
Tensión estator [V]
165.2
161
161.7
Tensión rotor [V]
Relación de transformación (a)
56.4
2.9
57.1
2.8
55.1
2.9
Relación de transformación promedio
2.9
Tabla 6.6: Resistencias en el estator
Rux
Rvy
Ruw
Rpromedio
1005,7mΩ
1003,4mΩ
1004,6mΩ
1004,6mΩ
Tabla 6.4: Resistencia del rotor
R1
235,3mΩ
R2
239,75mΩ
R2
251,2mΩ
Rpromedio
242,1mΩ
La resistencia promedio presentada en la tabla 6.4 es necesario referirla al estator, para
ello se determina la relación de transformación entre el rotor y el estator. Con el rotor abierto
e inyectando tensión en el estator se mide la tensión inducida en las bobinas rotóricas.
De esta manera, la resistencia del rotor vista desde el estator queda como sigue.
Rr0 = 242,08mΩ(2,9)2 = 2,028Ω
Para el caso del estator, se pueden medir las resistencias de cada bobina de forma independiente ya que se tiene acceso a ambos terminales de las bobinas.
6.2.2.
Corrección de la resistencia por temperatura
Como es sabido, la resistividad de un material varía con la temperatura, en la medida
en que esta aumenta, el material conductor posee más resistencia al paso de la corriente.
Particularmente en el caso del cobre, la resistencia mantiene una relación lineal con la
temperatura entre un rango bien definido de temperaturas como se observa en la figura
6.1. La línea azul representa la relación real entre ambas variables, sin embargo la línea
31
Figura 6.1: Efecto de la temperatura sobre la resistencia del cobre.[4]
Tabla 6.7: Resistencias en el estator de la máquina una vez operada
Rux
Rvy
Rzw
Rpromedio
1569mΩ
1354,5mΩ
1316,8mΩ
1413,4mΩ
entrecortada puede ser considerada como una aproximación válida, la cual corta el eje en
-234.5 ◦ C.
Por lo tanto, si se hace x igual a la distancia entre T1 y -234.5 ºC y y la distancia entre
T2 y -234.5 ºC, por la propiedad de triángulos semejantes se tiene la siguiente relación.
y
234,5 + T1
234,5 + T2
x
=
⇒
=
R1
R2
R1
R2
Una vez operada la máquina de inducción en el laboratorio, se midió nuevamente las
resistencias del estator para verificar su variación y la temperatura aproximada que alcanzó.
Una vez promediadas las resistencias se puede determinar la temperatura del cobre cuando
la máquina es operada considerando T1 = 23ºC.
R2
234,5 + T2
1413,4
234,5 + T2
=
⇒
= 1,407 =
⇒ T2 = 127,78ºC
R1
234,5 + T1
1004,6
234,5 + T1
Por lo tanto, las resistencias de la máquina se ven aumentadas aproximadamente en un
41 %.
Rr0 = 2,028Ω 1,407 = 2,853Ω
Re = 1004,6mΩ 1,407 = 1,413Ω
32
Tabla 6.8: Resistencias del estator y rotor en por unidad
Rr
0.0327
Re
0.066
6.2.3.
Pruebas de vacío y rotor bloqueado
6.2.3.1.
Prueba de vacío
La prueba de vacío se llevó a cabo a plena tensión con la máquina conectada en estrella,
se adquirieron las formas de onda de las tensiones y las corrientes en el estator.
Figura 6.2: Tensión en vacío
Figura 6.3: Corriente en vacío
33
Con estas variables se determinó la potencia instantánea que se presenta en la siguiente
figura.
(a)
(b) Potencia filtrada
Figura 6.4: Potencia instantánea
Bajo estás condiciones la máquina alcanzó una velocidad en el eje de 1795 rpm, lo que se
traduce en un deslizamiento de 0.0028, lo cual indica que la máquina no se encontraba en
una condición de vacío total, en vista de que este convertidor presentaba problemas en los
rodamientos, esto tendrá sus implicaciones en el desarrollo de los resultados finales.
Una vez procesadas las adquisiciones, se obtuvieron los siguientes valores.
34
Tabla 6.9: Variables de la operación en vacío
6.2.3.2.
Vlnrms
1.039
Irms
0.834
P3ϕ
0.308
Q3ϕ
2.563
Zin
0.148+j1.236
Prueba de rotor bloqueado
Se realizó la prueba hasta alcanzar la corriente efectiva nominal de la máquina.
Figura 6.5: Tensión a rotor bloqueado
35
Figura 6.6: Corriente a rotor bloqueado
Al igual que en la prueba de vacío, se determinó la potencia a partir de las variables
medidas.
36
(a)
(b) Potencia filtrada
Figura 6.7: Potencia instantánea
Tabla 6.10: Variables de la operación a rotor bloqueado
Vlnrms
0.2237
Irms
1.5
P3ϕ
0.3864
Q3ϕ
0.9272
Zin
0.057+j0.1376
Se procede a determinar por el método clásico los parámetros del convertidor.
37
Figura 6.8: Circuito equivalente durante la prueba de rotor bloqueado [3]
Mediante la prueba de rotor bloqueado se puede determinar la suma de la reactancia del
estator y del rotor, despreciándose así la rama de magnetización.
Xt = X1 + X2 =
0,9272/3
QRB
=
= 0,137 ⇒ X1 = 0,0687
2
IRB
1,52
A partir de la prueba de vacío, se determinan los parámetros de la rama magnetizante.
6.2.4.
I02 X1 +
V0
= Q0 ⇒ Xm = 1,19
Xm
I02 R1 +
V0
= P0 ⇒ Rm = 31,4
Rm
Cálculo optimizado de los parámetros[1]
En [1] se presenta un algoritmo que permite determinar los parámetros de la máquina a
partir de distintos puntos de operación, incluyendo los de vacío y rotor bloqueado y partiendo
de los parámetros obtenidos mediante el método clásico.
Para aplicar dicho algoritmo, es necesario determinar la impedancia de entrada en varios
puntos de operación, midiendo tensión y corriente a la entrada del convertidor.
A partir del circuito equivalente de la máquina de inducción en vectores espaciales (régimen permanente) que se muestra en la figura 6.9, se puede determinar la impedancia de
entrada teórica.
Zin (Re , Lσe , Rr , Lσr , Rm , Lm , s) = Ze + Zr k Zm
donde:
(6.1)
38
Figura 6.9: Circuito equivalente de la máquina de inducción.[1]
Ze = Re + jωLσe
(6.2)
Zr = Rr + jωLσr
(6.3)
Zm = Rm k jωLm =
jωLm · Rm
Rm + jωLm
(6.4)
El problema consiste en minimizarla función de coste cuadrática:
∗
n X
Zecal (si ) − Zemed (si ) Zecal (si ) − Zemed (si )
Ψ=
σi Zemed (si )
σi Zemed (si )
i=1
(6.5)
con:
Zemed (si )es la i-ésima impedancia medida en los ensayos para el deslizamiento Si
Zecal (si ) es la i-ésima impedancia calculada del modelo para el deslizamiento Si
σi es un factor de precisión de la medida i
n es el número total de medidas realizadas
Definida la función de costo de esta manera se implementa la función de matlab ’fminsearch’
para determinar los parámetros de la máquina a partir de las condiciones de vacío (s=0.003),
rotor bloqueado (s=1) y un punto de operación cualquiera (s=0.014).
[Zinmed ] =
h
0,131 + j1,2359 0,057 + j0,136 0,4845 + j0,9803
i
Los valores de las impedancias de entrada teóricos se calculan mediante las ecuaciones
de la máquina según el modelo de la figura 6.9. El vector de arranque del algoritmo está
39
conformado por los valores de las reactancias de dispersión del estator y rotor, la reactancia
y la resistencia de magnetización calculadas en el apartado 6.2.3 a partir de las pruebas de
vacío y rotor bloqueado.
[x0 ] =
h
Xe R m Xm X r
i
=
h
0,0687 11 1,2 0,0687
i
Los parámetros obtenidos de esta manera se presentan en la tabla 6.11.
Tabla 6.11: Parámetros de la máquina.
6.3.
Re
0.0324
Rr
0.066
Xe
0.0772
Xr
0.0772
Xm
1.2
Rm
11
Determinación de la curva de magnetización
Mediante un transformador trifásico variable, se energizó el motor desde una tensión de
80 V efectivos en el estator hasta alcanzar una tensión de 280 V efectivos, como en los casos
anteriores se registraron las formas de onda de las corrientes y las tensiones.
Como se indicó en la sección 2.2, la curva de saturación se determina a partir de las
curvas de histeresis de la máquina para cada nivel de tensión, dichas curvas se presentan a
continuación. Nótese que el área que encierra la curva de histéresis es bastante grande lo
que se traduce en grandes pérdidas debido a este fenómeno.
40
Figura 6.10: Curvas de histéresis
A partir de las curvas de la Figura 6.10 se determinan los puntos correspondientes a la
curva de saturación como el punto extremo de cada ciclo de histéresis, el cual está dado por
el punto que posee mayor radio con respecto al origen.
Figura 6.11: Determinación de los puntos extremos en el ciclo de histéresis
41
Figura 6.12: Curva de saturación resultante
De esta manera, es posible caracterizar la saturación de un convertidor electromecánico,
como se observa a continuación.
Para la utilización en las simulaciones de la característica expuesta en la Figura7.1 se
aproximará la misma por mínimos cuadrados. Para lograr un mejor ajuste se procesaron los
datos por tramos.
Tabla 6.12: Ecuaciones de los polinomios.
Intervalo de ajuste
Polinomio
Correlación (R2 )
0 ≤ λ ≤ 0,421
−1,0928λ2 + 1,1019λ
0.9982
0,421 ≤ λ ≤ 0,98
0,6371λ4 − 1,4896λ3 + 1,418λ2 − 0,2241λ + 0,204
0.9981
0,98 ≤ λ ≤ 1,579
2,6024λ4 − 10,596λ3 + 16,926λ2 − 11,778λ + 3,3913
0.999999
42
Figura 6.13: Aproximación polinómica por mínimos cuadrados de la curva de saturación
CAPÍTULO 7
RESULTADOS
7.1.
Curva de saturación
Para comparar los modelos analizados en este trabajo se utiliza la curva de saturación
de la máquina ensayada en el laboratorio. A dicha curva presentada en la figura 7.1 se ha
linealizado en la zona de flujos bajos. En esta zona es difícil determinar con precisión el
comportamiento de la curva en vista de que al momento de bajar mucho la tensión se pierde
par y la máquina no es capaz de mantenerse cercana a la velocidad sincrónica.
Esta curva posee una pendiente en la zona lineal de 2.2 y en la zona saturada de 0.12.
7.2.
Comparación de los modelos
Los distintos modelos que se contrastan en este trabajo presentan pocas variaciones en los
enlaces de flujos en el estator en vista de que como se dijo en la sección 2.1, estos resultan
Figura 7.1: Curva de saturación simplificada
44
de la integración de la tensión con la que se alimenta el motor. En estás simulaciones, la
tensión efectiva en el estator es 1 pu por lo tanto el flujo pico es, como se observa en la
√
Figura 7.2, de 2.
(a) Modelo de los enlaces de flujo
(b) Modelo en corrientes
(c) Modelo αβ
(d) Modelo en coordenadas primitivas
Figura 7.2: Flujos en el estator de la máquina
En el caso de las corrientes en el estator, el transitorio presenta, en los cuatro modelos,
magnitudes alrededor de 7 pu lo cual se ajusta a la reactancia de dispersión total que posee la
máquina (0.154 pu). Al observar esta corriente en régimen permanente, se puede notar que a
pesar de que todos consideran la curva de magnetización, ninguno de los modelos en vectores
espaciales refleja distorsión armónica. El modelo en coordendas αβ sí presenta distorsión
armónica en las corrientes del estator, sin embargo, dichas corrientes son diferentes en cada
fase lo cual no tiene sentido ya que la máquina de inducción considerada es simétrica,
esto deja en evidencia que al considerar un fenómeno no lineal como la saturación no es
válido el uso de transformaciones lineales al momento de modelar el convertidor. Por el
45
contrario, en el modelo en coordenadas primitivas Figura 7.4d, se presenta un alto grado de
distorsión armónica que a diferencia del modelo descrito anteriormente las tres corrientes en
el estator son iguales entre sí permitiendo, en este sentido, una representación coherente de
la máquina de inducción. Sin embargo, se debe destacar que este modelo no tiene en cuenta
las pérdidas por histéresis que al observar la Figura 6.10 se puede notar que son bastante
altas ya que el área que encierra cada ciclo es considerablemente grande, básicamente lo que
se ha considerado en este caso, es de alguna forma promediar dichas curvas de histéresis
para determinar así la curva de saturación que define la característica magnética del núcleo
del convertidor. Dichas pérdidas de histéresis pueden verse como carga para la máquina. En
referencia a lo dicho en la sección 1.2.1 la histéresis rotatoria suma aún más pérdidas a la
máquina en comparación con un transformador que no tiene piezas giratorias. Así mismo, al
observar las corrientes en vacío (Figura 6.3) se puede notar desbalances y armónicas de alta
frecuencia que también pueden ocasionar algún tipo de carga al convertidor electromecánico.
46
(a) Modelo de los enlaces de flujos
(b) Modelo en corrientes
(c) Modelo αβ
(d) Modelo en coordenadas primitivas
Figura 7.3: Corrientes en el estator
47
(a) Modelo de los enlaces de flujos
(b) Modelo en corrientes
(c) Modelo αβ
(d) Modelo en coordenadas primitivas
Figura 7.4: Corrientes en el estator (detalle)
No obstante a lo dicho anteriormente, las corrientes del modelo desarrollado tienen cierta
similitud con las corrientes en vacío de un transformador (figura 1.3) con la diferencia de
que en medio periodo estas corrientes son simétricas al aumentar y disminuir el flujo cosa
que en un transformadros real no pasa, ya que el fenómeno de la histéresis condiciona a que
el comportamiento al aumentar el flujo sea diferente que al disminuirlo.
Un estudio del contenido armónico de las corrientes obtenidas a partir del modelo en
coordenadas primitivas se presenta en la figura 7.5. En este espectro armónico se puede
apreciar que las corrientes contienen más de un 60 % de terceros armónicos con respecto
a la fundamental. En la sección 1.3 se mencionó que en los transformadores conectados
en delta, las corrientes de fase poseen terceros armónicos y se resaltaron las características
de dichas corrientes, las cuales se corresponden con muchas de las características de las
48
corrientes determinadas con este modelo de la máquina de inducción.
Figura 7.5: Espectro armónico de las corrientes del modelo en coordenadas primitivas.
El modelo en coordenadas primitivas desarrollado está basado en tres tensiones trifásicas
que alimentan las tres bobinas de la máquina, como consecuencia de esta excitación y
bajo los principios electromecánicos ya descritos, circulan las corrientes correspondientes
por cada bobina de la máquina y son éstas las que se determinan mediante las ecuaciones
matriciales anteriormente explicadas. Para ser coherentes con los principios básicos de los
sistemas trifásicos, se puede asumir que las bobinas de la máquina están en delta o en estrella
con el neutro conectado para que puedan circular las corrientes que se presentaron en la
figura 7.4d, ya que bajo estas configuraciones es posible que circulen corrientes de terceros
armónicos como se observa en el espectro armónico de la figura 7.5. Como las tensiones
utilizadas en la simulación del modelo son completamente balanceadas, estas corrientes son
de naturaleza homopolar esto permite comparar los resultados con lo observado y explicado
en la sección 1.3 en referencia a la figura 1.4. En este sentido, al momento de validar los
resultados del modelo con las curvas experimentales, es necesario que las corrientes de dicho
modelo estén libres de terceros armónicos en vista de que las corrientes medidas son de
línea y el neutro nunca estuvo conectado, es decir, no es posible la circulación de corrientes
homopolares. No obstante, como las tensiones que alimentaron a la máquina son reales
lo que puede implicar un cierto desbalance en la alimentación, la circulación de terceros
armónicos no queda completamente descartada, solo que de existir este orden armónico, no
poseerá un desfasaje de un periodo completo en cada fase de la máquina. Resulta conveniente
entonces asumir que la conexión del modelo es en delta por lo que las corrientes obtenidas
mediante el modelo desarrollado son las corrientes dentro de la delta. Definida la máquina
de tal manera es necesario determinar las corrientes que circulan por las líneas, las cuales
49
se pueden observar en la figura 7.6a.
(a) Modelo en coordenadas primitivas. Corrientes de
línea.
(b) Adquisición en el laboratorio. Corrientes en vacío
Figura 7.6: Corrientes absorbidas por la máquina
Las corrientes presentadas en la figura 7.6 se asemejan en la forma aplanada de la cresta
que en el modelo desarrollado es más pronunciado, sin embargo el desbalance en las corrientes
medidas establece claras diferencias entre ambas corrientes.
A nivel mecánico, los tres primeros modelos presentan básicamente la misma respuesta.
La presencia de armónicos en la corriente provoca que el par eléctrico tenga mayor ruido en
el modelo en coordenadas αβ y en el modelo en coordenadas primitivas.
50
(a) Modelo de los enlaces de flujos
(b) Modelo en corrientes
(c) Modelo αβ
(d) Modelo en coordenadas primitivas
Figura 7.7: Par eléctrico
51
(a) Modelo de los enlaces de flujos
(b) Modelo en corrientes
(c) Modelo αβ
(d) Modelo en coordenadas primitivas
Figura 7.8: Velocidad
Ahora se simula una carga mecánica de la forma Tm = kω 2 con k = 1,9 con lo cual
se alcanza un deslizamiento de 0.04. Las corrientes obtenidas en el modelo se presentan
en la figura 7.9a las cuales presentan menor distorsión armónica que en la simulación en
vacío, esto es un resultado coherente porque la contrafuerza electromotriz que se crea con la
carga ayuda a contrarrestar la saturación de la máquina. Estas corrientes presentan cierta
similitud con las corrientes medidas en el laboratorio, sin embargo, el desbalance en estas
últimas crea claras diferencias entre el modelo matemático y los valores experimentales.
52
(a) Modelo en coordenadas primitivas
(b) Adquisición en el laboratorio
Figura 7.9: Corriente en el estator. Máquina cargada s = 0,04
CONCLUSIONES Y RECOMENDACIONES
Conclusiones
Modelar la saturación en la máquina de inducción es importante en diversos casos, en la
mayoría de los modelos que se han desarrollado en vectores espaciales se logra amortiguar
los transitorios con lo cual los resultados de dichos modelos se acercan a la realidad. Sin
embargo, los mencionados modelos no presentan la saturación como un fenómeno que ha
de distorsionar las corrientes como consecuencia de la orientación de los dipolos magnéticos
en la medida en que aumenta el flujo de inducción. Mediante el modelo en coordenadas
primitivas presentado en este trabajo es posible representar matemáticamente la variación de
la permeanza del camino magnético. Este modelo permite obtener corrientes que presentan
armónicos al considerar una característica magnética no lineal
El modelo desarrollado en este trabajo no es del todo exacto en sus resultados ya que no
considera las pérdidas no conservativas de la histéresis que harán que los resultados finales
sean más ajustados a la respuesta experimental de la máquina de inducción estudiada. Otro
elemento que afecta los resultados son las pérdidas por corrientes Foucault que no se han
eliminado previamente de las variables medidas en el laboratorio y como se dijo en la sección
2.1, éstas ensanchan el ciclo de histéresis lo que se traduce en mayores pérdidas.
El comportamiento de la máquina de inducción saturada es muy similar al comportamiento
de un transformador trifásico operando en vacío, se introducen corrientes de tercer armónico
cuando la conexión permite su circulación (delta o estrella con neutro conectado), este
armónico hace que la corriente en el estator presente picos tal como se explicó en la sección
1.3.
Una vez determinado este modelo es posible estudiar y determinar un control adecuado
para una máquina de inducción alimentada por un convertidor puente asimétrico de manera
tal que se regule la saturación a la que se ve sometida la máquina en operación con el
mencionado convertidor de electrónica de potencia.
En la respresentación de fenómenos no lineales como la saturación no es válido la utilización de transformaciones lineales como las utilizadas en el modelo en coordenadas αβ.
Recomendaciones
Las modificaciones en el modelo que incluyan el fenómeno de la histéresis del convertidor
garantizarán que los resultados puedan ser validados con mayor precisión con los resultados
54
experimentales en vista de que dicho fenómeno puede ser considerado como una carga para
la máquina y como se vio en la figura 7.9 el modelo se ajusta bastante bien a los resultados
experimentales cuando es conectada una carga mecánica.
Se recomienda implementar el modelo con un convertidor puente asimétrico como el descrito en el Apéndice G para estudiar el comportamiento de la máquina cuando se considera
la saturación.
REFERENCIAS BIBLIOGRÁFICAS
[1]
ALLER, J. 2008. Máquinas Eléctricas Rotativas: Introducción a la Teoría General. Universidad Simón Bolívar. Departamento de Conversión y Transporte
de Energía. Editorial Equinoccio. Venezuela.
[2]
BUENO, A. 2000. Electrónica de Potencia: Aspectos Generales y Convertidores Electrónicos. Universidad Simón Bolívar. Departamento de Conversión y
Transporte de Energía. Venezuela.
[3]
FRAILE MORA, J. 2003. Máquinas eléctricas. McGraw-Hill. España.
[4]
Pearson Educación. Disponible en internet: http://www.pearsoneducacion.
net/boylestad/recursos/03-Anexo%2003%20063-100.pdf
[5]
Tang, N., Wu, H., Qiu, P. “A saturation model of induction machine by space
vector”, 2001. Fuzhou University, China.
[6]
CHAPMAN, S. 2000. Máquinas eléctricas. Mc Graw Hill. Australia.
[7]
Cabello, A., et al. “Control directo de par del motor de inducción usando un
convertidor puente asimétrico”, 2007. UNEXPO-USB, Caracas.
[8]
E. E. Staff - MIT. “Circuitos magnéticos y transformadores”, 1980. Editorial
Reverté, Argentina.
[9]
BUTCHER, J. C. 2008. Numerical Methods for Ordinary Differential Equations. 2a edición. John Wiley & Sons Ltd, Londres.
[10]
VIOLA, A. , VIOLA, J. 2006. Ecuaciones diferenciales ordinarias. Universidad
Simón Bolívar. Editorial Equinoccio. Venezuela.
[11]
Blas del Hoyo, Alfredo. 2005. “Modelización de la histéresis magnética y su
aplicación al cálculo numérico en máquinas eléctricas”. Barcelona, España.
[12]
Martín, Mª Elena. 2006. “Aportación al modelado del motor trifásico de inducción con consideración de la saturación y el efecto de doble jaula”. Barcelona,
España.
Apéndice A
VECTORES ESPACIALES
A.1.
Definición
En el análisis de los sistemas eléctricos de potencia, es común la implementación de trasformaciones modales, tales como: componentes simétricas, Clark, Park, entre otros. En sistemas
de potencia balanceados, conectados en estrella con el neutro aislado o en delta, la componente de secuencia cero es nula, y por tanto, puede ser despreciada. En estas condiciones,
las componentes de secuencia positiva y negativa poseen un comportamiento similar, en
especial, en sistemas simétricos; adicionalmente una es la compleja conjugada de la otra. A
partir de este principio, la transformación de vectores espaciales puede ser definida como
[?]:

→
−
x ≡
r
2 h
4π
2π
· 1 ej 3 ej 3
3

x
(t)
a
i


·  xb (t)  = xα + jxβ = x (t) · e jξ(t)
xc (t)
(A.1)
q
2
El coeficiente
es el factor necesario para mantener los valores de potencia, iguales
3
entre el sistema de coordenadas primitivas y el de vectores espaciales. En la Figura A.1, se
presenta la interpretación gráfica de la transformación a vectores espaciales.
57
Figura A.1: Representación gráfica del vector espacial de un sistema trifásico [1].
A.2.
Potencia Activa y Reactiva Instantánea
En sistemas de potencia trifásicos, la potencia activa trifásica instantánea P (t), puede ser
calculada por medio de la superposición de la potencia activa instantánea por cada una de
las fases del sistema.
P (t) = va (t) ia (t) + vb (t) ib (t) + vc (t) ic (t)
(A.2)
Por otra parte, la potencia aparente trifásica compleja S, puede ser escrita a partir de los
fasores de tensión fase-neutro y corriente de línea, como:
S = 3 · V · I∗ = P + jQ
(A.3)
Una expresión similar a la ecuación A.3, puede ser obtenida al utilizar vectores especiales:
−−→ −−→ −−→ ∗
s (t) = v (t) · i (t) = P (t) + jQ (t)
Donde:
(A.4)
58


va (t)
h
i
2
2π
4π


· 1 e j 3 e j 3 ·  vb (t) 
3
vc (t)
−−→
v (t) ≡
r
−−→ ∗
i (t) ≡
r
(A.5)

2 h
4π
2π
· 1 ej 3 ej 3
3

i
(t)
a
i


·  ib (t) 
ic (t)
(A.6)
Al sustituir las ecuaciones A.5 y A.6, en la ecuación A.4, se obtiene la expresión de potencia
instantánea en coordenadas primitivas [2]:
−−→
s (t) = P (t) + jQ (t) = [va (t) ia (t) + vb (t) ib (t) + vc (t) ic (t)]
(A.7)
√
+j
3
[vbc (t) ia (t) + vca (t) ib (t) + vab (t) ic (t)]
2
La potencia activa trifásica P (t) calculada a partir de la ecuación A.4, es válida en cualquier condición de operación, para sistemas de potencia de tres o cuatro hilos, para régimen
transitorio y estado estacionario, condición de operación balanceada y desbalanceada; y ante
formas de ondas sinusoidales o no sinusoidales. Por otra parte, la potencia reactiva trifásica
Q (t) no coincide siempre con la definición clásica de la potencia reactiva, expresada en la
ecuación A.3. Como caso especial, para un sistema trifásico sinusoidal balanceado, en estado estacionario, ambas potencias reactivas coinciden, ya que la tensiones y corrientes del
sistema conservan su amplitud y diferencia de fases [2].
Una de las principales ventajas de la definición de la potencia a través de vectores espaciales, es la posibilidad utilizarla de para estimar el comportamiento de la máquina de
inducción en régimen dinámico de operación.
A.3.
Interpretación Física
Es posible obtener una interpretación física de la expresión de potencia instantánea (ecuación A.7), si se considera la relación existente entre la fuerza electromotriz (e) y la intensidad
→
−
→
−
de campo eléctrico ( E ) por una parte y la intensidad de campo magnético ( H ) y la corriente
(i) por otra. En este sentido, el producto vectorial de estas dos intensidades de campo en
→
−
→
− →
−
cada punto del espacio y el tiempo, define el vector de Pointing S = E × H .
El vector de Pointing es un vector variable en el espacio y el tiempo; y representa el flujo
de potencia transferida por unidad de área, debido a los campos electromagnéticos. Para
59
el caso de las máquinas eléctricas rotatorias, en el entre hierro de las mismas, el vector de
Pointing en cada punto del espacio y del tiempo, tiene dos componentes: una en sentido axial
y otra en sentido tangencial. La componente axial, determina la potencia activa transferida
entre el estator y el rotor, mientras que la tangencial, representa la potencia que fluye en el
entrehierro para mantener el campo electromagnético rotatorio [2].
→
−
Dado que la corriente (i), está relacionado con la intensidad de campo magnético ( H ) por
la Ley de Ampère; y la fuerza electromotriz (e) está relacionada con la intensidad de campo
→
−
eléctrico ( E ) por la Ley de Faraday. Es posible pensar, que la potencia activa instantánea
(P (t)) está relacionada con la componente radial del vector de Pointing, y la potencia
reactiva instantánea (Q (t)) con la componente tangencial de este vector [2].
Apéndice B
MÉTODO DE EULER
El Método de Euler o de la Recta Tangente, fue publicado por el matemático suizo L.
Euler (1707-1783), en su trabajo de tres tomos: “Institutiones Calculi Integralis”, en los
años 1768 a 1770. Este método permite conocer la solución aproximada de una ecuación
diferencial ordinaria de primer orden, en forma numérica [9].
Considérese la siguiente ecuación diferencial ordinaria:
dy
= y 0 (x) = f (x, y) ,
dx
y (x0 ) = y0
(B.1)
La solución de la ecuación diferencial ordinaria B.1, puede ser aproximada numéricamente,
según el Método de Euler, utilizando la siguiente fórmula general:
yn+1 = yn + f (xn , yn ) · (xn+1 − xn )
(B.2)
El procedimiento consiste en construir una curva poligonal en n pasos, trazando en cada
punto (xn , yn ), una recta de pendiente f (xn , yn ). Dicha curva, representa la solución de la
ecuación diferencial [10].
Conforme (xn+1 − xn ) → 0, la solución de la ecuación diferencial obtenida por el Método
de Euler, representara con mayor precisión y exactitud la solución real del problema. Esto
se debe a que, para variaciones pequeñas de x, la pendiente f (xn , yn ), no varía significativamente, y por lo tanto, esta puede ser empleada para estimar el siguiente valor de la curva
de solución [10].
B.1.
Modo Matricial
Para un sistema de ecuaciones diferenciales ordinarias de primer orden, de soluciones:
y1 , y2 , . . . yN . Un equivalente a la ecuación B.1, puede ser escrita en forma matricial, de la
siguiente manera:
61






y10
y20
..
.
0
yN


f1 (x, y1 , y2 , . . . yN )
 
  f2 (x, y1 , y2 , . . . yN )
=
..
 
.
 
fN (x, y1 , y2 , . . . yN )




,







y1 (x0 )
y2 (x0 )
..
.
yN (x0 )


 
 
=
 
 
y10
y20
..
.






(B.3)
yN 0
La aplicación de la fórmula general de Euler (ecuación B.2) a cada fila del sistema de
ecuaciones diferenciales representado matricialmente en la ecuación B.3, permite obtener
numéricamente en forma aproximada, las curvas y1 , y2 , . . . yN .
Apéndice C
PROGRAMA COMPUTACIONAL PARA EL MODELO DE LOS
ENLACES DE FLUJOS
Programa principal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
% > > > > > > > > > > > > > > > > Modelo de los enlaces de flujo
<<<<<<<<<<<<<<<<<<<<<<<<
% > > > > > > > > > > > > > > > > > > > > > > > Programa rincipal
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
clear all
clc
close all
global vr Rr Rs Lsigr Lsigs Lm J pp PsiT tauT Mf Mi k Lm0 A
% Se definen los parámetros de la máquina
Lsigs =0.0772; % Inductancia de dispersión del estator
Lsigr =0.0772; % Inductancia de dispersión del rotor
Rr =0.066; % Resistencia del rotor
Rs =0.0324; % Resistencia del estator
Lm =1.2; % Inductancia de la rama de magnetización
% La tensión en las bobinas del rotor es cero por estar cortocircuitado
vr =0;
pp =2; % Número de pares de polos de la máquina
f =60; % Frecuencia nominal de operación ( Hz )
wb =2* pi * f ; % Frecuencia base de la máquina ( rad / s )
tb =1/ wb ; % Tiempo base
H =1.5; % Constante de inercia
J =2* H * wb / pp ; % Momento de inercia
k =0; % Constante de carga
y0 =[0 0 0]; % Vector de valores iniciales
A =1; % Tensión efectiva en el estator en por unidad
tsimul =0.5; % Tiempo de simulación
%Parámetros de ajustes de la curva de magnetización
Lm0 =2.2; % Inductancia en la zona lineal
Lmsat =0.12; % Inductancia en la zona
63
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
PsiT =1.6; % Nivel de flujo donde empieza a saturar la curva
fT =0.8; % Curvatura del codo de saturacion
tauT = fT / PsiT * Lm0 / Lmsat ;
Mf = 1/ Lmsat ;
Mi = (1/ Lm0 - 1/ Lmsat *(.5 - atan ( tauT * PsiT ) / pi ) ) /(.5+ atan ( tauT * PsiT ) /
pi ) ;
% Se resuelve numéricamente las ecuaciones del modelo
[t , sol ]= ode1 ( @fluxlinkageEC ,0 , tsimul / tb , y0 , pi () /120) ;
% Se redefinen los resultados obtenidos
lambs = sol (: ,1) ;
lambr = sol (: ,2) ;
wr = sol (: ,3) ;
%Cálculo de las corrientes y flujo de magnetización en vectores
espaciales
m = size ( sol ) ;
Isr = zeros ( m (1) ,2) ; % Vector de corrientes del estator y rotor
Lmm = zeros ( m (1) ,1) ; % Vector de inductancias de magnetización
imv = zeros ( m (1) ,1) ; % Vector de corrientes de magnetización
Lambdamv = zeros ( m (1) ,1) ; % Vector de enlaces de flujo de magnetización
Lmm (1 ,1) = Lm ;
Te = zeros ( m (1) ,1) ;
for k =1:1: m (1)
LL =[ Lsigs + Lmm ( k ) , Lmm ( k ) ; Lmm ( k ) , Lsigr + Lmm ( k ) ]; %Matriz de
inductancias
Isr (k ,:) =( inv ( LL ) *[ lambs ( k ) ; lambr ( k ) ]) ; % Cálculo de corrientes
imv ( k ) = Isr (k ,1) + Isr (k ,2) ; % Cálculo de corriente de magnetizción
Lambdamv ( k ) = Lmm ( k ) * imv ( k ) ; % Cálculo de flujo de magnetización
Lambdamm = abs ( Lambdamv ( k ) ) ;
imm =( Mf - Mi ) / pi *( (( Lambdamm - PsiT ) .* atan ( tauT *( Lambdamm - PsiT ) ) - PsiT *
atan ( tauT * PsiT ) ) + .5/ tauT *( log (1+( tauT * PsiT ) ^2) - log (1+ tauT ^2*(
Lambdamm - PsiT ) .^2) ) ) + Lambdamm .*( Mf + Mi ) /2;
imlin = inv ( Lm0 ) * Lambdamm ;
if imm - imlin <1 e -4
Lmm ( k +1) = Lm0 ;
else
Lmm ( k +1) = Lambdamm / imm ;
end
Te ( k ) =(3/2) * Lmm ( k ) * imag ( Isr (k ,1) * conj ( Isr (k ,2) ) ) ;
end
% Transformación a variables de fase
a = exp (1 i *2* pi /3) ;
% Corrientes en el estator
ia = sqrt (2/3) * real ( Isr (: ,1) ) ;
ib = sqrt (2/3) * real (( Isr (: ,1) ) * a ^2) ;
ic = -( ia + ib ) ;
64
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
% Flujos en el Estator
lambsa = sqrt (2/3) * real ( lambs (:) ) ;
lambsb = sqrt (2/3) * real (( lambs (:) ) * a ^2) ;
lambsc = -( lambsa + lambsb ) ;
% Flujos en el Rotor
lambra = sqrt (2/3) * real ( lambr (:) ) ;
lambrb = sqrt (2/3) * real (( lambr (:) ) * a ^2) ;
lambrc = -( lambra + lambrb ) ;
%> > > > > > > > > > > > > > > > > > > > Resultados obtenidos < < < < < < < < < < < < < < < < < < < < < < < < < < < <
% Límites de figuras
y1 =[0 0.5];
y2 =[0.35 0.4];
% Flujos en el estator
figure (1)
plot ( t * tb , lambsa , t * tb , lambsb , t * tb , lambsc , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Flujo ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
xlim ( y1 )
% Velocidad
figure (2)
plot ( t * tb , wr , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Velocidad ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
xlim ( y1 )
ylim ([0 1.2])
% Corrientes en el estator
figure (3)
plot ( t * tb , ia , t * tb , ib , t * tb , ic , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Corriente ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
xlim ( y1 )
% Corrientes en el rotor
figure (4)
plot ( t * tb , ii (: ,4) ,t * tb , ii (: ,5) ,t * tb , ii (: ,6) , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
65
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Corriente ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
xlim ( y1 )
% Flujos en el rotor
figure (5)
plot ( t * tb , lambra , t * tb , lambrb , t * tb , lambrc , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Flujo ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
xlim ( y1 )
% Par eléctrico
figure (6)
plot ( t * tb , Te , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Par eléctrico ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
xlim ( y1 )
Función utilizada
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function px = fluxlinkageEc (t , x )
global vr Rr Rs Lsigr Lsigs Lm J PsiT tauT Mf Mi k Lm0 A
%Se renombran las variables del programa
lambs = x (1) ;
lambr = x (2) ;
wr = x (3) ;
%Se define el vector espacial de tensión
vsa = A * sqrt (2) * sin ( t ) ;
vsb = A * sqrt (2) * sin (t -2* pi /3) ;
vsc = A * sqrt (2) * sin ( t +2* pi /3) ;
a = exp (1 i *2* pi /3) ;
vs = sqrt (2/3) *[1 a a ^2]*[ vsa ; vsb ; vsc ];
%Se calculan las corrientes de rotor y estator
L =[ Lsigs + Lm , Lm ; Lm , Lsigr + Lm ];
lamb =[ lambs ; lambr ];
Ii = inv ( L ) * lamb ;
%Se calculan los enlaces de flujos
66
18
19
20
21
22
23
24
25
26
27
28
29
30
A1 = vs - Rs * Ii (1) ; % Derivada del enlace de flujo del estator
A2 = vr - Rr * Ii (2) +1 i * wr * lambr ; %Derivada del enlace de flujo del rotor
%Ecuación de par
Tm = k * wr ^2;
Te =(3/2) * Lm * imag ( Ii (1) * conj ( Ii (2) ) ) ;
A3 =( Te - Tm ) / J ;
Lambdam = Lm * abs ( Ii (1) + Ii (2) ) ;
%Derivada de las variables de estado
px =[ A1 ; A2 ; A3 ];
%Se determina el valor de la inductancia asociada al flujo de
%magnetización obtenido
imsat = ( Mf - Mi ) / pi *( (( Lambdam - PsiT ) .* atan ( tauT *( Lambdam - PsiT ) ) PsiT * atan ( tauT * PsiT ) ) + .5/ tauT *( log (1+( tauT * PsiT ) ^2) - log (1+ tauT
^2*( Lambdam - PsiT ) .^2) ) ) + Lambdam .*( Mf + Mi ) /2;
imlin = inv ( Lm0 ) * Lambdam ;
31
32
33
34
35
36
if imsat - imlin <1 e -4
Lm = Lm0 ;
else
Lm = Lambdam / imsat ;
end
Apéndice D
PROGRAMA COMPUTACIONAL PARA EL MODELO EN
CORRIENTES
Programa principal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
% > > > > > > > > > > > > > > > > Modelo de los enlaces de flujo
<<<<<<<<<<<<<<<<<<<<<<<<
% > > > > > > > > > > > > > > > > > > > > > > > Programa rincipal
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
clear all
clc global
Rr Rs Lsigs Lsigr vr im J k PsiT tauT Mf Mi Lm0 pp A
%Parámetros de la máquina
Lsigs =0.0772; % Inductancia de dispersión del estator
Lsigr =0.0772; % Inductancia d dispersión del rotor
Rr =0.066; % Resistencia del rotor
Rs =0.0324; % Resistencia del estator
vr =0; %Tensión en las bobinas del rotor
pp =2; % Número de pares de polor
f =60; % Frecuencia eléctrica ( Hz )
wb =2* pi * f ; % Frecuencia base ( rad / s )
tb =1/ wb ; % Tiempo base ( s )
H =1; % Constante de inercia
J =2* H * wb / pp ; % Momento de inercia
k =0; % Constante de carga
tsimul =0.5; % Tiempo de simulación
y0 =[0 0 0 0 0]; % Vector de valores iniciales
A =1; % Tensión efectiva ( pu )
%Parámetros de ajustes de la curva de magnetización
Lm0 =2.2; % Inductancia en la zona lineal
Lmsat =0.12; % Inductancia en la zona
PsiT =1.6; % Nivel de flujo donde empieza a saturar la curva
fT =0.8; % Curvatura del codo de saturacion
tauT = fT / PsiT * Lm0 / Lmsat ;
Mf = 1/ Lmsat ;
68
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
Mi = (1/ Lm0 - 1/ Lmsat *(.5 - atan ( tauT * PsiT ) / pi ) ) /(.5+ atan ( tauT * PsiT ) /
pi ) ;
% Se resuelve numéricamente las ecuaciones del modelo
[ tc , sol ]= ode45 ( @currentmodelEc ,[0 tsimul / tb ] , y0 )
t = tc ;
is = sol (: ,1) ;
ir = sol (: ,3) ;
irconj = sol (: ,4) ;
wr = sol (: ,5) ;
% Corrientes en cada fase del estator
a = exp (1 i *2* pi /3) ;
isa = sqrt (2/3) * real ( sol (: ,1) ) ;
isb = sqrt (2/3) * real (( sol (: ,1) ) * a ^2) ;
isc = -( isa + isb ) ;
% Corrientes en cada fase del rotor
ira = sqrt (2/3) * real ( ir ) ;
irb = sqrt (2/3) * real (( ir ) * a ^2) ;
irc = -( ira + irb ) ;
%Cálculo de los flujos
n = size ( sol ) ;
lambm = zeros ( n (1) ,1) ; % Flujo de magnetización
lambs = zeros ( n (1) ,1) ; % Flujo en el estator
lambr = zeros ( n (1) ,1) ; % Flujo en el rotor
im = zeros ( n (1) ,1) ; % Corriente de magnetización
Te = zeros ( n (1) ,1) ; % Par eléctrico
for k =1: n (1)
imv =( ir ( k ) + is ( k ) ) ;
im ( k ) = abs ( imv ) ;
theta = angle ( imv ) ;
lambdam = fsolve ( @ ( x ) im ( k ) -(( Mf - Mi ) / pi *( (( x - PsiT ) .* atan ( tauT *( x PsiT ) ) - PsiT * atan ( tauT * PsiT ) ) + .5/ tauT *( log (1+( tauT * PsiT ) ^2) log (1+ tauT ^2*( x - PsiT ) .^2) ) ) + x .*( Mf + Mi ) /2) ,0.05) ;
%Determina si se encuentra en la zona lineal o en la saturada
imsat = ( Mf - Mi ) / pi *( (( lambdam - PsiT ) .* atan ( tauT *( lambdam - PsiT ) )
- PsiT * atan ( tauT * PsiT ) ) + .5/ tauT *( log (1+( tauT * PsiT ) ^2) - log
(1+ tauT ^2*( lambdam - PsiT ) .^2) ) ) + lambdam .*( Mf + Mi ) /2;
imlin = inv ( Lm0 ) * lambdam ;
%Se calcula la inductancia en estado estacionario y transitorio
if imsat - imlin <1 e -4
Lms = Lm0 ;
Lmt = feval ( @derivadaim , lambdam ) ;
else
Lms = lambdam / im ( k ) ;
Lmt = feval ( @derivadaim , lambdam ) ;
end
69
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
lambm ( k ) = Lms * imv ;
lambs ( k ) = Lsigs * is ( k ) + lambm ( k ) ;
lambr ( k ) = Lsigr * ir ( k ) + lambm ( k ) ;
Te ( k ) =(3/2) * Lms * imag ( is ( k ) .* irconj ( k ) ) ;
end
%Flujos en cada fase
%Estator
lambsa = sqrt (2/3) * real ( lambs (:) ) ;
lambsb = sqrt (2/3) * real (( lambs (:) ) * a ^2) ;
lambsc = -( lambsa + lambsb ) ;
%Rotor
lambra = sqrt (2/3) * real ( lambr (:) ) ;
lambrb = sqrt (2/3) * real (( lambr (:) ) * a ^2) ;
lambrc = -( lambra + lambrb ) ;
%> > > > > > > > > > > > > > > > > > > > Resultados obtenidos < < < < < < < < < < < < < < < < < < < < < < < < < < <
% Flujos en el estator
figure (1)
plot ( t * tb , lambsa , t * tb , lambsb , t * tb , lambsc , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Flujos en el estator ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
% Velocidad
figure (2)
plot ( t * tb , wr , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Velocidad ( rad / s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
% Corrientes en el estator
figure (3) plot ( t * tb , isa , t * tb , isb , t * tb , isc , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Corrientes en el estator ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
% Corrientes en el rotor
figure (4) plot ( t * tb , ira , t * tb , irb , t * tb , irc , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Corrientes en el rotor ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
70
112
113
114
115
116
117
118
119
120
121
122
123
124
125
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
% Flujos en el rotor
figure (5) plot ( t * tb , lambra , t * tb , lambrb , t * tb , lambrc , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Flujos en el rotor ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
% Par eléctrico
figure (6)
plot ( t * tb , Te , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Par eléctrico ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
Funciones utilizadas
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
function px = currentmodelEc (t , x )
global Rr Rs Lsigs Lsigr vr im J k PsiT tauT Mf Mi Lm0 pp A
% Se renombran las variables de la función
is = x (1) ;
isconj = x (2) ;
ir = x (3) ;
irconj = x (4) ;
palfa = x (5) ;
% Se definen las tensiones en las bobinas del estator
vsa = A * sqrt (2) * sin ( t ) ;
vsb = A * sqrt (2) * sin (t -2* pi /3) ;
vsc = A * sqrt (2) * sin ( t +2* pi /3) ;
% Vector espacial de tensión en el estator
a = exp (1 i *2* pi /3) ;
vs = sqrt (2/3) *[1 a a ^2]*[ vsa ; vsb ; vsc ];
%Corriente de magnetización
imv =( is + ir ) ;
im = abs ( imv ) ;
theta = angle ( imv ) ;
%Cálculo del flujo de magnetización asociado a la corriente de
%magnetización im
lambdam = fsolve ( @ ( x ) im -(( Mf - Mi ) / pi *( (( x - PsiT ) .* atan ( tauT *( x - PsiT ) )
- PsiT * atan ( tauT * PsiT ) ) + .5/ tauT *( log (1+( tauT * PsiT ) ^2) - log (1+
tauT ^2*( x - PsiT ) .^2) ) ) + x .*( Mf + Mi ) /2) ,0.05) ;
% Cálculo de la inductancia de magnetización transitoria y
estacionaria
71
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
1
2
3
4
5
6
7
8
9
10
11
12
13
imsat = ( Mf - Mi ) / pi *( (( lambdam - PsiT ) .* atan ( tauT *( lambdam - PsiT ) ) PsiT * atan ( tauT * PsiT ) ) + .5/ tauT *( log (1+( tauT * PsiT ) ^2) - log (1+ tauT
^2*( lambdam - PsiT ) .^2) ) ) + lambdam .*( Mf + Mi ) /2;
imlin = inv ( Lm0 ) * lambdam ;
if imsat - imlin <1 e -4
Lms = Lm0 ;
Lmt = feval ( @derivadaim , lambdam ) ;
else
Lms = lambdam / im ;
Lmt = feval ( @derivadaim , lambdam ) ;
end
Lo =( Lmt + Lms ) /2;
L2 =( Lmt - Lms ) /2;
N =[ Rs 0 0 0;0 Rs 0 0; -1 i .* palfa * Lms 0 Rr -1 i .* palfa *( Lsigr + Lms ) 0;0
1 i .* palfa * Lms 0 1 i .* palfa *( Lsigr + Lms ) + Rr ];
M =[ Lsigs + Lo , L2 * exp (2*1 i .* theta ) , Lo , L2 * exp (2*1 i .* theta ) ; L2 * exp
( -2*1 i .* theta ) , Lsigs + Lo , L2 * exp ( -2*1 i .* theta ) , Lo ; Lo , L2 * exp (2*1 i .*
theta ) , Lsigr + Lo , L2 * exp (2*1 i .* theta ) ; L2 * exp ( -2*1 i .* theta ) , Lo , L2 *
exp ( -2*1 i .* theta ) , Lsigr + Lo ];
Minvr = inv ( M ) ;
v =[ vs ; conj ( vs ) ; vr ; conj ( vr ) ]; %Vector de tensiones
ii =[ is ; isconj ; ir ; irconj ]; % Vector de corrientes
pisr = Minvr *( v - N * ii ) ; %Derivada de las corrientes
Tm = k * palfa ^2; %Par mecánico
Te =(3/2) * Lms * imag ( is .* irconj ) ; % Par eléctrico
pw =( Te - Tm ) / J ; %Derivada de la velocidad
px =[ pisr ; pw ]; % Derivada de las variables de estado
end
function df = derivadaim ( Lambdam )
% Esta función permite clacular la derivada de la corriente de
% magnetización con respecto al flujo de dicha rama
%Se utiliza la expresión arcotangente de la corriente de magnetización
Lm0 =2.2; % Inductancia en la zona lineal
Lmsat =0.12; % Inductancia en la zona
PsiT =1.6; % Nivel de flujo donde empieza a saturar la curva
fT =0.8; % Curvatura del codo de saturacion
tauT = fT / PsiT * Lm0 / Lmsat ;
Mf = 1/ Lmsat ;
Mi = (1/ Lm0 - 1/ Lmsat *(.5 - atan ( tauT * PsiT ) / pi ) ) /(.5+ atan ( tauT * PsiT ) /
pi ) ;
% Finalmente se evalúa en la derivada con el valor de flujo
df = inv (( Mf - Mi ) / pi *( atan ( tauT *( Lambdam - PsiT ) ) +( Lambdam - PsiT ) .*
inv (1+( tauT *( Lambdam - PsiT ) ) ^2) .* tauT -.5/ tauT * inv (1+ tauT ^2*(
Lambdam - PsiT ) .^2) *2* tauT ^2*( Lambdam - PsiT ) ) +( Mf + Mi ) /2) ;
72
14
end
Apéndice E
PROGRAMA COMPUTACIONAL PARA EL MODELO EN
COORDENADAS αβ
Programa Principal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
% > > > > > > > > > > > > > > > > Modelo en coordenadas alfa - beta
<<<<<<<<<<<<<<<<<<<<<<<
% > > > > > > > > > > > > > > > > > > > > > > > Programa rincipal
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
clc clear all global vr vra vrb vrc Lsigr Lsigs Lm Lsr R J K Lm0 Lmsat
PsiT fT a tauT Mf Mi A vec_esp f1
% Transformada a vectores espaciales
alfa = exp (1 j *2* pi /3) ;
alfa2 = alfa * alfa ;
vec_esp = sqrt (2/3) *[1 , alfa , alfa2 ];
A =1; %Amplitud de la tensión de entrada en pu
vr =[0;0]; % Tensión en las bobinas del rotor
f = sqrt (3) ;
f1 = inv ( f ) ;
f3 = sqrt (3/2) ;
% Parámetros de la máquina
Lsigs = f3 *0.0772; % Inductancia de dispersión del estator
Lsigr = f3 *0.0772; % Inductancia de dispersión del rotor
Lm =1.2; % Inductancia de magnetización
Lsr = Lm ;
Rralf =0.066; % Resistencia de la bobina alfa del rotor
Rrbet =0.066; % Resistencia de la bobina beta del rotor
Rsalf =0.0324; % Resistencia de la bobina alfa del estator
Rsbet =0.0324; % Resistencia de la bobina beta del estator
pp =2; % Número de pares de polos
K =0; % Constante de carga
f =60; % frecuencia ( Hz )
wb =2* pi * f ; % frecuncia base ( rad / s )
tb =1/ wb ; % Tiempo base ( s )
H =1; % Constante de inercia
74
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
J =2* H * wb / pp ; % Momento de inercia
y0 =[0 ,0 ,0 ,0 ,0 ,0]; % Vector de valores iniciales
tsimul =0.5; % Tiempo de simulación
a = alfa ;
%Parámetros de ajustes de la curva de magnetización
Lm0 =2.2; % Inductancia en la zona lineal
Lmsat =0.12; % Inductancia en la zona
PsiT =1.6; % Nivel de flujo donde empieza a saturar la curva
fT =0.8; % Curvatura del codo de saturacion
tauT = fT / PsiT * Lm0 / Lmsat ;
Mf = 1/ Lmsat ;
Mi = (1/ Lm0 - 1/ Lmsat *(.5 - atan ( tauT * PsiT ) / pi ) ) /(.5+ atan ( tauT * PsiT ) /
pi ) ;
%Matriz resistencias
R =[ Rsalf ,0 ,0 ,0;0 , Rsbet ,0 ,0;0 ,0 , Rralf ,0;0 ,0 ,0 , Rrbet ];
%Se resuelve numéricamente las ecuaciones del modelo
[t , sol ]= ode1 ( @Modelo_Saturacion_alfaBeta ,0 , tsimul / tb , y0 , pi () /120) ;
%Se renombran las variables
n = size ( sol (: ,1) ) ;
lambalfs = sol (: ,1) ;
lambbets = sol (: ,2) ;
lambalfr = sol (: ,3) ;
lambbetr = sol (: ,4) ;
theta = sol (: ,5) ;
wr = sol (: ,6) ;
%Se crean los vectores de flujo
lambr_vec = lambalfr +1 i * lambbetr ;
lambs_vec = lambalfs +1 i * lambbets ;
% Cálculo de los flujos en cada fase del estator
lambsa = sqrt (2/3) * real ( lambs_vec ) ;
lambsb = sqrt (2/3) * real ( lambs_vec * a ^2) ;
lambsc = -( lambsa + lambsb ) ;
% Cálculo de los flujos en cada fase del rotor
lambra = sqrt (2/3) * real ( lambr_vec ) ;
lambrb = sqrt (2/3) * real ( lambr_vec * a ^2) ;
lambrc = -( lambra + lambrb ) ;
%Cálculo de las corrientes
ii = zeros ( n (1) ,4) ;
is_vec = zeros ( n (1) ,1) ;
Te = zeros ( n (1) ,1) ;
iabcs = zeros (3 , n (1) ) ;
iabcr = zeros (3 , n (1) ) ;
for k =1: n (1)
Salfs = gradosaturacion2 ( f1 * abs ( lambalfs ( k ) ) ) ;
Sbets = gradosaturacion2 ( f1 * abs ( lambbets ( k ) ) ) ;
75
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
Salfr = gradosaturacion2 ( f1 * abs ( lambalfr ( k ) ) ) ;
Sbetr = gradosaturacion2 ( f1 * abs ( lambbetr ( k ) ) ) ;
Lsat =[ Lsigs + Lm / Salfs ,0 ,2* inv ( Salfs + Salfr ) * Lsr * cos ( theta ( k ) ) , -2* inv (
Salfs + Sbetr ) * Lsr * sin ( theta ( k ) ) ; 0 , Lsigs + Lm / Sbets ,2* inv ( Sbets + Salfr ) *
Lsr * sin ( theta ( k ) ) ,2* inv ( Sbets + Sbetr ) * Lsr * cos ( theta ( k ) ) ; 2* inv ( Salfs +
Salfr ) * Lsr * cos ( theta ( k ) ) ,2* inv ( Sbets + Salfr ) * Lsr * sin ( theta ( k ) ) , Lsigr + Lm
/ Salfr ,0;
-2* inv ( Salfs + Sbetr ) * Lsr * sin ( theta ( k ) ) ,2* inv ( Sbets +
Sbetr ) * Lsr * cos ( theta ( k ) ) ,0 , Lsigr + Lm / Sbetr ];
lamb =[ lambalfs ( k ) ; lambbets ( k ) ; lambalfr ( k ) ; lambbetr ( k ) ];
ii (k ,:) = inv ( Lsat ) * lamb ;
is_vec = ii (k ,1) +1 i * ii (k ,2) ;
lambs_vec = lambalfs ( k ) +1 i * lambbets ( k ) ;
Te ( k ) = - imag ( lambs_vec .* conj ( is_vec ) ) ;
end
% Corrientes de fase
%Estator
isa = sqrt (2/3) * ii (: ,1) ;
isb = sqrt (2/3) * real (( ii (: ,1) +1 i * ii (: ,2) ) * a ^2) ;
isc = -( isa + isb ) ;
%Rotor
ira = sqrt (2/3) * ii (: ,3) ;
irb = sqrt (2/3) * real (( ii (: ,3) +1 i * ii (: ,4) ) * a ^2) ;
irc = -( ira + irb ) ; y1 =[0 0.5]; y2 =[0.35 0.4];
%> > > > > > > > > > > > > > > > > > > > Resultados obtenidos < < < < < < < < < < < < < < < < < < < < < < < < < < < <
% Flujos en el estator
figure (1)
plot ( t * tb , lambsa , t * tb , lambsb , t * tb , lambsc , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Flujo ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
% Velocidad
figure (2)
plot ( t * tb , wr , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Velocidad ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
% Corrientes en el estator
figure (3) plot ( t * tb , isa , t * tb , isb , t * tb , isc , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Corriente ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
76
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
% Corrientes en el rotor
figure (4)
plot ( t * tb , ira , t * tb , irb , t * tb , irc , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Corriente ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
% Flujos en el rotor
figure (5)
plot ( t * tb , lambra , t * tb , lambrb , t * tb , lambrc , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Flujo ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
% Par eléctrico
figure (6)
plot ( t * tb , Te , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Par eléctrico ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
Funciones utilizada
1
2
3
4
5
6
7
8
9
10
11
12
13
14
function px = M o d e l o _ S a t u r a c i o n _ a l f a B e t a (t , x )
global vr vra vrb vrc Lsigr Lsigs Lm Lsr R J K Lm0 Lmsat PsiT fT a tauT
Mf Mi A vec_esp f1
% Se renombran las variables del programa
lambalfs = x (1) ;
lambbets = x (2) ;
lambalfr = x (3) ;
lambbetr = x (4) ;
theta = x (5) ;
wr = x (6) ;
%Se define la tensión en el estator
vsa = A * sqrt (2) * cos ( t ) ;
vsb = A * sqrt (2) * cos (t -2* pi /3) ;
vsc = A * sqrt (2) * cos ( t +2* pi /3) ;
% Se crea la tensión en coordenadas alfa - beta
77
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
1
2
3
4
5
6
7
8
9
10
11
12
v_vec = vec_esp *[ vsa ; vsb ; vsc ];
valfa = real ( v_vec ) ;
vBeta = imag ( v_vec ) ;
vs =[ valfa ; vBeta ];
v =[ vs ; vr ];
% Se determinan los grados de saturación
Salfs = gradosaturacion2 ( f1 * abs ( lambalfs ) ) ;
Sbets = gradosaturacion2 ( f1 * abs ( lambbets ) ) ;
Salfr = gradosaturacion2 ( f1 * abs ( lambalfr ) ) ;
Sbetr = gradosaturacion2 ( f1 * abs ( lambbetr ) ) ;
% Matriz de inductancias
Lsat =[ Lsigs + Lm / Salfs ,0 ,2* inv ( Salfs + Salfr ) * Lsr * cos ( theta ) , -2* inv ( Salfs +
Sbetr ) * Lsr * sin ( theta ) ; 0 , Lsigs + Lm / Sbets ,2* inv ( Sbets + Salfr ) * Lsr * sin (
theta ) ,2* inv ( Sbets + Sbetr ) * Lsr * cos ( theta ) ; 2* inv ( Salfs + Salfr ) * Lsr * cos (
theta ) ,2* inv ( Sbets + Salfr ) * Lsr * sin ( theta ) , Lsigr + Lm / Salfr ,0;
-2*
inv ( Salfs + Sbetr ) * Lsr * sin ( theta ) ,2* inv ( Sbets + Sbetr ) * Lsr * cos ( theta ) ,0 ,
Lsigr + Lm / Sbetr ];
lamb =[ lambalfs ; lambbets ; lambalfr ; lambbetr ]; % Flujos
ii = Lsat \ lamb ; % Corrientes
plamb =v - R * ii ; %Derivada del flujo
is_vec = ii (1) +1 i * ii (2) ;
lambs_vec = lamb (1) +1 i * lamb (2) ;
Te = - imag ( lambs_vec .* conj ( is_vec ) ) ; % Par eléctrico
Tm = K * wr ^2; % Par mecánico
pwr =( Te - Tm ) / J ; % Derivada de la velocidad
ptheta = wr ; % Derivada de la posición angular
px =[ plamb ; ptheta ; pwr ]; % Derivada de las variables de estado
end
function s = gradosaturacion2 ( lambda )
%Esta función permite determinar el grado de saturación a partir del
módulo
%del flujo y las curvas de magnetización real y lineal
global vr vra vrb vrc Lsigr Lsigs Lm Lsr J k I R Lm0 Lmsat PsiT fT a
tauT Mf Mi A dca dcb dcc vec_esp
imsat = ( Mf - Mi ) / pi *( (( lambda - PsiT ) .* atan ( tauT *( lambda - PsiT ) ) PsiT * atan ( tauT * PsiT ) ) + .5/ tauT *( log (1+( tauT * PsiT ) ^2) - log (1+ tauT
^2*( lambda - PsiT ) .^2) ) ) + lambda .*( Mf + Mi ) /2;
imlin = inv ( Lm0 ) * lambda ;
if abs ( imsat - imlin ) <1e -3
s =1;
else
s = imsat / imlin ;
end
end
78
Apéndice F
PROGRAMA COMPUTACIONAL PARA EL MODELO EN
COORDENADAS PRIMITIVAS
Programa principal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
%> > > > > > > > > > > > > > > Modelo de la máquina de inducción <<< <<<<< <<<<< < %
%> > > > > > > > > > > > > > > Modelo en coordenadas primitivas < << << << < << << << < %
%> > > > > > > > > > > > > > > > > > > > Programa Principal < < < < < < < < < < < < < < < < < < < < < < < < %
clear all
global vra vrb vrc Lsigr Lsigs Lm Lsr J K I R Lm0 PsiT fT tauT Mf Mi A vec_esp
%Se define la transfromación a vectores espaciales
alfa = exp (1 j *2* pi /3) ;
alfa2 = alfa * alfa ;
vec_esp = sqrt (2/3) *[1 , alfa , alfa2 ];
%Tensiones rotor
vra =0;
vrb =0;
vrc =0;
A =1; %Tensión efectiva en el estator en por unidad
%Parámetros de la máquina
Lsigs =0.0772; %Inductancia de dispersión del estator
Lsigr =0.0772; %Inductancia de dispersión del rotor
Lm =1.2; %Inductancia de magnetización
Lsr = Lm ;
Rr =0.066; %Resistencia de los devanados del rotor
Rs =0.0324; %Resistencia de los devanados del estator
pp =2; %Número de pares de polos
K =0; %La constante de carga
f =60; %Frecuencia eléctrica
wb =2* pi * f ; %Frecuencia base
tb =1/ wb ; %Tiempo base
H =1; %Constante de inercia
J =2* H * wb / pp ; %Momento de inercia
y0 =[0 ,0 ,0 ,0 ,0 ,0 ,0 ,0]; %Vector inicial
tsimul =0.5; %Tiempo de simulación
%Definición de las matrices invariantes
I = eye (3) ; %Matriz identidad
R =[ Rs *I , zeros (3) ; zeros (3) , Rr * I ]; %Matriz de resistencias de la maquina
%Parámetros de ajustes de la curva de magnetización
Lm0 =2.2; %Inductancia en la zona lineal
Lmsat =0.12; %Inductancia en la zona
80
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
PsiT =1.6; %Nivel de flujo donde empieza a saturar la curva
fT =0.8; %Curvatura del codo de saturacion
tauT = fT / PsiT * Lm0 / Lmsat ;
Mf = 1/ Lmsat ;
Mi = (1/ Lm0 - 1/ Lmsat *(.5 - atan ( tauT * PsiT ) / pi ) ) /(.5+ atan ( tauT * PsiT ) / pi ) ;
%Se resuelve numéricamente las ecuaciones de la máquina
[t , sol ]= ode1 ( @Modelo_Saturacion_Flujo ,0 , tsimul / tb , y0 , pi () /120) ;
%Cálculo de las corrientes
n = size ( sol ) ;
ii = zeros ( n (1) ,6) ;
Te = zeros ( n (1) ,1) ;
for k =1:1: n (1)
vsa = A * sqrt (2) * cos ( t ( k ) ) ;
vsb = A * sqrt (2) * cos ( t ( k ) -2* pi /3) ;
vsc = A * sqrt (2) * cos ( t ( k ) +2* pi /3) ;
%Determinanción de los grados de saturación en cada fase del estator y el
%rotor a partir de los enlaces de flujos
Sas = gradosaturacion ( abs ( sol (k ,1) ) ) ;
Sbs = gradosaturacion ( abs ( sol (k ,2) ) ) ;
Scs = gradosaturacion ( abs ( sol (k ,3) ) ) ;
Sar = gradosaturacion ( abs ( sol (k ,4) ) ) ;
Sbr = gradosaturacion ( abs ( sol (k ,5) ) ) ;
Scr = gradosaturacion ( abs ( sol (k ,6) ) ) ;
%Modelo de la máquina
th = sol (k ,8) ;
%Matriz de cosenos
Cn =[2* inv ( Sas + Sar ) * cos ( th ) , 2* inv ( Sas + Sbr ) * cos ( th +2* pi /3) , 2* inv ( Sas + Scr ) * cos ( th
+4* pi /3) ; 2* inv ( Sbs + Sar ) * cos ( th +4* pi /3) , 2* inv ( Sbs + Sbr ) * cos ( th ) , 2* inv ( Sbs + Scr
) * cos ( th +2* pi /3) ; 2* inv ( Scs + Sar ) * cos ( th +2* pi /3) , 2* inv ( Scs + Sbr ) * cos ( th +4* pi /3)
, 2* inv ( Scs + Scr ) * cos ( th ) ];
%Derivada de la matriz de cosenos
dCn = -[2* inv ( Sas + Sar ) * sin ( th ) , 2* inv ( Sas + Sbr ) * sin ( th +2* pi /3) , 2* inv ( Sas + Scr ) * sin (
th +4* pi /3) ; 2* inv ( Sbs + Sar ) * sin ( th +4* pi /3) , 2* inv ( Sbs + Sbr ) * sin ( th ) , 2* inv ( Sbs +
Scr ) * sin ( th +2* pi /3) ; 2* inv ( Scs + Sar ) * sin ( th +2* pi /3) , 2* inv ( Scs + Sbr ) * sin ( th +4* pi
/3) , 2* inv ( Scs + Scr ) * sin ( th ) ];
%Matriz de inductancias de magnetización del estator y rotor
Lms = Lm *[ inv ( Sas ) ,- inv ( Sas + Sbs ) ,- inv ( Sas + Scs ) ;...
- inv ( Sas + Sbs ) , inv ( Sbs ) ,- inv ( Sbs + Scs ) ;...
- inv ( Sas + Scs ) ,- inv ( Scs + Sbs ) , inv ( Scs ) ];
Lmr = Lm *[ inv ( Sar ) ,- inv ( Sar + Sbr ) ,- inv ( Sar + Scr ) ;...
- inv ( Sar + Sbr ) , inv ( Sbr ) ,- inv ( Sbr + Scr ) ;...
- inv ( Sar + Scs ) ,- inv ( Scr + Sbr ) , inv ( Scr ) ];
%Matriz de inductancias de la máquina
L =[( Lsigs * I + Lms ) , Lsr * Cn ; Lsr * Cn . ’ ,( Lsigr * I + Lmr ) ];
%Matriz de par
dL = Lsr *[ zeros (3) , dCn ; dCn . ’ , zeros (3) ];
%Flujos en el estator y rotor
lambs =[ sol (k ,1) ; sol (k ,2) ; sol (k ,3) ];
lambr =[ sol (k ,4) ; sol (k ,5) ; sol (k ,6) ];
lambda =[ lambs ; lambr ];
%Tensiones en el estator y rotor
vs =[ vsa ; vsb ; vsc ];
vr =[ vra ; vrb ; vrc ];
v =[ vs ; vr ];
81
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
%Corrientes en el estator y rotor
ii (k ,:) = inv ( L ) * lambda ;
%Par eléctrico
Te ( k ) =0.5* lambda . ’* inv ( L ) . ’* dL . ’* inv ( L ) * lambda ;
end
%Intervalo de gráficas
y1 =[0 0.5];
%> > > > > > > > > > > > > > > > > > > > Resultados obtenidos < < < < < < < < < < < < < < < < < < < < < < < < < < < < <
%Flujos en el estator
figure (1)
plot ( t * tb , sol (: ,1) ,t * tb , sol (: ,2) ,t * tb , sol (: ,3) , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Flujo ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
xlim ( y1 )
%Velocidad de la máquina en por unidad
figure (2)
plot ( t * tb , sol (: ,7) , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Velocidad ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
xlim ( y1 )
ylim ([0 1.2])
%Corrientes en el estator
figure (3)
plot ( t * tb , ii (: ,1) ,t * tb , ii (: ,2) ,t * tb , ii (: ,3) , ’ linewidth ’ ,1.5)
ylim ([ -10.5 10.5])
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Corriente ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
xlim ( y1 )
%Corrientes en el rotor
figure (4)
plot ( t * tb , ii (: ,4) ,t * tb , ii (: ,5) ,t * tb , ii (: ,6) , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Corriente ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’
Location ’ , ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
xlim ( y1 )
%Flujos en el rotor
figure (5)
plot ( t * tb , sol (: ,4) ,t * tb , sol (: ,5) ,t * tb , sol (: ,6) , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
82
136
ylabel ( ’ Flujo ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
legend ( ’ Fase a ’ , ’ Fase b ’ , ’ Fase c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’ Location ’ ,
’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
xlim ( y1 )
%Par eléctrico
figure (6)
plot ( t * tb , Te (:) , ’ linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Par eléctrico ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
xlim ( y1 )
%Corrientes de lineas
figure (8)
plot ( t * tb , ii (: ,1) - ii (: ,3) ,t * tb , ii (: ,2) - ii (: ,1) ,t * tb , ii (: ,3) - ii (: ,2) , ’
linewidth ’ ,1.5)
set ( gca , ’ fontsize ’ ,12 , ’ fontweight ’ , ’ bold ’) ;
grid
xlabel ( ’ Tiempo ( s ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
ylabel ( ’ Corriente ( pu ) ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’)
legend ( ’ I_l_a ’ , ’ I_l_b ’ , ’ I_l_c ’ , ’ FontSize ’ ,12 , ’ fontweight ’ , ’ bold ’ , ’ Location ’
, ’ SouthEast ’ , ’ Orientation ’ , ’ Horizontal ’)
xlim ( y1 )
Funciones utilizadas
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
f u n c t i o n px=Modelo_Saturacion_Flujo ( t , x )
g l o b a l vr vra vrb v r c L s i g r L s i g s Lm Lsr J K I R Lm0 Lmsat PsiT fT a tauT Mf Mi A
vec_esp
%Se renombran l a s v a r i a b l e s para s e r empleadas d e n t r o de l a f u n c i ó n
lambsa=x ( 1 ) ;
lambsb=x ( 2 ) ;
lambsc=x ( 3 ) ;
lambra=x ( 4 ) ;
lambrb=x ( 5 ) ;
lambrc=x ( 6 ) ;
wr=x ( 7 ) ;
th=x ( 8 ) ;
%Se d e f i n e l a t e n s i ó n en e l e s t a t o r
vsa=A∗ s q r t ( 2 ) ∗ ( c o s ( t ) ) ;
vsb=A∗ s q r t ( 2 ) ∗ ( c o s ( t −2∗ p i / 3 ) ) ;
v s c=A∗ s q r t ( 2 ) ∗ ( c o s ( t +2∗ p i / 3 ) ) ;
%Determinanción de l o s g r a d o s de s a t u r a c i ó n en cada f a s e d e l e s t a t o r y d e l
%r o t o r
Sas=g r a d o s a t u r a c i o n ( abs ( lambsa ) ) ;
Sbs=g r a d o s a t u r a c i o n ( abs ( lambsb ) ) ;
S c s=g r a d o s a t u r a c i o n ( abs ( lambsc ) ) ;
Sar=g r a d o s a t u r a c i o n ( abs ( lambra ) ) ;
Sbr=g r a d o s a t u r a c i o n ( abs ( lambrb ) ) ;
S c r=g r a d o s a t u r a c i o n ( abs ( lambrc ) ) ;
%Par mecánico
83
25 Tm=K∗wr ^ 2 ;
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
1
2
3
4
5
6
7
%Modelo de l a máquina
%M a t r i z de c o s e n o s
Cn=[2∗ i n v ( Sas+Sar ) ∗ c o s ( th ) , 2∗ i n v ( Sas+Sbr ) ∗ c o s ( th+2∗ p i / 3 ) , 2∗ i n v ( Sas+S c r ) ∗ c o s ( th
+4∗ p i / 3 ) ; 2∗ i n v ( Sbs+Sar ) ∗ c o s ( th+4∗ p i / 3 ) , 2∗ i n v ( Sbs+Sbr ) ∗ c o s ( th ) , 2∗ i n v ( Sbs+S c r ) ∗
c o s ( th+2∗ p i / 3 ) ; 2∗ i n v ( S c s+Sar ) ∗ c o s ( th+2∗ p i / 3 ) , 2∗ i n v ( S c s+Sbr ) ∗ c o s ( th+4∗ p i / 3 ) , 2∗
i n v ( S c s+S c r ) ∗ c o s ( th ) ] ;
%Deri vada de l a m a t r i z de c o s e n o s
dCn=−[2∗ i n v ( Sas+Sar ) ∗ s i n ( th ) , 2∗ i n v ( Sas+Sbr ) ∗ s i n ( th+2∗ p i / 3 ) , 2∗ i n v ( Sas+S c r ) ∗ s i n (
th+4∗ p i / 3 ) ; 2∗ i n v ( Sbs+Sar ) ∗ s i n ( th+4∗ p i / 3 ) , 2∗ i n v ( Sbs+Sbr ) ∗ s i n ( th ) , 2∗ i n v ( Sbs+S c r
) ∗ s i n ( th+2∗ p i / 3 ) ; 2∗ i n v ( S c s+Sar ) ∗ s i n ( th+2∗ p i / 3 ) , 2∗ i n v ( S c s+Sbr ) ∗ s i n ( th+4∗ p i / 3 ) ,
2∗ i n v ( S c s+S c r ) ∗ s i n ( th ) ] ;
%M a t r i c e s de m a g n e t i z a c i ó n d e l e s t a t o r y d e l r o t o r
Lms=Lm∗ [ i n v ( Sas ) ,− i n v ( Sas+Sbs ) ,− i n v ( Sas+S c s ) ; . . .
−i n v ( Sas+Sbs ) , i n v ( Sbs ) ,− i n v ( Sbs+S c s ) ; . . .
−i n v ( Sas+S c s ) ,− i n v ( S c s+Sbs ) , i n v ( S c s ) ] ;
Lmr=Lm∗ [ i n v ( Sar ) ,− i n v ( Sar+Sbr ) ,− i n v ( Sar+S c r ) ; . . .
−i n v ( Sar+Sbr ) , i n v ( Sbr ) ,− i n v ( Sbr+S c r ) ; . . .
−i n v ( Sar+S c s ) ,− i n v ( S c r+Sbr ) , i n v ( S c r ) ] ;
%M a t r i z de i n d u c t a n c i a s de l a máquina
L=[( L s i g s ∗ I+Lms) , L s r ∗Cn ; L s r ∗Cn . ’ , ( L s i g r ∗ I+Lmr) ] ;
%M a t r i z de par
dL=L s r ∗ [ z e r o s ( 3 ) , dCn ; dCn . ’ , z e r o s ( 3 ) ] ;
%F l u j o s en e l e s t a t o r y r o t o r
lambs =[ lambsa ; lambsb ; lambsc ] ;
lambr =[ lambra ; lambrb ; lambrc ] ;
lambda =[ lambs ; lambr ] ;
%C á l c u l o de c o r r i e n t e s en e l e s t a t o r y r o t o r
i i =i n v (L) ∗ lambda ;
%T e n s i o n e s en e l e s t a t o r y r o t o r
vs =[ vsa ; vsb ; v s c ] ;
vr =[ vra ; vrb ; v r c ] ;
v=[ vs ; vr ] ;
% Derivada de l o s e n l a c e s de f l u j o s
dlamb=v−R∗ i i ;
%C á l c u l o d e l par e l é c t r i c o
Te=0.5∗ lambda . ’ ∗ i n v (L) . ’ ∗ dL . ’ ∗ i n v (L) ∗ lambda ;
%Balance mecánico
dw=(1/J ) ∗ ( Te−Tm) ;
%Deri vada de l a p o s i c i ó n a n g u l a r
dth=wr ;
%D e r i v a d a s de l a s v a r i a b l e s a i n t e g r a r
px=[dlamb ; dw ; dth ] ;
end
%
>>>>>>>>>Funcion para e l c a l c u l o de l o s g r a d o s de s a t u r a c i o n <<<<<<<<<<<<<
%Esta f u n c i ó n p e r m i t e c a l c u l a r e l g ra d o de s a t u r a c i ó n a p a r t i r de l a
%e c u a c i ó n que d e f i n e l a c u r v a de m a g n e t i z a c i ó n c o n o c i d o e l e n l a c e de f l u j o
f u n c t i o n s=g r a d o s a t u r a c i o n ( lambda )
g l o b a l vr vra vrb v r c L s i g r L s i g s Lm Lsr J K I R Lm0 PsiT fT a tauT Mf Mi A
vec_esp
%C á l c u l o de l a c o r r i e n t e s a t u r a d a a p a r t i r de l a e c u a c i ó n de l a c u r v a de
%s a t u r a c i ó n
84
8
9
10
11
12
13
14
15
16
17
18
i m s a t = ( Mf−Mi ) / p i ∗ ( ( ( lambda−PsiT ) . ∗ atan ( tauT ∗ ( lambda−PsiT ) ) −PsiT ∗ atan ( tauT∗
PsiT ) ) + . 5 / tauT ∗ ( l o g (1+( tauT∗ PsiT ) ^2) − l o g (1+tauT ^2∗( lambda−PsiT ) . ^ 2 ) ) ) +
lambda . ∗ ( Mf+Mi ) / 2 ;
%C á l c u l o de l a c o r r i e n t e l i n e a l a p a r t i r de l a p e n d i e n t e en l a zona l i n e a l
%de l a c u r v a de v a c í o
i m l i n=i n v (Lm0) ∗ lambda ;
%Determinación d e l g r a d o de s a t u r a c i ó n como e l c o c i e n t e de l a c o r r i e n t e
%s a t u r a d a y l a c o r r i e n t e l i n e a l
i f abs ( imsat−i m l i n )<1e−3
s =1;
else
s=i m s a t / i m l i n ;
end
Apéndice G
PUENTE ASIMÉTRICO
El puente asimétrico permite la operación del convertidor aún cuando una o varias de
sus componentes fallan en la conmutación, evitando que la barra DC se vea cortocircuitada
como es natural que suceda en un puente convencional ante condiciones de falla.
G.1.
Puente convencional y puente asimétrico
El inversor trifásico de la G.1 permite la alimentación de carga entre los terminales a, b
y c, mediante la conmutación de los transistores Q1 , Q2 , Q3 , Q4 , Q5 y Q6 . Para alimentar
correctamente la carga es necesario que la activación de los transistores se haga en pares
cruzados para garantizar que ni la fuente, ni la carga se cortocircuiten en un momento
determinado, de esta manera, para alimentar las fases a y b los semiconductores Q1 y Q6
han de estar conduciendo y el resto apagado. Si Q1 y Q4 conducen al mismo tiempo, la fuente
de corriente contínua se ve cortocircuitada. De igual manera al conducir simultaneamente
Q1 y Q3 , la carga sufre cortocircuito. Para garantizar la correcta operación del puente se
debe garantizar que los semiconductores de una misma rama deben ser uno el negado del
otro.
Uno de los principales inconvenientes de estos equipos es el fallo en la conmutación de los
transistores que provoca cortocircuitos en la barra de corriente continua. Este inconveniente
se puede solventar implementando un puente asimétrico como el que se presenta en la G.2.
Figura G.1: Inversor trifásico convencional. [2]
86
Figura G.2: Inversor trifásico con puente asimétrico.[7]
Dada la disposición de los semiconductores no es posible que se cortocircuite la fuente de
corriente continua.
G.2.
Operación del puente asimétrico
El inversor con puente asimétrico posee 27 estados de operación de los cuales solo 5
permiten tener una salida no nula de tensión. La operación de este inversor permite tener tres
estados de tensión en la salida: tensión positiva cuando los transistores de una misma rama
se encuentran encendidos, tensión negativa cuando los transistores contiguos se encuentran
apagados y la corriente por la bobina es distinta de cero para que ésta provoque la conducción
de los diodos correspondientes, y tensión cero cuando sólo uno de los transistores de una
misma rama se encuentre encendido [7].
Resulta evidente que dependiendo del esquema de control del convertidor existe la posibilidad de tener inyecciones de corriente con valor DC distinto de cero ya que en un ciclo
de operación la forma de onda a la que se someten las bobinas pueden no ser simétricas
con respecto al eje de las abscisas. Esto en máquinas eléctricas se traduce en que el núcleo
magnético se puede ver altamente saturado.
G.3.
Aplicaciones del puente asimétrico
El puente asimétrico es comunmente usado en el accionamiento de los motores de reluctancia autoconmutados (SRM, sus siglas en inglés). Este dispositivo hizo su aparición en 1838,
pero no es sino a principio del siglo XXI que es altamente apreciado por su construcción
simple y robusta, bajos costos de fabricación, alta tolerancia a fallas y elevado rendimiento.
El número de polos del estator debe ser distinto al número de polos del rotor para impedir
la alineación completa del estator con el rotor.
El alto número de posibilidades de control de este convertidor de electrónica de potencia
representa una de las principales ventajas de su implementación.