triágulos - Emagister
Anuncio
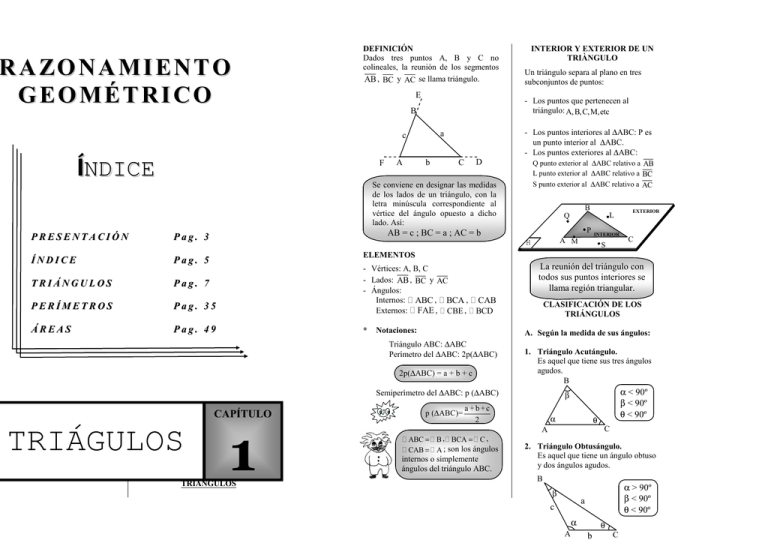
RAZONAMIENTO GEOMÉTRICO DEFINICIÓN Dados tres puntos A, B y C no colineales, la reunión de los segmentos AB , BC y AC se llama triángulo. E - Los puntos interiores al ∆ABC: P es un punto interior al ∆ABC. - Los puntos exteriores al ∆ABC: a c F b A Un triángulo separa al plano en tres subconjuntos de puntos: - Los puntos que pertenecen al triángulo: A, B, C, M,etc B ÍNDICE INTERIOR Y EXTERIOR DE UN TRIÀNGULO D C Q punto exterior al ∆ABC relativo a AB L punto exterior al ∆ABC relativo a BC S punto exterior al ∆ABC relativo a AC Se conviene en designar las medidas de los lados de un triángulo, con la letra minúscula correspondiente al vértice del ángulo opuesto a dicho lado. Así: B P AB = c ; BC = a ; AC = b PRESENTACIÓN Pag. 3 ÍNDICE Pag. 5 TRIÁNGULOS Pag. 7 PERÍMETROS Pag. 35 - Vértices: A, B, C - Lados: AB , BC y AC - Ángulos: Internos: ABC , BCA , CAB Externos: FAE , CBE , BCD ÁREAS Pag. 49 * INTERIOR A M H S EXTERIOR C ELEMENTOS Notaciones: La reunión del triángulo con todos sus puntos interiores se llama región triangular. CLASIFICACIÓN DE LOS TRIÁNGULOS A. Según la medida de sus ángulos: Triángulo ABC: ∆ABC Perímetro del ∆ABC: 2p(∆ABC) 2p(∆ABC) = a + b + c 1. Triángulo Acutángulo. Es aquel que tiene sus tres ángulos agudos. B Semiperímetro del ∆ABC: p (∆ABC) CAPÍTULO TRIÁGULOS L Q 1 TRIÁNGULOS p (∆ABC)= a +b+c 2 α θ C A ABC = B , BCA = C , CAB = A ; son los ángulos internos o simplemente ángulos del triángulo ABC. α < 90º β < 90º θ < 90º β 2. Triángulo Obtusángulo. Es aquel que tiene un ángulo obtuso y dos ángulos agudos. B β α > 90º β < 90º θ < 90º a c α A θ b C Segmento que parte de un vértice y llega al punto medio del lado opuesto. En el ∆ABC isósceles: α: medida de los ángulos en la base. θ: medida del ángulo en el vértice. *a>b ya>c A este triángulo se le llama: “triángulo ABC obtuso en A” A los triángulos acutángulos y obtusángulos se les denomina “OBLICUÁNGULOS” riángulo Rectángulo. s aquel que tiene un ángulo recto y os ángulos agudos. Se cumple que: α < 90º y α = 180º −θ ó α = 90º − θ 2 2 3. Triángulo Equilátero. Es aquel triángulo que tiene sus tres lados de igual longitud; en consecuencia, sus tres ángulos serán de 60º. B 60º AB y AC:Catetos β AB = BC = AC m A = m B = m C = 60º BC:Hipotenusa a 60º C b α + β = 90º 60º C A TEOREMAS FUNDAMENTALES 1. Suma de Ángulos Internos: “En todo triángulo la suma de las medidas de sus tres ángulos interiores es igual a 180º ” B ⇒ AB ≠ BC ≠ AC y además α ≠ β ≠ θ β α riángulo Isósceles. s aquel triángulo que tiene dos dos de igual longitud; en onsecuencia, los ángulos opuestos a chos lados serán de igual medida. B θ α 2. Suma de Ángulos Externos: (considerando uno por vértice) “ La suma de las medidas de los ángulos exteriores de un triángulo es igual a 360º ” B y AB = BC m A=m C Se cumple: x + y + z = 360º x α α BASE C α θ C 5. Teorema de EXISTENCIA (Desigualdad Triangular) “En todo triángulo, la longitud de uno de sus lados está comprendida entre la suma y la diferencia de los otros dos lados” B A Sea a ≥ b ≥ c ⇒ se cumple: a z C A b b-c<a<b+c BM es la mediana relativa al lado AC . B Q A P G C M G: Baricentro, Gravicentro o Centriode (Es el centro de gravedad del triángulo) Propiedad: El baricentro divide a la mediana en dos segmentos que están en relación de 2 a 1 BG 2 = GM 1 , AG = 2 , CG = 2 GP 1 GQ 1 2. ALTURA: Segmento perpendicular al lado opuesto o su prolongación. C También se cumple: B B a-c<b<a+c a-b<c<a+b LÍNEAS NOTABLES Y PUNTOS NOTABLES 1. MEDIANA: C M Nota: Si b > a: ⇒ β>α a c θ C A 4. Propiedad de Correspondencia: “ En todo triángulo se cumple que a mayor lado se opone mayor ángulo y viceversa ” B c A BM: mediana El punto de intersección de las medianas se llama BARICENTRO. C α + β + θ = 180º θ B e α A Se cumple: β C e = α+β A egún la medida de sus lados: riángulo Escaleno. s aquel triángulo que tiene sus tres dos de diferente magnitud. B β “Todo triángulo equilátero es equiángulo” ⇒c < a y b < a α 3. Teorema del Ángulo Exterior: “En todo triángulo, la medida de un ángulo exterior es igual a la suma de las medidas de dos ángulos interiores del triángulo no adyacentes a él ” B Se cumple: A H C H A BH es la altura relativa al lado AC . C nto de intersección de las alturas se ORTOCENTRO. - Equidista de los lados 4. MEDIATRIZ. I: Incentro I r r Es la recta o segmento de recta que divide a un segmento por su punto medio en forma perpendicular. r Acutángulo Rectángulo Re A SECTRIZ: Re C C L1: mediatriz de AC MP: mediatriz de AC Baricentro Ortocentro O Incentro Circuncentro O El punto de intersección de las mediatrices se llama CIRCUNCENTRO. - Equidista de los vértices del triángulo. Y se ubica: Todo triángulo tiene 3 ex-centros, uno relativo a cada lado ento limitado por el lado opuesto, vide a su ángulo en otros dos de medida. El Baricentro, es también ortocentro, incentro y circuncentro. - Centro de la circunferencia circunscrita Ea: Excentro relativo al lado BC - ∴ M A Ea entro si es acutángulo uera del mismo si es obtusángulo Fuera del mismo si es obtusángulo. 1. En todo triángulo equilátero, sus puntos notables se confunden. Re B n el vértice del ∠recto si es ctángulo - P Es centro de la circunferencia ex-inscrita. triángulo tiene un solo ortocentro y estar ubicado: En punto medio de la hipotenusa si es rectángulo. OBSERVACIONES Punto de intersección de dos bisectrices exteriores y una interior. - Dentro si es acutángulo. - L1 B EXCENTRO: ∆ Obtusángulo - 2. En todo triángulo isósceles las alturas relativas a los lados iguales son iguales. B E1 O B O E2 H B β A αα β C ∆ Acutángulo P ∆ Obtusángulo A P C E3 Q onde BP : bisectriz interior BQ : bisectriz exterior NTRO: de intersección de las bisectrices ores. ro de la circunferencia inscrita. CH = AP O Nota: Los mismo ocurre con las bisectrices y medianas. Donde: E1: Ex–centro relativo al lado AB E2: Ex–centro relativo al lado BC E3: Ex–centro relativo al lado AC C B ∆ Rectángulo Todo triángulo tiene un solo circuncentro y puede estar ubicado: K A B T M C A N C K = AT CM = AN a altura relativa al lado desigual, orta a éste un su punto medio. sta altura es mediana, mediatriz y sectriz a la vez, del lado desigual. B ∆ABE: θ = a + b (Angulo Exterior) ∆DEC: x = θ + c (Angulo Exterior) ∴ 2. β b Prolongamos AD hasta E (E en BC), para obtener triángulos: a α Demostración: M θ c O d b R C H α A e a Por eso cuando se tiene un triángulo isósceles se recomienda trazar su altura. ∆AMO: θ=a+b ∆ROC: θ = α + β (Angulo Exterior) ∴ a + b + c + d + e = 180º (Angulo Exterior) ∴ x = 90º − OPIEDADES IMPORTANTES B c opiedad del “PANTALONCITO” B b d a θ A c x I e En ACEI: (Propiedad del Pantaloncito) ⇒ θ=a+c+e x =a +b+c ∆BID: (Suma de Ángulos Internos) stración: ⇒ b + θ + d = 180º ∴ b a A A ω x= B̂ 2 C Demostración: ∆ACE: ω = α + x (Angulo Externo) ⇒ ω - α = x… (I) ∆ABC: 2α + B + 2θ = 180º 2 (α + θ) = 180º - B … (II) I en II: 2 (180º - x) = 180º - B ∆ABC: 2ω = 2α + 2B 2 (ω - α) = 2B … (II) I en II: 2 (x) = 2B ∴ x = 90º + B 2 5. Ángulo formado por dos Bisectrices Exteriores 3. Propiedad de la “Mariposa” o Propiedad de la “Corbatita” c ω α α Demostración: ∆ACI: α + x + θ = 180º ⇒ α + θ = 180º - x… (I) a + b + c + d + e = 180º E θ θ θ C b + (a + c + e) + d = 180º B D x x A E A 2 6. Ángulo formado por una Bisectriz Interior y otra Exteriores E B B̂ x = 90° + 2 I α α ω x D θ b a 4. Ángulo formado por dos Bisectrices Interiores C ω ∆ABC: 2φ + ( 180º − A ) + 2ω = 360º 2 (α + θ) =360º- (180º − A ) 2 (α + θ) = 180º + A … (II) I en II: 2 (180º - x) = 180º + A a+b=α+β Tu profe Markito Demostración: E A C ∆BEC: φ + x + ω = 180º ⇒ φ + ω = 180º - x… (I) β a B C φ φ E x ∴x = B 2 7. Ángulo formado la Bisectriz y la Altura que parten del mismo vértice B x ω A Â 2 x 180º − A C b y BH ⊥ AC φ φ a + b = α +β Propiedad de la “ESTRELLITA” ⇒ AH = HC Demostración: B x=a+b+c Si AB = BC x = 90° − C ω α A θ H D C α −θ 2 11. En todo Cuadrilátero se cumple: Si: MN es MEDIANA ⇒ AM = MB = MC = 1 AC β stración: B α 2 β ω θ θ α ω φ x φ+x α + β + θ + ω = 360º α θ H C D 12. Propiedad: α α + φ = 90º… (I) θ + 2x + φ = 90º … (II) α - θ - 2x = 0 α−θ ∴x = 2 opiedad: x b ∴∆APB es Isósceles 1. TEOREMA DE LA BASE MEDIA En todo triángulo, el segmento que une los puntos medios de dos lados es paralelo al tercero y mide su mitad. B x N MN es base media piedad: a+b x= 2 θ θ 2x A 3. Triángulo Rectángulo de 37º-53º ( 37º-53º) Sólo en los triángulos rectángulos de 37º-53º, SUS LADOS ESTAN EN PROGRESIÓN ARITMÉTICA. 53° ⇒ PA = PB y MN = A 2. MEDIANA RELATIVA A LA HIPOTENUSA: En todo triángulo rectángulo, la longitud de la mediana relativa a la hipotenusa es na mitad de ésta. B 1. Triángulo Rectángulo de 45º-45º ( 45º-45º) En todo triángulo rectángulo de 45º 45º, el cateto que se opone a un ángulo de 45º mide la mitad de la hipotenusa multiplicada por 2 . k n 45º k 2 k 45º 2 k A M C k 15° 15° 4k 75° ( 6 − 2)k 45º 45º θ 4. Triángulo Rectángulo de 15º-75º ( 15º-75º) En todo triángulo rectángulo de 15º 75º, se tiene: k 2 2 )k m+n =α+θ 37° 4k + ( 6 α 1 AC 2 5k 3k θ θ TRIÁNGULOS RECTÁNGULOS NOTABLES C b x O Si: AM = MB y CN = NB ⇒ MN // AC opiedad del “Pescadito” m P k 3 ⇒ OA = OB M α α 30º 4. TEOREMA DE LA BISECTRIZ “Todo punto que pertenece a la bisectriz de un ángulo equidista de los lados de dicho ángulo” uuur Si OP:Bi sec triz B θ θ α α a+b 2 y PROPIEDADESS GENERALES 2k k B A x 60° ⇒ AP = PB α+β = x + y β B: C: I): x= sur Si: L1 :Mediatriz AD es bisectriz: m ABD = m DBC = φ+ x a L1 P ( 6 + 2)k A 3. TEOREMA DE LA MEDIATRIZ “Todo punto de la mediatriz de un segmento equidista los extremos de dicha mediatriz ” 2. Triángulo Rectángulo de 30º-60º ( 30º-60º ) En todo triángulo rectángulo de 30º-60º, se cumple que: El cateto que se opone a un ángulo de 30º mide la mitad de la hipotenusa. El cateto que se opone a un ángulo de 60º mide la mitad de la hipotenusa multiplicada por 3 . (2 − 3)k x= 75° k Si viene un problema con ángulos de 15º o 75º, frecuentemente se usa la suma o resta de 30º y 45º Trazamos AH ⊥ BC , para obtener (45º-45º) y (30º-60º) Trazamos CH ⊥ AB , para obtener (45º-45º) y (30º-60º) Luego: Luego: AHB (30º-60º): Si AB = 20 ⇒ BH = 10 (Opuesto a 30º) y AH = 10 3 (Opuesto a 60º) iángulos Rectángulos de 53º y 37º 2 2 º 37º 2 k 5 k 10 k k CLAVE: a figura hallar el valor de AC, si = 20m. B 30º A) 2 B) D) E) 2 C 5 3m 2 2 B E h r C R ' 60º C ⇒ a b c h r R = = = = = =K a ' b' c ' h' r ' R ' 2. Si EF // AC B 2 45º H 30º A 45º C 60º 15º Prolongamos AB , así el ángulo externo en B seria 45º (Notable) C ' A' SEMEJANZA DE TRIÁNGULOS B 45º ' r F AB DE = BC EF Solución: ' R h C B A D H 30º 45º B A C) 2 2 ión: 20 1. Si ∆ABC ∼ ∆A'B'C' 15º C 6 3 lados que se oponen a ángulos congruentes. B A B) 10 2 m D) 10 3 m NOTA: Lados Homólogos son aquellos OBSERVACIONES 60º ) 10 m ) 10 6 m C Tres o más rectas paralelas, determinan sobre dos o más rectas secantes, segmentos cuyas longitudes son proporcionales. A A K : Constante o razón de semejanza TEOREMA DE THALES B 75º B Aˆ C = E Dˆ F AB = BC = AC = K A Bˆ C = D Eˆ F DE EF DF A Cˆ B = D Fˆ E C Hallar el valor del segmento AC , en el gráfico que se muestra a continuación, si BC = 2 m. MPLO 1 F C D ∴ AC = 2 EJEMPLO 2 EJEMPLOS A AHC (30º-60º): Como CH = 1 ⇒ AC = 2CH (Opuesto a 60º) AC = 2 (1) ∴ AC = 10 6 CLAVE: E BHC (45º-45º): Si BC = 2 ⇒ CH = 1 (Opuesto a 45º) AHC (45º-45º): Si AH = 10 3 ⇒ AC = AH 2 (Hipotenusa) AC = (10 3 ) 2 3k B Si dos triángulos son semejantes, entonces tienen sus ángulos respectivamente congruentes y sus lados homólogos respectivamente proporcionales. E A F C ' HC: Proyección ortogonal de BC sobre la hipotenusa BE BF = EA FC y ∆ EBF ∼ ∆ ABC ⇒ 1. Teorema del Cuadrado del Cateto: 2 2 a = n .b c = m .b EF // AC 2. Teorema de Pitágoras: E F n b A h 2= m . n C b . h = a .c NATURALEZA DE UN TRIÁNGULO A M A ∴ Acutángulo a c M' N Proyección Ortogonal de P sobre L Proyección Ortogonal de AB sobre L ELACIONES MÉTRICAS EN RIÁNGULOS RECTÁNGULOS B A C b Siendo: a > b y a > c Se tiene que: 1. Si: a2 < b2 + c2 ⇒ α < 90º Luego ∆ABC es Acutángulo 2. Si: a2 = b2 + c2 ⇒ α = 90º Luego ∆ABC es Rectángulo a c m H α N' n b 3. Si: C oyección ortogonal de AB sobre hipotenusa a2 > b2 + c2 ⇒ α > 90º Luego ∆ABC es Obtusángulo EJEMPLOS EJEMPLO 1 CLAVE: C y+5 5 O 12 x x+4 = ⇒ x=2 4 12 y y+5 5 = ⇒ y= 4 12 2 Finalmente: PERÍMETRO MRO = 12+(x+4)+(y+5) ∴ PERÍMETRO MRO = 25.5 m EJEMPLO 2 B B' C 18 Aplicamos las relaciones de la Naturaleza de un triángulo y se tendría: ⇒ α < 90º 202 < 182 + 152 Averiguaremos si un triángulo es acutángulo, rectángulo u obtusángulo, con las siguientes relaciones: B A' K Notamos que: ∆ ARK ∼ ∆ MRO Por los que usamos proporciones: θ 4. Teorema del producto de Catetos: a m = b n M 20 15 ROYECCIÓN ORTOGONAL P' 4 A x+4 B y ∆ EBF ∼ ∆ ABC P B) Obtusángulo D) Rectángulo Solución: 3. Teorema del Cuadrado de la Altura: B ⇒ A) Isósceles C) Acutángulo E) Equilátero y x 4 b 2= a 2+ c 2 m a R Los lados de un triángulo miden 15, 18 y 20 metros. ¿Qué tipo de triángulo es? Las bases de un trapecio miden 4m y 12m, y los lados no paralelos 4m y 5m. Hallar el perímetro del triángulo mayor que se forma al prolongar los lados no paralelos. (UNSAAC 2001 – II) A) 21,5m C) 27,5m E) 23.5m Solución: B) 29,5m D) 25,5m CLAVE: D EJEMPLO 3 Oswaldo hace un recorrido de la siguiente manera: 50 pasos al SUR, 100 pasos al NORTE, 70 pasos al ESTE, luego 80 pasos al SUR. ¿A cuantos pasos del punto de partida se encuentra? (UNSAAC 2001 – II) A) 58 10 B) 10 58 C) 10 85 D) 158 10 E) 58 58 Solución: Realizamos el gráfico de acuerdo a los datos del problema y se tiene: B N B Solución: 3 70 4 2 50 100 70 D 1 S 2 = 702 + 302 2 = 102 7 2 + 32 ( 3k )2 = n x b ( 2k )2 ( 3k )2 ∴ D = 10 58 … (II) ) 2 3 B) 2 3 3 E) 5 Dato: a – b = 20º… (II) (I) + (II) ⇒ a = 30º b externo) 20 = 4k A x + a + 40º = 180º 9 CLAVE: Cómo AC = 4K=20 ⇒ K = 5 Luego QC = 3K ⇒ QC = 15 ∴ PQ = 5 E A En la siguiente figura, calcular el valor de “x”, si el segmento AC es bisectriz del ángulo “A” y a- b = 20º CLAVE: Sabiendo que el segmento AB mide 40cm. Hallar la medida del segmento PQ. B En la figura, si la medida de AE es igual a la medida de BE, hallar la medida del ángulo “x”. D B 30º E 45º C O a 53º 40º b A A) 140º D) 100º D B) 150º E) 110º 25º x 30º Q A ión: A PROBLEMA 3 P x ⇒ PC = 20 QCA: (53º-37º) PROBLEMAS RESUELTOS B ⇒ AC = 20 Como AC = 20 PROBLEMA 2 C) 1 2 C PCA: (45º-45º) ∴ x = 110º PROBLEMA 1 3k=15 ABC: (30º-60º) Si AB = 40 x + 30º + 40º = 180º CLAVE: UNSAAC 2002 – I PRIMERA PCION) a + b = 40º… (I) ( Finalmente: MPLO 4 as longitudes de los catetos de un ángulo rectángulo son entre sí, omo 2 es a 3. ¿En que relación tán las longitudes de sus oyecciones sobre la hipotenusa? ∆ADO: nxb 20 37º b D nxa 5 Q A ∆BOA: = 40º a ∴a=4 CLAVE: B ) 4 9 a Dividimos (I) y (II) ) O P 45º 40 53º ( 2k )2 = m x b … (I) mente en el triángulo sombreado mos el Teorema de Pitágoras: 40º C n b Usamos los teoremas de Relaciones Métricas en triángulos rectángulos. (Teorema del Cuadrado del Cateto) 50 ( h N 30 C B x A m H 80 30º 3k 2k C) 90º A) 5 D) 20 B) 10 E) 25 C C) 15 A A) 20º D) 25º Solución: Solución: B) 10º E) 15º C C) 30º B D 25º x E θ 25º A 30º C B También 60º E = BE ⇒ BAE = ABE = 25º BE: θ = 25º+25º ( Externo) θ = 50º EC: θ = x + 30º ( Externo) 50 = x +30º ∴ x = 20º mos usar la propiedad de la posa” B D 25º x Si: AB = BC 2α = 50º ⇒ α = 50º ∆ ABE: α + 80º + x = 180º ∴ x = 75º Q CLAVE: 55º 35º C x En la figura adjunta determinar el valor de “a+b” (UNSAAC CBU 99 I) B QAC = 55º (Dato) ACQ = 35º ABC: ACB = 60º ⇒ 35º + x = 60º ∴ x = 25º A C En la figura AB = BC. Determinar el valor del ángulo ADC. (UNSAAC CBU 99 I) CLAVE: A a A) 3 − 3 D) 4 − 3 B) 8 + 3 E) 6 + 3 ) 35º ) 45º B) 15º E) 60º 2θ θ A 30º b=3 C B C) 25º 40º 40º x ión: α α A D E x x 50º H C A 45º a D 60º 3 O θ + x = 90° ∴ x = 75° CLAVE: B PROBLEMA 8 3 Hallar el valor del ángulo “x” en la siguiente figura, si BM=MC y AB=BC. (UNSAAC CBU INT 2000) ABC: (45° - 45°) ⇒ AC = BC AC = 3 ∴ a = 3− AMO: R 4θ + 30º = 90° θ = 15° C BCD: (30° - 60°) ⇒ BC = DC 3 b = 3( 3) b=3 ∆ ABC Isósceles ⇒ BH es bisectriz. ABH = HBC= 40º x CAR: α α C) 80º M θ LEMA 4 B) 105º E) 35º C C) 6 − 3 B 45º A C) 85º 30º D A) 75º D) 45º Solución: B) 75º E) 60º C 3 40º n el interior del triángulo equilátero BC, se sitúa un punto “A” de tal anera que el ángulo AQC mide 90º el ángulo QAC mide 55º. Hallar la edida del ángulo BCQ. A) 80º D) 70º 60º D Solución: B θ C PROBLEMA 5 25º + 25º = x + 30º ∴ x = 20º 2θ θ Solución: b 45º 30º 30º PROBLEMA 6 CLAVE: 25º A x A AQC: ⇒ Determinar el valor del ángulo x, en la figura: (UNSAAC CBU 99 II) B x 3 CLAVE: A 50º PROBLEMA 7 A M C Solución: ) 20º ) 45º B) 40º E) 30º C) 25º A) 8 2 B) 3 2 D) 13 2 E) 4 3 3 ión: B x 50º Propiedad del “Pantaloncito” En ABCF: θ=a+b+c x = 4k 53º B 2 2 = 3k A ABC: (37° - 53°) MBC = CLAVE: 2 2 = 3k ⇒ k = 2 2 3 MCB = 50º o en ∆ ABC Luego: 60º ∴x= 8 Calcular la longitud de AB en el triángulo ABC, de la figura: (UNSAAC CBU 2000 I) B A CLAVE: C A) 27 D) 20 C) 25 Solución: P R Q 53º B) 14 E) 8 37º A C) 16 25 B) 150º E) 180º C) 360º 2 2 30º x 13 16 H c E θ 37º x N 3 ⇒ AM = 3 QMN: (45° - 45°) 6 3 3 Si QM = 4 2 ⇒ MN = 4 RNB: (37° - 53°) C BHC (30º -60º) HC = 3 ⇒ BH = 3 3 Luego en C 45º M PAM: (30° - 60°) B Trazamos BH ⊥ AC para aprovechar el ángulo de 60º. x 60º C 60º e 4 2 Si AP = 6 La suma de las medidas de los ángulos “marcados” en la figura adjunta, es: (UNSAAC CBU 2000 I) A) 120º D) 270º B) 30 E) 28 6 16 A) 10 D) 12 Solución: A 53º B N 60º 3 PROBLEMA 10 n la siguiente figura determinar el alor de “x”. UNSAAC CBU INT 2000) M 2 E LEMA 9 45º A x = 4k ∴ x = 30º CLAVE: 53º 25 E 6 0 + (x + 50) + 50 = 180º R Q 4 2 6 PROBLEMA 11 BCA = 50º MC: Isósceles ⇒ P Luego: ∆FED: θ + d + e = 180º ∴ a + b +c + d +e = 180º C H BAC = Determinar la medida de AB , en la figura: (UNSAAC CBU 2000 I) C 50º 50º B PROBLEMA 12 Solución: BC: Isósceles ⇒ ∴ x = 14 CLAVE: 37º A x 2 = 13 2 + (3 3) 2 C) 8 2 3 BHA. (Teor. Pitagoras) Si RN = 25 RN = 5k = 25 ⇒ k=5 NB = 3k ⇒ NB = 15 Luego: AB = AM + MN + NB B ∴ x = 27 CLAVE: Solución: Solución: A A C L n la figura adjunta: AB = BC. allar la medida del ángulo X. UNSAAC CBU 2000 II) C 15 = 3k A 37º 12 B B) 20º E) 35º ión: D C) 25º ABC: (37° - 53°) CB = 15 X 40º B C Isósceles CAB = D B: x + x = 50º ( ∴ x = 25 CLAVE: n la figura adjunta, calcular el valor e X. UNSAAC CBU 2000 II) )5 )6 15 x x x x x C) 12 CLAVE: A CLAVE: C Nada puede conseguir el hombre si no es a través del sacrificio. Las bases de un trapecio miden 4 metros y 12 metros y los lados no paralelos 4 metros y 5 metros. Hallar el perímetro del triángulo mayor en metros, que se forma al prologarse los lados no paralelos. (UNSAAC CBU 2000 II) A) 20.5 B) 26.5 C) 25.5 D) 24.5 E) 18.5 Solución: x B) 130º E) 140º A 4 D 15 8 53º A Solución: K 5 4 B y x C) 180º En la figura: Hallar AE A) 9 + 4 3 D) 12 + 4 3 R C A) 120º D) 100º PROBLEMA 17 PROBLEMA 16 En la figura adjunta. Determinar el valor de 2X. (UNSAAC CBU 2000 II) B B) 10 E) 8 E PROBLEMA 15 X ∴ 2p = 25.5 C LEMA 14 37º 12 Finalmente el perímetro del triángulo MRO (2p) sería: 2p = (4 + x) + ( y + 5) + 12 ∴ 2x = 120º ∴x = 8 CLAVE: x+4 ⇒ x=2 12 y+5 ⇒ y = 2.5 12 Externo) Luego en ∆ LUZ tenemos sus 3 ángulos externos ⇒ 6x = 360º x = 60º x = 20 - 12 externo) Externo) x = 4 y = 4 ⇒ θ = 2x x = AB – 12 ACB = x I Externo) ( ∆ LIT: θ = x + x ( ⇒ AB = 20 Finalmente: K x α=x+x ( ⇒ α = 2x Luego: AB = 4k 50º ∆ ARK ∼ ∆ MRQ (son semejantes, por lo tanto usamos proporcionales) x Z U ∆ RUK: ⇒ k=5 3k = 15 C φ x T ∆ MAZ: φ = x + x ⇒ φ = 2x B x 4k = 20 θ α x M 40º X A x x LEMA 13 ) 30º ) 15º R 60º C B) 16 E) 13 E C) 21 B Si AE = 9 β 37º D 15 β 30º 8 53º A PROBLEMA 19 B α E C E φ 60º ω θ D C θ ⇒ k=3 ⇒ AC = 9 E: (30° - 60°) Si DE = 8 DE = 2a ero: CE = a Para empezar a resolver este problema, prolongamos AD hasta E (E en BC), con la finalidad de formar los triángulos ABE y DEC. ⇒ a=4 ⇒ CE = 4 Luego: ∆ ABE: φ = α + β (∠ externo) ∆ DEC: φ + θ + ω = 180º B E 30º 60º 6 3 8 45º D β A) 18 D) 30 B) 24 E) 20 C) 32 C BEC: (30° - 60°) Solución: E Si BC = 6 (Hipotenusa) B 45º ⇒ CE = 3 (Opuesto a 30º) β D ω 180º- ω 3k ABC: (30° - 60°) θ C θ A Propiedad del “Pantaloncito” C) 120º D E D OTRA FORMA: En C A B α 45º un x 37º x 45º es E C) 6 2 Solución: A 9 CLAVE: eterminar la suma de los ángulos arcados en la siguiente figura: ión: B) 9 E) 9 2 30º LEMA 18 B) 240º E) 360º A) 6 D) 6 3 ∴ α + β + θ + ω = 180º AE = 13 ) 160º ) 180º En la figura, ABCD rectángulo, hallar “x” (UNSAAC CBU 2001 II) 6 (α + β) + θ + ω = 180º CLAVE: E 30º “α+β+θ+ω“ E = AC + CE E=9+4 ∴ CLAVE: PROBLEMA 20 C: (37° - 53°) Si BC = 15 BC = 5k ero: AC = 3k mente: x= 9 2 45º En este problema nos están pidiendo: ces calculamos AC y CE ∴ x A figura: AE = AC + CE ⇒ AE = 9 2 Hallar el valor de “x” en la siguiente figura: ⇒ AC = 12 (Hipotenusa) Luego: AE = AC - CE ABCD: AE = 12 - 3 180º - ω = α + β + θ AE = 9 ∴ α + β + θ + ω = 180º CLAVE: D B Si BC = 6 (Opuesto a 30º) Finalmente: DEA (45° - 45°) 8 37º 8 x F 45º 3k 45º 45º A ABF: (45° - 45°) ⇒ AB = BF = 8 ECF: (45° - 45°) ⇒ EC = CF = 3k C 8 D Sumando las 4 ecuaciones se tiene: a + b + c + d + e + f + g + h + (α+β+θ+φ) = 720º B: (37° - 53°) Si: EC = 3k ⇒ BC = 4k 8 + 3k = 4k k=8 Pero en LUZE: α + β + θ + φ = 360º ∴ ∴ CLAVE: CLAVE: C eterminar la suma de los ángulos saltados. UNSAAC CBU 2001 II) L2 P CLAVE: θ + (180º-α) = 60º ∴ α = 160º E CLAVE: PROBLEMA 23 En la longitud adjunta, determinar la longitud “x”. (UNSAAC CBU 2001 II) x 45º 30º En la figura L1 // L2, calcular “α”, sabiendo que el triángulo ABC es equilátero. (UNSAAC CBU INT 2002) B 100º L1 C PROBLEMA 24 En la siguiente figura. Hallar la medida del ángulo θ: (UNSAAC CBU 2002 I) C A D L2 α 8 ) 180º ) 240º ión: B) 720º E) 360º Z d e β U α θ h L I C) 10 2 A) 80º D) 100º Solución: B) 120º E) 140º U θ x θ 30º 45º 12 60º A C) 160º O iden: “a + b + c + d + e + f + g + h” ces tomamos los triángulos: a + f + β = 180º b + e + φ = 180º c + h + θ = 180º d + g + α = 180º T 180º-α 30º B 60º 8 4 C BEC: (30° - 60°) Si BC = 8 (Hipotenusa) ⇒ CE = 4 (Opuesto a 30º) M L1 D 4x ABC: (30° - 60°) Si BC = 8 (Opuesto a 30º) ⇒ AC = 16 (Hipotenusa) P L2 α C Como el ∆ABC es equilátero: ∠A = ∠B = ∠C = 60º ∆BUM: C) 90º x D E B) 80º E) 100º C 100º 2x f B A) 60º D) 20º Solución: A 60º g θ 2x C B 45º E φ a B) 14 2 E) 9 2 A K c S A) 12 2 D) 8 2 Solución: C) 540º R b Z: A: S: O: 180º-α E PROBLEMA 22 LEMA 21 L1 A 60º DEA (45° - 45°) Si AE = 12 ∴ x = 12 2 a + b + c + d + e + f + g + h = 360º x = 32 U θ Finalmente: Finalmente: a + b + c + d + e + f + g + h + (360º) = 720º o: x = 3k + 8 Luego: AE = AC - CE AE = 16 - 4 AE = 12 θ + 60º = 100º (∠ externo) θ = 40º Luego: Propiedad del “Serruchito” 2x 4x θ B A E Si AD = DB ⇒ ∆ADB Isósceles Luego: DAB = DBA= 2x ∆ADB: CDB = 2x + 2x (∠ externo) CDB = 4x Si CD = CB ⇒ ∆DCB Isósceles Luego: CDB = CBD = 4x ∆DCB: 4x + 4x + x = 180º ∴ x = 30 x = 20º mente: B: CLAVE: CBE = 2x + x (∠ externo) θ = 3x θ = 3 (20º) C A PROBLEMA 26 D LEMA 25 alcular el valor del ángulo “x”, si B = AC; BD = BC UNSAAC CBU 2002 I) 6 3 ∆BAD: Finalmente: CLAVE: D CLAVE: 30º x E 37º C ) 40º ) 25º ión: B) 36º E) 50º B) 8 2 E) 10 A) 6 3 D) 8 C) 30º C) 6 A) 15º B) 20º D) 30º E) 45º Solución: B) 30º E) 60º C) 10º Solución: E A 20º B 30º 30º x 50º β E 63 β θ A 50º A ien AB = AC ⇒ ∆BAC Isósceles o: ∠ ABC = ∠ACB = 50º 60º x =8 45º C E 6 53º 8 45º 37º BD = BC ⇒ ∆DBC Isósceles o: ∠BAC = ∠BCD = 50º mente: C: 50 + (x + 50) + 50 = 180 C) 10º Solución: D 50º En un triángulo isósceles EFG, de base FG , se toman los puntos M y N sobre EF y EG respectivamente, de modo que: FM = MN = EN. Si el ángulo G del triángulo dado mide A) 20º D) 80º 50º A PROBLEMA 28 C D B E 80º, hallar el ángulo MNF . (UNSAAC CBU 2002 II) x B x = 15º PROBLEMA 27 C E 45º (I) en (II): θ + 30º = (θ + x) + x ∴ En la figura, ABC es un triángulo isósceles (AB = AC). Determinar x si AD = AE. (UNSAAC CBU 2002 II) 30º ADC = θ + 30º (∠ externo) β + x = θ + 30º… (II) A A H (Opuesto a 37º) (Opuesto a 53º) AEB (45º - 45º) ⇒ AE = BE ∴ AE = 8 Calcular la medida del lado AE del siguiente polígono ABCDEA. (UNSAAC CBU 2002 I) ∴ θ = 60º CLAVE: Si EC = 6 ⇒ BE = 8 B DEC (30º-60º): Si DE = 6 3 (Opuesto a 60º) ⇒ EC = 6 (Opuesto a 30º) CEB (37º-53º): B N 20º θ x M C D x C x Si ∆ABC isósceles ⇒ AB = AC Luego: m ABC = ACB = θ. Si AD = AE ⇒ ∆ADE isósceles Luego: ADE = AED = β. ADE = θ + x β = θ + x … (I) 80º G Como FG es la base ⇒ EF = EG Luego: ∠ EGF = ∠ EFG = 80º Seguidamente: ∆DEC: 80º F (∠ externo) ∆EFG: ∠EGF + ∠EFG + ∠FEG = 180º 80º + 80º + ∠FEG = 180º ∠ FEG = 20º A) D) an: MN=NE MEN es Isósceles B) 2 C) E) 3 + 1 3 2 −1 Solución: • Cuando vemos “p” en alguna fórmula, esto significa semiperímetro, y es la mitad del perímetro. : MN = MF ⇒ ∆MNF es Isósceles r 15º 45º 1 H x mente: 20º = 2x C 30º A 2 CLAVE: C El ÉXITO es la envoltura del sacrificio. LEMA 29 n la figura AC = 2, determinar 2x. UNSAAC CBU 2002 II) 2p(∆ABC) = a + b + c 45º Semiperímetro del ∆ABC (p) CHA (30º-60º): Si CA = 2 (Hipotenusa) ⇒ CH = 1 (Opuesto a 30º) y HA = 3 (Opuesto a 60º) p= El perímetro de un Polígono Regular es igual al número de lados multiplicado por la longitud de un lado. BDA (30º-60º) Si BD = x (Opuesto a 30º) ⇒ AB = 2x (Hipotenusa) 2p = n l AB = 1 + 3 ∴ 2x = 3 +1 CLAVE: a +b+c 2 PERÍMETROS DE POLÍGONOS REGULARES CHB (45º-45º): Si CH = 1 (Opuesto a 45º) ⇒ HB = 1 (Opuesto a 45º) Pero: C Perímetro del ∆ABC: 2p(∆ABC) Trazamos CH ⊥ AB para aprovechar los ángulos de 30º y 45º ∴ x = 10º b A E 30º A PERÍMETROS Donde: n: número de lados l: longitud de un lado CÍRCULO Donde: O: Centro (del círculo o la circunferencia) r : Radio (del círculo o la circunferencia) P: Punto de la circunferencia O: Punto interior de la circunferencia ⇒ O no pertenece a la circunferencia pero si al círculo. Por lo tanto: - La circunferencia tiene longitud, más no área. - El círculo tiene área y su perímetro es la longitud de su circunferencia. LONGITUD DE LA CIRCUNFERENCIA (Lc) Es el límite hacia el cual se aproximan los perímetros (P) de los polígonos regulares inscritos cuando su número de lados aumenta indefinidamente. CIRCUNFERENCIA: EsCAPÍTULO la curva plana y cerrada, cuyos puntos equidistan de un punto interior llamado centro. 2 * La distancia de un punto cualquiera de la circunferencia al centro, se denomina RADIO. CÍRCULO: Es la suma de las medidas de los lados de una figura geométrica. Se representa con “2p” O P 3 1 D a c 2x 60º (∠externo) PERÍMETRO CIRCUNFERENICIA B o: ∠MNF = ∠MFN = x C Es el conjunto de todos los puntos de la circunferencia y de los interiores a la misma. B o: ∠MEN = ∠NME = 20º NME = x + x 2 +1 Es la región plana determinada por la unión de la circunferencia y su interior. lim P = Lc n→ ∞ EL NÚMERO “ π ” El número “pi”, también llamado “Número LEUDOLFINO” (en honor a Ludolf Van Ceulen, Matemático Alemán u Holandés que determino su valor hasta con 354 lugares decimales); es el valor ante de la razón de la longitud de rcunferencia (Lc) a su diámetro. Lc D ⇒ Lc = π D ero D = 2r ⇒ Lc = 2π r = Y otros han aportado valores racionales aproximados de “pi”; tales como: Lc = 2πr A B πDθ 360º L AB = PROPIEDADES 355 = 3.1415929... 113 Sabemos por la propiedad anterior que: 1. LONGITUD DE EN FUNCIÓN AL DIÁMETRO DE UNA SEMICIRCUNFERENCIA ALOR DE “ π ” mero “pi” es el más importante de la a matemática, y es mensurable, así también como su ado, su cubo, etc. lor aproximado es: 3.14159265359 adrado es: 9.869604401089 bo es: 31.0062766803 verso es: 0.318309886184 íz Cuadrada es: 1.772453850906 r 3927 = 3.1416... 1250 LAB LONGITUD DE UN ARCO A (π = 3 ) ( 2 decimales ) ( 7 decimales ) ( 8 decimales ) ( 16 decimales ) ( 35 decimales ) ( 73 decimales ) ( 127 decimales ) ( 140 decimales ) ( 200 decimales ) ( 440 decimales ) ( 530 decimales ) r O L AB θ r B L AM 180º = 2πr 360º AB Pero r = 2 Cuando se realizan trabajos de mucha precisión se usa π = 3.1416 , que viene a ser un trabajo aproximado por exceso con un error menor que 0.0001. garitmo en Base 10 es: 0.497149872 mero “pi” siempre a sido un número sante para los matemáticos, así os: B A Los Hindúes: ⇒ L AB AB = π 2 2. LONGITUD DE UNA LÍNEA CURVA FORMADA POR SEMICIRCUNFERENCIAS Pero: Lc = 2π r ⇒ L AB AM + MN + NB π 2 L AM + LMN + L NB = AB π 2 AB π 2 La propiedad anterior, también la podemos aplicar si la figura se presenta de esta forma: La suma de las longitudes de las semicircunferencias con sus diámetros sobre AB, equivale a la longitud de una semicircunferencia de diámetro AB. B A A θ ⇒ L AB = Lc 360º LAM + LMN + L NB = ∴ LAB = Realizamos una Regla de Tres Simple: Lc → 360º LAB → θ º AM π 2 MN L MN = π 2 NB π L NB = 2 AM MN NB + L MN + L NB = π+ π+ π 2 2 2 L AM = 2 16 = 3.16049... 9 AB π 2 Luego, también se tendía: Papiro de Ahmés: B os Babilonios rquímedes ancois Viette étius drien Romanus V. Ceulen HARPS agny ega hase utherford hangks = AB 22 = 3.142... 7 Adriano Mecio: =2r ⇒ L Como D = 2r Arquímedes: L AB = L AB = B AB π 2 3. SEMICIRCUNFERENCIAS CUYOS DIÁMETROS ESTÁN FORMADAS SOBRE UN SEGMENTO Demostración: θ = 2π r 360º A M AB π 2 N B uma de las longitudes de las ircunferencias con sus diámetros un segmento AB, es igual a la a de AB, multiplicada por π y da por 2. B B D) 10(π+2) Solución: B r Debes tener cuidado, cuando te pregunten: “de la figura sombreada”, por que en este ejemplo vemos que la figura sombreada esta formada por semicircunferencias y también por segmentos. C A R D C B AB = CD L AB AB = π 2 RA 3 . AB + BC = AC + 2r PROPIEDAD AB + BC = 2R + 2r Las tangentes comunes exteriores a dos circunferencias son iguales. De ahora en adelante: M Q Significa longitud de las curvas (semicircunferencias) en AB , y es igual a: L AB = AB π 2 M 2. TEOREMA DE PITOT N C PROPIEDAD angentes trazadas desde un punto or a una circunferencia son iguales. P A R O R B O C Sabemos que: MO π 2 y que : L MA + L AR + L RC + L CO = L MO L MO = MO π + MO 2 20 = π + 20 2 Perím.SOMBR. = MN = PQ Perím.SOMBR. 1. TEOREMA DE PONCELET ∴ D A “En todo triángulo rectángulo, la suma de los catetos es igual a la hipotenusa mas el diámetro de la circunferencia inscrita” Perím.SOMBR. = 10 ( π + 2 ) CLAVE: AB + CD = BC + AD D EJEMPLO 2 EJEMPLOS Se anuncia también así “En todo triángulo rectángulo, la suma de los catetos es igual a la suma de los diámetros de las circunferencias inscrita y circunscrita” R Luego: B TEOREMAS IMPOTANTES PIEDADES DE LAS TANGENTES A UNA CIRCUNFERENCIA A Perím.SOMBR. = L MO+ L MA + L AR + L RC + L CO En todo cuadrilátero circunscrito a una circunferencia, la suma de dos lados opuestos es igual a la suma de los otros dos lados. P Las curvas formadas sobre AB son todas semicircunferencias. E) 20(π+1) A EJEMPLO 1 Hallar el perímetro de la figura sombreada, si los arcos formados sobre este segmento son todos semicircunferencias; y el segmento MO mide 20µ. Hallar el perímetro de la figura sombreada, si los arcos mostrados son semicircunferencias; y el segmento AB mide 20µ. PA = PB PROPIEDAD ngentes comunes exteriores a dos ferencias son iguales. M A) 10π O B) 20π C) 5π B A A) 10π D) 10(π+2) B) 20π E) 20(π+1) C) 5π D) 8π E) 4(π+3) PROBLEMA 2 ión: x Solución: En este caso, la figura sombreada esta limitada solamente por semicircunferencias. B C A A M N B m.SOMBR. = m.SOMBR. Perím.SOMBR. = 13 AB BC AC π+ π+ π 2 2 2 A 4 4 4 Perím.SOMBR. = π + π + π 2 2 2 ∴ Perím.SOMBR. = 20π CLAVE: CLAVE: C 5 6 P 6 H 13 5 Solución: C 5π B A 13 Perím.SOMBR. = 6π B D A) 20π cm. B) 20(π + 4) cm. B) 20 (π + 1) cm. D) 10 (π + 4) cm. E) 20 (π + 2) cm. Perím.SOMBR. = L AB+ L BC + LAC 20 20 = π+ π 2 2 B B) 11 + 61 m D) 25 + 61 m B AB AB π+ π 2 2 A Solución: Luego: AB = BC = AC = 4µ m.SOMBR. = 10π + 10π ∴ A) 19 + 61 m C) 18 + 61 m E) 20 + 61 m Dato: PERIM. ∆ABC = 12µ ⇒ AB + BC + AC = 12µ m.SOMBR. = L AB+ LAB En el cuadrado ABCD de 10 cm. de lado, se ha trazado semicircunferencias en cada lado. Calcular el perímetro de la región sombreada. x 2 C 13 5π 5π 10 D BHA: (Teorema de Pitágoras) EJERCICIOS MPLO 3 triángulo ABC es un triángulo quilátero, los arcos son micircunferencias. Hallar el erímetro de la región sombreada, si perímetro del triángulo es 12µ. B PROBLEMA 1 El lado del rombo mide 13 m y la diagonal menor mide 10m. Hallar el perímetro de la región sombreada. (UNSAAC CBU 99 I) 132 = 52 + BH 2 ⇒ BH = 12 D 5π BHA: (Teorema de Pitágoras) PS = L CURVAS + L SEGMENTOS PC2 = 52 + PH 2 PC2 = 52 + 62 ⇒ PC = 61 Finalmente: Donde: P s = Perímetro Sombreado Dato: Lado del Cuadrado = 10 cm. PerímSOMBREADO = BP + BC + PC ) 3π ∴ PerímSOMBREADO = 19 + C C) 6π ( 61 CLAVE: B) 4π Luego: AB = BC = CD = AD = 10 cm. Primero calculamos la suma se las longitudes de los segmentos que limitan a la región sombreada L . SEGMENTOS PerímSOMBREADO = 6 + 13 + 61 A C A ) L SEGMENTOS = AB + BC + CD + AD = 10 + 10 + 10 + 10 MENTOS = 40 damente calculamos la suma se las udes de las curvas que limitan a la n sombreada L , para lo CURVAS ( E 2 ) B samos la propiedad. L AB AB = π 2 RVAS VAS = L AB + L BC + L CD + L AD =π VAS 1 A) 2(2A + B) C) 4A + B E) 7A − 4B 2 B) 8 + π D) 12 + π A B 6 2 = 20 π mente: 6 D C P ERÍMETRO = AB + BC + CD + LDEA ∴ P S= 20 ( π + 2) CLAVE: D TA: Para no operar tanto debemos darnos cuenta que: Si AB = BC = CD = AD P ERÍMETRO AD = 6+2+6+π 2 n la figura AEB es una micircunferencia, ¿cuál es el erímetro de la figura cerrada DCBEA? UNSAAC CBU INT 2000) C) 3 Solución: A 1 A B B B A Para calcular el perímetro, sumamos todos los lados de la región sombreada. Empezando del lado indicado en un solo sentido (en este caso en sentido horario) PERIM = 4A + 2B CLAVE: C PROBLEMA 4 Calcular el perímetro de la región sombreada que tiene forma de la letra “L”, sabiendo que consta de dos rectángulos iguales contiguos, cada uno de largo “A” metros y ancho “B” metros. (UNSAAC CBU INT 2000) P2 1 P5 1 P4 2 P1 1 De la figura: P1 = P 2 = P3 = P4 = P5 = P6 = K ∴ PERIM = 2 ( 2A + B ) ∴ P ERÍMETRO= 14 + π P6 2 P3 PERIM = A + B + (A − B) + A + B + (A + B) 2 P ERÍMETRO = 14 + π 2 ⇒ LAB = LBC = LCD = LAD LEMA 3 B) 2 E) 2 A-B E 0 + 20π A) 4 D) 1 2 B 1 L CURVAS + L SEGMENTOS B) 2A + 2B D) 4A – 2B Solución: Solución: AB BC CD AD +π +π +π 2 2 2 2 10 10 10 10 +π +π +π VAS = π 2 2 2 2 C 6 A) 16 + π C) 14 + π E) 13 + π o: perímetro de la región sombreada al perímetro de la región no sombreada; es: (UNSAAC CBU 2000 I) D A INICIO MENTOS Luego: CLAVE: A NOTA: También podemos sumar todos los segmentos horizontales y luego todos los verticales, y al final ambos resultados parciales para obtener el total. PROBLEMA 5 En la figura se tiene seis triángulos rectángulos isósceles. La razón del PS = P1 + P3 + P4 + P6 ⇒ PS = 4K PNS = P2 + P5 ⇒ 2K Finalmente: Ps = 4K PNS 2K ∴ Ps =2 PNS CLAVE: B LEMA 6 Hallamos PINTERIOR n la figura adjunta, ABCD es un uadrado de lado 4 cm. El perímetro e la región sombreada en cm es: UNSAAC CBU 2000 I) C B PINTERIOR = MR + NP + MN + PR PINTERIOR = 4 + 4 + π(2) 2 π(2) 2 + 4 4 PINTERIOR = 8 + 2π Hallamos AP y PB en D CLAVE: P B 2 PROBLEMA 7 ∴ PSOMBREADO = N 2π+4 CLAVE: B PROBLEMA 9 E En la figura adjunta, determinar en centímetros el perímetro de la región sombreada, si todos los círculos tienen un radio igual a 2 centímetros: Hallar la suma de los perímetros de los 4 triángulos equiláteros, sabiendo que AB mide 12 cm. R O 2 2 D A) figura: BREADO CLAVE: PROBLEMA 8 2 A ∴ PERÍMETRO = 36 PSOMBREADO = 2 + 2 + 2 π C 2 O PERÍMETRO = 3(12) PSOMBREADO = AP + PB + LAB 2 4M PERÍMETRO = 3(a + b + c + d) Finalmente: En la figura adjunta. Determinar el perímetro de la región sombreada. (UNSAAC CBU 2000 II) ión: Finalmente: AB (Propiedad) 2 2 2 ⇒ LAB = 2 π LAB = π 2 A AB = 12 ⇒ a + b + c + d = 12 LAB = π ∴ P SOMBREADO = 2(12 + π ) B) 2(5 + π) D) 20 + π Pero nos dan: Hallamos L AB PSOMBREADO = (16) + (8 + 2π) ) 2(12 + π) ) 10 + π ) 2(10 + 2π) PERÍMETRO = 3(a + b + c + d) APB (45º-45º) Si: AB = 2 2 ⇒ AP = PB = 2 Finalmente: A PERÍMETRO = 3a + 3b + 3c + 3d PSOMBREADO = AP + PB + LAB = PEXTERIOR + PINTERIOR A B) π + 4 D) 4π + 2 2π−4 C) π + 4 2 E) 2 π + 4 A) 18 cm. C) 26 cm. E) 72 cm. Solución: Solución: o: B A) 16π D) 8π B) 36 cm. D) 40 cm. L mos PEXTERIOR = AB + BC + CD + AD EXTERIOR = 4+4+4+4 EXTERIOR = 16 a a 2 A De la figura: b b c 2 45º A 45º O 2 2 a B De la figura: C) 4π Solución: P EXTERIOR B) 18π E) 24π b M cd c A R V O K I T S d d B Y U Z De la figura el perímetro de la región sombreada es igual a la suma las longitudes de los arcos exteriores: E A A A , LO, OV, VEZ, ZU, UY arcos interiores: 5x 3x , LRY, UKO, OIU, ZTV, VSZ nos podemos dar cuenta que al los arcos YML y LRY se obtiene unferencia MLRY, de manera r en los otros arcos al sumarlos se e una circunferencia, luego mos hallar el perímetro de la región eada de la siguiente forma: B A) 28 D) 24 C 2x + 4 B) 20 E) 30 C) 34 + LLO + LOIU + LUY = LC LZTV + LVEZ = LC B PerímetroSOMBREADO = 4 LC mente: 5x 2x + 4 C ( 25x 2 = 9x 2 + 4x 2 + 16x + 16 12x 2 − 16x − 16 = 0 erímetro SOMBREADO = 4 2π ( 2 ) 3x 2 − 4x − 4 = 0 CLAVE: ⇒ x=2 A LEMA 10 allar el perímetro del triángulo ctángulo ABC. UNSAAC CBU 2001 II) P = LAOB + LBOC + LAC P= AB BC θ π+ π + 2π r 2 2 360º PERÍMETRO = 12x P= 6 6 90º π + π + 2π (6) 2 2 360º PERÍMETRO = 12(2) P = 3π + 3π + 3π ∴ PERÍMETRO = 24 ∴ P = 9π CLAVE: ) C 6 m De la figura: ( 5x )2 = ( 3x )2 + ( 2x + 4 )2 erímetro SOMBREADO = 4 ( 2π r ) ∴ Perímetro SOMBREADO = 16π B Finalmente el perímetro: PERÍMETRO = 5x + 3x + 4x ABC (Teorema de Pitágoras) Las cuatro circunferencias tienen iguales por los tanto tienen la a longitud de circunferencia. C 2x 12+34 4x ⇒ x=2 Solución: 3x + LOV + LVSZ + LZU = LC O B O 6 Luego: 4x = 2x + 4 A LYML + LLRY = LC 5x 3x CLAVE: D A PROBLEMA 12 PROBLEMA 11 Hallar el perímetro de la región sombreada. (UNSAAC CBU 2001 II) En la figura mostrada, hallar el perímetro de la región sombreada, si el radio de la circunferencia es r = 2a. (UNSAAC CBU 2002 I) A Luego, el perímetro sería: PERÍMETRO = 5x + 3x + ( 2x + 4 ) r 6 r r r r PERÍMETRO = 10x + 4 PERÍMETRO = 10(2) + 4 ∴ PERÍMETRO = 24 OTRA FORMA (MÁS RÁPIDA): Observemos que este es un triángulo Notable (3-4-5), entonces: B A) 9π D) 18π Solución: 6 B) 10π E) 6π C C) 12π A) 32 π a B) 12 π a C) 16 π a D) 8 π a E) 20 π a Solución: Resolvimos un problema muy similar anteriormente, por lo que podemos afirmar que: PerímetroSOMBREADO = 5 L erímetroSOMBREADO = 5 [2π (2a)] ∴ Perímetro SOMBREADO = 20 π a Perím SOMBR = 2π(8) 8 8 + π+ π 4 2 2 CLAVE: Áreas ∴ Perím SOMBR = 12π CLAVE: CAPÍTULO E 3 E PROBLEMA 14 LEMA 13 alcular el perímetro de la región mbreada en la siguiente figura, si O = OB y los arcos son porciones e circunferencias. UNSAAC CBU 2002 II) A Determinar el perímetro de la región sombreada, de la figura. (UNSAAC CBU 2002 II) ) 15π ) 16π B) 10π E) 12π A) 16a (π + 2) C) 8a (π + 2) E) 8a (2 - π) C) 6π B) 4a (π + 2) D) 8a (π - 2) A1 ≡ A2 O figura podemos ver que : m SOMBR = L AB + LAO + L OB m SOMBR = 2πR OA OB + π+ π 4 2 2 D1 D2 S1 D12 r12 = = S2 D22 r22 1. FÓRMULA GENERAL: l = 4a II. Las Figuras Semejantes tienen igual forma, y sus áreas son proporcionales a los cuadrados de sus elementos homólogos. - h A b B De la figura, se deduce que: Perím SOMBR = 4l + 4L - N Perím SOMBR = 4(4a) + 4[2π (a)] A = 8 a (π π + 2) CLAVE: C S= bh 2 Triángulo Rectángulo C S1 (r = a) C H Caso de 2 Triángulos Semejantes: a ∴ Perím SOMBR Triángulo Acutángulo B Por ejemplo: 8 S2 r2 A. REGIONES TRIÁNGULARES A1 = A 2 B 8 r1 PRINCIPALES FÓRMULAS DE FIGURAS CONOCIDAS Solución: ión: A S1 I. Las Figuras Equivalentes tienen igual área, sin importar la forma. a O El área de una superficie limitada cualquiera es su extensión, indicada por un número positivo único acompañada de la unidad adecuada (cm2, m2, u2, etc.). DEBEMOS RECORDAR QUE: B 8 Caso de 2 Círculos: ÁREA: S2 C M h L S1 AB2 BC2 AC 2 = = = S2 MN 2 NL2 ML2 A b B S= bh 2 INFORMES E INSCRIPCIONES Av. de la Cultura 1020 Of. 203. 2do. Nivel. 244856 49 Triángulo Obtuso B c a r A H S= bh 2 a c b S= 3 C b abc 4R a C S = ab D 7. TRIÁNGULO RECTÁNGULO CIRCUNSCRITO 3. PARALELOGRAMO: A m C n r S = a b Senθ 8. EN FUNCIÓN A LOS EX-RADIOS E INRADIO C. REGIONES POLIGONALES 4. ROMBO: 1. POLÍGONO CIRCUNSCRITO: B S= c b c Sen θ 2 B C b Dd S= 2 d θ S = pr b b ÓRMULA TRIGONOMÉTRICA: 2 8. CUADRILÁTERO CIRCUNSCRITO h θ a + b + c+ d ( p − a ) ( p −b ) ( p −c ) ( p −d ) S = bh a p = d S= B r c a D2 = a2 + b 2 S = mn h2 3 S= 3 4 7. CUADRILÁTERO INSCRITO: b L L L L H 2 S = R A A D2 2 2. RECTÁNGULO: B h S= 6. EN FUNCIÓN AL CIRCUNRADIO B RIÁNGULO EQUILÁTERO: L D L C b A DdSen θ 2 S = L2 S = pr h b S= 1. CUADRADO: B r Ra Rc S = pr D r ÓRMULA DE HERÓN: A C 5. TRAPECIO: 2. POLÍGONO REGULAR b B p= a b a+b+c 2 Rb S= h C S = p ( p −a ) ( p −b ) ( p − c ) N FUNCIÓN DE SU INRADIO: (B+b ) h 2 ap S = p x ap B S# ABC = r R a R b R c 6. TRAPEZOIDE: B. ÁREAS DE REGIONES CUADRANGULARES D. REGIONES CIRCULARES 1. θ d D Círculo: SZC = S CD − S AB R S = π r2 5. Corona Circular: SCC = π(R 2 − r 2 ) θ SSECTOR = π r 2 360° 6. Trapecio Circular: B AT 2 S S S S S S r R O θ S S A R L ASECTOR R ( STC = π R 2 − r 2 LR = 2 ) 360θ ° El área de un Trapecio Circular, también se puede calcular con la fórmula para un trapecio y sería así: B egmento Circular: r θ R L1 O B S S S S= AT 4 S= AT 2 S I) Se cumple que: S S= J) Propiedad del Triángulo Rectángulo: D) Se cumple que: S1 S1 S2 S1 = S2 D S S Si los lados de un triángulo rectángulo son líneas homologas de figuras semejantes construidas sobre ellos, entonces la suma de las áreas de regiones construidas sobre los catetos es igual al área de la región apoyada en la hipotenusa. Por consiguiente: S1 S2 L + L2 STC = 1 (R − r) 2 A) Propiedad de la Mediana. S2 S3 L2 ALGUNAS RELACIONES IMPORTANTES DE ÁREAS S AT 4 S R-r π r 2 θ r 2 Senθ S AB = − 360° 2 B AT 6 E) Se cumple que: A ona o Faja Circular: S= C) 2DA Propiedad de los Puntos Medios Al Sector Circular, también se le conoce como Triángulo Circular o Triángulo Mixtilíneo y su área se calcula así: O S= S B) 1RA Propiedad de los Puntos Medios R O G) Se cumple que: r A θ AT 2 H) Se cumple que: ector Circular: O S= S1 + S2 = S3 A T = S1 + S2 K) Lúnulas de Hipócrates: F) Se cumple que: S S= AT 2 C PROBLEMA 1 S2 ABCD es un cuadrado, M y N son puntos medios. ¿Qué parte de la figura falta sombrear? S1 B A M ÓRMULAS GEOMÉTRICAS IMPORTANTES B A B) 4/8 E) 6/8 Solución: B C) 7/8 S RECTA SECANTE O TRANSVERSAL A E C abc = xyz ∴ A NS 5S 8S PROBLEMAS As = 12 × 6 12 × 6 + 2 2 ∴ As = 72 cm A Así ponemos “A” a la mitad del área de la región que encierra en cuadrado. 2 Luego: También podemos usar la propiedad: A 2 ⇒ As = 5 = AT 8 Donde: E Punto Interior. As AT = 6A 12A 2 12 2 ∴ As = 1 AT 2 ∴ As = 72 cm 2 CLAVE: PROBLEMA 2 A Sabemos que en este tipo de problemas, es conveniente poner un valor al área de la región más pequeña, que en nuestro caso es la mitad de un cuadrado, que puede ser un rectángulo o un triángulo. D As = A∆ AEA + A∆BEC As = D A A 12 D Finalmente: AT A C 6 En ∆CNA MO mediana ⇒ A∆NOA = A∆NOC = S De manera similar para las otras regiones = A 2A 2A Usamos la propiedad de la mediana vista en la teoría, por ejemplo: A NS A 6 2S N C) 1/2 Solución: A 12 B C S B B) 1/6 E) 2/5 E C A A) 3/8 D) 5/8 B) 72 cm2 D) 70 cm2 S 3S O EOREMA DE MENELAO secante a un triángulo, determina dos lados del triángulo, cuatro entos parciales, y con la ngación del tercero otros dos entos parciales. de tal forma que el cto de tres de ellos no consecutivos ual al producto de los otros tres co consecutivos” D Solución: M a b A A) 36 cm2 C) 86 cm2 E) 75 cm2 D N A) 3/8 D) 5/8 a + c = b + 2r r C O SABC = S1 + S2 odo triángulo rectángulo, la suma de tetos es igual a la hipotenusa mas el tro de la circunferencia inscrita” B ¿Qué fracción representa la región sombreada de la siguiente figura? C B EOREMA DE PONCELET Hallar el área de la región sombreada, sí ABCD es un cuadrado de 12cm de lado y ABE es un triángulo equilátero. D CLAVE: PROBLEMA 3 B CLAVE: PROBLEMA 4 C ncontrar la fracción que representa región sombreada en el siguiente uadrado: UNSAAC CBU 99 I) ) 1/8 ) 3/16 En la figura mostrada; si el área de la región sombreada es 200 cm2. Hallar el área del cuadrado ABCD, sabiendo que BOC y COD son semicírculos. (UNSAAC CBU 99 I) B D A B) 5/16 E) 1/2 C) 1/4 O C A) 4 5 m2 C) 4 3 m2 E) 3 m2 D A B) 2 3 m2 D) 2 5 m2 2 A) 172 u2 D) 156 u2 2 A) 400 cm C) 600 cm2 E) 300 cm2 B) 100 cm D) 800 cm2 B 60° E Para calcular el área necesitamos hallar la altura. Solución: C B 60° 60° D 5# = AT 16 # As A C 6 Deducimos que ∆BEA es equilátero ⇒ AE = 2 Usamos la fórmula trigonométrica para hallar el área de la región triangular DEA. ∴ As = 5 AT 16 CLAVE: B ∴ S# DEA = 2 3 m 2 S ABCD ABCD = 2S# DEA S ABCD = 2 ( 200 ) S ABCD = 400 m B N D 8 Trazamos los radios OA y OB , para formar triángulos rectángulos, entonces: En ONA (37º-53º): b=6 En BOM (37º-53º): a=8 MN = 14 (Altura del Trapecio) Luego: 2 A 16 + 12 = 14 2 ∴A CLAVE: PROBLEMA 7 8 ⇒ MN = a + b 2 S ∴ CLAVE: PROBLEMA 6 En este tipo de problemas sabemos que debemos trasladar regiones para obtener una región de área conocida; así obtenemos: S# DEA = 4x 2 Luego: S# Sen120º DEA = 2 4x 2 3 S# DEA = 2 2 A D A 60° vamos que podemos dividir la en triángulos congruentes. o contamos el número de triángulos eados y el total de triángulos que n, para obtener la siguiente ón: O b 10 4 C a 10 120° 4 C) 164 u2 sombreada, 6 M 6 B 2 2 B) 196 u2 E) 144 u2 Solución: Solución: 2 En la figura mostrada: 12 y 16 unidades son las medidas de las bases del trapecio isósceles inscrito en la circunferencia de 10 unidades de radio. ¿Cuál es el área del trapecio? (UNSAAC CBU 99 I) C B E ión: LEMA 5 En el triángulo equilátero mostrado en la figura; AC = 6m, DC = 4m, AE = 4m. Calcular el área del triángulo AED. (UNSAAC CBU 99 I) A = 196µ 2 CLAVE: PROBLEMA 8 B Hallar el área del sector circular de 4m de radio y 8m de arco. (UNSAAC CBU 99 I) A) 4 m2 D) 32 m2 B) 64 m2 E) 12 m2 C) 16 m2 D A O 4 A Dato a = 4 ⇒ a = 2 A Para calcular rápidamente el área de esta región, usamos la fórmula para el Triangulo Circular. C AS = 2 2 O A BD x AH BD x CQ + 2 2 As = 4× 6 4× 4 + 2 2 B A) 6 (9 - π) cm2 C) 48 - 9π cm2 E) 32 + 9π cm2 BC = 4 2 C ( S =π 2 2 ∴ As = 4π LEMA 9 ) 2 −π E 6 A En la figura mostrada, cada “cuadradito” tiene un área de 4 cm2. ¿Cuál es el área de la región sombreada? (UNSAAC CBU 99 I) h A bh A= 2 b D 12 Nos dan el radio del cuadrante ⇒ CD = CB = 6cm Por lo tanto la base menor del trapecio mide 6 cm. Luego: Que en este problema vino así: AS = A − A C A C Recuerda que el área de un triángulo obtusángulo se calcula así: mente: −A 6 B CLAVE: o el radio del círculo sería 2 2 AS = A B) 9 (6 +π) cm2 D) 9 (6 - π) cm2 Solución: PROBLEMA 10 C = AB = 4 D ∴ AS = 20cm2 CLAVE: BAC es un cuadrante (la cuarta de una circunferencia) BAC (45º-45º): 8× 4 2 AS = ∴ AS = 16 m2 2 2 4 A Luego: 8 ión: C 4 AS = A# BAD + A# BCD B) 2 π cm2 D) 4 π cm2 4 H 6 B 2 B ) 3 π cm2 ) 5 π cm2 ) 6 π cm2 C Q Solución: C La figura ABCD es un trapecio y BCD un cuarto del círculo de radio igual a 6cm. Hallar el área de la región sombreada si AD = 12 cm. (UNSAAC CBU 99 I) B a=2 a=2 n la figura mostrada, hallar el área e la región sombreada, sabiendo que sector circular ABC, es la cuarta arte de un círculo de radio AB = cm. UNSAAC CBU 99 I) B b 42 4 A 2 CLAVE: D A) 23 cm C) 16 cm2 E) 20 cm2 Solución: 2 B) 18 cm D) 15 cm2 A= bh 2 12 + 6 π ( 6 ) AS = 6− 4 2 2 ∴ AS = 9(6 − π)cm2 CLAVE: h PROBLEMA 11 PROBLEMA 12 C alcular el perímetro de la región mbreada, sabiendo que el área del uadrado ABCD es 64 cm2 A B En el cuadrado ABCD, de 20 cm. de lado, los puntos M, N, P, Q, E, F, G y H son puntos medios, respectivamente. ¿Cuál es el área del cuadrado EFGH? A M B H C ) 4 ( 3 2 + 4) cm. B) 3 ( 3 2 + 4) cm. ) 3 ( 4 2 + 3) cm. D) 2 ( 4 2 + 3) cm. ) 2 ( 3 2 + 4) cm. ión: H C Q A) 200 cm2 C) 100 cm2 E) 250 cm2 A B) 50 cm2 D) 150 cm2 ABCD = 16A# 202 = 16A# Finalmente: A Solución: B A 4 2 D M A L = 64 ⇒ L = 8 AMNPQ = : Si L = 8 ⇒ BH = HC = 4 o usamos el (45º-45º) DO = OB = OC = 4 2 MNPQ = A MNPQ = mente PERIM # AHO + PERIM # DOC ) ( ( ) A ) = 4 3 2 + 4 cm CLAVE: A EFGH = A D AABCD 2 53º A 30 m A) 350 m2 C) 450 m2 E) 300 m2 ABCD 2 202 ⇒ A 2 A MNPQ = 200 ABC = 30 x 20 2 CLAVE: E Hallar el área de la región sombreada, si el triángulo ABC es equilátero de lado 12m y E, F, G son puntos medios de los lados AB , BC y AC , respectivamente. B C B) 400 m2 D) 250 m2 F E Solución: G A B C 37º MNPQ = 100 CLAVE: OTRA FORMA: A# MNPQ 2 200 A EFGH = ⇒ A 2 LEMA 13 AC x BH 2 C Calcular el área del triángulo ABC Luego: A ABC = ∴ A# ABC = 300cm2 B 2 4 2 +8 + 8 2 +8 P Q ABCD = 64 A A# PROBLEMA 14 C A Finalmente: PROBLEMA 15 C L=8 (Opuesto a 53º) N 4 4 2 4 (Opuesto a 37º) BH = 4(5) ⇒ BH = 20 EFGH = 4A# CLAVE: B O 4 2 ⇒ A# = 25 ∴ AEFHG = 100cm2 Usamos la siguiente propiedad: 4 Si AH = 3k= 15 Luego: BH = 4k G C Q Observamos que existen 16 triángulos en el cuadrado ABCD, entonces: G D BHA: (37º-53º) D N P Luego AH = HC = 15. ⇒ k=5 N P F E D Dividimos el cuadrado en triángulos congruentes: M B A E F C A 53º 15 H Como AB = BC ⇒ ∆ABC isósceles C A) 12(3 3 -π) m2 B) 3(12 3 -π) m2 C) 3( 3 -12π) m2 D) 12( 3 -π) m2 E) 3(4 3 -π) m2 Solución: B 6 E 6 6 A2 F 6 2 r A2 A3 A4 A1 A5 Dato: figura: AS = 2A1 + A 2 mos A1: A1 = π ( 3) 2 2 ⇒ A1 = 9 π 2 hallamos A2. 2 2 = AS = A1 + A 2 + A3 + A4 + A5 122 3 2 60º − 2 π ( 6) 4 360º ASOMB = 2A1 + A2 9π ASOMB = 2 + 36 3 − 12π 2 ∴ ASOMB = 3 (12 ) 3 − π m2 CLAVE: B A = π (12 ) 2 A NS 9A = AS 16A = 144π CLAVE: 2 ×10 A1 = = 10 2 8× 6 A2 = = 24 2 4× 4 A3 = =8 2 A 4 = 12 × 4 = 48 6×8 A5 = = 24 2 C ∴ A NS = 9 As 16 PROBLEMA 18 CLAVE: ¿Qué fracción del área del cuadrado, representa la parte no sombreada de la figura? (UNSAAC CBU 99 II) ∴ En la figura, ¿qué fracción del área del cuadrado MNPQ representa la región sombreada? N P M Q AS = 114cm 2 CLAVE: D A) 9/16 D) 4/5 PROBLEMA 17 Si la longitud de la circunferencia es 24π. ¿Cuánto mide el área del círculo? (UNSAAC CBU 99 II) B) 100 cm2 D) 114 cm2 A) 122 π D) 24 π B) 12 π E) 14 π C) 144 π B) 1/2 E) 3/16 C) 7/16 Solución: En este problema, observamos que el cuadrado mayor queda dividido en 4 cuadrados, si cada uno de ellos tiene un área de “4A”, entonces se tiene el siguiente esquema: A) 2 5 B) 2 3 D) 3 4 E) 1 2 Solución: Solución: A A A A A A A A 2A A PROBLEMA 19 AS = A1 + A 2 + A3 + A 4 + A5 alcular el área de la región mbreada, si cada cuadrito tiene cm. de lado. ión: Luego tendríamos: Luego: Finalmente: LEMA 16 ) 96 cm2 ) 80 cm2 ) 120 cm2 2 π r = 24 π ⇒ r = 12 ∴A Entonces, calculamos: = 36 3 − 12π o: Dividimos la región total, en 5 regiones de áreas conocidas (4 triángulos rectángulos y un rectángulo); luego tendríamos: Lc = 24π C) 4 5 o de trasladar regiones, para obtener, gión de área conocida, tenemos: N 8 = 2π r ⇒ r = P = π r2 4 A = π π ∴A = Q M E CLAVE: C Determinar el área sombreada de la figura; Si AB = 16 cm. ) 16 cm2. π ) 16 π cm2. D C 9k r A) 60 π cm C) 64 π cm2 E) 12 π cm2 B) 25 cm D) 45 cm2 B) 32 π cm D) 16 π cm2 53º D 18 Trazamos CH ⊥ AD para obtener el A A B B Pero: 2 BD = CH = 4k CH = 8 CH = AD = 8 (Altura del Trapecio) Luego: 8 ⇒ BD = 2 2 BD = 2 2 ⇒ AB = AD = 2 ABCD = 8 o, por condición del problema: erímetro H 3k = 6 D h Luego: C: (45º- 45º) erímetro 12 BAC: (37º- 53º) ⇒ HD = 3K = 6 K=2 Trasladamos regiones así tenemos: y 3k 4k =8 2 Solución: 2 A C 37º Solución: 2 2 12 B B A B E F A) 30 cm C) 80 cm2 E) 20 cm2 C B) 150 cm2 D) 120 cm2 h=8 3k A 2 ión: A) 100 cm2 C) 140 cm2 E) 110 cm2 Solución: 2 B) 4 cm2 π D) π cm2 4 18 PROBLEMA 22 PROBLEMA 21 n círculo tiene igual perímetro que n cuadrado cuya diagonal mide 8 cm. El área del círculo es: π cm2. 16 E 53º 16 2 cm π En la figura adjunta, el área del trapecio ABCD es 40 cm2. Entonces el área del rectángulo ABEF es: LEMA 20 12 2 CLAVE: CLAVE: (UNSAAC CBU 2000 I) ∴ A ABEF = 20 cm 2 ∴ AS = 1 AT 2 o: ) A Finalmente: 20 A ABEF = 3 3 4 π ABCD = Lc ces: Lc = 2π r D F 3k 9k E C ∴ A ABCD = 40 9k + 3k h = 40 2 Luego: A As = 2 A 2 2 18 + 12 8 2 ABCD = ∴A ABCD = 120cm 2 As = 32π CLAVE: 20 ⇒ kh = 3 A ABEF = ( 3k ) h ⇒ As = π (8) CLAVE: B D PROBLEMA 24 PROBLEMA 23 Hallar el área de la siguiente figura: En la figura, calcular el área en metros cuadrados de toda la región mbreada, ABC es micircunferencia. UNSAAC CBU 2000 I) a una a B a M C b P h B b 4b N 2b C O 2m B) 2 E) 1 ión: B C)7 ATRAPECIO A# ABC O 2m 1 ⇒ As = 2 (1) 2 ∴ As = 1m2 CLAVE: E 1 2 1 ) 4 ión: A PAM = A ABCD − ( A BAM + ACPM + A PAD ) D Finalmente: A ABCD = ( 2a ) x ( 4b ) 1 3 1 E) 6 C) 2 5 D A 2 A) 120 m C) 106 m2 E) 92 m2 Solución: 2 B) 64 m D) 96 m2 En la figura adjunta. Determinar el área del círculo sombreado en cm2. (UNSAAC CBU 2000 II) A ABCD = 8 (12 ) ∴ A ABCD = 96m2 CLAVE: D Calcular el área del triángulo isósceles en m2, si su altura es 12 m y el perímetro del triángulo es 36 m (UNSAAC CBU 2000 II) A) 36 D) 80 B) 60 E) 120 Solución: B b B PROBLEMA 28 PROBLEMA 27 B) 2a x 12 2 CLAVE: C 3a A# ABC = Finalmente: a M ⇒a =5 ∴ A ABCD = 60m2 A ABCD = 8ab Hallar el área del cuadrilátero ABCD, si el área del triángulo AMP es 30 m2. (UNSAAC CBU 2000 II) AHB: Remplazamos (I) en (II): 11ab ⇒ ab = 12 m 2 30 = 8ab − 2 CLAVE: B Teorema de Pitágoras en (18 − a )2 = a 2 + 122 a 4b a b 2a 3b 30 = 2a x 4b − x + x + x 2 2 2 PROBLEMA 26 LEMA 25 2a + 2b = 36 a + b = 18 b = 18 − a … (I) b 2 = a 2 + 122 … (II) De la figura: ah ASOMBREADA 2 = A TRAPECIO 3a + a h 2 ∴ ASOMBRADA = 1 A TRAPECIO 4 C 1 D 2a Perímetro# ABC = 36 ⇒ No nos dicen que es un cuadrado, por eso colocamos lados diferentes. Finalmente se tiene: a relación entre el área sombreada y área del trapecio isósceles es: UNSAAC CBU 2000 I) ) ah 2 a + 3a = h 2 ASOMBREADA = 1 A A Primero hallamos: )3 )5 Dato: 2 cm A 3a 12 C) 90 2 cm A) (3 + 2 2 ) π C) (3 - 2 2 ) π E) (3 - 2 ) π Solución: b B) (2 - 3 2 ) π D) (2 + 3 2 ) π B C r 4 2cm 1 AS (Opuesto a 45º) (Hipotenusa) De la figura: AS = L2 − π r 2 AS = 42 − π(2) 2 A = π r2 A =π ∴A ( ) 2 −1 ( CLAVE: ) C LEMA 29 área de la región sombreada en m2, en la figura dada es: UNSAAC CBU 2000 II) ión: A A 2A 2A 2A 2A D Por lo tanto se tendría: AS Hallar el área de la región no sombreada en cm2. Si el radio del círculo mayor mide 2 cm. y el ángulo AOB mide 120º. (UNSAAC CBU 2000 II) B A 18A 30A 120º AS = π (2)2 360º ATOTAL ∴ AS = 4 π ∴ AS = 3 ATOTAL = 5 CLAVE: B CLAVE: B PROBLEMA 32 PROBLEMA 31 PROBLEMA 30 En la figura, cada cuadradito tiene un área de 4 cm2. ¿Qué parte del área total del rectángulo ABCD es el área sombreada? (UNSAAC CBU 99 II) B C En la figura, ¿Qué fracción del área del rectángulo ABCD representa la región sombreada? (UNSAAC CBU 99 II) B C A D O 4 cm ) 4 (8 - π) ) 8 (4 + π) ) 2 (16 - π) Luego: B = 3−2 2 π CLAVE: 2A El área de cada triángulo es “A”; por la tanto el área de cada cuadradito sería “2A”. 3 ∴ AS = 4 ( 4 − π ) 2 2A A θ AS = π r 2 360º Finalmente: o: 2 −1 A O Pero “A” es la cuarta parte de un círculo, por lo tanto: 4 A = A de la figura: AC = 1 + 2 r + 1 2 2 =2+2r mente: A 120º r =2 AS = A ABCD − 4 A AS = A ABCD − 4 A AS = A ABCD − A r= A 4 calcular el área del círculo, bastará ar el radio del dicho círculo. A B A D 2cm D (45º - 45º) omo: AB = 2 ⇒ AC = 2 2 C B A r A A Trasladamos regiones y obtenemos un sector circular de 120º, como se muestra: A A 1 A 4 cm B) 4 (4 - π) D) 4 (8 + π) A) 4 π 3 D) 8 π 3 Solución: B) 3 π 4 E) 4 π C) 3 π 8 D A) 4 B) 3 C) 8 5 D) 2 3 5 E) 2 7 15 Solución: A) 1 B) 5 C) 1 3 8 4 D) 2 E) 1 3 2 Solución: M B A A C A A# ABC = A r 60º El hexágono es regular por lo que lo dividimos en 6 triángulos equiláteros. r AS 2A = A TOTAL 6A D: AN es mediana ⇒ A# ACN = A# AND = A ∴ AS = 1 ATOTAL A# ABC = [ 2(1)]2 3 CLAVE: AS 2A = A TOTAL 4A E PROBLEMA 34 ∴ AS = 1 ATOTAL 2 E LEMA 33 En la figura adjunta el área de la región sombreada es 3 − π cm2 . 2 Determinar el área en cm2 del triángulo formado al unir los centros de las circunferencias siendo estas iguales. n la figura adjunta. ¿Qué parte del ea del hexágono regular representa región sombreada? 4 3 D) 2 Solución: 3 CLAVE: Al unir los centros A, B y C se obtiene un triángulo equilátero; para calcular el área que encierra este triángulo equilátero ABC necesitamos saber cuánto mide su lado, para lo que necesitamos calcular el radio de la circunferencia. Dato: A = S B 3 3 E) 3 3 C) 5 3− Hallar el área de la región sombreada: 4 π 2 4 Pero de la figura: AS = A# ABC − 3A Luego: 3− B) ∴ A# ABC = C AS = A) 3 4 r 3 PROBLEMA 35 mente: C) 5 6 60º Trasladamos la región indicada y luego: C: AM es mediana ⇒ A# ABM = A# AMC = A B) 3 8 E) 1 3 r A os la propiedad de la mediana: CLAVE: 4 B A A D mos AC ⇒ A# ABC = A# ACD ión: r 60º N A A ) 2 3 ) 1 2 r A L2 3 L2 3 4 θ − 3 π r 2 360º 2 π (2r) 3 60º = − 3 π r 2 2 4 360º 2 3− π 2 πr =r 3− 2 2 3− π 2 π =r 3− 2 2 ⇒ r =1 Finalmente: A) 5 D) 3 B) 7 E) 9 C) 2 Solución: 4 B P 1 M H C 2 3 N 2 A 2 Q ABQ: PM // AQ 2 2 D M es Base Media de AQ M= AQ ⇒ PM = 1 2 3A como PM = 1 r O C MN x QH 2 # MQN = # MQN 3 2 = x 2 D ión: Solución: 53º A O ∴ ATRAPECIO = 5 CLAVE: C) 2 3 B Nada es imposible, a menos que uno esté de acuerdo en que lo es. PROBLEMA 37 37º 20 ∴ AS = 2 (100 3 − 48 ) CLAVE: E A 30º E 40 20 ADE (37º-53º): AE = 20 (Hipotenusa) 2 B 4cm Buscando la respuesta de las alternativas se tiene: C 3 120º ABC (30º-60º): Como AC = 40 (Hipotenusa) ⇒ AB = 20 (Opuesto a30º) y BC = 20 3 (Opuesto a60º) 4 +1 A TRAPECIO = 1 2 ) En la figura: AC y BC son tangentes al círculo. El área de la región sombreada, es: (UNSAAC CBU 2001 I) 4k 3k BC + OA A TRAPECIO = CA 2 20 x 20 3 12 x16 − 2 2 PROBLEMA 38 D Finalmente: n la figura adjunta. Determinar el ea en cm2 del trapecio AOBC. B) 5 2 E) 2 5 C A) 2( 3 - 48) B) 20 ( 3 - 96) D) 100 (2 3 -48) D) 2(200 3 -96) E) 2 (100 3 -48) CD + CB = BD +2 r 3 + 4=5+2r r=1 LEMA 36 C 30º 37º 40 E B CLAVE: AS = ( En este trapecio para hallar el su área de la región que encierra, necesitamos su altura (r) y su base menor (r). ∴ AS = 3 ABx BC AD x DE − 2 2 AS = 8 25 3 − 12 A Para hallar “r” aplicamos el Teorema de Poncetet en DCB. AS = AS = 200 3 − 96 D B DCB Triángulo Notable (37º-53º) ⇒ BD = 5 mente: ) 3 2 B 4 ién de la figura: QH = 2 )3 5 r la figura MN = 3 m A En la figura, “E” es el punto medio de AC . El área de la región sombreada, es: (UNSAAC CBU 2001 I) D 5k = 20 ⇒ k = 4 AD = 3k (Opuesto a30º) ⇒ AD = 12 BC = 4k (Opuesto a60º) y BC = 16 Luego: AS = A# ABC − A# ADE C 3 B A) 3 3 − π 3 B) 9 3 − π 3 C) 9 π + 3 3 D) 3 π + 3 3 E) 3 ( Solución: 3−π ) A 3 3 3 O 60º 60º 30º 30º 3 C El porcentaje del área sombreada, es: (UNSAAC CBU 2001 I) En la figura: los vértices del triángulo equilátero de lado de longitud 12 son centros de círculos de radio 6. El área de la región sombreada, es: (UNSAAC CBU 2001 I) Si en el gráfico P y Q son puntos medios. ¿Qué parte del círculo falta sombrear? (UNSAAC CBU 2001 I) 3 3 B A) 50% D) 60% ro trazamos OC para obtener ulos rectángulos notables de 30º y C (30º-60º): OA = 3 (Opuesto a 30º) ⇒ AC = 3 3 (Opuesto a 60º) B) 40% E) 45% Solución: A) 6π + 3 B) 16π + 3 3 ( ) E) 18 ( π + 2 3 ) D) 9 π + 3 ( D) 4 4π + 3 3 2 3 1 D) 2 ) h ) ( ( B A TOTAL 6 = 2 bxh 6 M 12 P CLAVE: A Trasladamos regiones y se obtiene un triángulo equilátero y un semicírculo: ) Para calcular el área de la región sombreada hemos usado esta formula: AS = A# ABC + A1 ndo la forma en la que esta esta se presenta en las alternativas, ne: ∴ AS = 9 π 3− 3 B a Q Área del círculo menor (A1): A1 = π a 2 Área del círculo mayor (A2): 2 ⇒ A2 = 4π a 2 A2 = π ( 2a ) Finalmente: AS = (12 )2 4 3 + π (6) 2 2 A1 π a2 = A2 4 π a 2 h AS = 36 3 + 18π CLAVE: 1 4 1 A TOTAL 2 C 6 a 2a ∴ AS = 50% ATOTAL A 9 3 − 3π 3 3 3−π AS AS = 3 x3 3 120º − π ( 3 )2 2 2 360º C) bxh A1 6 2 A# OAC − ASECTOR AOB B) Solución: b A OACB − ASECTOR AOB 1 3 3 E) 4 A) Solución: o: Q P C) 55% ∴ AS = 18 ( π + 2 3 ) CLAVE: LEMA 39 PROBLEMA 40 ∴ A1 = 1 A 2 b E AS = PROBLEMA 41 4 bxh CLAVE: 2 PROBLEMA 42 C Qué fracción representa la parte mbreada respecto al área total? UNSAAC CBU 2001 II) Hallar el área de la región sombreada, si: AB = BC; DC = DE; BD = 30 cm. (UNSAAC CBU 2001 II) B A) 54 cm2 C) 36 cm2 E) 12 cm2 30 cm D A E C 2 B) 3 5 2 E) 5 C) 1 3 B Dato: 30 cm D a b A E C Aplicamos el Teorema de Pitágoras en el BCD: d =3 2 2 A = AS = 2 + LEMA 43 L 2 … (II) Remplazando (I) en (II) 2 ⇒ x = 20 5 20 = x 5 2 Finalmente: = 36cm 2 CLAVE: C A ROMBO = BD x AC 2 2 PROBLEMA 45 A ROMBO = Hallar el área de un rombo cuya diagonal mayor es el doble de la menor y su perímetro es igual a 80cm. (UNSAAC CBU 2001 II) Remplazando (I) en (II). 900 AS = 2 ∴ AS = 450cm2 CLAVE: PROBLEMA 44 PerímetroROMBO = 80 4L = 80 ⇒ L = 20 … (I) L=x 5 bxb a 2 + b2 … (II) AS = 2 CLAVE: C Dato: L2 = x 2 + ( 2x ) d2 2 (6 2 ) = ∴A AS = A ABC + A CDE 3 2x L Aplicamos el Teorema de Pitágoras en BOA: Finalmente sabemos que: A axa D ⇒ d=6 2 b Luego: ∴ AS = 1 ATOTAL C O x D a 2 + b2 = 900 … (I) ATOTAL x d a 2 + b2 = 302 6# = 18 # C A ión: AS A L 2x Solución: Solución: a o: L B) 18 2 cm2 D) 36 2 cm2 B) 300 cm D) 150 cm2 B imos el la figura en triángulos, para er regiones de áreas iguales, como estra a continuación: B 2 A) 900 cm C) 250 cm2 E) 450 cm2 ) 2 3 ) 3 4 Hallar el área de un cuadrado, si la mitad de su diagonal mide 3 2 cm. (UNSAAC CBU 2001 II) E A) 300 cm2 C) 64 5 cm2 E) 160 cm2 Solución: B) 300 5 cm2 D) 320 cm2 ( 4x ) x ( 2x ) A ROMBO = 4 x A ROMBO 2 2 20 = 4 5 2 ∴ A ROMBO = 320cm2 CLAVE: PROBLEMA 46 D n la figura, el área del triángulo BH es igual a 4m2; además CD x H = 12m2. Hallar el área del apecio ABCD. UNSAAC CBU 2001 II) A 8 A B C H ) 10 m2 ) 30 m2 ) 40 m2 8 D B) 15 m2 C) 20 m2 b A 8 A) 8 + 16 π C) 16 + 8 π E) 8 + 4 π O A) 310 cm2 C) 320 cm2 E) 200 cm2 B) 16 + 4 π D) 8 + 8 π C a A O ⇒ b x h =8 D CD x AH =12 ⇒ a x h =12 De la figura: o: ATRAPECIO ah + bh a+b = h = 2 2 ATRAPECIO = 12 + 8 2 LEMA 47 4 A1 A2 4 O A3 4 C F 2 L = 20 AS = A1 + A 2 + A3 AS = 1 Trazamos OE ⊥ AD 2L x 5L 2 + 2L x 3L 2 ( + 4L x 2L ) AS = 5L2 + 3L2 + 8L2 ⇒ AS = 16L2 AS = 16 ( 20 ) C AS = A PDA ( − A 1 D ⇒ AE = ED = 1 AOE +A OED π (1)2 1 x 1 2 45º AS = π ( 2 ) − + 360º 4 2 ∴ AS = π + 1 4 CLAVE: C PROBLEMA 49 E Luego de la figura: ∴ AS = 320cm2 CLAVE: 45º A 2 De la figura: π ( 4 )2 + 42 AS = 2 4 PROBLEMA 48 P E G A AS = 2A1 + A 2 A C 4 M N C D ∴ AS = 16 + 8π ∴ AS = 10m2 CLAVE: B A2 Dato: A1 B) π + 1 4 2 D) 3π −1 Solución: L B A1 ién nos dan este dato: A) π − 1 4 2 C) π − 2 E) π − 1 3 2 B L A# ABH = 4 =4 B) 280 cm2 D) 230 cm2 Solución: Dividimos la región en tres regiones conocidas (un cuadrado y dos cuartos de círculo) H D A C Solución: B h 2 C B ión: bxh La figura ABCD es un cuadrado de lado igual a 2 cm. Hallar el área en cm2 de la región sombreada. (UNSAAC CBU INT 2002) B 8 D Hallar el área de la figura sombreada. Si cada cuadradito tiene un área de 20cm2. (UNSAAC CBU INT 2002) En la figura, hallar el área de la región sombreada. (UNSAAC CBU 2001 II) 2 CLAVE: PROBLEMA 50 B ) n la figura, ABCD es un trapecio ósceles, EBCF es un cuadrado de 64 2 de área y AD = 26m. Calcular la ma de áreas de las regiones angulares ABE y CFD. UNSAAC CBU 2002 I) B CLAVE: B F C C 13 PROBLEMA 51 A 2 D R O A 2 A) 25 m D) 8 m2 B) 16 m E) 20 m2 Solución: B 5 2 12 B C) 9 m Teorema de Pitágoras: ABC: AC2 = 122 + 52 ⇒ AC = 13 C B A A semicircunferencia es R = 5m. (UNSAAC CBU 2002 I) B En la figura mostrada: ABCD y PQRC son cuadrados, siendo “P” punto medio del lado BC. Calcular qué parte del área de la región no sombreada es el área de la región sombreada. (UNSAAC CBU 2002 I) C E ∴ x + y = 72 D 5 2 P 2 ) 36 m ) 64 m2 ) 48 m2 B) 72 m D) 81 m2 A x Ox D DOC: 52 = (2x)2 + x2 ⇒ x2 = 5 C D ión: B 64 x h L D 26 ato: A BCFE 2A 2A 2A 2A 2A 2A AD = 26 As 8A = A NS 20A 2h + L = 26 ⇒ h = 9 8(9) x= = 36 2 CLAVE: E C PROBLEMA 53 Hallar el área del círculo inscrito en el triángulo ABC, si AB, = 5 cm y BC = 12cm (UNSAAC CBU 2002 I) A A A A En el siguiente cuadriculado, cada “cuadradito” tiene un área de 9 cm2. El área de la región sombreada, es: (UNSAAC CBU 2002 I) C De la figura se tiene: Lh x= 2 ∴ Acírculo = 4π 2 CLAVE: 2A L = 64 ⇒ L = 8 x=y Luego: A círculo = π ( 2 )2 AABCD = 4 x 2 ⇒ AABCD = 4 (5) = 64 2 uego: C) 3/2 Teorema de Poncelet: 5 + 12 = 13 + 2r r=2 PROBLEMA 54 F h Luego AABCD = (2x) 2 ∴ A ABCD = 20m 2A y L B) 5/6 E) 5/12 R Solución: L E ero: A) 2/3 D) 2/5 C L 2x Q ∴ AS = 2 5 A NS A CLAVE: D PROBLEMA 52 Hallar el área que encierra el cuadrado ABCD, si el radio de la 2 A) 2π cm D) 6π cm2 Solución: B B) 9π cm2 E) 8π cm2 C) 4π cm2 A) 54 cm2 C) 36 cm2 E) 27 cm2 Solución: B) 72 cm2 D) 24 cm2 l=3 B 3 C A A2 A1 H A ato: l = 9 ⇒ l = 3 2 e la figura: F 3C 16 6×9 6×9 As = + 2 2 A 3 CLAVE: CLAVE: ⇒A E Q PROBLEMA 58 B ABCD = 2A# AEB ∴ AS = 64u2 E A D Calcular el área de la región cuadrangular ABCD, inscrito en el semicírculo de centro O y radio R. Si el área del semicírculo sombreado Qué parte de la región sombreada, presenta la región no sombreada? UNSAAC CBU 2002 II) En el triángulo AEB, los segmentos interiores son medianas. Hallar el área de la región rectangular ABCD; si el área de la región triangular PBQ es 2u2. (UNSAAC CBU 2002 II) E D (UNSAAC CBU 2002 II) B B) 1/3 E) 1/2 C) 2/3 B A MBN N 3A o, se tendría: C 2 B) 60 u E) 64 u2 A = ABC 4 A D A Luego tendríamos: C) 18 3 u 2 E) 27 u2 D) 36 u2 r D O B) 16 u2 E) 15 π u2 B 2 r C) 20 u2 A r C S r r O B C R 2r C B) 27 3 u 2 D A B C) 65 u A A) 27 2 u 2 Solución: Solución: Usamos la propiedad de la mediana: B os la siguiente propiedad: A Q A) 32 u D) 72 u2 ión: M A 2 B A Solución: C P C R A) 20 π u2 D) 25 u2 ) 1/4 ) 3/4 C mide 5π u 2 . PROBLEMA 56 2 LEMA 55 Determinar el área de la región de un trapecio isósceles ABCD. Si el área del círculo es 36 π u2; donde CD es la mitad del diámetro AB . (UNSAAC CBU 2002 II) PROBLEMA 57 B C P 2 CLAVE: ∴ A NS = 1 AS ∴ AS = 54cm2 2 4 A NS A +B+C+ D+E + F = AS 3 ( A + B + C + D + E + F) As = A1 + A2 2 8 3E A NS A+ B+C+D+ E +F = AS 3A + 3B + 3C + 3D + 3E + 3F F 9 ABCD = 20u CLAVE: C 9 ∴A C E D B 3A D E D 3F 3D 3B Dato: A = 36π π r 2 = 36π ⇒ r=6 A r O r D Luego observamos que: el área pedida es igual a 3 triángulos equiláteros: 5π 2 Dato: A = u 2 πr 2 5π = ⇒ r2 = 5 2 2 Luego: A ABCD = ( 2r ) 2 A TRAPECIO = 3 ( S ) r2 3 A TRAPECIO = 3 4 ∴ ATRAPECIO = 27 3 CLAVE: B medidas iguales; E es el centro del cuadrado ABCD.¿Cuánto mide el área de la región cuadrangular ABCD, si el área de la region sombreada mide 4 2 m 2 ? LEMA 59 A allar el área de la región sombreada, ABCD es un cuadrado de lado 2m. UNSAAC CBU 2002 II) 60º E C C H a) 36 d) 31 A) 16 m 2 B) 12 2 m2 D) 8 2 m2 E) 16 2 m 2 B) π m2 D) 2 m2 c) 32 c a d f c Hallar la suma de los angulos : a + b + c + d + 2e + 2f + i a) 360º d) 620º b) 270º e) 540º c) 720º 6. En la figura adjunta, AD = DC = 6m, si CB = CA. Calcular DB. (UNSAAC CBU 2003 II) b B e f E 1/2 1/2 b) 29 e) 30 e b 2. En la siguiente figura, determinar : a+b+c+d+e+f (UNSAAC CBU 2003 I) C B d i D A x C) 12 m 2 Solución: Trazamos las diagonales (estas se cortan en el punto E) ión: a ¿Cuántas estacas se necesitan, si las estacas se colocan cada 3 metros? (UNSAAC CBU 2003 I) F D ) π/2 m2 ) 4 m2 ) 3 m2 C A G A ¿Cuánto mide el perímetro de dicho triángulo rectángulo? a) 12cm b) 10cm c) 13cm d) 15cm e) 14cm 5. En la siguiente figura (UNSAAC CBU 2003 II) 30 3m D B B un terreno que tiene la forma de la figura siguiente: B A a) 360º d) 180º 1 b) 270º e) 720º c) 540º C 2 C B H D A e la figura se tiene que: B G s = [A ABCD - A ] + 8x E A ∴A ∴ AS = 4m2 C LEMA 60 n la figura ABCD y EFGH son uadrados cuyos lados tienen ABCD C x Luego de trasladar la región: π(1/ 2)2 s = [22 - π(1) 2 ] + 8 2 CLAVE: 3. En la siquiente figura, ABCD es un cuadrado y AED es un triángulo equilátero. Hallar el valor del ángulo “x”. (UNSAAC CBU 2003 I) F = 4 As ABCD = 16 2 m2 D A CLAVE: E PROBLEMAS PROPUESTOS SOBRE TRIÁNGULOS 1. Se desea cercar los lados AB y AC de a) 80º d) 75º b) 105º e) 115º c) 100º 4. Los lados de un triangulo miden, respectivamente; 10, 9 y 8 cm. Si cada lado se disminuye en “x” cm, se convierte en un triangulo rectangulo. D a) 3 5 m b) 8 m d) 6 5 m e) 10 5 m c) 10 m 7. Se da un trapecio con bases de longitudes 3cm. y 6cm. y con altura de 4cm. de longitud. Hallar la distancia del punto de intersección de los lados no paralelos a la base mayor. (UNSAAC 2000 II) a) 6cm b) 9cm c) 8cm d) 4cm e) 5cm 8. La bisectriz del ángulo recto de un triángulo rectángulo forma con la hipotenusa un ángulo de 115°. El ángulo que forma dicha bisectriz con bisectriz exterior del menor de los ngulos agudos, mide: UNSAAC 2001 II) 25° 35° b) 30° e) 45° (UNSAAC 2000 I) B A c) 20° B R Q UNSAAC 2002 PRIMERA OPCIÓN) 8 5 b) 3 5 5 3 8 5 e) 3 A a) 2 2 m b) 3m d) 2m e) 15° d) 15m 45° x 3 e) c) 2 2 6 a hipotenusa de un triángulo ctángulo mide 10cm. y uno de los tetos mide 8cm. Hallar la altura del ángulo tomando como base la potenusa. UNSAAC 2000 I) 6cm 3.5cm b) 4.8cm e) 10cm A 2m c) 4cm n el triángulo ABC mostrado en la gura BH = 4m, AC = 4m. Hallar la ngitud del lado del cuadrado scrito PQRS. b) 6m e) 6 e) 16 3 c) 12 b) 32m e) 21m b) 19 e) 22 c) 20 20. El la figura hallar “x” 80º 40º x 20º 100º n 60° 37° 3 a) 30º d) 60º b) 40º e) 80º c) 50º 21. De la figura hallar “φ” a) 4 − 3 b) 7 − 3 c) 7 + 3 d) 3 − 3 100° φ e) 8 + 3 40° 18. Calcular “x” en el gráfico a) 10° d) 30° b) 15° e) 40° c) 20° 22. Hallar “x” en la figura 10 100° x c) 28m 16. Calcular el valor de “x” en la figura. c) 16 3 D 8 a) 18 d) 21 17. Calcular el valor de “m + n” en la figura. m 15. Los lados de un triángulo rectángulo forman una progresión aritmética cuya razón es 3m. Hallar el perímetro del triángulo. a) 36m d) 24m b) 16 d) 32 3 3m b) 11 e) 14 C a) 32 c) 9m 14. Se tiene un triángulo en donde dos de sus lados miden 3 y 4. Hallar el perímetro del triángulo. Si el tercer lado es el doble de uno de los otros dos lados. a) 10 d) 13 B c) 1 m 4 3 metros de altura, de modo que sus extremos superiores coinciden. Los ángulos que forman la escalera con el piso y la pared con el piso son de 30° y 90° respectivamente. Hallar la distancia del extremo inferior de la escalera a la pared. (UNSAAC 2000 I) a) 12m 6 b) 2 3 α C 13. Una escalera se apoya a una pared de UNSAAC 2002 PRIMERA OPCIÓN) 3 2 S P H C 2 x 8 3 c) 8 n la siguiente figura, la longitud de x”, es: 10 x 30º n un triángulo rectángulo, la longitud la hipotenusa y uno de los catetos iden 12m y 4 5 m , respectivamente. a longitud de la altura relativa a la potenusa mide (en m.): Calcular la suma del máximo y mínimo valor entero que puede tener “x”. D a) 40 2 b) 40 d) 20 e) 10 2 19. En la figura se sabe que ∀ > 90º, y que AC es un número entero. x 70° c) 20 2 a) 50° d) 80° b) 60° e) 40° c) 70° 23. Si AB = DC y DA = DB, hallar “x”. B 35. Si sabemos que “E” es el punto medio de AB . Además ABCD es un cuadrado. Hallar θ : 3 D x x A 10° 45° C b) 20° e) 53° n un triángulo rectángulo uno de sus ngulos agudos mide 22°30´; si ueremos calcular la longitud de la potenusa ¿entre qué número ebemos de dividir a la hipotenusa? 2 2 b) 2 2 e) 3 a) 4 d) 8 α c) 30° a) 30° d) 16° b) 37° e) 15° c) 53° 29. Calcular “ α ” en: 32. En la figura calcular el valor del ángulo “ α ” si AD y BC son bisectrices de los ángulos A y C respectivamente. 30° D 20° a) 20° d) 45° φ φ 12 15 D 10 b) 16 e) 18 C c) 20 a hipotenusa y un cateto suman 62m. Si el otro cateto mide 80m. allar la hipotenusa. 82m 90m b) 68m e) 86m 4 7 b) 5 e) 8 c) 6 alcular “ α ”, si los 2 cuadrados son ongruentes. b) 35° e) 60° c) 37° 30. En la figura siguiente la medidas de ˆ son 60° y ˆ y ACB los ángulos BAC 90° respectivamente, además se trazan las bisectrices de los ángulos interiores las que se intersectan en el punto D. Sea DM la mediana del triángulo ADB hallar la medida de ˆ . los ángulo MDB C a) 95° d) 120° b) 110° e) 125° c) 115° C D a) 12° d) 16° 33. Cuatro rectas se intersecan como se muestra en la figura. Calcular el valor de: (x + y + z + w) b) 14° e) 20° c) 15° D C A B a) 3π( 3 + 1)cm z°° b) π( 3 + 3) cm c) (2 3 + 3π) cm d) 2π( 2 + 2)cm y°° e) 2π( 3 + 3)cm x°° w°° 37. Si AB = 5m y BC = 12 , hallar la C c) 84m n el interior de un cuadrado ABCD toma el punto P y luego se traza H ⊥ BC, tal que BH=2 y HC=8. Si ∠APD=90°, hallar PH. A C θ 36. En la figura se muestra una lámina metálica de forma rectangular. Si y AB = 4 3 cm. AD = 4 cm. Calcular la longitud que recorre el vértice A cuando la lamina haya dado una vuelta completa en el sentido indicado. 60° α B B D c) 4 α E F c) 6 B n la figura, hallar BC A 6 b) 5 e) 9 B A A medida de MN a) 360° d) 630° D A M a) 20° d) 55° b) 30° e) 60° 31. Calcular el valor de “x”: B c) 45° b) 450° e) 720° c) 540° B αα θ θ 34. Hallar el ángulo formado por la intersección de las bisectrices de los ángulos exteriores de los ángulos agudos de un triángulo rectángulo. a) 60° d) 65° b) 45° e) 75° c) 30° A a) 1 d) 4 M N b) 2 e) 5 C c) 2.5 allar el valor del ángulo “ α ” si bemos que ABCD es un cuadrado. A B PROBLEMAS PROPUESTOS SOBRE PERÍMETROS 1. Hallar el perímetro de la figura sombreada: C D 100° 116° b) 105° e) 150° c) 110° b m 15 a) 44 d) 64 a 3a b) 28a e) 34a c) 30a b) 36 e) 62 c) 54 5. En la figura adjunta. Determinar el perímetro de la región sombreada (UNSAAC CBU 2000 II) a) 30πR d) 36πR b) 25πR e) 32πR c) 38πR 8. En la siguiente figura, hallar el perímetro de la región sombreada. (UNSAAC 2002 PRIMERA OPCIÓN) 2. Hallar el perímetro de la siguiente figura: 4 a 3 1 a n ab b) 2a + b 3a + b e) 2ab a+b c) ab B 1 c b C 4 2a d a) 22 a a n la figura ABCD es un cuadrado de do “a”. Calcular el radio de la rcunferencia. 2 6R 4 a) 20a d) 32a x +b ab b +b 3 4 a alcular el valor de “x” en: es: (UNSAAC CBU INT. 2003) 8 a a a 2a α 4. Hallar el perímetro de la región sombreada, de la figura: (UNSAAC CBU 2000 I) a) 2(a + 2b + c – d) c) 2a + 4b + c – 2d e) 5(a + 3b + 10c – d) b) 2(a + 2b – c + d) d) a + 2b + 2c – 2d 3. Hallar el perímetro de la siguiente figura: b) 7 a 3 11a d) 3 3 3a e) 22 c) 20 a 3 6. Hallar el perímetro de la siguiente figura. (UNSAAC CBU 2002 I) b b a) π + 4 d) 2π + 3 b) 2(4+3π) e) 2(4 + π ) c) 3(2+π) 9. Un arquitecto diseña la siguiente reja para ventana. Si los arcos son semicircunferencias iguales y 22 asumiendo ; hallar la π = 7 longitud total de acero que se requiere. 2 A b 6 c 2 70 D A b) a 2 3a e) 8 c) a 3a 5 6 a) 30 d) 36 b) 46 e) 42 c) 40 a) 2 (a – b + 2c) c) 2 (a + b + c) e) 2 (2a + b + c) b) 2 (a + 2b + c) d) 2 (a + 2b + 2c) 7. El peimetro de la region sombreada, a) 490 d) 680 b) 560 e) 620 c) 720 allar el perímetro de la siguiente gura: c d b c 13. En un triángulo equilátero de lado 4; se unen los puntos medios de los lados, formando otro triángulo equilátero, y se repite la operación indefinidamente. Hallar el límite de la suma de los perímetros de todos los triángulos. a) 21 d) 18 a b) 8 e) 12 17. Del gráfico calcule el perímetro del polígono ABCDE B C 3m D 4m A ) 2 (a + b – d) ) 4 (a + b – d) 2 (2a + b – c) b) 2 (a + b + d ) d) 3 (a – b – d) allar el perímetro de la figura mbreada si todas las curvas son micircunferencias. 14. Cuál es el perímetro de la figura, si ABCD es un cuadrado de 10 cm. de lado y los dos arcos son semicircunferencias. A B 1. El perímetro de un cuadrado es el doble del perímetro de un triángulo equilátero, cuya área es igual a 2 9 3 cm . Hallar el área del cuadrado. (UNSAAC CBU 2003 II) 2m c) 24 5m a) 64cm2 d) 81cm2 E a) 2 6 +15 b) 3 6 +14 d) 5 6 +15 e) 7 6 +15 PROBLEMAS PROPUESTOS SOBRE ÁREAS c) 3 6 10. Hallar el perímetro del trapecio, si la altura es igual a la base menor: 4 b) 100cm2 e) 121cm2 2. Calcular el perimetro de la región sombreada en cm, sabiendo que P, Q, R y S son puntos medios en el cuadrados ABCD cuyo lado mide 10cm . (UNSAAC CBU INT. 2003) Q D 10 6 D a) 10(π+2) d) 20(π+2) 8 8π 6(π+3) b) 16π e) 12(π+2) c) 12π C b) 5(π+2) e) 10(π+4) c) 5π 15. Hallar el perímetro de la región marcada si cada cuadradito tiene 1cm. de lado. M B S a) 10 2 b) 11 3 d) 12 2 e) 8 3 c) 8 5 3. En la figura: AB = AP y CD = DP, el area del cuadrilátero ABCD es: (UNSAAC CBU 2003 II) B C b) 27 e) 24 c) 28 16. Se tiene un pentágono ABCDE tal que: AB = BC = CD = DE = b y ABC = ACD = ADE = 90º . Calcular el perímetro del pentágono ABCDE. c) 160cm A B a) 26 d) 25 b) 184cm e) 240cm R c) 24 19. Calcular el perímetro de la región sombreada, si AB = 15. a figura mostrada está formada por exágonos regulares iguales. Hallar perímetro de toda la figura si cada exágono tiene 48 cm. de perímetro. 176cm 168cm b) 22 e) 28 A C P 10 a) 20 d) 26 c) 49cm2 a) 2b d) 10b b) 6b e) 12b c) 8b a) 20 d) 35 N b) 25 e) 40 c) 30 y 20. Se tiene un cuadrado ABCD, sobre el lado AD se traza una semicircunferencia interior, luego desde C se traza una tangente a la semicircunferencia la cual corta a AB en F. Hallar el perímetro del triángulo BCF si el lado del cuadrado mide 6. a) 12 d) 22 b) 14 e) 24 C x c) 18 A D P a) (x + y) 2 2 b) 4 2 c) (x + y) 2 2 e) x + xy + y x + xy + y 2 2 2 2 d) x + y 2 2 4 4. En la siguiente figura, el diámetro el círculo de centro O, mide 8cm. allar el área de la región sombreada. B P A 18cm2 16cm2 C O a) 600m2 d) 100m2 Q D b) 20cm2 e) 17cm2 perímetro es igual a 74m., mientras que el cuadrado de su diagonal es igual a 769m2. ¿Cuál es el área del lote? (UNSAAC 2000 II) c) 14cm2 n la figura, el área de la region mbreada y no sombreada en el rculo mayor de radio R = 4 metros, n de igual medida. El área en etros cuadrados de la región mbreada, es: b) 150m2 e) 300m2 c) 500m2 9. Si el área de la figura sombreada es 8m2. entonces el lado del cuadrado ABCD mide: (UNSAAC 2001 II) B A D C a) 6 2 m d) 4 m 6π 10π b) 4π e) 8π c) 12π e quiere revestir un piso rectangular on losas circulares de igual radio, olocadas tangentes unas con otras. se sabe que tanto a lo largo como a ancho entran losas completas. Cuál es el máximo porcentaje que se ubrirá del piso con las losas? AN MARCOS 2003) 27.5π% 30π% b) 20π% e) 22.5π% b) 576 e) 288 c) 72 n lote de terreno es de forma ctangular y se sabe que su c) 2 m 10. En la siguiente figura se tiene dos circunferencias concéntricas donde OA = AB = 1. Si OB = BC = OC, calcular el área de la región sombreada. (UNSAAC 2002 II) D C (UNSAAC 2002 PRIMERA OPCIÓN)) A) 250 D) 450 B) 500 E) 325 C) 300 12. Hallar el área del círculo inscrito en un hexágono regular, cuya área es de 36 3 m2. A A) 18π m2 C) 24 3 π m2 E) 26 3 π m2 B) 30 3 π m2 D) 18 3 π m2 13. Calcular el área del círculo que está inscrito en un sector circular de 60° de ángulo central y 15cm de radio. (UNSAAC 2002 I) A) 15πcm2 D) 20πcm2 B) 25πcm2 E) 30πcm2 C) 18πcm2 14. Calcular el área de la región de un triángulo rectángulo si su hipotenusa mide 8 y uno de sus ángulos internos mide 22°30” A) 4 B) 8 D) 12 2 E) 8 2 c) 2π − 3 d) π − 3 2 3 π e) − 4 3 6 3 11. La pintura de un cuadro tiene un largo de 60 cm. y un ancho de 35 cm. Calcular el área del marco rectangular B) 4 E) 10 C) 6 17. El cubo mostrado tiene 2m. de arista. Hallar el área de la figura limitada por el triángulo sombreado. B) D) 2 3 E) 4 3 B) 2(5-π) E) 3(6-π) C) 3 2 18. Hallar el área de la región sombreada en la siguiente figura: Y -2 -1 0 1 2 X A) (π- 3 ) u2 B) 2(π+ 3 ) u2 C) 2(π- 3 ) u2 D) (π+ 3 ) u2 2 19. Los lados de un triángulo son tres números consecutivos, el perímetro es 60m. El área de triángulo es: 8 A) 3(4-π) D) 4(6-π) 3 3 2 A) 4 3 E) 3 3 u 6 b) π − 3 A) 5 D) 8 C) 2 2 B a) 3π − 3 región es igual a 4/9 del área de la región del primer hexágono. (UNSAAC 2002 PRIMERA OPCIÓN) 15. Si el triángulo es rectángulo, hallar el área marcada en: O c) 25π% os lados no paralelos y la base enor de un trapecio isósceles son uales entre sí y miden 15 metros. Si base mayor mide 33m. El área del apecio en metros cuadrados, es: UNSAAC 2000 I) 128 144 b) 6 m e) 4 2 m en cm2, si se tiene un ancho igual a 2,5cm. C) 6(4-π) 16. El lado de un hexágono regular mide 9. Determine el lado de otro hexágono regular, cuya área de su A) 152.4 m2 C) 120.6 m2 E) 170 m2 B) 145.8 m2 D) 172.3 m2 20. En la figura E, F, G y H son puntos medios del cuadrado ABCD. Entonces la razón entre el área 10 mbreada y el área no sombreada : F B C A H 3 13 2 ) 15 7 A) 10 6 D) 17 B) C) 5 13 A ) 60 m ) 50 m2 C A) a 2 B) a2 2 a2 3 E) a2 5 D) π B) 1 − R 2 4 π D) 4 − R 2 4 B) 80 m E) 65 m2 A) 10 D) 36 D C R B) 20 E) 38 C) 32 27. Calcular el área de la sombreada en el cuadrado. A región B C M A) 7a 2 10 B) 8a 2 15 D) 11a 2 20 E) 7a 2 10 C) 9a 2 20 30. Determinar el área de la región sombreada, si ABCD es un cuadrado de lado “a”. Además M y N son puntos medios. a B D 2 D A E C) a2 4 5a 2 2 B) 4a 2 5 D) 5a 2 3 E) 5a 2 7 C) 6a 2 7 28. En el cubo de arista 4m., calcular el área sombreada: B C 2 C) 40 m allar la relación entre el área mbreada y el área no sombreada. D C) 3R 2 ( π − 6) D) 2R 2 (8π − 3) E) 2R 2 (32 − 9π ) 26. El área del cuadrado ABCD es 40m2. Hallar el área sombreada sabiendo que M, N, O, y R son puntos medios de los lados. F E A) 8 2 D) 16 B) 4 2 E) 8 C M A) 2a 2 46 B) 5a 2 41 D) 5a 2 35 E) 7a 2 35 C) 5a 2 48 31. Si las bases de un trapecio miden 4 y 6 metros y su altura es de 2m. Calcular el área del triángulo cuyos vértices son los puntos medios de las diagonales y el punto de corte de los lados no paralelos. R B) 2R 2 (15 − 2π ) N D A A) R 2 (16 − 2π) B C A) 25. Hallar el área sombreada de la figura: a altura de un triángulo es los 3/4 de base más 4m. Si la base es la lución positiva de: 2x2 -13x-24 = 0 , área del triángulo es: 2 7 C) 10 D L π ) 2 − R2 4 3π 2 ) R 4 N a R π 2 R 4 6 B) 13 7 E) 13 B O M 24. Hallar el área sombreada, si consideramos que la figura ABCD es un cuadrado, además DB = DE = a 2 . el lado de un cuadrado inscrito en n círculo C1 es L, entonces el área e la figura sombreada, en función el radio R de la circunferencia C1, : A B 3 4 D 5 16 7 E) 13 ) ) 4 G E N A C) 2 2 29. En el cuadrado ABCD, de lado “a” M y N son puntos medios. Hallar el área de la región sombreada. A) 2.4 m2 D) 2.7 m2 B) 2.5 m2 E) 2.8 m2 C) 2.6 m2 32. En la figura mostrada ABCD es un cuadrado: Calcular el área sombreada si tenemos que “O” es el centroide del cuadrado. A L Z 4 D ) 3( π − 2) ) 3( π − 1) B A C 4 B) 2( π + 2) E) 3( π − 3) A N 2 C) 2π π allar el área sombreada, si AB = 8 , endo ABCD un cuadrado. A B 2 A) 4π m . D) 6π m2. 2 C) π/2 m B) 8π m . E) 3π m2. 36. Si Rr = 5 R, hallar el área de la región sombreada. A) D) 2 R 4 B) 3 2 R 4 E) M B U 2 3R 16 C) R 3 3 R 3 R C D B) 8π(7 − 3 5) ) 8π(6 − 5) D) 8π(7 + 2 2) ) 9π(7 − 3 5) área del cuadrado ABCD es igual a 0m2, siendo M y N puntos medios. allar el área del triángulo mbreado. A M C) 12π π 37. En la figura mostrada calcular el área sombreada si AB = AC = 2 , además F y M son centros de las semicircunferencias. B A 60° B A) 2 D) 3 M C D π 3 3 A) 2 − 3 8 C B) 4 E) 6 C) 5 alcular el área de la región mbreada, si MN mide 4m. y AB, N y AM son diámetros. 3 4 3 D) 5 A) C π 2 3 B) 2 − 2 3 π 3 3 π 2 2 C) 3 − D) 4 − 4 3 7 3 E) 2π π 38. Hallar el área de la región sombreada si: m∠LUZ = 120°. y “U” es centro de las dos semicircunferencias. (AU = R) B) 20m2 E) 50m2 48 25 3 E) 7 B) B) 4 E) 1 B) 75 m2 E) 12 m2 C) 30m2 43. Hallar el área del cuadrado ABCD siendo “R” el radio del semicírculo y “r” el radio del círculo. r B R C) 13 4 D C B) R 2 − r 2 A) Rr D) 4Rr 2 C) 2Rr 2 E) 2(R + r ) 44. Calcula el sombreada: área A de la región B C) 6 24 41. En una pirámide regular de base cuadrada de 10m de lado )cuál es el área de la sombra que proyecta una de sus caras laterales en su base a las 12 meridiano. A) 100m2 D) 25m2 A) 10m2 D) 40m2 R 40. En un cuadrado ABCD de lado 3 2 , se toma Q, en la diagonal BD, de modo que las áreas ABCQ y CQD sean iguales. Hallar DQ. F N A C x A B r B) 10π π E) 20π π A 8 2 r A) 8π π D) 15π π y 2 39. En la figura mostrada, calcular el área sombreada de la región ABC. Si r=4 y R=6. B ) 4π(2 − 3 2) )3 ) 5.5 sombreada es 10m2. (“x” e “y” son semicircunferencias) M B C) 50 m2 42. En la figura mostrada calcular la suma de las áreas “x” e “y”. Si el área del triángulo mixtilíneo AMBC es 40m2. y el área de la lúnula D 24 C A) 222 2 B) 250 2 C) 267 2 D) 278 2 E) 288 2 45. En la figura mostrada se pide calcular el área sombreada, si los radios miden 6 m. y 2 m. P y Q trisecan a BC y MN trisecan a AC) B O1 2 O ) 22π − 8 3 30π ) −8 3 ) 40π − 8 3 Q 6 P B) 28π − 9 A 3 35π D) −8 4 a) 1 m . d) 16 m2. perímetro de un trapecio es 42m. la base menor mide 3m. Hallar el ea del trapecio (en m2) si sus agonales son bisectrices de los ngulos obtusos. ) 96 ) 102 B) 84 E) 114 B) 5/4 E) 1/2 C) 1 alcular el área de la región mbreada, si el área de la región angular ABC es 14m2. B 2b A ) 1 m2. ) 4 m2. a M a N a B) 2 m2. E) 5 m2. N 2 b) 4 m . e) 25 m2. C c) 9 m2. 50. En la figura ABCD es un cuadrado, si AB = 10 . Calcular el área de la región sombreada aproximada. A B D C C) 90 alcular el área del cuadrado scrito en un semicírculo de dio " 1m" sabiendo que uno de us lados está sobre su diámetro ) 4/5 ) 3/2 M 2 P b C C) 3m2 n la figura mostrada calcular el área e la región sombreada si el área de región triangular ABC es 70m2. (Si A) 50.25 D) 55.02 B) 52.38 E) 56.38 C) 53.42 Parábola de la Educación Iba un hombre caminando por el desierto cuando oyó una voz que le dijo:: “Levanta algunos guijarros, mételos en tu bolsillo y mañana te sentirás a la vez triste y contento”. Aquel hombre obedeció. Se inclinó, recogió un puñado de guijarros y se los metió en el bolsillo. A la mañana siguiente, vio que los guijarros se habían convertido en diamantes, rubíes y esmeraldas. Y se sintió feliz y triste. Feliz, por haber cogido guijarros; triste por no haber cogido más. Lo mismo ocurre con la educación W. Cunningham








