Proyecto 1 Yesid

RAÍCES E INTERPOLACIÓN
Universidad Industrial de Santander
Métodos Numéricos y Probabilidad
Profesor: Ilia Davidovich Mikhailov
Yesid Román Gómez Código:2121030
27 de Junio 2014
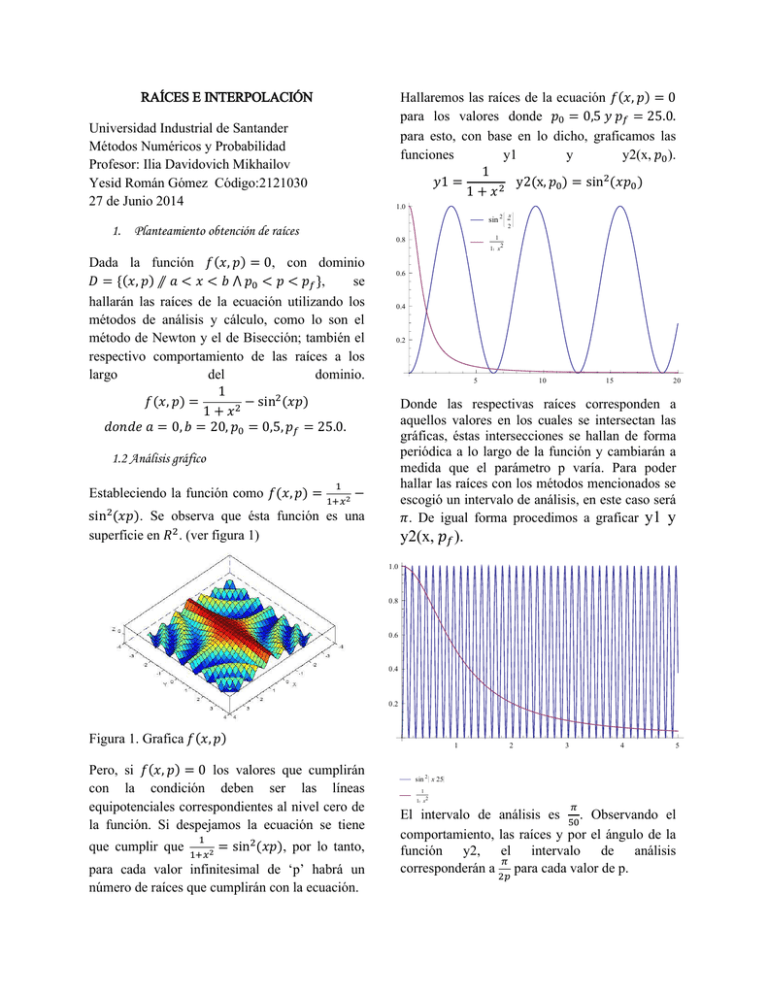
Hallaremos las raíces de la ecuación ( )
para los valores donde
para esto, con base en lo dicho, graficamos las
funciones
y1
y
y2(x, ).
(
(
x
1
0.8
1 x2
0.6
0.4
0.2
5
)
10
15
20
Donde las respectivas raíces corresponden a
aquellos valores en los cuales se intersectan las
gráficas, éstas intersecciones se hallan de forma
periódica a lo largo de la función y cambiarán a
medida que el parámetro p varía. Para poder
hallar las raíces con los métodos mencionados se
escogió un intervalo de análisis, en este caso será
. De igual forma procedimos a graficar y1 y
1.2 Análisis gráfico
Estableciendo la función como (
)
2
)
Dada la función (
, con dominio
( )
,
se
hallarán las raíces de la ecuación utilizando los
métodos de análisis y cálculo, como lo son el
método de Newton y el de Bisección; también el
respectivo comportamiento de las raíces a los
largo
del
dominio.
)
(
1.0
sin 2
1. Planteamiento obtención de raíces
(
)
)
( ). Se observa que ésta función es una
superficie en . (ver figura 1)
y2(x,
).
1.0
0.8
0.6
0.4
0.2
Figura 1. Grafica (
)
1
Pero, si ( )
los valores que cumplirán
con la condición deben ser las líneas
equipotenciales correspondientes al nivel cero de
la función. Si despejamos la ecuación se tiene
que cumplir que
(
), por lo tanto,
para cada valor infinitesimal de ‘p’ habrá un
número de raíces que cumplirán con la ecuación.
2
3
4
5
sin 2 x 25
1
1 x2
El intervalo de análisis es . Observando el
comportamiento, las raíces y por el ángulo de la
función y2, el intervalo de análisis
corresponderán a para cada valor de p.
1.3 Métodos de raíces
Continuando, se usó el código de programación
‘C’ para hallar las raíces con una precisión
deseada de
. Inicialmente se realizó con
el método de la bisección, que se muestra a
continuación, en el cual las raíces halladas se
encuentran en la tabla 1.
No. Raíz
Raíz
1
1.306542
2
5.950173
3
6.584620
4
12.405500
5
12.723241
6
18.742950
7
18.954971
Tabla 1. Raíces de f(x,p) para p=0.5
Se utilizó códigos de programación ya que
usualmente se presentan cálculos bastante
extensos volviéndose imposible realizarlos a
mano. Como se ve para cuando p=25.0 se
presentan 319 raíces distintas en el intervalo de
.
0.060418
0.065446
0.181321
0.196247
0.302413
0.326793
0.423789
0.456968
0.545511
0.586710
0.667604
0.716006
0.790068
0.844875
0.912882
0.973354
1.036018
1.101488
1.159441
1.283118
1.356896
1.407016
1.484249
1.531107
1.611412
1.655365
1.738411
1.779768
1.865271
1.904297
1.992009
2.028936
2.118643
2.153671
2.245186
2.278490
2.371649
2.403382
2.528340
2.624376
2.653355
2.750654
2.778421
2.876884
2.903533
3.003071
3.028685
3.129220
3.153874
3.255335
3.279096
3.381419
3.404348
3.507474
3.529627
3.633505
3.654930
3.780256
3.885499
3.905601
4.011466
4.030965
4.137416
4.156347
4.263350
4.281743
4.389270
4.407155
4.515175
4.532579
4.641068
4.658016
4.766950
4.783464
4.892820
4.908923
1.229321
5.034392
5.144532
5.159869
5.270375
5.285355
5.396210
5.410849
5.522037
5.536351
5.647857
5.661859
5.773671
5.787375
5.899478
5.912896
6.025279
6.038423
6.151075
6.163955
6.276866
2.498043
6.289492
6.402652
6.415035
6.528433
6.540581
6.654210
6.666132
6.779983
6.791688
6.905752
6.917247
7.031517
7.042809
7.157278
7.168376
7.283037
7.293945
7.408792
7.419518
7.534544
3.759512
7.545093
7.660294
7.670671
7.786040
7.796253
7.911784
7.921836
8.037526
8.047422
8.163265
8.173011
8.289002
8.298602
8.414737
8.424194
8.540470
8.549789
8.666200
8.675386
8.791929
5.018681
8.800985
8.917656
8.926586
9.043382
9.052188
9.169105
9.177792
9.294827
9.303397
9.420548
9.429004
9.546267
9.554613
9.671984
9.680223
9.797701
9.805834
9.923415
9.931447
10.049129
10.057061
10.174842
10.182676
10.300553
10.308292
10.426263
10.433910
10.551972
10.559528
10.677680
10.685148
10.803387
10.810768
10.929093
10.936390
11.054798
11.062012
11.180502
11.187636
11.306205
11.313260
11.431907
11.438885
11.557609
11.564511
11.683309
11.690138
11.809009
11.815766
11.934708
11.941394
12.060407
12.067023
12.186104
12.192653
12.311801
12.318283
12.437498
12.443914
12.563193
12.569546
12.688888
12.695179
12.814583
12.820812
12.940277
12.946445
13.065970
13.072079
13.191663
13.197714
13.317355
13.323349
13.443047
13.448985
13.568738
13.574622
13.694428
13.700258
13.820118
13.825896
13.945808
13.951534
14.071497
14.077172
14.197186
14.202810
14.322874
14.328450
14.448562
14.454089
14.574250
14.579729
14.699937
14.705370
14.825623
14.831010
14.951310
14.956651
15.076996
15.082293 16.338727 17.595190
15.202681 16.459518 17.716327
15.207935 16.464372 17.720837
15.328366 16.585200 17.842007
15.333577 16.590017 17.846485
15.454051 16.710882 17.967686
15.459220 16.715663 17.972133
15.579736 16.836564 18.093365
15.584863 16.841309 18.097782
15.705420 16.962245 18.219044
15.710506 16.966955 18.223430
15.831104 17.087926 18.344723
15.836149 17.092602 18.349079
15.956787 17.213607 18.470401
15.961793 17.218248 18.474728
16.082470 17.339287 18.596080
16.087438 17.343895 18.600377
16.208153 17.464967 18.721758
16.213082 17.469542 18.726026
16.333836 17.590647 18.847436
Tabla 2. Raíces de f(x,p) para p=25.0
18.851676
18.973113
18.977325
19.098791
19.102975
19.224468
19.228625
19.350145
19.354276
19.475822
19.479926
19.601499
19.605577
19.727176
19.731227
19.852852
19.856878
19.978529
19.982529
scanf("%lf", &b);
printf("Ingrese el valor del parametro p:");
scanf("%lf", &p);
printf("tolerancia:");
scanf("%lf", &tol);
inter=PI/(2*p);
xl1=a;
xr1=a+inter;
while(xl1<b){
xl=xl1;
xr=xr1;
y0=function(xl,p)*function(xr,p);
if(y0<0.0){
wid=(xr-xl)/2.0;
while(wid>tol){
xm=(xr+xl)/2.0;
y1=function(xl,p)*function(xm,p);
if(y1<0.0)xr=xm;
else xl=xm;
wid=(xr-xl)/2.0; }
x[i]=xm;
i++;}
xl1=xr1;
xr1=xr1+inter;}
-----------------------------------------------------------
raiz=fopen("raices.txt","w");
fprintf(raiz,"Raíces para %lf\n", p);
for(j=0;j<i;j++)fprintf(raiz,"%lf\n", x[j]);
fclose(raiz);
return 0;}
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define PI 3.14159265358979323846
double function(double x, double p){
double y;
y=(1/(1+(x*x)))-(sin(x*p)*sin(x*p));
return y;}
double function(double x, double p);
-----------------------------------------------------------
El código usado para hallar las raíces se presenta
a continuación.
int main(){
double a, b, p, tol, inter, xl, xr, y0, xl1, xr1, wid,
xm, y1, x[340];
int i=0,j=0;
FILE *raiz;
printf("Por favor introduzca el intervalo [a,b] en
el que desea hallar la raiz\n");
printf("a:");
scanf("%lf", &a);
printf("b:");
1.3 Comportamiento y número de raíces
Se encontró éste incremento significativo de
raíces; para un análisis más detallado se halló el
número de raíces N con respecto al crecimiento
del parámetro P a un paso iterativo de 0.6 y se
graficó respecto su incremento. El código
utilizado en C para realizar el conteo es el
siguiente.
-----------------------------------------------------------
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define PI 3.14159265358979323846
Los datos obtenidos se organizaron en la tabla 3,
se graficó la dependencia de las variables
encontrando un crecimiento lineal.
P
N
12,5
160
0,5
7
13,1
167
1,1
15
13,7
175
1,7
22
14,3
183
2,3
30
14,9
190
2,9
37
15,5
198
3,5
45
16,1
205
4,1
53
16,7
213
4,7
60
17,3
221
5,3
68
17,9
228
5,9
76
18,5
236
6,5
83
19,1
244
7,1
91
19,7
251
7,7
99
20,3
259
8,3
106
20,9
267
8,9
114
21,5
274
9,5
121
22,1
282
10,1
129
22,7
290
10,7
137
23,3
297
11,3
144
23,9
305
11,9
152
24,5
312
Tabla 3. Datos del número de raíces contra el
valor de P, las tercera y cuarta columna
corresponden a la continuación de la primera y
segunda respectivamente.
double function(double x, double p);
int main(){
double a,b,p[500],p0,pf,inter,xl,xr,y0,j,x[500];
int i=0,s=0;
FILE *raiz;
printf("Por favor introduzca el intervalo [a,b] en
el que desea hallar la raiz\n");
printf("a:");
scanf("%lf", &a);
printf("b:");
scanf("%lf", &b);
printf("Por favor introduzca el intervalo [p0,pf]
del parametro p:\n");
printf("p0:");
scanf("%lf", &p0);
printf("pf:");
scanf("%lf", &pf);
for(j=p0;j<=pf;j=j+0.6){
p[s]=j;
i=0;
inter=PI/(2*j);
xl=a;
xr=a+inter;
while(xl<b){
y0=function(xl,j)*function(xr,j);
if(y0<0.0)i++;
xl=xr;
xr=xr+inter;}
x[s]=i;
s++;}
N Vs P
300
raiz=fopen("numeros.txt","w");
fprintf(raiz,"p
raíz\n");
for(i=0;i<s;i++)fprintf(raiz,"%lf \n", x[i]);
fclose(raiz);
250
system("pause");
return 0;}
100
double funtion(double x, double p){
double y;
y=(1/(1+(x*x)))-(sin(x*p)*sin(x*p));
return y;}
200
150
50
0
0
5
10
15
Gráfica 1. Número de raíces Vs P
20
25
1.4 Error entre métodos
De igual forma, se halló la primera raíz con el
método de Newton, agregando un contador en
éste, comparando con el método de Bisección se
encontró que en éste último se requirió una
cantidad de 28 iteraciones mientras con el
método de Newton sólo 2. Por lo tanto, mientras
cumpla las condiciones es recomendable usar el
método de Newton ya que consume menos
memoria en cálculos extensos. El código para
hallar las raíces con el método de Newton es:
#include <stdio.h>
#include <math.h>
#include<stdlib.h>
#define pi 3.14159265358979323846
double fun(double x, double p);
double fund(double x, double p);
double fun2d(double x, double p);
double newton(double a,double b,double p,
double tol);
int main (){
double a,b,tol,p,inter,xl1,xr1,xl,xr,yt;
double x[330];
int i=0,j=0,n=0;
FILE *raiz;
printf("Por favor introduzca el intervalo [a,b] en
el cual desea hallar la raiz\n");
printf("a:");
scanf("%lf", &a);
printf("b:");
scanf("%lf", &b);
printf("tolerancia:");
scanf("%lf", &tol);
printf("Ingrese el valor del parametro p: ");
scanf("%lf", &p);
inter=(pi/(2*p*1000));
xl=a;
xr=a+inter;
while(xl<b){
yt=fun(xl,p)*fun(xr,p);
if(yt<0.0){
x[i]=newton(xl,xr,p,tol);
printf("1\n");
i++;}
xl=xr;
xr=xr+inter;}
raiz=fopen("raicesnewton.txt","w");
fprintf(raiz,"Raíces para %lf\n", p);
for(j=0;j<i;j++)fprintf(raiz,"%lf \n", x[j]);
fclose(raiz);
return 0;}
double newton(double a,double b,double p,
double tol){
double y,yl,yr,wid,u;
yl=fun(a,p)*fun2d(a,p);
yr=fun(b,p)*fun2d(b,p);
if(yl>0.0)y=a;
if(yr>0.0)y=b;
wid=sqrt((fun(y,p)/fund(y,p))*(fun(y,p)/fund(y,p)
));
while(wid>tol){
y=(y)-(fun(y,p)/fund(y,p));
wid=sqrt((fun(y,p)/fund(y,p))*(fun(y,p)/fund(y,p)
)); }
return y;}
double fun(double x, double p){
double y;
y=(1/(1+(x*x)))-(sin(x*p)*sin(x*p));
return y;}
double fund(double x, double p){
double y;
y=(-2*x/pow((x*x+1),2))(2*p*sin(p*x)*cos(p*x));
return y;}
double fun2d(double x, double p){
double y;
y=((2*pow((x*x+1),2)+8*x*x*pow((x*x+1),2))/pow(
x*x+1,4))-(2*x*x*(pow(cos(p*x),2)pow(sin(p*x),2)));
return y;}
2 Interpolación
Cuando se tiene un conjunto de valores de
variables dependientes respecto a unas
independientes de una función desconocida y se
desea hallar otros posibles valores en un rango
específico, se pueden utilizar distintos métodos
para encontrar funciones que modelen su
comportamiento y, a partir de esta función,
obtener datos con una precisión específica.
2.1 Función
Inicialmente se estableció una función conocida
( ) de la cual hallamos valores equidistantes
entre el rango
y encontramos sus
imágenes respectivas
.
( )
A partir de los valores de la imágenes les
aplicamos un ruido aleatorio de la siguiente
forma
donde
es la
precisión, éste proceso se realizará para una
precisión de
y
(ver tabla 4).
Raíces para =0.100000
x[i]
yex[i]
y[i]
0.000000 0.000000 0.000000
0.314159 0.086913 0.088834
0.628318 0.247702 0.249690
0.942478 0.346619 0.347034
1.256637 0.350702 0.358166
1.570796 0.288401 0.296479
1.884955 0.198660 0.202461
2.199114 0.112148 0.113720
2.513274 0.047221 0.047384
2.827433 0.010617 0.010630
3.141592 0.000000 0.000000
Raíces para =0.000010
x[i]
yex[i]
y[i]
0.000000 0.000000 0.000000
0.314159 0.086913 0.086914
0.628318 0.247702 0.247703
0.942478 0.346619 0.346619
1.256637 0.350702 0.350702
1.570796 0.288401 0.288401
1.884955 0.198660 0.198660
2.199114
2.513274
2.827433
3.141592
0.112148
0.047221
0.010617
0.000000
0.112149
0.047221
0.010617
0.000000
Programa
----------------------------------------------------------#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
#define PI 3.14159265358979323846
double function(double x);
int main(){
double a,b,e,m,n,u,rnd,j;
int v,k,i=0,s=0;
FILE *variable1;
srand (time(NULL));
printf("Por favor introduzca el intervalo [a,b] en
el que desea hallar la raiz\n");
printf("a:");
scanf("%lf", &a);
printf("b:");
scanf("%lf", &b);
printf("númebro de nodos: ");
scanf("%d", &v);
printf("precision: ");
scanf("%lf", &e);
double x[v],y[v];
m=(b-a)/(v-1);
n=(b-a)/(k-1);
u=rand() % 100000 + 0;
rnd=u/100000;
j=a;
x[i]=j;
y[i]=function(j)*(1+e*rnd);
while(j<=b){
j=j+m;
i++;
u=rand() % 100000 + 0;
rnd=u/100000;
x[i]=j;
y[i]=function(j)*(1+e*rnd);}
variable1=fopen("tabla interpolación.txt","w");
fprintf(variable1,"%d %lf %lf %lf\n", v,e,a,b);
for(s=0;s<=i;s++)fprintf(variable1,"%lf
%3lf\n", x[s],y[s]);
fclose(variable1);
return 0;}
double function(double x){
double y;
y=(sin(x)*sin(x))/(1+(x*x));
return y;}
----------------------------------------------------------Continuando, aplicamos el método de
interpolación de Lagrange para los dos casos y
hallamos las imágenes de una malla de 201 nodos
contenida en el mismo intervalo [a,b], así
obteniendo una gráfica de la función (ver gráfica
2 y 3).
Ya teniendo los N valores (
), con el
programa anterior, el programa de interpolación
de Lagrange global es:
----------------------------------------------------------#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
#define PI 3.14159265358979323846
double function(double xn);
double lagrange(double x[],double
N,double xn);
int main(){
double e,a,b,I;
char t;
int s,i=0,N;
FILE *variable1;
variable1=fopen("tabla interpolación.txt","r");
fscanf(variable1,"%d
%lf
%lf
%lf",
&N,&e,&a,&b);
double x[N],y[N];
for(i=0;i<N;i++)fscanf(variable1,"%lf
%lf\n",
&x[i], &y[i]);
fclose(variable1);
printf("Introduzca el número
interpolar: ");
scanf("%d", &s);
double yn[s],yp[s],xn[s];
Gráfica 2. Valores de x Vs y para ᢄ=0.1
y[],int
de
nodos
a
I=(b-a)/(s-1);
xn[0]=a;
for(i=0;i<s;i++){
yn[i]=lagrange(x,y,N,xn[i]);
yp[i]=function(xn[i]);
printf("%lf\n", xn[i]);
xn[i+1]=xn[i]+I;}
variable1=fopen("interpolado.txt","w");
fprintf(variable1,"xn[i]
yn[i]
yp[i]\n");
for(i=0;i<s;i++)fprintf(variable1,"xn[%d]:%lf
yn[%d]:%lf
yp[%d]:%lf\n",
i,xn[i],i,yn[i],i,yp[i]);
fclose(variable1);
Gráfica 3. Valores de x Vs y para ᢄ
system("pause");
return 0;}
double lagrange(double x[],double y[],int
N,double xn){
double yn=0.0,L=1.0;
int i=0,j=0;
for(i=1;i<=N;i++){
L=1.0;
for(j=1;j<=N;j++){
if(i!=j)L=L*(xn-x[j])/(x[i]-x[j]);}
yn=yn+L*y[i];}
return yn;}
double function(double xn){
double yp;
yp=(sin(xn)*sin(xn))/(1+(xn*xn));
return yp;}
----------------------------------------------------------Finalmente, con el fin de comparar, se realizó el
mismo procedimiento con interpolaciones
segmentarias lineal y parabólica; lo que se obtuvo
fue lo siguiente:
Gráfica 4. Valores de x Vs y para ᢄ=0.1
Interpolación Cuadrática
Gráfica 5. Valores de x Vs y para ᢄ
Interpolación Cuadrática
El código para realizar
segmentaria o lineal es:
Gráfica 4. Valores de x Vs y para ᢄ=0.1
Interpolación lineal
la
interpolación
----------------------------------------------------------#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define PI 3.14159265358979323846
double segmentadaL(double a,double h,double
y[],int N,double xn);
double segmentadaC(double a,double h,double
y[],int N,double xn);
double function(double xn);
Gráfica 5. Valores de x Vs y para ᢄ
Interpolación Lineal
int main(){
double e,a,b,h,he;
int s,i=0,N,P;
FILE *variable1;
variable1=fopen("tabla interpolación.txt","r");
fscanf(variable1,"%d
%lf
%lf
%lf",
&N,&e,&a,&b);
double x[N],y[N];
for(i=0;i<N;i++)fscanf(variable1,"%lf
%lf\n",
&x[i], &y[i]);
fclose(variable1);
printf("Introduzca el número de nodos a
interpolar: ");
scanf("%d", &s);
double yn[s],yp[s],xn[s];
printf("Introduzca el tipo de interpolación
segmentaria deseada: ");
scanf("%d", &P);
double segmentadaC(double a,double h,double
y[],int N,double xn){
double yn,xs1,xs2;
int k;
k=(xn-a)/h;
if(k==(N-1))k=k-1;
y[5]=y[4];
xs1=a+(k)*h;
xs2=xs1+h;
yn=y[k]+((y[k+1]-y[k])*(xn-xs1)/h)+((y[k+2]2*y[k+1]+y[k])*(xn-xs1)*(xnxs2)/(2*pow(h,2)));
return yn;}
variable1=fopen("segmentariado.txt","w");
fprintf(variable1,"xn[i]
yn[i]
yp[i]\n");
for(i=0;i<s;i++)fprintf(variable1,"xn[%d]:%lf
yn[%d]:%lf
yp[%d]:%lf\n",
i,xn[i],i,yn[i],i,yp[i]);
fclose(variable1);
double function(double xn){
double yp;
yp=(sin(xn)*sin(xn))/(1+(xn*xn));
h=(b-a)/(N-1);
he=(b-a)/(s-1);
xn[0]=a;
Comparando con los dato originales (ver gráfica
6) se observa que en estos casos es conveniente
realizar una interpolación por el método de
Lagrange y dejar un margen de error bastante
pequeño, ya que proporciona una exactitud
mayor a los datos
for(i=0;i<s;i++){
if(P==1)yn[i]=segmentadaL(a,h,y,N,xn[i]);
if(P==2)yn[i]=segmentadaC(a,h,y,N,xn[i]);
yp[i]=function(xn[i]);
xn[i+1]=xn[i]+he;}
return yp;}
0.35
0.30
variable1=fopen("segmentariado.txt","w");
fprintf(variable1,"xn[i]
yn[i]
yp[i]\n");
for(i=0;i<s;i++)fprintf(variable1,"%lf\n", yn[i]”);
fclose(variable1);
0.25
0.20
0.15
return 0;}
double segmentadaL(double a,double h,double
y[],int N,double xn){
double yn,xs;
int k;
k=(xn-a)/h;
if(k==(N-1))k=k-1;
xs=a+(k)*h;
yn=y[k]+(y[k+1]-y[k])*(xn-xs)/h;
return yn;}
0.10
0.05
0.5
1.0
1.5
2.0
2.5
3.0
Gráfica 6. Función ( )
Los datos exactos y los interpolados por
lagrange, Newton lineal y Newton cuadrática se
pueden encontrar en el documento Datos.xlsx
anexo a la carpeta comprimida.
mikhail2811@gmail.com
3.5