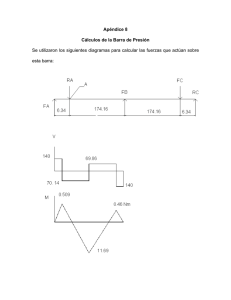
TP1 - Solicitación Axil
Anuncio
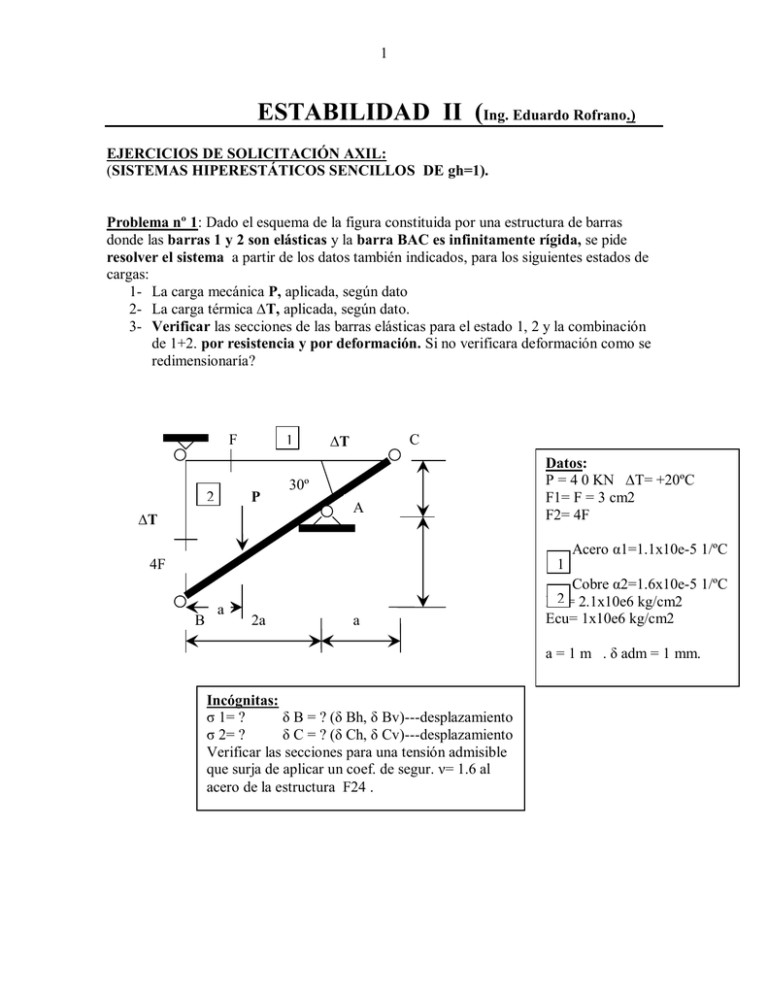
1 ESTABILIDAD II (Ing. Eduardo Rofrano.) EJERCICIOS DE SOLICITACIÓN AXIL: (SISTEMAS HIPERESTÁTICOS SENCILLOS DE gh=1). Problema nº 1: Dado el esquema de la figura constituida por una estructura de barras donde las barras 1 y 2 son elásticas y la barra BAC es infinitamente rígida, se pide resolver el sistema a partir de los datos también indicados, para los siguientes estados de cargas: 1- La carga mecánica P, aplicada, según dato 2- La carga térmica ∆T, aplicada, según dato. 3- Verificar las secciones de las barras elásticas para el estado 1, 2 y la combinación de 1+2. por resistencia y por deformación. Si no verificara deformación como se redimensionaría? F 2 1 P ∆T ∆T C 30º A Datos: P = 4 0 KN ∆T= +20ºC F1= F = 3 cm2 F2= 4F Acero α1=1.1x10e-5 1/ºC 4F 1 B a 2a a a Incógnitas: ζ 1= ? δ B = ? (δ Bh, δ Bv)---desplazamiento ζ 2= ? δ C = ? (δ Ch, δ Cv)---desplazamiento Verificar las secciones para una tensión admisible que surja de aplicar un coef. de segur. ν= 1.6 al acero de la estructura F24 . Cobre α2=1.6x10e-5 1/ºC 2 2.1x10e6 kg/cm2 Eaº= Ecu= 1x10e6 kg/cm2 a = 1 m . δ adm = 1 mm. 2 Problema nº 2: Dado el esquema de la figura constituida por una estructura de barras donde las barras 1, 2, 3 y 4 son elásticas y la barra BAC es infinitamente rígida, se pide resolver el sistema (obtener las incógnitas explicitas) a partir de los datos también explícitos, para los siguientes estados de cargas: 1-La carga mecánica P, aplicada, según dato 2-La carga térmica ∆T, aplicada, según dato. 4-Verificar las secciones de las barras elásticas para el estado 1, 2 y la combinación de 1+2. Por resistencia. 5- Verificar por deformación el desplazamiento máximo de los extremos B y C. Si no verificara deformación como se redimensionaría? 45º L 45º 2 1 3 ∆T ∆T ∆T B C a/2 a P Datos: P = 80 KN ∆T= +30ºC F2= F3 = 6 cm2 F1= F4 =3 cm2 Todas las barras son de Acero α=1.1x10e-5 1/ºC Eaº= 2.1x10e5 MN/m2 a=3m Alternativa: Contracción en barra 3 con ∆T = -35ºC Dilatación en el resto de las barras con∆T = +20ºC A a L ∆T 4 Incógnitas: ζ 1= ? ζ 2= ? ζ 3= ? ζ 4= ? δ B = ? (δ Bh, δ Bv)desplazamiento δ C = ? (δ Ch, δ Cv)desplazamiento Verificar las secciones para una tensión admisible que surja de aplicar un coef. de segur. ν= 1.6 al acero de la estructura F24 . δ adm = 2 mm. 3 Problema nº3: Dado el esquema de la figura constituida por una estructura de barras donde la barra vertical 1, 2, 3 es de sección variable y elástica, siendo la barra ABC infinitamente rígida, se pide resolver el sistema (obtener las incógnitas) a partir de los datos también explícitos, para el estado de carga dado por la fuerza P. Verificar las secciones para una tensión admisible que surja de aplicar un coef. de segur. ν= 1.6 al acero de la estructura F24. Verificar el desplazamiento máximo del extremo C del voladizo. A a a a B 1 P C 2 Incógnitas: ζ 1= ? ζ 2= ? ζ 3= ? δ C = ? (δ Ch, δ Cv)desplazamiento δ adm = a/200 3 2a Datos: P = 40KN F2= 2F1 F3= 2F2 E = 2x10e5 MN/m2 a=2m Alternativa: ∆T= +20ºC en todos los tramos . a Problema nº4: Dada la barra biempotrada de sección variable sometida a una carga P y una carga térmica uniforme ∆T en toda la barra, obtener las tensiones en ambos tramos, previa obtención de los esfuerzos en las barras y calcular el corrimiento del punto C de cambio de sección. Para ambos estados por separado. Dimensionar para el estado más desfavorable: 1) P 2) TΔ 3) P+ΔT (combinación de los dos estados de cargas). Considerar una relación de rigideses igual a 2 (dos). Determinar los Diagramas N(x), u(x) ε (x) ζ (x). Determinar el estado de tensión y de deformación de un punto ubicado en la barra 1. Analizar el estado de tensión para un plano transversal al eje de la barra y otro que forma un ángulo α cualquiera. Cual será la máxima tensión tangencial y el ángulo donde actúe. Cuales serán las tensiones principales y sus planos correspondientes. Analizar el cubo elemental y la circunferencia de Mohr asociada, en forma cualitativa sin escala. 1 C 2 P E1 α1 A F1 L1 E2 α2 L2 Datos: P= 5t ∆T= +20ºC λ1= 1x10-5 1/c° λ2 = 2.3x10-5 1/c° L1=L2=1m E1= Aº (Acero) = 2.1 x106 Kg/cm2 E2= Al (Aluminio) = 7x106 Kg/cm2 B F2 Recordar: Rigidez axil= EF/L Flexibilidad axil= L/EF 4 Problema 5: Dado el esquema estructural, solicitado por una carga térmica uniforme, determinar: 1- El esfuerzo en los tramos de la barra y el desplazamiento del apoyo intermedio. 2- El ET y ED de un punto cualquiera de ambos tramos de barra, determinando los tensores correspondientes. L1= 3m L2= 4m ΔT = 20ºc F1 = 10 cm2 λ = 1x10- 5/ºc F2 = 5 cm2 E = 21000 KN/cm2 μ =0.25 Problema 6: Determinar las tensiones desarrolladas en las dos barras de materiales distintos, vinculadas a dos cabezales infinitamente rígidos, siendo la exterior hueca y la interior maciza, habiéndose sometido a los dos estados de carga siguientes, por separado: 1) La carga P. 2) Al cilindro exterior a una variación uniforme de temperatura ΔT. L=1m ΔT = +45°C λ= 1x10-51/°C P= 6 KN E1= 210000 MPa F1=3 cm2 E2= 100000 MPa F2= 1,5F1 P 2 1 L P Problema 7: Un recipiente esférico de radio interior Ri, contiene un gas a una presión pi. Se solicita: a. Determinar el mínimo espesor del recipiente que asegure el cumplimiento de la condición de resistencia: tensión principal máxima <= 120 MPa.b. Estudiar el estado de tensión y de deformación para un punto, de la superficie interior y para otro de la exterior, del recipiente. Trazar las circunferencias de Mohr. Hallar las tensiones tangenciales máximas e indicar en un cubo elemental (y circunferencia de Mohr asociada) las mismas y los planos en donde ellas actúan. (Para ambos puntos) Ri = 1,5m e=? pi = 15 atm E = 210.000 MPa μ= 0,3. 5 PROBLEMAS DE ESTADO DE DEFORMACION -RELACION CON - ET- LEY GENERALIZADA DE HOOKEEjercicio Nº 1: Mediante la aplicación de una roseta equiangular (120º) (captadores tensométricos de resistencia o galgas extensométricas) en un punto de la superficie interior de una tubería a presión cuya presión interior es de pi= 20 Mpa, se han obtenido las siguientes lecturas: ε0 = 2.5x10-3 ; ε120 = 1.5x10-3 ; ε-120 = 1.1x10-3. Considerando un material de E = 2x105 Mpa y coeficiente de Piosson μ = 0.3, determinar analíticamente: 1- Las deformaciones específicas principales y sus direcciones en el punto considerado. 2- Las tensiones principales. 3- Calcular εnn y γnt para una dirección n que forma un ángulo α = 50º con x y γ= 90º con z (n┴t). 4- Trazar la circunferencia de Mohr de tensiones y verificar los valores del punto 2-. z x t pi n y Ejercicio Nº 2: Un tanque cilíndrico de almacenamiento de gas a presión, tiene un diámetro interior D y un espesor de pared e (delgada). Se colocan extensómetros en la superficie del tanque en direcciones transversal y longitudinal. Estos indican las deformaciones εt y εl respectivamente. Sabiendo que un ensayo de torsión ha mostrado que el módulo de elasticidad transversal del material del tanque es de G = 800000 kg/cm2 determinar: a- La presión manométrica en el interior del tanque. b- Las tensiones principales y la tensión tangencial máxima en la pared del tanque y las direcciones correspondientes. c- El módulo de elasticidad E y el coeficiente de Piosson μ del material del tanque. t Datos: l D = (550/650) mm e = (17/25) mm εt = (23x10-5/28x10-5). εl = (5.5x10-5/6.5x10-5). 6 Ejercicio Nº 3: Para el estado de tensión dado determinar las deformaciones específicas asociadas a la dirección normal del plano π. z ζz ζx = ζz = 120 Mpa E = 2.1x105 Mpa. ζx μ = 0.3. π x y Ejercicio Nº 4: Dado el siguiente estado de deformación, correspondiente a un estado plano de tensión, se pide determinar las deformaciones específicas asociadas a la dirección normal del plano π. z ζz = 0 E = 2.1x105 Mpa. μ = 0.3. εx = εy = 1.5x10-3 π x τxy = 0 y Ejercicio Nº 5: Para el cubo de la figura cargado como se indica, y que encaja perfectamente en un canal abierto e indeformable, se pide: a- Calcular las fuerzas actuantes sobre las caras del cubo. b- Determinar la variación de la longitud de sus lados. p Datos: P = 150 Mpa a = 10 cm. a E = 2.1x105 Mpa. μ = 0.3.