EJERCICIOS TEMA 17: CIRCUITOS DIGITALES

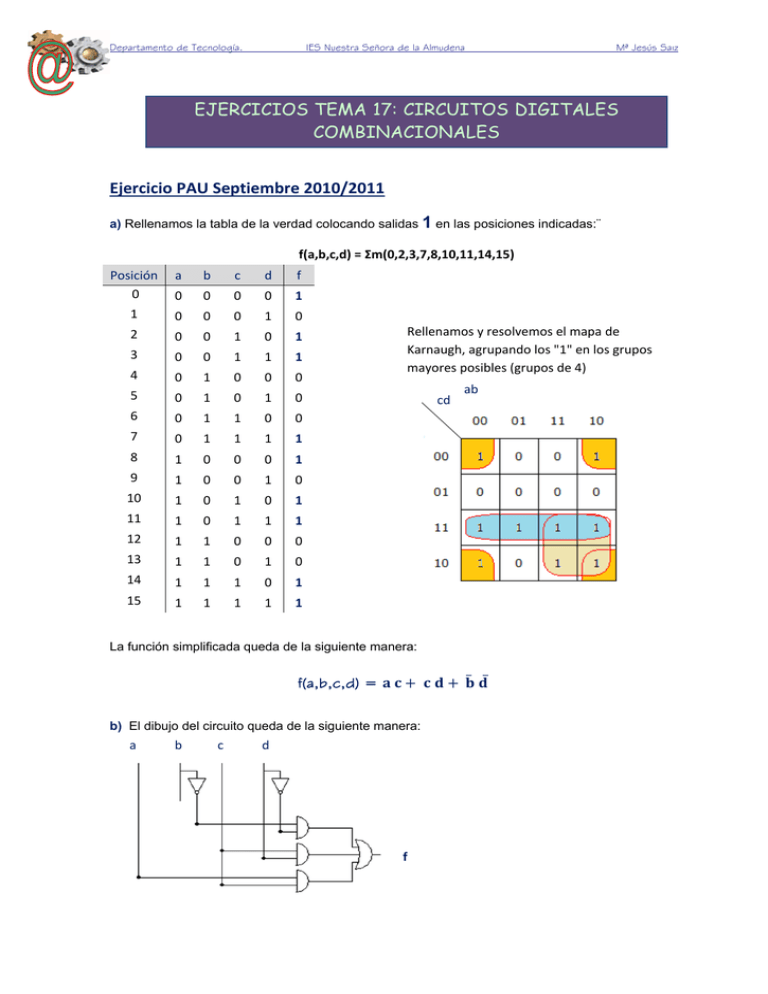
Departamento de Tecnología.
IES Nuestra Señora de la Almudena
Mª Jesús Saiz
EJERCICIOS TEMA 17: CIRCUITOS DIGITALES
COMBINACIONALES
Ejercicio PAU Septiembre 2010/2011
a) Rellenamos la tabla de la verdad colocando salidas 1 en las posiciones indicadas:¨
f(a,b,c,d) = Σm(0,2,3,7,8,10,11,14,15)
Posición
0
a
b
c
d
f
0
0
0
0
1
1
0
0
0
1
0
2
0
0
1
0
1
3
0
0
1
1
1
4
0
1
0
0
0
5
0
1
0
1
0
6
0
1
1
0
0
7
0
1
1
1
1
8
1
0
0
0
1
9
1
0
0
1
0
10
1
0
1
0
1
11
1
0
1
1
1
12
1
1
0
0
0
13
1
1
0
1
0
14
1
1
1
0
1
15
1
1
1
1
1
Rellenamos y resolvemos el mapa de
Karnaugh, agrupando los "1" en los grupos
mayores posibles (grupos de 4)
cd
La función simplificada queda de la siguiente manera:
f(a,b,c,d) =
b) El dibujo del circuito queda de la siguiente manera:
a
b
c
d
f
ab
Departamento de Tecnología.
IES Nuestra Señora de la Almudena
Mª Jesús Saiz
Ejercicio PAU Septiembre 2010/2011
a) -78(10)
Primero pasamos el numero decimal positivo 78 a numero binario y le añadimos ceros a la
izquierda para completar los ocho dígitos
Cociente Resto
78:2
39:2
19:2
9:2
4:2
2:2
39
19
9
4
2
1
0
1
1
1
0
0
1001110 = 01001110
Para transformar el número binario positivo a un número binario negativo se utiliza el
método de complemento a dos. Empezando a leer el número por la derecha, se
mantienen iguales todos los “ceros” y el primer “uno” que encontremos, y después se
cambian los dígitos restantes (los ceros por unos y los unos por ceros)
Solución:
-78(10) = 10110010(C2)
b) 93(10)
Cociente Resto
93:2
46:2
23:2
11:2
5:2
2:2
46
23
11
5
2
1
1
0
1
1
1
0
1011101 = 01011101
Los números decimales positivos no se complementan
Solución:
93(10) = 01011101(C2)
c) 10110100(C2)
Por ser un número complementado a dos y que empieza por "1", se trata de un número
negativo.
Primero hay que descomplementar a dos (se mantienen iguales todos los “ceros” y el primer
“uno” que encontremos por la derecha, y después se cambian los dígitos restantes (los
ceros por unos y los unos por ceros)).
01001100.
Este valor es el número binario en positivo. Ahora lo pasamos a número
decimal
01001100 = 0. 27 +1. 26 + 0. 25 + 0. 24 + 1. 23 + 1. 22 + 0. 21 + 0. 20 = 76
Solución:
10110100(C2) = -76(10)
Departamento de Tecnología.
IES Nuestra Señora de la Almudena
Mª Jesús Saiz
d) 01110001(C2)
Por ser un número complementado a dos y que empieza por "0", se trata de un número
positivo y los números positivos no se complementan, por lo que no hay que
descomplementar a dos
01110001(C2) = 0. 27 +1. 26 + 1. 25 + 1. 24 + 0. 23 + 0. 22 + 0. 21 + 1. 20 = 113
Solución:
01110001 (C2) = 113(10)
Ejercicio PAU Junio 2010/2011
a) Solución:
-26(10) = 11100110(C2)
b) Solución:
11510) = 01110011(C2)
c) Solución:
10010010(C2) = -110(10)
d) Solución:
00010010 (C2) = 18(10)
Ejercicio PAU Septiembre 2009/2010, tema 17
a) Para realizar el mapa de Karnaugh hay que operar en la función hasta conseguir que se
parezca a una suma de productos o a un producto de sumas. Para operar aplicamos los
teoremas de Morgan
f (a,b,c) =
+ a) =
) + a) =
=
=
Rellenamos la tabla de la verdad, colocando con lógica positiva las combinaciones que dan
salida 1:
Posición
0
a
b
c
f
0
0
0
1
1
0
0
1
0
2
0
1
0
0
3
0
1
1
1
4
1
0
0
0
5
1
0
1
0
6
1
1
0
1
7
1
1
1
1
Resolvemos el mapa de Karnaugh,
agrupando los "1" en los grupos mayores
posibles (2 grupos de 2 y 1 grupo de 1)
ab
c
b) La función simplificada queda de la siguiente manera:
f(a,b,c) =
Departamento de Tecnología.
IES Nuestra Señora de la Almudena
Mª Jesús Saiz
Ejercicio PAU Septiembre 2009/2010
a) 87CB (16)
87CB = 8.163+7.162+12.161+11.160 = 34763
b) 5F10
5
F
5
15
1
0
Hexadecimal
1
0
Decimal
(10)
0101 1111 0001 0000 Binario
Solución 5F10(16)= 0101111100010000
(2)
c) 46102
Cociente
Resto
46102:16 2881
6
2881:16
180
1
180:16
11 = B
4
Solución 46102
(10)
= B416
B416
(16)
d) 1101110100100010
1101 1101 0010 0010 Binario
13
13
2
2
Decimal
D
D
2
2
Hexadecimal
Solución 1101110100100010
(2)
= DD22
(16)
Ejercicio PAU Junio 2009/2010
Necesitamos realizar la tabla de la verdad y para ello hay que operar en la función hasta
conseguir que se parezca a una suma de productos o a un producto de sumas. Para operar
aplicamos los teoremas de Morgan
f (a,b,c,d) =
)) =
=
Rellenamos la tabla de la verdad, colocando con lógica positiva las combinaciones que dan
salida 1:
Departamento de Tecnología.
IES Nuestra Señora de la Almudena
Mª Jesús Saiz
Posición
a
b
c
d
f
0
0
0
0
0
1
Nuestra solución son las posiciones que dan salida 1
1
0
0
0
1
1
2
0
0
1
0
1
Solución f (a,b,c,d)
=∑(0,1,2,3,4,5,6,7,10,11,13,14,15)
3
0
0
1
1
1
4
0
1
0
0
1
5
0
1
0
1
1
6
0
1
1
0
1
7
0
1
1
1
1
8
1
0
0
0
0
9
1
0
0
1
0
10
1
0
1
0
1
11
1
0
1
1
1
12
1
1
0
0
0
13
1
1
0
1
1
14
1
1
1
0
1
15
1
1
1
1
1
Ejercicio PAU Septiembre 2012/2013
a) Obtener expresiones de conmutación en función de a, b, c y d de las señales lógicas x1, x2,
x3 y z
x1=
x2=
x3=
z=
+ + + =
Departamento de Tecnología.
IES Nuestra Señora de la Almudena
Mª Jesús Saiz
b) Obtener la tabla de la verdad
Posición
a
b
c
d
f
0
0
0
0
0
1
1
0
0
0
1
1
2
0
0
1
0
1
3
0
0
1
1
0
4
0
1
0
0
1
5
0
1
0
1
1
6
0
1
1
0
1
7
0
1
1
1
1
8
1
0
0
0
1
9
1
0
0
1
1
10
1
0
1
0
0
11
1
0
1
1
1
12
1
1
0
0
1
13
1
1
0
1
1
14
1
1
1
0
1
15
1
1
1
1
1
Ejercicio PAU Junio 2009/2010
a) Obtener las expresiones de conmutación:
=
x1=
x2=
=
x3= x1. x2 =
x4 =
(
=
z = x3 + x4 =
+
b ) Simplificar por el método de Karnaugh. Primero debemos realizar la tabla de la verdad,
rellenando las siguientes combinaciones
Departamento de Tecnología.
IES Nuestra Señora de la Almudena
Mª Jesús Saiz
( 0 0 - -)
Posición
0
a
b
c
d
f
0
0
0
0
1
1
0
0
0
1
1
2
0
0
1
0
1
3
0
0
1
1
1
4
0
1
0
0
1
5
0
1
0
1
0
6
0
1
1
0
1
7
0
1
1
1
0
8
1
0
0
0
0
9
1
0
0
1
0
10
1
0
1
0
1
11
1
0
1
1
0
12
1
1
0
0
0
13
1
1
0
1
0
14
1
1
1
0
1
15
1
1
1
1
0
Ejercicio PAU Septiembre 2008/2009
a) En 5 segundos se podrán almacenar 48 . 5 = 240 kB
240 kB . 1024 B/KB . 8 bit/B = 1966080 bites
b) Como la capacidad es de 16 GB
16 GB . 220 B/KB = 224 kB = 16777216 kB
c) 224 kB / 48 = 349525,3 segundos
Resolvemos el mapa de Karnaugh,
agrupando los "1" en grupos de 4
cd
ab
Solución:
f(a,b,c,d ) =
Departamento de Tecnología.
IES Nuestra Señora de la Almudena
Mª Jesús Saiz
Ejercicio PAU Septiembre 2008/2009
a) Simplificar por Karnaugh la siguiente suma de minterms
f(a,b,c,d) = Σm(4,5,6,7,11,15)
Rellenamos la tabla de la verdad colocando salidas 1 en las posiciones indicadas:¨
Posición
0
a
b
c
d
f
0
0
0
0
0
1
0
0
0
1
0
2
0
0
1
0
0
3
0
0
1
1
0
4
0
1
0
0
1
5
0
1
0
1
1
6
0
1
1
0
1
7
0
1
1
1
1
8
1
0
0
0
0
9
1
0
0
1
0
10
1
0
1
0
0
11
1
0
1
1
1
12
1
1
0
0
0
13
1
1
0
1
0
14
1
1
1
0
0
15
1
1
1
1
1
Rellenamos y resolvemos el mapa de
Karnaugh, agrupando los "1" en los grupos
mayores posibles (grupos de 4 y 2)
Solución:
f(a,b,c,d ) =
b) Realizar el circuito, usando únicamente puertas NAND. Para conseguirlo aplicamos dos
veces los teoremas de Morgan.
=
aa
aa b
acd
Departamento de Tecnología.
IES Nuestra Señora de la Almudena
Mª Jesús Saiz
Ejercicio PAU Junio 2012/2013
a) Obtener las expresiones de conmutación:
de la señal Z
Multiplexor X1
c
d
X1
0
0
1
0
1
1
1
0
0
1
1
1
c
d
X2
0
0
0
0
1
1
1
0
1
1
1
1
X1 =
Multiplexor X2
X2 =
a
b
Z
0
0
X1
0
1
c
1
0
X2
1
1
d
Multiplexor Z
=
Z=
=
=
+
+
a
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
b
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
c
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
d
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
f
1
1
0
1
0
0
1
1
0
1
1
1
0
1
0
1
b) Para simplificar por el método de Karnaugh, primero debemos
realizar la tabla de la verdad, rellenando con "1" las combinaciones
obtenidas en el apartado a
Solución:
Z(a,b,c,d ) =
=
Departamento de Tecnología.
IES Nuestra Señora de la Almudena
Mª Jesús Saiz
Ejercicio PAU Septiembre 2013/2014
a) Obtener la expresión de
conmutación de la señal Z
Z = S0 + S3 + S6
I2
0
0
0
0
1
1
1
1
I1
0
0
1
1
0
0
1
1
I0
0
1
0
1
0
1
0
1
S0
1
0
0
0
0
0
0
0
S1
0
1
0
0
0
0
0
0
S2
0
0
1
0
0
0
0
0
S3
0
0
0
1
0
0
0
0
S4
0
0
0
0
1
0
0
0
S5
0
0
0
0
0
1
0
0
S6
0
0
0
0
0
0
1
0
S7
0
0
0
0
0
0
0
1
Para ello escribimos la tabla de la
verdad del decodificador y
resolvemos S0 , S3 y S6
S0 =
S3 =
S6 =
Del dibujo obtenemos:
I2 = a+c
I1 = a
I0 = abc
Y sustituimos:
+
Z = S0 + S3 + S6 =
+
=
=
b) Para simplificar por el método de Karnaugh, primero debemos realizar la tabla de la verdad,
rellenando con "1" las combinaciones obtenidas en el apartado a
a
b
c
Z
0
0
0
1
0
0
1
0
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
0
Resolvemos el mapa de Karnaugh, agrupando los "1" en
los grupos mayores posibles (2 grupos de 4)
Solución:
Z(a,b,c) =