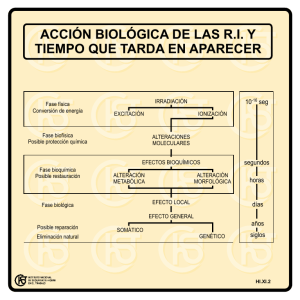
Ejemplos de aplicación
Anuncio
Técnicas ópticas en biofísica Nieves Andrés Departamento de Física Aplicada Grupo TOL del I3A Sólidos: Moteado en superficies (Speckle) Flujos: Sembrado partículas Fotografía Microscopía Interferometría Holografía Digital Tecnologías Ópticas en Biofísica Tecnologías Ópticas en Biofísica Formación del moteado (Speckle) “Granularidad” debido a la interferencia de la luz proveniente de todos los puntos de la superficie Intensidad resultante puede tener “cualquier” valor , predominan las zonas oscuras Iluminado con luz blanca Iluminado con luz láser Análisis estadístico Información de la superficie p( I ) = 1 e I − I I λ Tecnologías Ópticas en Biofísica Tamaño del moteado Tamaño transversal relacionado con: mínimo periodo de la interferencia entre dos ondas o tamaño de la figura de difracción Promedio estadístico de la distancia entre regiones adyacentes de intensidad nula o máxima Moteado formado en una pantalla: moteado objetivo Moteado con sistema formador de imagen: moteado subjetivo α d s = 1.2 λL D ≈ λ α El tamaño se reduce cuando nos acercamos a la superficie rugosa (al revés que con cualquier objeto) d s = 1.2 d s = 1.2 λa ' D ≈ λ α (1 + M )λf = 1.2(1 + M )λF D Tecnologías Ópticas en Biofísica Fotografía de moteado / Digital Speckle Photography (DSP) Detección de cambios en la intensidad Matriz de intensidades Registro de dos exposiciones: I1(x,y), I2(x,y) Disminuyendo M aumenta la zona de medida pero empeora la resolución espacial Análisis 2D Campo de desplazamientos locales transversales del moteado 2D Correlación cruzada 2D Autocorrelación * Registro separado de los dos moteados * SI se obtiene signo del desplazamiento * Registro conjunto de los dos moteados * NO se obtiene el signo del desplazamiento A(∆X ) = I1 ( X ) I1 ( X + ∆X ) Ventanas 32x32 C (∆X ) = I1 ( X ) I 2 ( X + ∆X ) Precisión subpixel Se detecta la posición del máximo de la función A(∆X) o C(∆X) Mapa 2D del desplazamiento en el plano de cada punto Tecnologías Ópticas en Biofísica Holografía Proceso de registro o( x, y ) = Ao ( x, y )e iϕ r(x,y) o ( x, y ) ; r ( x, y ) = Ar ( x, y )e iϕ r ( x, y ) I ( x, y ) = o( x, y ) + r ( x, y ) = o + r + r * o + ro* = 2 Y 2 2 Ao + Ar + 2 Ao Ar cos(ϕ o − ϕ r ) 2 Z o(x,y) Sensor 2 Intensidad en z=0 Proceso de reconstrucción Se ilumina el holograma con un onda c(x,y) La onda que sale del holograma será: s ( x, y ) = c( x, y ) I ( x, y ) = r c + o c + cr * o + cro* = s1 + s2 + s3 + s4 2 Para c(x,y)=r(x,y) s3 2 s1+s2 Para c(x,y)=r*(x,y) s4 Holograma s3 ( x, y ) = r o 2 s1+s2 Holograma s 4 ( x, y ) = r o * 2 Tecnologías Ópticas en Biofísica Interferometría de moteado / Digital Speckle Pattern Inteferometry (DSPI) Registro digital Detección de cambios en la fase Haz de referencia moteado Haz de referencia suave E o = A o e iϕ o Er = Ar eiϕ r Ao y ϕo aleatorios Ao y ϕo varia de forma continua Interferencia Moteograma 2 2 2 I i = Eo + Er = Ao + Ar + 2 Ao Ar cos(ϕ R ) ϕ R = ϕ o − ϕ r Moteograma: Registro de un campo de moteado subjetivo (haz objeto) + campo moteado o suave (haz de referencia) Tecnologías Ópticas en Biofísica Interferometría de moteado Dos exposiciones Primera exposición Segunda exposición I i = Eo + Er = Ao + Ar + 2 Ao Ar cos(ϕ R ) 2 2 2 E 'o = Ao ei (ϕo + ∆ϕ ) ϕ R = ϕo − ϕr cambia la fase del objeto sin cambiar su amplitud I f = E 'o + Er = Ao + Ar + 2 Ao Ar cos(ϕ R + ∆ϕ ) 2 2 2 Análisis de los moteogramas Diferencia, suma o correlación Mapa de diferencia fases I f − I i = 4 Ao Ar sin(ϕ R + ∆ϕ ∆ϕ ) sin( ) 2 2 Mapa de intensidad, detectar máximos y mínimos I = I o + I M cos ∆ϕ Relacionada con la diferencia de fase en el objeto en cada punto Tecnologías Ópticas en Biofísica Interferometría de moteado Relación entre el cambio de fase y el desplazamiento ϕo = 2π λ (OP + PQ + QR ) = k1 ⋅ r1 + k 2 ⋅ r2 + k 3 ⋅ r3 2π ki = ; k i ri ϕ 'o ≈ k '1 ⋅r '1 + k ' 2 ⋅r ' 2 + k 3 ⋅ r3 λ x z K: vector sensibilidad L = ( Lx , L y , Lz ) ∆ϕ = ϕ f − ϕ i ≈ ϕ 'o −ϕ o = (k '1 ⋅r '1 + k ' 2 ⋅r ' 2 ) − (k1 ⋅ r1 + k 2 ⋅ r2 ) r '1 = r1 + L; r ' 2 = r2 − L; (k '1 −k1 )⊥ r1 ; (k '2 −k 2 )⊥ r2 ∆ϕ ≈ (k1 − k 2 )⋅ L = K ⋅ L Campo de desplazamientos en la dirección de K Tecnologías Ópticas en Biofísica Fotografía vs Interferometría 1C 2C Lo fija el espacio imagen: 0.1 pix a 10 pix depende de M Rango de desplazamientos, L 7 µm a 700 µm para M=0.1 0.7 µm a 70 µm para M=1 0.050 µm a 15 µm L≤ 𝑑𝑑𝑠𝑠 L≥ 𝑑𝑑𝑠𝑠 Independiente de M ∆𝐿𝐿 0.1 𝑝𝑝𝑝𝑝𝑝𝑝 = = 3 10−3 ∆𝑥𝑥 32 𝑝𝑝𝑝𝑝𝑝𝑝 Lo fija el espacio objeto: 0.1 λ a 30 λ Independiente de M Rango de gradientes, ∆𝐿𝐿 ∆𝑥𝑥 Depende de M λ ∆𝐿𝐿 = ∆𝑥𝑥 30 𝑝𝑝𝑝𝑝𝑝𝑝 ∗ 7𝜇𝜇𝜇𝜇/𝑀𝑀 3 10−4 para M=0.1 3 10−3 para M=1 Tecnologías Ópticas en Biofísica Desplazamiento temporal Técnicas de desplazamiento de la fase Introducir un desfase adicional conocido modificando la fase del haz de referencia Mover 170 µm λ= 600 nm n=1.5 α=6’ Desfase π/2 Desplazamiento relativo de dos cuñas Desplazamiento de un espejo El desfase adicional se introduce en el haz de referencia en instantes sucesivos de tiempo. I i = I o + I M cos(∆ϕ + α i ) Mapa de ∆ϕ Tres interferogramas αi es el desfase introducido entre dos fotogramas sucesivos. I1 (α1 = 0 ) Cuatro interferogramas α1 = 0; α 2 = π 2 I2 α 2 = 2π 3 ; α3 = π ; α4 = 4π I3 α 3 = 3 3π 2 I −I ∆ϕ = arctg 3 2 I1 − I 2 I −I ∆ϕ = arctg 4 2 I1 − I 3 Tecnologías Ópticas en Biofísica Técnicas de desplazamiento de la fase Desplazamiento espacial Modulación espacial del moteado: Se introduce una variación espacial lineal de la fase: desfase conocido entre un pixel y el siguiente Se ajusta el haz de referencia tal que forme un pequeño ángulo con el haz objeto Pérdida de resolución espacial pero mejora la resolución temporal a’ I ( m, n, t ) = I o (m, n, t ) + I M (m, n, t ) cos[ϕ (m, n, t ) + nψ ] Sin modulación espacial Con modulación espacial nψ = 2π∆x n∆ λa ' ∆, dimensión del pixel Tamaño del moteado mínimo 3 pixel Tecnologías Ópticas en Biofísica Técnicas de desplazamiento de la fase Desplazamiento espacial Análisis del moteado modulado espacialmente Comparando la intensidad de cada pixel Registrada amplitud y fase de la onda Calculando la transformada de Fourier Interferometría fase Diferencia de las fases Mapa diferencia fase Diferencia de fases filtrado Plano de la FFT Fotografía de moteado amplitud HOLOGRAFÍA DIGITAL IMAGEN Mapa de intensidades de una imagen Tecnologías Ópticas en Biofísica Técnicas de desplazamiento de la fase Desfase temporal vs Desfase espacial Requiere ambiente estable Se puede medir en condiciones adversas Dispositivo para generar el desfase temporal Desfase espacial no requiere dispositivo especial sino ajuste especial Adquisición secuencial de varios interferogramas/imágenes Sólo se adquiere un interferograma/imagen Mayor resolución espacial Menor resolución espacial Menor resolución temporal: apto sólo para fenómenos lentamente variables Mayor resolución temporal: permite análisis de procesos dinámicos Mayor precisión en la medida Menor precisión en la medida Permiten conocer el signo de la fase pero no su valor absoluto Requieren postprocesado para eliminar el ruido y desplegar la fase Tecnologías Ópticas en Biofísica Medida de campos de desplazamientos Medida de desplazamientos Lz Iluminación y observación perpendiculares k1 = −kˆ k 2 = kˆ 2π ˆ 2k K =− Ki λ Ko ∆ϕ 2 Lz = λ 2π m= ∆Lz = λ 2 x z por franja K no es constante Iluminación oblicua, observación perpendicular k1 = −senθ î − cosθ k̂; k 2 = kˆ 2π K =− senθ î + (1 + cosθ )k̂ [ λ m= ] Ki θ sen θ Lx + (1 + cosθ )Lz ∆LK = Ko λ λ por franja 2 cos(θ 2 ) x z K no es constante Tecnologías Ópticas en Biofísica Medida de campos de desplazamientos Medida de desplazamientos en el plano: Lx,Ly Dos haces de iluminación con ángulos simétricos θ1 = θ; θ 2 = −θ 2π (senθ + senθ ) î + (cosθ - cosθ )k̂ = − 2π 2 sen θî K =− ] [ λ m= 2 senθ Lx λ ∆Lx = Ki1 λ Ko Ki2 λ por franja 2 sen θ K es constante Iluminación con fibra óptica en los dos haces K es constante, con ligeros cambios en su dirección Dispositivo de TPS: cilindro piezoeléctrico para control del camino óptico de un haz Ki Ki Ko SPS no es posible Tecnologías Ópticas en Biofísica Medida de formas Registros con diferente longitud de onda • Multiplexado espacial (un solo registro) t1, t2 deformacion ∆φ ( x, y ) = CCD Ref 𝜆𝜆1 forma 2π 2 Z ( x, y ) Λ Longitud de onda sintética Λ= Beam Splitter Illumination 𝜆𝜆1 𝜆𝜆2 Ref 𝜆𝜆2 λ1, λ2 λ1λ2 λ1 − λ2 λ1 = 659.477 nm λ2 = 659.597 nm Λ = 3.6mm Acoplador de fibra optica Tecnologías Ópticas en Biofísica Ejemplos de aplicación Medida de la deformación de la superficie del corazón Medida de desplazamientos en el plano: Lx,Ly Fotografía de moteado: Digital speckle photography-DSP 6.25 µm/pixel Mapa de deformaciones Partículas de carburo de silicio, 40 µm de dia. Deformación unitaria (strain) 2 D Ventana de análisis: 0.2mm x 0.2mm Resolución espacial: 0.1 mm Sonomicrometría vs DSP Tecnologías Ópticas en Biofísica Ejemplos de aplicación Medida de desplazamientos en el plano: Lx,Ly Medida de grandes deformaciones mecánicas de membranas biológicas con DSPI φ= 19.3º, 0.96 µm / franja Dos montajes DSPI : uno por componente Muestras traslúcidas Luz transmitida Vista superior Sistema experimental Vista lateral Tecnologías Ópticas en Biofísica Ejemplos de aplicación Medida de desplazamientos en el plano: Lx,Ly Medida de grandes deformaciones mecánicas de membranas biológicas con DSPI Mapas de diferencia de fase Membrana de pericardio canino: 10 mm diametro, 0.25 mm espesor Lx Campo de tensiones F/A Ly Desplazamientos Desplazamiento máximo de 7 µm Tecnologías Ópticas en Biofísica Ejemplos de aplicación Medida de desplazamientos perpendiculares: Lz Plataforma de fuerzas para medir pequeñas fuerzas con DSPI Montaje experimental desplazamientos de micras para fuerzas de gramos 0.267 µm/franja Fase plegada Desplazamiento Valor de la fuerza y punto de aplicación a partir del campo de desplazamientos Tecnologías Ópticas en Biofísica Ejemplos de aplicación Plataforma de fuerzas para medir pequeñas fuerzas con DSPI Tecnologías Ópticas en Biofísica Ejemplos de aplicación Medida de desplazamientos perpendiculares: Lz Plataforma de fuerzas para medir pequeñas fuerzas con DSPI Ratón con una enfermedad moto neuronal Macho, 57 días, 19.18 g de peso Apoyo de diferentes patas del ratón en su paso por la placa Posición de la F DSPI mide el campo de desplazamientos verticales de la placa Teoría de elasticidad proporciona el valor y posición de F Experimentos estáticos muestran un desplazamiento máximo de 3 µm para 10 g de peso Se ha medido la evolución de la fuerza de apoyo de una pata en ratones de sólo 20 g de peso F máxima es del orden del 50% del peso F y desplazamiento máximo Tecnologías Ópticas en Biofísica Ejemplos de aplicación Medida de desplazamientos perpendiculares: Lz DSPI endoscópico para inspección de cavidades internas en medicina Experimentos in vitro con una pared intestinal Estimulación con una aguja Análisis de la elasticidad del tejido Tejido sano 0.267 µm / franja Tejido canceroso Tecnologías Ópticas en Biofísica Ejemplos de aplicación Medida de forma Medida de la forma de un objeto grande Mapa de fase Mapa de fase filtrado Unwrapped Mapa 2D de la superficie • Grandes valores de Z ( 40 mm) • No contacto Z mm Tecnologías Ópticas en Biofísica Ejemplos de aplicación Medida de forma Medida de la forma de un tubo Mapa de fase Mapa de fase sin fondo Mapa de fase filtrado Unwrapped Tecnologías Ópticas en Biofísica Ejemplos de aplicación Medida de forma Medida de la forma de un vena de oveja Bad visibility Object Mapa de fase , λ2) Mapa de de fase fase sin (λ1fondo Mapa Mapa Object de fase filtrado Unwrapped Filtrado * 2D mapa de la superficie de la vena • Valores de 4 mm, dificil de medir sin contacto Tecnologías Ópticas en Biofísica